Roller-Integrated Acoustic Wave Detection Technique for Rockfill Materials
Abstract
1. Introduction
2. Methodologies
2.1. Theoretical Analysis
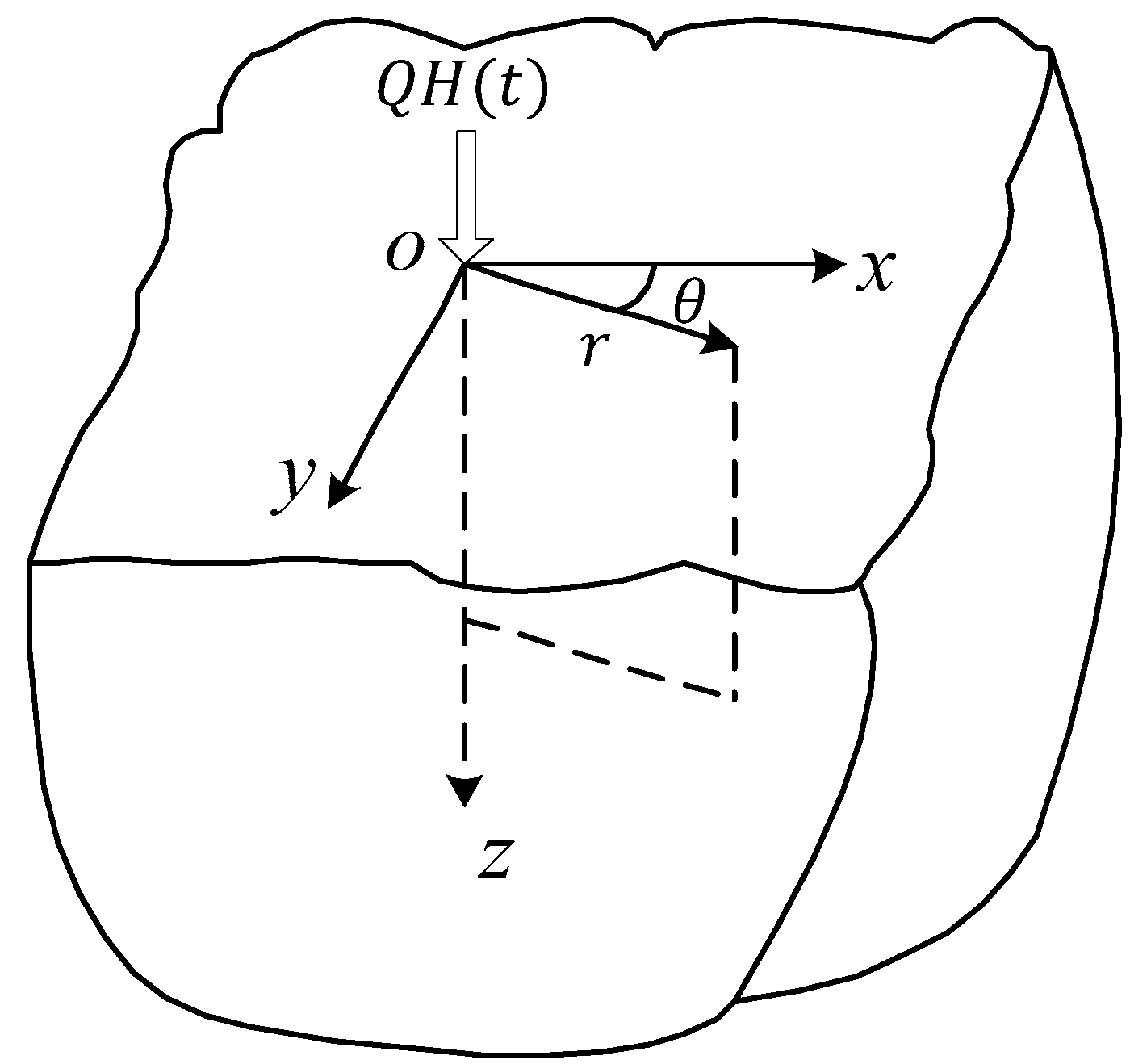
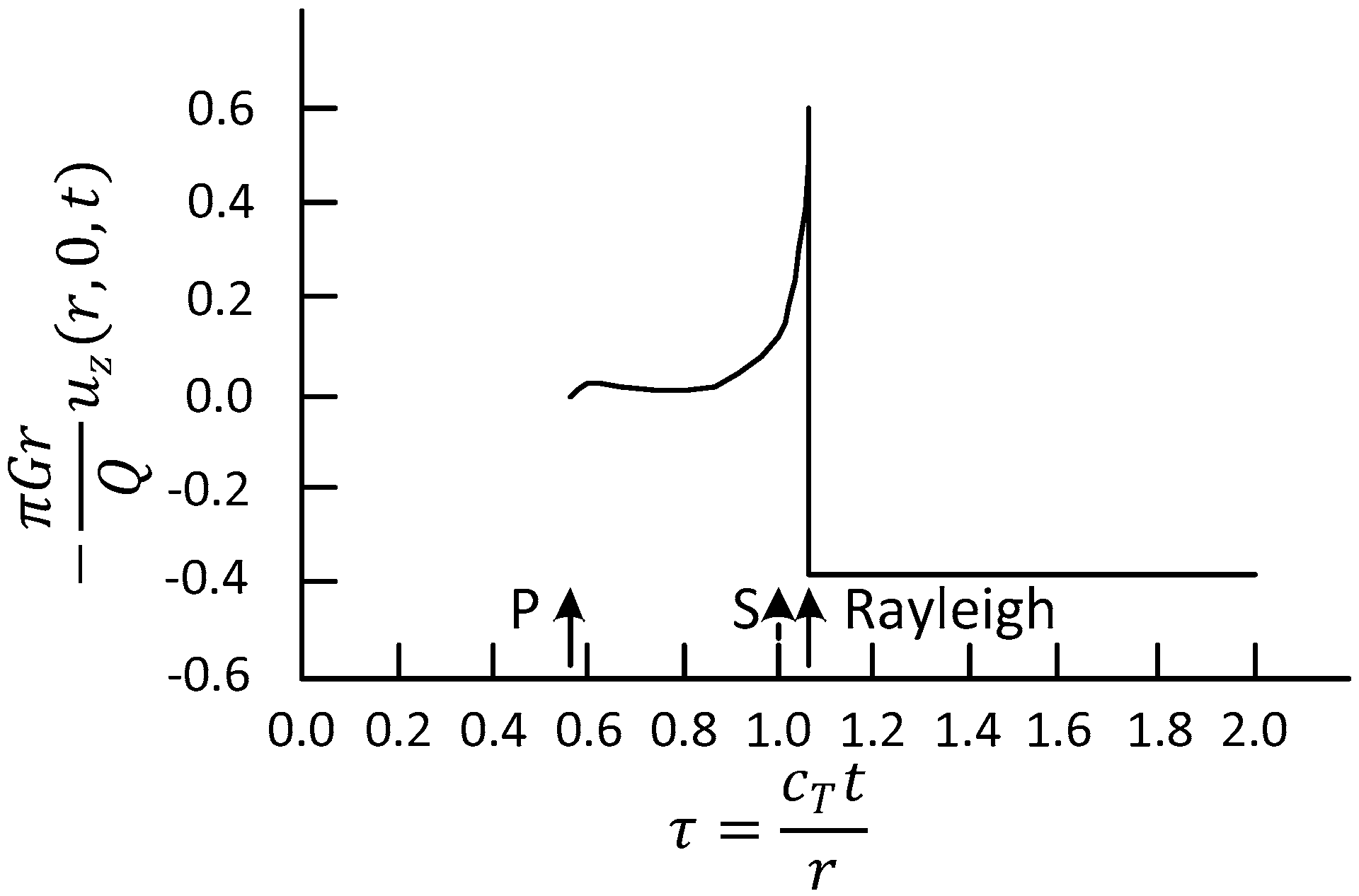
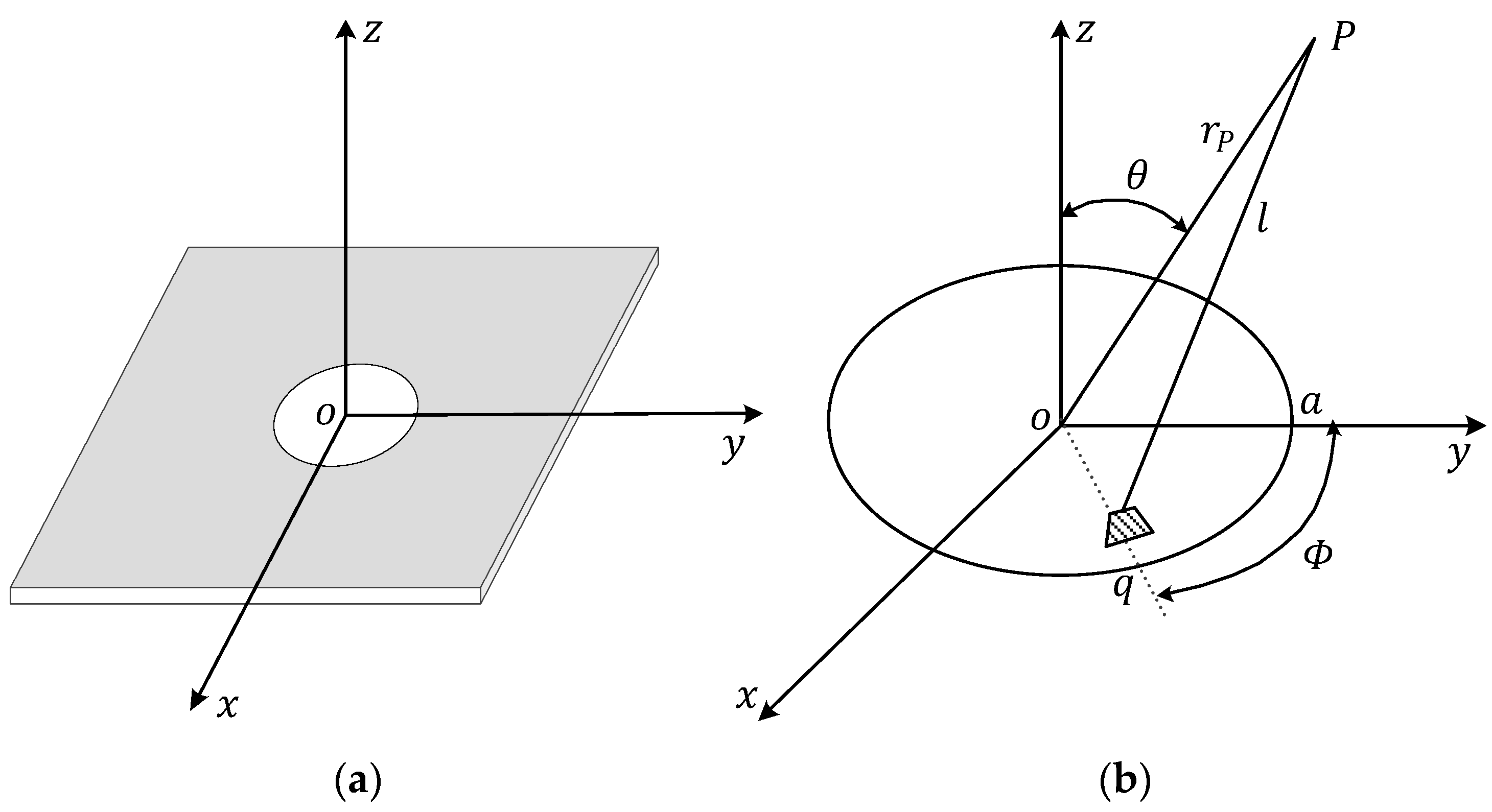
2.1.1. Lamb’s Problem
- (1)
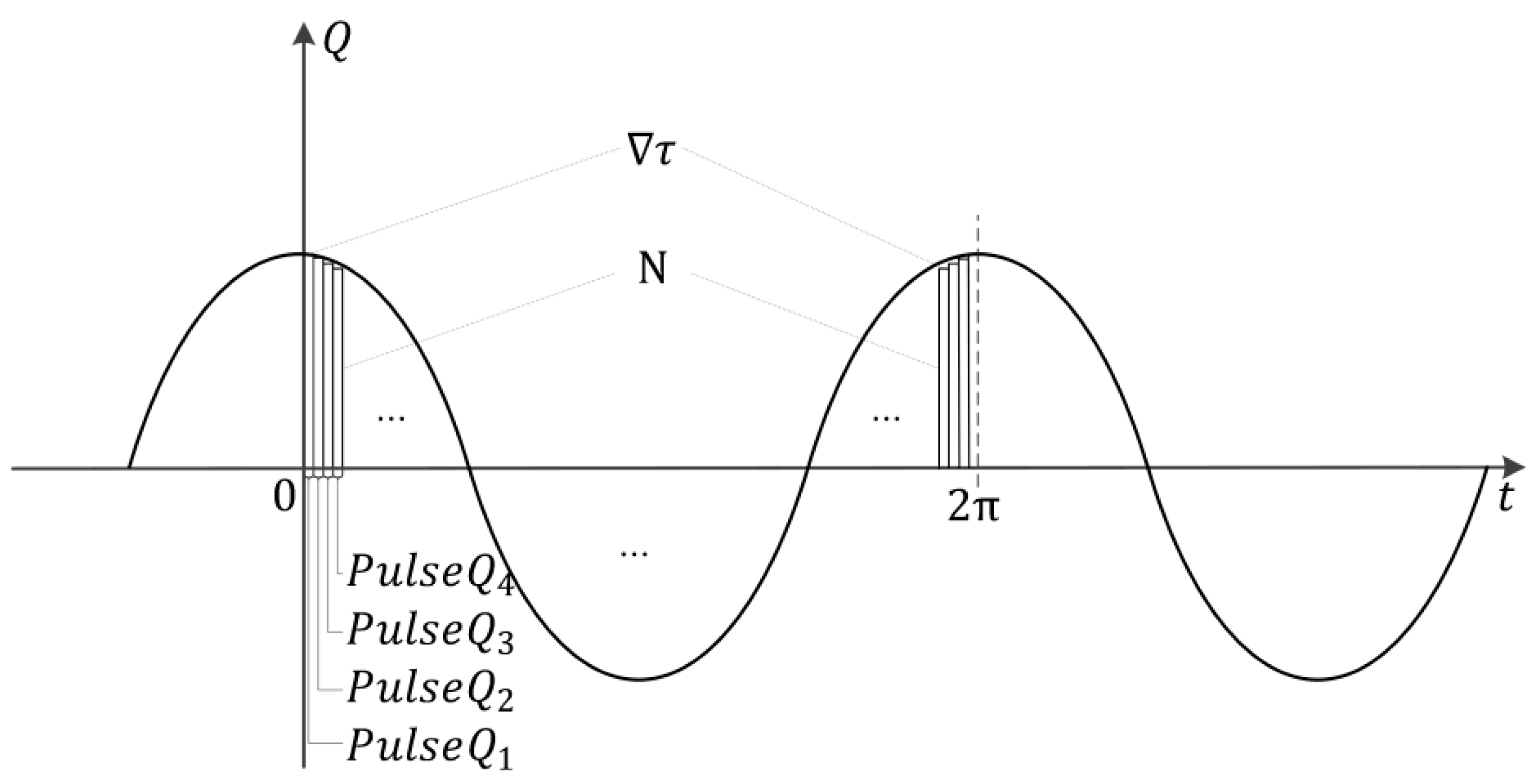
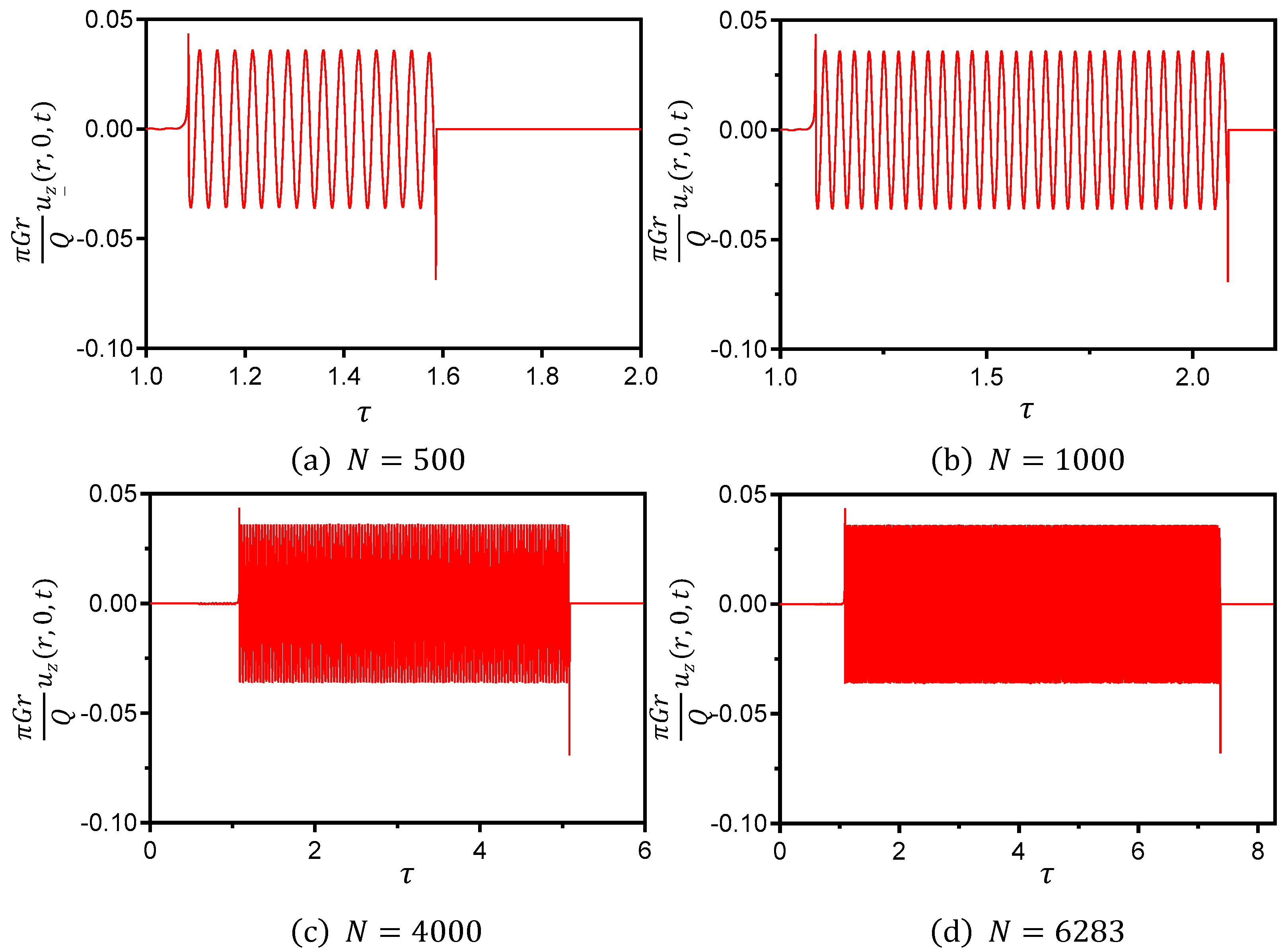
- Firstly, the periodic harmonic load excitation is discretized into N parts, then the Nth excitation pulse is (), as shown in Figure 3.
- (2)
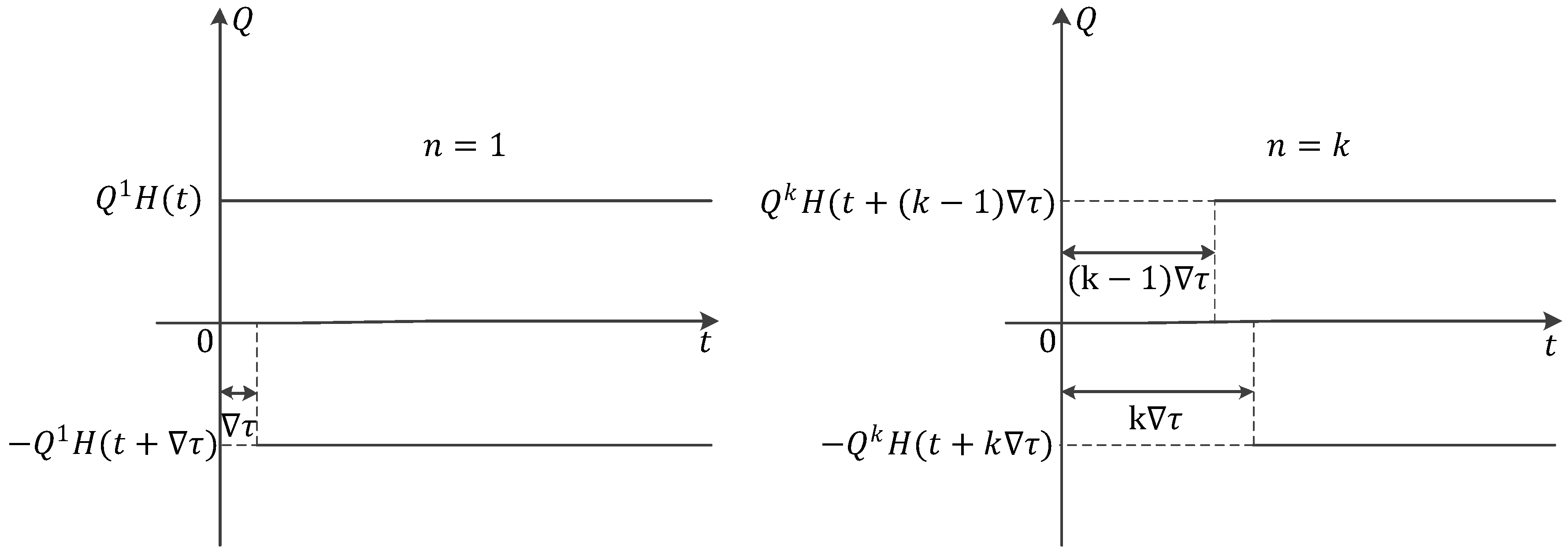
- Then, assuming , is the delay time and , as shown in Figure 4.
- (3)
- Impulse excitation are applied to the origin , respectively, and the vertical displacement () at the distance from the origin is obtained when the different pulse loads act on the semi-space surface. When , the true vertical displacement of the soil under the simple harmonic load at any time in a cycle can be obtained by integrating the vertical displacement response of the pulse excitation. The displacement is as follows:where and is an integer.
2.1.2. Infinite Baffle Piston Radiation Acoustic Field
2.1.3. Analytical Solution
2.1.4. Numerical Solution
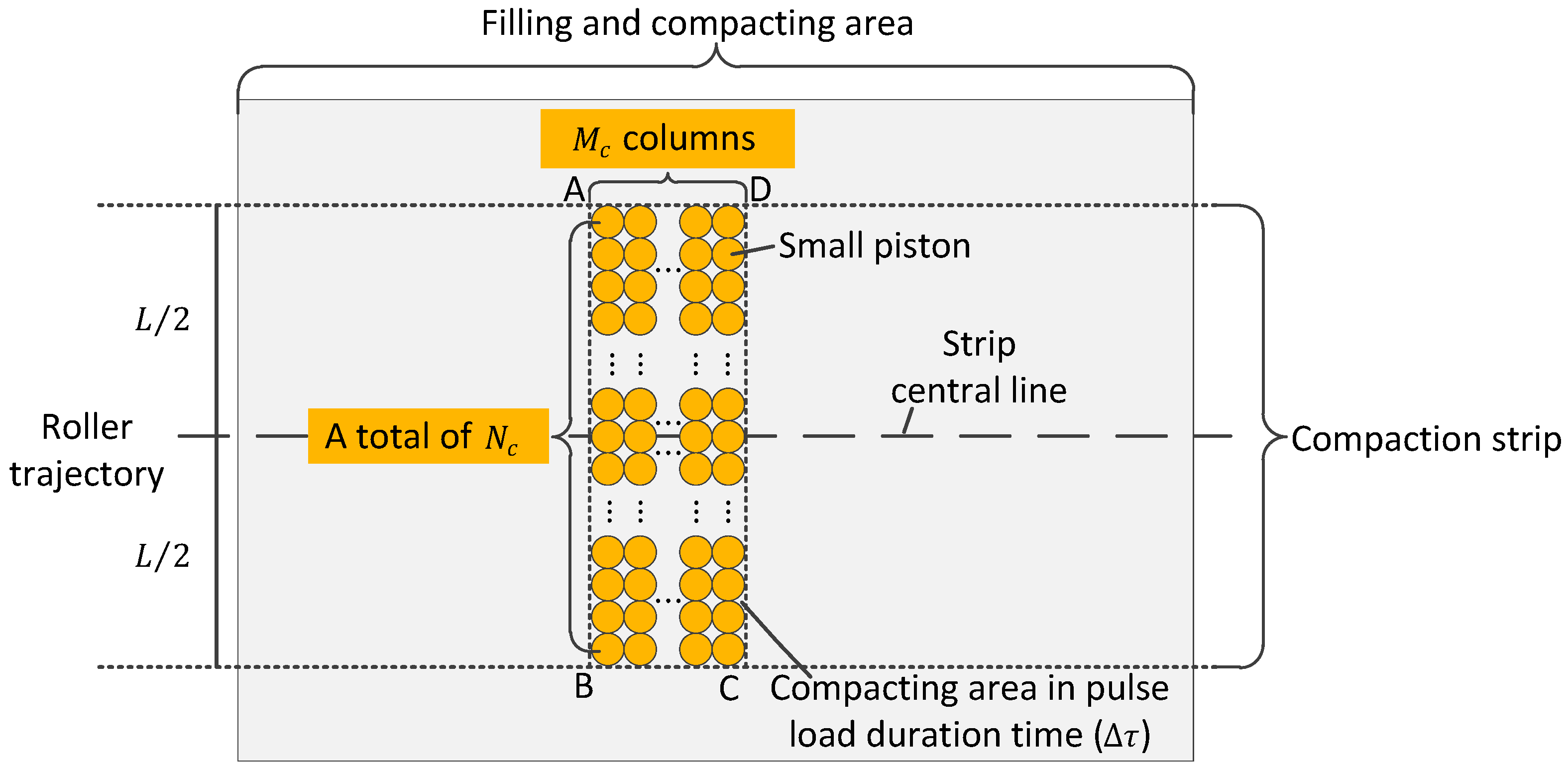
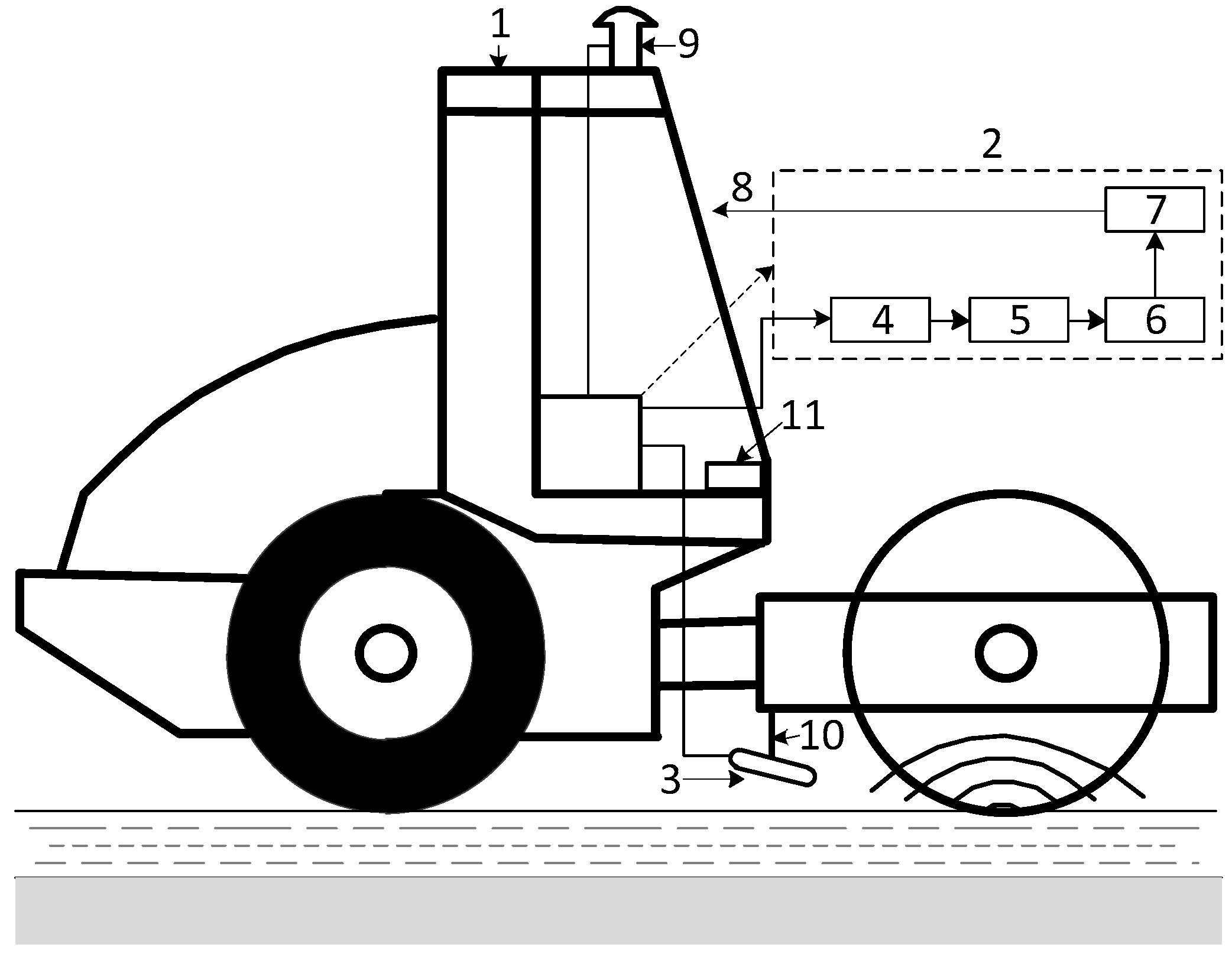
2.2. Technical Implementation
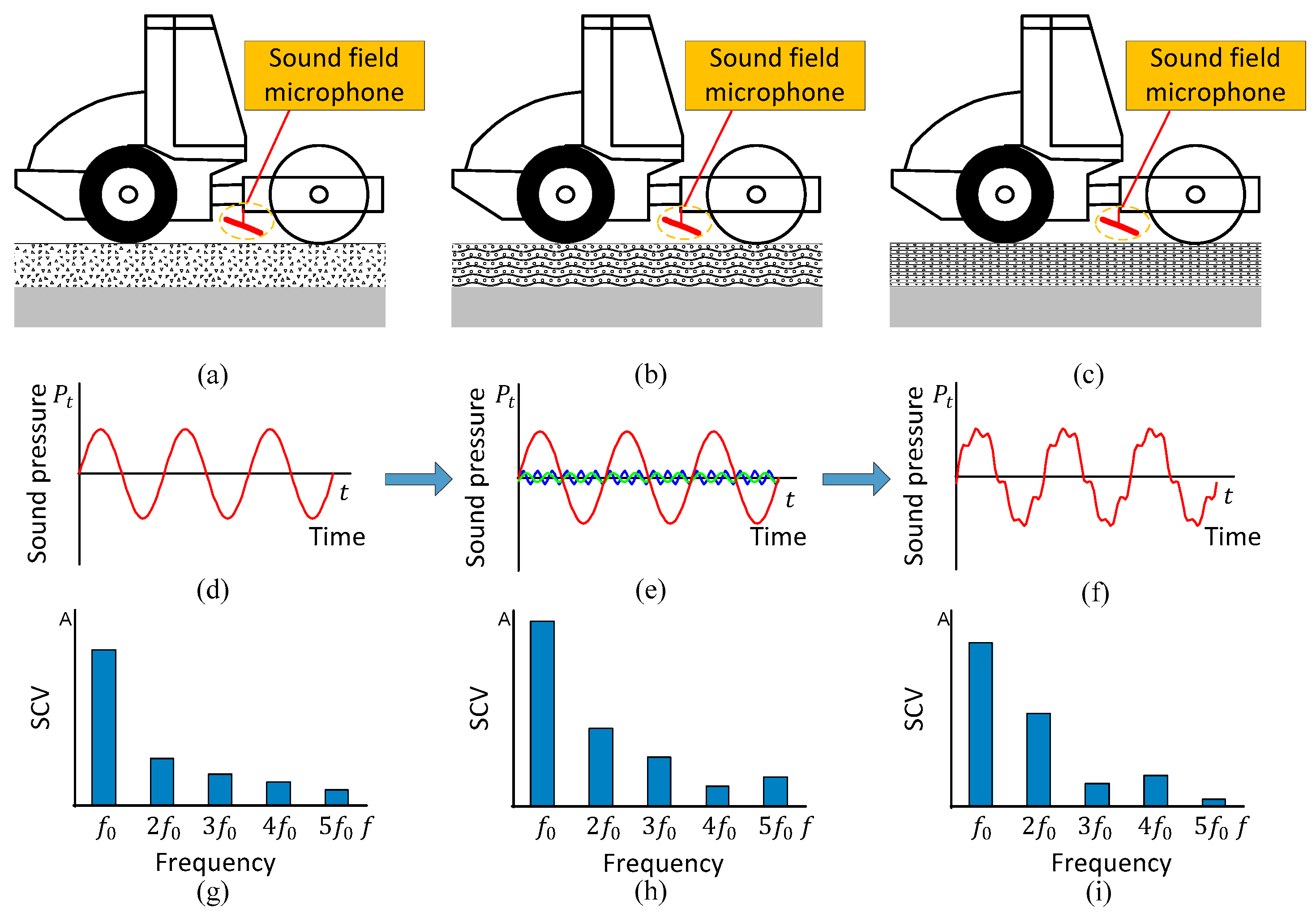
2.3. Sound Compaction Value
3. Case Study
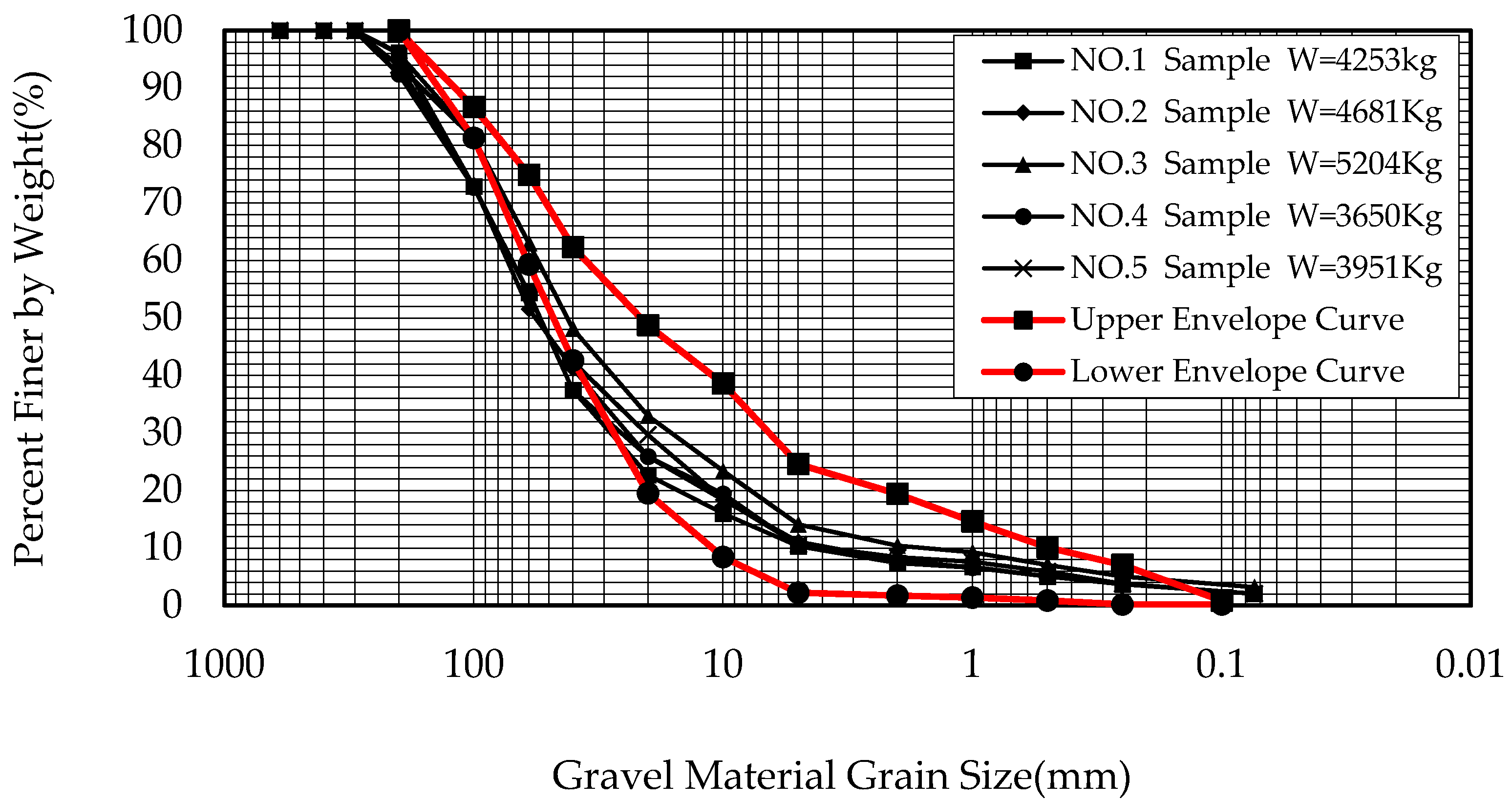
3.1. Testing Site and Materials
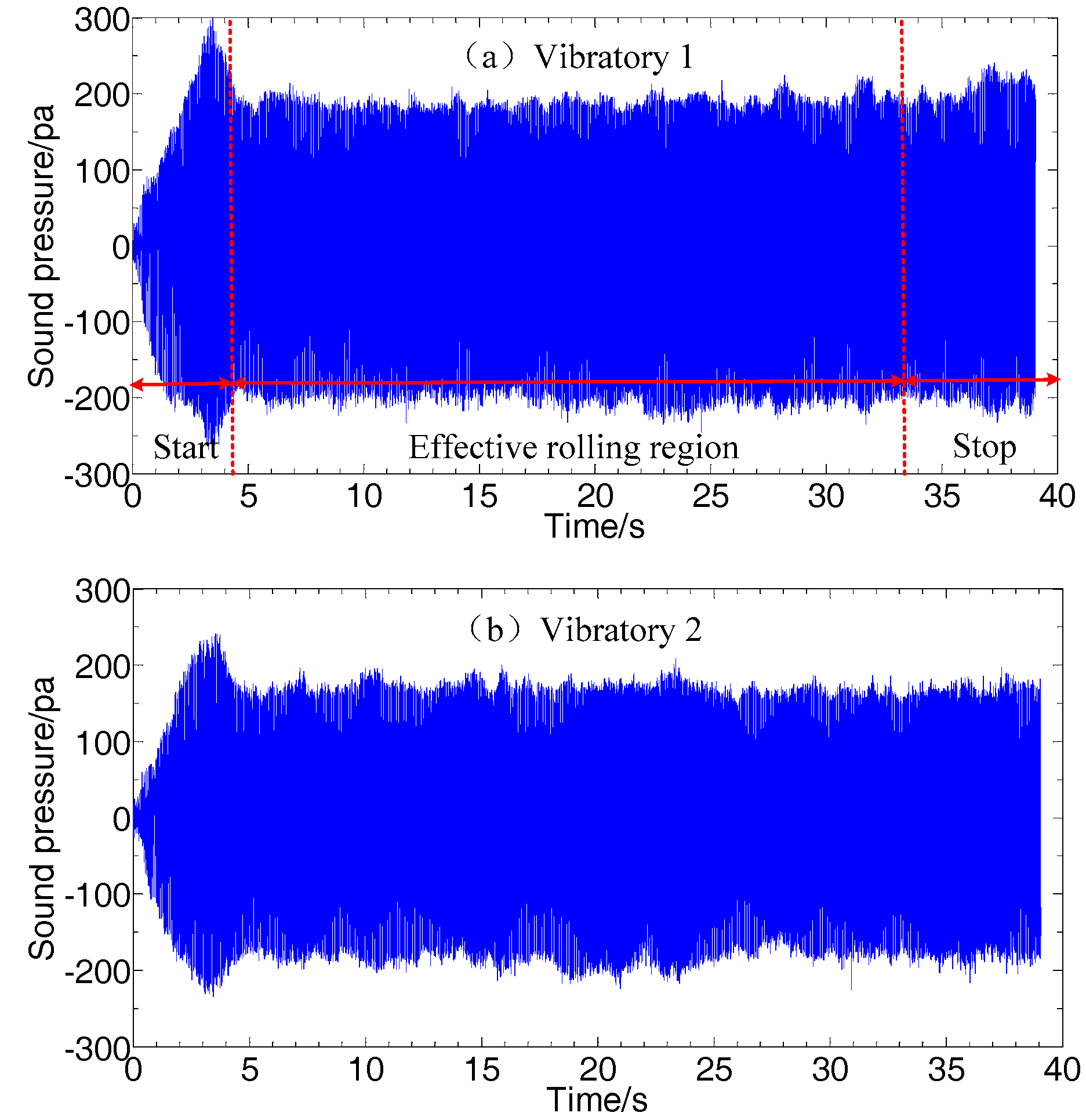
3.2. Testing Program
4. Results and Discussions
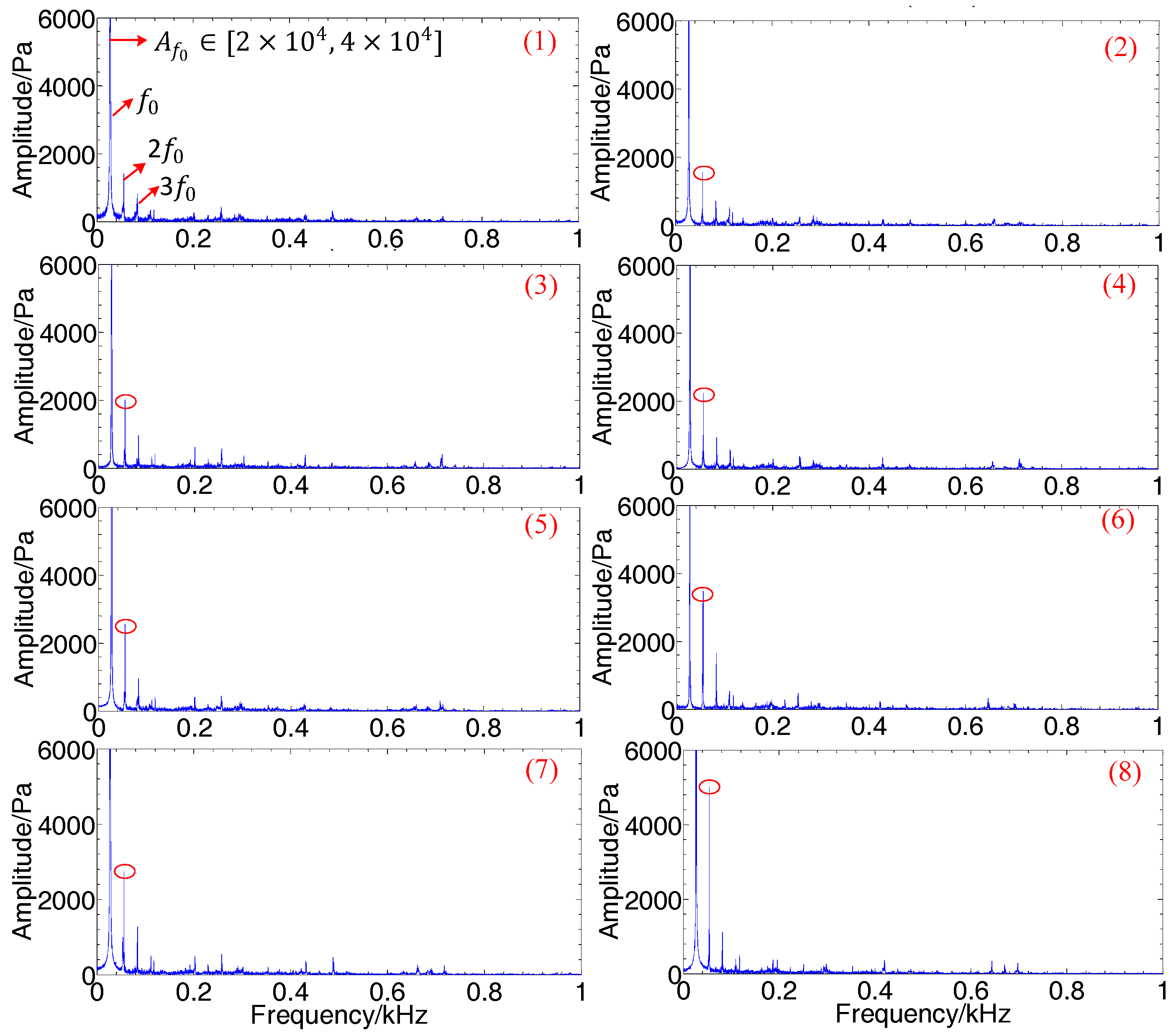
4.1. Spectrum Analysis of Detection Results
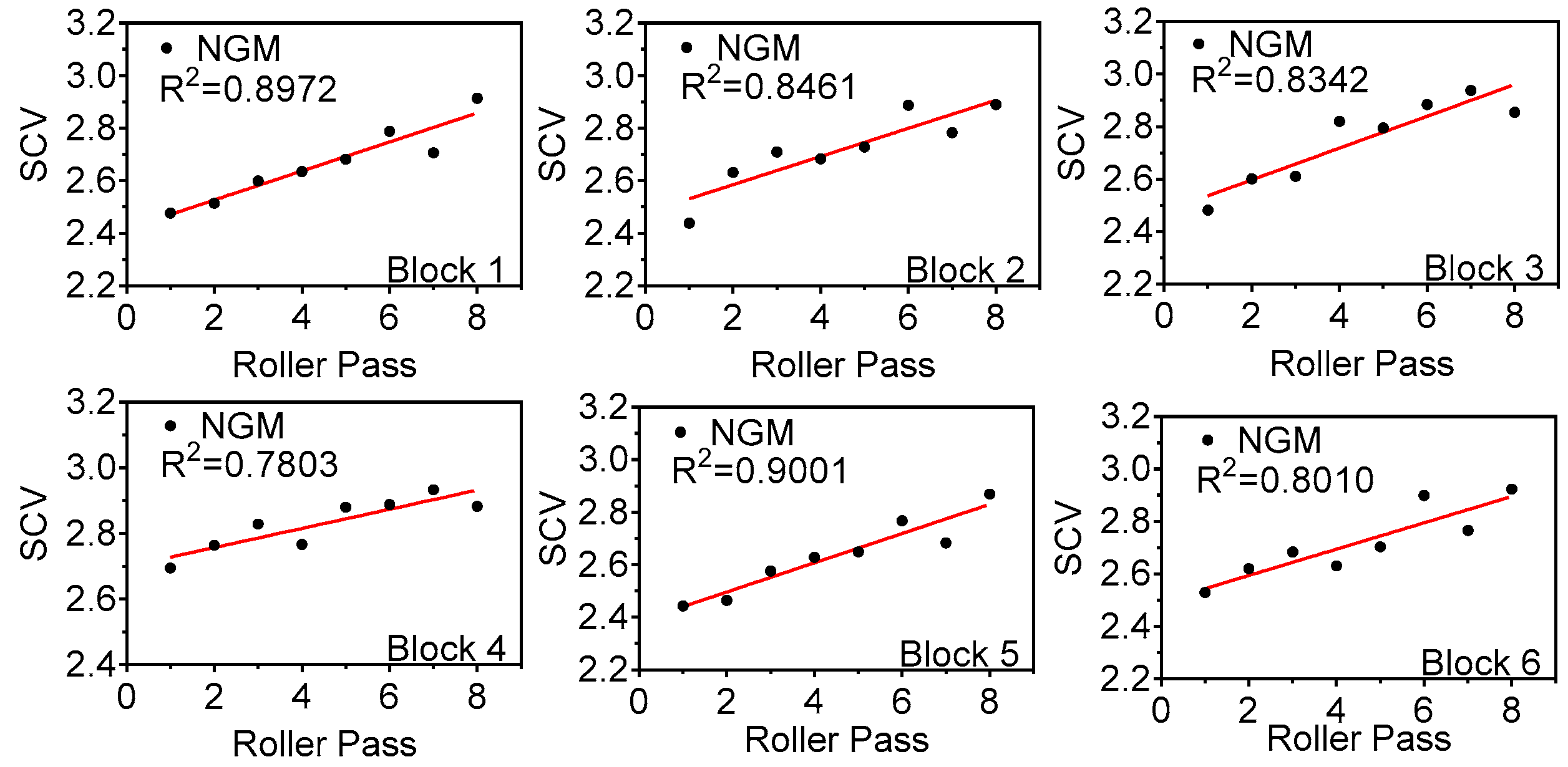
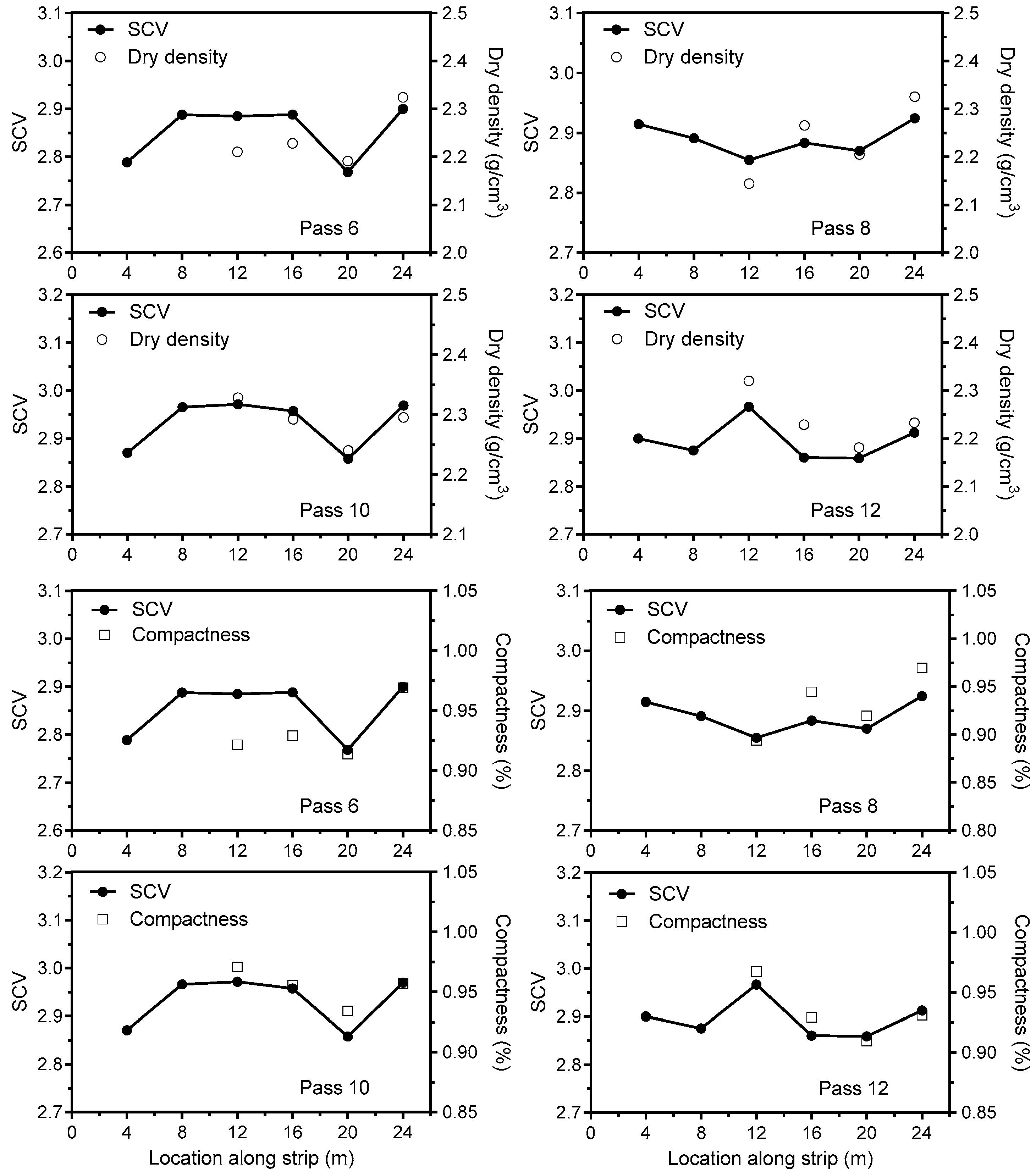
4.2. Correlations between Compaction Parameters and SCV
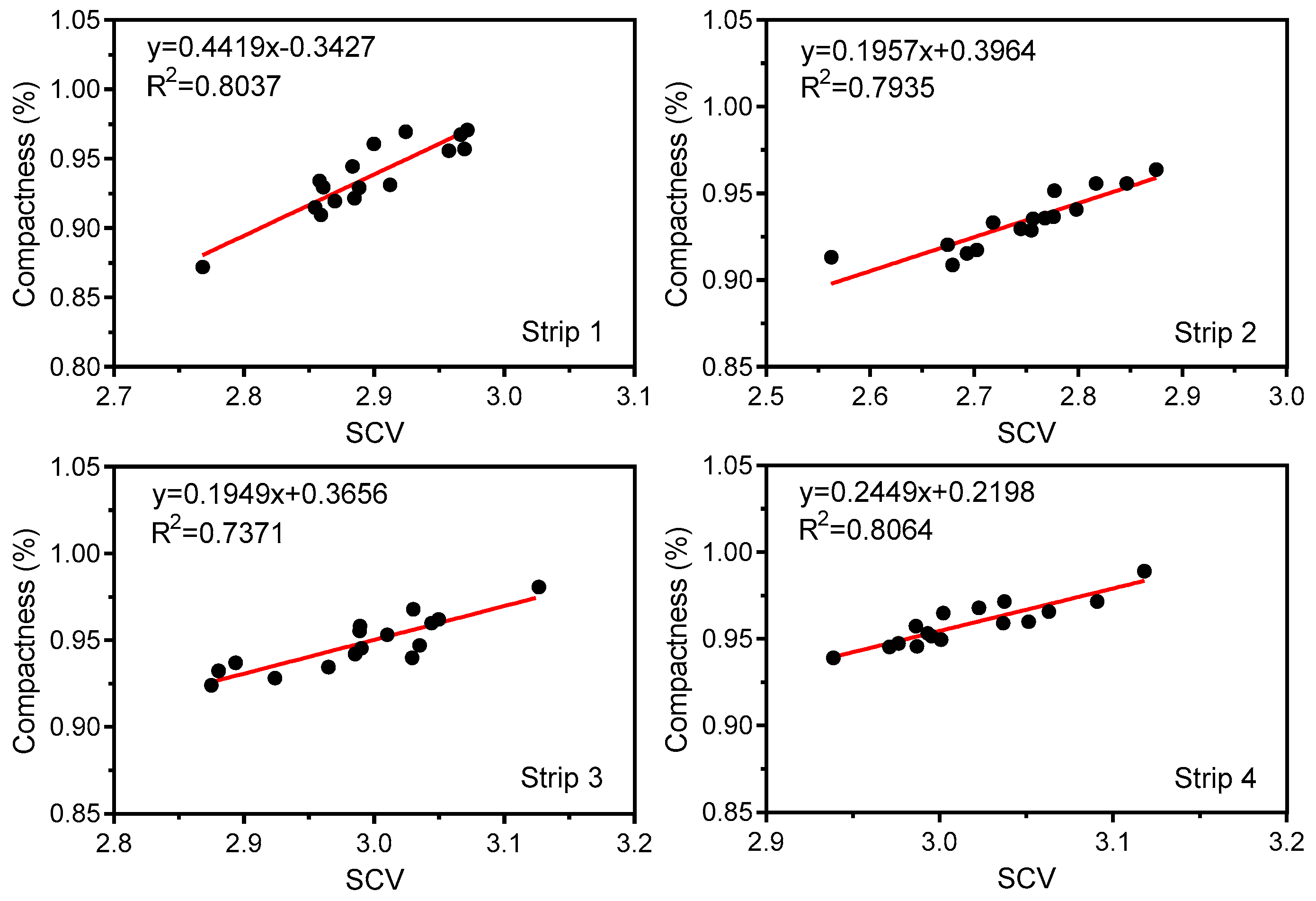
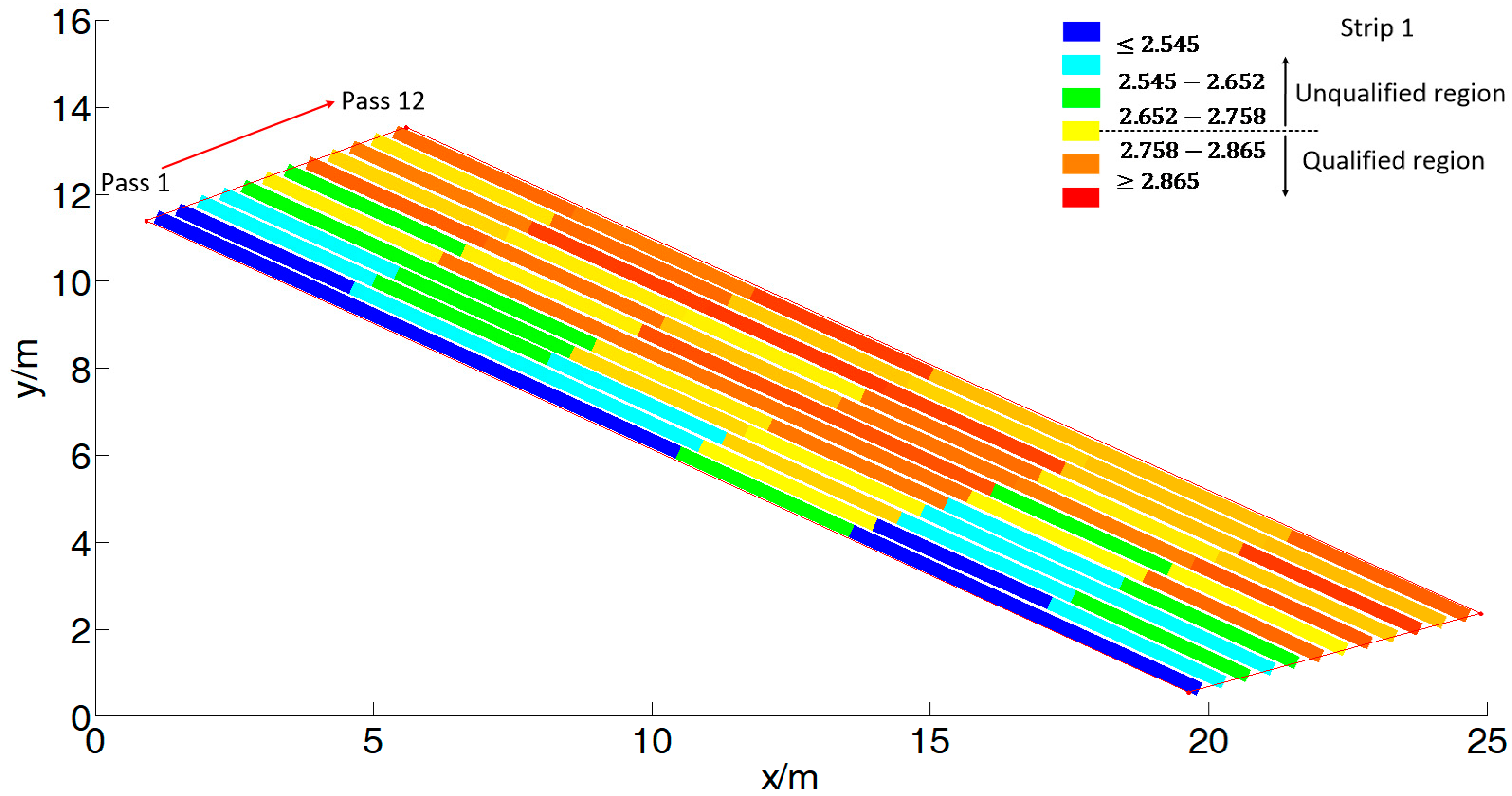
4.3. Correlations between SCV and Compaction Quality of Rockfill Materials
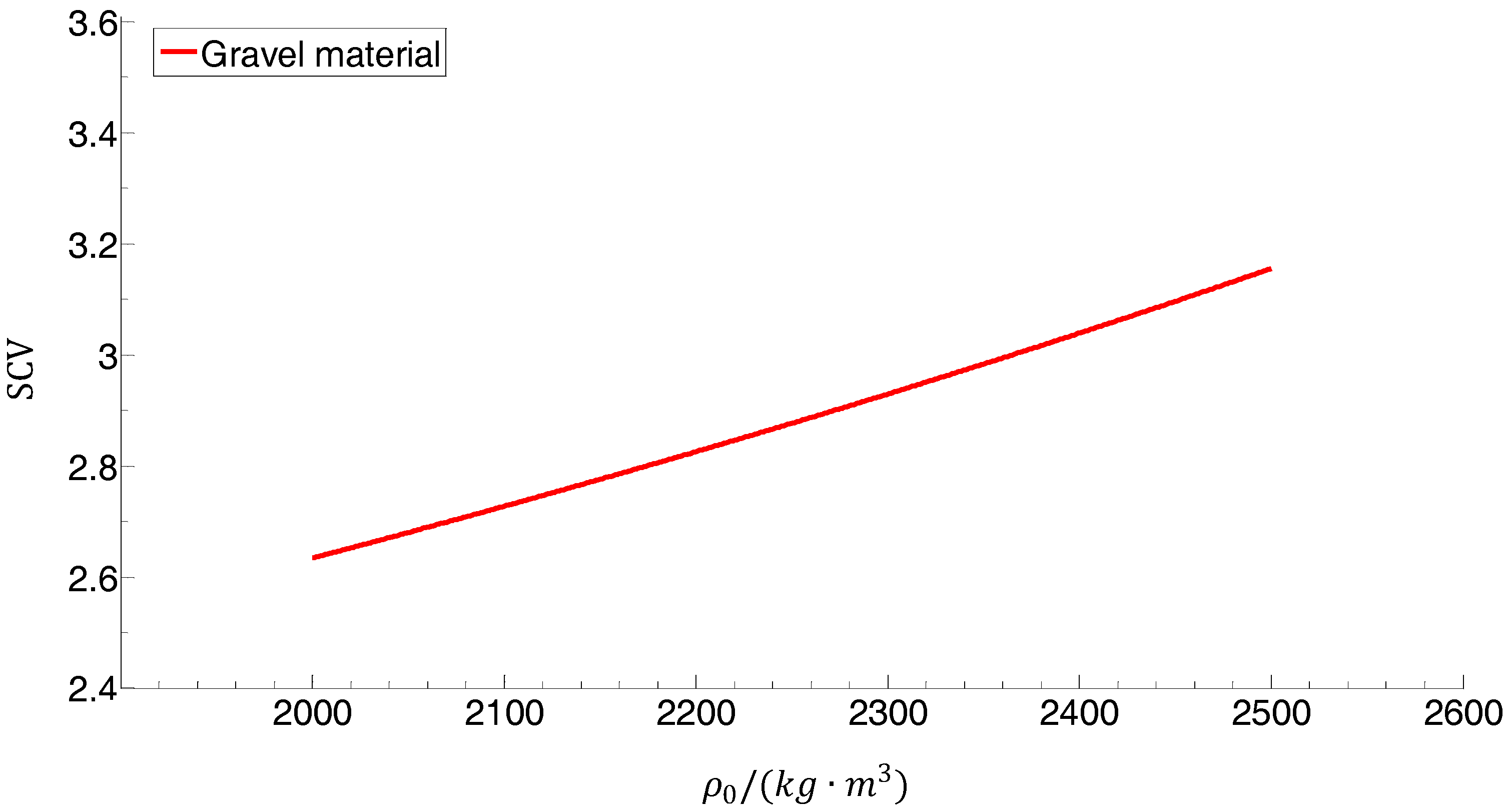
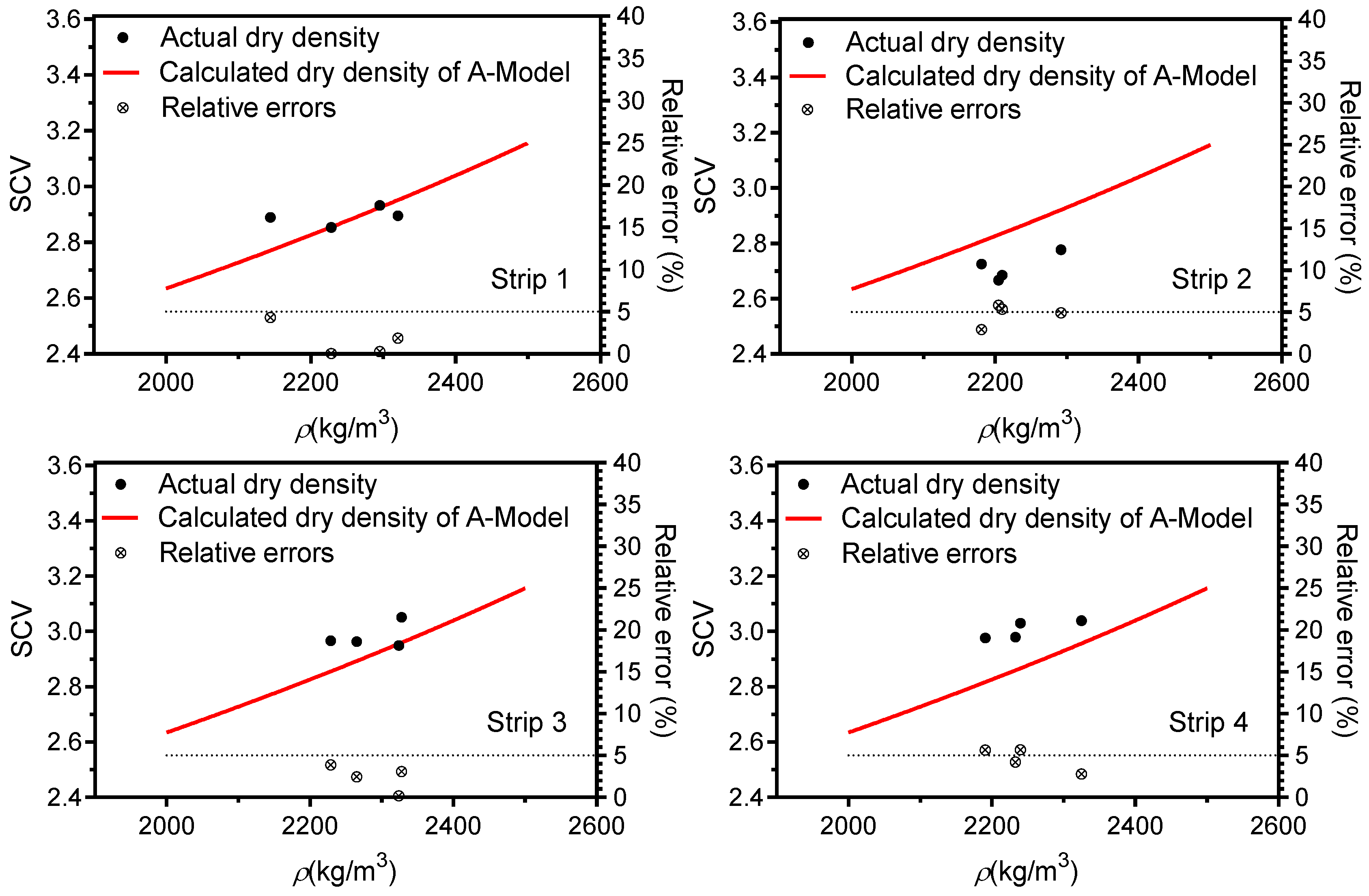
4.4. Relations between the Theoretical Model and In Situ Measurements
5. Conclusions
- (1)
- The SCV value increased with the increase of the number of compaction times. Furthermore, the SCV increased with the increase of the compactness or dry density and vice versa. Moreover, the SCV had a strong linear correlation with the number of compaction times ( ranged from 0.7803 to 0.9696) as well as the compactness ( ranged from 0.7371 to 0.8064). The comparison analysis of the actual and calculated dry density based on A-model showed that the relative errors were between 0.04% and 5.80%, and the average relative errors were less than 5%.
- (2)
- A-model, namely, a relational model between the SCV and the dry density of the NGM, was established. During the modeling process, an innovative differential pulse excitation method was proposed and used to solve the numerical solution of the vertical displacement of the soil surface under harmonic loads. The A-model has been experimentally verified to have high accuracy and can meet the requirements of practical projects.
- (3)
- Statistical averaging of in situ measurements in each test strip of the field tests mitigated measurement variations and revealed the high accuracy of the calculated values based on the A-model. This data processing method conforms to the design specifications of rockfill dams and the calculation results based on the A-model are reliable.
- (4)
- Compared with existing contact techniques and methods and CMV-based RICM techniques, the new technique proposed in this paper demonstrated several advantages, such as higher accuracy, smaller discreetness, convenience, and suitability for detecting the compactness of rockfill materials with particle sizes larger than 200 mm. In addition, based on the CAWDS developed in this study and the RTK-GPS technique, the SCV could automatically be acquired and used to characterize the compaction status of the NGM as a nephogram. Based on the nephogram, the compaction performance in the entire work areas could be clearly determined and support could be provided for quality control in a timely manner. The above results showed that the SCV could serve as a real-time monitoring index characterizing the compaction quality of rockfill dam materials.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, D.H.; Sun, J.; Zhong, D.H.; Song, L.G. Compaction quality control of earth-rock dam construction using real-time field operation data. J. Constr. Eng. Manag. 2012, 138, 1085–1094. [Google Scholar] [CrossRef]
- Krebs, R.D.; Walker, E.D. Highway Materials; McGraw-Hill Book Co.: New York, NY, USA, 1971. [Google Scholar]
- Rahman, F.; Hossain, M.; Hunt, M.M.; Romanoschi, S.A. Soil stiffness evaluation for compaction control of cohesionless embankments. Geotech. Test. J. 2008, 31, 442–451. [Google Scholar]
- Meehan, C.L.; Tehrani, F.S.; Vahedifard, F. A comparison of density-based and modulus based in situ test measurements for compaction control. Geotech. Test. J. 2012, 35, 387–399. [Google Scholar] [CrossRef]
- Melbouci, B. Compaction and shearing behavior study of recycled aggregates. Constr. Build. Mater. 2009, 23, 2723–2730. [Google Scholar] [CrossRef]
- Zabilska-Adamska, K.; Sulewska, M.J. Dynamic CBR test to assess the soil compaction. J. Test. Eval. 2014, 43, 1028–1036. [Google Scholar] [CrossRef]
- Resende, L.R.M.; Oliveira Filho, W.L.; Nogueira, C.L. Use of the DCP test for compaction control of staged dikes in mining tailings dams. REM Rev. Esc. Minas 2013, 66, 493–498. [Google Scholar] [CrossRef]
- Kongkitkul, W.; Saisawang, T.; Thitithavoranan, P.; Kaewluan, P.; Posribink, T. Correlations between the surface stiffness evaluated by light-weight deflectometer and degree of compaction. Tunn. Undergr. Constr. Geo Shanghai 2014, 65–75. [Google Scholar] [CrossRef]
- Umashankar, B.; Hariprasad, C.; Kumar, G. Compaction quality control pavement layers using LWD. J. Mater. Civ. Eng. 2016, 28. [Google Scholar] [CrossRef]
- Swinford, J.M.; Meyer, J.H. An evaluation of a nuclear density gauge for measuring infield compaction in soils of the South African sugar industry. S. Afr. Sugar Technol. Assoc. 1985, 19, 218–224. [Google Scholar]
- White, D.J.; Thompson, M.T.; Morris, M. Power-based compaction monitoring using vibratory padfoot roller. Proc. Geo-Congr. 2016, 1–6. [Google Scholar] [CrossRef]
- Thurner, H.; Forsblad, L. Compaction Meter on Vibrating Rollers; Res Bulletin Nr 8022 Monograph; Swedish National Road and Transport Research Institute (VTI): Linköping, Sweden, 1978. [Google Scholar]
- Forssblad, L. Compaction meter on vibrating rollers for improved compaction control. Proc. Int. Conf. Compact. 1980, 2, 541–546. [Google Scholar]
- Anderegg, R.; Kaufmann, K. Intelligent Compaction with Vibratory Rollers-Feedback Control Systems in Automatic Compaction and Compaction Control; Transportation Research Board: Washington, DC, USA, 2004; pp. 124–134. [Google Scholar]
- White, D.J.; Thompson, M.J. Relationships between in situ and roller-integrated compaction measurements for granular soils. J. Geotech. Geoenviron. Eng. 2008, 134, 1763–1770. [Google Scholar] [CrossRef]
- Anderegg, R.; von Felten, D.A.; Kaufmann, K. Compaction monitoring using intelligent soil compactors. GeoCongress 2006 2006. [Google Scholar] [CrossRef]
- Thompson, M.J.; White, D.J. Estimating compaction of cohesive soils from machine drive power. J. Geotech. Geoenviron. Eng. 2008, 134, 1771–1777. [Google Scholar] [CrossRef]
- White, D.J.; Jaselskis, E.J.; Schaefer, V.R.; Cackler, E.T. Real-Time Compaction Monitoring in Cohesive Soils from Machine Response; Transportation Research Record No. 1936; Transportation Research Board: Washington, DC, USA, 2005; pp. 173–180. [Google Scholar]
- Komandi, G. An evaluation of the concept of rolling resistance. J. Terrramech. 1999, 36, 159–166. [Google Scholar] [CrossRef]
- Adam, D. Continuous compaction control (CCC) with vibratory rollers. In Proceedings of the GeoEnvironment 97: 1st Australia-New Zealand Conference on Environmental Geotechnics, Melbourne, Australia, 26–28 November 1997; pp. 245–250. [Google Scholar]
- Mooney, M.; Rinehart, R. Field Monitoring of roller vibration during compaction of subgrade soil. J. Geotech. Geoenviron. 2007, 133, 257–265. [Google Scholar] [CrossRef]
- Rinehart, R.; Mooney, M. Instrumentation of a roller compactor to monitor vibration behavior during earthwork compaction. Automat. Constr. 2008, 17, 144–150. [Google Scholar] [CrossRef]
- Singh, D.; Zaman, M.; Commuri, S.; Zaman, M. Application of intelligent compaction technology for estimation of effective modulus for a multilayered asphalt pavement. J. Test. Eval. 2015, 43, 1–11. [Google Scholar] [CrossRef]
- Xu, Q.; Chang, G.K. Adaptive quality control and acceptance of pavement material density for intelligent road construction. Automat. Constr. 2016, 62, 78–88. [Google Scholar] [CrossRef]
- Liu, D.H.; Lin, M.; Li, S. Real-time quality monitoring and control of highway compaction. Automat. Constr. 2016, 62, 114–123. [Google Scholar] [CrossRef]
- Karray, M.; Lefebvre, G.; Ethier, Y.; Bigras, A. Assessment of deep compaction of the Peribonka dam foundation using “modal analysis of surface waves” (MASW). Can. Geotech. J. 2010, 47, 312–326. [Google Scholar] [CrossRef]
- Donohue, S.; Forristal, D.; Douohue, L.A. Detection of soil compaction using seismic surface waves. Soil Tillage Res. 2013, 128, 54–60. [Google Scholar] [CrossRef]
- Shangguan, P.; Al-Qadi, I.; Coenen, A.; Zhao, S. Algorithm development for the application of ground-penetrating radar on asphalt pavement compaction monitoring. Int. J. Pavement Eng. 2016, 17, 189–200. [Google Scholar] [CrossRef]
- Liu, D.H.; Li, Z.L.; Lian, Z.H. Compaction quality assessment of earth-rock dam materials using roller-integrated compaction monitoring technology. Automat. Constr. 2014, 44, 234–246. [Google Scholar] [CrossRef]
- Sandström, Å. Numerical Simulation of a Vibratory Roller on Cohesionless Soil; Internal Report; Geodynamic: Stockholm, Sweden, 1994; pp. 1–22. [Google Scholar]
- Vennapusa, P.K.R.; White, D.J.; Morris, M.D. Geostatistical analysis for spatially referenced roller-integrated compaction measurements. J. Geotech. Geoenviron. 2010, 136, 813–823. [Google Scholar] [CrossRef]
- Lamb, H. On the propagation of an elastic solid. Proc. R. Soc. Lond. 1904, 203, 1–42. [Google Scholar]
- De Hoop, A.T. A modification of Cagniard’s method for solving seismic pulse problems. Appl. Sci. Res. 1960, 8, 349–356. [Google Scholar] [CrossRef]
- Reissner, E. Stationäre, axialsymmetrische, durch eine schüttelnde Masse erregte Schwingungen eines homogenen elastischen Halbraumes. Ing. Arch. 1936, 7, 381–396. [Google Scholar] [CrossRef]
- Quinlan, P.M. The elastic theory of soil dynamics. In Symposium on Dynamic Testing of Soils; ASTM STP 156; ASTM International: West Conway Hocken, PA, USA, 1953; pp. 3–34. [Google Scholar] [CrossRef]
- Sung, T.Y. Vibration in semi-infinite solids due to periodic surface loadings. In Symposium on Dynamic Testing of Soils; ASTM STP 156; ASTM International: West Conway Hocken, PA, USA, 1953; pp. 35–54. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of deformation and acoustic propagation in porous media. J. Appl. Phys. 1962, 33, 1482–1498. [Google Scholar] [CrossRef]
- Paul, H.S. On the displacements produced in a porous elastic semi-space by an impulsive line load (non-dissipative case). Pure Appl. Geophys. 1976, 114, 605–614. [Google Scholar] [CrossRef]
- Philippacopoulos, A.J. Lamb’s problem for fluid-saturated porous media. Bull. Seismol. Soc. Am. 1988, 78, 908–923. [Google Scholar]
- Wang, L.Z.; Chen, Y.M.; Wu, S.M.; Ding, H.J. A solution to saturated elastic semi-space under harmonic force of low frequency. J. Hydraul. Eng. 1996, 2, 84–88. [Google Scholar]
- Cai, Y.Q.; Meng, K.; Xu, C.J. Stable response of axisymmetric two-phase water-saturated soil. J. Zhejiang Univ. Sci. 2004, 5, 1022–1027. [Google Scholar] [CrossRef] [PubMed]
- Jin, B.; Liu, H. Vertical response of a disk on a saturated poroelastic semi-space. Soil. Dyn. Earthq. Eng. 1999, 18, 437–443. [Google Scholar]
- Jin, B.; Liu, H. Horizontal vibrations of a disk on a poroelastic semi-space. Soil Dyn. Earthq. Eng. 2000, 19, 269–275. [Google Scholar] [CrossRef]
- Senjuntichai, T.; Sapsathiarm, Y. Forced vertical vibration of circular plate in multilayered poroelastic medium. J. Eng. Mech. 2003, 129, 1330–1341. [Google Scholar] [CrossRef]
- Pekeris, C.L. The seismic surface pulse. Proc. Natl. Acad. Sci. USA 1955, 41, 469–480. [Google Scholar] [CrossRef] [PubMed]
- Lade, P.V.; Nelson, R. Modeling of the elastic behavior of granular materials. Int. J. Numer. Anal. Methods Geomech. 1987, 11, 521–542. [Google Scholar] [CrossRef]
- Liu, H.B.; Zou, D.G.; Liu, J.M. Constitutive modeling of dense gravelly soils subjected to cyclic loading. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1503–1518. [Google Scholar] [CrossRef]

| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Material | Strip | Passes (Static) | Passes (Vibratory) | Vibration Frequency () | Velocity () | Lift Thickness () | Vibration Status |
|---|---|---|---|---|---|---|---|
| NGM | 1~4 | 2 | 12 | 31 | 3 | About 0.8 | HFHA |
| Strip | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Block | |||||
| 1 | 0.8972 | 0.8085 | 0.8147 | 0.9096 | |
| 2 | 0.8461 | 0.8316 | 0.8237 | 0.9204 | |
| 3 | 0.8342 | 0.8775 | 0.9696 | 0.8416 | |
| 4 | 0.7803 | 0.8628 | 0.9232 | 0.8052 | |
| 5 | 0.9001 | 0.7961 | 0.8679 | 0.8714 | |
| 6 | 0.8010 | 0.8619 | 0.7955 | 0.8968 | |
| Strip | Maximum Relative Error (%) | Minimum Relative Error (%) | Average Relative Error (%) |
|---|---|---|---|
| 1 | 4.31 | 0.04 | 1.63 |
| 2 | 5.80 | 2.91 | 4.74 |
| 3 | 3.89 | 0.18 | 2.39 |
| 4 | 5.66 | 2.79 | 4.58 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Liu, T.; Li, Q. Roller-Integrated Acoustic Wave Detection Technique for Rockfill Materials. Appl. Sci. 2017, 7, 1118. https://doi.org/10.3390/app7111118
Zhang Q, Liu T, Li Q. Roller-Integrated Acoustic Wave Detection Technique for Rockfill Materials. Applied Sciences. 2017; 7(11):1118. https://doi.org/10.3390/app7111118
Chicago/Turabian StyleZhang, Qinglong, Tianyun Liu, and Qingbin Li. 2017. "Roller-Integrated Acoustic Wave Detection Technique for Rockfill Materials" Applied Sciences 7, no. 11: 1118. https://doi.org/10.3390/app7111118
APA StyleZhang, Q., Liu, T., & Li, Q. (2017). Roller-Integrated Acoustic Wave Detection Technique for Rockfill Materials. Applied Sciences, 7(11), 1118. https://doi.org/10.3390/app7111118





