A New Fuzzy Sliding Mode Controller with a Disturbance Estimator for Robust Vibration Control of a Semi-Active Vehicle Suspension System
Abstract
1. Introduction
2. Problem Formulation
3. Design of a New FSMC
3.1. Structure FSMC
3.2. Control Law of FSMC
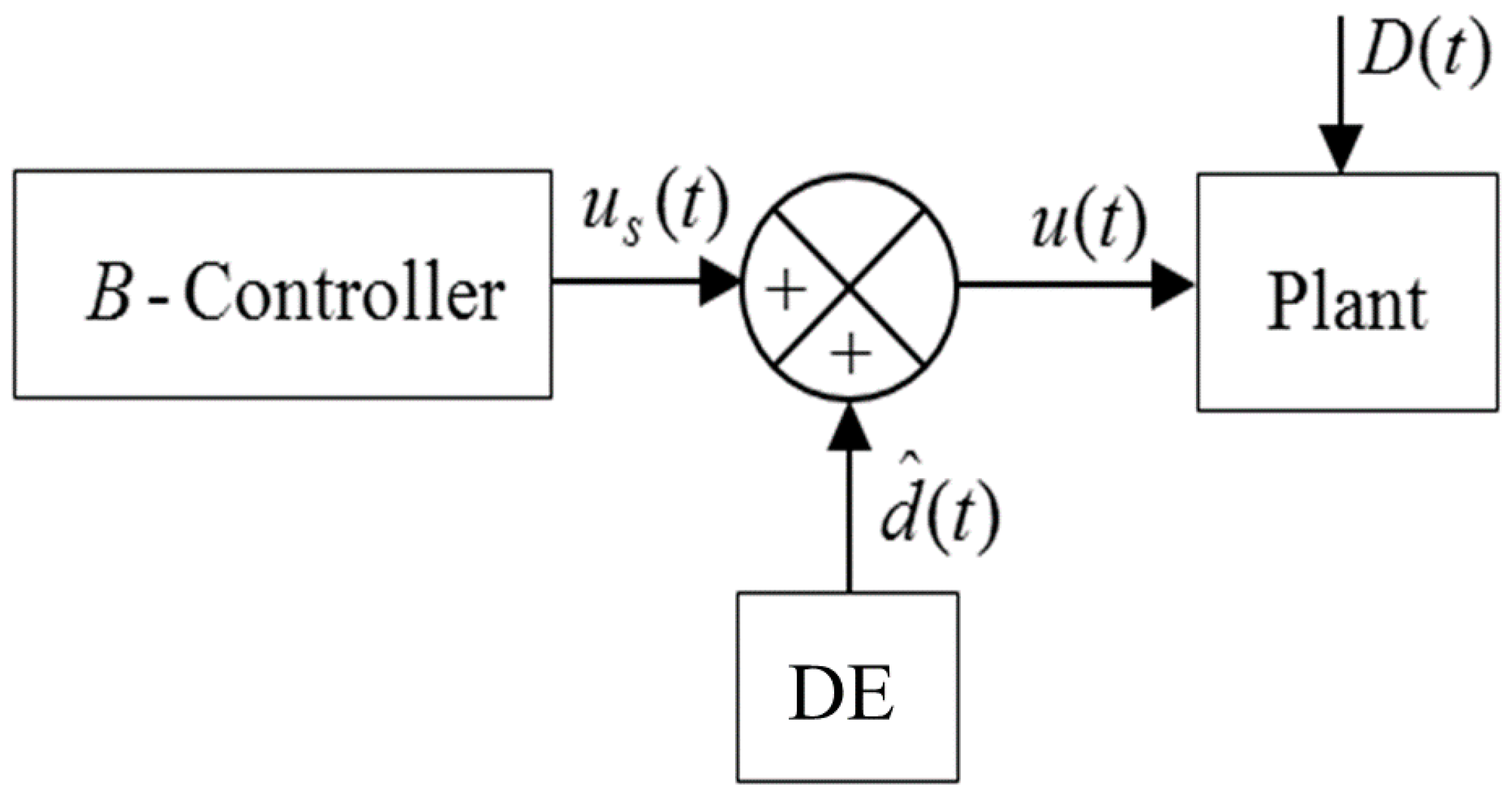
4. Design of Disturbance Estimator
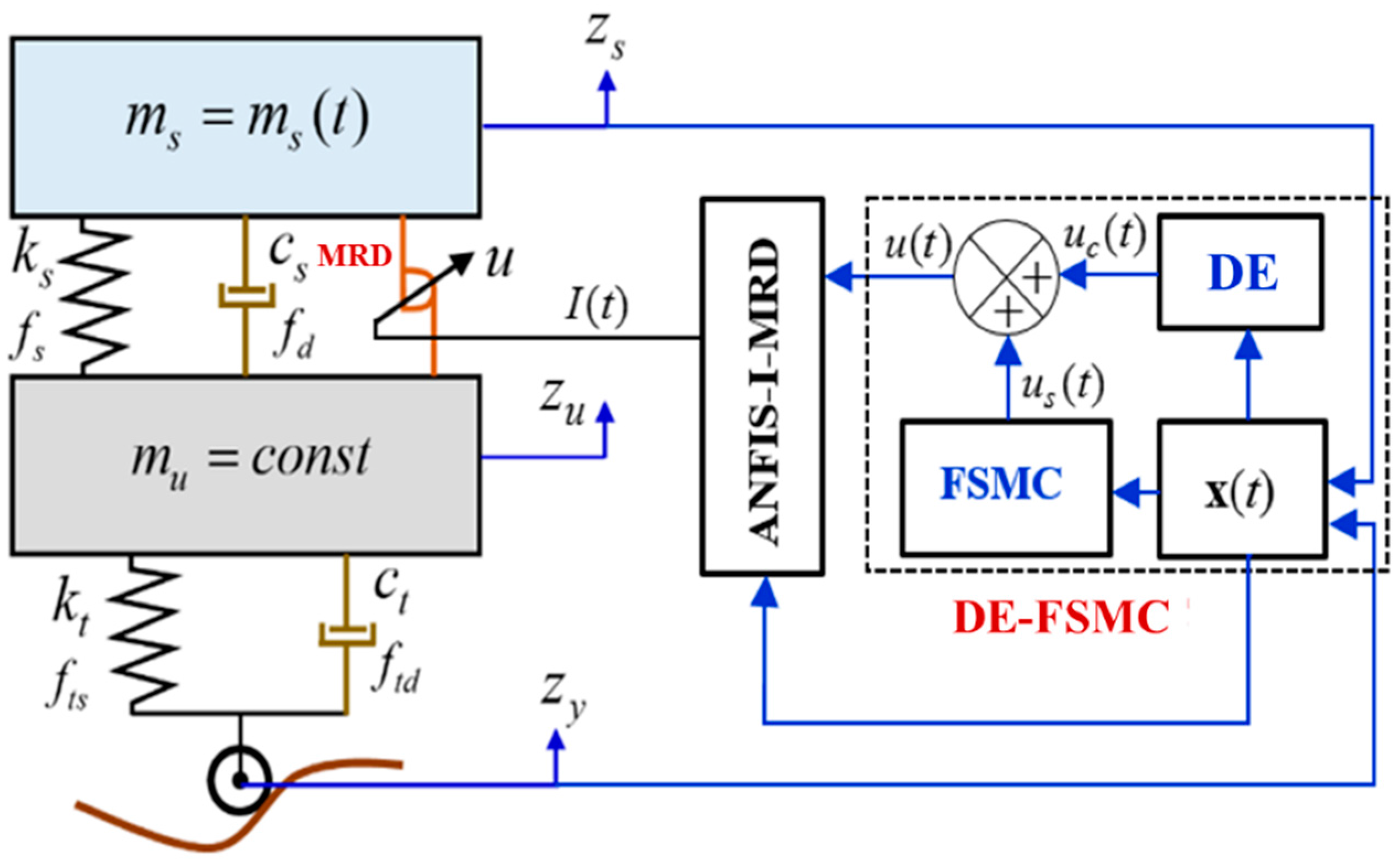
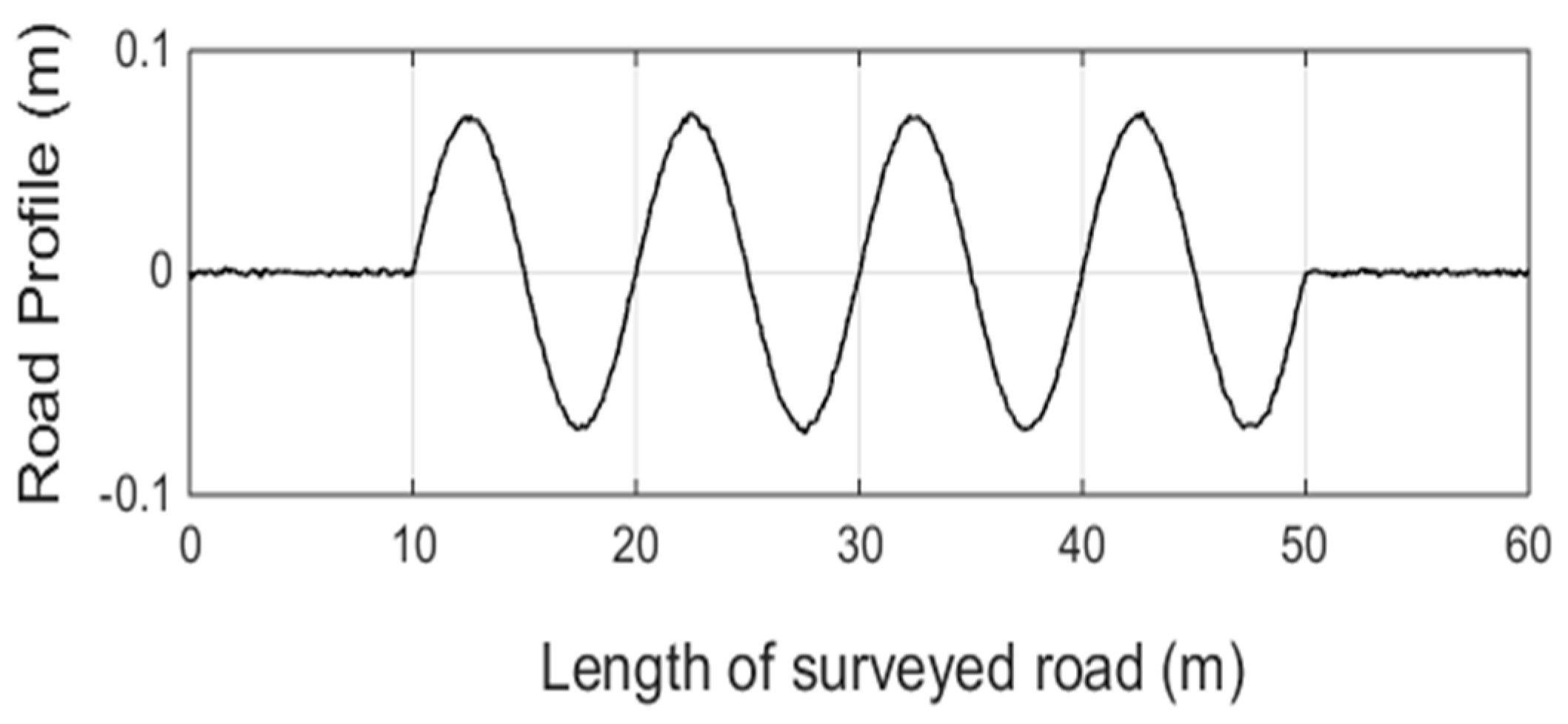
5. Application to Vehicle Suspension System
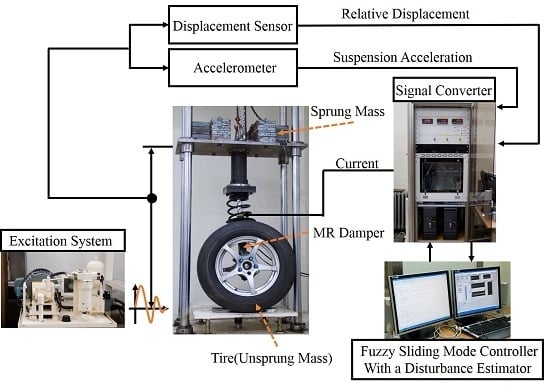
5.1. Experimental Apparatus
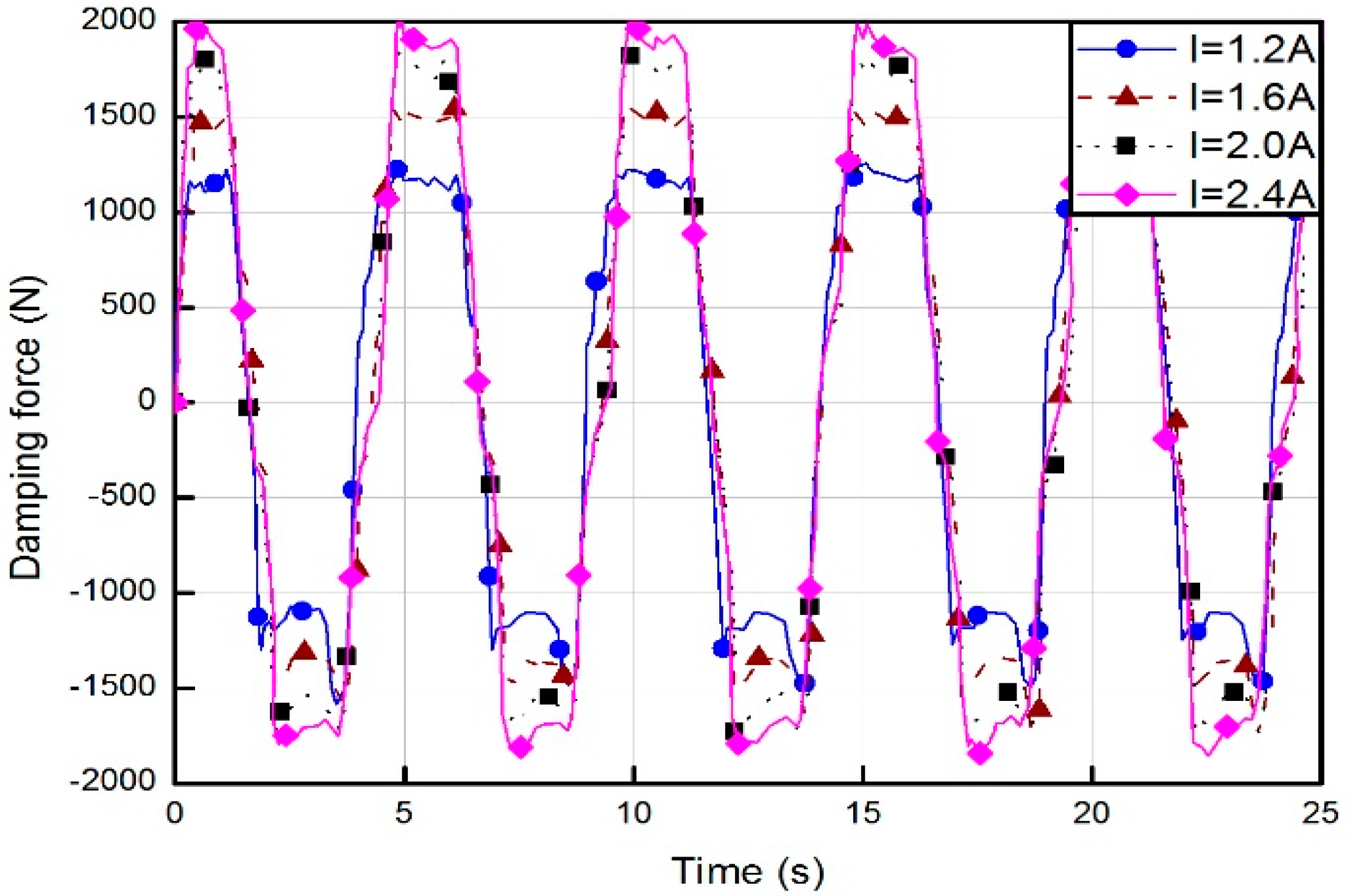
5.2. Building of ANFIS-I-MRD
5.3. Formulation of DE-FSMC
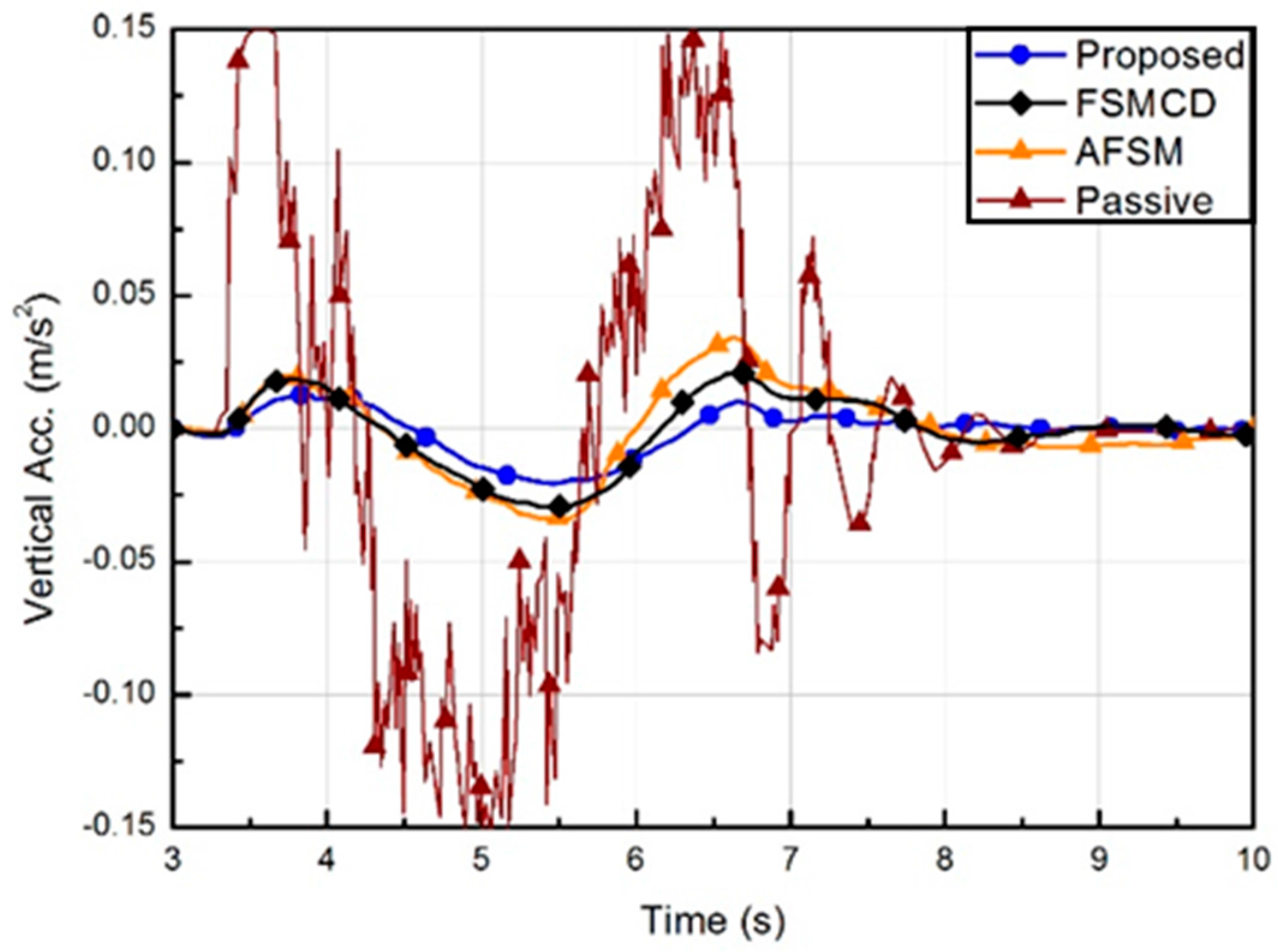
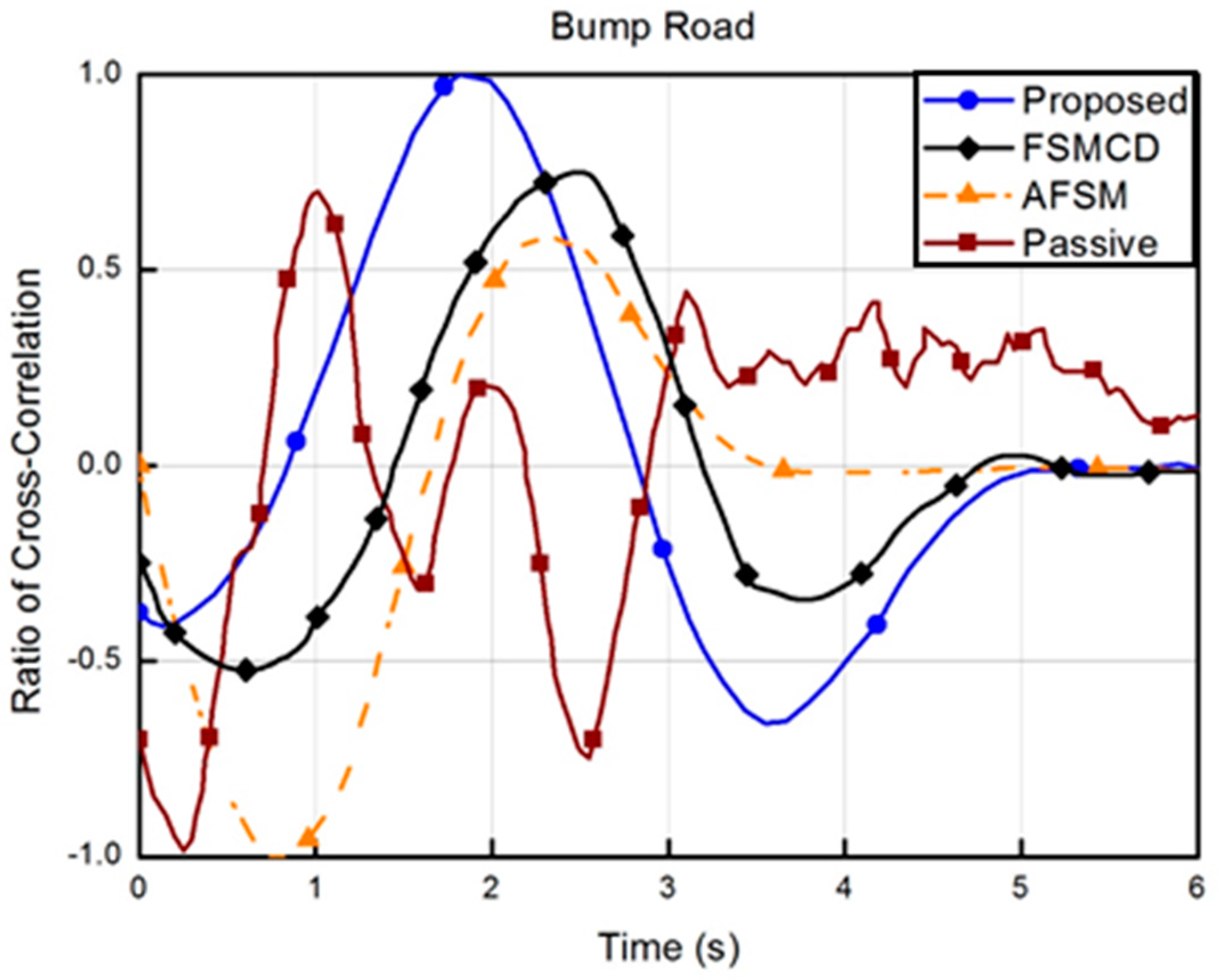
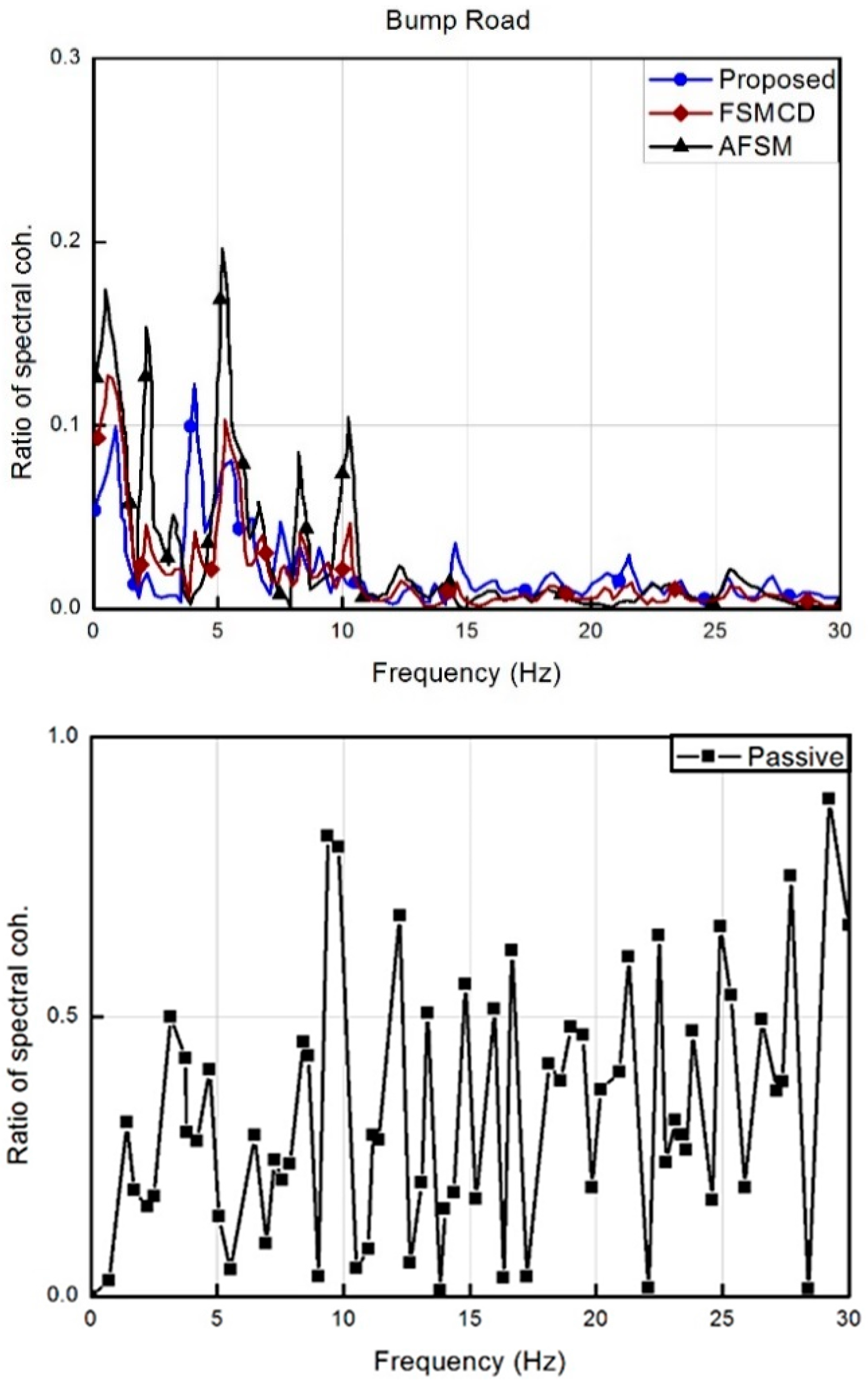
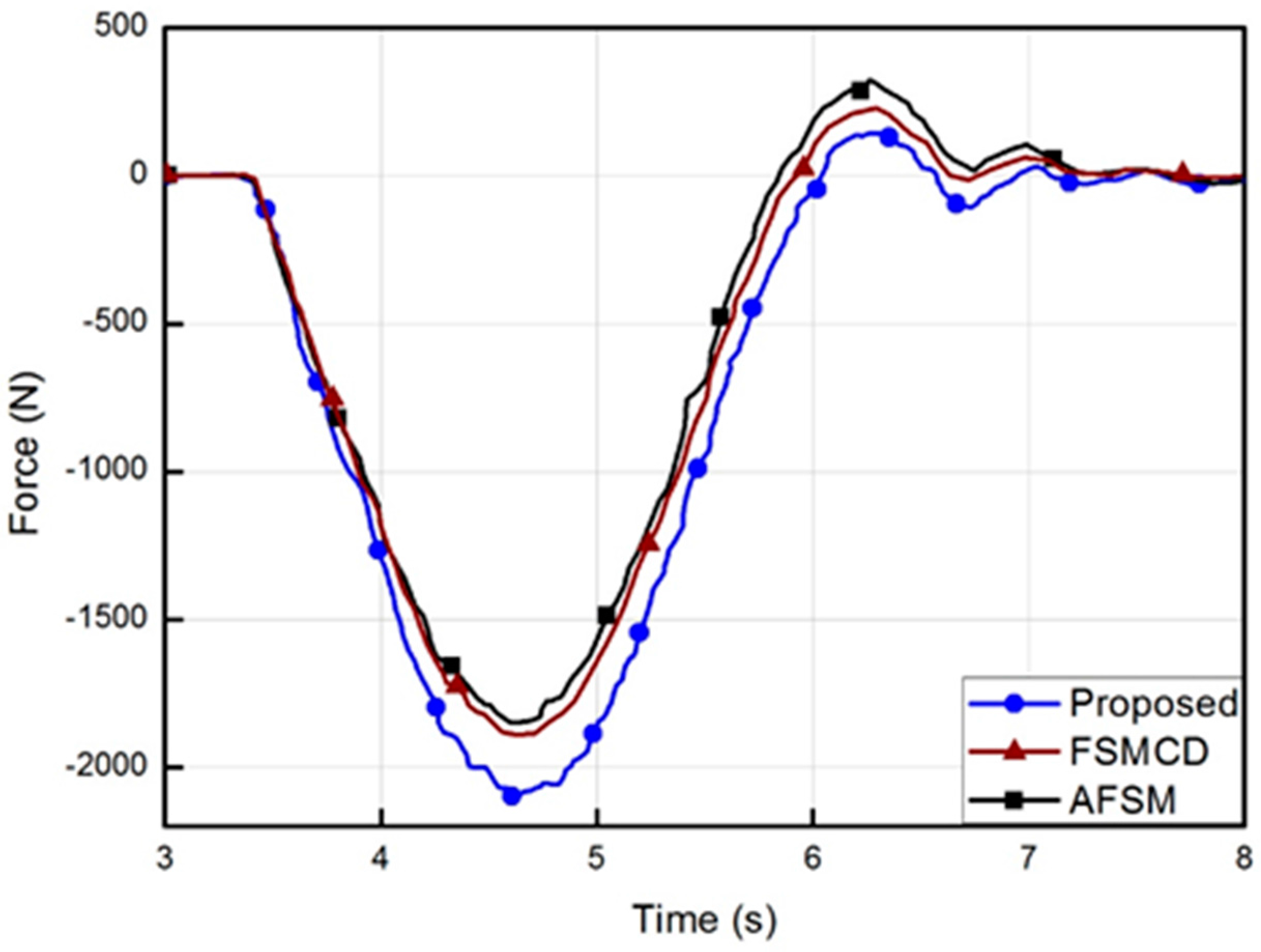
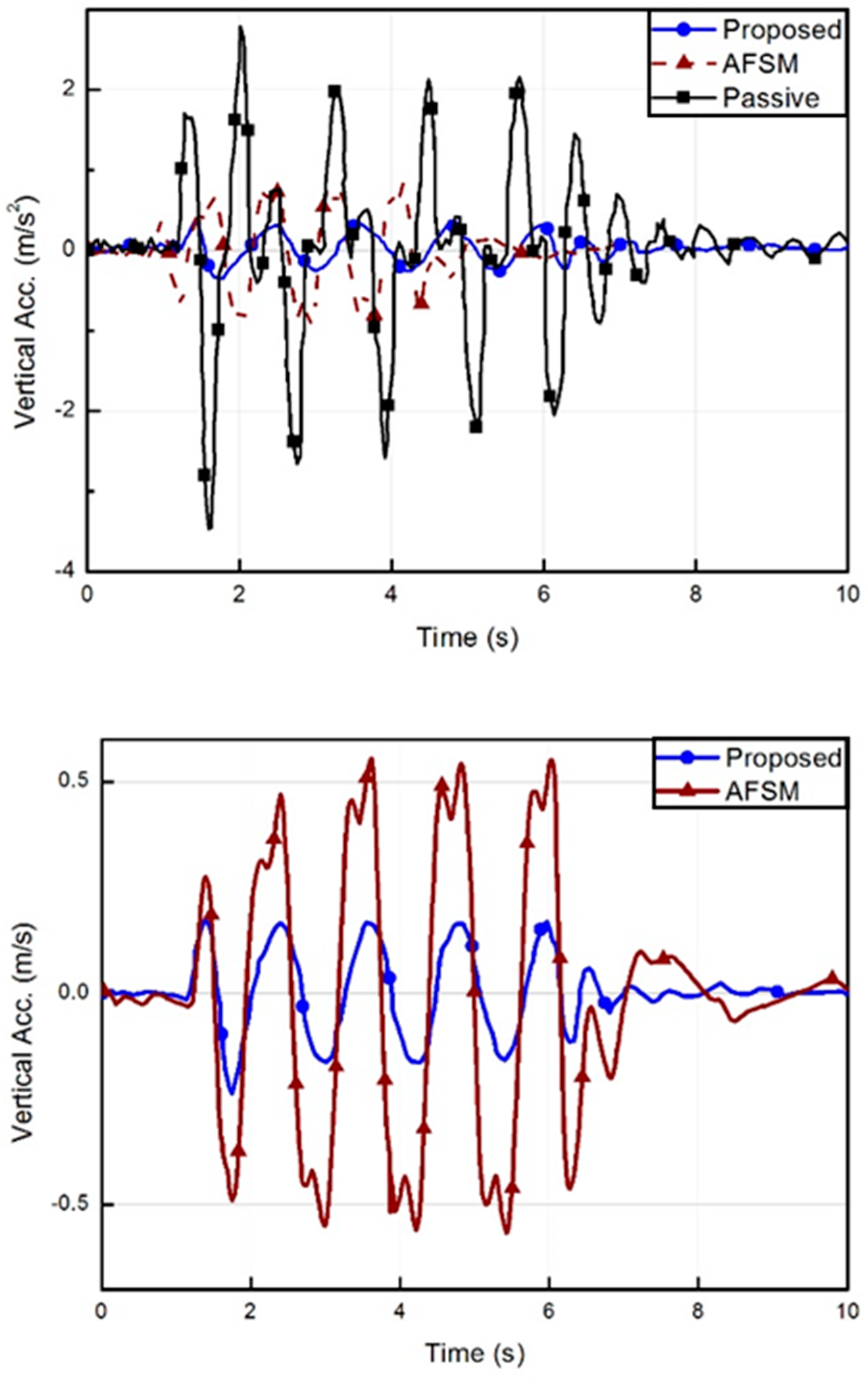
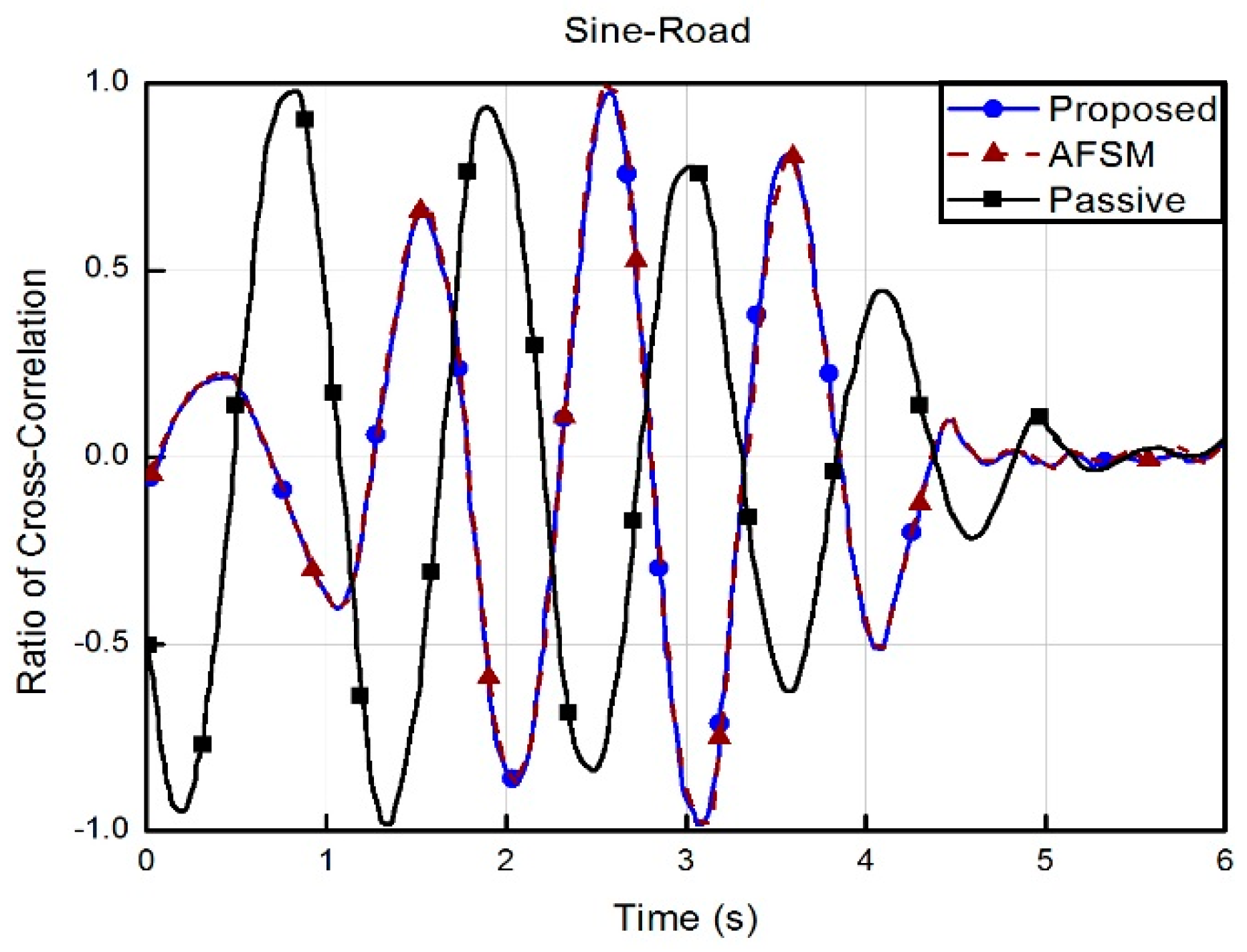
5.4. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nguyen, S.D.; Nguyen, Q.H. Design of active suspension controller for train cars based on sliding mode control, uncertainty observer and neuro-fuzzy system. J. Vib. Control. 2015, 23, 1334–1353. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Choi, S.B. Design of a new adaptive neuro-fuzzy inference system based on a solution for clustering in a data potential field. Fuzzy Sets Syst. 2015, 279, 64–86. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Nguyen, Q.H.; Choi, S.B. Hybrid clustering based fuzzy structure for vibration control—Part 1: A novel algorithm for building neuro-fuzzy system. Mech. Syst. Signal Process 2014, 50–51, 510–525. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Nguyen, Q.H.; Choi, S.B. Hybrid clustering based fuzzy structure for vibration control—Part 2: An application to semi-active vehicle seat-suspension system. Mech. Syst. Signal Process 2014, 56–57, 288–301. [Google Scholar] [CrossRef]
- Sivanandan, S.N.; Sumathi, S.; Deepa, S.N. Inductionto Fuzzy Logic Using MATLAB; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Castillo, O.; Melin, P. A review on the design and optimization of interval type-2 fuzzy controllers. Appl. Soft Comput. 2012, 12, 1267–1278. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.D.; Phadke, S.B. Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 26, 98–107. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Shendge, P.D.; Phadke, S.B. Active suspension systems for vehicles based on a sliding-mode controller in combination with inertial delay control. Proc. IMechE Part D 2013, 227, 675–690. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Mohan, B.; Shendge, P.D.; Phadke, S.B. Disturbance observer based sliding mode control of active suspension systems. J. Sound Vib. 2014, 333, 2281–2296. [Google Scholar] [CrossRef]
- Ling, F.X.; Yue, Z. Sliding-mode output feedback control for active suspension with nonlinear actuator dynamics. J. Vib. Control. 2013, 21, 2721–2738. [Google Scholar]
- Mahmoodabadi, M.J.; Taherkhorsandi, M.; Talebipour, M.; Castillo-Villar, K.K. Adaptive robust PID control subject to supervisory decoupled sliding mode control based upon genetic algorithm optimization. Trans. Inst. Meas. Control. 2015, 37, 505–514. [Google Scholar] [CrossRef]
- Mohammad, R.; Mohammad, H.; Mohammad, R. An optimal and intelligent control strategy for a class of nonlinear systems: Adaptive fuzzy sliding mode. J. Vib. Control. 2014, 22, 159–175. [Google Scholar]
- Pan, Y.; Wei, W.; Furuta, K. Hybrid sliding sector control for a wheeled mobile robot. ProcIMechE Part I 2008, 222, 829–837. [Google Scholar] [CrossRef]
- Zhang, B.L.; Han, Q.L.; Zhang, X.M.; Yu, X. Sliding Mode Control with Mixed Current and Delayed States for Offshore Steel Jacket Platforms. IEEE Trans. Control. Syst. Technol. 2013, 22, 1769–1783. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mech. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Madoński, R.; Herman, P. Survey on methods of increasing the efficiency of extended state disturbance observers. ISA Trans. 2015, 56, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Wang, C.; Zeng, Q. Observer-based sliding mode control for a class of uncertain nonlinear neutral delay systems. J. Frankl. Inst. 2008, 345, 233–253. [Google Scholar] [CrossRef]
- Chan, P.T.; Rad, A.B.; Wang, J. Indirect adaptive fuzzy sliding mode control: Part II: Parameter projection and supervisory control. Fuzzy Sets Syst. 2001, 122, 31–43. [Google Scholar] [CrossRef]
- Liang, J.W.; Chen, H.Y.; Wu, Q.W. Active suppression of pneumatic vibration isolators using adaptive sliding controller with self-tuning fuzzy compensation. J. Vib. Control. 2013, 21, 246–259. [Google Scholar] [CrossRef]
- Nekoukar, V.; Erfanian, A. Adaptive fuzzy terminal sliding mode control for a class of MIMO uncertain nonlinear systems. Fuzzy Sets Syst. 2011, 179, 34–49. [Google Scholar] [CrossRef]
- Oguz, Y.; Hasan, A. Neural based sliding-mode control with moving sliding surface for the seismic isolation of structures. J. Vib. Control. 2011, 17, 2103–2116. [Google Scholar]
- Hosseini, R.; Qanadli, S.D.; Barman, S.; Mazinani, M.; Ellis, T.; Dehmeshki, J. An automatic approach for learning and tuning Gaussian interval type-2 fuzzy membership functions applied to lung CAD classification system. IEEE Trans. Fuzzy Syst. 2012, 20, 224–234. [Google Scholar] [CrossRef]
- Ho, H.F.; Wong, Y.K.; Rad, A.B. Adaptive fuzzy sliding mode control with chattering elimination for nonlinear SISO systems. Simul. Model. Pract. Theory 2009, 17, 1199–1210. [Google Scholar] [CrossRef]
- Yao, J.L.; Shi, W.K. Development of a sliding mode controller for semi-active vehicle suspensions. J. Vib. Control. 2013, 19, 1152–1160. [Google Scholar] [CrossRef]
- Li, H.; Yu, J.; Hilton, C.; Liu, H. Adaptive Sliding-Mode Control for Nonlinear Active Suspension Vehicle Systems Using T-S Fuzzy Approach. IEEE Trans. Ind. Electron. 2013, 60, 3328–3338. [Google Scholar] [CrossRef]
- Khazaee, M.; Markazi, A.H.D.; Omidi, E. Adaptive fuzzy predictive sliding control of uncertain nonlinear systems with bound-known input delay. ISA Trans. 2015, 59, 314–324. [Google Scholar] [CrossRef] [PubMed]
- Mobayen, S.; Javadi, S. Disturbance observer and finite-time tracker design of disturbed third-order nonholonomic systems using terminal sliding mode. J. Vib. Control. 2015, 23, 181–189. [Google Scholar] [CrossRef]
- Wang, J.; Rad, A.B.; Chan, P.T. Indirect adaptive fuzzy sliding model control—Part I: Fuzzy switching. Fuzzy Sets Syst. 2001, 122, 21–30. [Google Scholar] [CrossRef]
- Geravand, M.; Aghakhani, N. Fuzzy Sliding Mode Control for applying to active vehicle suspensions. WSEAS Trans. Syst. Control. 2010, 5, 48–57. [Google Scholar]
- Sharkawy, A.B.; Salman, S.A. An Adaptive Fuzzy Sliding Mode Control Scheme for Robotic Systems. Intell. Control Autom. 2011, 2, 299–309. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Karimi, H.R. Fuzzy Sliding Mode Controller Design Using Takagi-Sugeno Modelled Nonlinear Systems; Hindawi Publishing Corporation: New York, NY, USA, 2013. [Google Scholar]
- Khanesar, M.A.; Kaynak, O.; Yin, S.; Gao, H. Adaptive indirect fuzzy sliding mode controller for networked control systems subject to time-varying network-induced time delay. IEEE Trans. Fuzzy Syst. 2015, 23, 205–214. [Google Scholar] [CrossRef]
- Chen, W.H. Nonlinear disturbance observer-enhanced Dynamic inversion control of missiles. J. Guid. Control. Dyn. 2003, 26, 161–166. [Google Scholar] [CrossRef]
- Prattichizzo, D.; Mercorelli, P. On some geometric properties of active suspensions systems. Kybernetika 2000, 36, 549–570. [Google Scholar]
- Bittanti, S.; Savaresi, S.M. On the parameterization and design of an ex tended Kalman filter frequency tracker. IEEE Trans. Autom. Control. 2000, 45, 1718–1724. [Google Scholar] [CrossRef]
- Bittanti, S.; dell Orto, F.; Di Carlo, A.; Savaresi, S.M. Notch filtering and multi-rate control for radial tracking in high-speed dvd-players. IEEE Trans. Consum. Electron. 2002, 48, 56–62. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Bittanti, S.; So, H.C. Closed-form unbiased frequency estimation of a noisy sinusoid using notch filters. IEEE Trans. Autom. Control. 2003, 48, 1285–1292. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z. Differential Evolution With Ranking-Based Mutation Operators. IEEE Trans. Cybern. 2013, 43, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Bendat, J.; Piersol, A. Engineering Applications of Correlation and Spectral Analysis, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Bendat, J.; Piersol, A. Random Data: Analysis and Measurement Procedures, 4nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2010. [Google Scholar]


| kg | |
| N/m | |
| Ns/m |
| Sliding Surface | |
| 1.51 | |
| 1.73 | |
| 1 | |
| 150 | |
| Number of fuzzy laws | 49 |
| Controller | (m/s2) | (s) |
|---|---|---|
| Proposed | 0.0190 | 1.869 |
| FSMCD | 0.0256 | 1.321 |
| AFSM | 0.0374 | 0.905 |
| Passive | 0.2394 | 0.264 |
| Controller | (m/s2) | (s) |
|---|---|---|
| Proposed | 0.1269 | 4.28 |
| FSMCD | 0.1985 | 5.05 |
| AFSM | 0.2175 | 5.45 |
| Passive | 0.9208 | 47.08 |
| Controller | (m/s2) | (s) |
|---|---|---|
| Proposed | 0.3642 | 2.545 |
| AFSM | 0.5742 | 1.359 |
| Passive | 3.6587 | 0.793 |
| Controller | (Hz) | |
|---|---|---|
| Proposed | 0.4672 | 24.03 |
| AFSM | 0.5195 | 70.54 |
| Passive | 0.8140 | 89.92 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.-K.; An, J.-H.; Choi, S.-B. A New Fuzzy Sliding Mode Controller with a Disturbance Estimator for Robust Vibration Control of a Semi-Active Vehicle Suspension System. Appl. Sci. 2017, 7, 1053. https://doi.org/10.3390/app7101053
Song B-K, An J-H, Choi S-B. A New Fuzzy Sliding Mode Controller with a Disturbance Estimator for Robust Vibration Control of a Semi-Active Vehicle Suspension System. Applied Sciences. 2017; 7(10):1053. https://doi.org/10.3390/app7101053
Chicago/Turabian StyleSong, Byung-Keun, Jin-Hee An, and Seung-Bok Choi. 2017. "A New Fuzzy Sliding Mode Controller with a Disturbance Estimator for Robust Vibration Control of a Semi-Active Vehicle Suspension System" Applied Sciences 7, no. 10: 1053. https://doi.org/10.3390/app7101053
APA StyleSong, B.-K., An, J.-H., & Choi, S.-B. (2017). A New Fuzzy Sliding Mode Controller with a Disturbance Estimator for Robust Vibration Control of a Semi-Active Vehicle Suspension System. Applied Sciences, 7(10), 1053. https://doi.org/10.3390/app7101053