1. Introduction
Since industrialization, the use of fossil fuel energy has increased exponentially. Consequently, the awareness and concern for the entirety life on Earth is growing due to side effects, such as global warming. As a result, the importance of renewable energy is on the rise, and energy sources that use wind, sun and geothermal heat are at the commercialization stage [
1].
Among the sources for renewable energy that await commercialization in the near future is wave energy [
2]. Although the idea of wave energy has existed for a long time, the commercialization has been slower than other sources of renewable energy. Unlike sunlight or wind that have relatively uniform energy flow, wave energy has a reciprocating motion, high energy density with slow speed and seasonal variations in heights and periods [
3]. As a result, wave energy converters (WECs) must have a complicated mechanism, solidity and flexibility corresponding to each attribute.
In addition, since waves generally have higher energy density at a deep water depth and the density becomes lesser as they get closer to the shore, it is appropriate to install the WECs in the distant sea, which has a deep water depth [
4]. Hence, the accessibility is poor, and a long sub-sea transmission line is needed. As the accessibility is low, WECs should be more robust so that less maintenance is required. To reduce the proportion of the cable installation cost in the capital expenditure of the WEC, a large-capacity wave energy farm should be built. Consequently, it requires more complete initial verification than other renewable energy sources for commercialization [
5].
One of the aforementioned disadvantages of wave energy is that the area of high wave energy density is far away from the on-grid. However, depending on the location, it can actually work as an advantage. One of these locations would be remote islands that are off-grid and therefore do not receive electricity from the mainland. Diesel generators are used for sourcing electricity in these islands. Since the power production unit price of a diesel generator is higher than that of the mainland, renewable energy sources in the islands are cost competitive. This has been represented in the example of Samsø Island in Denmark [
6]. Wave energy can be seen as the most suitable option for creating an energy self-sufficient island.
In consideration of such a situation, the wave power company INGINE has created a wave power generator called
INWAVE. Currently, there are three full-scale prototype devices installed in Jeju Island as a test run [
7]. The company seeks to start commercial operations in the latter half of 2016. This device, a tight moored moving body-type WEC, shares similar concepts with Fred Olsen’s Lifesaver WEC, in that the buoy has six degrees of freedom for movement and is connected to the sea-floor via stiff mooring ropes. While the Lifesaver [
8] is installed at a medium water depth of about 50 m,
INWAVE is installed along the coast. The
INWAVE device can follow the theoretical analysis of the Lifesaver since the basic concept is similar to this device. In the papers dealing with the Lifesaver, however, there is no modeling description for the multi-mooring and multi-degree motion of the WEC, but a point absorber modeling with heave motion is only described. In [
9], meanwhile, a multi-point tight moored body-type WEC is presented. However, only the frequency domain analysis is applied to the optimal control theory. Hence, there are limits to using this modeling approach directly.
In order to realize the modeling of the
INWAVE device, it is necessary to derive the kinematic relations of mooring ropes between the buoy and PTO (power take off) module and to build up the ratchet gear modeling in the PTO module. The ratchet gear is a mechanical element that converts the reciprocating motion of the mooring rope into a uni-directional rotation to the generator. This process is determined by the relationship between the angular velocities of the rope drum and the generator. As the ratchet gear connects or disconnects the rope drum with the generator, the dynamic modeling of the PTO module has discontinuity that causes the systemic errors and instability. To solve this problem, we introduce the PTO modeling, which does not cause discontinuous change by applying the virtual torsion spring element to the ratchet gear. We present the
INWAVE modeling including this PTO module based on the Newtonian mechanics and linear wave theory (LWT) [
10,
11]. Finally, we carry out simulations under JONSWAPirregular waves in various wave periods, to demonstrate the characteristics of the device.
2. Explanation of the Device
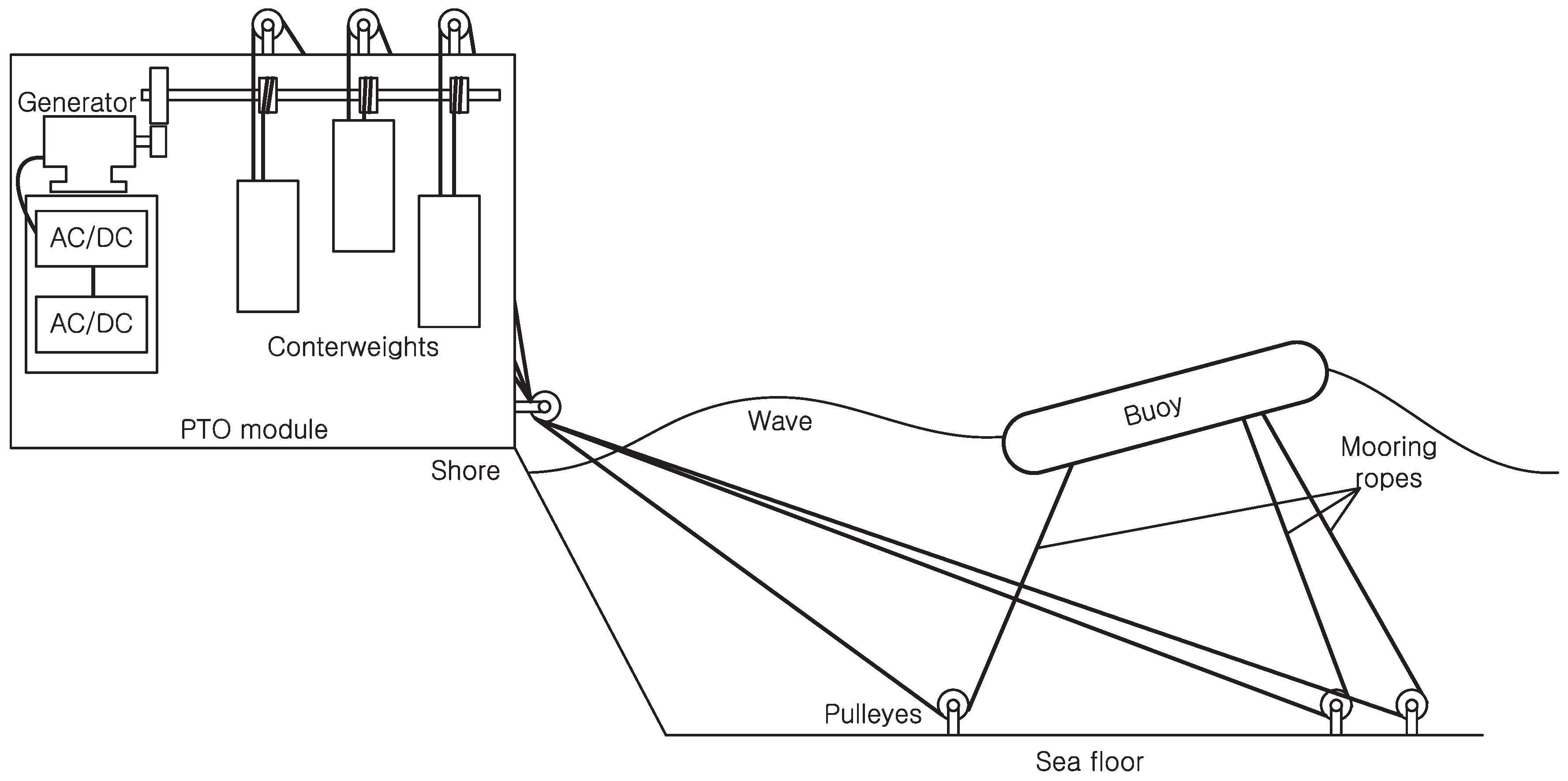
As shown in
Figure 1,
INWAVE (INGINE Inc., Seoul, Korea) consists of the buoy and the power take off (PTO) module, which is located on land. The buoy is discus shaped and is connected to ropes by three points on the bottom, and this rope is connected to the PTO module located on land via a pulley fixed to the sea-floor. The PTO module consists of a counterweight, the gearbox module (which includes the ratchet gears) and the generator. Individual ropes that are connected to the buoy are connected to a counterweight. The counterweight provides tension on the rope consistently, and this tension gives the buoy dynamic stability.
In calm water conditions, the buoy maintains equilibrium due to the weight, buoyancy and tension from the weights. The buoy goes through a complex movement that can be divided into heave, surge, sway, roll, pitch and yaw, as the wave passes over it. Depending on the movement of the buoy, ropes are pulled, and the counterweights either rise or lower. Each rope is wound on the rope drum, and the rope drum is connected to the generator. The ratchet gear, which is mounted on the rope drum, only sends the power to the generator when the buoy pulls the ropes, and as such, the counterweight is rising. Since the motion of the three ropes is not in the same phase, the time point for the sending of the power by the individual rope drum is different, which results in a mechanical smoothing effect. The generator uses a 20-kW permanent magnet synchronous generator (Yaskawa, Tokyo, Japan) and is linked to the grid through an AC/DC converter (LSIS, Gyeonggi-do, Korea) and a DC/AC inverter (LSIS, Gyeonggi-do, Korea). As shown in
Figure 2, currently, three modules are installed on Jeju Island’s northern coastal region for a test run. It was installed in September of 2015 and seeks to start operating commercially in the latter half of 2016.
3. Modeling of the Device’s Dynamics
3.1. Buoy-Counterweight Modeling
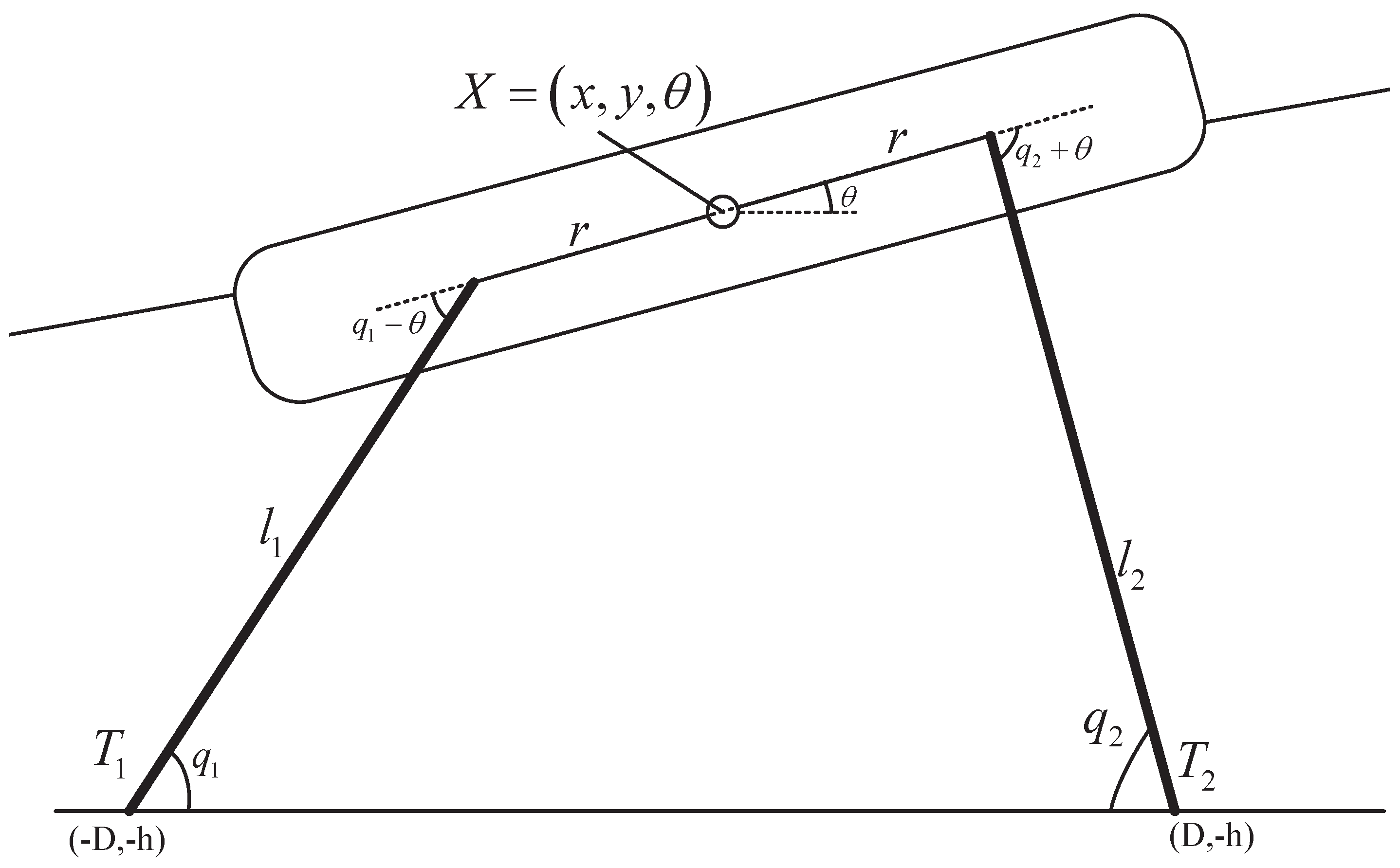
A buoy and PTO module are mechanically connected by the rope tensions that are applied by vector decomposition in each moving direction from the relationship between the buoy’s posture and pulleys on the sea-bed. In this chapter, to derive this relationship easily, we assume a two-dimensional analysis of the device with two-mooring points. This analysis has the advantage that intuitive consideration can be made by matching the dimension of the traveling direction of the waves and the movement dimension of the mooring ropes. The two-dimensional analysis will be a comparative case that can prove the validity of the complex three-dimensional analysis results. For this reason, we assume a discus-shaped model with mooring points connected by two points that are away from the center of the buoy by
r; as seen in
Figure 3, even the actual device is a discus-shaped buoy with the mooring point connected by three different points. The buoy has a radius
R and is submerged a distance of
d since it is connected by the counterweight. For the sake of convenience, let us name the left and right mooring ropes as 1, 2, respectively, and the related variables will follow suit.
The origin of the coordinate is on the water surface; the water depth is
h; and fixed pulleys are away from the origin by
D. In two dimensions, the buoy only moves in the directions of surge, heave and pitch, corresponding to the movements in the directions of
x,
y and
, respectively. The buoy’s posture is
; the lengths of the mooring ropes are
and
, and the angles of them are
and
, respectively. Then, the angles and lengths of the mooring ropes with the posture of the buoy have a geometric relation as follows:
The mooring ropes supply the buoy with tension
and
that are expressed as follows:
and are the mass of the counterweights connected to Ropes 1 and 2, respectively, since this counterweight only moves vertically (acceleration of gravity g). and are the load forces related to the generator.
Then, the dynamic equation of the buoy is expressed as follows [
10]:
Here,
is the mass and inertia matrix of buoy and the added mass effect, and
H is the geometric matrix related to how the rope’s tensions
and
that affect the movement of the buoy. These are expressed as follows:
and are the buoy’s mass and the buoy’s inertia in the direction of pitch movement, respectively. , and are the added masses for the buoy’s surge, heave and pitch motion, respectively. Diag[] is the diagonal matrix.
is the excitation force vector as follows:
where:
is the wave elevation and
and
are the summation of the Froude–Krylov force and diffraction force vector (or named the excitation force) in the frequency domain and its kernel function in the time domain, respectively. We set the negative sign in front of
in (
6) because the wave progresses to the left, as seen in
Figure 1.
is the radiation force vector and is expressed as follows:
where:
is the radiation damping kernel function in the time domain. is the radiation damping in the frequency domain.
is the spring coefficient dependent on buoyancy. Since there is no buoyancy in the surge direction, it is zero.
and
are buoyancy in the
y and
direction, respectively, and are defined as follows:
where:
Here,
is the density of the seawater.
is the spring constant when the buoy rotates by
of the small displacement in the pitching direction and is obtained as follows:
When substituting (
1) and (
2) into (
3), we can obtain the combined dynamics of counterweights and the buoy, expressed as follows:
where:
3.2. Power Take Off Module Modeling
A buoy undergoes complex motions in the heave, surge and pitch directions in the two dimensions. While heave and pitch receive restoring force due to buoyancy, the restoring force in the surge direction is solely dependent on the tension of the ropes. The further away it gets from the origin and in the surge (x) direction, the difference between angles and grows, leading it to return back to the origin.
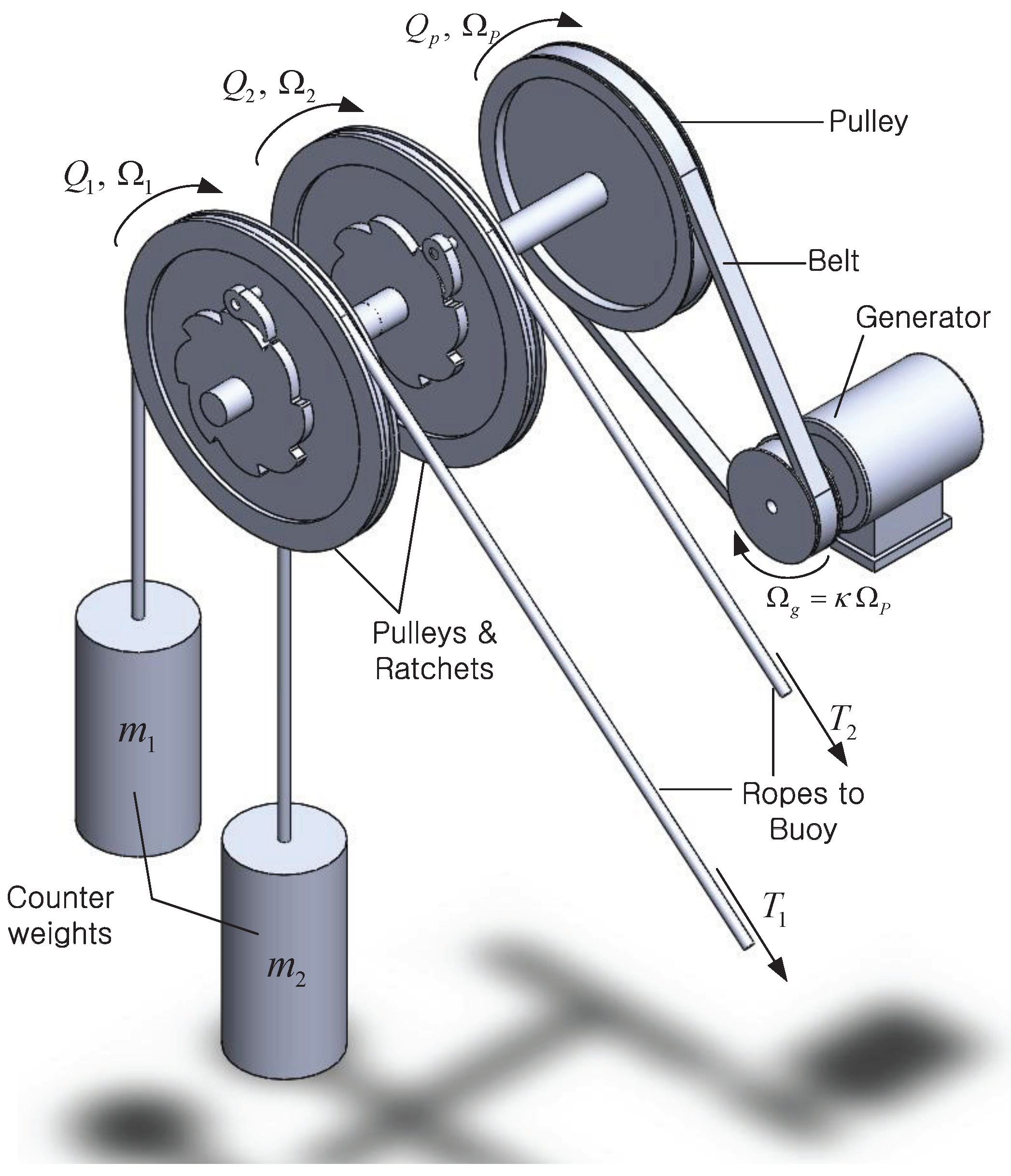
Rope drums (or rope pulleys) connected to the ropes repeat the winding and unwinding with the rope’s back and forth movements. In order to deliver the torques from pulleys to the one-way electrical generator, bi-directional winding motions should be converted into a uni-directional rotation using a ratchet gear as seen in
Figure 4. The use of the ratchet mechanism divides the power transmission processes as follows: when the buoy pulls on the rope, the rope pulls on the counterweight, making it rise. Simultaneously, it provides the driving torque to the generator. Conversely, when the counterweight falls, the driving torque is not transmitted to the generator, and it only provides the restoring force to the buoy through the rope tension.
The reverse setting that driving torque is connected when the counterweight is falling is also possible. However, this mechanism is risky because unless the counterweight is sufficient, the load of the generator will result in the rope losing tension. Then, the rope can deviate from the pulley or drum, which can result in breaking of the rope. For this reason, the reverse setting requires careful consideration of the relationship between the generator load and the mass of the counterweight. In this paper, we deal only with the former ratchet mechanism, in which the driving torque is transmitted when the counterweight rises.
Figure 4 shows the overall configuration of the PTO module. The angular velocities of the pulleys that Ropes 1 and 2 are pulled over are
and
, respectively, where
and
are the radii of the pulleys. The angular velocities of the generator and the pulley connected to it are
and
, respectively, which have the relation of
where
κ is the radius ratio between the pulley and generator. For numerical simplicity, it is assumed that the inertia of the pulleys and shafts can be ignored. Then, the dynamics of the generator can be expressed as follows:
where
is the inertia of the generator rotor.
,
and
are the induced torques from Pulleys 1, 2 and the generator, respectively.
and
have the following relation with
and
in (
2) expressed as:
We assume that induced torque from the generator
is proportional to the angular velocity
and is given as follows:
where
is the generator damping coefficient. Then, the instantaneous power output from the generator is:
Furthermore, the time-averaged output power is denoted by
. Since the LWT is premised [
11], the output power is proportional to the square of the wave amplitude. Hence, the output power per unit amplitude can be defined as
, and accordingly, time averaged power per unit amplitude is denoted as
[
12].
The instantaneous power that the rope delivers to the pulley is:
Additionally, in order to define how efficiently the power is transmitted from pulleys to the generator, we denote the ratchet efficiency as follows:
3.3. Schematization of Ratchet Gears
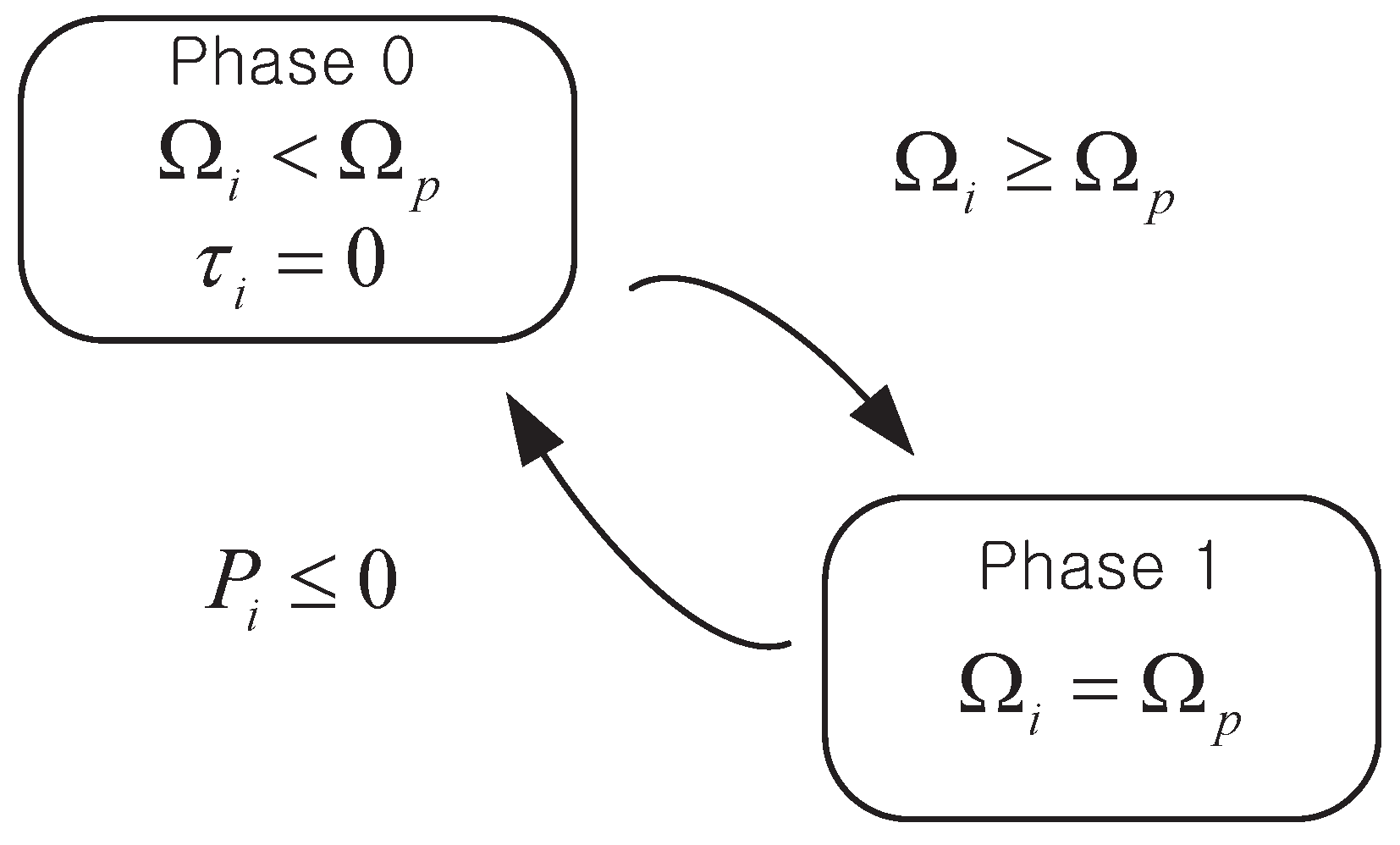
A ratchet gear modeling that rope pulley only transmits the torque with forward rotation to the generator while repeating the forward and reverse rotations is required and can be simply analyzed as follows:
The moment
(for
) is greater than
; both are equivalent, and the torque
is transmitted from the rope pulley to the generator. Thereafter, at the moment that the transmitted power
becomes negative,
and
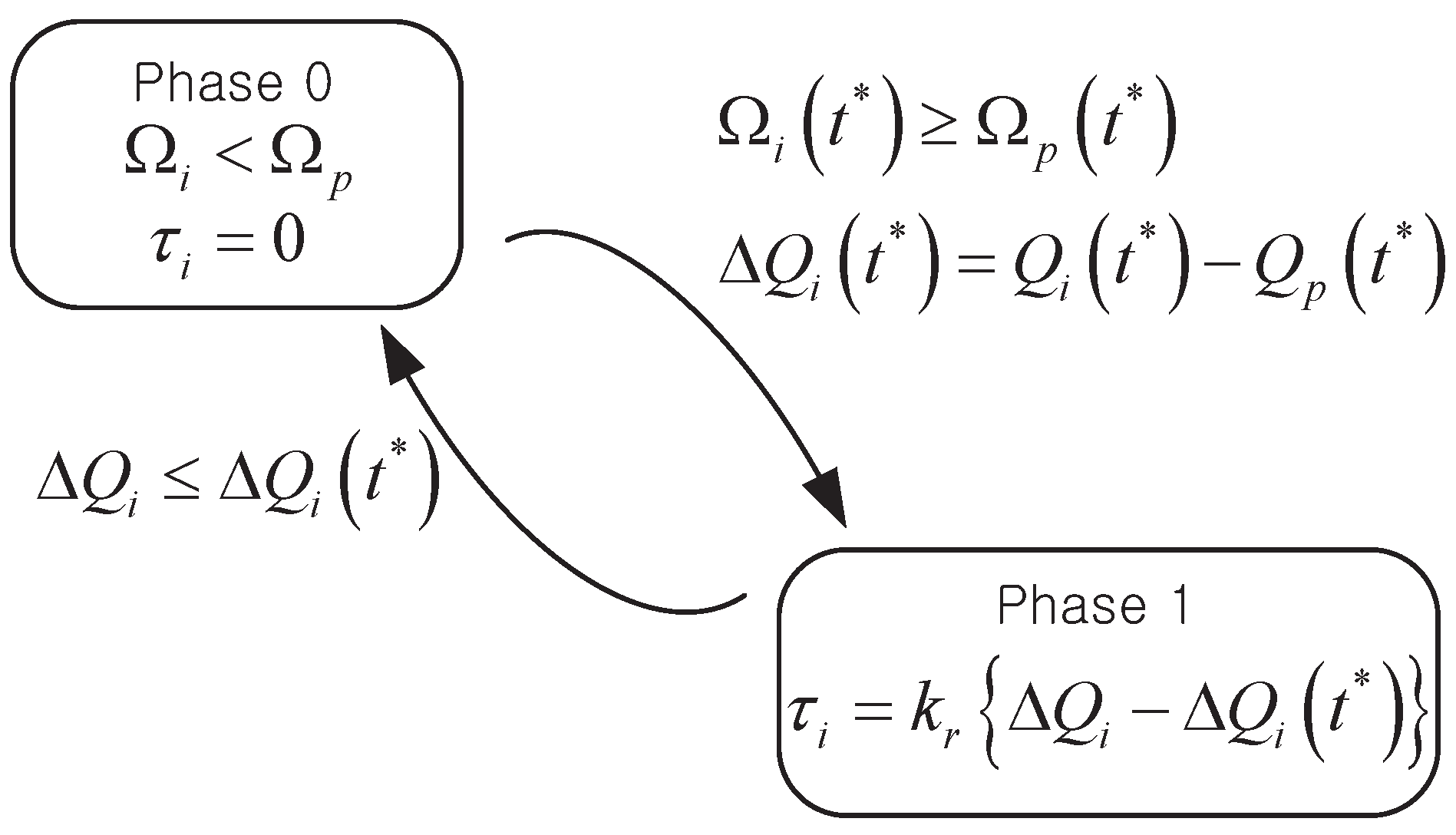
are separated, and the torque is not delivered anymore. With the definitions of Phases 0 and 1 denoting the states for whether torque is transmitted or not, the ideal ratchet modeling can be schematized as shown in
Figure 5.
However, it is not easy to implement this modeling in the simulation, even when assumed with extremely short sampling time in the time domain analysis. At the moment of state transition, it must be concurred that and change from some positive to zero, which are the modeling errors.
To overcome this difficulty, we present a ratchet modeling with the addition of the spring element, as shown in
Figure 6. Let us define the angle difference between the pulleys
i and
p as
and also define
when
is the moment that the phase changes from 0 to 1 (
outpaces
). Then, from this moment
, we assume that the pulleys
i and
p are connected by virtual torsion spring, and the torque between them is defined as:
where
is the virtual torsion spring coefficient.
As long as is greater than , is transmitted; otherwise, the phase changes from 0 to 1, and becomes zero. This modeling distinguishes the phases via the relation between and its certain value at the specific moment , but does not force the identification between and , unlike the modeling without the spring element. At the phase transition moment, must be greater than , but the gap between them is getting smaller due to the spring effect. Hence, there is no discontinuity in the resulting in no impulse torque that provides the stability in the simulation. It is emphasized that the power (or torque) transmission propensity is dependent on the spring coefficient .
Let us analyze the effect of
through the comparison of simple simulations by assigning arbitrary parameters and rope tensions in the PTO module. In
Figure 4, the masses of counterweights
and
are assumed to be 200 kg;
and
are 1 m;
κ = 1; and
is 0.1 kg·m
. Then, tensions on the ropes from the buoy are applied as:
By combining (
12) and (
17) and substituting the assumed parameters and tensions, we can obtain the simulation results as seen in
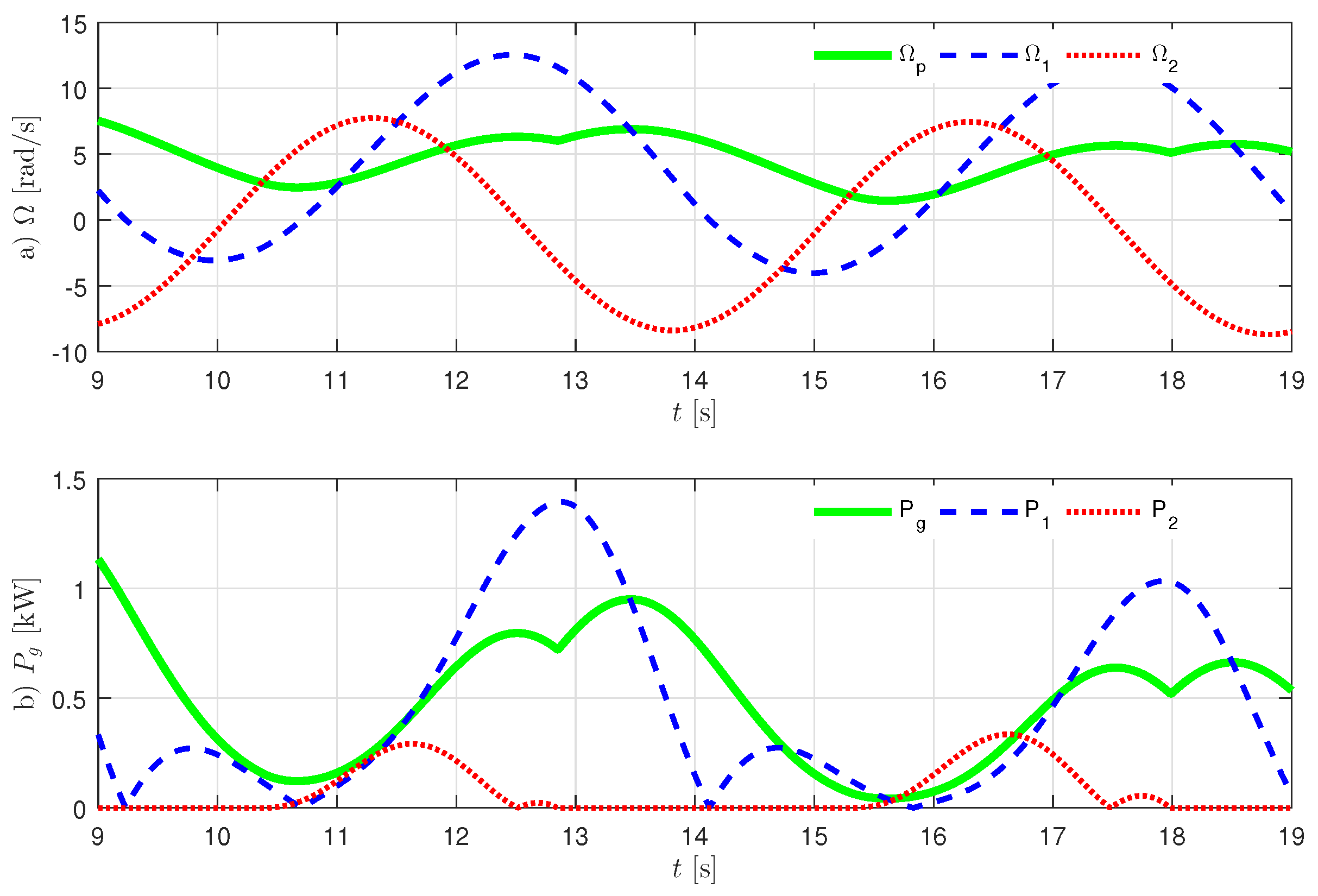
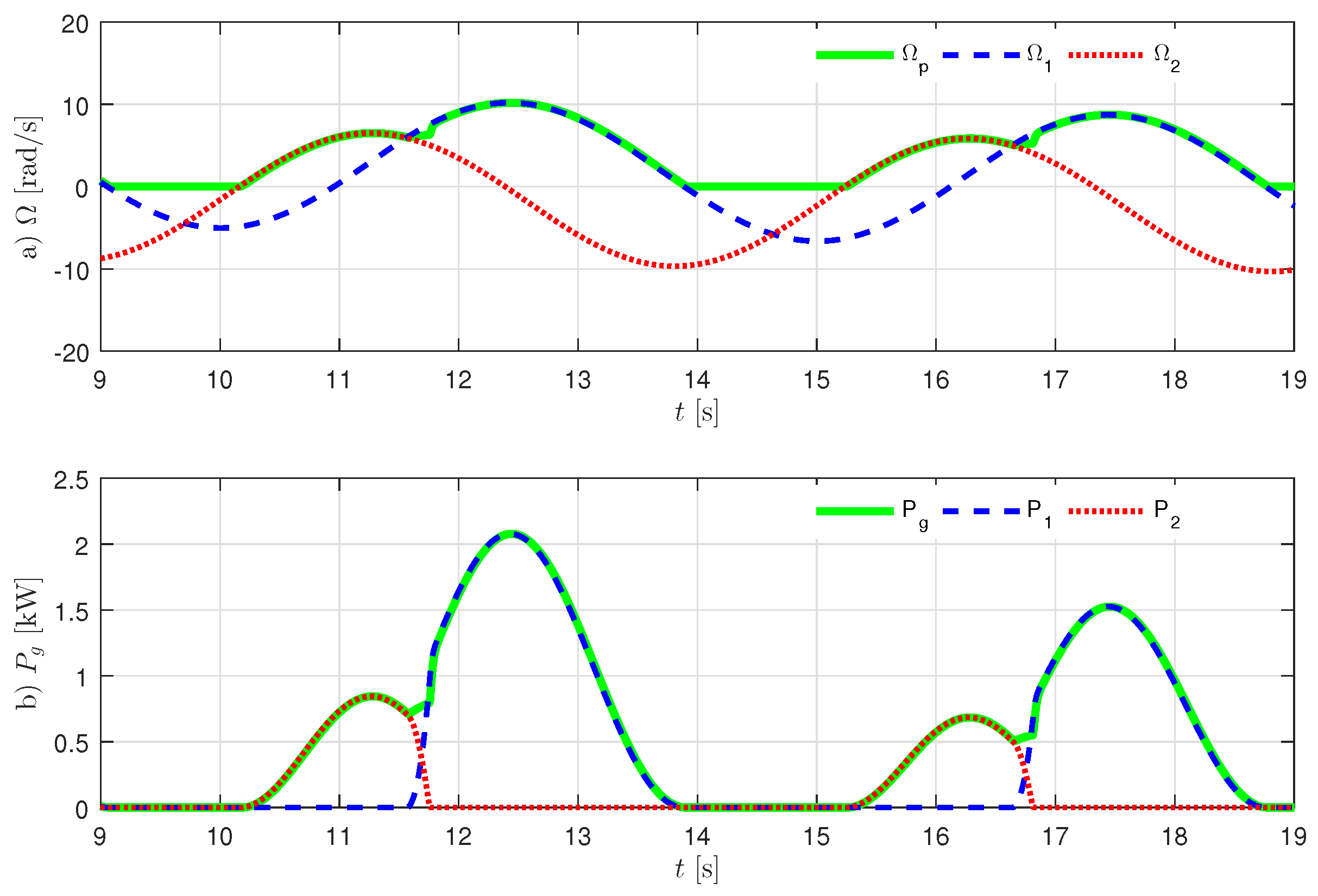
Figure 7 and
Figure 8 that
are set to 10 and
, respectively. When
= 10, it can bee seen that
does not track
, and power from the generator
also does not track the trajectory of larger value of
and
. Otherwise, when
, it results that
can track the trajectory of larger value of
and
, and the graph for power provides the equivalent result. The average ratchet efficiency
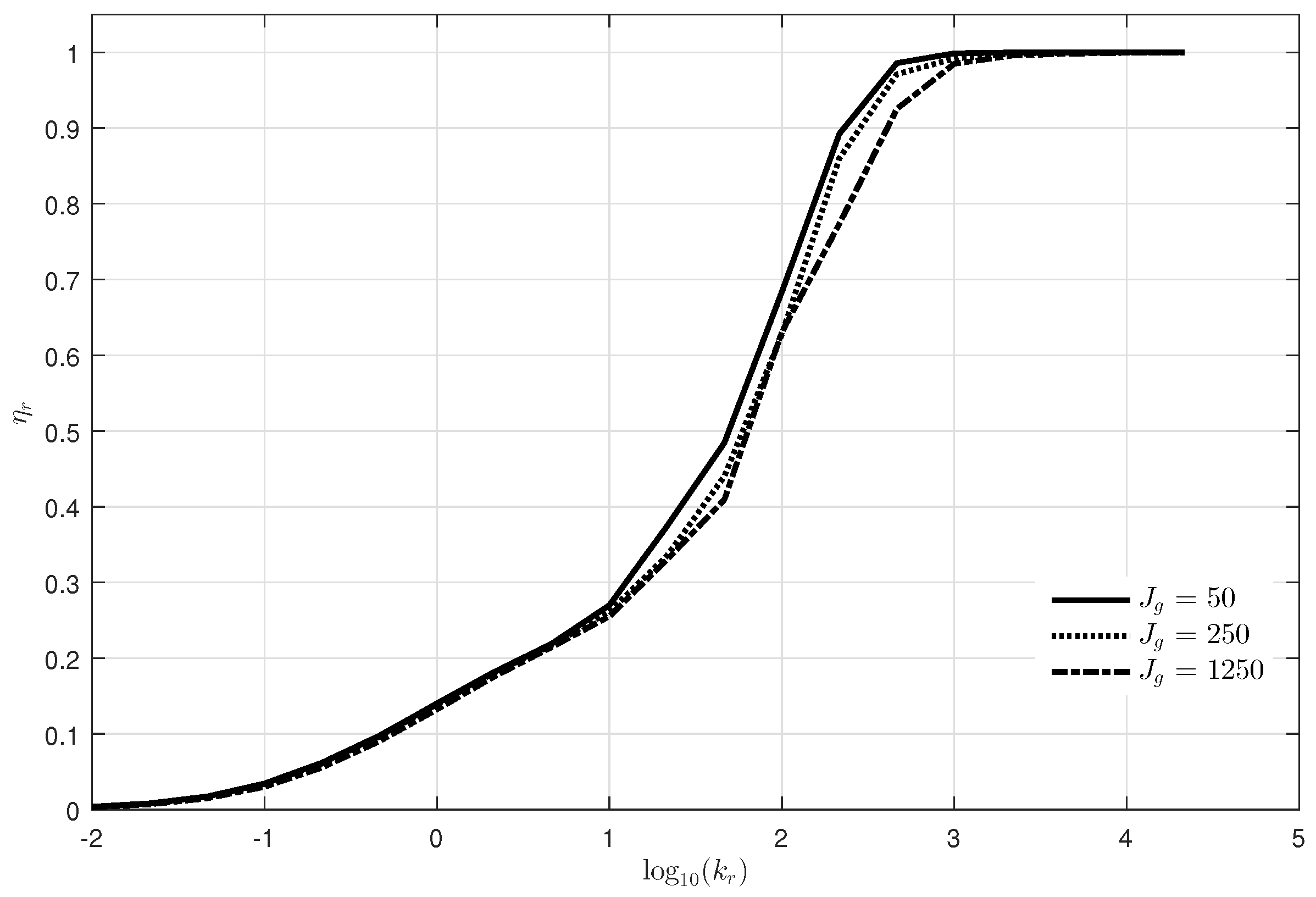
defined in (
16) according to
is presented in
Figure 9, which
increases as
increases and approaches almost one with
beyond
. Furthermore, larger inertia results in slightly lower efficiency, since heavy inertia provides the slow response speed like the small
effect, as seen in
Figure 7. The actual inertia, including generator rotor, shaft and gear ratio, is about
kg·m
. Hence,
in the following simulation will be set to
in order to ignore the power loss in the ratchet gears.
3.4. JONSWAP Wave Spectrum Model and Capture Width Ratio
For irregular wave input, typical wave spectra include JONSWAP, Pierson–Moskowitz, Bretschneider and the Gaussian distribution [
13]. We chose the JONSWAP wave model since the area where the
INWAVE device has been installed has
of the JONSWAP spectrum [
14]. When the significant wave height is
and the peak period is
, it is expressed in the frequency domain with wave angular frequency
as:
where:
Then, the wave power per unit crest length is defined as:
where
is the group velocity given by:
and
is the phase velocity:
Here, the wave number
(
: the wave length) is obtained from:
We also define the normalized wave power per unit crest length and unit wave amplitude as:
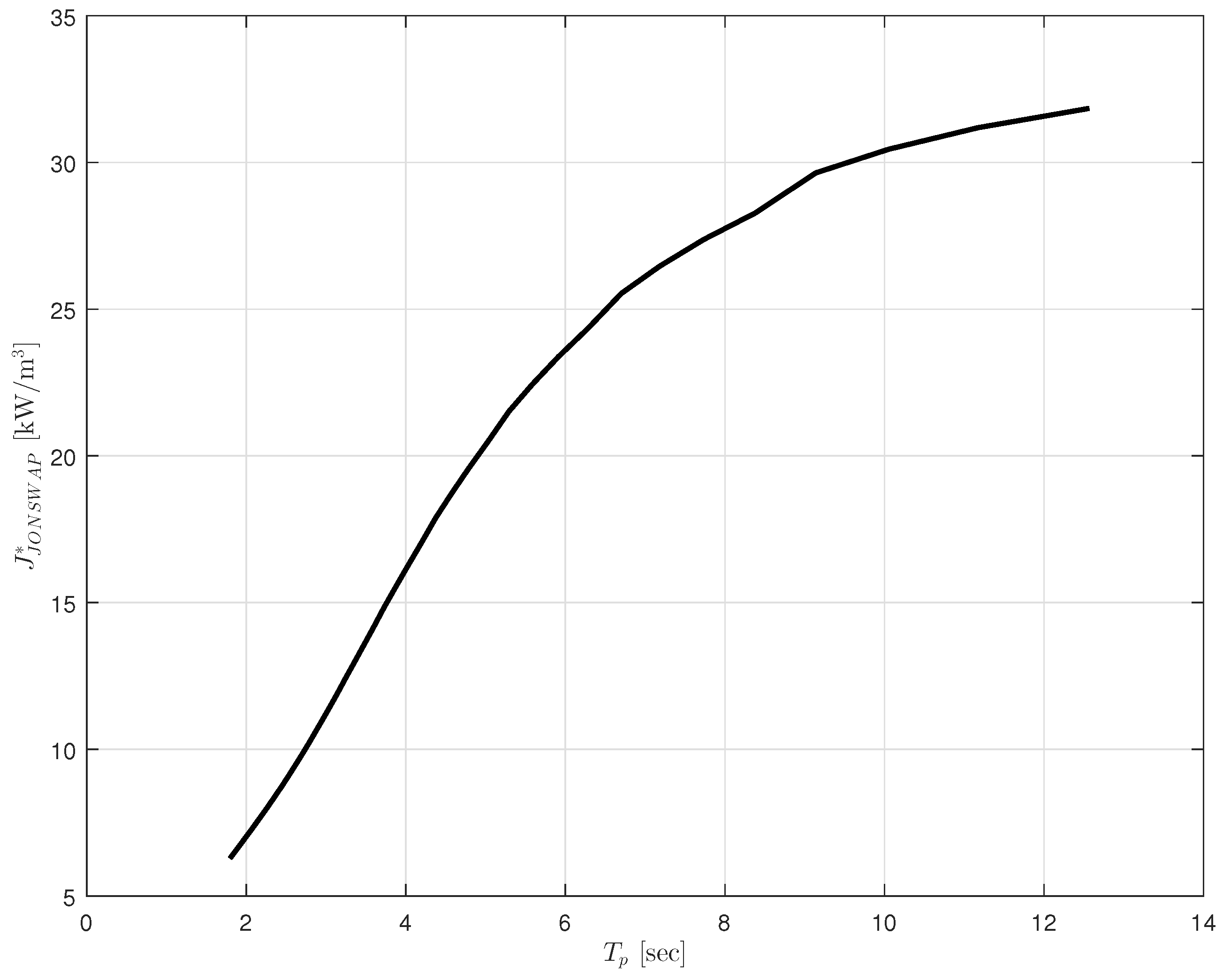
This is only a function of the wave period and can be seen in
Figure 10 with
, which is the water depth of the installation area.
In order to quantify the power performance with the consideration of the device’s dimension, the capture width ratio (CWR)
is widely used and is defined as follows [
15]:
where
is the characteristic dimension and
is the maximum horizontal cross-sectional area of the device. In this paper, for a cylindrical buoy,
is simply equal to
. Hence,
where
R is the radius of the buoy.
4. Simulation in the Time Domain
In this section, simulation of the buoy and PTO combined dynamics is carried out in the time domain under the irregular wave condition with the JONSWAP wave model [
16]. For time domain analysis, the Runge–Kutta method was applied for solving the dynamics [
17].
We obtained the hydrodynamic parameters of the buoy from AQWA (version 14, ANSYS, Pittsburgh, PE, USA) [
18]. In order to calculate kernel function of excitation force
and radiation damping
, the frequency domain responses for excitation forces
, radiation
and added mass
need to be calculated. In the AQWA simulation, the buoy has a
m for diameter, with 0.5 m of draft, which reflects the actual size of the prototype buoy. It is floating in the ocean cube that has a 500 by 500
surface and
m of water depth, which is the actual depth of the installation area, and only surge, heave and pitch motions of the body are allowed. The frequency domain response should have a truncation frequency of 5 rad/s with a frequency spacing of 0.05 rad/s [
19].
The lines in
Figure 11 display the kernel functions of excitation force
and radiation damping force
from the calculations of (
7) and (
9), respectively.
A JONSWAP wave model is adapted in order to generate irregular waves in the simulation. For time series calculations, the spectral distribution (
18) is discretized as the sum of a large number
M of regular waves, written as:
Here, , where is the lowest frequency, is a small frequency interval, and the spectrum does not contain a significant amount of energy outside the frequency range . and are the amplitude of the wave component of order m and the initial phase randomly chosen in the interval , respectively.
With the excitation force vector formed by substituting (
22) into (
6), the combined dynamics with (
11)–(
13) and (
17) was performed according to the Runge–Kutta method with 0.001 s sampling time [
17]. A summary of the parameters and values used in the simulations is given in
Table 1.
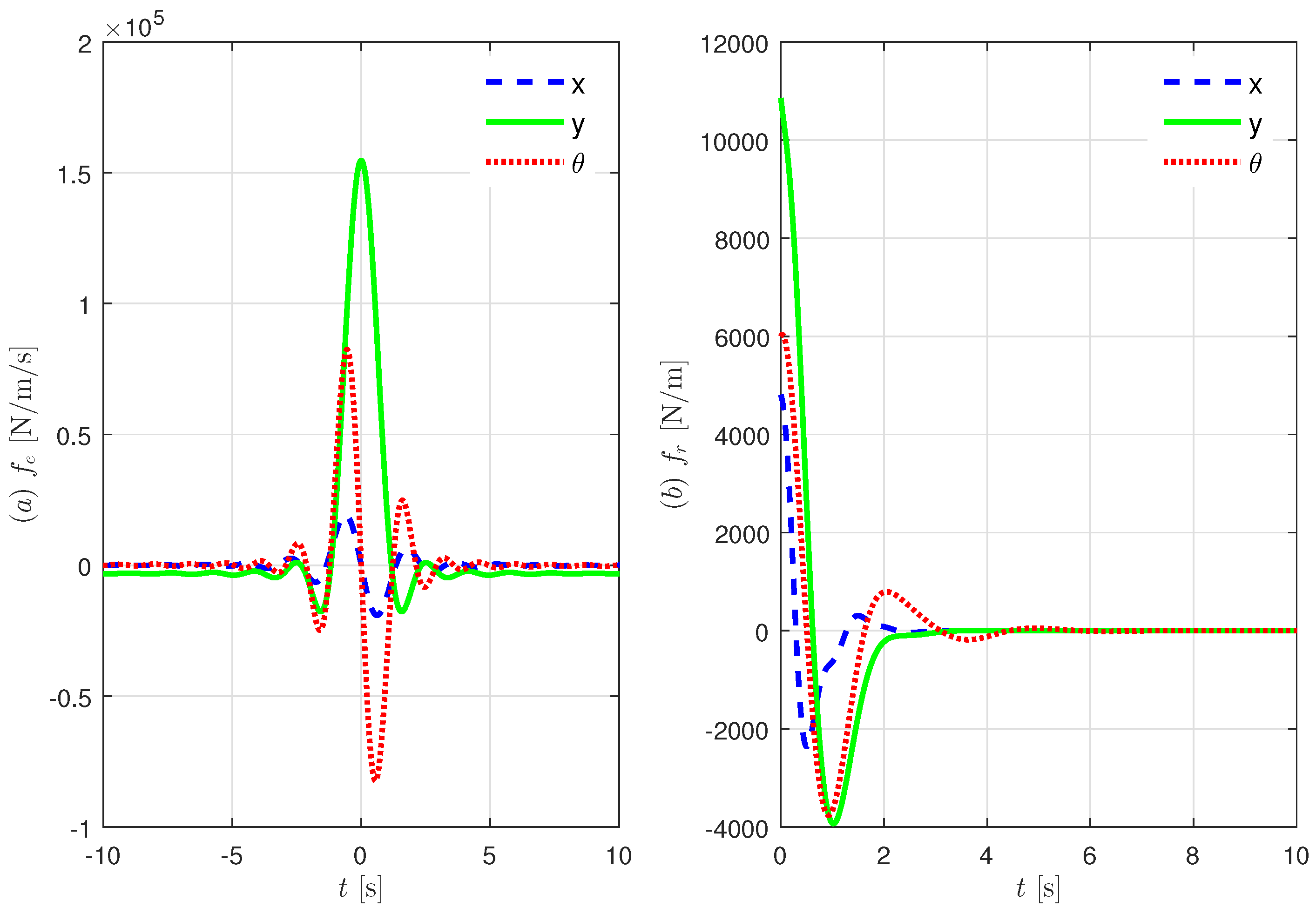
Figure 12 displays the result of wave elevation, the buoy’s posture, the angular speed of pulleys, the tension of ropes and the power output from the generator in the time domain when
= 4.5 s,
= 1 m and
= 5 Nm s/rad.
In
Figure 12, irregular waves yield complex motions of surge, heave and pitch. Furthermore, angular velocities of pulleys connected to the ropes and the generator also have very complex trajectories. The pulley speed
somewhat tracks the positive max value of
and
with small error. Finally, as
increases, the power from generator
also increases. Tensions
and
are only 0.25 tons of counterweight when power is not transmitted, and
is generated as tension increases. During the 30-min duration of the simulation, the average power output is 10.56 kW.
The power output varies sensitively in accordance with
.
Figure 13 displays the graphs of
with varying
under irregular waves with
= 4.5 s. Let us define
and
as
and
, respectively, at the peak of the power output. In
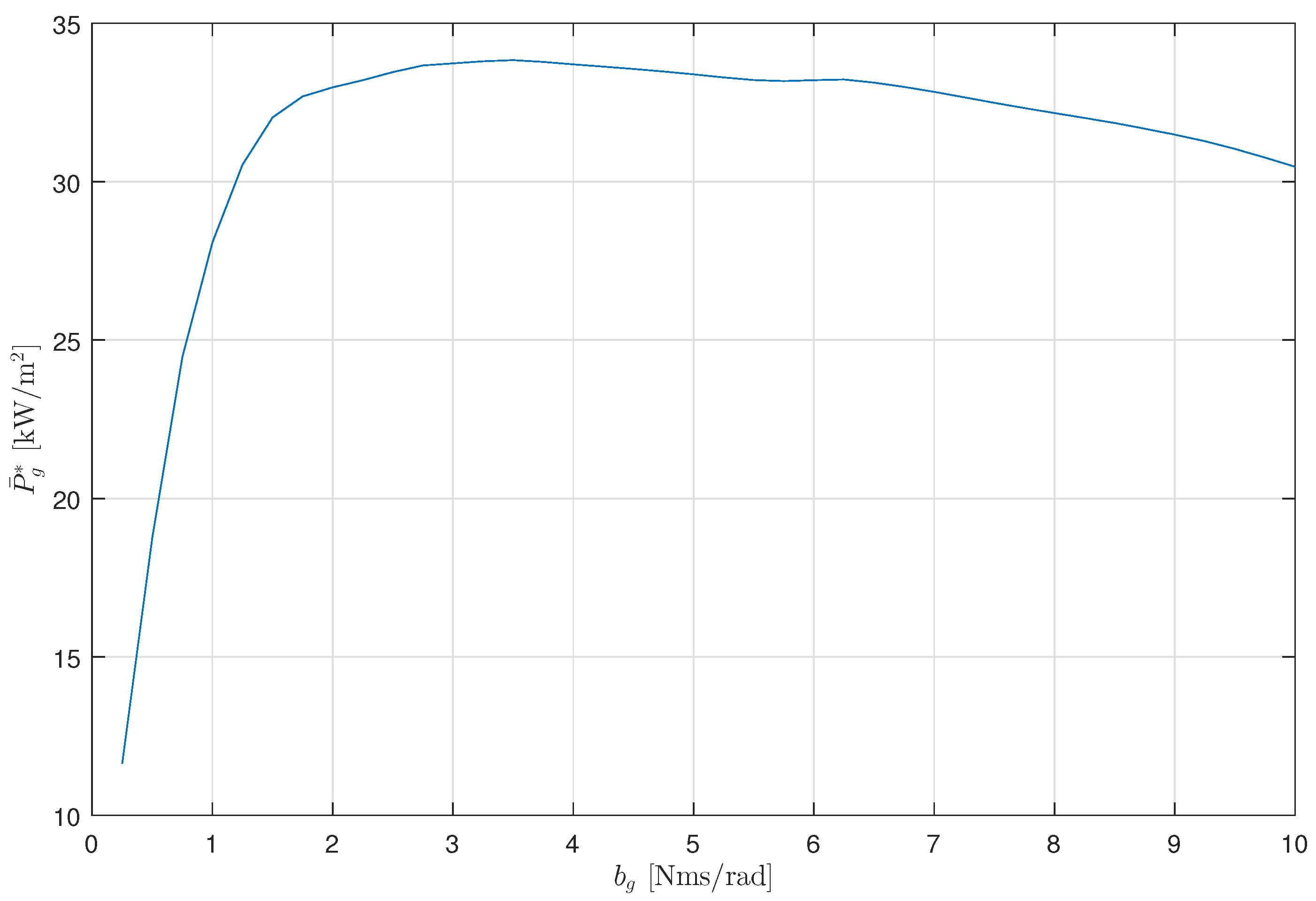
Figure 13, it can be seen that
rapidly increases when
,
= 33.8 kW at
= 3.8 and gradually decreases when
.
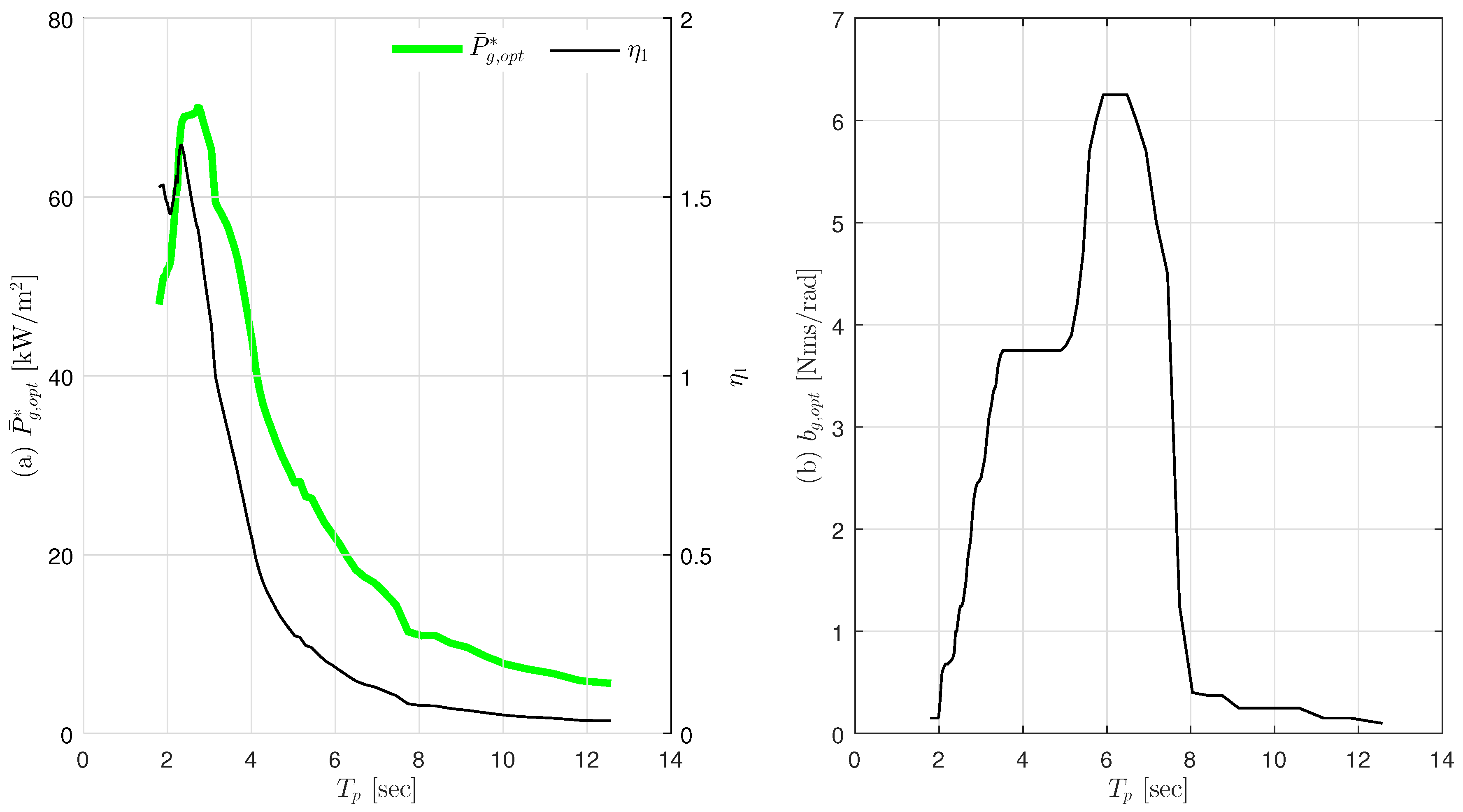
According to the LWT, the normalized power output is mainly a function of
and
. We calculate
for varying
, and
Figure 14 shows the results of the
and
for varying
between 2.5 and 12 s. It can be seen that
has 70
of maximum output at
= 2.7 s, and the maximum value of CWR
reaches almost 1.645 at
= 2.31 s. The optimal damping coefficient
increases with
and
s and the levels between them, but drastically decreases when
> 6.5 s. Since our targeted installation area has the
between 2.5 and 4.3 s, the simulation that displays the maximum power between 2 and 4 s of
, we can see that the design of the
INWAVE somewhat meets the design direction.
5. Characteristics of the INWAVE Device
Commonly, a point absorber is installed in an area deeper than 20 m of water. CETO [
20] and the Lysekil project [
21] pick the center of the buoy as the single point mooring and connect it to PTO because these locations have high enough energy density to concentrate mainly on the heave motions. As water depths become shallower, the wave moves more in the direction of the surge than heave. As such, the
INWAVE device focuses on the surge and pitch motion and is installed nearer to the coast. Waves in shallow water are affected by sea-bed topography, resulting in irregular motions. To overcome this, the
INWAVE device is connected via three ropes that are on the bottom of the buoy. It is designed to respond to all motions within six degrees of freedom. The three ropes that are connected to the buoy are also connected to the counterweight on land via underwater pulleys. The ropes also spin the rope drum. Each rope drum transmits the torque to the electrical generator through the ratchet mechanism. While all three ropes move back and forth irregularly according to the movement of the buoy, they do not move in phase with each other. Accordingly, the time point in which each rope drum sends power to the generator is different. This reduces the effect of the inhomogeneity of electricity, which is one of disadvantages of wave power energy.
Ropes are preferentially considered when designing the device. Due to the tension that is always in action between the buoy and the counterweight, ropes must have toughness to endure stress, the ability to endure salinity and sunlight, as well as the friction created as it winds up on the underwater pulley and the rope drums. While this paper’s analysis was done with the assumption that power is supplied to the generator only when the buoy pulls on the rope and the counterweight rises, in reality, torque can be supplied to the generator when the counterweight is descending, as well. For this to occur, the ratchet mechanism needs to be designed in such a way that it allows for the generator to spin in one direction, regardless of the direction of the counterweight’s movement. Currently, both ratchet mechanisms are undergoing field tests. In terms of smoothing of the created electricity, the best method would be to send all of the power created by two-way directional spin. However, to do so, we must carefully consider the relationship between the mass of the counterweight and the maximum wave height. The greatest function of the counterweight is providing the buoy with restorability. While heave and pitch motion gets restorability from buoyancy, surge motion gets its restorability from the tensions supplied from the rope by the counterweight. If the counterweight sends force to the generator on its way down, the tension supplied to the buoy will inevitably be smaller. If the tension supplied becomes zero, the rope will become loose. The moment the counterweight rises, it will put sudden shock on the rope, causing the rope to potentially break, or breakaway from the rope drum. This would not be a problem if the mass of the counterweight is sufficient. However, this would require the rope to be tougher, so that it can endure higher tension. Thus, we did not simulate this kind of situation because it would require more complex hardware. However, in future works, we plan to compare and analyze the data given by the prototypes.
6. Conclusions
This paper introduced the INWAVE device developed by INGINE Inc. In order to evaluate its theoretical performance, dynamic analysis based on the Newtonian mechanics was derived in the two dimensions, and the time domain simulation was carried out under the LWT. The parameters used in the simulation were obtained by using the ANSYS AQWA simulator and inverse Fourier transform. In order to overcome the dynamic discontinuity of the ratchet gear mechanism in the time domain simulation, we suggest the modeling of the ratchet gear by introducing the virtual torsion spring element and prove its efficiency under various generator inertia and torsion spring coefficients. In the simulation, the JONSWAP wave model with was adapted to generate irregular waves, to ensure that the model is reflecting the actual installation area. The simulation results provide the theoretical capture width ratio with the optimal operation condition. There are two limitations in the paper; the LWT was applied at a low water depth condition, and the effect of viscous damping was ignored. If the low depth and viscous damping were considered, the CWR would have been lower. In addition, as mentioned in the previous section, the physical limitation of the rope, the non-linearity of the generator (including the inverter process) and friction loss with the threshold of the mechanical components should be addressed.
Despite the inaccuracies of the buoy’s hydrodynamic modeling, this modeling has become a reference for practical design decisions. This is because the modeling uncertainty can be offset by multiplying the safety margin factor. For example, we have found the design criteria for rope tension that determine the thickness of the rope, the diameter of the rope drum and the diameter of the shaft in the PTO module. In addition, a relationship between the generator’s torque limit and the inertia of the gear module on the power output has been researched, which is reflected in the design of the next prototype. We will present the three-dimensional modeling analysis and discuss the optimization of mechanical elements including the hardware limitations in the future.