Analysis of MPPT Failure and Development of an Augmented Nonlinear Controller for MPPT of Photovoltaic Systems under Partial Shading Conditions
Abstract
:1. Introduction
- (1)
- The output characteristics of the PV arrays are analyzed using the PV array model under PSC, and the V–P curve is found to demonstrate a multi-peak trend. The reasons for the failure of the conventional MPPT algorithm are analyzed under the premise of rapid and continuous irradiance changes.
- (2)
- For the MPPT failures caused by the timings of the irradiance changes, this paper proposes a hybrid MPPT method that uses an artificial neural network (ANN) to estimate the MPP and an augmented state feedback precise linearization (AFL) controller for the DC/DC converter to meet the fast and frequent changes in irradiance.
- (3)
- Considering the influence of the multi-peak output of the PV array on the small signal of the DC/DC converter under PSC, this paper designs a nonlinear control method with precise state feedback linearization.
2. Grid-Connected PV Generation System
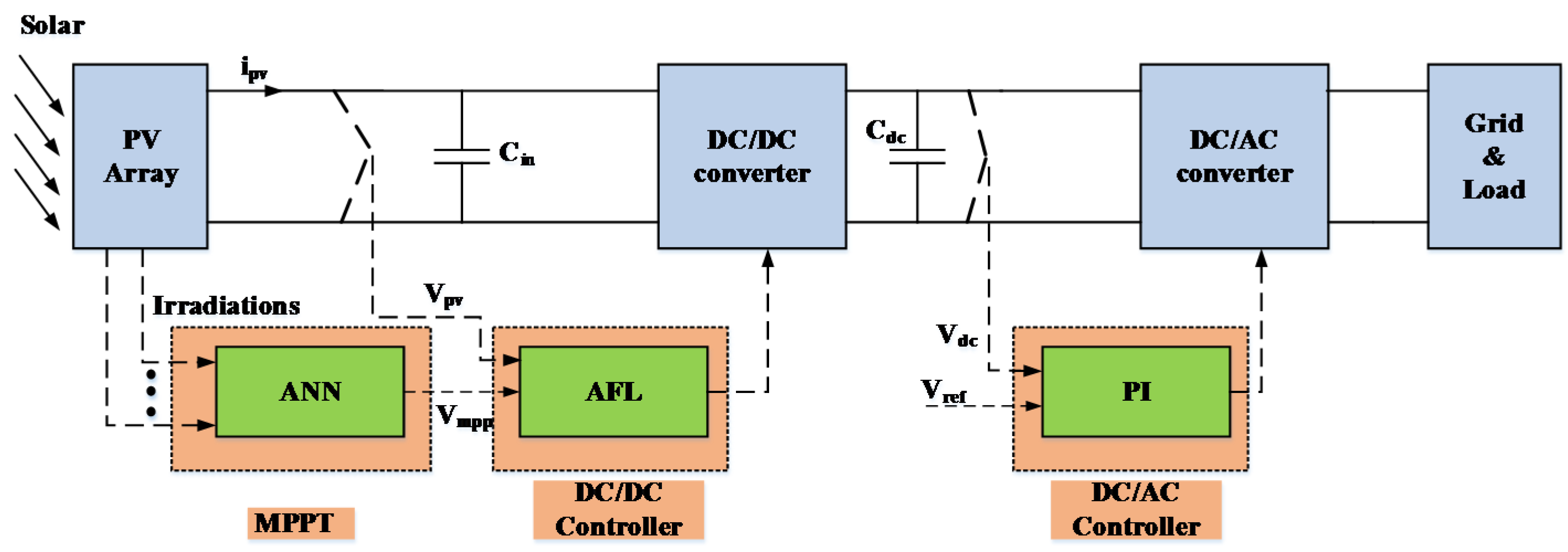
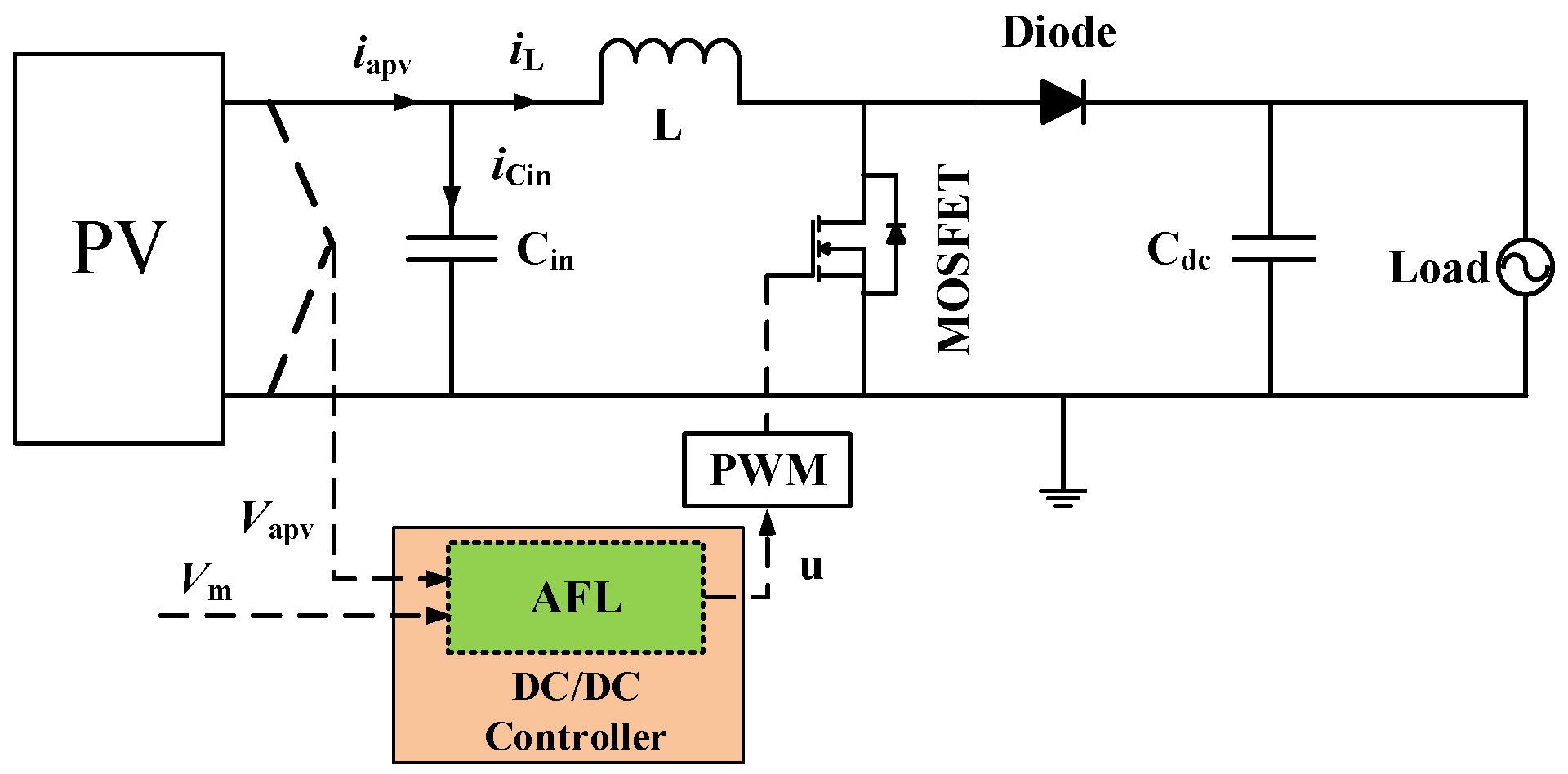
2.1. Structure of the Proposed System
2.2. PV Array Model under PSC
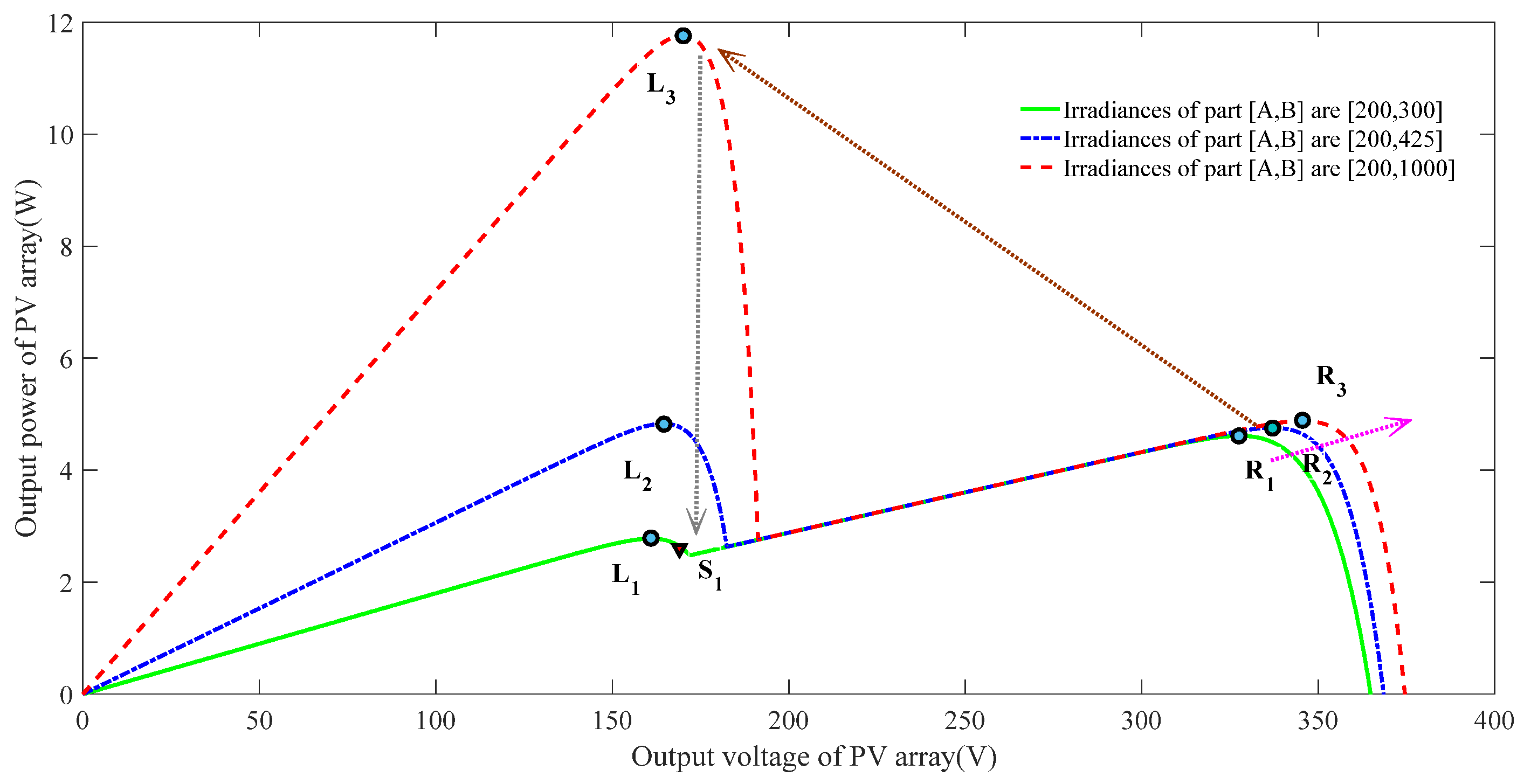
2.3. Failure Analysis of GMPPT under PSC
- (1)
- Assuming that the illumination characteristic of the PV array at the moment t is given by the L3–R3 curve, and that the lighting condition changes at moment t + 1, the output characteristic curve of the PV array becomes L1–R1, and the actual PV output becomes S1. As the PV curve exhibits a multi-peak shape, the traditional MPP R1 cannot be obtained by searching the LMPP L1 using the gradient information as in the P & O and INC methods. Some experts found that the overall output power of the PV array changed greatly in this process. Global search algorithms such as the particle swarm optimization (PSO) algorithm or the artificial bee colony (ABC) algorithm can be used for global optimization, by using the amplitudes of the output power variations and the t + 1 global optimal solution R1 to solve the local shadow problems of the PV output characteristics with multiple peaks.
- (2)
- The light characteristic curve of the PV array is assumed to be the L1–R1 curve at moment t, and the curve of the PV characteristic becomes L3–R3 at moment t + 1, which indicates that the MPP of the PV system should change from R1 to L3.
3. ANN Method for Maximum Power-Point Tracking (MPPT)
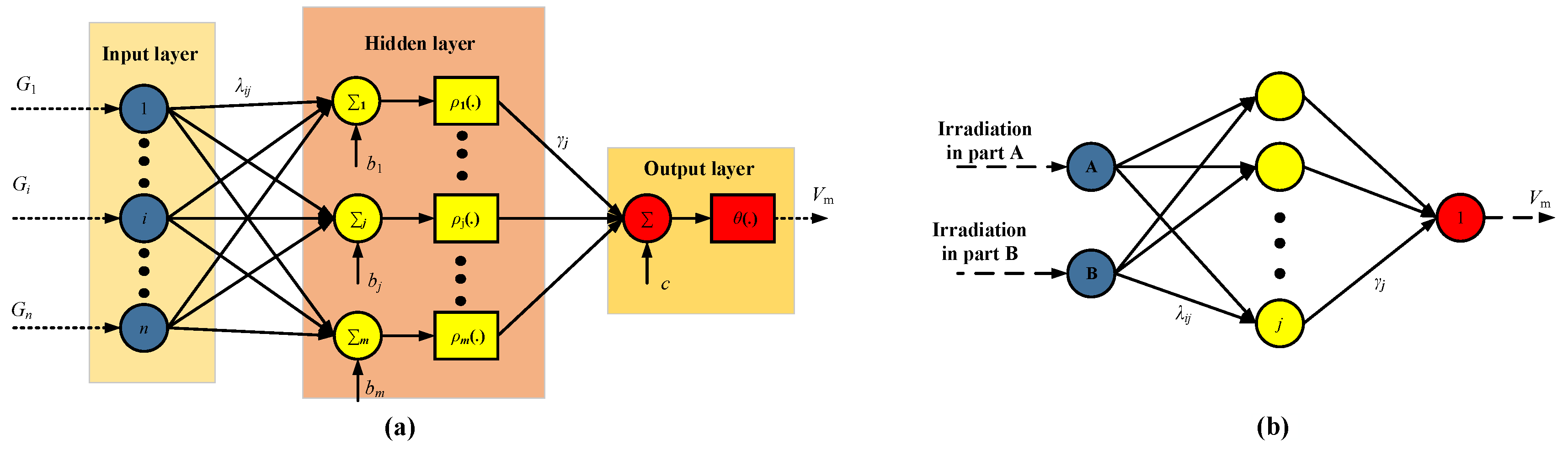
3.1. Neural Network Construction for MPPT
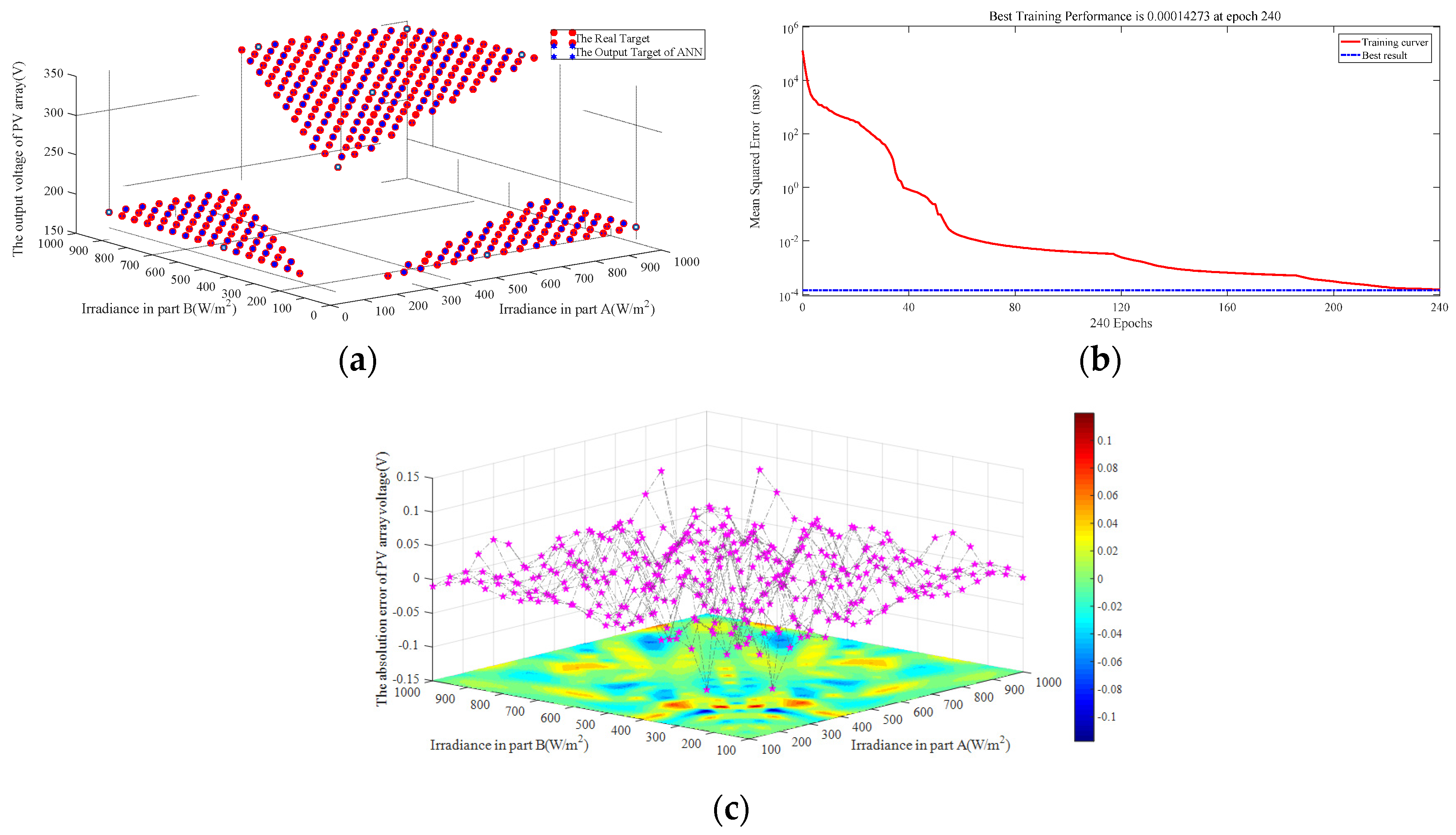
3.2. Neural Network Analysis for MPPT
4. Topology and Control Strategy for Proposed Power Converter
4.1. Nonlinear Model of DC/DC Converter
4.2. Augmented-State Feedback Linearization (AFL) Control for Nonlinear Systems
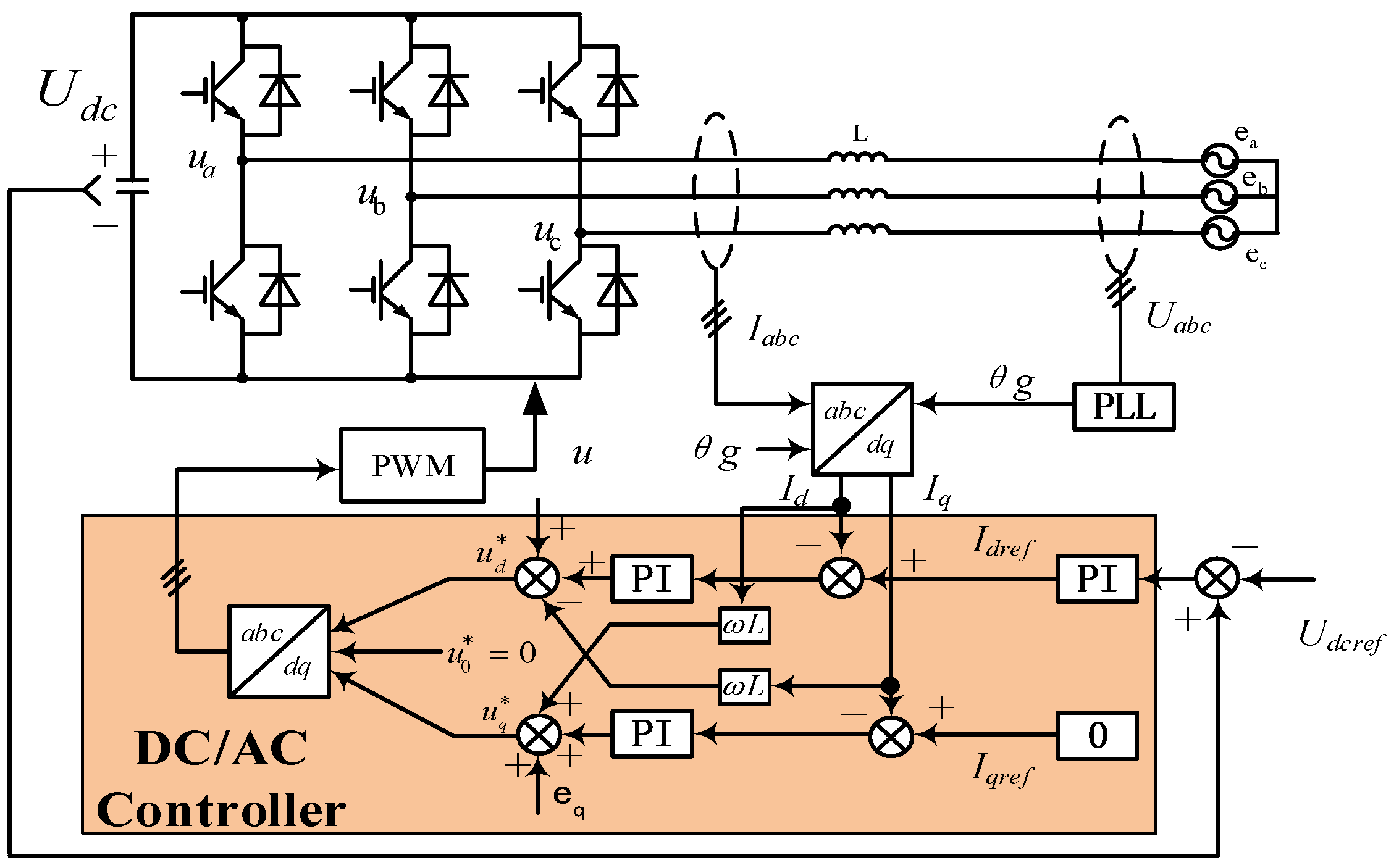
4.3. DC/AC Inverter and Control
5. Digital Simulation Experiments and Analysis
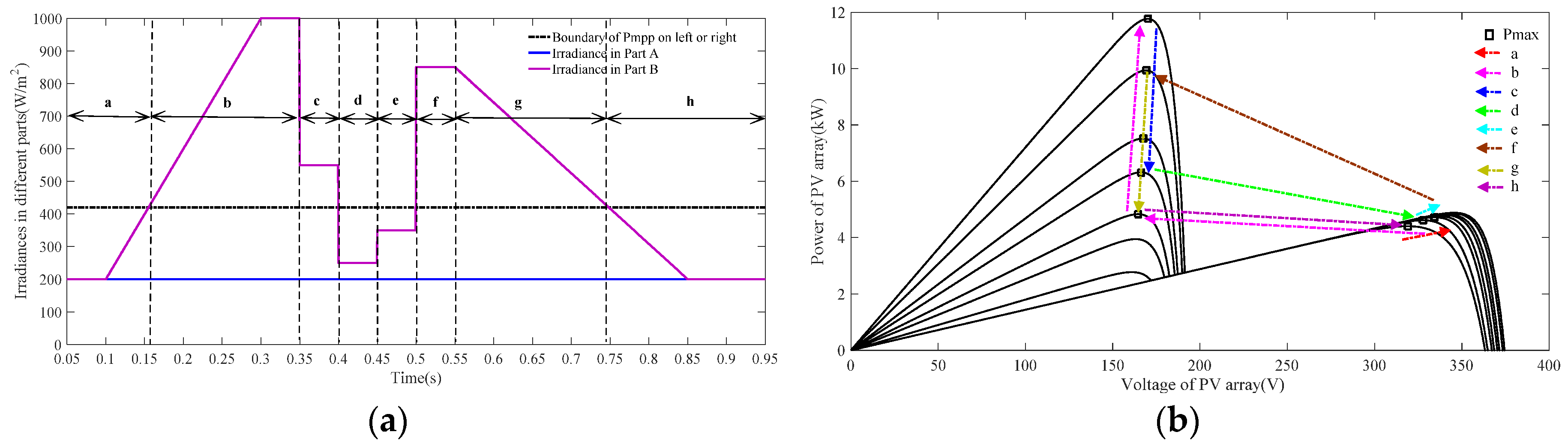
5.1. Simulation Case 1
5.2. Simulation Case 2
- (1)
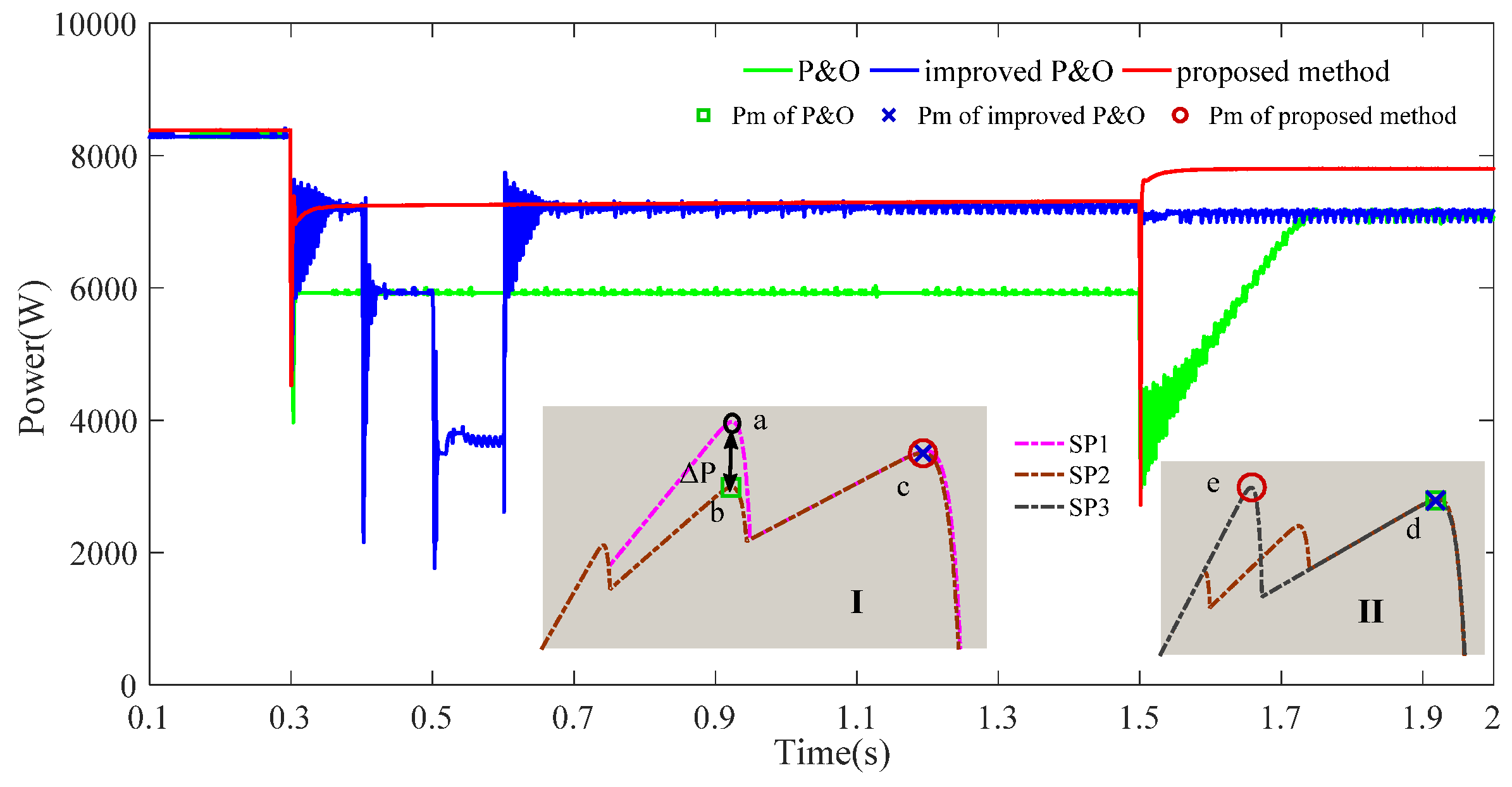
- As shown in Part I of Figure 14, when the shading condition changes to SP2 from SP1, the PV output characteristic changes from the pink curve to the brown curve. The traditional P & O algorithm (the green curve in Figure 14) can track the MPP (point a) in section SP1. However, only the local MPP (point b) in section SP2 can be tracked by the traditional P & O algorithm, which indicates that the traditional P & O algorithm for MPPT fails to track the GMPP in section SP2. Since the instantaneous power change ΔP is large, the improved P & O algorithm (the blue curve in Figure 14) can start the global search module and track the GMPP (point c), similar to the method proposed in this paper (the red curve in Figure 14). It is clear from the dynamic process that the response time of the proposed method is much less than that of the improved P & O algorithm, and that the tracking speed is increased more than 6-fold. By combining this inference with the information in Table 3, it can be inferred that the steady-state maximum power of the proposed method is also superior to that of the improved P & O algorithm.
- (2)
- When the shading condition changes to SP2 from SP3, the PV output characteristic changes from the brown curve to the black curve, as shown in Figure 14II. It can be seen that the MPP (point c) of the SP2 shading condition is near the local MPP (point d) of the SP3 shading condition. It is difficult to start the global search because the power change due to the shading condition change is not large enough. Therefore, the improved P & O and traditional P & O algorithms track the local MPP (point d) in identical manners, which indicates that the GMPP tracking fails in the cases of the improved P & O and traditional P & O algorithms. It can be seen from Table 3 that the power loss caused by MPPT failure is 699 W, which accounts for approximately 10% of the maximum power. The method proposed in this paper can track the MPP (point e) quickly and accurately, and effectively solve the MPPT failure problem caused by local shadow conditions.
6. Conclusions
- (1)
- The PV output characteristics were modeled and analyzed under PSC, and the complex nonlinear multi-peak morphology of the PV array output was verified. It was found that the timings of irradiance changes might cause the failure of traditional MPPT methods or make it difficult to define the starting conditions, especially for MPPT algorithms based on voltage or current information.
- (2)
- Based on the above analysis, an artificial neural training network model was designed based on environmental variables and irradiance information, and GMPPT was realized efficiently and effectively using the hybrid method (ANN + AFL) for the DC/DC converter. A comparison of the proposed MPPT method with the conventional P & O method and the improved P & O method was illustrated through simulations. The GMPPT failure caused by the timing of the irradiance change was solved.
- (3)
- For the problems caused by the partial shading process, such as the MPP voltage of the PV output being shifted greatly, the static operating point of the system being changed, or the difficulty of designing a PI controller to eliminate the steady state under small-signal modeling, this paper proposed an AFL control method for nonlinear systems to accurately track the MPP without static errors. The control parameters were clear and easy to design and apply.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Nonlinearity Control Theory and Parameter Analysis in Third-Order Systems
A.1. Some Definitions in Nonlinearity Control Theory
A.2. Multi-Input Feedback Linearization Theorem
- (i)
- a nonsingular state feedback:where K(x) is a smooth function from V0 into Rn, β(x) is an m × m matrix with smooth entries, nonsingular in V0;
- (ii)
- a local diffeomorphism in V0: ,if, and only if, in U0:
- (i)
- , is involutive and of constant rank.
- (ii)
- , Rank Gn−1 = n.
Appendix B. Description of the Detailed Model
B.1. Simulation Parameters
B.2. Simulation Model in Matlab/Simulink

Abbreviations
| C1, C2 | parameters of the PV panels under standard test conditions (STCs) |
| Vpv | PV substring voltage |
| Ipv | PV substring current |
| Iapv | PV array current |
| Vapv | PV array voltage |
| Papv | PV array power |
| Iscn | short-circuit current |
| Vocn | open-circuit voltage |
| Im | MPP current |
| Vm | MPP voltage |
| Ns | number of PV modules in series |
| Np | number of PV modules in parallel |
| Gi | PV cells irradiance |
| γj, λij | weights |
| bj, c | biases for each joint from the input layer to the output layer |
| Pm | MPP power |
| Vdc | DC-link voltage |
| ed, eq | d–q components of the grid voltage |
| id, iq | d–q components of the output current |
| pdc | DC-link power |
References
- Mathiesen, B.V.; Lund, H.; Karlsson, K. 100% renewable energy systems, climate mitigation and economic growth. Appl. Energy 2011, 88, 488–501. [Google Scholar] [CrossRef]
- Carcangiu, G.; Dainese, C.; Faranda, R.; Leva, S.; Sardo, M. New network topologies for large scale photovoltaic systems. In Proceedings of the IEEE Power Tech Conference 2009, Bucharest, Romania, 28 June–2 July 2009; pp. 1–7.
- Mamarelis, E.; Petrone, G.; Spagnuolo, G. A two-steps algorithm improving the P & O steady state MPPT efficiency. Appl. Energy 2014, 113, 414–421. [Google Scholar]
- Hiren, P.; Vivek, A. Maximum Power Point Tracking Scheme for PV Systems Operating Under Partially Shaded Conditions. IEEE Trans. Power Electron. 2008, 55, 1689–1698. [Google Scholar]
- Nicola, F.; Giovanni, P.; Giovanni, S.; Massimo, V. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar]
- Qiang, M.; Mingwei, S.; Liying, L.; Guerrero, J.M. A Novel Improved Variable Step-Size Incremental-Resistance MPPT Method for PV Systems. IEEE Trans. Ind. Electron. 2011, 58, 2427–2434. [Google Scholar]
- Alberto, D.; George, C.L.; Sonia, L.; Giampaolo, M. Experimental investigation of partial shading scenarios on PV (photovoltaic) modules. Energy 2013, 55, 466–475. [Google Scholar]
- Singh, M.D.; Shine, V.J.; Janamala, V. Application of artificial neural networks in optimizing MPPT control for standalone solar PV system. In Proceedings of the 2014 International Conference on Contemporary Computing and Informatics (IC3I), Mysore, India, 27–29 November 2014; pp. 162–166.
- Faranda, R.; Leva, S.; Maugeri, V. MPPT techniques for PV systems: Energetic and cost comparison. In Proceedings of the IEEE Power and Energy Society 2008 General Meeting, Pittsburgh, PA, USA, 20–24 July 2008.
- Berrera, M.; Dolara, A.; Faranda, R.; Leva, S. Experimental test of seven widely-adopted MPPT algorithms. In Proceedings of the 2009 IEEE Bucharest PowerTech: Innovative Ideas Toward the Electrical Grid of the Future, Bucharest, Romania, 28 June–2 July 2009.
- Martınez-Moreno, F.; Munoz, J.; Lorenzo, E. Experimental model to estimate shading losses on PV arrays. J. Sol. Energy Mater. Sol. Cells 2010, 94, 2298–2303. [Google Scholar] [CrossRef]
- Yazdani, A.; Di Fazio, A.R.; Ghoddami, H.; Russo, M.; Kazerani, M.; Jatskevich, J.; Strunz, K.; Leva, S.; Martinez, J.A. Modeling guidelines and a benchmark for power system simulation studies of three-phase single stage photovoltaic systems. IEEE Trans. Power Deliv. 2011, 26, 1247–1264. [Google Scholar] [CrossRef]
- Potnuru, S.R.; Pattabiraman, D.; Ganesan, S.I.; Chilakapati, N. Positioning of PV panels for reduction in line losses and mismatch losses in PV array. Renew. Energy 2015, 78, 264–275. [Google Scholar] [CrossRef]
- Sahu, H.S.; Nayak, S.K.; Mishra, S. Maximizing the Power Generation of a Partially Shaded PV Array. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 626–637. [Google Scholar] [CrossRef]
- Patel, H.; Agarwal, V. MATLAB-Based Modeling to Study the Effects of Partial Shading on PV Array Characteristics. IEEE Trans. Energy Convers. 2008, 23, 302–310. [Google Scholar] [CrossRef]
- Liu, X.; Qi, X.; Zheng, S.; Wang, F.; Chen, D. Model and Analysis of Photovoltaic Array under Partial Shading. Power Syst. Technol. 2010, 34, 192–197. [Google Scholar]
- Dıaz-Dorado, E.; Cidras, J.; Carrillo, C. Discrete I–V model for partially shaded PV-arrays. Sol. Energy 2014, 103, 96–107. [Google Scholar] [CrossRef]
- Alberto, D.; Sonia, L.; Manzolini, G. Comparison of different physical models for PV power output prediction. Sol. Energy 2015, 119, 83–99. [Google Scholar]
- Kadri, R.; Andrei, H.; Gaubert, J.-P. Modeling of the photovoltaic cell circuit parameters for optimum connection model and real-time emulator with partial shadow conditions. Energy 2012, 42, 57–67. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An Improved Method to Predict the Position of Maximum Power Point during Partial Shading for PV Arrays. IEEE Trans. Ind. Inform. 2015, 11, 1378–1387. [Google Scholar] [CrossRef]
- Ji, Y.-K.; Jung, D.-Y.; Kim, J.-G.; Kim, J.-H.; Lee, T.-W.; Won, C.-Y. A Real Maximum Power Point Tracking Method for Mismatching Compensation in PV Array under Partially Shaded Conditions. IEEE Trans. Power Electron. 2011, 26, 1001–1009. [Google Scholar] [CrossRef]
- Murtaza, S.; Chiaberge, M.; Spertino, F.; Boero, D.; De Giuseppe, M. A maximum power point tracking technique based on bypass diode mechanism for PV arrays under partial shading. Energy Build. 2014, 73, 13–25. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Vignesh kumar, V.; Palani, S. Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions. Renew. Energy 2015, 75, 308–317. [Google Scholar] [CrossRef]
- Hajighorbani, S.; Radzi, M.A.M.; Ab Kadir, M.Z.A.; Shafie, S.; Zainuri, M.A.A.M. Implementing a Novel Hybrid Maximum Power Point Tracking Technique in DSP via Simulink/MATLAB under Partially Shaded Conditions. Energies 2016, 9, 1–25. [Google Scholar] [CrossRef]
- Ghasemi, M.A.; Forushani, H.M.; Parniani, M. Partial Shading Detection and Smooth Maximum Power Point Tracking of PV Arrays Under PSC. IEEE Trans. Power Electron. 2016, 31, 6281–6292. [Google Scholar] [CrossRef]
- Liu, T.-H.; Chen, J.-H.; Huang, J.-W. Global maximum power point tracking algorithm for PV systems operating under partially shaded conditions using the segmentation search method. Sol. Energy 2014, 103, 350–363. [Google Scholar] [CrossRef]
- Lyden, S.; Haque, M.E. A Simulated Annealing Global Maximum Power Point Tracking Approach for PV Modules Under Partial Shading Conditions. IEEE Trans. Power Electron. 2016, 31, 4171–4181. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Syafaruddin; Karatepe, E.; Hiyama, T. Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions. IET Renew. Power Gener. 2009, 3, 239–253. [Google Scholar] [CrossRef]
- Rizzo, S.A.; Scelba, G. ANN based MPPT method for rapidly variable shading conditions. Appl. Energy 2015, 145, 124–132. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Huang, S.-C.; Huang, J.-W.; Liang, W.-C. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating Under Partially Shaded Conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar] [CrossRef]
- Benyoucef, A.S.; Chouder, A.; Kara, K. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar] [CrossRef]
- Jiang, L.L.; Nayanasiri, D.R.; Maskell, D.L.; Vilathgamuwa, D.M. A hybrid maximum power point tracking for partially shaded photovoltaic systems in the tropics. Renew. Energy 2015, 76, 53–65. [Google Scholar] [CrossRef]
- Elobaid, L.M.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial neural network-based photovoltaic maximum power point tracking techniques: A survey. IET Renew. Power Gener. 2015, 9, 1043–1063. [Google Scholar] [CrossRef]
- Trejos, A.; Gonzalez, D.; Ramos-Paja, C.A. Modeling of Step-up Grid-Connected Photovoltaic Systems for Control Purposes. Energies 2012, 5, 1900–1926. [Google Scholar] [CrossRef]
- Manganiello, P.; Ricco, M.; Petrone, G.; Monmasson, E.; Spagnuolo, G. Optimization of Perturbative PV MPPT Methods through Online System Identification. IEEE Trans. Ind. Electron. 2014, 61, 6812–6821. [Google Scholar] [CrossRef]
- Renaudineau, H.; Donatantonio, F.; Fontchastagner, J.; Petrone, G.; Spagnuolo, G.; Martin, J.-P.; Pierfederici, S. A PSO-Based Global MPPT Technique for Distributed PV Power Generation. IEEE Trans. Ind. Electron. 2015, 62, 1047–1058. [Google Scholar] [CrossRef]
- Mamarelis, E.; Petrone, G.; Spagnuolo, G. An Hybrid Digital-Analog Sliding Mode Controller for Photovoltaic Applications. IEEE Trans. Ind. Inf. 2103, 9, 1094–1103. [Google Scholar] [CrossRef]
- Haroun, R.; Aroudi, A.E.; Cid-Pastor, A.; Garcia, G.; Olalla, C.; Martinez-Salamero, L. Impedance Matching in Photovoltaic Systems Using Cascaded Boost Converters and Sliding-Mode Control. IEEE Trans. Power Electron. 2015, 30, 3185–3199. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Abbasi, M.H.; Moradian, H. Improving the performance of a nonlinear boiler-turbine unit via bifurcation control of external disturbances: A comparison between sliding mode and feedback linearization control approaches. Nonlinear Dyn. 2016, 85, 229–243. [Google Scholar]
- Ding, X.; Sinha, A. Hydropower Plant Frequency Control Via Feedback Linearization and Sliding Mode Control. J. Dyn. Syst. Meas. Control-Trans. ASME 2016, 138, 074501. [Google Scholar] [CrossRef]
- Alonge, F.; Cirrincione, M.; Pucci, M.; Sferlazza, A. Input- Output Feedback Linearization Control with On-Line MRAS-Based Inductor Resistance Estimation of Linear Induction Motors Including the Dynamic End Effects. IEEE Trans. Ind. Appl. 2016, 52, 254–266. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitation of voltage-oriented PI current control of grid-connected PWM rectifier with LCL filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Dannehl, J.; Fuchs, F.W.; Hansen, S.; Thogersen, P.B. Investigation of active damping approaches for PI-based current control of grid-connected pulse width modulation converter with LCL filters. IEEE Trans. Ind. Appl. 2010, 46, 1509–1517. [Google Scholar] [CrossRef]
- Dannehl, J.; Fuchs, F.W.; Thogersen, P.B. PI state current control of grid-connected PWM converters with LCL filters. IEEE Trans. Power Electron. 2010, 25, 2320–2330. [Google Scholar] [CrossRef]
- Hwang, T.S.; Park, S.Y. A seamless control strategy of a distributed generation inverter for the critical load safety under strict grid disturbances. IEEE Trans. Power Electron. 2013, 28, 4780–4790. [Google Scholar] [CrossRef]

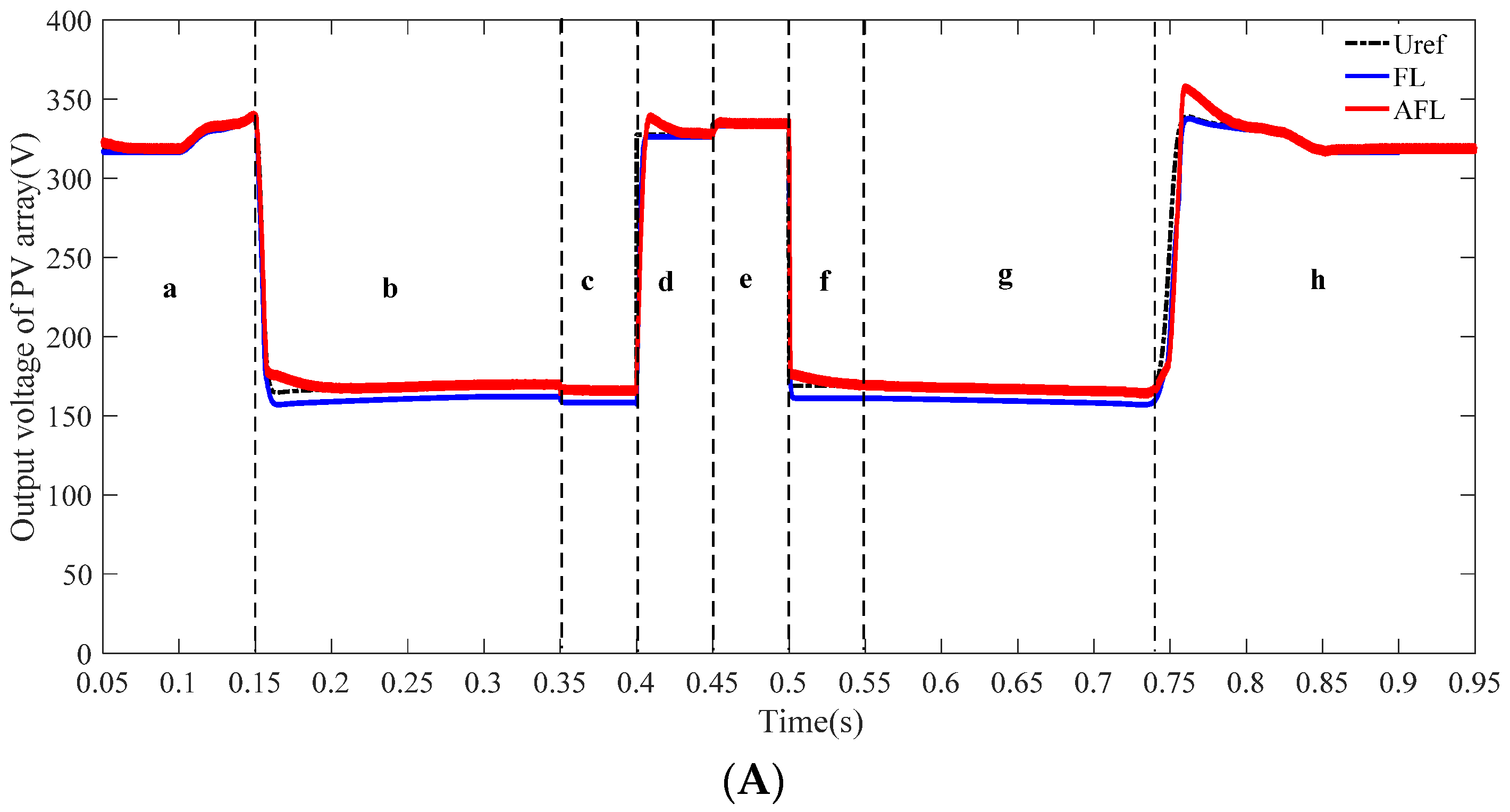
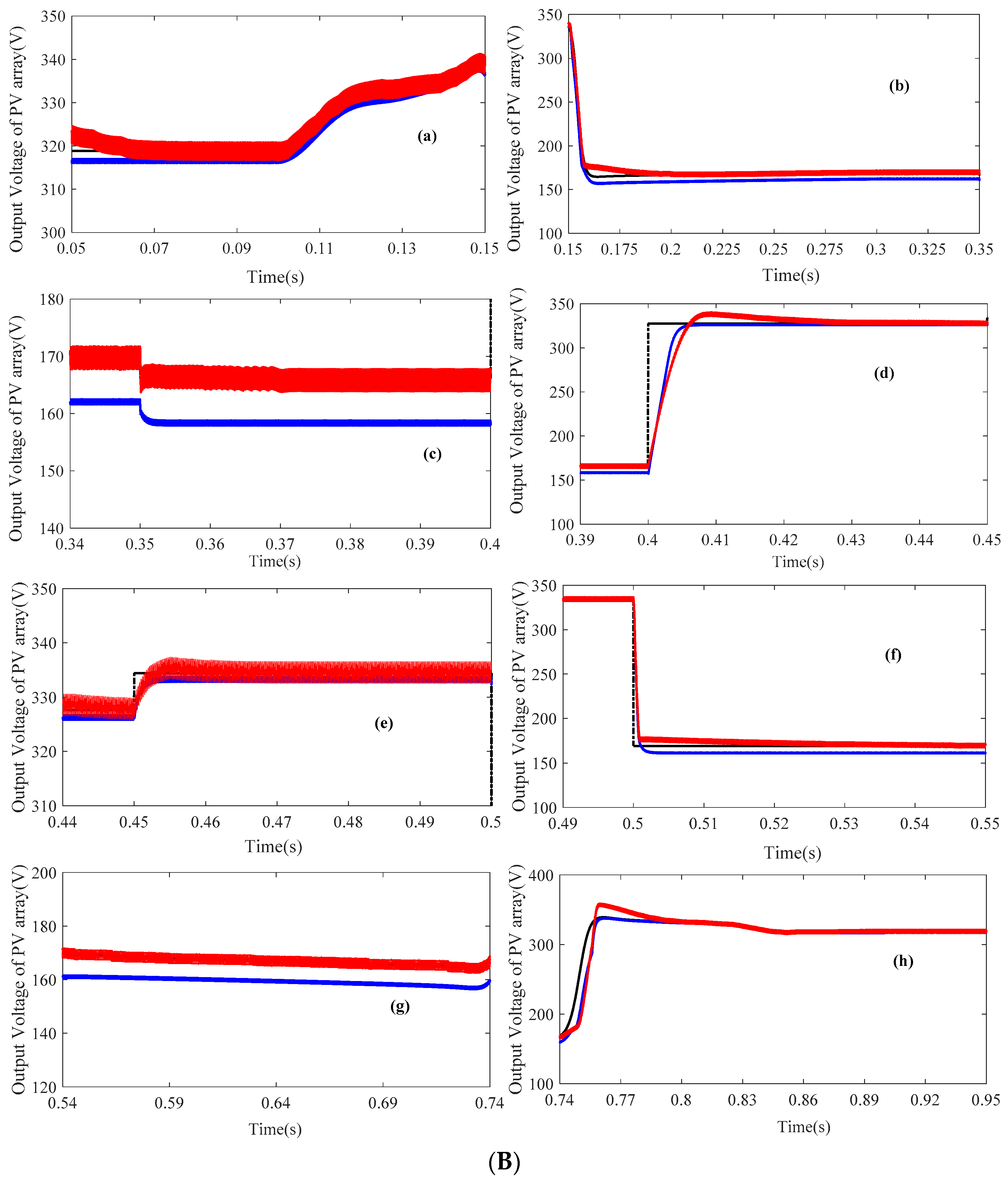
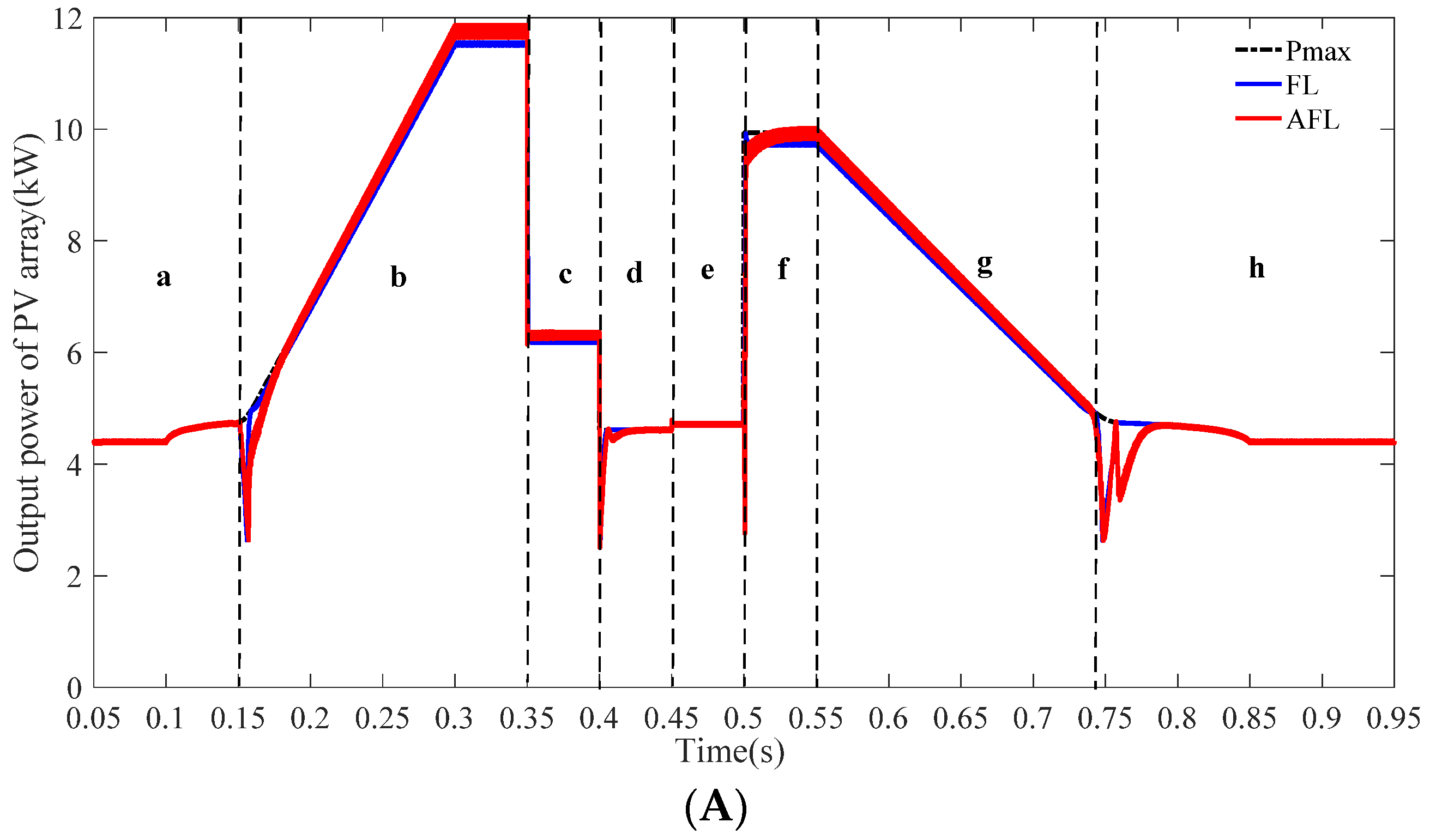
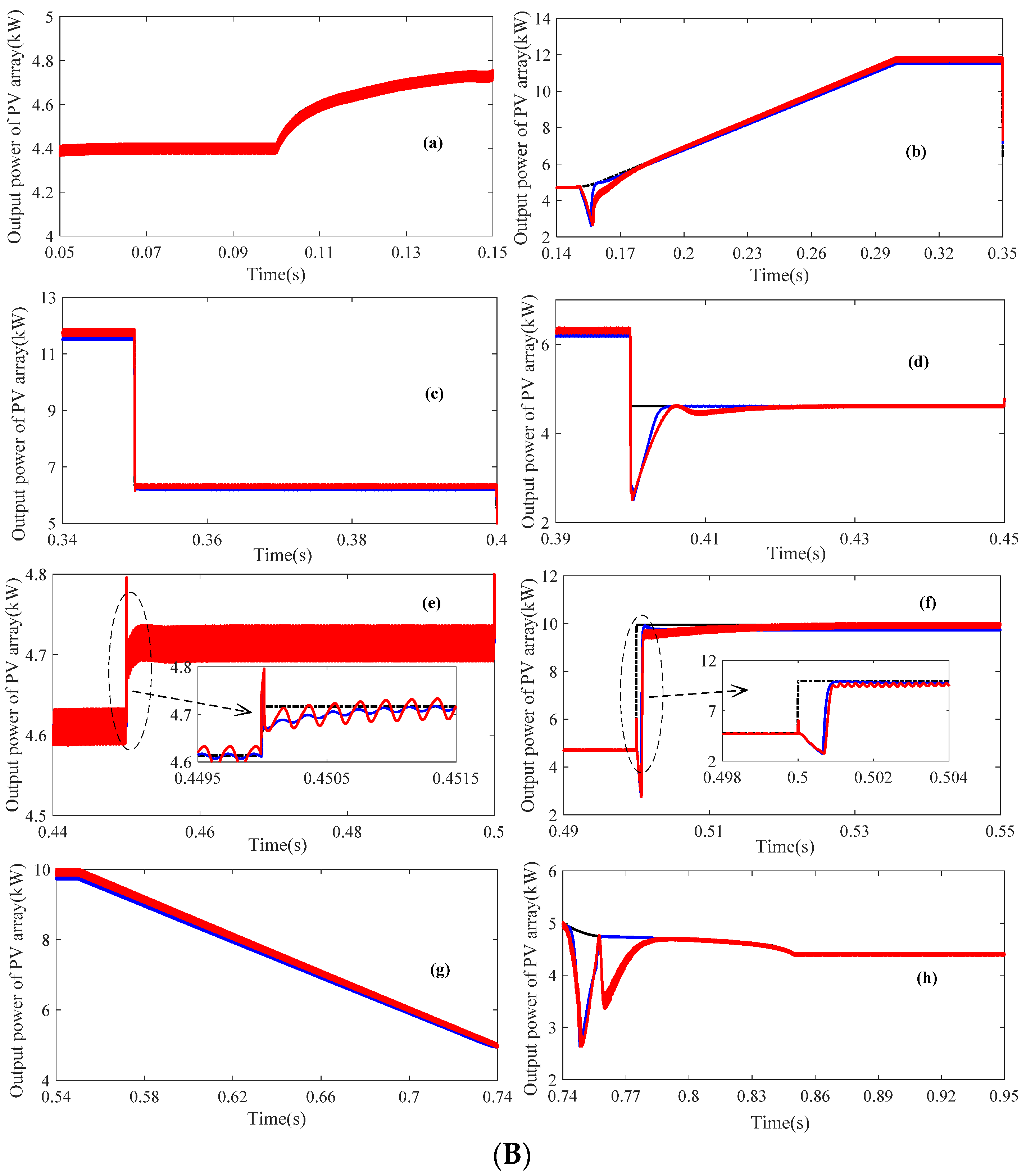

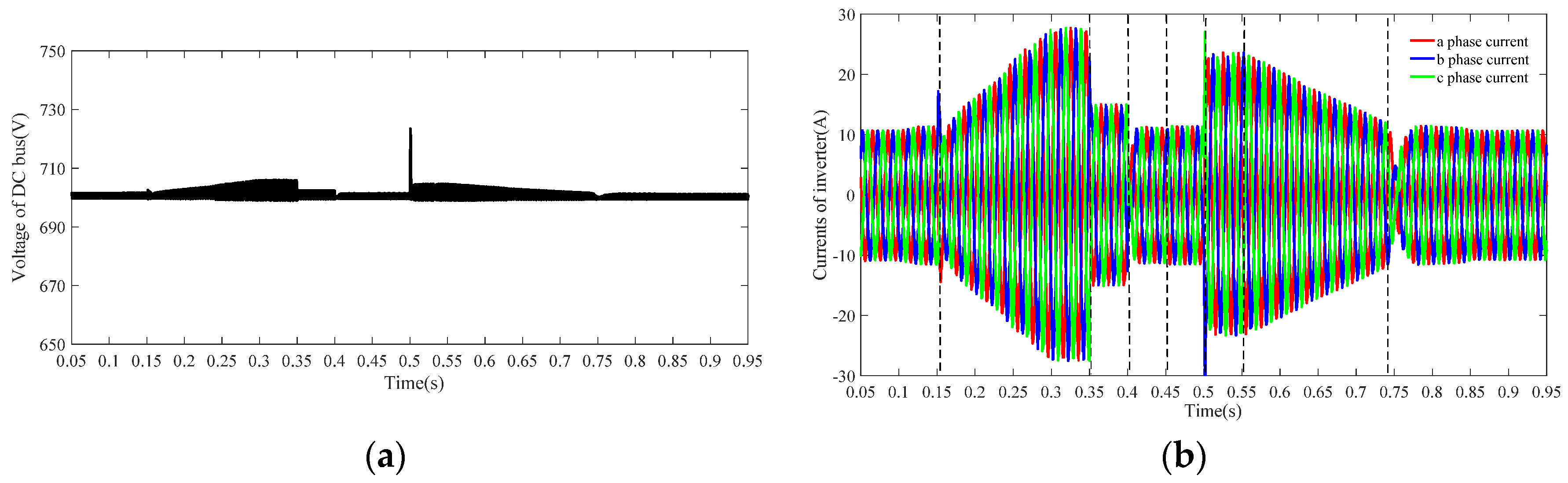
| Parameter | Value |
|---|---|
| Voc (open-circuit voltage) | 65.2 V |
| Isc (short-circuit current) | 5.96 A |
| Vm (MPP (maximum power point) voltage) | 54.7 V |
| Im (MPP current) | 5.58 A |
| Pm (MPP power) | 305.2 W |
| Section No. | Time (s) | Shading Pattern [G1,1~12, G2,1~12, G3,1~12, G4,1~12, G5,1~12, G6,1~12] (W/m2) |
|---|---|---|
| SP1 | 0.1~0.3 | [300, 300, 300, 1000, 700, 700] |
| SP2 | 0.3~1.5 | [300, 300, 300, 1000, 500, 500] |
| SP3 | 1.5~2.0 | [300, 300, 300, 1000, 1000, 300] |
| Section No. | Ideal Maximum Power (W) | Output Power Obtained (W) | ||
|---|---|---|---|---|
| P & O | Improved P & O | ANN + AFL 1 | ||
| SP1 | 8393.4 | 8282.9 | 8283.1 | 8381.4 |
| SP2 | 7341.3 | 5989.2 | 7225.3 | 7311.2 |
| SP3 | 7811.6 | 7108.4 | 7112.6 | 7798.8 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Ma, S.; Wu, J.; Huang, L. Analysis of MPPT Failure and Development of an Augmented Nonlinear Controller for MPPT of Photovoltaic Systems under Partial Shading Conditions. Appl. Sci. 2017, 7, 95. https://doi.org/10.3390/app7010095
Chen M, Ma S, Wu J, Huang L. Analysis of MPPT Failure and Development of an Augmented Nonlinear Controller for MPPT of Photovoltaic Systems under Partial Shading Conditions. Applied Sciences. 2017; 7(1):95. https://doi.org/10.3390/app7010095
Chicago/Turabian StyleChen, Mingxuan, Suliang Ma, Jianwen Wu, and Lian Huang. 2017. "Analysis of MPPT Failure and Development of an Augmented Nonlinear Controller for MPPT of Photovoltaic Systems under Partial Shading Conditions" Applied Sciences 7, no. 1: 95. https://doi.org/10.3390/app7010095
APA StyleChen, M., Ma, S., Wu, J., & Huang, L. (2017). Analysis of MPPT Failure and Development of an Augmented Nonlinear Controller for MPPT of Photovoltaic Systems under Partial Shading Conditions. Applied Sciences, 7(1), 95. https://doi.org/10.3390/app7010095






