Abstract
The main purpose of the paper is to present an innovative higher-order structural theory to accurately evaluate the natural frequencies of laminated composite shells. A new kinematic model is developed starting from the theoretical framework given by a unified formulation. The kinematic expansion is taken as a free parameter, and the three-dimensional displacement field is described by using alternatively the Legendre or Lagrange polynomials, following the key points of the most typical Layer-wise (LW) approaches. The structure is considered as a unique body and all the geometric and mechanical properties are evaluated on the shell middle surface, following the idea of the well-known Equivalent Single Layer (ESL) models. For this purpose, the name Equivalent Layer-Wise (ELW) is introduced to define the present approach. The governing equations are solved numerically by means of the Generalized Differential Quadrature (GDQ) method and the solutions are compared with the results available in the literature or obtained through a commercial finite element program. Due to the generality of the current method, several boundary conditions and various mechanical and geometric configurations are considered. Finally, it should be underlined that different doubly-curved surfaces may be considered following the mathematical framework given by the differential geometry.
1. Introduction
The development of refined structural models or higher-order theories currently represents one of the most active areas for many researchers in the structural mechanics field. Their interest in this subject is mainly due to the fact that the use of advanced materials has shown inadequacy of the classical or first-order theories to capture the effective mechanical behavior of this class of materials, such as laminated composites or functionally graded materials [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In these particular circumstances, the fundamental hypotheses of a lower-order model could lead to inaccurate results since some effects are neglected or not even considered. A typical situation is the case of structures made of a combination of highly heterogeneous materials in the lamination scheme. As highlighted in the work by Librescu and Reddy [21], many refined approaches arose to predict a more coherent structural behavior. For the sake of completeness, the readers can find some examples of these approaches in [22,23,24,25,26,27,28,29,30,31,32,33]. It should be noted that the aforementioned papers were mainly focused on plates and shells.
The insufficiency of classical plate and shell theories can also be highlighted in the dynamic analysis. In order to evaluate the natural frequencies of composite structures correctly, several higher-order shear deformation theories (HSDTs) were developed. In general, two different approaches are followed, namely, equivalent single layer (ESL) and layer-wise (LW) models (see Reddy [1] for a brief review). The former is able to study a composite structure by referring each geometric and mechanical parameter on the middle surface of the structure, which is taken as reference domain for the governing equations. In a similar manner, the degrees of freedom of the problem under consideration are evaluated on the middle surface, independently from the enrichment of the kinematic model [33,34,35,36,37,38,39,40,41,42,43,44,45,46]. On the other hand, the latter approach takes into account each layer (or ply) that composes the structure separately from the others. In general, a LW model defines the kinematic expansion, and consequently the degrees of freedom, along the thickness of each layer. As a result, this approach is able to deal with continuous displacements but characterized by discontinuous derivatives at the interfaces [46,47,48,49,50,51,52,53,54,55,56].
The works [57,58,59] represent a turning point in the advancement of HSDTs. In fact, they provided the basis for the development of a unified formulation (UF), which is able to analyze and use several structural models within a single framework. As a matter of fact, the order of kinematic expansion can be arbitrarily chosen in order to obtain the desired theory that is more appropriate to deal with a particular physical phenomenon. In the review paper [57] a complete treatise about both ESL and LW approaches is presented. It is important to cite also the works [58,59], where the so-called zig-zag theories for layered structures were discussed. For the sake of completeness, it should be recalled that a zig-zag theory is actually an ESL model embedded with a specific function that allows to consider continuous through-the-thickness displacements characterized by different slope at the interface between two plies, similar to a LW theory [31,32,33]. This aspect is commonly denoted as zig-zag effect and it is generally given by the choice of different materials along the transverse direction of the structure. For instance, this effect is particularly evident when a soft-core is included into the lamination scheme of a generic plate or shell (sandwich structure). In general, the Murakami’s function is employed for this purpose.
Recently, a huge number of scientific papers based on the UF is available in the literature. For the sake of completeness, the works [60,61,62,63,64,65,66,67,68,69,70,71,72,73,74] can be considered as examples of higher-order ESL models. On the other hand, the papers [75,76,77,78,79,80,81,82,83] can be cited as the proof of the use of this unified formulation to develop higher-order LW approaches. It should be noticed that the UF was generalized by Demasi [84], who developed the so-called Generalized Unified Formulation (GUF). The research provided by Demasi represents the starting point for the development of more general theories. For this purpose, the work by D’Ottavio [85] must also be mentioned. He proposed an optimized approach able to consider the structure as the sum of packages of layers, each of them governed by a peculiar structural model. This approach was named Sublaminate Generalized Unified Formulation (S-GUF). Analogously, the paper by Fazzolari [86,87,88] and by Fazzolari and Banerjee [89] represent a significant extension of the GUF. Their works aimed to extend the contributions first given by Demasi in [84] for plates to the structural analysis of beams and shells. At this point, it is the authors’ intention to apologize for the omissions in the present review of those papers that could be considered as important steps in the development of HSDTs.
The main aim of the present work is to introduce a new higher-order structural model based on the aforementioned unified formulation for the structural analysis of doubly-curved laminated composite plates and shells, which has some elements in common with both the ESL and LW approaches. According to the proposed methodology, the overall mechanical properties of the composites are computed on the shell middle surface, taking into account all the layers that compose the structure. It should be noticed that there is no limitation on the choice of the constituents, as well as their orientation and stacking sequence, due to the general features of this approach. The displacement field is written as a function of an arbitrary order of kinematic enrichment, whereas the Legendre and the Lagrange polynomials are employed to describe the kinematic expansion. The degrees of freedom of the problem are not defined on the shell middle surface as in a typical ESL model, but they are related to specific points placed along the thickness of the structure according to what is typically done for each layer by the LW theory. The term Equivalent Layer-Wise (ELW) is introduced to define this approach. Once the governing equations are obtained, they are numerically solved by means of the Generalized Differential Quadrature (GDQ) method [90], whose main features are illustrated in detail by Tornabene et al. in the review paper [91]. The accuracy, reliability and stability characteristic of this numerical tool can be checked considering the excellent results shown in the works [39,40,41,61,62,63,64,65,66,67,68,69,70,71,72,73,74,79,80,81,82,83,92,93,94,95,96,97,98,99,100,101,102], which have been obtained in different kinds of structural problems related to plates and shells.
2. Definition of the Geometry
As highlighted by Kraus in his book [103], each shell structure is a three-dimensional body which is bounded by two close surfaces, whose distance measured along the normal direction defines the thickness of the shell. The middle surface is clearly equidistant from these two external surfaces and can be taken as reference domain for the governing equations. Its importance is evident, since its define the shape of the structure under consideration and rules the mechanical behavior of a shell structure if a two-dimensional structural model is considered. By means of the differential geometry, several kinds of shells can be studied in a general and unified manner. For instance, the same theoretical approach is used to define the geometry of doubly-curved, singly-curved and degenerate shells (or plates). With reference to Figure 1, in which a generic shell element is depicted, the position vector is introduced to identify each point of the three-dimensional medium as follows
where the dimensionless quantity denotes the distance of the point from its projection on the reference domain.
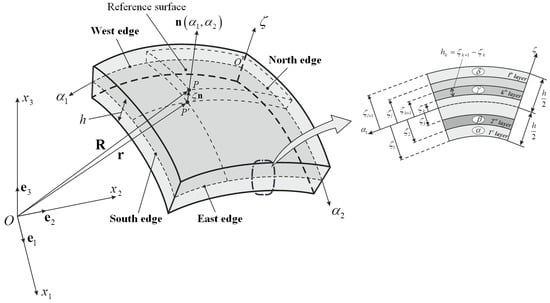
Figure 1.
Representation of a generic doubly-curved shell element, edge identification and lamination scheme.
On the other hand, is the position vector that describe the middle surface, which assumes different meanings according to the investigated geometry. A curvilinear orthogonal coordinates system must be defined on the shell middle surface. In particular, the coordinates denote the lines of main curvature of the middle surface, whereas is the normal direction that can be specified by the following outward unit normal vector
where the symbol “” represents the vector product. For conciseness purposes, the notation , for , is introduced. For the sake of completeness, it should be highlighted that the curvilinear coordinates vary according to the considered structure. For example, they assume the following meaning for a doubly-curved shell of revolution, whereas the notation is introduced for a singly-curved shell of translation. In the case of a flat panel, such as a rectangular plate, they can be assumed equal to . This aspect is to underline the effectiveness of the differential geometry. In general, the position vector of any reference surface is expressed as
where , for are arbitrary functions needed to describe the surface under consideration. On the other hand, the symbols , for , denote the unit vectors of axes of the global reference system as depicted in Figure 1. In the following sections, the position vector will be specified for the various shell structures under consideration. Further details concerning these features, as well as a wide range of shell structures, can be found in the recent books by Tornabene et al. [2,3]. In general, the curvilinear coordinates in hand must be bounded by specific values to define a finite domain. Without loss of generality, a three-dimensional shell is defined if the following limits are specified
It should be noticed that the total thickness of the shell is defined as the summation of the thickness of each layer (or lamina) , if a laminated composite material is taken into account. For a lamination scheme that consists of layers as the one shown in Figure 1, the overall thickness is given by
It is evident that the symbol is used to define all the geometric and mechanical properties related to the -th layer. The differential geometry provides also the definition of the well-known Lamè parameters and , which can be evaluated once the position vector is specified as follows
where the symbol “” is introduced to specify the scalar product. Finally, the main radii of curvature of the reference surface and can be computed using the definition shown below
in which the notation , for , is employed. Expressions (7) are valid only if the curvilinear coordinates are orthogonal and principal. The three-dimensional effect of a shell structure is taken into account by the parameters and , which are defined as follows
3. Higher-Order Equivalent Layer-Wise Approach
As already illustrated in the introduction, the well-known UF represents an extremely valid and efficient tool to analyze a huge variety of HSDTs, which are classified in general as Equivalent Single Layer (ESL) theories [61,62,63,64,65,66,67,68,69,70,71,72,73,74] and Layer-Wise (LW) models [79,80,81,82,83]. The former approach establishes that all the mechanical and geometric parameters are evaluated on the shell middle surface, whereas each layer is analyzed independently from the others in the latter method. The main novelty introduced by the present work is a new higher-order formulation which keeps the main features of the ESL approaches but uses the kinematic expansion of the displacement field commonly employed in the LW models. For this purpose, the term Equivalent Layer-Wise (ELW) is introduced. Let us consider the three-dimensional displacements , , and . They can be defined in each point of the shell structure according to the following expressions
in which , for , specify the thickness functions related to the -th order of kinematic expansion. On the other hand, , , and , for , are the degrees of freedom of the current model and denote the displacements of the section placed at the height of the shell, as it can be noticed from Figure 2. This aspect represents the main difference in comparison with the ESL approach, where each degree of freedom is always evaluated on the shell middle surface. In other words, the -th order of kinematic expansion is strictly related to the number of points along the shell thickness (Figure 2).
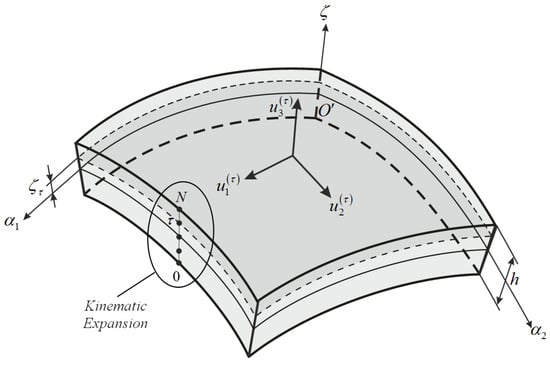
Figure 2.
Kinematic expansion and degrees of freedom related to the order for the Equivalent Layer-Wise (ELW) approach.
For the sake of clarity, it should be noticed that the displacements linked to the order of expansion are the displacements of the points laying on the shell bottom surface (for ). On the contrary, the displacements are related to the order of kinematic expansion and represent the displacements of the top surface of the shell.
Similarly to the ESL approach, the -th order of kinematic expansion is always related to the well-known Murakami’s function, which can be introduced to capture the zig-zag effect that can be noticed especially if a sandwich structure is analyzed. Having in mind Figure 1, in which a general lamination scheme is depicted, the Murakami’s function can be defined as follows
The non-dimensional parameter is assumed equal to the following expression
in which represents the boundary coordinate of the -th layer along the normal direction. Thus, if a soft-core effect must be studied, one gets . The reader can find further details concerning the use and the peculiar features of the Murakami’s function in the works [57,58,59]. Let us consider the thickness functions related to the other orders of kinematic expansions. The first possible choice consists in assuming them equal to the corresponding Legendre polynomials. In other words, they can be defined as follows
in which the symbol is introduced to specify the -th order Legendre polynomial. They can be computed conveniently in the closed interval by using the following recursive formula (as shown in [3])
for , assuming and . For clarity purposes, let us consider a fourth order of kinematic expansion (). The displacement field (9) becomes
if the Murakami’s function is embedded in the model. Due to expressions (12) the first five Legendre polynomials are required
As a consequence, the thickness functions needed for the kinematic expansion at issue take the following aspect
It should be pointed out that is evidently the Murakami’s function (). If the Legendre polynomial are used, the coordinates which define the kinematic expansion can be located by evaluating the roots of the Legendre polynomial of highest order.
Alternatively, the Lagrange polynomials can be used as thickness functions simply assuming , in which denotes the Lagrange polynomial of order defined as follows
for . The coordinates , for , can be chosen taking into account an arbitrary distribution of points in the closed interval . In the present paper, a uniform (or equally spaced) grid distribution is considered for the sake of simplicity. If the Lagrange polynomials are employed as thickness functions, one gets
For the sake of completeness, it should be noted that the displacement field (9) without the Murakami’s function is equivalent to the displacement approximation of the sampling surfaces (SaS) formulation presented in the works [104,105], if the Lagrange polynomials (17)–(18) are employed as thickness functions.
As in the previous approach, the -th thickness function is still given by the Murakami’s function (). Using both the Legendre polynomials and the Lagrange ones, the thickness functions have the following properties
with . As a consequence, the relations shown below can be easily deduced
This means that the three-dimensional displacement evaluated at the height coordinate linked to the -th order of kinematic expansion coincides with the corresponding degree of freedom of the model, except for the Murakami’s function. At this point it should be specified also that the kinematic expansion is not affected by either the lamination scheme or the placement of the various layers that compose the laminate, since this aspect is considered only when the elastic coefficients of the composite are evaluated as it will be shown in the following paragraphs. Finally, it should be noticed that the same kinematic model just illustrated is typically used for the LW approach to describe the displacement field of each lamina [79,80,81,82,83]. A peculiar notation can be introduced now to specify univocally the various higher-order ELW models that are employed in the following. Each theory is identified by the maximum order of kinematic expansion . In particular, the structural theories used in the current work are listed below for various orders of expansion
where “” specifies that an ELW approach is considered, whereas “” means that the governing equations will be written in terms of generalized displacements. If the Murakami’s function must be embedded in the model, the following theories are obtained for several orders of kinematic expansion
where “” stands clearly for the Murakami’s function (zig-zag effect).
Once the kinematic model is defined, both the constitutive relations and the motion equations are formally equal to the ones used for the ESL approach [61,62,63,64,65,66,67,68,69,70,71,72,73,74]. Thus, in the following only the main aspects of the model are presented for conciseness purposes. At this point, the vector that collects the degrees of freedom for each order of kinematic expansion can be conveniently introduced
for . The generalized strain components for each order of kinematic expansion can be collected in the corresponding algebraic vector defined as follows
The generalized strains can be directly related to the degrees of freedom of the problem for according to the following equation in vector notation
The differential operator assumes the following matrix notation
where are the Lamè parameters (6), and the principal radii of curvature (7) of the shell middle surface.
The complete treatise concerning the definition of the generalized strain components, as well as further details about their meaning, can be found in the books by Tornabene et al. [2,3]. As highlighted above, the interested reader can notice some similarities between the present approach and the aforementioned SaS formulation. In particular, the definitions of the first six generalized strains collected in (24) coincide exactly with the corresponding strain parameters of the SaS formulation [104,105].
The stress resultants related to the -th order of kinematic expansion can be collected in the algebraic vector , whose extended vector form is shown below
Due to the duality between strains and stresses, the generalized stresses (or stress resultants) can be related directly to the degrees of freedom of the model for according to the following equation
where the constitutive operator is introduced for each order of kinematic expansion (for ). It should be noticed that represents the stiffness matrix of the considered shell structure. In particular, if a laminated composite structure made of orthotropic layers is considered, the constitutive operator takes the following aspect
Each term collected in the stiffness matrix can be evaluated by means of the following definitions
for , , and . It should be noticed that the symbols specify the thickness function order, whereas denote that the derivatives of the corresponding thickness functions with respect to must be evaluated. It is pointed out that this evaluation can be easily performed since the definition of the thickness functions is shown in extended form in (12) and (18), respectively. Quantities are defined as follows
for and
for . This distinction is performed to introduce the shear correction factor that has to be included in the model if the chosen order of kinematic expansion does not provide a parabolic profile of the through-the-thickness shear stresses. Typically, a constant value is used to define the shear correction factor . In the present paper, the value is used for this purpose. Nevertheless, it should be noticed that a parabolic function can be chosen as shear correction function as illustrated in the work by Tornabene and Reddy [92]. On the other hand, quantities , for , represent the elastic constant of the material of the -th layer. They can assume different meanings depending on the case. If the strain along the shell thickness is neglected, the plane-stress-reduced elastic coefficients are needed (). On the contrary, if the stretching effect is taken into account the non-reduced elastic coefficients must be used (). The trace over these symbols means that these quantities must be evaluated in the local reference system . In other words, the constitutive equations of each lamina must be transferred into the geometric coordinate system by means of the proper transformation laws which take into account the different orientation that can be given to an orthotropic medium. In fact, since each layer can be arbitrarily oriented with respect to the laminate reference system as shown in Figure 1, in which the symbols are introduced for this purpose, the constitutive relations of each lamina must be converted into the local reference system . Further details concerning these relations can be found in the book by Reddy [1]. For the sake of completeness, it should be specified that in the present work the mechanical properties of each layer are fully described by means of the engineering constants of the materials, which are , , , , , , , , for an orthotropic medium, and , , for an isotropic one. In any case, the lamination scheme is identified by the notation , in which represent the orientation of each ply. It should be recalled that in the current approach each layer is assumed to be linear elastic. In any circumstance, the use of both the shear correction factor and the plane stress-reduced elastic coefficients is specified by adding a proper notation to the acronym of the structural theory. In particular, the superscript is added to specify the use of the constant value for the shear correction factor, whereas the subscript stands for “Reduced Stiffness” and means that the reduced elastic coefficients are employed.
The motion equations are obtained by means of the well-known Hamilton’s variational principle. For the sake of conciseness, only the equations at issue are shown. For each order of kinematic expansion , the free vibration problem is governed by the following matrix equation
The equilibrium operator takes the following aspect
in which represent the Lamè parameters defined in (6), and are the principal radii of curvature of the shell middle surface shown in (7). On the contrary, the matrix collects the inertia terms for every order of kinematic expansion as follows
If denotes the mass density of the -th ply, the definition shown below is used to evaluate the inertia masses of the laminated composite in hand
It is clear that represents the generalized acceleration component vector defined as follows
for . By inserting definition (28) into the motion equation shown in (33), the governing system can be conveniently written as a function of the degrees of freedom of the problem. As a consequence, one gets
where the so-called fundamental operator is introduced. In matrix form, it assumes the following aspect
For conciseness purposes, the definition of each term , for , is omitted in the present paper. Nevertheless, the reader can find their complete meaning in the work by Tornabene et al. [61]. It should be noticed that they are formally equal to the ones employed in the ESL approach. Relation (38) represents the fundamental nucleus of the ELW approach and it identify a set of three differential equations for each order of kinematic expansions. Thus, equations must be solved to obtain the solution of this structural problem. In order to fully characterize the problem at issue, the proper set of boundary conditions must be enforced along each external edge. For a clamped edge (denoted by letter “C”), these conditions are written in terms of displacements. On the contrary, specific prescription are given to the generalized stress resultants for a free edge (indicated by letter “F”). Let us consider Figure 1 to identify each external edge. In particular, if an edge is defined by or , for , the boundary conditions become
These edges are the Southern (S) and the Northern (N) ones in Figure 1. On the other hand, if the coordinates of an edge are or , for , one gets
This is clearly the case of the Western (W) and Eastern (E) edges. In the present paper, the boundary conditions are specified for the panel under consideration following the sequence WSEN. For instance, this means that the acronym FCCF specifies that the Western and the Northern edges are free, whereas the other two are completely clamped.
4. Generalized Differential Quadrature Method
In the present paper, the governing equations shown in matrix form in (38) are solved by means of the GDQ method. According to this numerical technique, it is possible to approximate the -th derivative of a sufficiently smooth function at a generic point within the reference domain as a weighted linear sum of the values that the function assumes in some chosen grid points. Starting from this definition, it is clear that the strong form of the governing equations is solved. Let us consider a two-dimensional domain, as the one needed to describe any doubly-curved surface, in which a generic function is defined. Three types of derivative can be computed at a generic point for and : the -th derivative with respect to the first coordinate
the -th derivative with respect to the second coordinate
and the mixed derivative of order
It is pointed out that denote the overall number of discrete points within the reference domain. The symbols and are introduce to specify the weighting coefficients for the derivatives at issue. It is clear that the key points of the present numerical approach are the choice of a proper discrete grid point distribution and the evaluation of the weighting coefficients. If the Lagrange polynomials are chosen to approximate the function, there is no restriction on the choice of the grid points. This aspect represents one of the main advantages of the GDQ method. In addition, the weighting coefficients can be easily evaluated if the recursive formulae given by Shu are employed [90]. Further details concerning this technique and its major applications can be found in the review paper by Tornabene et al. [91]. As far as the choice of the grid points is concerned, several distributions can be used, as highlighted in the work [91]. Some examples of grid distributions typically employed in many structural problems are listed in Table 1. It should be recalled that a discrete grid must be applied along the two principal coordinates as shown in the following relations

Table 1.
Eight different kinds of grid distributions. The indices and specify respectively and , when direction is taken into account. On the other hand, they correspond to and when direction is considered. Finally, if the grid distribution has to be applied along the coordinate , one gets and . It should be noted that denotes the Legendre polynomials.
The values of and , for and , can be found in Table 1.
5. Generalized Integral Quadrature Method
A numerical approach has to be introduced to evaluate the integrals needed to compute the elastic constants , , , defined in (30). In the present paper, the Generalized Integral Quadrature (GIQ) method is employed for this purpose. In fact, a numerical solution to the integrals in (30) must be found since it is impossible to solve them analytically due to their definition. According to this approach, the integral of a smooth function defined in a close domain can be evaluated as a weighted linear sum of the values that the function assumes in each point of the reference domain. In other words, this definition can be written as follows
where represents the number of discrete points defined within the reference domain, whereas are the weighting coefficients for the integration. These last quantities can be computed directly from the definitions of the corresponding weighting coefficients of the first order derivatives, as illustrated in depth in the review paper by Tornabene et al. [91]. It is clear that the GIQ method shares the same fundamentals with the GDQ method. Thus, the same recursive formulae given by Shu can be used once again to evaluate the weighting coefficients at issue, once an arbitrary grid distribution is chosen to discretize the reference domain. It should be noticed that differently from the well-known Gaussian integration schemes, this method is able to compute the weighting coefficients without any restriction on the position of the points within the reference domain. Therefore, all the different kinds of grid distributions listed in Table 1 can be used with this aim. For the sake of clarity, it should be specified that the one-dimensional domain in which the integrals in (30) must be evaluated is defined along the coordinate of the local reference system.
In other words, the integration procedure is performed through the shell thickness. As a consequence, the discrete nodes in which the functions are evaluated are placed following the definition shown below
for . The values of , for , can be found in Table 1, as well. For the sake of simplicity, in the present paper the Chebyshev-Gauss-Lobatto grid distribution is employed in any numerical test with due to its accuracy and stability features.
6. Free Vibration Analysis
The free vibrations of a doubly-curved laminated composite shell can be evaluated starting from the fundamental equation (38) by means of the GDQ method. A solution to the fundamental system can be found in the following form
in which the vector collects the mode shapes for each order of kinematic expansion . On the other hand, the symbol is introduce to specify the corresponding circular frequencies, which allow to compute the natural frequencies as . Once the first and second order derivatives with respect to the time variable of definition (49) are evaluated and substituted into relation (38), one gets
for . It should be recalled that equation (50) is the fundamental equation system which rules the free vibrations of any laminated composite shell. The system (50) can be easily solved by means of the GDQ method illustrated in the previous section. Once each derivative is discretized following definitions (42)–(44), the governing system can be conveniently written in its discrete form as follows
where denotes the global stiffness matrix, the inertia matrix, and the mode shape vector. Relation (51) is clearly a generalized linear eigenvalue problem, whose eigenvalues are the circular frequencies by definition. It is clear that the corresponding eigenvectors allow to define the mode shapes of the structures under consideration. The well-known kinematic condensation of non-domain degrees of freedom, the quantities related to the internal points of the domain (denoted by the subscript “”) can be separated from the ones linked to the boundaries (specified by the subscript “”). In this manner, the initial problem is noticeably simplified and can be written as follows
from which the following relation is carried out
assuming that is the identity matrix. The vector that collects the degrees of freedom is clearly subdivided into and , respectively. For the sake of clarity, denotes the vector of the degrees of freedom along the boundary, whereas represents the vector related to the internal degrees of freedom. The same partition is performed for both the stiffness matrix and the mass matrix . The solution of the system (53) allows to obtain the circular frequencies and consequently the natural frequencies.
7. Numerical Results
In the present section, several applications are presented to show the validity of both the present theoretical approach and the numerical methods for the evaluation of the free vibrations of various laminated composite shells. For this purpose, a preliminary convergence analysis is performed for two different mechanical configurations. Then, six shell structures are investigated. The results are compared with the natural frequencies available in the literature and the solutions obtained by means of a Finite Element model (FEM). The GDQ analysis is performed through a MATLAB code [106], whereas the commercial software Strand 7 is employed to obtain the FEM solution. It should be noticed that a specific tool has been developed to export the geometry of the considered doubly-curved shells into the commercial finite element code, as specified in the work [98]. For the sake of completeness, it should be specified that a different FEM model is used according to the investigated structure. For thick plates and shells, a three-dimensional model made of 20-node hexahedrons (“Hexa20”) is employed. On the other hand, a two-dimensional model made of 9-node quadrilateral elements (“Quad9”) is used for thin structures. The notations 3D-FEM and 2D-FEM are introduced to denote these solutions, respectively.
7.1. Convergence Analysis
A flat panel is considered in order to perform the convergence analysis. The length of each edge of the plate is equal to , whereas the thickness is given by . Two different lamination schemes are taken into account in order to prove the capability of the current approach to deal with different mechanical configurations. In particular, an isotropic plate made of Aluminum is considered firstly. Then, the same structure is taken with as lamination scheme. In this circumstance, each ply has the same thickness and is made of the same material (Graphite-Epoxy). For conciseness purposes, the mechanical properties of the materials employed in this section are summarized in Table 2. As far as the boundary conditions are concerned, the structure under consideration is fully clamped along each edge (CCCC). Figure 3 shows the convergence characteristics of the first three natural frequencies as a function of the total number of grid points varying the grid distribution. It can be easily noticed that the current approach reaches the maximum level of convergence with a number of point equal to , for both the two lamination schemes. In a similar manner, the various grids lead to similar tendency. It should be noticed that the graphs depicted in Figure 3 are related to the model. This means that both the reduced elastic coefficients and the shear correction factor () are employed.

Table 2.
Mechanical properties of the materials employed in the numerical analyses.
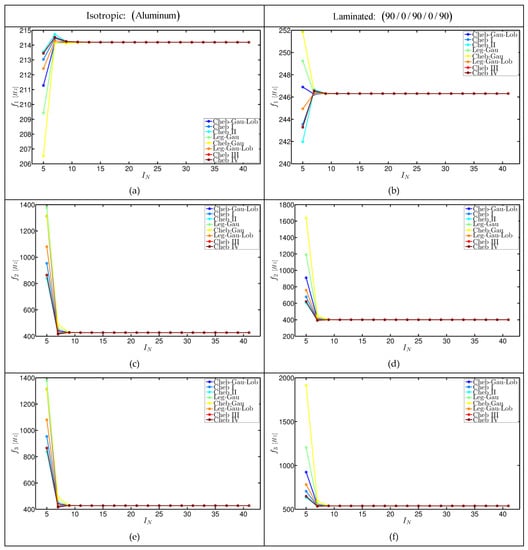
Figure 3.
Convergence characteristics of the first three frequencies for a completely clamped (CCCC) square plate () of thickness for two different lamination schemes as a function of the number of grid points , varying the grid distribution. The ELW theory is the in both the circumstances. (a) and (b) are related to the first frequency, (c) and (d) to the second one and (e) and (f) to the third one.
The same graphs could be achieved also for higher-order theories, whose results are just summarized in Table 3 (for the isotropic case) and in Table 4 (for the laminated one) for conciseness purposes. It should be noticed that the natural frequencies presented in Table 3 and Table 4 are obtained considering the Cheb-Gau-Lob grid distribution with . In addition, the 3D-FEM solution (9000 brick elements “Hexa20”) is also included in these tables. The GDQ solution is evidently in good agreement with the one used as a reference. For the sake of completeness, the analysis is carried out considering HSDTs with and without the Murakami’s function for the laminated composite plate (Table 4). In this circumstance, since the mechanical properties of each layer are the same, the benefits introduced by embedding this function are negligible. It should be noticed also that the reduced elastic coefficients are used only for a first order kinematic expansion (). On the other hand, a constant value of the shear correction factor equal to is used for both the first-order and second order theories () due to the reasons illustrated in the previous sections.

Table 3.
First 10 natural frequencies ([Hz]) for a CCCC isotropic square plate () of thickness for several higher-order ELW approaches. The Cheb-Gau-Lob grid distribution is used for the numerical solution assuming .

Table 4.
First 10 natural frequencies ([Hz]) for a CCCC laminated square plate () of thickness for several higher-order ELW approaches, with and without the Murakami’s function. The Cheb-Gau-Lob grid distribution is used for the numerical solution assuming .
7.2. Free vibrations of Laminated Composite Shells
In this paragraph, the free vibrations are investigated for the six structures depicted in Figure 4, in which the GDQ grid and local coordinate reference systems are shown for each geometry.
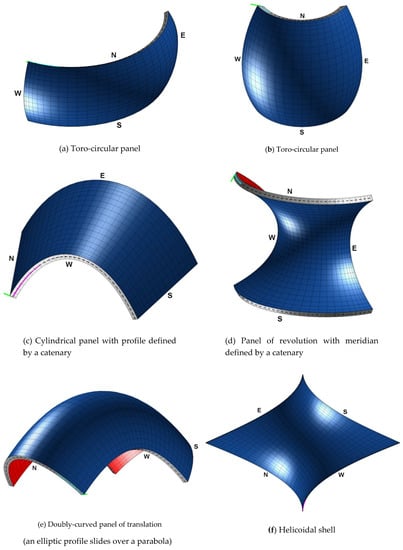
Figure 4.
Definition of the geometry of six shell structures: Generalized Differential Quadrature (GDQ) grid and local coordinate reference system representation.
The first two laminated shells are taken from the work by Wang et al. [13] and they are employed to compare the results given by the current approach with the ones obtained by using the Fourier-Ritz Method. The reference surface of the toro-circular panel at issue (Figure 4a,b) can be described by the following position vector
where are the curvilinear coordinates of the surface. is the radius of the circular meridian and represents an offset from the revolution axis. The first toro-circular panel is obtained by setting , whereas the second one can be achieved by using . In both these circumstances, the surfaces are bounded assuming the limitations and , whereas the thickness of the shells is . In order to perform the validation test, the following mechanical properties are employed for each orthotropic ply: , , , , , and . The natural frequencies are written in their non-dimensional form in Table 5 for the toro-circular panel with , whereas the results shown in Table 6 are related to the second surface (). Several lamination schemes and boundary conditions are taken into account. As far as the GDQ solutions are concerned, the natural frequencies are computed by using the Cheb-Gau-Lob grid distribution assuming and for the first case, and for the second one. As in the previous example, various orders of kinematic expansion are considered for the ELW approach without embedding the Murakami’s function. From Table 5 and Table 6, the excellent agreement with the reference solution can be easily noticed independently from the HSDTs, for each boundary condition and lamination scheme. It should be noted that in the reference work by Wang [13], a modified Fourier series approach in conjunction with a Ritz method is used to obtain a semi-analytical solution based on the First-order Shear Deformation Theory (FSDT).

Table 5.
Comparison of the frequency parameter for a laminated composite toro-circular panel () with different boundary conditions and lamination schemes. The ELW solutions are obtained by means of the GDQ method, using the Cheb-Gau-Lob grid distribution and assuming and .

Table 6.
Comparison of the frequency parameter for a laminated composite toro-circular panel () with different boundary conditions and lamination schemes. The ELW solutions are obtained by means of the GDQ method, using the Cheb-Gau-Lob grid distribution and assuming .
The next structure is a CCFC singly-curved cylindrical panel whose profile is defined by a catenary section (Figure 4c). It can be obtained by sliding a catenary curve on an inclined straight line, whose slope is equal to . The reference surface can be described by the following position vector
in which are the curvilinear coordinates of the surface, assuming and , with and . The structure is made of five layers of equal thickness and material (Graphite-Epoxy) oriented according to the scheme . The numerical solution is obtained by employing the Cheb-Gau-Lob grid distribution with and .
The first 10 natural frequencies of this structure are shown in Table 7 for different higher-order ELW models. As in the previous tests, each order of kinematic expansion is taken with and without the Murakami’s function to investigate its contribution. It is easy to notice that in the present case all the theories give the same results, independently from this function. The accuracy of the numerical technique is proven also by the comparison with the 3D-FEM solution (8000 brick elements “Hexa20”), which is nearly equal to the proposed ones. It should be recalled that the same considerations illustrated above concerning the use of both the shear correction factor and the reduced elastic coefficients are still valid. Finally, the first nine mode shapes for the shell structure at issue are depicted in Figure 5.

Table 7.
First 10 natural frequencies ([Hz]) for a CCFC laminated cylindrical surface with as lamination scheme for several higher-order ELW approaches, with and without the Murakami’s function. The Cheb-Gau-Lob grid distribution is used for the numerical solution assuming and .
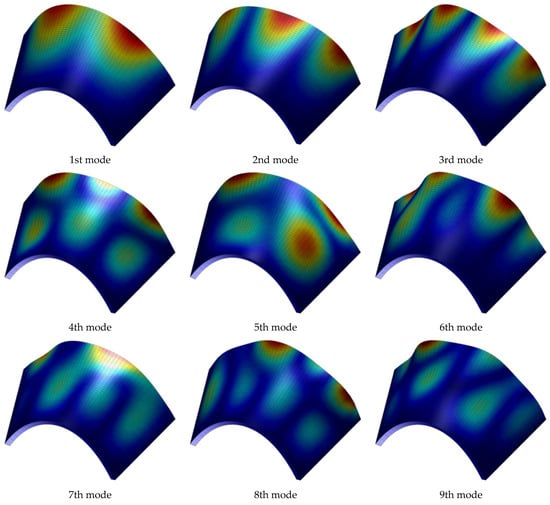
Figure 5.
First nine mode shapes for a CCFC laminated cylindrical surface with as lamination scheme.
The following structure is a CCCC doubly-curved revolution shell, whose reference surface is generated by the rotation about the revolution axis of a branch of a catenary (Figure 4d).
where are the curvilinear coordinates of the surface defined in the intervals and , with . The lamination scheme is chosen to define a so-called sandwich structure in which the core exhibits mechanical properties that are considerably different from the ones that characterize the external face-sheets, especially along the transverse direction.
In other words, if the stiffness of the constituent materials along the transverse direction is really different the zig-zag effect is generated. As a consequence, the Murakami’s function is embedded in the kinematic model to represent the effective behavior of the structure. The lamination scheme here is given by , assuming that the external orthotropic layers have equal thickness and are made of Graphite-Epoxy. On the other hand, the isotropic core is made of Ceramic Foam and it is defined by a thickness equal to . With reference to the mechanical properties of Table 2, it is easy to notice that . Thus, the shell falls into the class of sandwich structures. The first 10 natural frequencies are shown in Table 8 and are evaluated by using the Cheb-Gau-Lob grid distribution with . In the same table, the 3D-FEM solution is also reported for comparison purposes. It should be noticed that the first two orders of kinematic expansion () are taken into account with and without the shear correction factor. From Table 8 it can be noted that the use of the shear correction factor leads to a solution that are slightly different from the others. On the other hand, if the correction is not applied (which means ) the natural frequencies are similar to the ones obtained for higher-order theories, as well as the ones given by the 3D-FEM (11560 brick elements “Hexa20”). This aspect has been noticed by the authors in their previous work [69], where the same considerations were made for the corresponding theories based on the ESL approach embedded with the Murakami’s function. Thus, the shear correction factor should be neglected in those structural theories with the Murakami’s function, if a sandwich structure is analyzed. Finally, the related first nine mode shapes can be found in Figure 6.

Table 8.
First 10 natural frequencies ([Hz]) for a CCCC sandwich panel of revolution with as lamination scheme for several higher-order ELW approaches embedded with the Murakami’s function. The Cheb-Gau-Lob grid distribution is used for the numerical solution assuming .
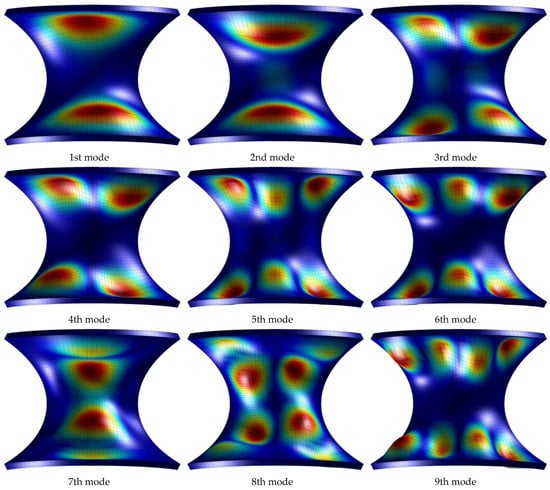
Figure 6.
First nine mode shapes for a CCCC sandwich panel of revolution with as lamination scheme.
The next structure is a CFCF (clamped-free-clamped-free) doubly-curved panel of translation, obtained by sliding an elliptic profile (defined by the semi diameters ) over a parabola (described through the parameters ). It should be noticed that this surface is obtained by moving the elliptic curve along the parabolic curve, keeping the plane containing the ellipse always orthogonal to the parabola (Figure 4e). The position vector , which defines the doubly-curved translational surface in hand, can be written as a function of the curvilinear coordinates
where the quantities expressed as a function of the coordinate are related to the parabola (curve which the other curve is sliding on), whereas the geometric parameters that depend on are linked to the ellipse (curve that is moving on the other one). As far as the parabolic branch is concerned, one gets
where is the characteristic parameter of the curve at issue, assuming the following values , , , . Further details concerning the geometric features of the parabolic arch, as well as the meaning of each parameter, can be found in the work [68]. On the other hand, the following terms are related to the elliptic curve
in which the characteristic parameter of the ellipse is given by , with and . The doubly-curved panel of translation is defined by setting and . The total thickness of the structure is equal to and the lamination scheme is . Each ply made of Graphite-Epoxy has the same thickness. The GDQ solution is obtained by using the Cheb-Gau-Lob grid distribution and the number of grid points is equal to and . The natural frequencies are shown in Table 9 for several higher-order ELW approaches, with and without the Murakami’s function. In the same table, the 3D-FEM solution is also given for comparison purposes. The use of the shear correction factor and the reduced elastic coefficients follows the same considerations illustrated before. It should be noticed that the analyses are carried out considering both the two types of Thickness functions defined in the previous sections. In the first row, the natural frequencies are obtained by means of the Legendre Polynomials, whereas in the second raw the results are related to the Lagrange ones. It can be noticed that the solutions are not affected by this choice, since the natural frequencies are the same independently from the approach. Even in this circumstance, the solutions are in excellent agreement with the ones provided by the FEM (9600 brick elements “Hexa20”). The first nine mode shapes are depicted in Figure 7. It is important to noticed that the deformed shapes follow the boundary conditions applied to the structure. It should be noted that all the structures considered until now are included in the category of thick and moderately thick shells.

Table 9.
First 10 natural frequencies ([Hz]) for a CFCF (clamped-free-clamped-free) laminated panel of translation with as lamination scheme for several higher-order ELW approaches, with and without the Murakami’s function. The Cheb-Gau-Lob grid distribution is used for the numerical solution assuming and .
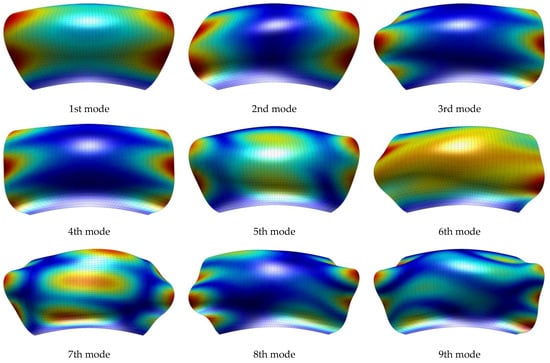
Figure 7.
First nine mode shapes for a CFCF laminated panel of translation with as lamination scheme.
The last example is focused on the free vibration analysis of a completely clamped (CCCC) thin helicoidal shell, whose geometry is shown in Figure 4f. The reference surface can be described in principal curvilinear coordinates according to the following position vector
in which , whereas the domain is defined by the limits and . The structure is made of four plies (Graphite-Epoxy) of equal thickness oriented as . The overall thickness is given by . The first 10 natural frequencies for this shell are shown in Table 10 for various ELW models. The GDQ solution is achieved by setting for the Cheb-Gau-Lob grid distribution. On the other hand, the solution obtained by the FEM is two-dimensional (1600 plate elements “Quad9”).

Table 10.
First 10 natural frequencies ([Hz]) for a CCCC thin laminated helicoidal surface with as lamination scheme for several higher-order ELW approaches. The Cheb-Gau-Lob grid distribution is used for the numerical solution assuming .
It can be noticed from the proposed results match perfectly even in this case. The Murakami’s function is not taken into account due to the reduced value of thickness that allows to neglect the possible zig-zag effect. The first nine mode shapes are depicted in Figure 8. This last example has clearly proven also the accuracy of the present method for the free vibration analysis of thin shells.
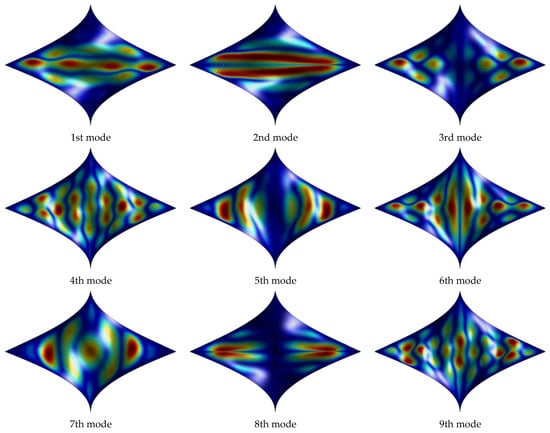
Figure 8.
First nine mode shapes for a CCCC thin laminated helicoidal shell with as lamination scheme.
7.3. Comparison with the LW and ESL Approaches
In this last paragraph, the results obtained by means of the proposed ELW approach are compared to the ones achievable through the ESL and LW models. For this purpose, the laminated conical shell described in the works [61,83] is considered. The same work can be taken as a reference for both the geometric and mechanical properties of the laminated composite shell at issue. For completeness purposes, the conical surface in hand is given by the following position vector
where . The constant angle represents the slope of the straight meridian profile, whereas is the radius measured at the top of the shell. The two-dimensional domain is bounded by the limitations and , with , and . The shell is made of two layers of Graphite-Epoxy characterized by the same thickness value . On the other hand, the lamination scheme is given by . As far as the boundary conditions are concerned, the conical shell is completely clamped along the top edge, whereas the lower circumference is free.
The GDQ method is employed to obtain the numerical solution even in this circumstance, for all the considered approaches. Since various orders of kinematic expansion are taken into account, the comparison should be performed by considering the corresponding higher-order displacement field for each approach (ESL, ELW, and LW). In particular, the ESL solutions are taken from the paper [61], whereas the work [83] is the reference for the LW ones. The same grid distributions and total values of discrete points specified in the works [61,83] are used also in the present paper. The natural frequencies of the conical shell are shown in Table 11, where the solutions obtained through a three-dimensional finite element model are presented too. It should be noted that both the ESL and ELW models are taken with and without the Murakami’s function. In general, the ELW approach provides values of natural frequencies placed between the ones given by the corresponding ESL and LW models. In other words, the results obtained by the ELW approach are closer to the LW solutions, as well as to the 3D-FEM, than the corresponding ESL ones. Nevertheless, the computational cost of the ELW model is reduced if compared to the one that characterizes the LW approach, since the proposed methodology does not require to consider each layer separately. For the sake of completeness, the reader can refer to the papers [61,83] to understand the meaning of the ESL and LW models introduced in Table 11.

Table 11.
Comparison of the natural frequencies for a laminated composite conical shell [61,83]. The solutions obtained through the present approach are compared to the results given by the corresponding ESL and Layer-Wise (LW) models.
8. Conclusions
A new higher-order approach is presented to analyze the natural frequencies of thin and thick laminated composite shells. The method, named Equivalent Layer-Wise (ELW) method, is used to evaluate the overall mechanical and geometric properties directly on the shell middle surface, as commonly done in the Equivalent Single Layer (ESL) approaches, and the displacement field has been described by using the same kinematic expansions employed in the most typical Layer-Wise (LW) models, but without considering each layer separately. The governing equation are solved numerically by the GDQ method. This new approach has been validated by comparison with the results available in the literature and those obtained using a commercial finite element code. It has been illustrated that the solutions are in excellent agreement with the reference ones for several boundary conditions and various mechanical configurations. When compared to the corresponding three-dimensional finite element model, the present methodology requires a lower number of degrees of freedom to reach the same level of accuracy. In addition, since the differential geometry is employed to describe the reference doubly-curved surface, several geometric shapes have been easily obtained and analyzed. In fact, the domain has been defined using only one element, whereas the FEM models required many brick or plate elements to describe the same geometry accurately. It should be noted that the present methodology provides a physical meaning to the degrees of freedom of the problem for each order of kinematic expansion, different from the ESL approach, in which the generalized displacements related to higher-order expansions represent a mathematical parametrization of these quantities. Furthermore, the structural analysis of a laminated composite structure has not required the same computational resources needed by the LW methods. Thus, the computational time has been noticeably reduced when compared to the LW models. It should be noted also that the use of the Murakami’s function has been also investigated by taking into account a sandwich structure. The linear static analysis of laminated composite shell structures can be seen as a future development of the present approach. Finally, it should be highlighted that the presented methodology could be used to deal with some typical aerospace applications which require an efficient tool to analyze composite structures characterized by complex geometries, with different material and thickness distributions.
Acknowledgments
The research topic is one of the subjects of the Centre of Study and Research for the Identification of Materials and Structures (CIMEST)-“M. Capurso” of the University of Bologna (Italy).
Author Contributions
All the authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Reddy, J.N. Mechanics of laminated composite plates and shells, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential Geometry Higher-order Structural Theories, 1st ed.; Societa Edirtrice Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential and Integral Quadrature. Strong Formulation Finite Element Method, 1st ed.; Societa Edirtrice Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Fantuzzi, N.; Brischetto, S.; Tornabene, F.; Viola, E. 2D and 3D Shell Models for the Free Vibration Investigation of Functionally Graded Cylindrical and Spherical Panels. Compos. Struct. 2016, 154, 573–590. [Google Scholar] [CrossRef]
- Brischetto, S.; Tornabene, F.; Fantuzzi, N.; Viola, E. 3D Exact and 2D Generalized Differential Quadrature Models for Free Vibration Analysis of Functionally Graded Plates and Cylinders. Meccanica 2016, 51, 2059–2098. [Google Scholar] [CrossRef]
- Gutierrez Rivera, M.; Reddy, J.N.; Amabili, M. A new twelve-parameter spectral/hp shell finite element for large deformation analysis of composite shells. Compos. Struct. 2016, 151, 183–196. [Google Scholar] [CrossRef]
- Groh, R.M.J.; Weaver, P.M. A computationally efficient 2D model for inherently equilibrated 3D stress predictions in heterogeneous laminated plates. Part I: Model formulation. Compos. Struct. 2016, 156, 171–185. [Google Scholar]
- Groh, R.M.J.; Weaver, P.M. A computationally efficient 2D model for inherently equilibrated 3D stress predictions in heterogeneous laminated plates. Part II: Model validation. Compos. Struct. 2016, 156, 186–217. [Google Scholar]
- Amabili, M. A new third-order shear deformation theory with non-linearities in shear for static and dynamic analysis of laminated doubly curved shells. Compos. Struct. 2015, 128, 260–273. [Google Scholar] [CrossRef]
- Maturi, D.A.; Ferreira, A.J.M.; Zenkour, A.M.; Mashat, D.S. Analysis of Laminated Shells by Murakami’s Zig-Zag Theory and Radial Basis Functions Collocation. J. Appl. Math. 2013, 2013, 1–14. [Google Scholar] [CrossRef]
- Kulikov, G.M.; Mamontov, A.A.; Plotnikova, S.V.; Mamontov, S.A. Exact geometry solid-shell element based on a sampling surfaces technique for 3D stress analysis of doubly-curved composite shells. Curved Layer. Struct. 2016, 3, 1–16. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M. Free vibrations and buckling analysis of laminated plates by oscillatory radial basis functions. Curved Layer. Struct. 2016, 3, 17–21. [Google Scholar] [CrossRef]
- Wang, Q.; She, D.; Pang, F.; Liang, Q. Vibrations of Composite Laminated Circular Panels and Shells of Revolution with General Elastic Boundary Conditions via Fourier-Ritz Method. Curved Layer. Struct. 2016, 3, 105–136. [Google Scholar] [CrossRef]
- Piskunov, V.G.; Verijenko, V.E.; Adali, S.; Summers, E.B. A Higher-order Theory for the Analysis of Laminated Plates and Shells with Shear and Normal Deformation. Int. J. Engng. Sci. 1993, 31, 967–988. [Google Scholar] [CrossRef]
- Wu, C.-P.; Hung, Y.-C. Asymptotic theory of laminated circular conical shells. Int. J. Engng. Sci. 1999, 37, 977–1005. [Google Scholar] [CrossRef]
- Brischetto, S. An exact 3d solution for free vibrations of multilayered cross-ply composite and sandwich plates and shells. Int. J. Appl. Mechanics 2014, 6, 1450076. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. Exact 3D solutions and finite element 2D models for free vibration analysis of plates and cylinders. Curved Layer. Struct. 2014, 1, 59–92. [Google Scholar] [CrossRef]
- Le, K.C.; Yi, J.-H. An asymptotically exact theory of smart sandwich shells. Int. J. Eng. Sci. 2016, 106, 179–198. [Google Scholar]
- Ye, T.; Jin, G.; Zhang, Y. Vibrations of composite laminated doubly-curved shells of revolution with elastic restraints including shear deformation, rotary inertia and initial curvature. Compos. Struct. 2015, 133, 202–225. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J.N. A general third-order theory of functionally graded plates with modified couple stress effect and the von Kármán nonlinearity: Theory and finite element analysis. Acta Mech. 2015, 226, 2973–2998. [Google Scholar] [CrossRef]
- Librescu, L.; Reddy, J.N. A few remarks concerning several refined theories of anisotropic composite laminated plates. Int. J. Eng. Sci. 1989, 27, 515–527. [Google Scholar] [CrossRef]
- Whitney, J.M.; Pagano, N.J. Shear Deformation in Heterogeneous Anisotropic Plates. J. Appl. Mech.-T. ASME 1970, 37, 1031–1036. [Google Scholar] [CrossRef]
- Whitney, J.M.; Sun, C.T. A Higher Order Theory for Extensional Motion of Laminated Composites. J. Sound Vib. 1973, 30, 85–97. [Google Scholar] [CrossRef]
- Reissner, E. On transverse bending of plates, including the effect of transverse shear deformation. Int. J. Solids Struct. 1975, 11, 569–573. [Google Scholar] [CrossRef]
- Murthy, M.V.V. An Improved Transverse Shear Deformation Theory for Laminated Anisotropic Plates; NASA Technical Paper; NASA: Hampton, VA, USA, 1981.
- Green, A.E.; Naghdi, P.M. A theory of composite laminated plates. IMA J. Appl. Math. 1982, 29, 1–23. [Google Scholar] [CrossRef]
- Bert, C.W. A Critical Evaluation of New Plate Theories Applied to Laminated Composites. Compos. Struct. 1984, 2, 329–347. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech.-T. ASME 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Shirakawa, K. Bending of plates based on improved theory. Mech. Res. Commun. 1985, 10, 205–211. [Google Scholar] [CrossRef]
- Reddy, J.N.; Liu, C.F. A higher-order shear deformation theory for laminated elastic shells. Int. J. of Eng. Sci. 1985, 23, 319–330. [Google Scholar]
- Reddy, J.N. A Generalization of the Two-Dimensional Theories of Laminated Composite Plates. Commun. Appl. Numer. M. 1987, 3, 173–180. [Google Scholar] [CrossRef]
- Reddy, J.N. On Refined Theories of Composite Laminates. Meccanica 1990, 25, 230–238. [Google Scholar] [CrossRef]
- Robbins, D.H.; Reddy, J.N. Modeling of Thick Composites Using a Layer-Wise Laminate Theory. Int. J. Numer. Meth. Eng. 1993, 36, 655–677. [Google Scholar] [CrossRef]
- Alibeiglooa, A.; Shakeri, M.; Kari, M.R. Free vibration analysis of antisymmetric laminated rectangular plates with distributed patch mass using third-order shear deformation theory. Ocean Eng. 2008, 35, 183–190. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, K.-M. Free vibration analysis of symmetric laminated composite plates by trigonometric shear deformation theory and inverse multiquadric RBF. Thin Wall. Struct. 2009, 47, 304–310. [Google Scholar] [CrossRef]
- Amabili, M.; Reddy, J.N. A new non-linear higher-order shear deformation theory for large-amplitude vibrations of laminated doubly curved shells. Int. J. Nonlinear Mech. 2010, 45, 409–418. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. Free vibration of laminated composite plates using two variable refined plate theory. Int. J. Mech. Sci. 2010, 52, 626–633. [Google Scholar] [CrossRef]
- Kumar, A.; Chakrabarti, A.; Bhargava, P. Vibration of laminated composites and sandwich shells based on higher order zigzag theory. Eng. Struct. 2013, 56, 880–888. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. General Higher-Order Shear Deformation Theories for the Free Vibration Analysis of Completely Doubly-Curved Laminated Shells and Panels. Compos. Struct. 2013, 95, 639–666. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. Static Analysis of Completely Doubly-Curved Laminated Shells and Panels Using General Higher-order Shear Deformation Theories. Compos. Struct. 2013, 101, 59–93. [Google Scholar] [CrossRef]
- Viola, E.; Rossetti, L.; Fantuzzi, N.; Tornabene, F. Static Analysis of Functionally Graded Conical Shells and Panels Using the Generalized Unconstrained Third Order Theory Coupled with the Stress Recovery. Compos. Struct. 2014, 112, 44–65. [Google Scholar] [CrossRef]
- Sahoo, R.; Singh, B.N. A new trigonometric zigzag theory for buckling and free vibration analysis of laminated composite and sandwich plates. Compos. Struct. 2014, 117, 316–332. [Google Scholar] [CrossRef]
- Vidal, P.; Polit, O.; D’Ottavio, M.; Valot, E. Assessment of the refined sinus plate finite element: Free edge effect and Meyer-Piening sandwich test. Finite Elem. Anal. Des. 2014, 92, 60–71. [Google Scholar] [CrossRef]
- Wang, X.; Shi, G. A refined laminated plate theory accounting for the third-order shear deformation and interlaminar transverse stress continuity. Appl. Math. Model. 2015, 39, 5659–5680. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.; Chen, X.; Xie, Y.; Miao, H. Analysis of laminated composite plates using wavelet finite element method and higher-order plate theory. Compos. Struct. 2015, 131, 248–258. [Google Scholar] [CrossRef]
- Viola, E.; Rossetti, L.; Fantuzzi, N.; Tornabene, F. Generalized Stress-Strain Recovery Formulation Applied to Functionally Graded Spherical Shells and Panels Under Static Loading. Compos. Struct. 2016, 156, 145–164. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Farid, M.; Zahedinejad, P. A three-dimensional layerwise-differential quadrature free vibration analysis of laminated cylindrical shells. Int. J. Pres. Ves. Pip. 2008, 85, 450–458. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Afsari, A.; Zahedinejad, P.; Bahadori, R. Three-dimensional layerwise-finite element free vibration analysis of thick laminated annular plates on elastic foundation. Appl. Math. Model. 2010, 34, 776–790. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Guedes Soares, C. A new trigonometric layerwise shear deformation theory for the finite element analysis of laminated composite and sandwich plates. Comput. Struct. 2012, 94–95, 45–53. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Carrera, E.; Nguyen-Xuan, H. Isogeometric analysis of laminated composite and sandwich plates using a layerwise deformation theory. Compos. Struct. 2013, 104, 196–214. [Google Scholar] [CrossRef]
- Mantari, J.L.; Guedes Soares, C. Generalized layerwise HSDT and finite element formulation for symmetric laminated and sandwich composite plates. Compos. Struct. 2013, 105, 319–331. [Google Scholar] [CrossRef]
- Guo, Y.; Nagy, A.P.; Gürdal, Z. A layerwise theory for laminated composites in the framework of isogeometric analysis. Compos. Struct. 2014, 107, 447–457. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Layer-wise dynamic stiffness solution for free vibration analysis of laminated composite plates. J. Sound Vib. 2014, 333, 200–227. [Google Scholar] [CrossRef]
- Yazdani, S.; Ribeiro, P. A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Compos. Struct. 2015, 120, 531–542. [Google Scholar] [CrossRef]
- Band, U.N.; Desai, Y.M. Coupled higher order and mixed layerwise finite element based static and free vibration analyses of laminated plates. Compos. Struct. 2015, 128, 406–414. [Google Scholar] [CrossRef]
- Li, D.H. Extended layerwise method of laminated composite shells. Compos. Struct. 2016, 136, 313–344. [Google Scholar] [CrossRef]
- Carrera, E. Theories and Finite Elements for Multilayered, Anisotropic, Composite Plates and Shells. Arch. Comput. Meth. Eng. 2002, 9, 87–140. [Google Scholar] [CrossRef]
- Carrera, E. Historical review of zig-zag theories for multilayered plates and shells. Appl. Mech. Rev. 2003, 56, 287–308. [Google Scholar] [CrossRef]
- Carrera, E. On the use of the Murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 2004, 82, 541–554. [Google Scholar] [CrossRef]
- Biscani, F.; Giunta, G.; Belouettar, S.; Hu, H.; Carrera, E. Mixed-dimensional modeling by means of solid and higher-order multi-layered plate finite elements. Mech. Adv. Mat. Struct. 2016, 23, 960–970. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Fantuzzi, N. General higher-order equivalent single layer theory for free vibrations of doubly-curved laminated composite shells and panels. Compos. Struct. 2013, 104, 94–117. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Carrera, E. Static Analysis of Doubly-Curved Anisotropic Shells and Panels Using CUF Approach, Differential Geometry and Differential Quadrature Method. Compos. Struct. 2014, 107, 675–697. [Google Scholar] [CrossRef]
- Tornabene, F; Fantuzzi, N.; Viola, E.; Reddy, J.N. Winkler-Pasternak Foundation Effect on the Static and Dynamic Analyses of Laminated Doubly-Curved and Degenerate Shells and Panels. Compos. Part B-Eng. 2014, 57, 269–296. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Local GDQ Method Applied to General Higher-Order Theories of Doubly-Curved Laminated Composite Shells and Panels: The Free Vibration Analysis. Compos. Struct. 2014, 116, 637–660. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Free vibrations of free-form doubly-curved shells made of functionally graded materials using higher-order equivalent single layer theories. Compos. Part B Eng. 2014, 67, 490–509. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Batra, R.C. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 2015, 119, 67–89. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Higher-Order Theories for the Free Vibration of Doubly-Curved Laminated Panels with Curvilinear Reinforcing Fibers by Means of a Local Version of the GDQ Method. Compos. Part B-Eng. 2015, 81, 196–230. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of Agglomeration on the Natural Frequencies of Functionally Graded Carbon Nanotube-Reinforced Laminated Composite Doubly-Curved Shells. Compos. Part B-Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Local GDQ Method for the Natural Frequencies of Doubly-Curved Shells with Variable Thickness: A General Formulation. Compos. Part B-Eng. 2016, 92, 265–289. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E. Inter-Laminar Stress Recovery Procedure for Doubly-Curved, Singly-Curved, Revolution Shells with Variable Radii of Curvature and Plates Using Generalized Higher-Order Theories and the Local GDQ Method. Mech. Adv. Mat. Struct. 2016, 23, 1019–1045. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The GDQ Method for the Free Vibration Analysis of Arbitrarily Shaped Laminated Composite Shells Using a NURBS-Based Isogeometric Approach. Compos. Struct. 2016, 154, 190–218. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Eisenberger, M.; Fantuzzi, N.; Tornabene, F.; Viola, E. Vibration Analysis of Variable Thickness Plates and Shells by the Generalized Differential Quadrature Method. Compos. Struct. 2016, 156, 218–237. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear Static Response of Nanocomposite Plates and Shells Reinforced by Agglomerated Carbon Nanotubes. Compos. Part B-Eng. 2016, in press. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. On the Mechanics of Laminated Doubly-Curved Shells Subjected to Point and Line Loads. Int. J. Engng. Sci. 2016, 109, 115–164. [Google Scholar] [CrossRef]
- Dozio, L. A hierarchical formulation of the state-space Levy’s method for vibration analysis of thin and thick multilayered shells. Compos. Part B-Eng. 2016, 98, 97–107. [Google Scholar] [CrossRef]
- Dozio, L.; Alimonti, L. Variable kinematic finite element models of multilayered composite plates coupled with acoustic fluid. Mech. Adv. Mater. Struct. 2016, 23, 981–996. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L. A variable-kinematic model for variable stiffness plates: Vibration and buckling analysis. Compos. Struct. 2016, 142, 15–26. [Google Scholar] [CrossRef]
- Wenzel, C.; D’Ottavio, M.; Polit, O.; Vidal, P. Assessment of free-edge singularities in composite laminates using higher-order plate elements. Mech. Adv. Mat. Stuct. 2016, 23, 948–959. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Accurate Inter-Laminar Recovery for Plates and Doubly-Curved Shells with Variable Radii of Curvature Using Layer-Wise Theories. Compos. Struct. 2015, 124, 368–393. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Dynamic Analysis of Thick and Thin Elliptic Shell Structures Made of Laminated Composite Materials. Compos. Struct. 2015, 133, 278–299. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Free Vibrations of Composite Oval and Elliptic Cylinders by the Generalized Differential Quadrature Method. Thin-Wall. Struct. 2015, 97, 114–129. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Higher-Order Structural Theories for the Static Analysis of Doubly-Curved Laminated Composite Panels Reinforced by Curvilinear Fibers. Thin-Wall. Struct. 2016, 102, 222–245. [Google Scholar] [CrossRef]
- Tornabene, F. General Higher Order Layer-Wise Theory for Free Vibrations of Doubly-Curved Laminated Composite Shells and Panels. Mech. Adv. Mat. Struct. 2016, 23, 1046–1067. [Google Scholar] [CrossRef]
- Demasi, L. ∞3 Hierarchy plate theories for thick and thin composite plates: The generalized unified formulation. Compos. Struct. 2008, 84, 256–270. [Google Scholar] [CrossRef]
- D’Ottavio, M. A Sublaminate Generalized Unified Formulation for the analysis of composite structures. Compos. Struct. 2016, 142, 187–199. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Reissner's Mixed Variational Theorem and variable kinematics in the modelling of laminated composite and FGM doubly-curved shells. Compos. Part B-Eng. 2016, 89, 408–423. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Quasi-3D beam models for the computation of eigenfrequencies of functionally graded beams with arbitrary boundary conditions. Compos. Struct. 2016, 154, 239–255. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Modal characteristics of P- and S-FGM plates with temperature-dependent materials in thermal environment. J. Therm. Stresses 2016, 39, 854–873. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Banerjee, J.R. Axiomatic/asymptotic PVD/RMVT-based shell theories for free vibrations of anisotropic shells using an advanced Ritz formulation and accurate curvature descriptions. Compos. Struct. 2014, 108, 91–110. [Google Scholar] [CrossRef]
- Shu, C. Differential quadrature and its application in engineering; Springer: Berlin, Germany, 2000. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67, 020801. [Google Scholar] [CrossRef]
- Tornabene, F.; Reddy, J.N. FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: A GDQ solution for static analysis with a posteriori stress and strain recovery. J. Indian Inst. Sci. 2013, 93, 635–688. [Google Scholar]
- Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Viola, E.; Tornabene, F.; Fantuzzi, N.; Zenkour, A.M. Analysis of Thick Isotropic and Cross-Ply Laminated Plates by Generalized Differential Quadrature Method and a Unified Formulation. Compos. Part B-Eng. 2014, 58, 544–552. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Strong Formulation Finite Element Method: Stability and Accuracy. Fract. Struct. Integr. 2014, 29, 251–265. [Google Scholar]
- Fantuzzi, N.; Bacciocchi, M.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. Radial Basis Functions Based on Differential Quadrature Method for the Free Vibration of Laminated Composite Arbitrary Shaped Plates. Compos. Part B-Eng. 2015, 78, 65–78. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. A New Approach for Treating Concentrated Loads in Doubly-Curved Composite Deep Shells with Variable Radii of Curvature. Compos. Struct. 2015, 131, 433–452. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong Formulation Isogeometric Analysis (SFIGA) for Laminated Composite Arbitrarily Shaped Plates. Compos. Part B-Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Neves, A.M.A.; Ferreira, A.J.M. MLSDQ Based on RBFs for the Free Vibrations of Laminated Composite Doubly-Curved Shells. Compos. Part B-Eng. 2016, 99, 30–47. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Dimitri, R.; Tornabene, F. A SFEM-Based Evaluation of Mode-I Stress Intensity Factor in Composite Structures. Compos. Struct. 2016, 145, 162–185. [Google Scholar] [CrossRef]
- Tornabene, F.; Dimitri, R.; Viola, E. Transient Dynamic Response of Generally-Shaped Arches Based on a GDQ-Time-Stepping Method. Int. J. Mech. Sci. 2016, 114, 277–314. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free Vibration Analysis of Arbitrarily Shaped Functionally Graded Carbon Nanotube-Reinforced Plates. Compos. Part B-Eng. 2016, in press. [Google Scholar] [CrossRef]
- Dimitri, R.; Fantuzzi, N.; Tornabene, F.; Zavarise, G. Innovative Numerical Methods Based on SFEM and IGA for Computing Stress Concentrations in Isotropic Plates with Discontinuities. Int. J. Mech. Sci. 2016, 118, 166–187. [Google Scholar] [CrossRef]
- Kraus, H. Thin Elastic Shells; John Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Kulikov, G.M.; Carrera, E. Finite deformation higher-order shell models and rigid-body motions. Int. J. Solids Struct. 2008, 45, 3153–3172. [Google Scholar] [CrossRef]
- Kulikov, G.M.; Plotnikova, S.V. On the use of sampling surfaces method for solution of 3D elasticity problems for thick shells. Z. Angew.Math. Mech. 2012, 92, 910–920. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. DiQuMASPAB Software. Bologna, Italy, 2013. Available online: http://software.dicam.unibo.it/diqumaspab-project.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).