Output Filter Design for a Novel Dual-Input PV-Wind Power Converter by Energy Balance Principle
Abstract
:1. Introduction
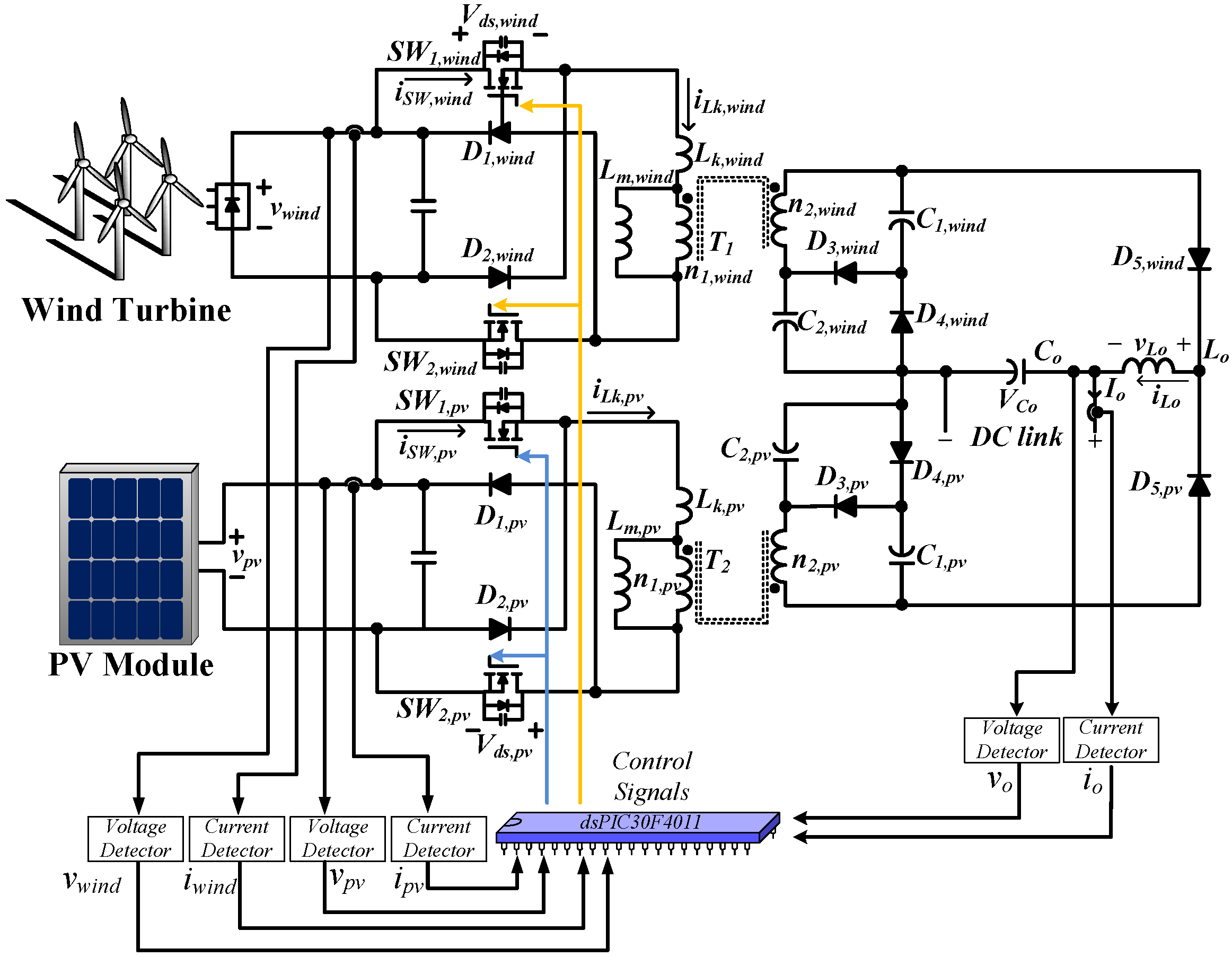
2. Characteristics of Proposed Converter
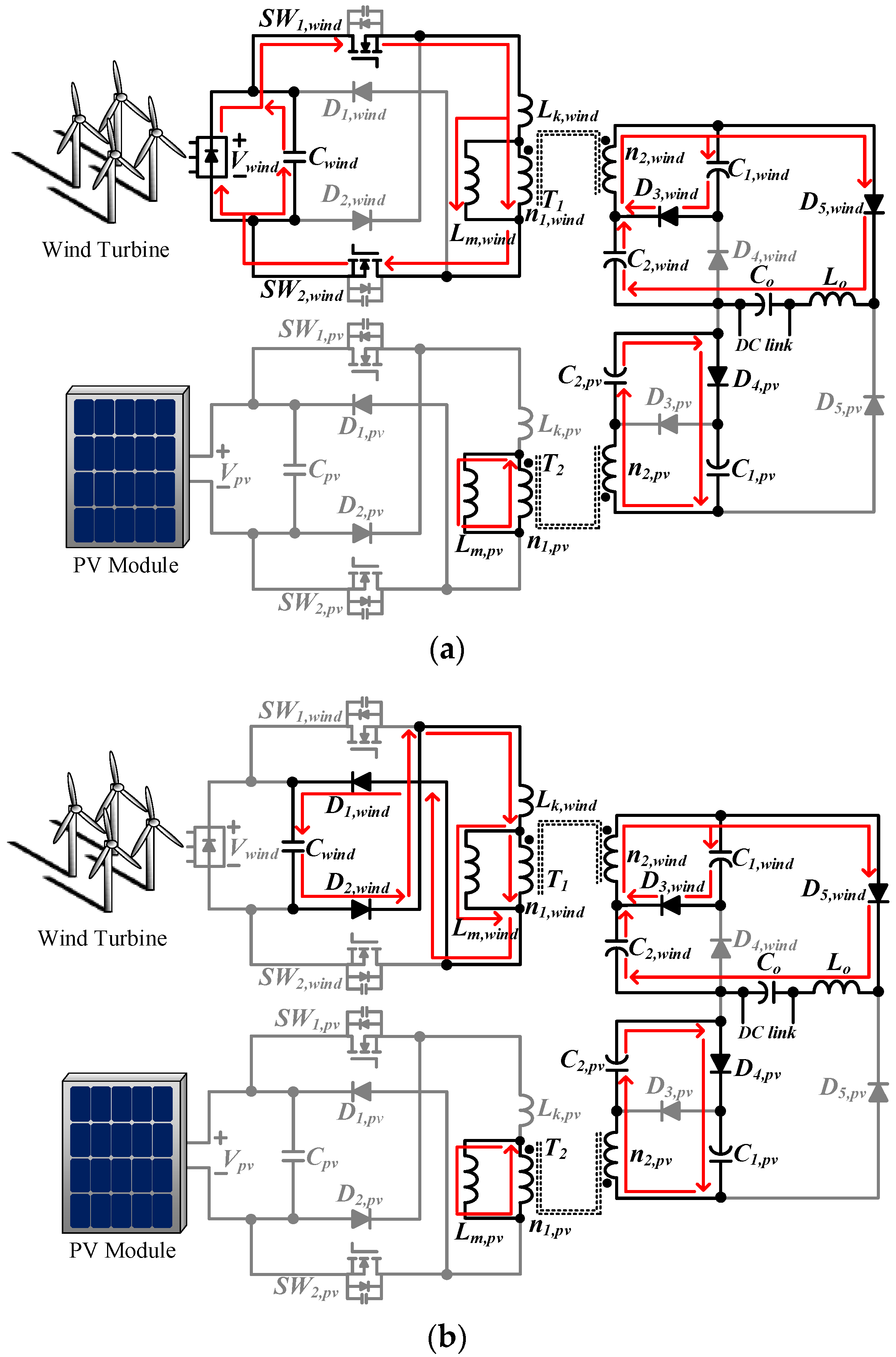
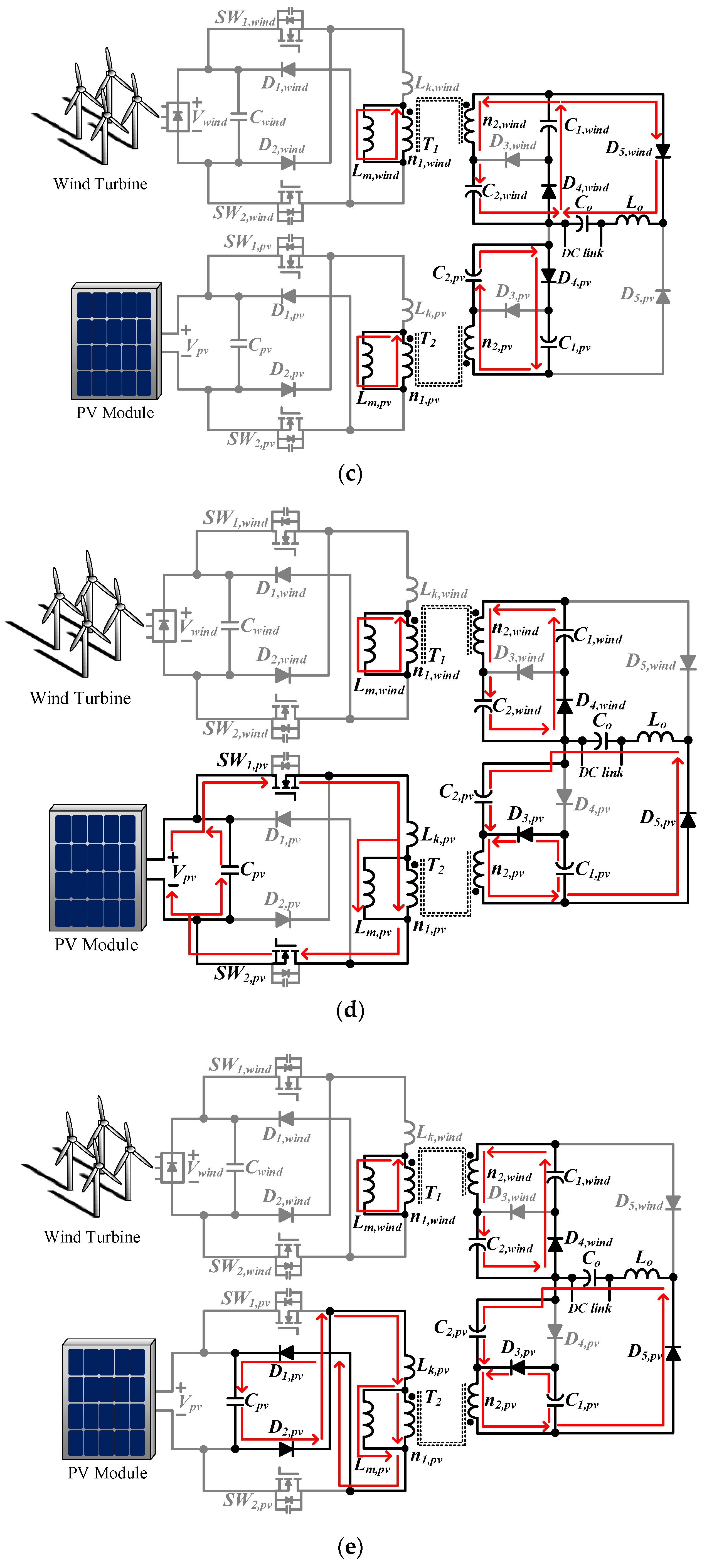
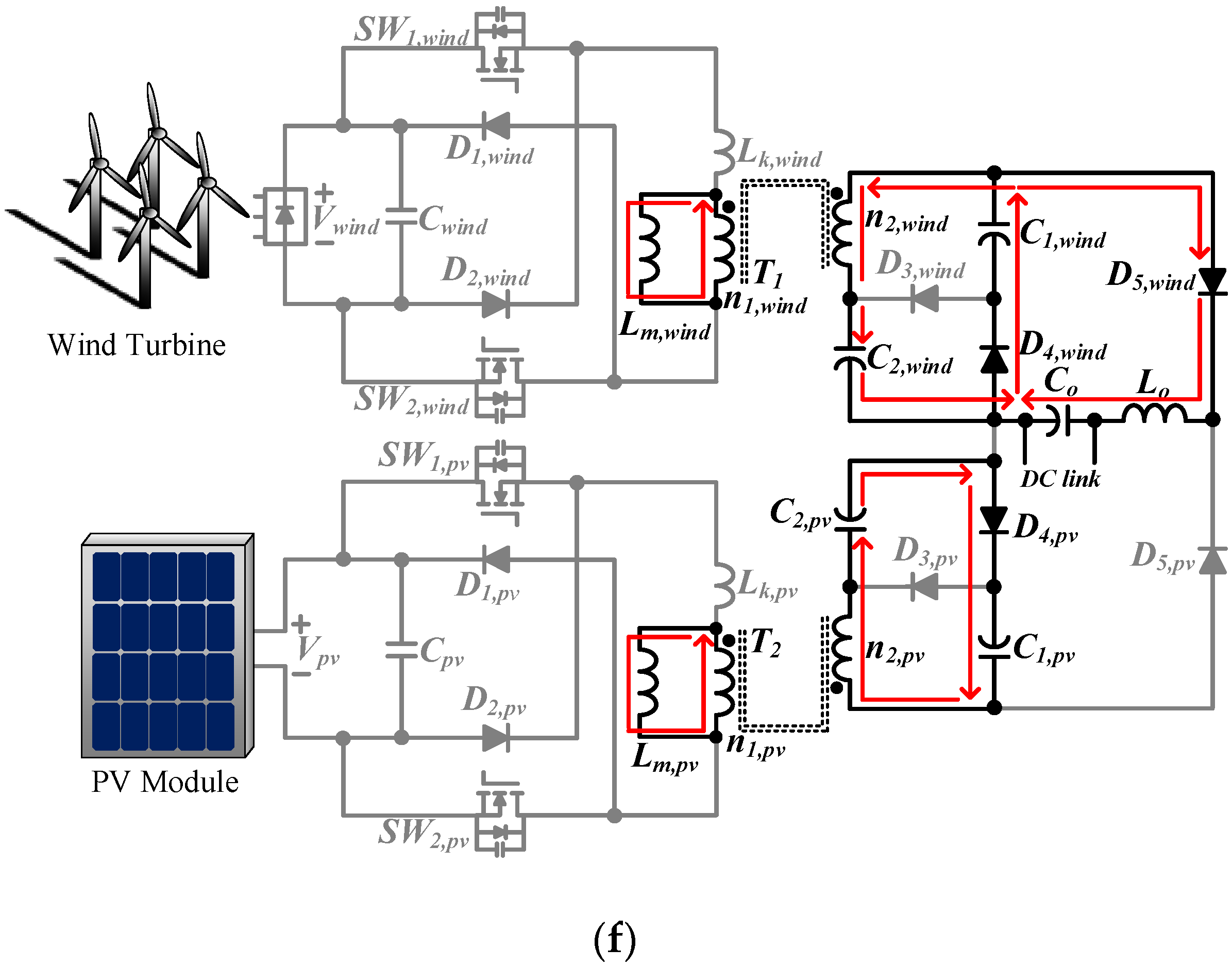
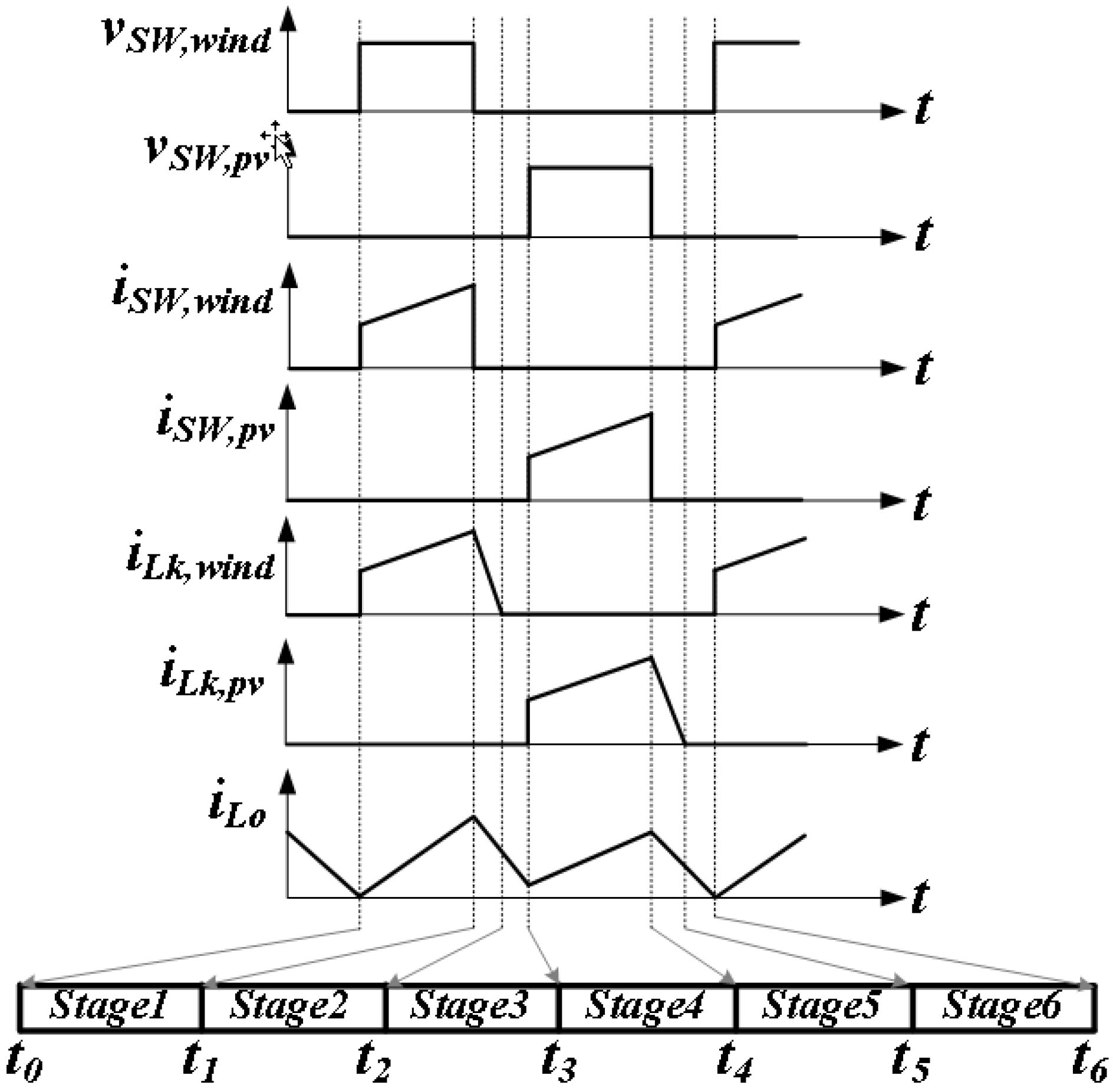
3. Operation Principle
- (1)
- In Figure 2, capacitances of C1,wind, C2,wind, C1,pv, and C2,pv are large enough so that all the voltages across them can be regarded as constant in a switching cycle.
- (2)
- The internal resistances and parasitic capacitances in all active switches are neglected.
- (3)
- All diodes are ideal.
4. Inductance Derivation
- Step 1:
- Find the voltages across C1,wind and C1,pv, VC1,wind and VC1,pv.
- Step 2:
- Apply energy balance principle to Lm,wind and Lm,pv to determine the voltages across C2,wind and C2,pv, respectively.
- Step 3:
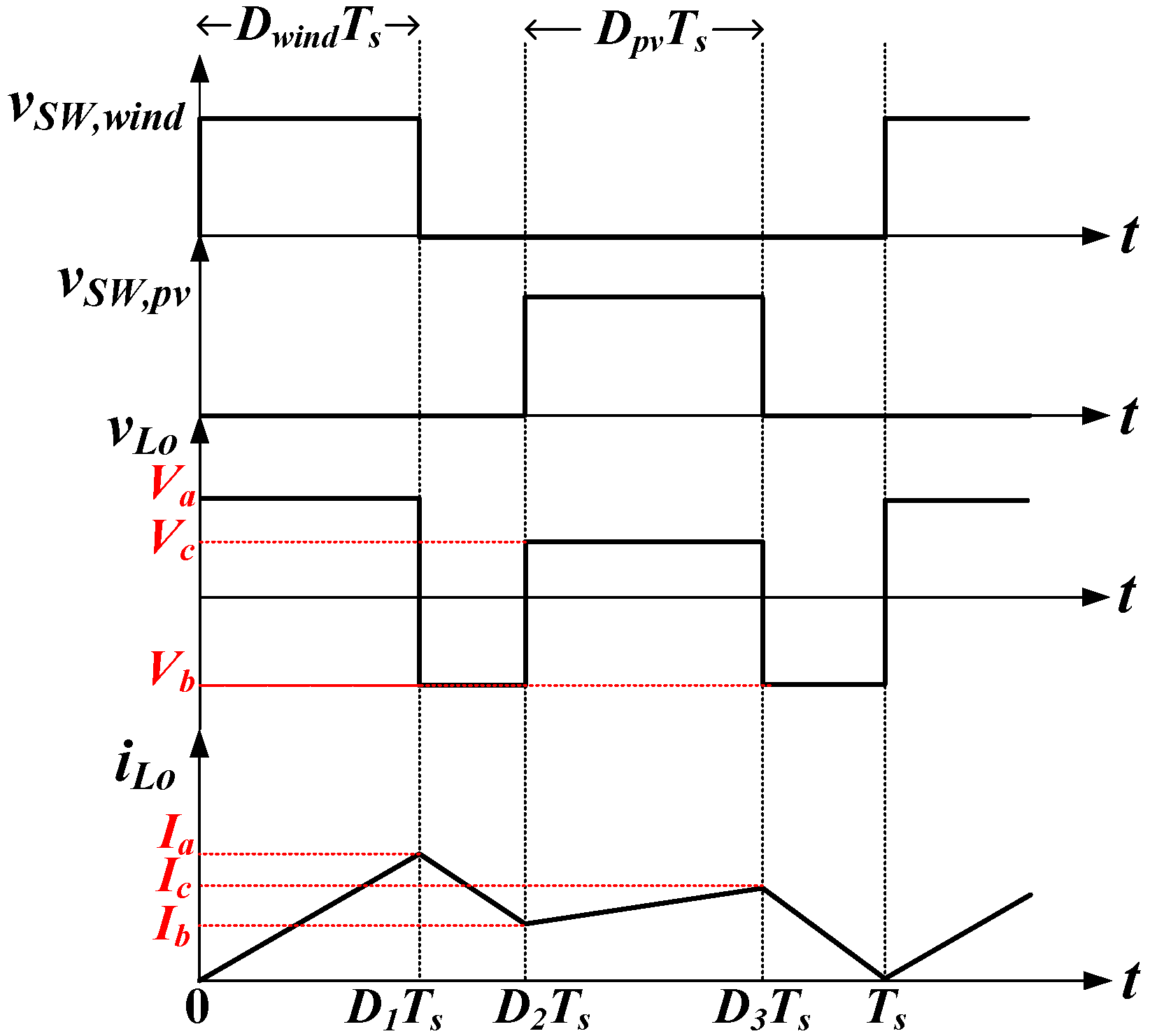
- Apply volt-second balance criterion (VSBC) to Lo to determine the output capacitor voltage VCo.
- Step 4:
- After obtaining all capacitor voltages VC1,wind, VC2,wind, VC1,pv, VC2,pv, and VCo, calculate the voltage levels of Lo during the intervals of DwindTs, DpvTs, and (1 − Dwind − Dpv)Ts.
- Step 5:
- Step 6:
- Estimate the average current of Lo, ILo,avg.
- Step 7:
- From the equation of ILo,avg obtained in Step 6, find the minimum inductance of Lo for the CCM operation.
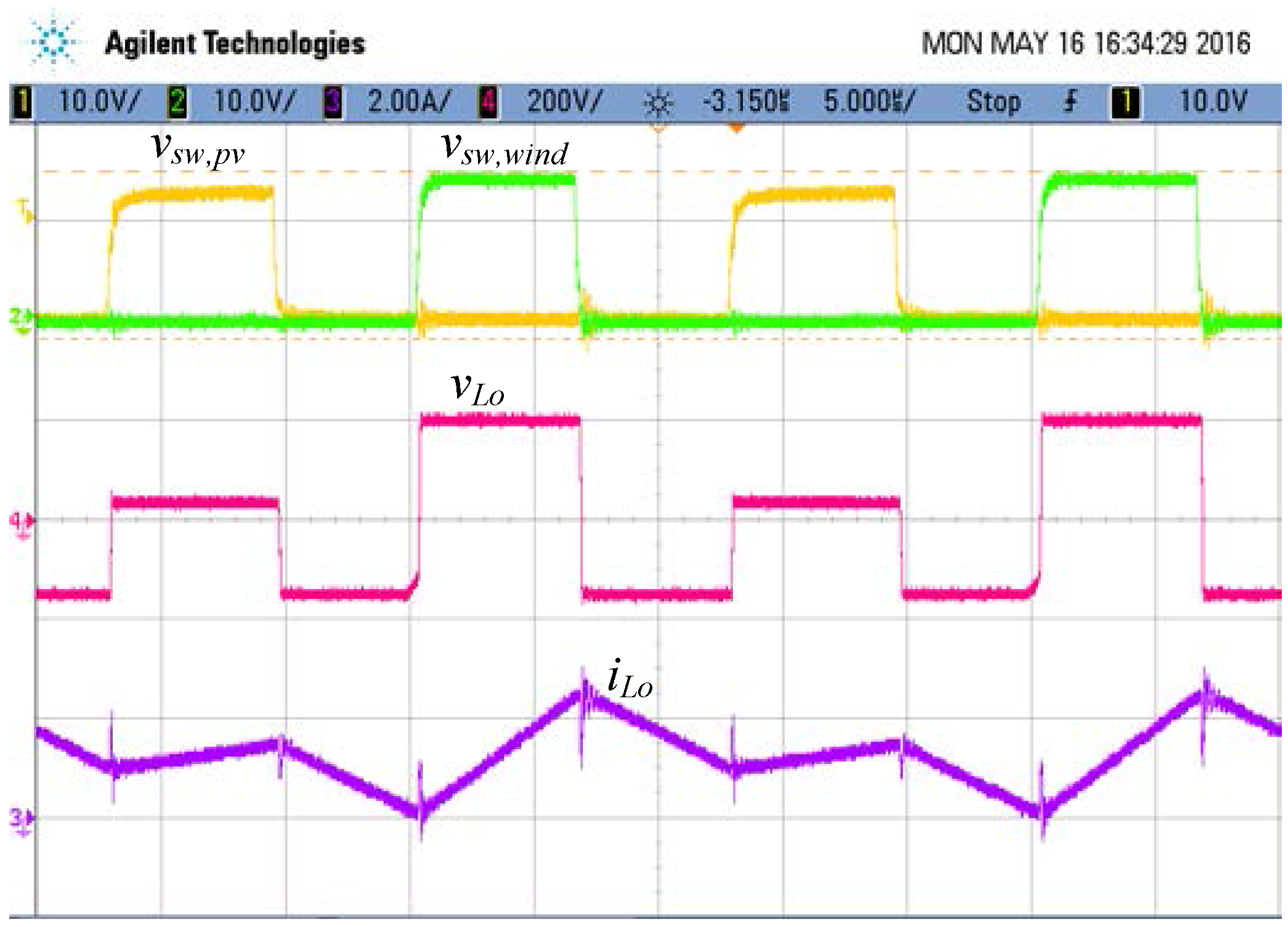
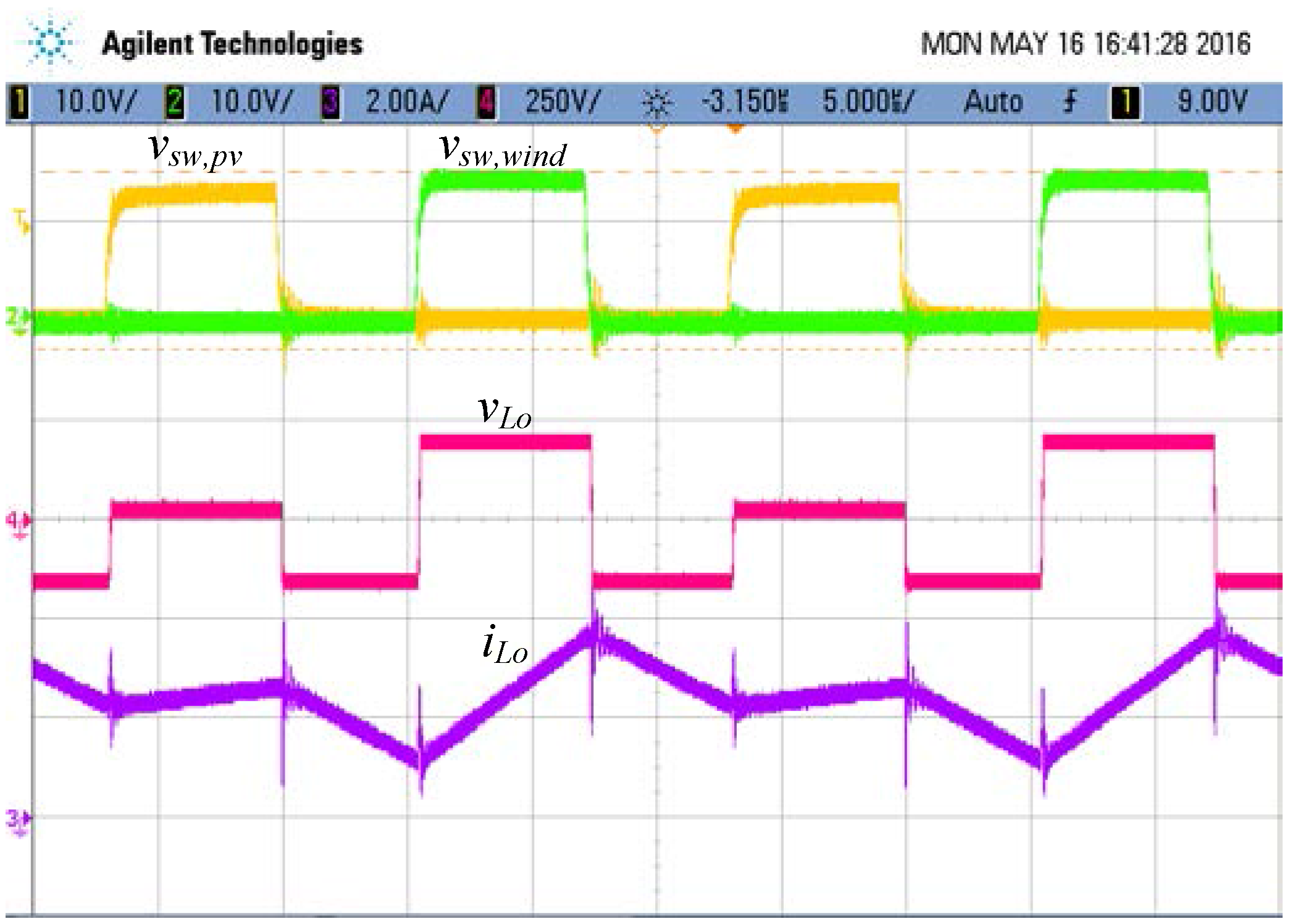
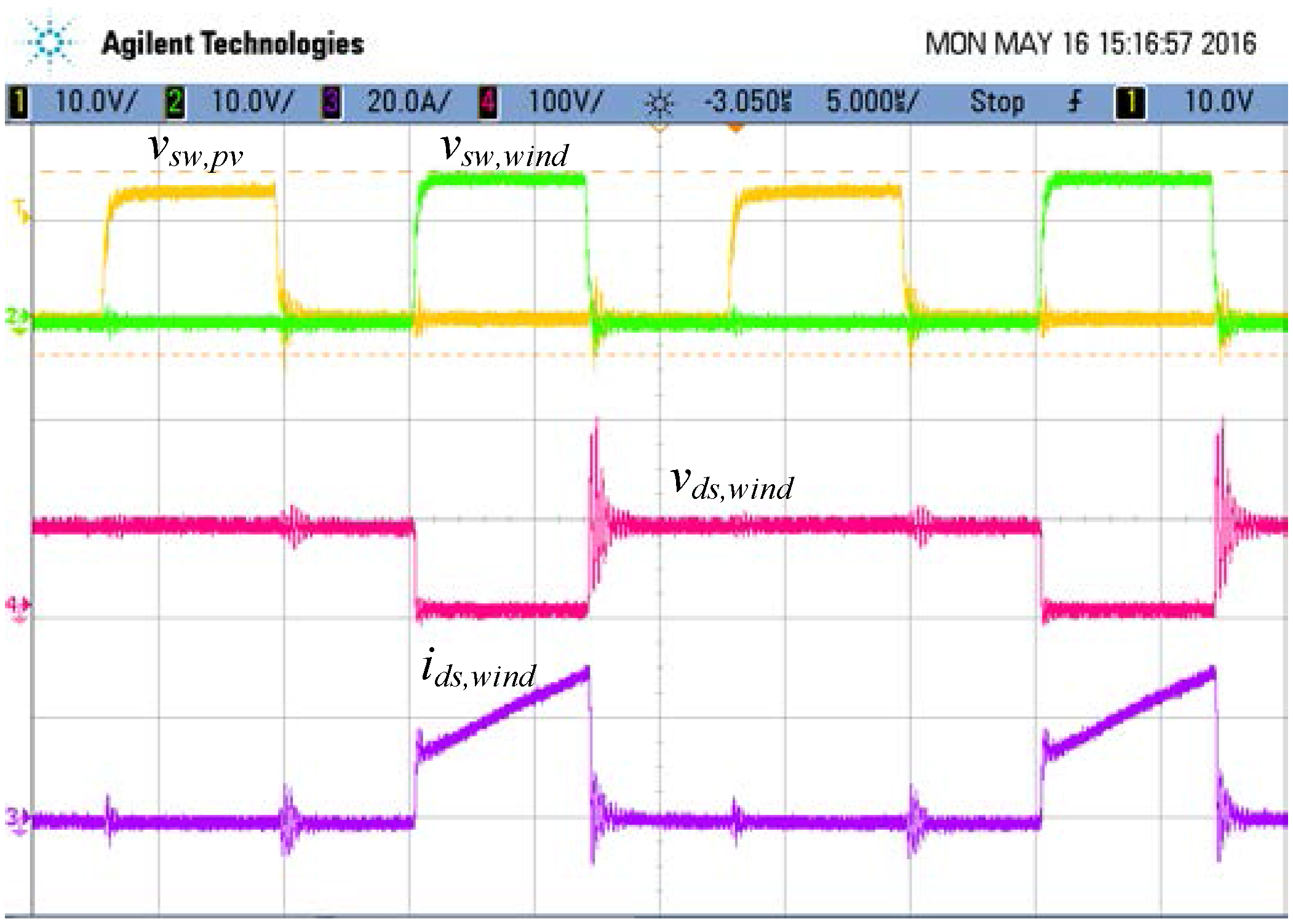
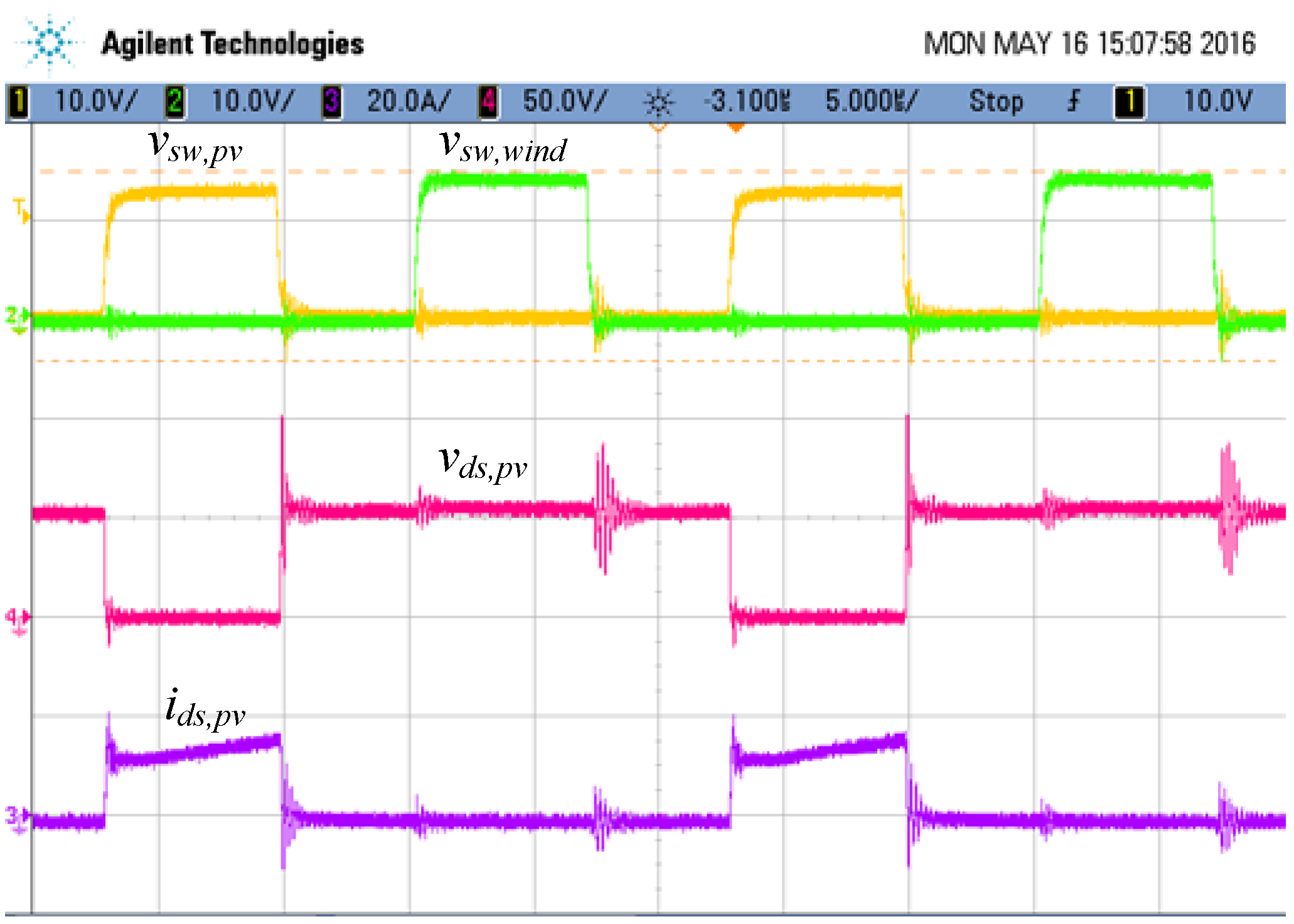
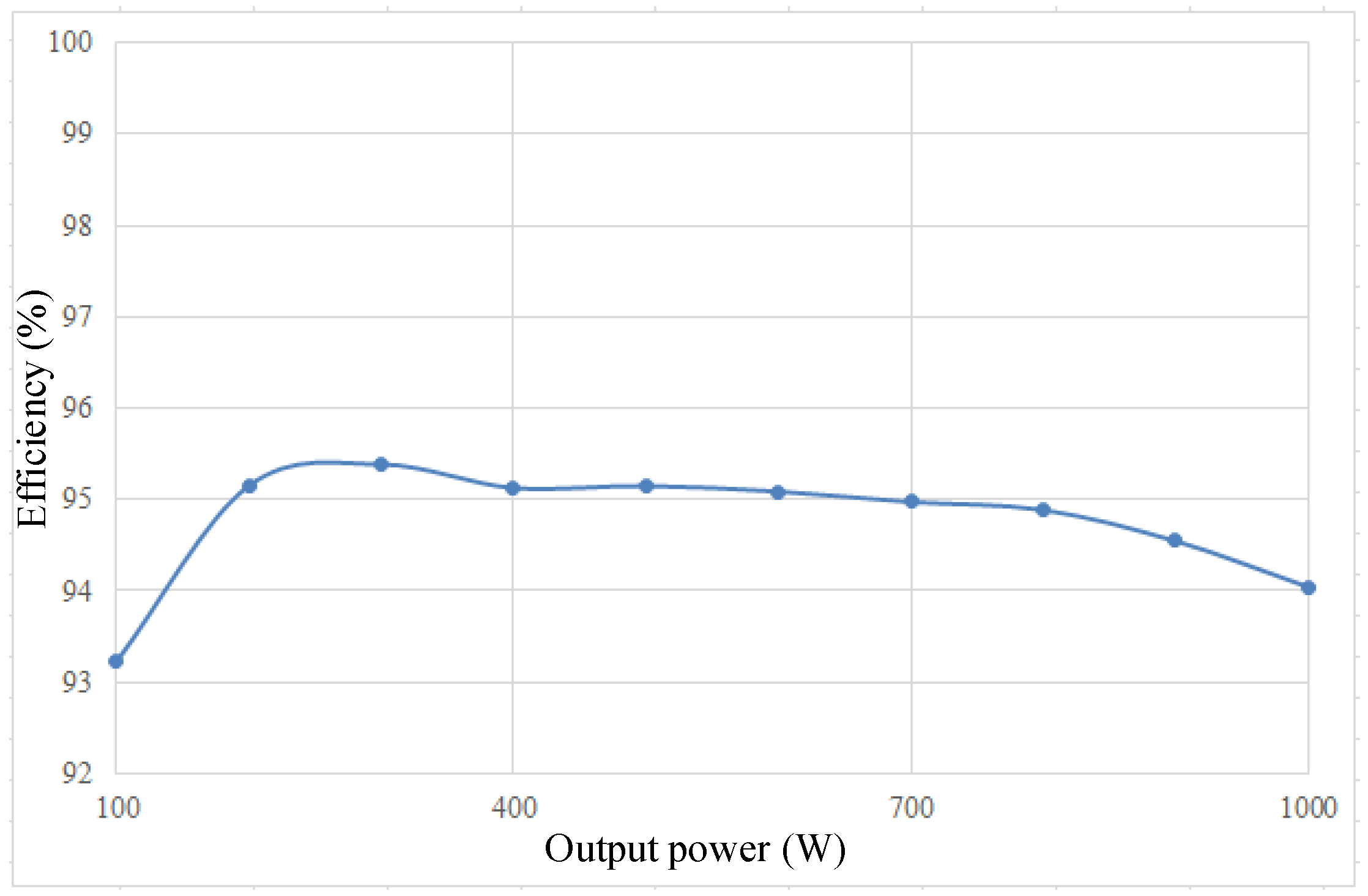
5. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alireza, K.; Mohamed, Y.A.R.I. Networked-based hybrid distributed power sharing and control for islanded microgrid systems. IEEE Trans. Power Electron. 2015, 30, 603–617. [Google Scholar]
- Chunhua, P.; Peng, X.; Lei, P.; Rong, Y. Flexible robust optimization dispatch for hybrid wind/photovoltaic/hydro/thermal power system. IEEE Trans. Smart Grid. 2016, 7, 751–762. [Google Scholar]
- Hussein, M.M.; Senjyu, T.; Orabi, M.; Wahab, M.A.A.; Hamada, M.M. Control of a stand-alone variable speed wind energy supply system. Appl. Sci. 2013, 3, 437–456. [Google Scholar] [CrossRef]
- Yamada, H.; Kimura, K.; Hanamoto, T.; Ishiyama, T.; Sakaguchi, T.; Takahashi, T. A novel MPPT control method of thermoelectric power generation with single sensor. Appl. Sci. 2013, 3, 545–558. [Google Scholar] [CrossRef]
- Lai, C.-M.; Yang, M.-J. A high-gain three-port power converter with fuel cell, battery sources and stacked output for hybrid electric vehicles and DC-microgrids. Energies 2016, 9, 180. [Google Scholar] [CrossRef]
- Ramalu, T.; Mohd Radzi, M.A.; Mohd Zainuri, M.A.A.; Abdul Wahab, N.I.; Abdul Rahman, R.Z. A photovoltaic-based sepic converter with dual-fuzzy maximum power point tracking for optimal buck and boost operations. Energies 2016, 9, 604. [Google Scholar] [CrossRef]
- Liu, F.; Wang, Z.; Mao, Y.; Ruan, X. Asymmetrical half-bridge double-input DC/DC converters adopting pulsating voltage source cells for low power applications. IEEE Trans. Power Electron. 2014, 29, 4741–4751. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, Y.; Wang, W.; Wang, B.; Zhang, Z. Alternative source-port-tolerant series-connected double-input DC–DC converter. IEEE Trans. Power Electron. 2015, 30, 2733–2742. [Google Scholar] [CrossRef]
- Banaei, M.R.; Ardi, H.; Alizadeh, R.; Farakhor, A. Non-isolated multi-input–single-output DC/DC converter for photovoltaic power generation systems. IET Trans. Power Electron. 2014, 7, 2806–2816. [Google Scholar] [CrossRef]
- Yang, P.; Chi, K.T.; Xu, J.; Zhou, G. Synthesis and analysis of double-input single-output DC/DC converters. IEEE Trans. Ind. Electron. 2015, 62, 6284–6295. [Google Scholar] [CrossRef]
- Tsai, C.-T.; Shen, C.-L.; Su, J.-C. A power supply system with ZVS and current-doubler features for hybrid renewable energy conversion. Energies 2013, 6, 4859–4878. [Google Scholar] [CrossRef]
- Piegari, L.; Rizzo, R.; Spina, I.; Tricoli, P. Optimized adaptive perturb and observe maximum power point tracking control for photovoltaic generation. Energies 2015, 8, 3418–3436. [Google Scholar] [CrossRef]
- Park, S.; Park, Y.; Choi, S.; Choi, W.; Lee, K.-B. Soft-switched interleaved boost converters for high step-up and high-power applications. IEEE Trans. Power Electron. 2011, 26, 2906–2914. [Google Scholar] [CrossRef]
- Hu, Y.; Deng, Y.; Long, J.; Lu, X. High step-up passive absorption circuit used in non-isolated high step-up converter. IET Trans. Power Electron. 2014, 7, 1945–1953. [Google Scholar] [CrossRef]
- Li, W.; Xiang, X.; Li, C.; Li, W.; He, X. Interleaved high step-up ZVT converter with built-in transformer voltage doubler cell for distributed PV generation system. IEEE Trans. Power Electron. 2013, 28, 300–313. [Google Scholar] [CrossRef]
- Liu, H.; Li, F.; Ai, J. A novel high step-up dual switches converter with coupled inductor and voltage multiplier cell for a renewable energy system. IEEE Trans. Power Electron. 2016, 31, 4974–4983. [Google Scholar] [CrossRef]
- Liu, H.; Li, F. a novel high step-up converter with a quasi-active switched-inductor structure for renewable energy systems. IEEE Trans. Power Electron. 2016, 31, 5030–5039. [Google Scholar] [CrossRef]
- Shen, C.-L.; Chiu, P.C. Buck-boost-flyback integrated converter with single switch to achieve high voltage gain for PV or fuel-cell applications. IET Trans. Power Electron. 2016, 9, 1228–1237. [Google Scholar] [CrossRef]
- Tseng, S.-Y.; Wang, H.-Y. A photovoltaic power system using a high step-up converter for DC load applications. Energies 2013, 6, 1068–1100. [Google Scholar] [CrossRef]
- Shen, C.-L.; Chen, H.-Y.; Chiu, P.-C. Integrated three-voltage-booster DC-DC converter to achieve high voltage gain with leakage-energy recycling for PV or fuel-cell power systems. Energies 2015, 8, 9843–9859. [Google Scholar] [CrossRef]
- Lai, C.-M. Development of a novel bidirectional DC/DC converter topology with high voltage conversion ratio for electric vehicles and DC-microgrids. Energies 2016, 9, 410. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Liu, Y.-C.; Wu, F.-Y. Multi-input DC/DC converter based on the multiwinding transformer for renewable energy applications. IEEE Trans. Ind. Appl. 2002, 38, 1096–1104. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, J.; Guo, X. An efficiency-optimized isolated bidirectional DC-DC converter with extended power range for energy storage systems in microgrids. Energies 2013, 6, 27–44. [Google Scholar] [CrossRef]
- Abramovitz, A.; Liao, C.-S.; Smedley, K. State-plane analysis of regenerative snubber for flyback converters. IEEE Trans. Power Electron. 2013, 28, 5323–5332. [Google Scholar] [CrossRef]
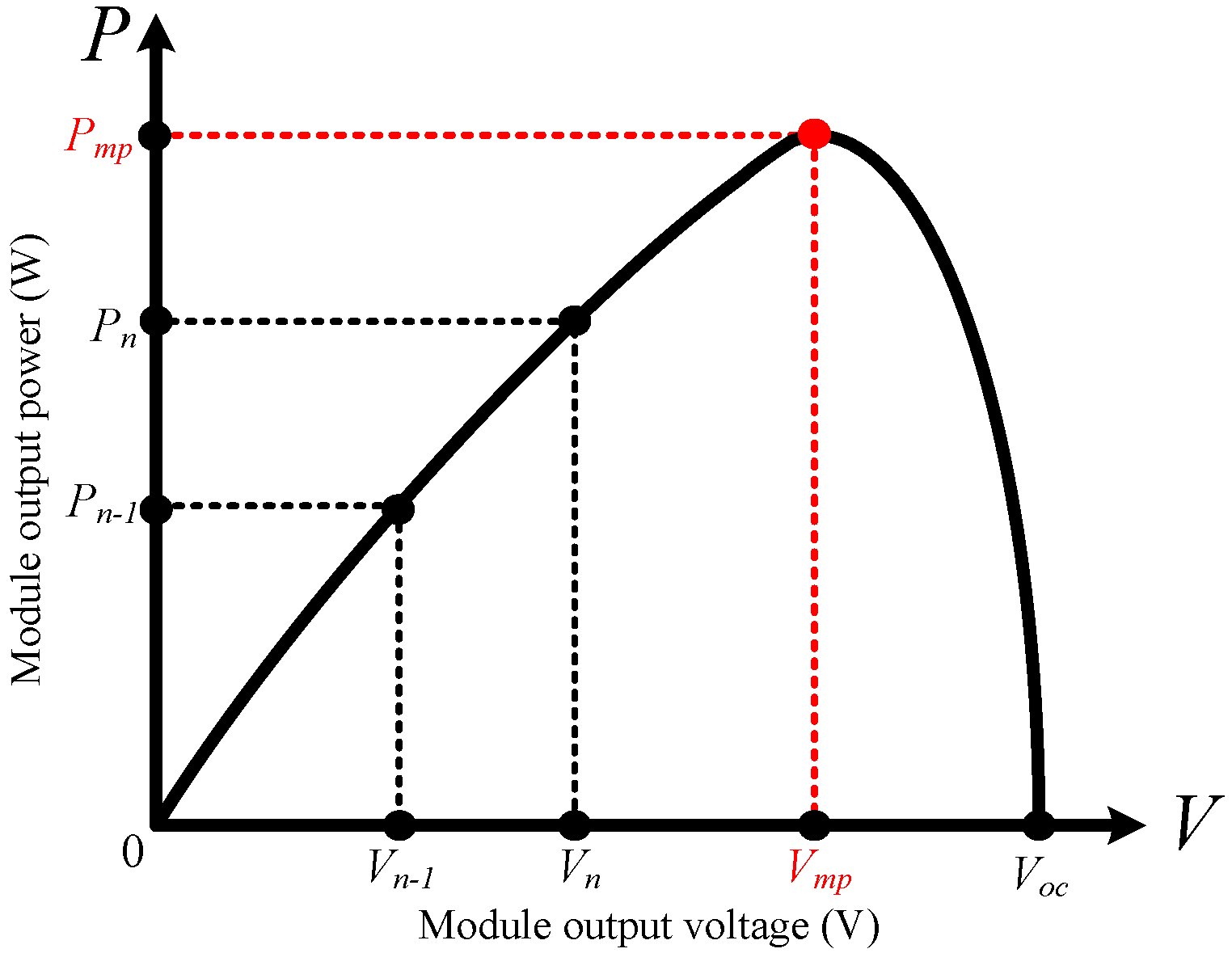
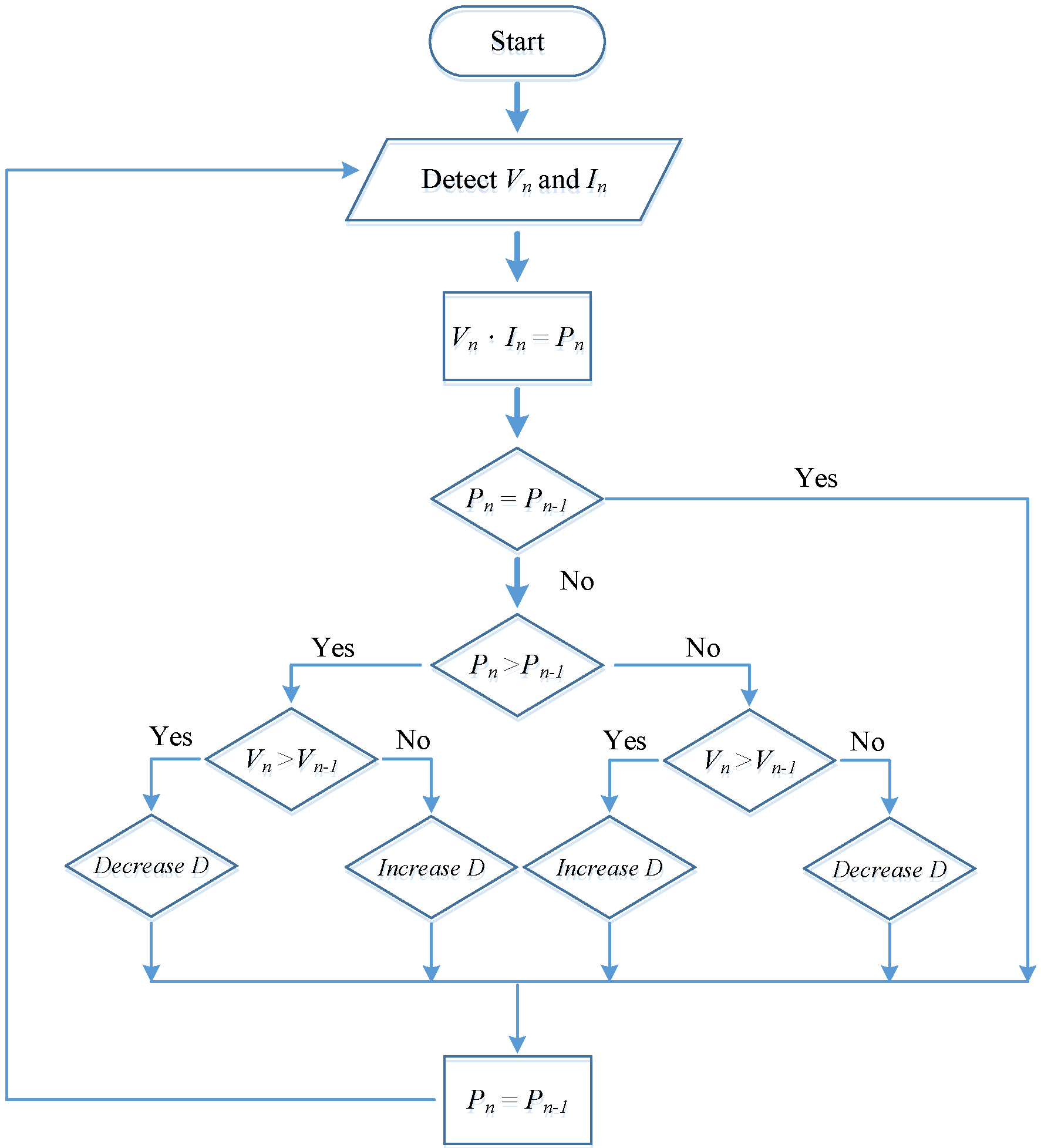




| Pn > Pn-1 | Vn > Vn-1 | Related Position | Duty Cycle (D) |
|---|---|---|---|
| True | True | Left | Decrease |
| True | False | Right | Increase |
| False | True | Right | Increase |
| False | False | Left | Decrease |
| Symbols | Values & Types |
|---|---|
| vwind (wind-turbine voltage) | 120 V |
| vpv (PV voltage) | 80 V |
| VCo (output voltage) | 400 V |
| Po (output power) | 1 kW |
| fs (switching frequency) | 40 kHz |
| Lm,wind (magnetizing inductance) | 1.09 mH |
| Lm,pv (magnetizing inductance) | 1 mH |
| Lk,wind (leakage inductance) | 4.2 μH |
| Lk,pv (leakage inductance) | 4 μH |
| Lo (output inductance) | 584 μH |
| nwind (turns ratio of T1) | 2.12 |
| npv (turns ratio of T2) | 2 |
| C1,wind and C2,wind (capacitors) | 47 μF |
| C1,pv and C2,pv (capacitors) | 33 μF |
| Co (output capacitor) | 220 μF |
| SW1,wind and SW2,wind (switches) | IXFH120N20P |
| SW1,pv and SW2,pv (switches) | IXFH120N15P |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.-L.; Shen, Y.-S. Output Filter Design for a Novel Dual-Input PV-Wind Power Converter by Energy Balance Principle. Appl. Sci. 2016, 6, 263. https://doi.org/10.3390/app6090263
Shen C-L, Shen Y-S. Output Filter Design for a Novel Dual-Input PV-Wind Power Converter by Energy Balance Principle. Applied Sciences. 2016; 6(9):263. https://doi.org/10.3390/app6090263
Chicago/Turabian StyleShen, Chih-Lung, and You-Sheng Shen. 2016. "Output Filter Design for a Novel Dual-Input PV-Wind Power Converter by Energy Balance Principle" Applied Sciences 6, no. 9: 263. https://doi.org/10.3390/app6090263
APA StyleShen, C.-L., & Shen, Y.-S. (2016). Output Filter Design for a Novel Dual-Input PV-Wind Power Converter by Energy Balance Principle. Applied Sciences, 6(9), 263. https://doi.org/10.3390/app6090263






