Abstract
Wind turbine power curves are calibrated by turbine manufacturers under requirements stipulated by the International Electrotechnical Commission to provide a functional mapping between the mean wind speed and the mean turbine power output . Wind plant operators employ these power curves to estimate or forecast wind power generation under given wind conditions. However, it is general knowledge that wide variability exists in these mean calibration values. We first analyse how the standard deviation in wind speed affects the mean and the standard deviation of wind power. We find that the magnitude of wind power fluctuations scales as the square of the mean wind speed. Using data from three planetary locations, we find that the wind speed standard deviation systematically varies with mean wind speed , and in some instances, follows a scaling of the form ; C being a constant and a fractional power. We show that, when applicable, this scaling form provides a minimal parameter description of the power curve in terms of alone. Wind data from different locations establishes that (in instances when this scaling exists) the exponent varies with location, owing to the influence of local environmental conditions on wind speed variability. Since manufacturer-calibrated power curves cannot account for variability influenced by local conditions, this variability translates to forecast uncertainty in power generation. We close with a proposal for operators to perform post-installation recalibration of their turbine power curves to account for the influence of local environmental factors on wind speed variability in order to reduce the uncertainty of wind power forecasts. Understanding the relationship between wind’s speed and its variability is likely to lead to lower costs for the integration of wind power into the electric grid.
1. Introduction
The wind turbine power curve relates the speed of wind blowing past a turbine to the power generated by the turbine. Wind plant operators forecast the power they expect to generate by feeding wind speed forecasts from numerical weather models to these power curves [1,2]. The power curves are supplied to operators by turbine manufacturers, who calibrate them under standards specified by the International Electrotechnical Commission (IEC) [3]. The IEC standard considers the average behaviour between the mean wind speed ( being the time-average of a time-varying quantity ) and mean power output , and hence does not locally hold in time for instantaneous measurements. Indeed, instantaneous values of wind speed and wind power exhibit significant scatter about the mean profile (Figure 1). Several studies [4,5,6,7,8] have focused on the factors contributing to this variability, including turbulent fluctuations, wind shear, directional shear, directional fluctuations, etc., with the aim of accurately modeling the “mean” profile of the wind turbine power curve [9,10,11,12].
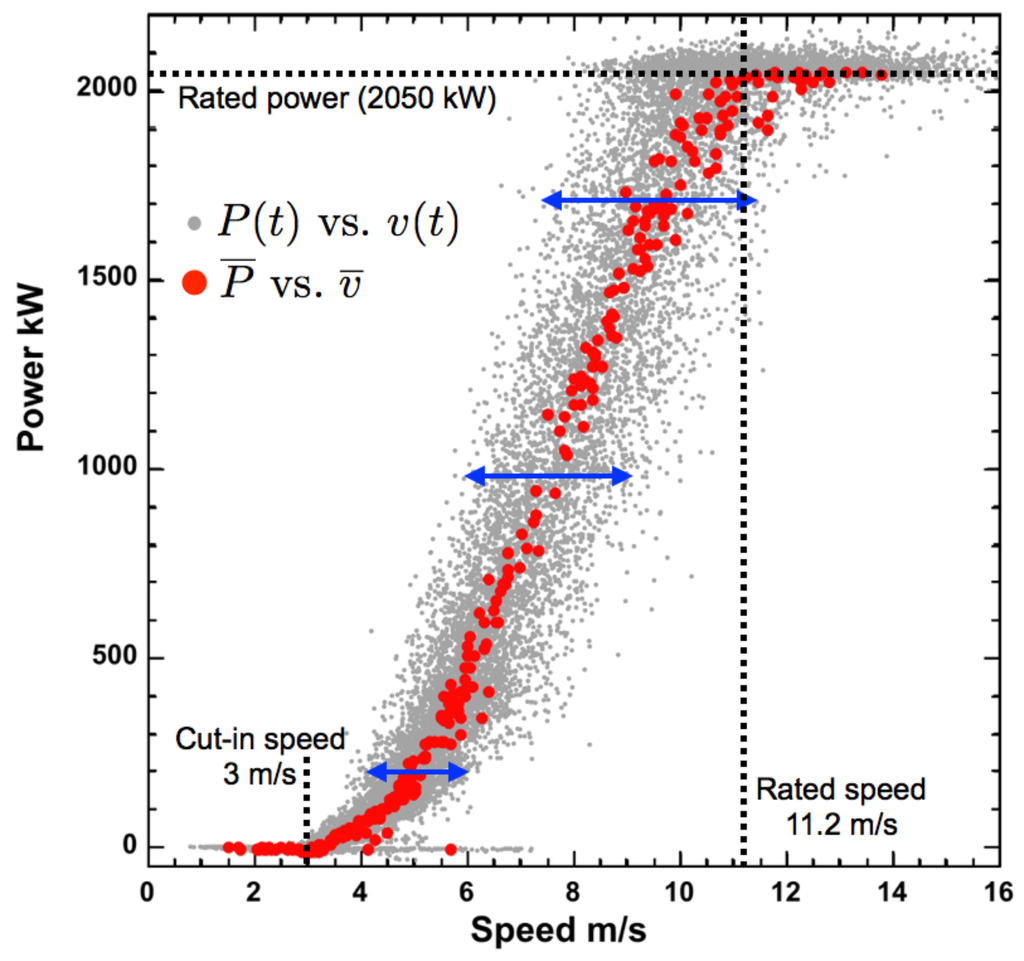
Figure 1.
Instantaneous power versus instantaneous wind speed (solid grey circles) and time-averaged power versus time-averaged wind speed (solid red circles) for the Howard data set (Table 1). Considerable scatter in versus occurs about the time-averaged power curve. The scatter increases with mean speed , as qualitatively shown with blue arrows at 5, 7, and 9 m/s.
In this article, we first establish that the wind turbine power curve has features that are sensitive to local environmental factors. We then employ a combination of theory and empirical results to self-consistently account for this dependence on local factors. Our proposed approach was especially developed within the framework of IEC standard 614001-12-1 to ensure its easy adoption by wind plant operators. In particular, we present a minimal parameter description of wind speed variability and wind power variability in terms of the mean wind speed . Our objective here is to remain faithful to the IEC standard [3] that prescribes the power curve with mean wind speed as its only parameter. We present empirical evidence that the standard deviation in wind speed systematically varies with mean wind speed . At least in some instances, this monotonic variation follows algebraic scaling of the form , where C is a constant and is a fractional power. This scaling form—which we attribute to residual signal correlations that remain post-averaging—then affords a description of mean wind power and its standard deviation in terms of alone.
Our analysis of wind data obtained from three different planetary locations (Table 1) reveals that in instances when the above scaling form is satisfied, the power-law exponent varies with geographic location, and hence must reflect local environmental factors not captured by manufacturer-supplied calibration power curves. Consequently, when these calibration power curves are applied to forecast wind power, wind speed variability transforms into power forecast uncertainty. Since the variability always increases in tandem with mean speed, the resulting forecast error is multiplicative, so it substantially increases uncertainty in wind power forecasts. We conclude with a proposal that wind plant operators should recalibrate turbine power curves at the plant location to properly account for variability arising from local environmental factors. This will help to reduce the uncertainty of wind power forecasts.

Table 1.
Details of data sets analysed in the present study.
At first sight, the monotonic increase in wind speed variability with mean speed seems at odds with the general belief that the turbulence intensity decreases with speed. In many instances, one observes that fluctuations exhibit non-monotonic behaviour with steady increase in mean speed (and Reynolds number Re) [13]. In particular, frictional losses with the walls cause loss of pressure head in water flow down a river or pipe. This in turn causes loss in mean speed (), but fluid shear with the wall can increase fluctuations and eventual transition to turbulence [14]. Atmospheric flows close to the Earth’s surface share close correspondence with pipe and river flows, in that the Earth’s surface behaves like a rough wall, but the flow is unbounded from above, where a second confining wall is absent. Fluctuations (and therefore turbulence intensity I) will vary non-monotonically with mean speed close to Earth’s surface. However, within the range of wind speeds between the cut-in and cut-out speed of a turbine, this variation should exhibit monotonic increase in with a concomitant rise in .
Whereas the IEC standard considers only mean quantities, as we show below, both mean power output (Equation (5)) and its standard deviation (Equation (7)) strongly depend upon wind speed variability , in addition to mean wind speed . Strong local environmental dependence of wind speed fluctuations naturally affects both the mean profile of the power curve and its variability. When not properly accounted for, this increases forecast uncertainty, which in turn adds costs to renewable energy production [15,16]. Understanding the source of variability and utilising it appropriately therefore brings tangible benefits to the global renewable energy community.
2. Influence of Wind Speed Variability on Wind Power
The starting point of our analysis is the instantaneous kinetic energy flux in wind with air density , blowing past a hypothetical turbine of cross-sectional area A:
Here is the time-varying streamwise component of velocity blowing past the turbine. We ignore directional fluctuations merely in the interest of keeping our arguments accessible (as also recently explained by Hedevang [8]), but the subsequent analysis can be easily extended to include directional fluctuations [4].
Performing Reynolds decomposition on the time-varying velocity into a time-independent mean speed and a time-varying fluctuation whose long-time average by definition, and substituting it in Equation (1), we obtain:
Owing to the turbine experiencing a drag force, it does not extract all the energy available in the wind. Indeed, the power generated by the turbine is given by:
where and is the efficiency factor representing the theoretical upper bound for power conversion. We now take the long-time average of Equation (3) to obtain the mean power extracted by the turbine, which upon performing an appropriate time-average of each term on the right-hand side (RHS) yields:
Term I in RHS of Equation (4) represents the turbine’s mean power output under steady (time-independent) wind speed conditions. Term II is zero, since by definition. can take both positive and negative values, owing to its being an odd function of time t. Consequently, Term IV on the RHS of Equation (4) takes a very small but non-zero value, and will be neglected in the foregoing analysis. Term III captures wind speed variability, and , being quadratic (an even function in time t), is always positive. Indeed, , the quantity of specific interest to our present analysis. As a point of comparison, a 20 day long-time average for the Howard dataset (Table 1) yielded the values m/s for term I, m/s for term III, and m/s for term IV. We are therefore justified in keeping term III (64% of term I) and dropping term IV (only 8% of term I). Dropping terms II and IV and re-arranging terms I and III, Equation (4) can be re-expressed as:
where is the turbulent intensity, or alternatively the coefficient of variation in wind speed.
The presence of a second fluctuation term in Equation (5) requires a comparison of its strength relative to the mean term (). When the turbulent intensity is low (), wind conditions are close to steady, and the mean power follows the standard relation. If the fluctuation magnitude is a significant fraction of mean speed (), then . Two scenarios must then be considered: one where the standard deviation of wind speed remains constant or decreases with increasing mean wind speed , and the second where increases with . A consideration of the two scenarios becomes important, because a constant leads to additive variability, whereas increasing with leads to multiplicative variability, which in turn has implications for the error. Our analysis of wind data presented below always shows an increase in with , hence we discuss only the case of multiplicative variability.
The standard deviation of power can also be computed as a function of and . Defining instantaneous power as , where is the fluctuation about the time-independent mean , whose long time average is zero by definition (), and using Equations (3) and (4):
An algebraic expansion of Equation (6) followed by a long-time average of individual terms yields:
Keeping only the leading order term and ignoring all higher order terms, we arrive at a first order approximation for the standard deviation of wind power:
From Equation (7), we see that scales linearly with , but is amplified by a factor of . More importantly, we see that the magnitude of wind power fluctuations scales quadratically with mean wind speed (). We note that the functional form for in Equation (7) is expected to apply between the cut-in and rated speeds.
In Figure 1, we plot the power curve ( vs. , solid red circles) with the instantaneous power against speed ( vs. , solid grey circles) overlaid on top of the power curve for a 2.05 MW REPower MM92 turbine (cut-in speed: 3 m/s, rated speed: 11.2 m/s, cut-out speed: 24 m/s, rated power: 2050 kW) located at a wind farm operated by EverPower Wind Holdings in Howard, NY (Table 1). The solid blue arrows marking the scatter in instantaneous wind speed values at = 5, 7, and 9 m/s qualitatively demonstrate the monotonic increase in wind speed variability with mean speed; i.e., the case of multiplicative variability.
Before proceeding, we note a nuance concerning the time-average for and . IEC standard 61400-12-1 [3] requires that each value of and in the power curve be determined by averaging a 10 min time record (sampled at 1 Hz or higher) of and , respectively. This translates to an average over 600 s × 1 Hz = 600 samples—at least—for each time-averaged value in the power curve. Since the Howard data set (see Table 1) was sampled at 0.2 Hz, a pertinent question to ask is whether 600 s × 0.2 Hz = 120 samples are sufficient to achieve statistical convergence of the mean. We performed a bootstrap protocol [17] for the Howard time series to generate ten different time series by randomly shuffling values of the originally measured time series for and . We then measured the mean for each bootstrap time series as a function of increasing sample size for wind speed and wind power. Figure 2 shows how the mean wind speed (Figure 2a) and mean wind power (Figure 2b) converge as a function of increasing sample size. Since each sample is measured 5 s apart in our data set, 120 samples equate to a 10 min interval prescribed by the IEC standard. As is evident from Figure 2, asymptotic statistical convergence of the mean values is achieved only at about 400 samples. Following from this statistical convergence test, we constructed the power curve in Figure 1 by averaging over 400 samples (i.e., a 33.3 min time record for each value of and ). We emphasise that the bootstrap protocol tests for statistical convergence in the absence of correlations. The successive values in the measured time series are correlated; i.e., the nth value will lie within a certain band relative to the th and th values, depending upon correlation strength and correlation time. When this measured series is randomly shuffled to generate a synthetic series for the bootstrap test, the correlations between successive values in the time series are lost. On the other hand, when using the actual time series for and in constructing the power curve from averages, such correlations persist and reveal themselves in the variability, as we discuss below.
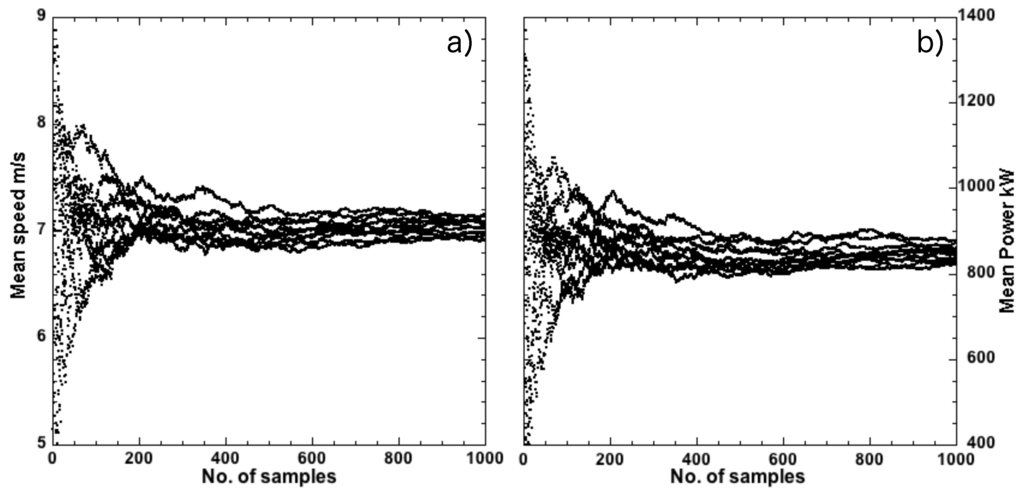
Figure 2.
Statistical convergence of (a) mean wind speed; and (b) mean wind power versus number of samples contributing to the average. Each trace represents a separate data set generated with a bootstrap protocol by randomly shuffling values of the original Howard time series (Table 1). The averages approach asymptotic convergence around 400 samples.
3. Results and Discussion
We analysed three data sets (Table 1), one (Howard) containing both wind speed and wind power time series, and the other two (Big Bear Lake and Atacama) containing only wind speed time series. Figure 3a plots the standard deviations of wind speed and wind power versus mean wind speed and wind power , respectively, for the Howard data set. The standard deviation of wind speed (solid red circles in Figure 3a) scales algebraically relative to the mean wind speed with a power-law fit that follows the form (solid line in Figure 3a). The standard deviation of wind power fluctuations (solid blue squares in Figure 3a) also exhibits algebraic scaling, albeit shallower than wind speed, with a power-law fit of the form (dashed line in Figure 3a). Wind speed standard deviation for the Big Bear Lake data set plotted in Figure 3b (red solid circles) exhibits a similar algebraic scaling, but with a different power-law exponent (, solid black line in Figure 3b) from the Howard data set. Finally, for the Atacama data set, although exhibits a systematic increase with (solid blue squares in Figure 3c), we find that the scatter is too high to make a conclusive determination of power-law scaling. We do include a power-law fit (dashed line in Figure 3c), but one should not derive any inferences from this fit. Be that as it may, the fact that exhibits monotonic increase with for all data sets establishes the scenario of multiplicative variability.
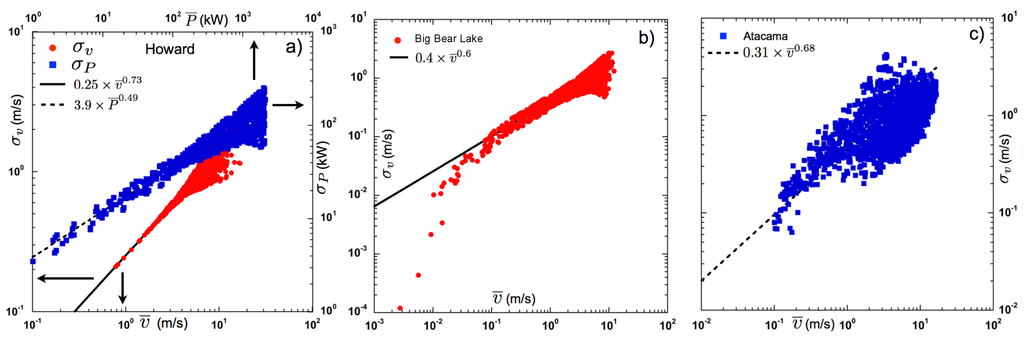
Figure 3.
(a) log–log scale: The standard deviation of wind speed fluctuations (red solid circles) versus mean wind speed and the standard deviation of wind power fluctuations (blue solid squares) versus mean wind power for the Howard data set. Power-law fits to the data provided (solid line) and (dashed line); (b) Whereas vs. for Big Bear Lake (red solid circles) exhibits power-law scaling with a fit value of (solid line); and (c) the Atacama data set (blue solid squares) reveals a monotonic increase in vs. . Although we include a power-law fit (dashed line) for illustrative purposes, the scatter in the data does not permit one to place any confidence in the fit value of the exponent.
The observed scaling for power fluctuations () is significant given that Calif et al. [18] have recently reported the same scaling for a single turbine as well as for wind farms at various planetary locations. They interpreted this scaling within the context of the “Taylor Rule” [19] (not to be confused with Taylor’s Hypothesis in turbulence theory [20]), also called “Fluctuation Scaling” [21] in physics, where the 1/2 scaling exponent forms one of two limiting cases. However, based on additional empirical evidence for wind speed fluctuations and calculations resulting in Equation (7), we proffer an alternative interpretation for this scaling.
Consider a time-varying signal with a signal correlation time . The mean and standard deviation become truly time-independent when the average is taken over several multiples of the correlation time . Instead, if the averaging interval , residual correlations persist in and (subscript τ now denotes the averaging interval) which vary with averaging time τ. Wind speed (and therefore wind power) fluctuations which reflect atmospheric turbulence possess long time correlations extending up to 24 h timescales [22,23,24,25,26], whereas the IEC standard [3] specifies a 10 min time average for calculation of and . Even our bootstrap protocol specifically tests for statistical convergence in the absence of temporal correlations; generating a new randomised time series from the original time series destroys temporal correlations in the signal. Consequently, and retain residual correlations, which are revealed as systematic variation in relative to (the same applies to and ). Such relative scaling between moments of a distribution is well known via Extended Self Similarity (ESS) scaling [27], and was fruitfully exploited to accurately estimate deviations from scalings predicted by the Kolmogorov theory of turbulence [28]. Our observed scalings between the mean and standard deviation of wind speed follow in the same spirit. One cannot escape the residual correlations—and hence the power-law relationship between and —unless the averaging time is increased from the IEC-stipulated 10 min to the signal correlation time of order 24 h. A 24 h averaging time for each point on the power curve calls for several months worth of data collection effort, and hence is clearly impractical. A more tractable—and still quantitatively defensible—approach is to incorporate the power-law scaling between and to self-consistently account for residual correlations in the power curve and its variability, as we show below in Equation (8).
Equation (8) therefore provides a minimal parameter description of and as a function of alone, thereby keeping our analysis in accord with the requirements of IEC standard 61400-12-1 [3]. Even when a scaling form for is unavailable (e.g., the Atacama data set), one can still exploit the monotonic variation in versus and numerically input and into Equation (7) and calculate to establish confidence intervals around for forecast projections. Failing this, the wind speed variability feeds into and amplifies wind power variability, and transforms into forecast uncertainty.
Equation (8) applies between the turbine’s cut-in and rated speeds. Furthermore, we emphasize the fact that Equation (8b) is only a leading order approximation for wind power variability between the cut-in and rated speeds. Between the rated and cut-out speeds, mean power decouples from mean speed, and the turbine acts to rectify wind power fluctuations, thereby suppressing any increase in power variability. When wind power fluctuations are considered as a whole between the cut-in and cut-out speeds, should follow a shallower scaling than would be suggested by Equation (8b). Given that the range of speeds between the rated and cut-out speeds is roughly half the entire operating range of wind speeds for any given turbine, it may explain why seems to hold universally.
It is, however, revealing that the Howard and Big Bear Lake data sets do not share the same scaling exponent , despite sharing the same averaging duration. This suggests that environmental factors local to the measurement location strongly influence wind dynamics, thereby controlling the value of the scaling exponent . A clue to this effect is revealed by the strongly anomalous behaviour of the Atacama data set, which does not exhibit as clear a scaling (Figure 3c) as the other two. The Atacama location (Chajnantor, Chile) differs significantly from Howard and Big Bear Lake in at least two respects. Firstly, Howard, NY and Big Bear Lake, CA are at 605 m and 2085 m elevations, respectively, whereas Chajnantor in Atacama has an elevation of 5080 m above sea level. This strong disparity in elevations translates to difference in air density and wind profiles, which must certainly affect wind speed variability.
Second, Big Bear Lake is adjacent to forested mountain ridges that rise several hundred meters above the lake. The rural farmland in Howard, NY has interspersed forest and cultivated land. On the other hand, the Chajnantor location in the Chilean Andes is a desert. The influence of surface roughness on the atmospheric boundary layer is well known in the environmental sciences, where internal atmospheric boundary layers are associated with the horizontal advection of air across a discontinuity in some surface property [29]. Identification of the precise environmental factors will require field observations, and cannot be achieved with wind speed data alone; hence, this lies beyond the scope of the current work. Furthermore, the sub-linear power-law scaling of relative to mean speed points to the existence of a hidden length scale, either in the atmospheric flow or in the planetary surface roughness. This hidden length scale—if identified through extensive observational measurements—could potentially extend the phenomenology of flow within the shear boundary layer beyond mean wind profiles to include fluctuations. Such a phenomenology would of course mark an advancement in geophysical fluid dynamics, but would also benefit the wind engineering community. High time-resolution wind data sets that extend over several days are few, and are prized by researchers. The generation of such data sets in several locations would be a worthy goal for national research agencies.
4. Summary
Before closing, we observe that collective interactions between turbines in a wind plant also change the local flow field in the plant’s vicinity [30,31], in turn compromising plant efficiency [32,33]. Decomposing plant-induced variability from natural environmental factors is often complicated [30,34]. The methods we employ are agnostic to the source of variability, hence can account for both natural (environmental) and artificial (plant-induced) sources of variability, while working within the framework of IEC standard 61400-12-1 [3].
In summary, we have explained the functional dependence of and in terms of and . From empirical evidence, we exploited systematic variation of with to recast expressions for and solely in terms of , thus keeping in accord with IEC standard 61400-12-1 [3]. Given the dependence of the fluctuation scaling exponent on local environmental factors, we propose that wind operators should recalibrate their turbine power curves post-installation at the site to accurately account for the site’s multiplicative variability. We believe that doing so, and including confidence intervals for wind power variability about the mean power curve profiles, would reduce wind power forecast uncertainty.
Acknowledgments
Mahesh M. Bandi was supported by the Collective Interactions Unit at the Okinawa Institute of Science and Technology Graduate University. Jay Apt received support from the Carnegie Mellon Electricity Industry Center and from the Carnegie Mellon Climate and Energy Decision Making Center (CEDM) formed through a cooperative agreement between the National Science Foundation and CMU (SES-0949710). We thank Dhaval Balodia and EverPower Wind Holdings for access to the Howard wind and wind turbine power data. Mahesh M. Bandi acknowledges helpful discussions with P. Chakraborty.
Author Contributions
M.M.B. and J.A. conceived and performed the research. M.M.B. wrote the manuscript and J.A. edited it.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Landberg, L. Short-term prediction of the power production from wind farms. J. Wind Eng. Ind. Aerodyn. 1999, 80, 207–220. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef]
- IEC. Wind Turbines–Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines; IEC61400-12-1; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Choukulkar, A.; Pichugina, Y.; Clack, C.T.M.; Calhoun, R.; Banta, R.; Brewer, A.; Hardesty, M. A new formulation for rotor equivalent wind speed for wind resource assessment and wind power forecasting. Wind Energy 2015. [Google Scholar] [CrossRef]
- Wharton, S.; Lundquist, J.K. Atmospheric stability affects wind turbine power collection. Environ. Res. Lett. 2012, 7. [Google Scholar] [CrossRef]
- Paiva, L.T.; Rodrigues, C.V.; Palma, J.M.L.M. Determining wind turbine power curves based on operating conditions. Wind Energy 2014, 17, 1563. [Google Scholar] [CrossRef]
- Sumner, J.; Masson, C. Influence of Atmospheric Stability on Wind Turbine Power Performance Curves. J. Sol. Energy Eng. 2006, 128, 531–538. [Google Scholar] [CrossRef]
- Hedevang, E. Wind turbine power curves incorporating turbulence intensity. Wind Energy 2014, 17, 173. [Google Scholar] [CrossRef]
- Carrillo, C.; Montaño, A.F.O.; Cidràs, J.; Díaz-Dorado, E. Review of power curve modelling for wind turbines. Renew. Sustain. Energy Rev. 2013, 21, 572–581. [Google Scholar] [CrossRef]
- Litong-Palima, M.; Bjerge, M.H.; Cutululis, N.A.; Hansen, L.H.; Sørensen, P. Modeling of the dynamics of wind to power conversion including high wind speed behavior. Wind Energy 2015. [Google Scholar] [CrossRef]
- Mücke, T.A.; Wächter, M.; Milan, P.; Peinke, J. Langevin power curve analysis for numerical wind energy converter models with new insights on high frequency power performance. Wind Energy 2015, 18. [Google Scholar] [CrossRef]
- Gottschall, J.; Peinke, J. How to improve the estimation of power curves for wind turbines. Environ. Res. Lett. 2008, 3. [Google Scholar] [CrossRef]
- Allen, J.J.; Shockling, M.; Kunkel, G.; Smits, A.J. Turbulent flow in smooth and rough pipes. Philos. Trans. R. Soc. A 2007, 365. [Google Scholar] [CrossRef] [PubMed]
- Gioia, G.; Chakraborty, P. Turbulent friction in rough pipes and the energy spectrum of the phenomenological theory. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef] [PubMed]
- Lueken, C.; Cohen, G.E.; Apt, J. Costs of Solar and Wind Power Variability for reducing CO2 Emissions. Environ. Sci. Technol. 2012, 46, 9761–9767. [Google Scholar] [CrossRef] [PubMed]
- Katzenstein, W.; Apt, J. The cost of wind power variability. Energy Policy 2012, 51, 233–243. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Calif, R.; Schmitt, F.G. Taylor Law in Wind Energy Data. Resources 2015, 4, 787–795. [Google Scholar] [CrossRef]
- Taylor, L.R. Aggregation, Variance and the Mean. Nature 1961, 189, 732–735. [Google Scholar] [CrossRef]
- Taylor, G.I. The spectrum of turbulence. Proc. R. Soc. Lond. A 1938, 164. [Google Scholar] [CrossRef]
- Eisler, Z.; Bartos, I.; Kertész, J. Fluctuation scaling in complex systems: Taylor’s law and beyond. Adv. Phys. 2008, 57, 89–142. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D.; Stanway, J.D. Direct Evidence of Multifractal Atmospheric Cascades from Planetary Scales down to 1 km. Phys. Rev. Lett. 2001, 86, 5200–5203. [Google Scholar] [CrossRef] [PubMed]
- Muzy, J.F.; Baïle, R.; Poggi, P. Intermittency of surface-layer wind velocity series in the mesoscale range. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Apt, J. The spectrum of power from wind turbines. J. Power Sources 2007, 169, 369–374. [Google Scholar] [CrossRef]
- Calif, R.; Schmitt, R.; Huang, Y. Multifractal description of wind power fluctuations using arbitrary order Hilbert spectral analysis. Physica A 2013, 392, 4106–4120. [Google Scholar] [CrossRef]
- Bel, G.; Connaughton, C.P.; Toots, M.; Bandi, M.M. Grid-scale Fluctuations Forecast Error in Wind Power. New J. Phys. 2016, 18. [Google Scholar] [CrossRef]
- Benzi, R.; Ciliberto, S.; Tripiccione, R.; Baudet, C.; Massaioli, F.; Succi, S. Extended self-similarity in turbulent flows. Phys. Rev. E 1993, 48, R29. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence: The legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Makridis, A.; Chick, J. Validation of a CFD model of wind turbine wakes with terrain effects. J. Wind Eng. Ind. Aerodyn. 2013, 123, 12–29. [Google Scholar] [CrossRef]
- Castellani, F.; Astolfi, D.; Garinei, A.; Proietti, S.; Sdringola, P.; Terzi, L.; Desideri, U. How wind turbines alignment to wind direction affects efficiency? A case study through SCADA data mining. Energy Procedia 2015, 75, 697–703. [Google Scholar] [CrossRef]
- González-Longatt, F.; Wall, P.; Terzija, V. Wake effect in wind farm performance: Steady-state and dynamic behavior. Renew. Energy 2012, 39, 329–338. [Google Scholar] [CrossRef]
- Kim, S.H.; Shin, H.K.; Joo, Y.C.; Kim, K.H. A study of the wake effects on the wind characteristics and fatigue loads for the turbines in a wind farm. Renew. Energy 2015, 74, 536–543. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Modeling turbine wakes and power losses within a wind farm using LES: An application to the Horns Rev offshore wind farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).