The Spotting Distribution of Wildfires
Abstract
:1. Introduction
1.1. The Havoc Caused by Spotting
1.2. The Primary Questions of This Article
- 1.
- What is the spotting distribution, or the probability of spot fire ignition, at each location downwind of an existing fire front?
- 2.
- What is the probability that a fire will breach an obstacle?
- 3.
- What role does spotting play on the rate of spread of a fire front? Can spotting cause a wildfire to quickly traverse a region across which it would spread slower with purely local spread?
- 4.
- Can spotting accelerate a fire’s advance?
1.3. Prior and Concurrent Models Coupling Spotting with Local Spread
1.4. The Types of Spotting Considered in This Paper
1.5. Ignition of Fuel Beds by Firebrands
- The species of plants emitting firebrands.
- Landed firebrand characteristics like diameter, length, and mass.
- The travel time from launch to landing.
- The moisture content of the fuel bed and local weather.
- The surface area, and thermal conductivity between firebrand and fuel.
- Whether the firebrand is in a “glowing” or “flaming” state upon landing.
- Variability of firebrand type within the launching stand (e.g., a coniferous tree might emit both small brands or cones).
- Whether there is a “re-settling” after landing due to slope or wind.
- Whether there is a shading effect from the sun due to the presence of the convection column.
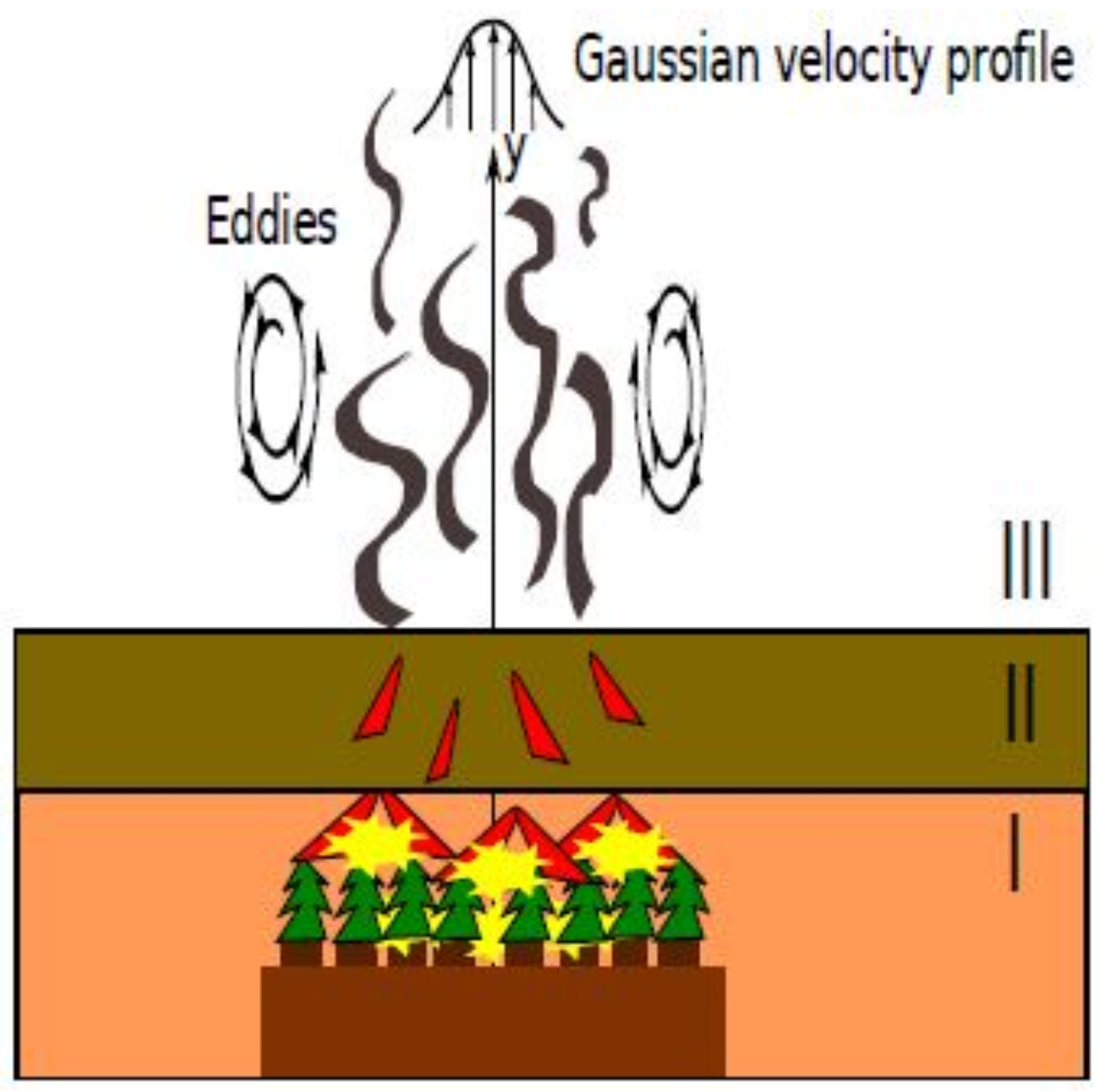
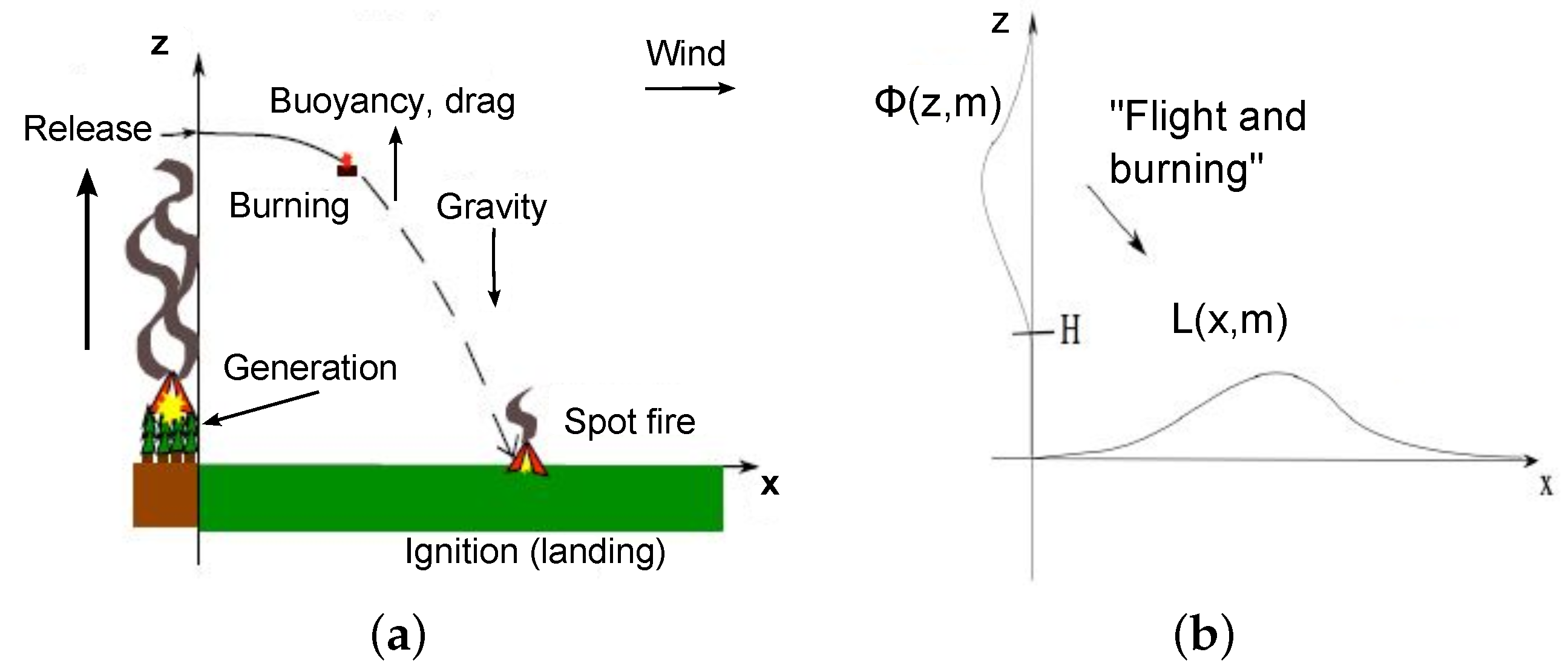
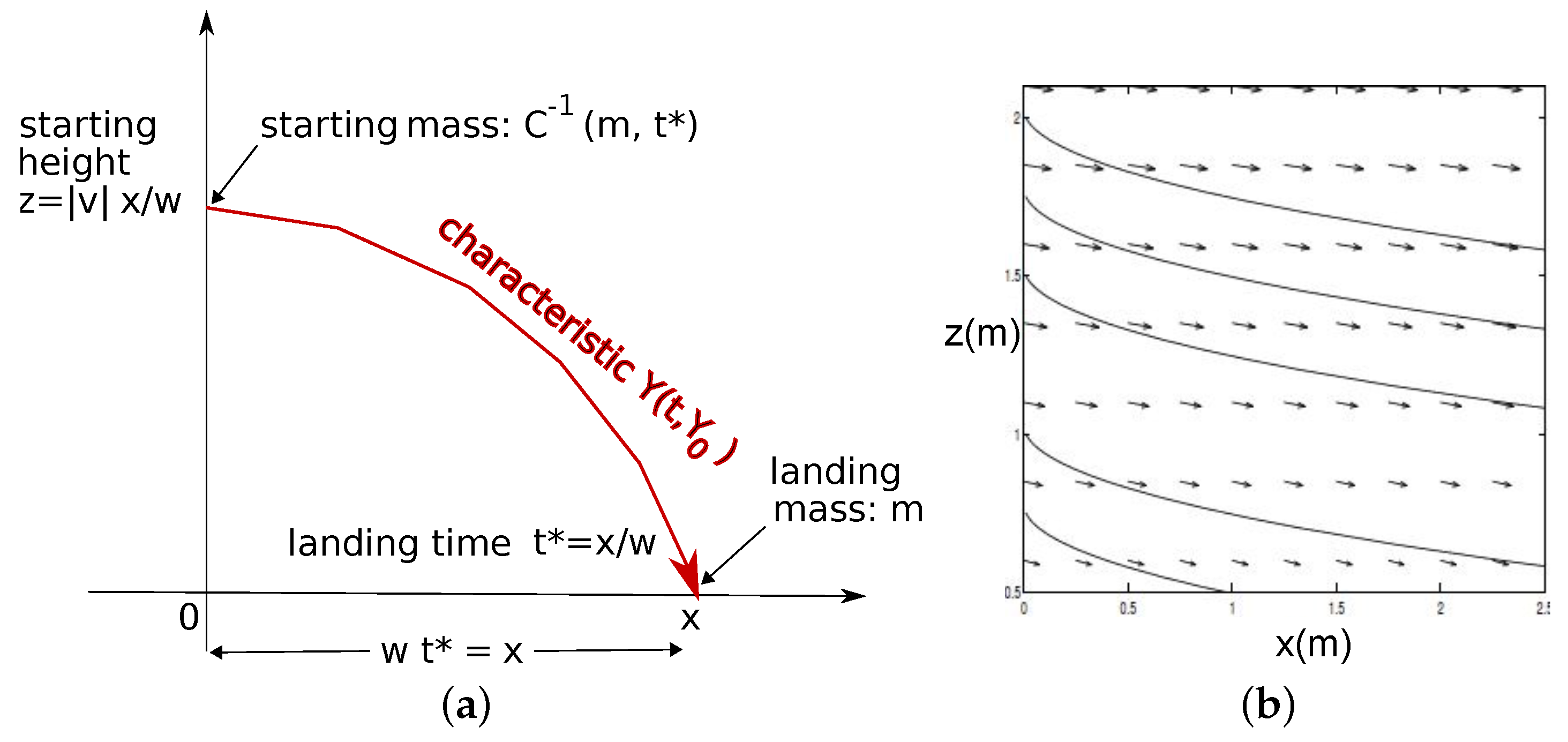
2. A Transport Model for Firebrand Transport and Combustion
- Launching: The launching distribution describes how many fire brands of mass m are launched into the convection column to the height z. We assume a maximal loftable mass of , such that . We use H to denote the canopy height (in metres) such that lofting is only considered for heights . The launching distribution is a true probability density on , normalized and dimensionless. We measure heights z in metres, and masses m in kilograms (though it will be noted that typical firebrand masses are on the order of grams). Notice that one may be interested in many more characteristics of the firebrands launched: the firebrand type, for example, could be important [46,47].
- Horizontal wind profile: We describe the horizontal windspeed (in metres per second), parallel to the downwind direction (or perpendicular to the front), by , which, depending on the physical model, might depend on the height z (in metres).
- Terminal falling velocity: We assume that flying fire brands quickly reach their terminal velocity (measured in metres per second), where falling through gravity and frictional drag are in equilibrium. We make the strong assumption that as soon as the ember leaves the convection column; in reality, we would expect turbulent up-drafts in a neighbourhood of the convection column. It is an interesting challenge to properly describe the vertical and horizontal variation in the strength of such updrafts in a neighbourhood of the convection column, though it is beyond the scope of this paper to do so. However, as discussed in the Appendix, outside the region of significant updrafts, the assumption that the brand will rapidly assume its terminal speed and falling orientation is well-justified, established through wind tunnel experiments [5,9,17].
- Burning rate: With we denote the combustion rate of a brand of mass m at height z in a well oxygenated environment. The combustion rate f has units of kilograms per second. While the burning rate depends on the relative firebrand velocity, in most models we will assume this dependence is negligible.
- Ignition probability: The ignition probability describes the probability that a landed burning mass m starts a spot fire. As a probability density on the space (with masses in kilograms), it is normalized to take on values between zero and one, and is dimensionless. Of course, ignition generally depends on the local fuel conditions, moisture content and temperature amongst other variables, so we are making a simplifying assumption that ignition is homogeneous in space. Notice further that we are implicitly assuming that thermal energy transfer, proportional to firebrand mass, depends only on mass and not for example on firebrand geometry (the latter being known to influence energy transfer).
2.1. The Impulse Release IBVP
2.2. Solution of the Transport Model
2.3. From Landed Firebrands to the Spotting Distribution
3. Examples of the Spotting Distribution
3.1. Case (W1,V1): Constant Wind and Terminal Velocity
3.2. Case (W3,V1): Power-Law for Wind, Constant Terminal Velocity
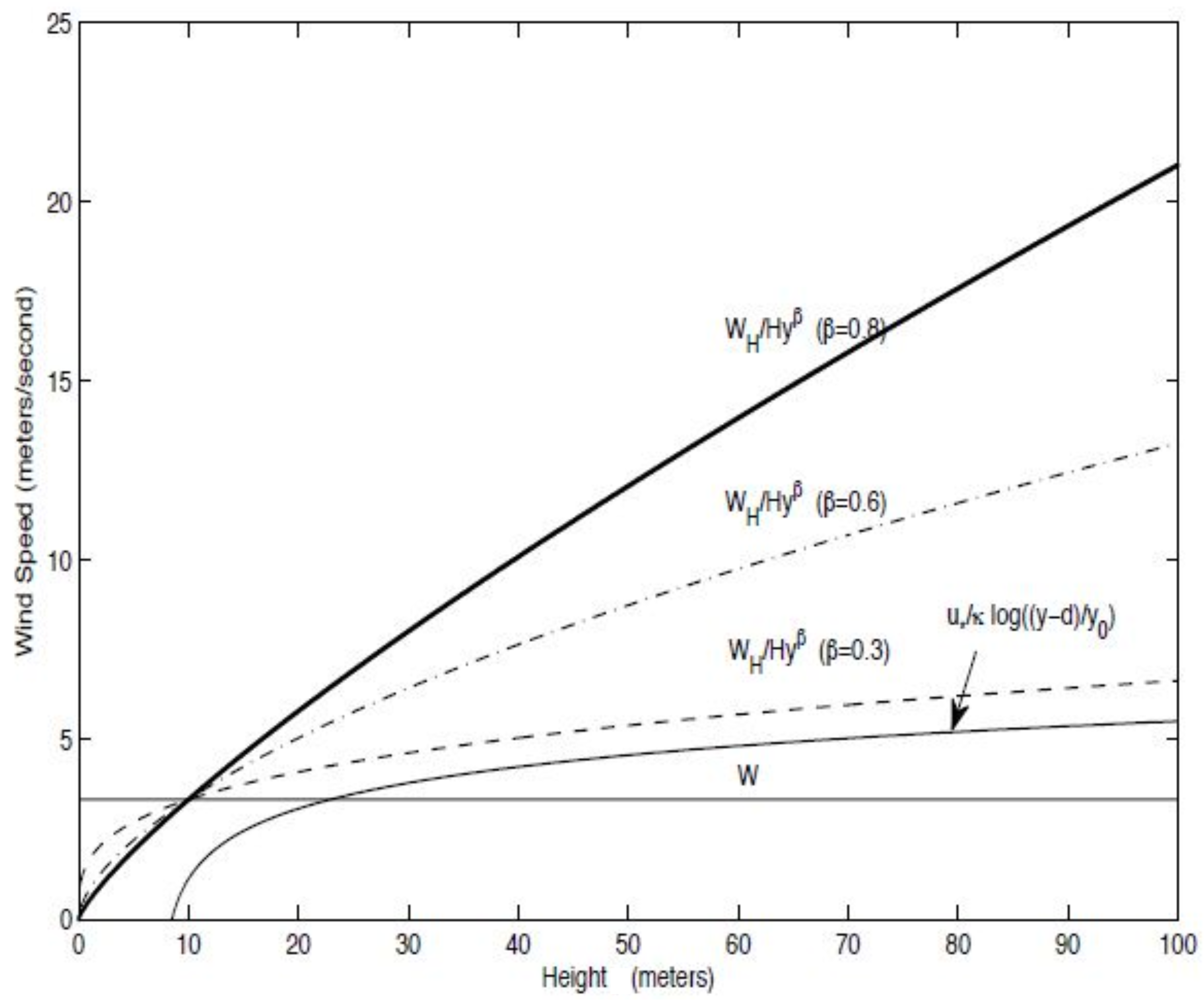
3.3. Case (W2,V1): Logarithmic Profile for w, Constant Vertical Velocity
3.4. The Spotting Distribution Determined from
3.5. Case (W1,V1, F0, L3, I3): A Family of Simple Spotting Kernels
3.6. Applications: Examples of the Spotting Distribution
4. Discussion
4.1. Usage of the Spotting Distribution
4.2. Measurements of Spotting Distributions
4.3. Future Studies
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix. Ember Release, Burning, Flying and Fuel Ignition
Appendix A.1. The Launching Distribution
| Process | Number, Description | Reference |
|---|---|---|
| launching | L1, Unique launching height | [1,21,22]. |
| L2 , Normally distributed | New. | |
| L3, Heights and masses independent: | ||
| New. | ||
| launched mass | G1, Power law | New; [44] |
| G2, Slash burning | [32]. | |
| Wind transport | W1, Constant horizontal wind | New. |
| w | W2, Logarithmic wind profile | [1,15]. |
| W3, Power-law wind profile | [1,13]. | |
| Terminal vertical | V1, Constant v | [9,68]. |
| velocity v. | V2, Experiments on | |
| cylindrical firebrands. | [16]. | |
| Combustion models | F0, Constant burn rate | New. |
| f | F1, Tarifa’s model | [1] |
| F2, Simplified Tarifa’s model | New. | |
| F3, Negligible combustion | New. | |
| F4, Fernandez-Pello model | [69]. | |
| F5, Refinements to | ||
| Fernandez-Pello model | [22,70]. | |
| F6, Albini’s line | ||
| thermal model | [3]. | |
| Ignition probability | I1, Piecewise linear | [32,46,47]. |
| I2, Heaviside step function | New. | |
| I3, Smoothed step function | New. | |
| Temperature | T1, Newton’s Law of Cooling, | |
| T2, Stefan-Boltzmann law | [22]. |
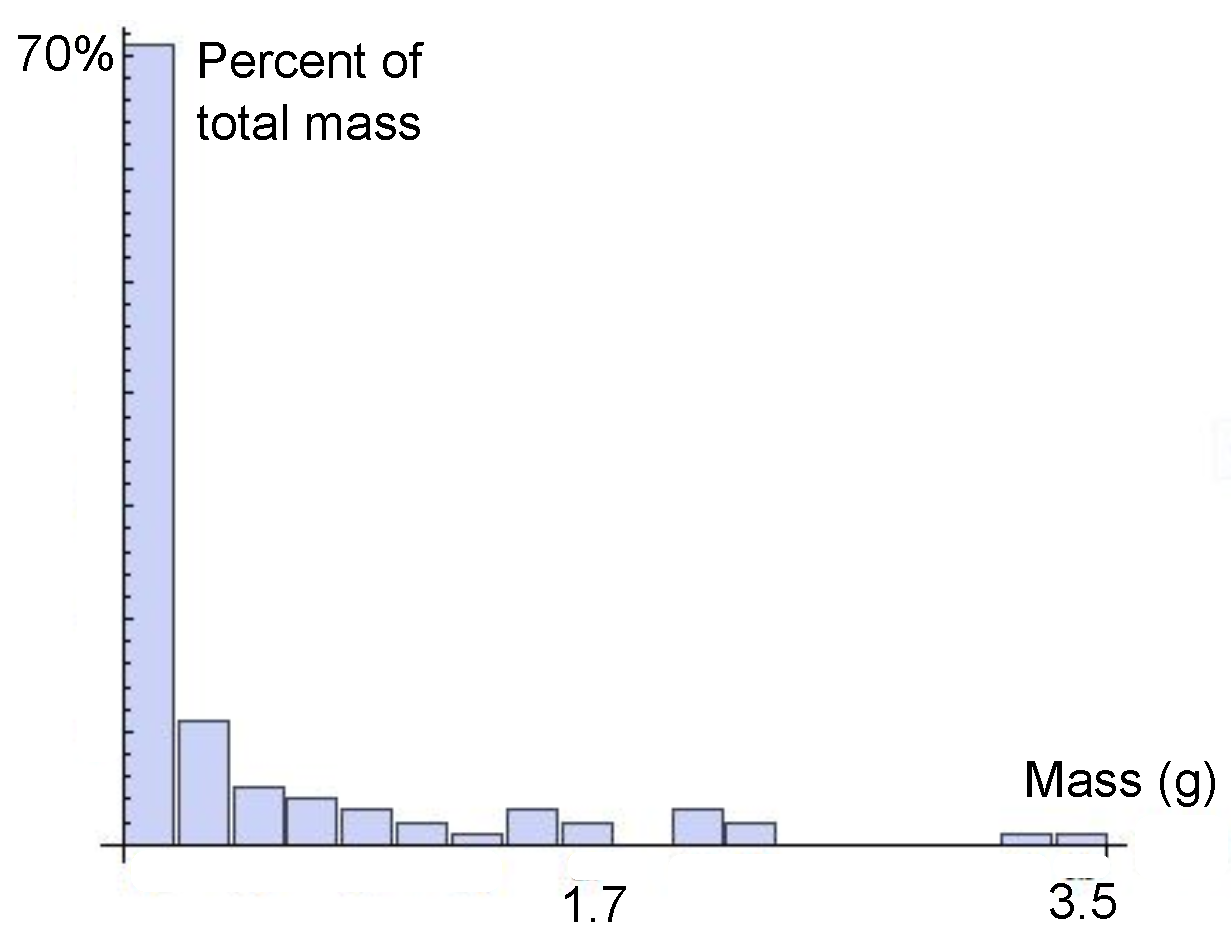
Appendix A.2. Distribution of Launched Masses
Appendix A.3. The Atmospheric Boundary Layer
Appendix A.4. Drag, Gravity and Terminal Velocity
Appendix A.5. Firebrand Combustion
Appendix A.6. Ignition Models
Appendix A.7. Models for Firebrand Temperature
References
- Albini, F.A. Spot Fire Distance From Burning Trees—A Predictive Model; Technical Report; Intermountain Forest and Range Experiment Station, Forest Service, US Department of Agriculture: Ogden, UT, USA, 1979.
- Clark, T.; Jenkins, M.A.; Coen, J.; Packham, D. A coupled atmospheric-fire model: Convective feedback on fire line dynamics. J. Appl. Meteorol. 1996, 35, 875–901. [Google Scholar] [CrossRef]
- Alexander, M.E.; Cruz, M.G. Evaluating a model for predicting active crown fire rate of spread using wildfire observations. Can. J. For. Res. 2006, 36, 3015–3028. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. Assessing crown fire potential in coniferous forests of western north america: A critique of current approaches and recent simulation studies. Int. J. Wildland Fire 2010, 19, 377–398. [Google Scholar] [CrossRef]
- Manzello, S.L.; Cleary, T.G.; Shields, J.R.; Yang, J.C. On the ignition of fuel beds by firebrands. Fire Mater. 2006, 30, 77–87. [Google Scholar] [CrossRef]
- University of California. Man, Fire and Chapparal: A Conference on Southern California Wildland Research Problems; University of California Conference Center at Lake Arrowhead: Lake Arrowhead, CA, USA, 1961. [Google Scholar]
- Woycheese, J.P.; Pagni, P.J.; Liepmann, D. Brand propagation from large-scale fires. J. Fire Protect. Eng. 1999, 10, 32–44. [Google Scholar] [CrossRef]
- Schroeder, M.; Buck, C. Fire Weather: A Guide for Application of Meteorological Information to Forest Fire Control Operations; Forest Service, US Department of Agriculture: Washington, DC, USA, 1970. [Google Scholar]
- Ellis, P.F. The Aerodynamic and Combustion Characteristics of Eucalypt Bark—A Firebrand Study. Ph.D. Thesis, Australian National University, Canberra, Australia, 2000. [Google Scholar]
- Luke, R.H.; McArthur, A.G. Bushfires in Australia; Technical Report; Australian Government Publishing Service: Canberra, Australia, 1978. [Google Scholar]
- McArthur, A.G. Fire Behaviour in Eucalypt Forests; Technical Report; Forestry and Timber Bureau: Canberra, Australia, 1967. [Google Scholar]
- Koo, E.; Pagni, P.J.; Weise, D.R.; Woycheese, J.P. Firebrands and spotting ignition in large-scale fires. Int. J. Wildland Fire 2010, 19, 818–843. [Google Scholar] [CrossRef]
- Albini, F.A. Transport of firebrands by line thermals. Combust. Sci. Technol. 1983, 32, 277–288. [Google Scholar] [CrossRef]
- Johnson, E.A.; Miyanishi, K. Forest Fires; Academic Press: Waltham, MA, USA, 2001. [Google Scholar]
- McIlveen, R. Fundamentals of Weather and Climate, 2nd ed.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Muraszew, A.; Fedele, J.B.; Kuby, W.C. Trajectory of firebrands in and out of fire whirls. Combust. Flame 1977, 30, 321–324. [Google Scholar] [CrossRef]
- Clark, T.; Coen, J.; Latham, D. Description of a coupled atmosphere-fire model. Int. J. Wildland Fire 2004, 13, 49–63. [Google Scholar] [CrossRef]
- Clark, T.; Jenkins, M.A.; Coen, J.; Packham, D. A coupled atmospheric-fire model: Convective Froude number and dynamic fingering. Int. J. Wildland Fire 1996, 6, 177–190. [Google Scholar] [CrossRef]
- Finney, M.A. Farsite: Fire Area Simulator—Model Development and Evaluation; Technical Report; USDA Forest Service: Washington, DC, USA, 2004. [Google Scholar]
- Tymstra, C. Prometheus—The Canadian Wildland Fire Growth Model: Development and Assessment; Technical Report; Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 2007. [Google Scholar]
- Baum, H.R.; McCaffrey, B.J. Fire Induced Flow Field—Theory and Experiment, Fire Safety Science; Technical Report; Hemisphere: Washington, DC, USA, 1983. [Google Scholar]
- Bhutia, S.; Jenkins, M.A.; Sun, R. Comparison of firebrand propagation prediction by a plume model and a coupled-fire/atmosphere large-eddy simulator. J. Adv. Model. Earth Syst. 2010. [Google Scholar] [CrossRef]
- Sun, R.; Jenkins, M.A.; Krueger, S.K.; Mell, W.; Charney, J.J. An evaluation of fireplume properties simulated with the fire dynamics simulator (FDS) and the clark coupled wildfire model. Can. J. For. Res. 2006, 36, 2894–2908. [Google Scholar] [CrossRef]
- Sun, R.; Krueger, S.K.; Jenkins, M.A.; Zulauf, M.A.; Charney, J.J. The importance of fire-atmosphere coupling and boundary-layer turbulence to wildfire spread. Int. J. Wildland Fire 2009, 18, 50–60. [Google Scholar] [CrossRef]
- Sofiev, M.; Ermakova, T.; Vankevich, R. Evaluation of the smoke-injection height from wild-land fires using remote-sensing data. Atmos. Chem. Phys. 2012, 12, 1995–2006. [Google Scholar] [CrossRef]
- Kot, M.; Lewis, M.; van den Driessche, P. Dispersal data and the spread of invading organisms. Ecology 1996, 77, 2027–2042. [Google Scholar] [CrossRef]
- Bullock, J.M.; Kenward, R.E.; Hails, E.R.S. Dispersal Ecology, 1st ed.; British Ecological Society: London, UK, 2002. [Google Scholar]
- Robbins, T. Seed Dispersal and Biological Invasion: A Mathematical Analysis. Ph.D. Thesis, University of Utah, Salt Lake City, UT, USA, 2003. [Google Scholar]
- Martin, J. Mathematical Modelling and Analysis of a Model for Wildfire Spread Including Spotting. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2013. [Google Scholar]
- Hillen, T.; Greese, B.; Martin, J.; de Vries, G. Birth-jump processes, with applications to wildfire spotting. J. Theor. Biol. 2015, 9 (Suppl. S1), 104–127. [Google Scholar]
- Sardoy, N.; Consalvi, J.-L.; Porterie, B.; Fernandez-Pello, A.C. Modeling transport and combustion of firebrands from burning trees. Combust. Flame 2007, 150, 151–169. [Google Scholar] [CrossRef]
- Wang, H.H. Analysis on downwind distribution of firebrands sourced from a wildland fire. Fire Technol. 2011, 47, 321–340. [Google Scholar] [CrossRef]
- Boychuk, D.; Braun, W.J.; Kulperger, R.J.; Krougly, Z.L.; Stanford, D.A. A stochastic model for forest fire growth. INFOR 2008, 45, 9–16. [Google Scholar] [CrossRef]
- Forestry Canada Danger Group. Development and Structure of the Canadian Forest Fire Behaviour Prediction System; Technical Report; Forestry Canada: Edmonton, AB, Canada, 1992. [Google Scholar]
- Kaur, I.; Mentrelli, A.; Bosseur, F.; Filippi, J.B.; Pagnini, G. Turbulence and fire-spotting effects into wild-land fire simulators. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 300–320. [Google Scholar] [CrossRef]
- Alexander, M.E.; Tymstra, C.; Frederick, K.W. Incorporating Breaching and Spotting Considerations into Prometheus, the Canadian Wildland Fire Growth Model; Technical Report; Foothills Model Forest: Hinton, AB, Canada, 2004. [Google Scholar]
- Pagnini, G.; Mentrelli, A. Modelling wildland fire propagation by tracking random fronts. Nat. Hazards Earth Syst. Sci. 2014, 14, 2249–2263. [Google Scholar] [CrossRef]
- Mandel, J.; Beezley, J.D.; Kochanski, A.K. Coupled atmosphere-wildland fire modeling with WRF 3.3 and SFIRE 2011. Geosci. Model Dev. 2011, 4, 591–610. [Google Scholar] [CrossRef] [Green Version]
- Bova, A.S.; Mell, W.E.; Hoffman, C.M. A comparison of level set and marker methods for the simulation of wildland fire front propagation. J. Appl. Meteorol. 2015, 25, 229–241. [Google Scholar] [CrossRef]
- Alexander, M.E. Crown Fire Thresholds in Exotic Pine Plantations of Australasia. Ph.D. Thesis, Australian National University, Canberra, Australia, 1998. [Google Scholar]
- Ryu, S.D.; University of Alberta, Edmonton, AB, Canada. The seven types of spotting. Private communication, 2013. [Google Scholar]
- Blackmarr, W.H. Moisture Content Influences Ignitability of Slash Pine Litter; Technical Report; USDA Forest Service South-Eastern Forest Experimental Station: Asheville, NC, USA, 1972. [Google Scholar]
- Muraszew, A.; Fedele, J.B. Firebrand Investigation; Technical Report; The Aerospace Corporation: El Segundo, CA, USA, 1975. [Google Scholar]
- Manzello, S.L.; Maranghides, A.; Mell, W.E. Firebrand generation from burning vegetation. Int. J. Wildland Fire 2007, 16, 458–462. [Google Scholar] [CrossRef]
- Manzello, S.L.; Maranghides, A.; Shields, J.R.; Mell, W.E.; Hayashi, Y. Mass and size distribution of firebrands generated from burning Korean pine trees. Fire Mater. 2009, 33, 21–31. [Google Scholar] [CrossRef]
- Gentaume, A.; Lampin-Maillet, C.; Guijarro, M.; Hernando, C.; Jappiot, M.; Fonturbel, T.; Perez-Gorostiaga, P.; Vega, J. Spot fires: Fuel ammability and capability of firebrands to ignite fuel beds. Int. J. Wildland Fire 2009, 18, 951–969. [Google Scholar] [CrossRef]
- Gentaume, A. Laboratory characterization of firebrands involved in spot fires. Ann. For. Sci. 2011, 68, 531–541. [Google Scholar] [CrossRef]
- Ellis, P.F. Fuelbed ignition potential and bark morophology explain the notoriety of eucalypt messmate ‘stringybark’ for intense spotting. Int. J. Wildland Fire 2011, 20, 897–907. [Google Scholar] [CrossRef]
- Okubo, A.; Levin, S.A. Diffusion and Ecological Problems: Modern Perspectives, 2nd ed.; Springer-Verlag: New York, NY, USA, 2002. [Google Scholar]
- Evans, L.C. Partial Differential Equations; AMS Press: New York, NY, USA, 1998. [Google Scholar]
- Muraszew, A. Firebrand Phenomena; Technical Report; The Aerospace Corporation: El Segundo, CA, USA, 1974. [Google Scholar]
- Asensio, M.I.; Ferragut, L. On a wildland fire model with radiation. Int. J. Numer. Meth. Eng. 2002, 54, 135–157. [Google Scholar] [CrossRef]
- Mandel, J.; Bennethum, L.S.; Beezley, J.D.; Coen, J.L.; Douglas, C.C.; Kim, M.; Vodacek, A. A wildland fire model with data assimilation. Math. Comput. Simul. 2008, 79, 584–606. [Google Scholar] [CrossRef]
- Ellis, P.F. Spotting and firebrand behaviour in dry eucalypt forest and the implications for fuel management in relation to fire suppression and to “ember” (firebrand) attack on houses. In Proceedings of the 3rd International Wildland Conference, Sydney, Australia, 3–6 October 2003.
- Gould, J.S.; Cheney, N.P.; McCaw, L. Project Vesta-Research into the effects of fuel structure and fuel load on behaviour of moderate to high-intensity fires in dry eucalypt forest: Progress Report. In Proceedings of the Australasian Bushfire Conference, Christchurch, New Zealand, 3–6 July 2001; pp. 104–127.
- Chandler, C.C. Fire Behaviour of the Basin Fire, Sierra National Forest; Technical Report; USDA Forest Service Pacific Southwest Forest and Range Experiment Station: Berkeley, CA, USA, 1961. [Google Scholar]
- Butler, B.W.; Bartlette, R.A.; Bradshaw, L.S.; Cohen, J.D.; Andrews, P.L.; Putnam, T.; Mangan, R.J. Fire Behaviour Associated with the 1994 South Canyon Fire on Storm King Mountain, Colorado; Technical Report; USDA Forest Service Rocky Mountain Research Station: Asheville, NC, USA, 1998. [Google Scholar]
- Butler, B.W.; Reynolds, T.D. Wildfire Case Study: Butte City Fire, Southeastern Idaho, July 1, 1994; Technical Report; USDA Forest Service Intermountain Research Station: Asheville, NC, USA, 1997. [Google Scholar]
- Baden, W.; Klem, T.; Teague, P.E. The Oakland/Berkeley Hills Fire; Technical Report; National Wildland/Urban Interface Fire Protection Initiative: Quincy, MA, USA, 1991. [Google Scholar]
- Martin, J.; Coville, J.; Hamel, F. Generalized transition waves for nonlocal equations with periodic heterogeneous dispersal. Unpublished work. 2016. [Google Scholar]
- Quintiere, J.G. Fundamentals of Fire Phenomena; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ai, S.; Huang, W. Travelling wavefronts in combustion and chemical reaction models. Proc. R. Soc. Edinb. 2007, 137A, 671–700. [Google Scholar] [CrossRef]
- Cunningham, P.; Goodrick, S.L.; Hussaini, M.Y.; Linn, R.R. Coherent vertical structures in numerical simulations of buoyant plumes from wildland fires. Int. J. Wildland Fire 2005, 14, 61–75. [Google Scholar] [CrossRef]
- Cunningham, P.; Linn, R.R. Numerical simulations of grass fires using a coupled atmosphere-fire model: Dynamics of fire spread. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Mercer, G.N.; Weber, R.O. Plumes above line fires in a cross wind. Int. J. Wildland Fire 1994, 4, 201–207. [Google Scholar] [CrossRef]
- Nmira, F.; Consalvi, J.J.; Boulet, P.; Porterie, B. Numerical study of wind effects on the characteristics of flames from non-propagating vegetation fires. Fire Saf. J. 2010, 45, 129–141. [Google Scholar] [CrossRef]
- Porterie, P.; Louraud, J.C.; Morvan, D.; Larini, M. A numerical study of buoyant plumes in cross-flow conditions. Int. J. Wildland Fire 1999, 9, 101–108. [Google Scholar] [CrossRef]
- Sanchez, C.T.; del Notario, P.P.; Moreno, F.G. On the flight paths and lifetimes of burning particles of wood. Symp. Int. Combust. 1967, 10, 1021–1037. [Google Scholar]
- Tse, S.D.; Fernandez-Pello, A.C. On the flight paths of metal particles and embers generated by power lines in high winds—A potential source of wildland fires. Fire Saf. J. 1998, 30, 333–356. [Google Scholar] [CrossRef]
- Kanuri, A.M. Introduction to Combustion Phenomena; Gordon and Breach Science: New York, NY, USA, 1995. [Google Scholar]
- McCaffrey, B. Momentum implications for buoyant dffusion flames. Combust. Flames 1983, 52, 149–167. [Google Scholar] [CrossRef]
- Linn, R.; Winterkamp, J.; Edminster, C.; Colman, J.J.; Smith, W.S. Coupled influences of topography and wind on wildland fire behaviour. Int. J. Wildland Fire 2007, 16, 183–195. [Google Scholar] [CrossRef]
- Zdunkowski, W.; Bott, A. Dynamics of the Atmosphere: A Course in Theoretical Meteorology; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Lynch, A.H.; Cassano, J.J. Applied Atmospheric Dynamics; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Taylor, M.E. Partial Differential Equations I: Basic Theory; Springer-Verlag: New York, NY, USA, 1996. [Google Scholar]
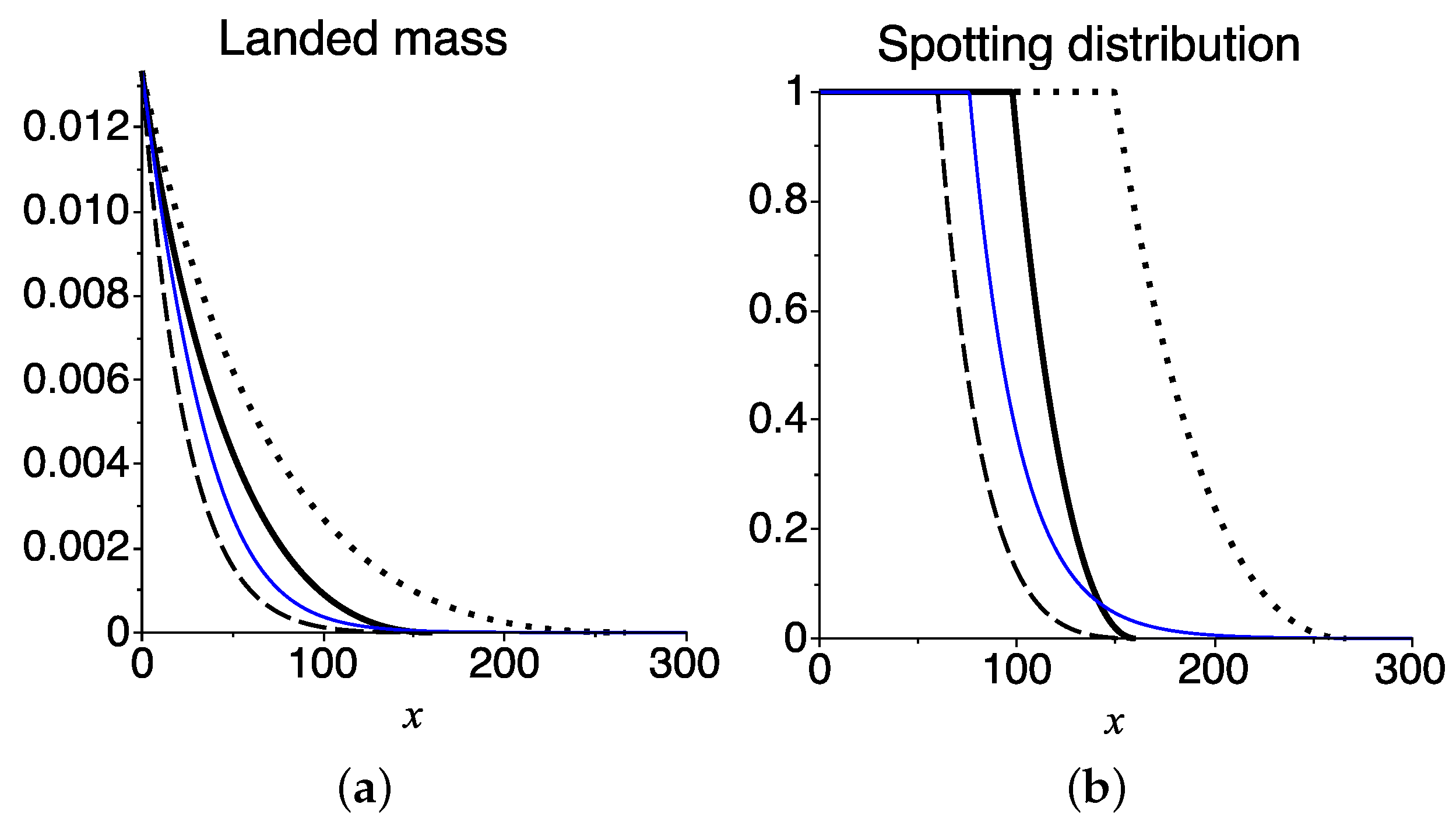
| Parameter | w | v | a | κ | N | λ | |||
|---|---|---|---|---|---|---|---|---|---|
| base case (thick solid) | 2 | −1 | 0.004 | 0.001 | 7.91 | 0.00005 | 1000 | 0.01 | 160 |
| slow burner (dotted) | 2 | −1 | 0.004 | 0.001 | 7.91 | 0.00003 | 1000 | 0.01 | 266.66 |
| lower release height (dashed) | 2 | −1 | 0.004 | 0.001 | 7.91 | 0.00005 | 1000 | 0.05 | 160 |
| Parameter | |||||||||
| Tarifa’s case (thin blue) | 2 | −1 | 0.004 | 0.001 | 7.91 | 0.000286 | 1000 | 0.01 | ∞ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martin, J.; Hillen, T. The Spotting Distribution of Wildfires. Appl. Sci. 2016, 6, 177. https://doi.org/10.3390/app6060177
Martin J, Hillen T. The Spotting Distribution of Wildfires. Applied Sciences. 2016; 6(6):177. https://doi.org/10.3390/app6060177
Chicago/Turabian StyleMartin, Jonathan, and Thomas Hillen. 2016. "The Spotting Distribution of Wildfires" Applied Sciences 6, no. 6: 177. https://doi.org/10.3390/app6060177
APA StyleMartin, J., & Hillen, T. (2016). The Spotting Distribution of Wildfires. Applied Sciences, 6(6), 177. https://doi.org/10.3390/app6060177





