Validation of a Mathematical Model for Green Algae (Raphidocelis Subcapitata) Growth and Implications for a Coupled Dynamical System with Daphnia Magna
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Asymptotic Theory
2.3. Boostrapping
- First estimate from the entire sample using OLS.
- Using this estimate, define the standardized residualsfor , where n is the number of data points, and p are the number of model parameters. Set , which will represent the total number of artificial samples we will create.
- Create a bootstrapping sample of size n using random sampling with replacement from the data (realizations) to form a bootstrapping sample .
- Create bootstrap sample pointsfor .
- Obtain a new estimate from the bootstrapping sample using OLS.
- Set and repeat steps 3–5 until (this can be any large value, but for these experiments we used ).
2.4. Model Comparison: Nested Restraint Tests
2.5. Akaike Information Criterion
3. Models
3.1. Logistic Model
3.2. Bernoulli Model
3.3. Gompertz Growth Model
3.4. Logistic Model: Numerical Discretization
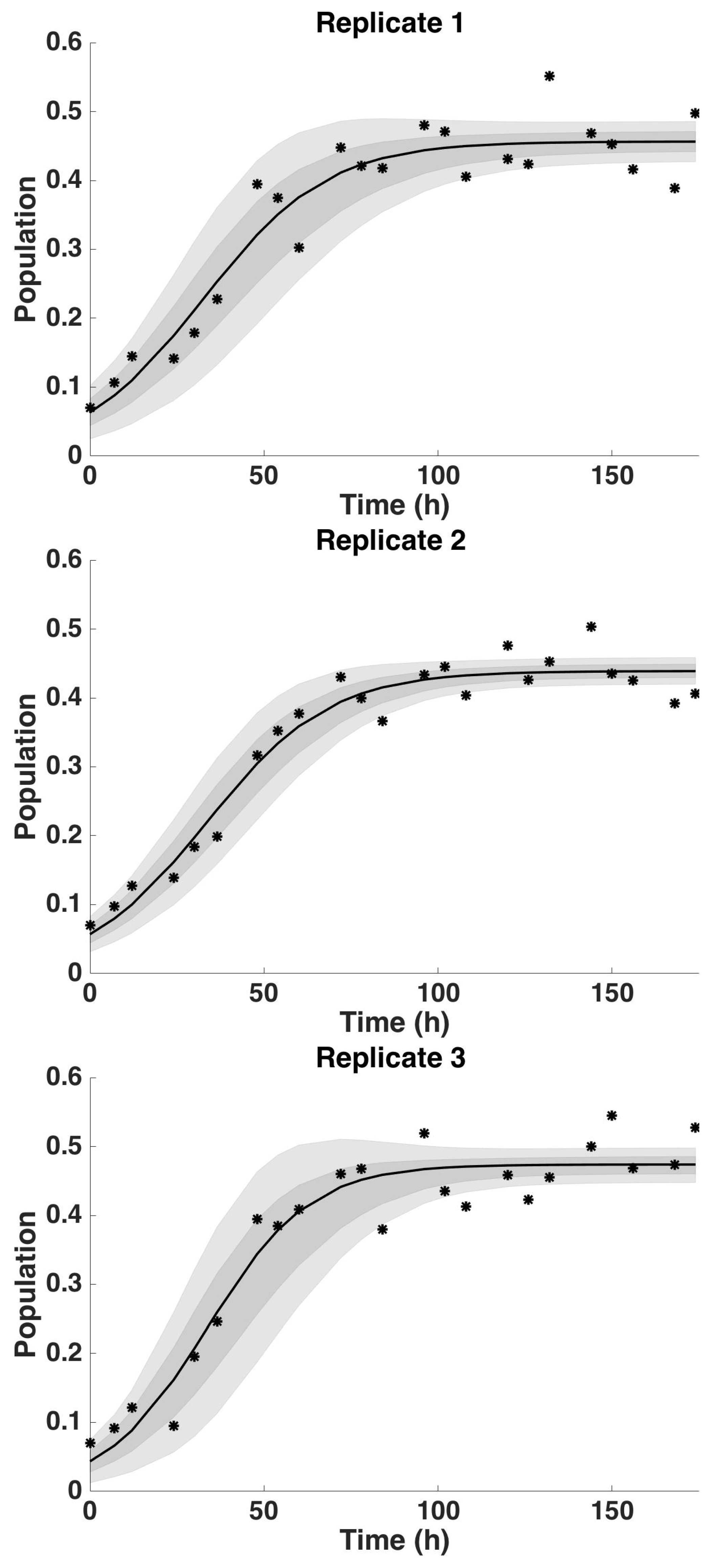
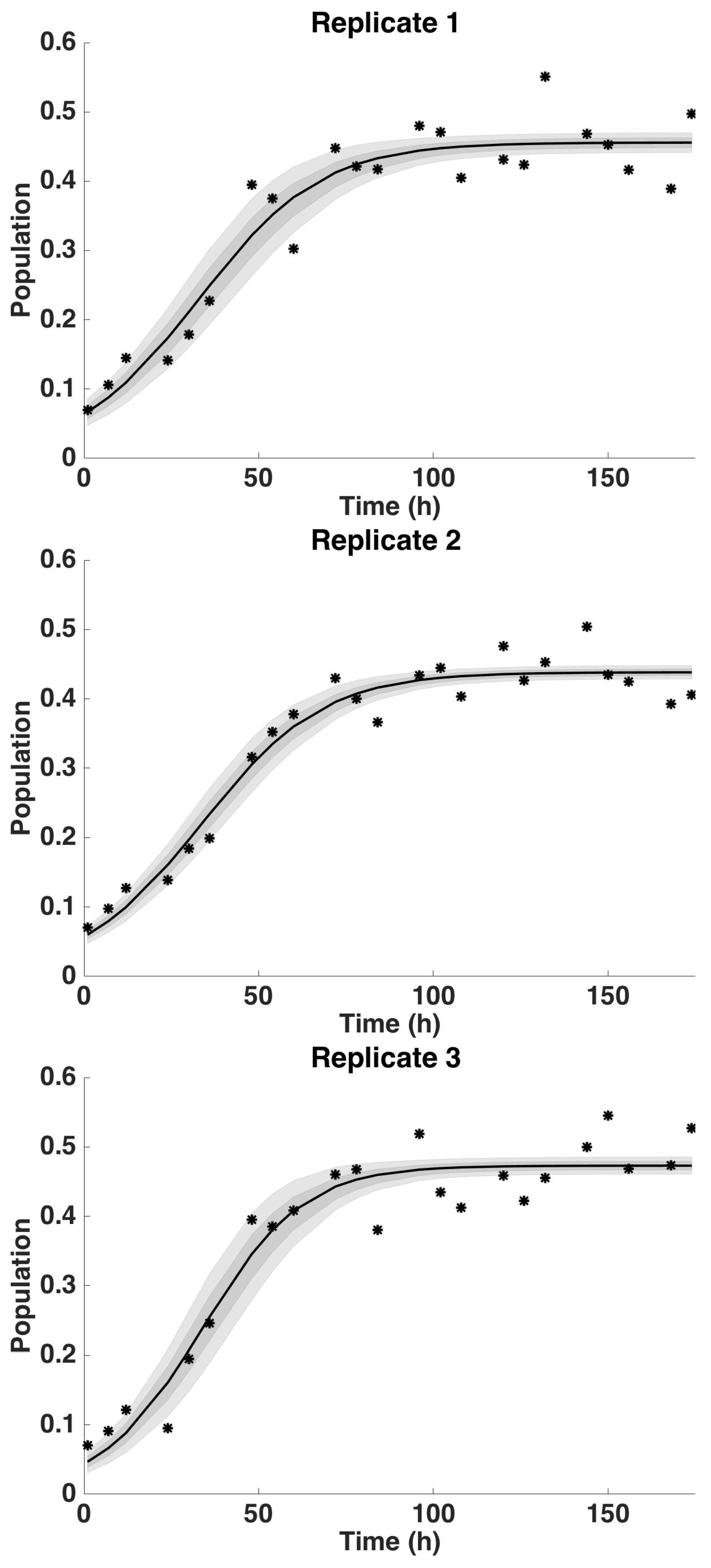
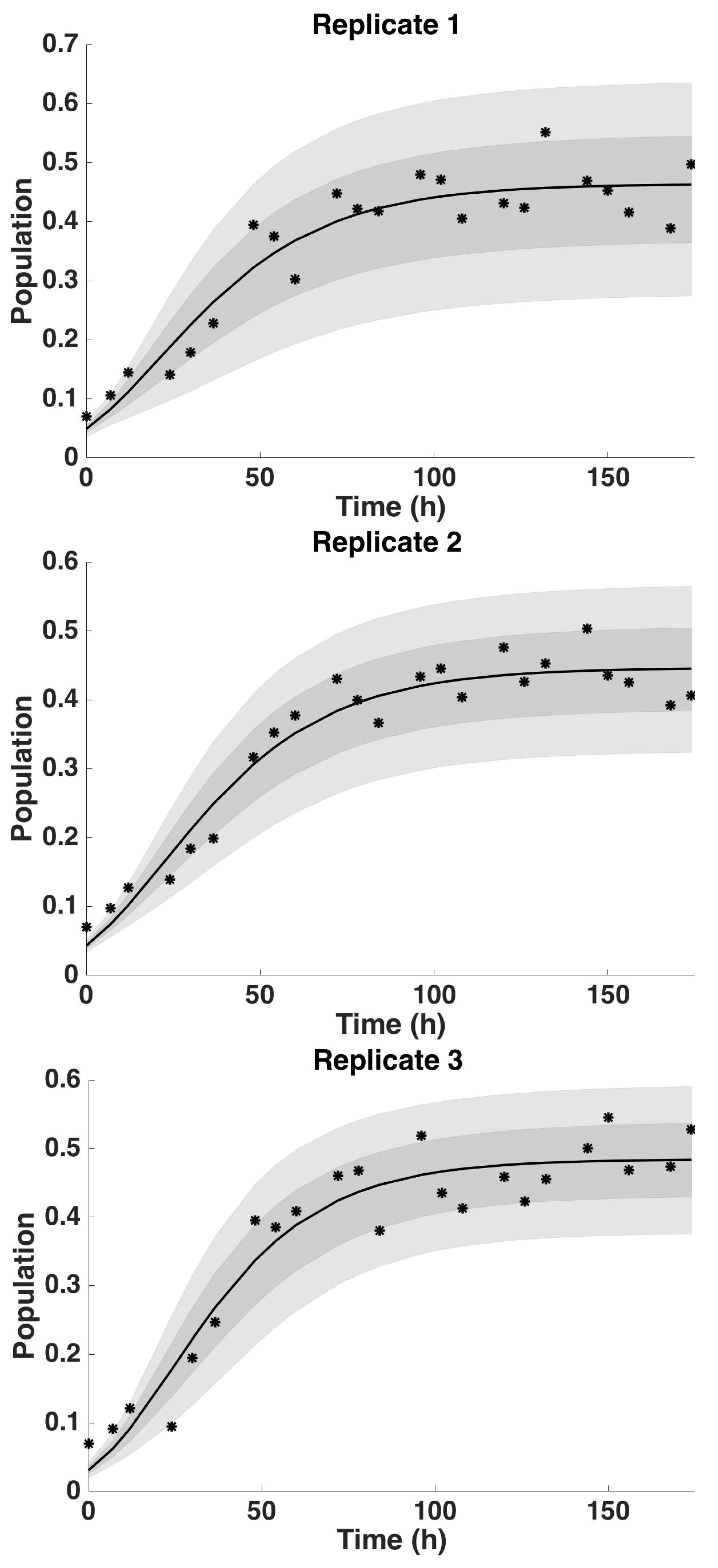
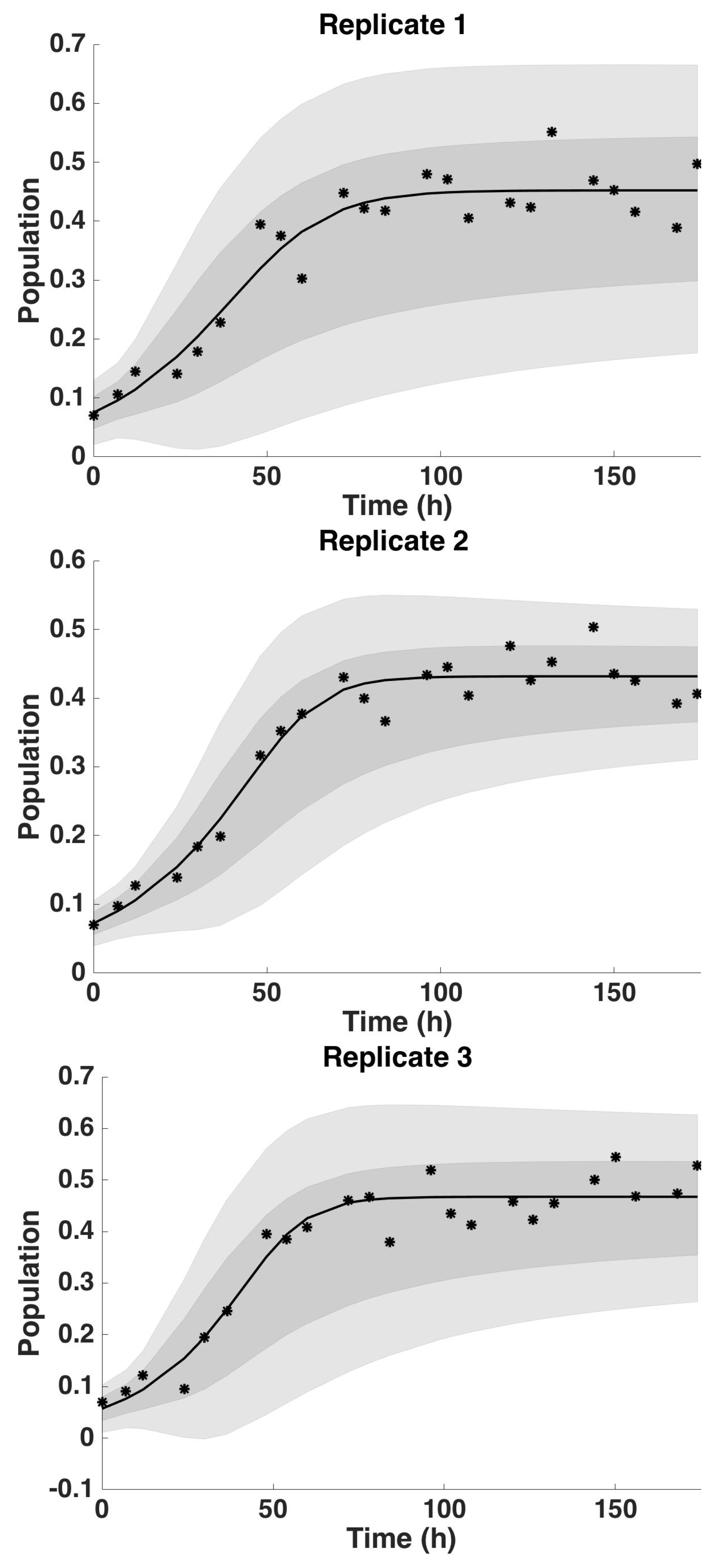
4. Results
4.1. Data fitting and Model Comparisons
4.2. Uncertainty Analysis
4.2.1. Uncertainty Analysis: Initial Condition
4.2.2. Uncertainty Analysis: Growth Rate
4.2.3. Uncertainty Analysis: Saturation Parameter
4.2.4. Uncertainty Analysis: Bernoulli Model Parameter β
4.3. Coupling to the Discrete-Time Daphnia magna Population Model
5. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- McCauley, E.; Murdoch, W.W. Cyclic and stable populations: Plankton as paradigm. Am. Nat. 1987, 129, 97–121. [Google Scholar] [CrossRef]
- Benincà, E.; Dakos, V.; van Nes, E.H.; Huisman, J.; Scheffer, M. Resonance of plankton communities with temperature fluctuations. Am. Nat. 2011, 178, E85–E95. [Google Scholar]
- McCauley, E.; Nisbet, R.M.; Murdoch, W.W.; de Roos, A.M.; Gurney, W.S. Large-amplitude cycles of Daphnia and its algal prey in enriched environments. Nature 1999, 402, 653–656. [Google Scholar] [CrossRef]
- Scheffer, M.; Rinaldi, S.; Kuznetsov, Y.A.; van Nes, E.H. Seasonal dynamics of Daphnia and algae explained as a periodically forced predator-prey system. Oikos 1997, 80, 519–532. [Google Scholar] [CrossRef]
- Adoteye, K.; Banks, H.T.; Cross, K.; Eytcheson, S.; Flores, K.B.; LeBlanc, G.A.; Nguyen, T.; Ross, C.; Smith, E.; Stemkovski, M. Statistical validation of structured population models for Daphnia magna. Math. Biosci. 2015, 266, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Wang, G.; LeBlanc, G.A. Cloning and characterization of the retinoid X receptor from a primitive crustacean Daphnia magna. Gen. Comp. Endocrinol. 2007, 150, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Caperon, J. Population growth in micro-organisms limited by food supply. Ecology 1967, 48, 715–722. [Google Scholar] [CrossRef]
- Schanz, F.; Zahler, U. Prediction of algal growth in batch cultures. Schw. Zeit. Hydr. 1981, 43, 103–113. [Google Scholar] [CrossRef]
- Thompson, P.-A.; Couture, P. Short-and long-term changes in growth and biochemical composition of Selenastrum capricornutum populations exposed to cadmium. Aqua. Toxic. 1991, 21, 135–143. [Google Scholar] [CrossRef]
- Banks, H.T.; Thompson, W.C.; Hu, S. Modeling and Inverse Problems in the Presence of Uncertainty; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Banks, H.T.; Tran, H.T. Mathematical and Experimental Modeling of Physical and Biological Processes; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Seber, G.A.; Wild, C.J. Nonlinear Regression; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Banks, H.T.; Banks, J.E.; Dick, L.K.; Stark, J.D. Estimation of dynamic rate parameters in insect populations undergoing sublethal exposure to pesticides. Bull. Math. Biol. 2007, 69, 2139–2180. [Google Scholar] [CrossRef] [PubMed]
- Banks, H.T.; Davis, J.L.; Ernstberger, S.L.; Hu, S.; Artimovich, E.; Dhar, A.K. Experimental design and estimation of growth rate distributions in size-structured shrimp populations. Inv. Probl. 2009, 25, 095003. [Google Scholar] [CrossRef]
- Banks, J.E.; Dick, L.K.; Banks, H.T.; Stark, J.D. Time-varying vital rates in ecotoxicology: Selective pesticides and aphid population dynamics. Ecol. Model. 2008, 210, 155–160. [Google Scholar] [CrossRef]
- Wood, S.N. Obtaining birth and mortality patterns from structured population trajectories. Ecol. Monogr. 1994, 64, 23–44. [Google Scholar] [CrossRef] [PubMed]
- May, R.M.; Conway, G.R.; Hassell, M.P.; Southwood, T.R.E. Time delays, density-dependence and single-species oscillations. J. Anim. Ecol. 1974, 43, 747–770. [Google Scholar] [CrossRef]
- Wang, Y.H.; Kwon, G.; Li, H.; LeBlanc, G.A. Tributyltin synergizes with 20-Hydroxyecdysone to produce endocrine toxicity. Toxicol. Sci. 2011, 123, 71–79. [Google Scholar] [CrossRef] [PubMed]

| Replicate | Gompertz | Logistic | Bernoulli | Discrete Euler-Method Logistic (DEL) |
|---|---|---|---|---|
| 1 | −69.4203 | −71.5919 | −69.2189 | −72.6155 |
| 2 | −84.2435 | −89.0016 | −89.3905 | −90.4114 |
| 3 | −71.3972 | −74.2560 | −72.4414 | −75.3515 |
| Bernoulli Restricted to: | Bernoulli Restricted to: | |
|---|---|---|
| Replicate | Logistic | Logistic with X0 fixed |
| 1 | 0.5935 | 0.7233 |
| 2 | 2.4718 | 3.6216 |
| 3 | 1.1733 | 3.4118 |
| Asymptotic Results: β | Replicate | Estimate | SE |
| 1 | 2.1646 | 2.5440 | |
| 2 | 3.4574 | 2.8118 | |
| 3 | 2.8188 | 2.8758 | |
| Bootstrapping Results: β | Replicate | Estimate | SE |
| 1 | 38.31 | 113.72 | |
| 2 | 29.78 | 92.89 | |
| 3 | 43.27 | 113.81 |
| Parameter/Variable | Description | Units |
|---|---|---|
| Number of daphnids of age i | # of daphnids | |
| Total population size at time t | # of daphnids | |
| q | Density-dependent fecundity constant | dimensionless |
| Density-independent fecundity rates | # neonates·daphnid−1·day−1 | |
| μ | Density-independent survival rate | day−1 |
| τ | Delay for density-dependent fecundity | days |
| c | Density-dependent survival constant | dimensionless |
| Total biomass at time t | mm | |
| k | Average maximum daphnid size (major axis) | mm |
| r | Average daphnid growth rate | mm/hour |
| Average neonate size (major axis) | mm | |
| R | Intrinsic growth rate of algae | cells L−1·day−1 |
| K | Algal population carrying capacity | cells L−1 |
| δ | Density dependent predation constant | mm−1·cells |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stemkovski, M.; Baraldi, R.; Flores, K.B.; Banks, H.T. Validation of a Mathematical Model for Green Algae (Raphidocelis Subcapitata) Growth and Implications for a Coupled Dynamical System with Daphnia Magna. Appl. Sci. 2016, 6, 155. https://doi.org/10.3390/app6050155
Stemkovski M, Baraldi R, Flores KB, Banks HT. Validation of a Mathematical Model for Green Algae (Raphidocelis Subcapitata) Growth and Implications for a Coupled Dynamical System with Daphnia Magna. Applied Sciences. 2016; 6(5):155. https://doi.org/10.3390/app6050155
Chicago/Turabian StyleStemkovski, Michael, Robert Baraldi, Kevin B. Flores, and H.T. Banks. 2016. "Validation of a Mathematical Model for Green Algae (Raphidocelis Subcapitata) Growth and Implications for a Coupled Dynamical System with Daphnia Magna" Applied Sciences 6, no. 5: 155. https://doi.org/10.3390/app6050155
APA StyleStemkovski, M., Baraldi, R., Flores, K. B., & Banks, H. T. (2016). Validation of a Mathematical Model for Green Algae (Raphidocelis Subcapitata) Growth and Implications for a Coupled Dynamical System with Daphnia Magna. Applied Sciences, 6(5), 155. https://doi.org/10.3390/app6050155






