4.1. Analyses of Liquid Bridge Force, Van der Waals force, and Electrostatic Force
In general, when the particle size is less than several tens of micrometers, the effects of the surface force generated from the van der Waals force, electrostatic force, and liquid bridge force are strengthened and this surface force becomes greater than the force of gravity [
11].
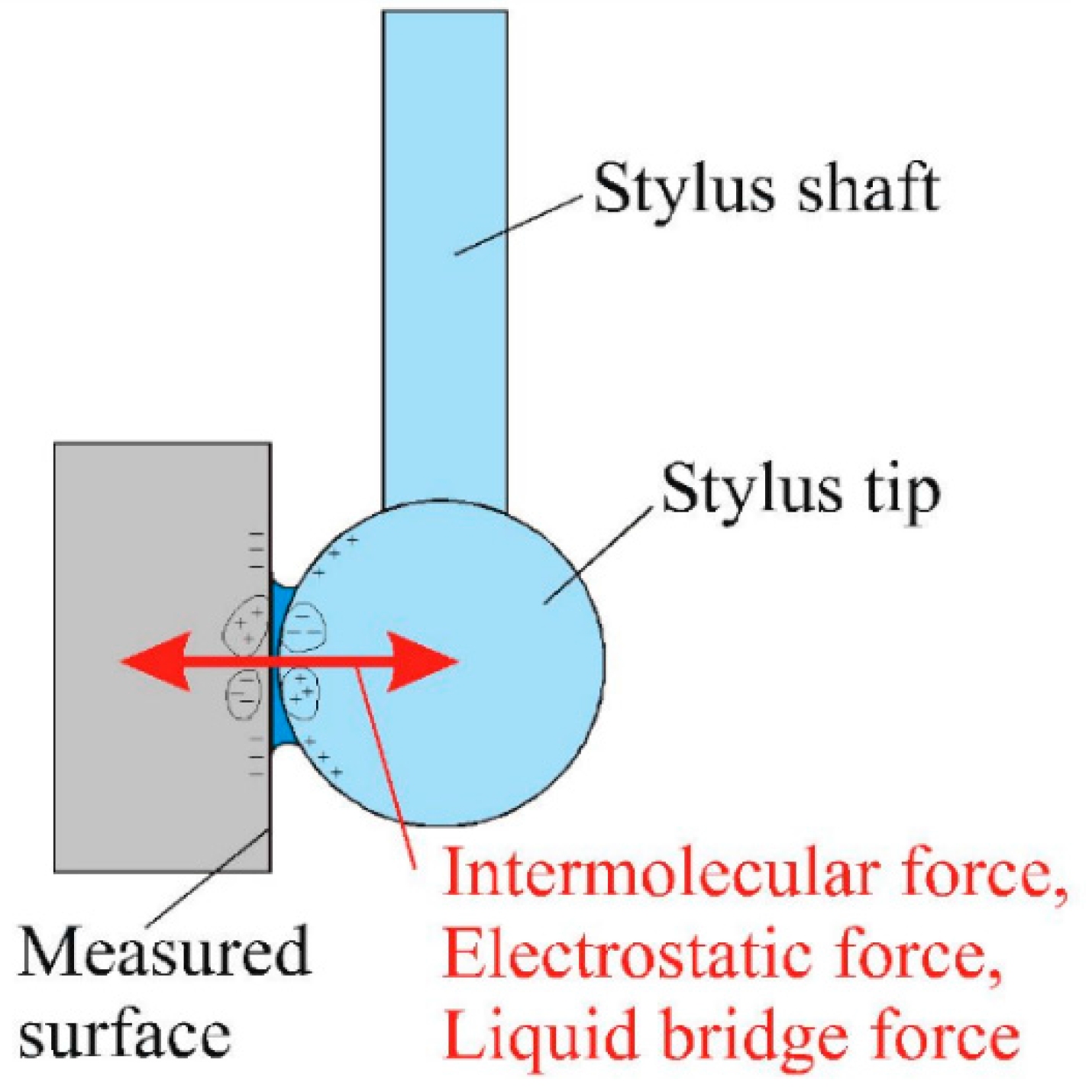
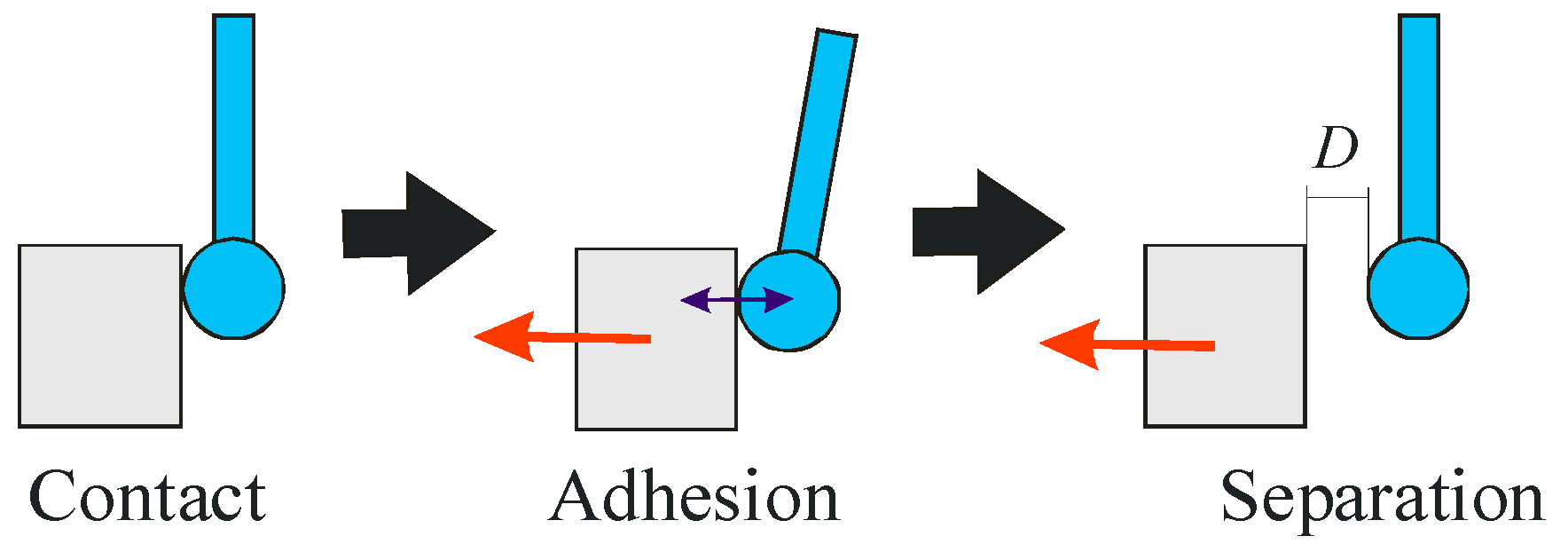
Figure 5 shows a schematic diagram of the surface force between the stylus tip and the measurement surface. Because the fiber stylus has a 5-µm-diameter sphere on its tip, the measurement surface draws the stylus tip closer when the stylus tip approaches it, and the distance between the stylus tip and the measured surface is less than the regular displacement. When the stylus tip comes into contact with the measured surface, it adheres to the surface and cannot be separated from it. When the measured surface is scanned point by point in the touch-trigger mode, the measurement time increases because the stylus tip is required to be separated from the measured surface on account of the surface force. When the measured surface is scanned continuously in the scanning mode, measurement accuracy reduced because of the bending of the stylus shaft due to the adhesion. The observed adhesion, which is influenced by environmental factors (e.g., humidity) and the roughness of the measured surface, is not reproducible.
These surface forces are analyzed with the aim of investigating the causes of adhesion. First, we examine the liquid bridge force. This force has a large effect on adhesion in a humid environment; it is generated by the capillary action of condensed water near the contact zone of the stylus tip and measured surface. This force increases with increasing relative humidity. The liquid bridge force
Fl experienced in the case of a stylus tip of diameter
d and under a relative humidity of %
RH can be calculated using the empirical formula in Equation (3) [
11]. This is the empirical formula of the liquid bridge force between a particle and a plate with a hard and clean surface. As indicated by this formula, the liquid bridge force increases with increasing relative humidity.
Next, we examine the van der Waals force. This force acts between molecules, and it is a general force of interaction that acts between objects at all times. The van der Waals force
FV can be calculated using the Hamaker constant
A and the distance
z between the stylus tip and the measured surface as given in Equation (4) [
11]. The Hamaker constant
A is a constant specific to materials, and it is expressed as in Equation (5), where
n and Λ are the number of atoms per unit volume and the constant of proportionality of London forces, respectively. When the molecules of the stylus tip and the measured surface come close to each other by the van der Waals force, intermolecular repulsive force is generated between the molecules of the stylus tip and the measured surface. The molecules are stabilized at the most stable position, which corresponds to the position with the smallest potential energy. At this instant, the separation distance
z is about 0.4 nm.
Finally, the electrostatic force generated by an interaction between a charged particle and an uncharged surface is examined. When a charged particle comes into contact with an uncharged surface, the generated electrostatic force
Fe can be calculated using Equation (6) in the case that the distance between the stylus tip and the measured surface is negligible because it is remarkably small compared with the diameter of the stylus tip [
11].
where ε
0, ε, and σ are the dielectric constant of the vacuum, the dielectric constant of the measured surface, and the marginal surface density of the charge of the stylus tip, respectively.
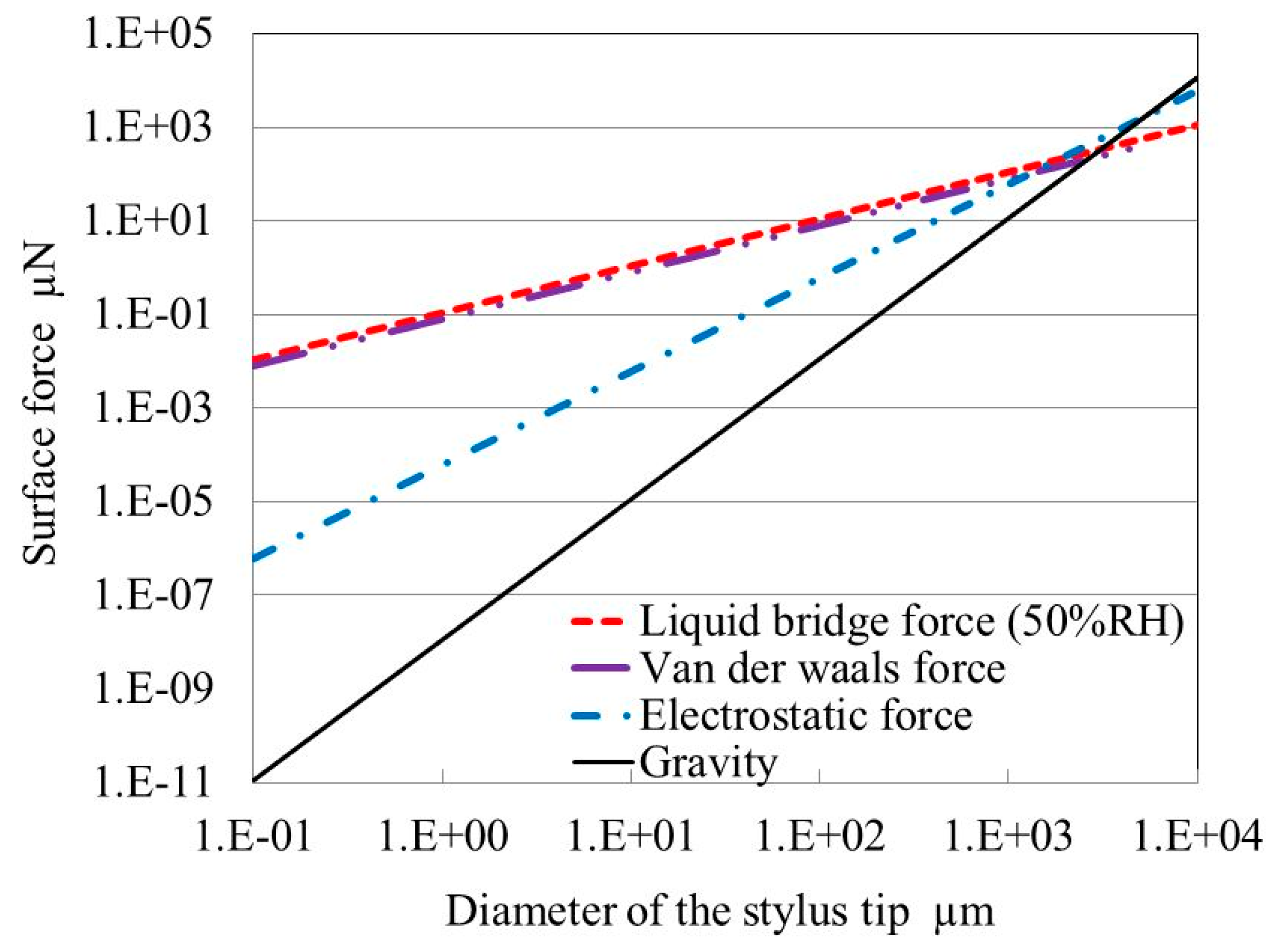
Figure 6 shows the relationship between the stylus tip diameter and the surface forces calculated using Equations (3), (4), and (6). Here, the horizontal axis represents the stylus tip diameter and the vertical axis represents the van der Waals force, electrostatic force, liquid bridge force, and gravity. It can be seen from this figure that when the stylus tip diameter is less than about 1 mm, the effects of surface force generated from the van der Waals force, electrostatic force, and liquid bridge force are strengthened and the surface force becomes greater than the force of gravity.
This confirms that the primary cause of adhesion is the liquid bridge force. The van der Waals force and liquid bridge force are approximately equal. However, the electrostatic force is much smaller than the van der Waals force and liquid bridge force. When the surface forces are calculated using Equations (3), (4), and (6) for a stylus tip 5 µm in diameter, the liquid bridge force (50%
RH), van der Waals force, and electrostatic force are 0.54 µN, 0.36 µN, and 0.0016 µN, respectively. In this case, the sum of the surface forces is approximately 0.9 µN.
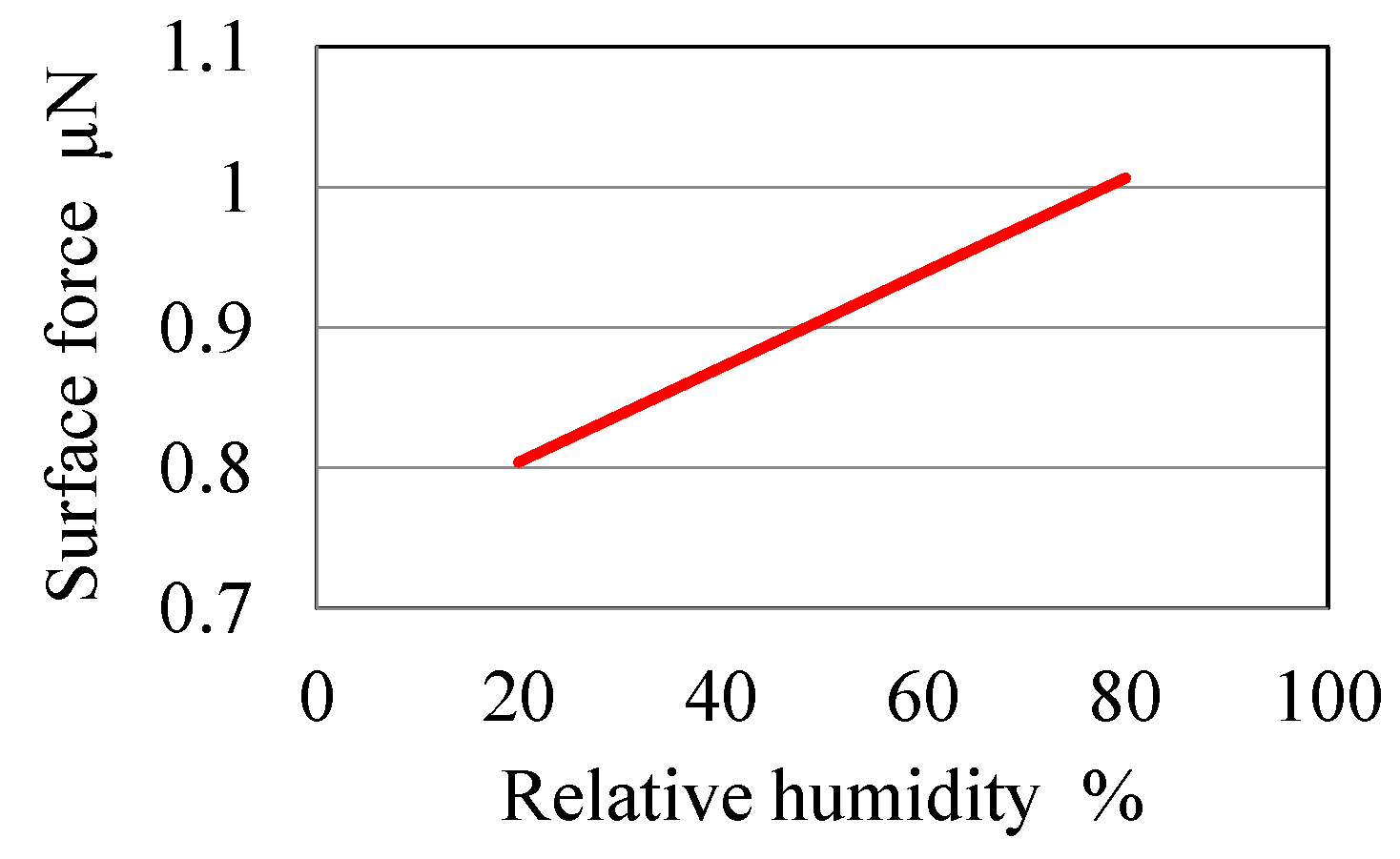
Figure 7 shows the relationship between the relative humidity and the sum of surface forces (
Fl +
Fv +
Fe) calculated using Equations (3), (4), and (6). It can be seen from this figure that the liquid bridge force increases with increasing relative humidity.
4.2. Effect of Relative Humidity on the Liquid Bridge Force
As stated in the discussion above, the primary cause of adhesion is the liquid bridge force, which increases with increasing relative humidity. When the measured surface is scanned point by point in the touch-trigger mode, the measurement time increases because the stylus tip is required to be separated from the measured surface on account of the surface force. When the measured surface is scanned continuously in the scanning mode, the measurement accuracy reduces owing to the bending of the stylus shaft due to the adhesion. Therefore, in our previous work, a vibration mechanism was introduced to prevent the adhesion of the stylus tip to the measurement surface caused by the surface force [
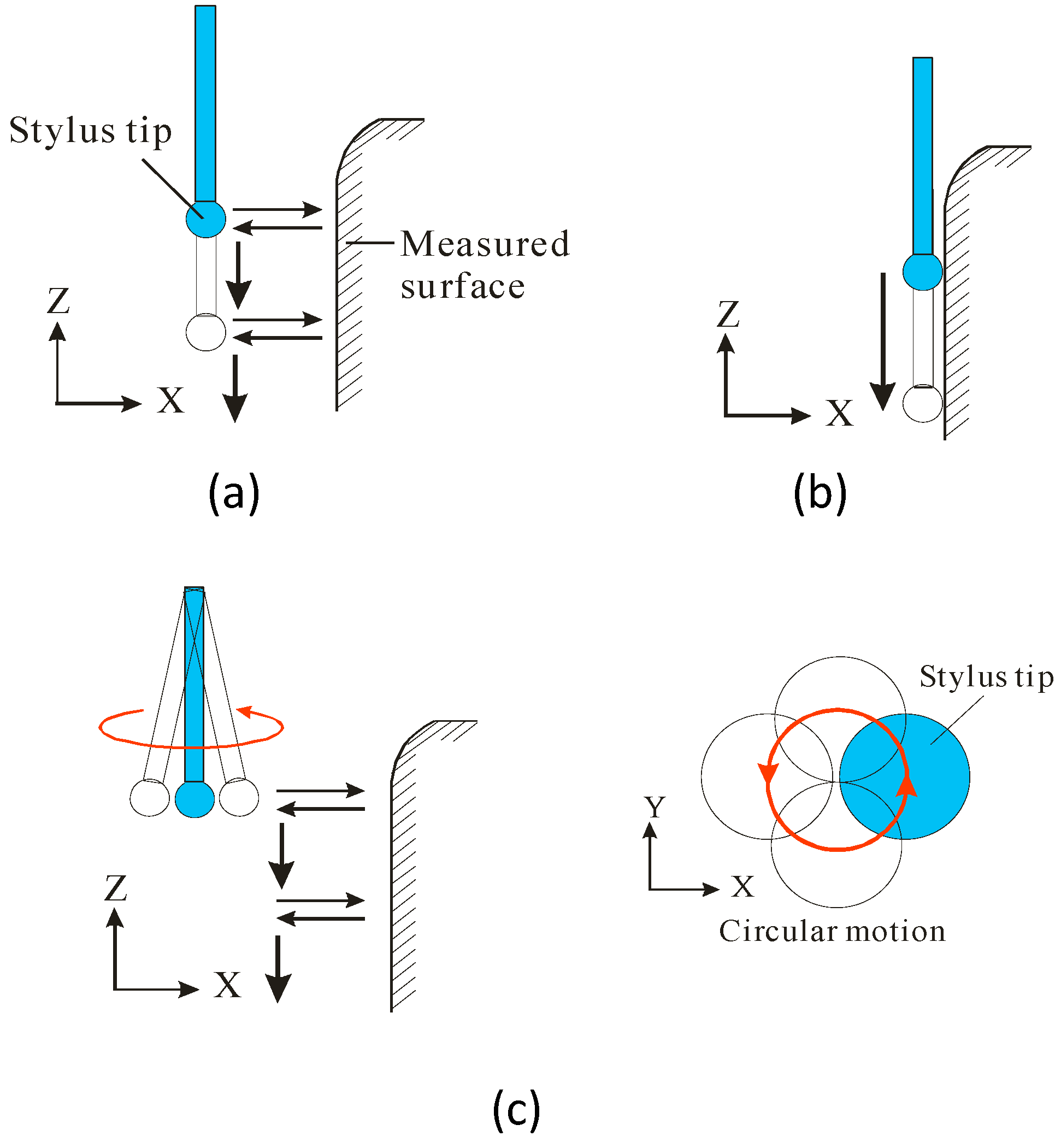
12]. By this mechanism, the stylus tip is set to vibrate in a circular motion, where it traces a circle of diameter 0.4 µm in the
X-
Y plane. However, the stylus shaft actually traces an elliptical path. The difference between the profile of the perfect circle and that of the actual elliptical path of the stylus tip leads to measurement errors. Moreover, the surface roughness cannot be measured in the scanning mode when using the vibrating fiber probe.
Therefore, the measurement system, placed in a vacuum vessel, is constructed suitably to prevent adhesion of the stylus tip to the measured surface caused by the surface force.
Figure 8 shows a photograph of the measurement system in the vacuum vessel. The effects of pressure inside the vacuum vessel on the surface force are evaluated experimentally. In the experiment, the relative humidity is 61% and the temperature is 25.1 °C.
First, the measurement method of the surface force is explained as follows. There are many techniques for measuring surface forces, such as those involving the surface forces apparatus (SFA), atomic force microscopy (AFM), micro cantilever (MC), optical trapping (OT),
etc. [
13,
14,
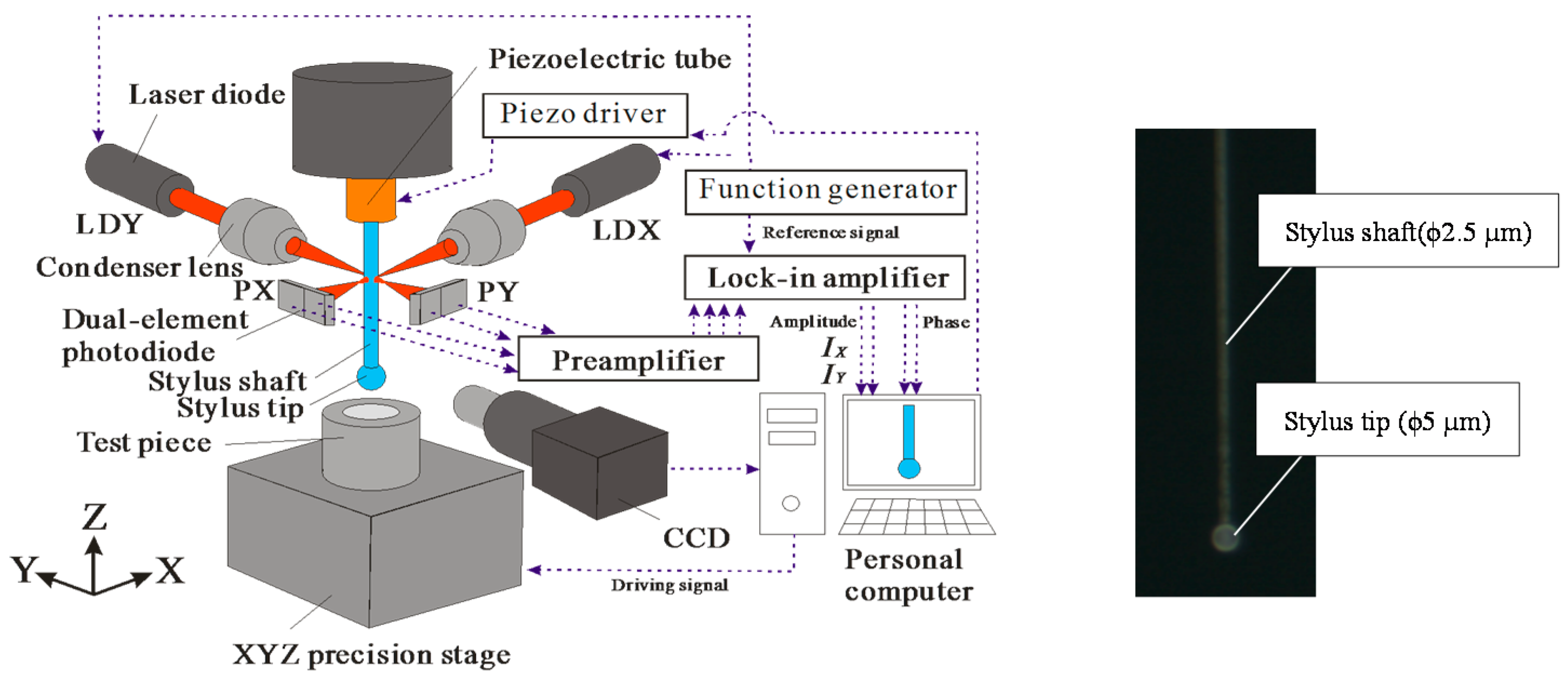
15]. The SFA can directly measure the force between two surfaces in controlled vapors or immersed in liquids. The force sensitivity of the SFA is about 10 nN. The SFA contains two curved molecularly smooth surfaces of mica between which the interaction forces are measured using a variety of force-measuring springs. AFM is, in principle, similar to the SFA except that forces are measured not between two macroscopic surfaces but between a fine tip and a surface. The force sensitivity of AFM is 1–10 pN. The measuring method using the optical fiber probe is, in principle, similar to the SFA and AFM. As shown in
Figure 9, after the stylus tip comes into contact with the measured surface, the stylus tip is displaced in the backward direction by using the piezoelectric stage, due to which it separates from the measured surface. Because the stylus tip is displaced while maintaining its contact with the measured surface, the stylus shaft is deflected and the force required to separate the stylus tip from the measured surface is generated by the deflection of the stylus shaft. With an increase in the displacement of the stylus tip, this required force also increases. Therefore, the stylus tip can be separated from the measured surface when the displacement
D of the stylus tip exceeds a certain value.
The load acting on the stylus tip,
i.e., the surface force, is calculated by assuming that the optical fiber probe, 2.5 µm in diameter and 0.38 mm in length, is equal to the cantilever of the fixed support. In other words, the surface force is calculated by the deflection of the stylus shaft. The surface force
F is calculated using Equation (7).
where
E,
I, and
L are the Young’s modulus, the geometrical moment of inertia, and the length of the stylus shaft, respectively.
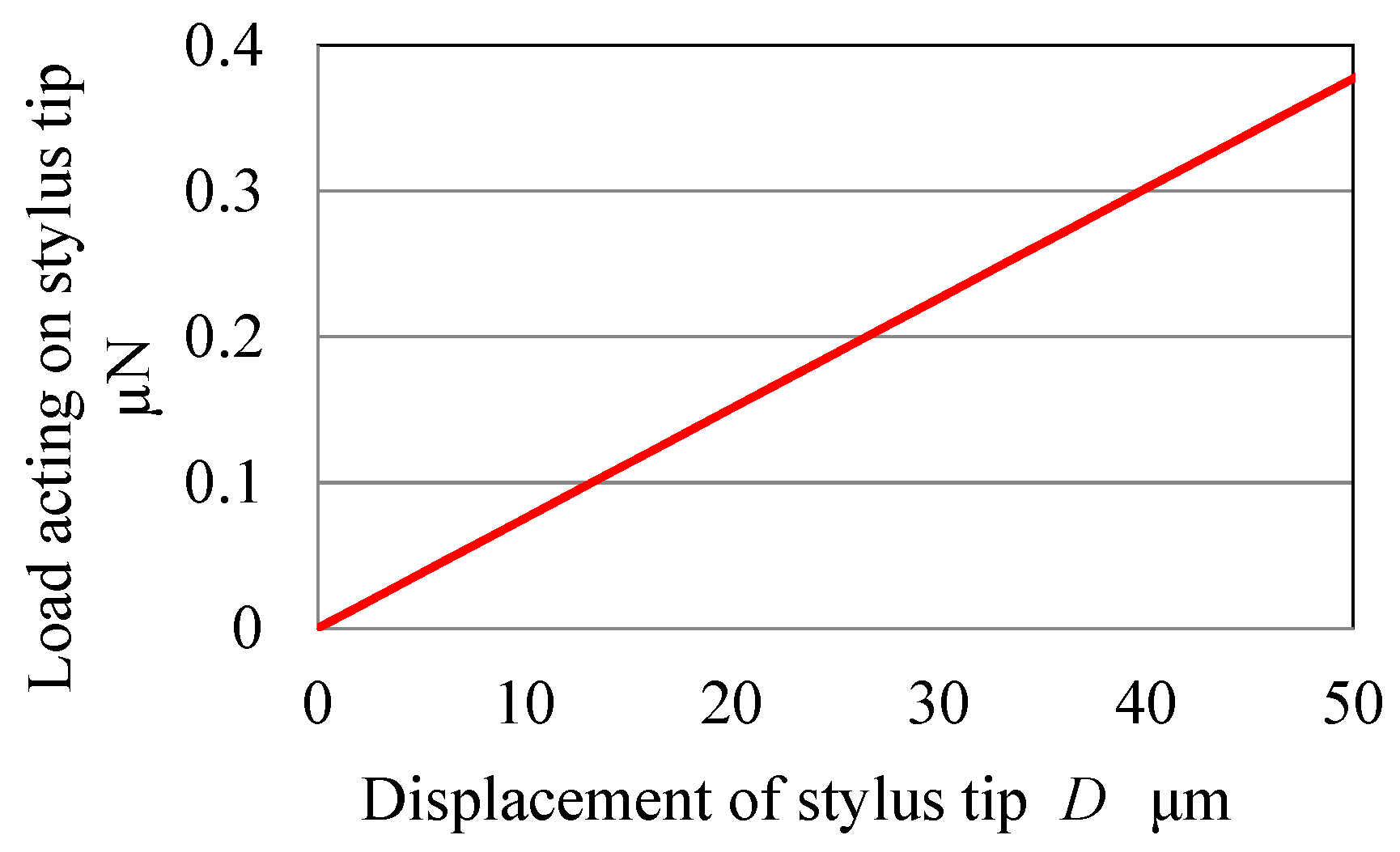
Figure 10 shows the load acting on the stylus tip under the assumption that the stylus shaft (Young’s modulus
E = 72 GPa) is equivalent to the cantilever of the fixed support. In this figure, the horizontal axis represents displacement of the stylus tip, and the vertical axis represents the load acting on the stylus tip. For example, when the displacement
D required to separate the stylus tip from the measured surface is about 20 µm, the load acting on the stylus tip is about 0.15 µN immediately before the stylus tip is separated from the measured surface as shown in
Figure 10. Therefore, this value of 0.15 µN is regarded as the surface force. In this experiment, the spring constant of the stylus shaft is not calibrated. However, to accurately measure the surface force, it is necessary to calibrate it [
16,
17,
18,
19].
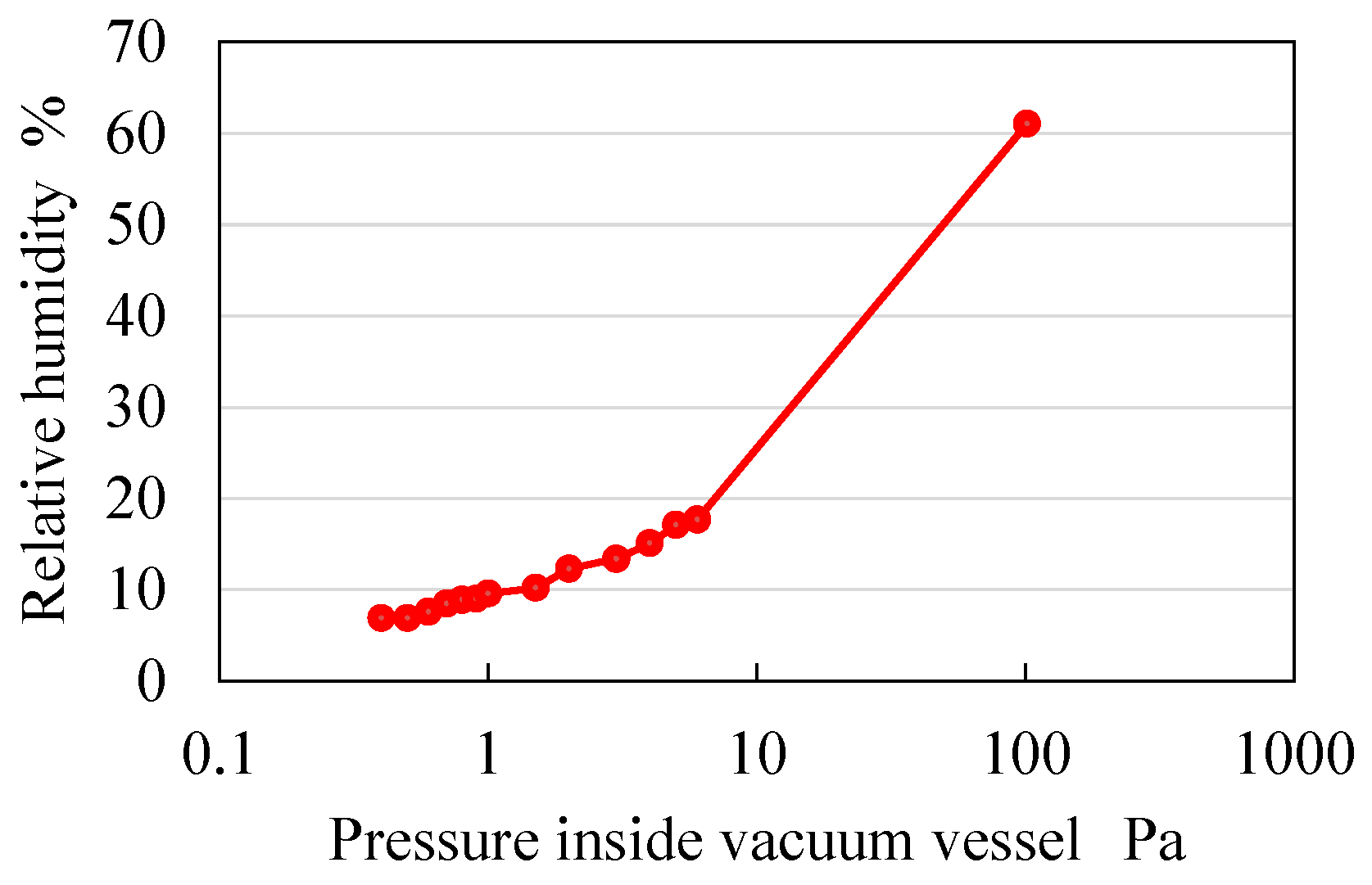
Figure 11 shows the relationship between the pressure inside the vacuum vessel and the relative humidity. Further,
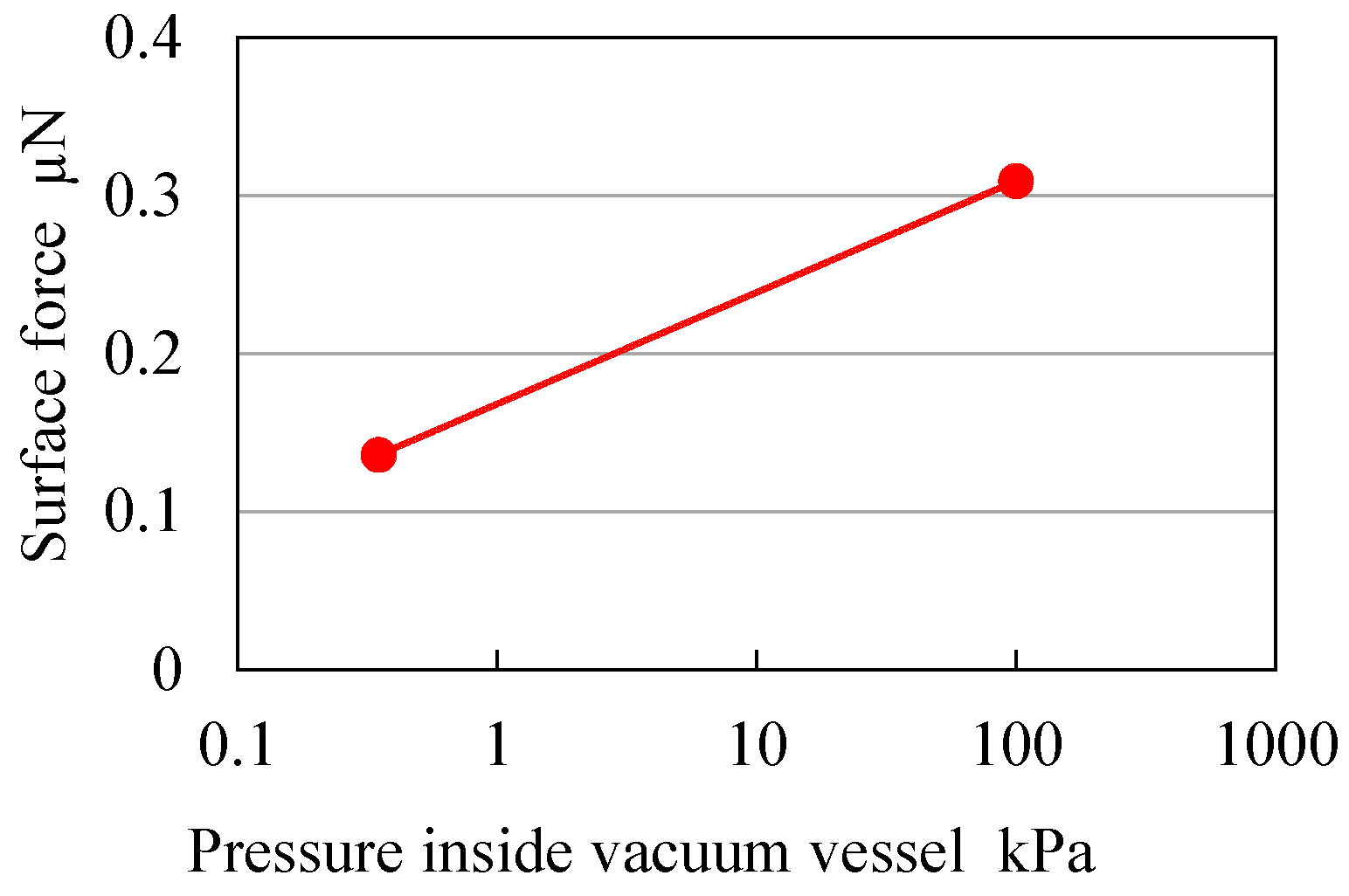
Figure 12 shows the relationship between the pressure inside the vacuum vessel and the surface forces. Finally,
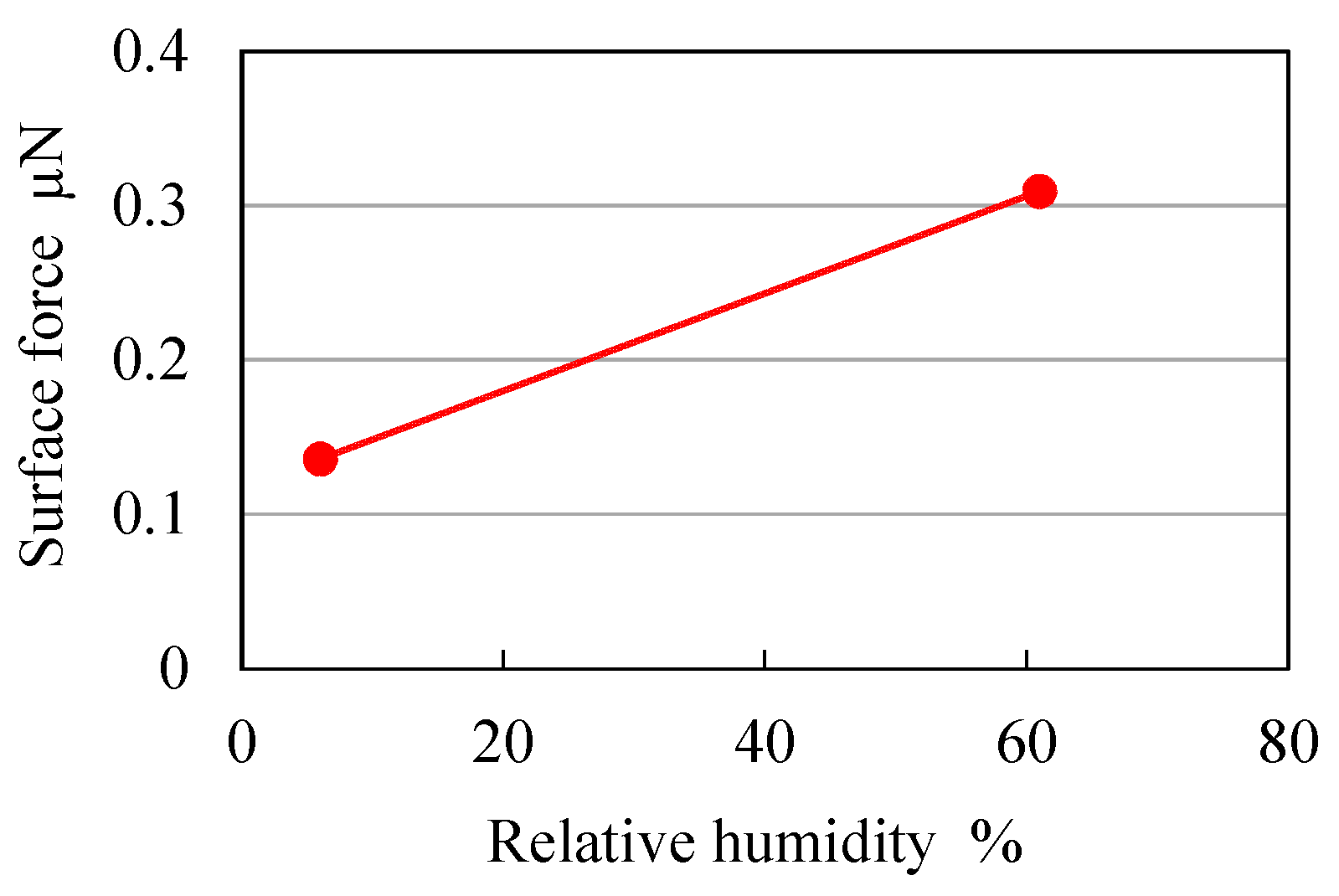
Figure 13 shows the relationship between the relative humidity and the surface force. From
Figure 13, it is confirmed that surface force decreases with decreasing relative humidity. It is found that the surface force is 0.13 µN when pressure inside the vacuum vessel and relative humidity are 350 Pa and 7%
RH, respectively. This effect is equivalent to a 60% reduction in the surface force in the atmosphere. However, a large residual surface force still acts between the stylus tip and the measured surface. This is because the amount of van der Waals force is almost the same as that of the liquid bridge force. Therefore, the surface force is thought to reduce by slightly a little more than 60%. When the stylus tip diameter is 5 µm as shown in
Figure 6, the theoretical van der Waals force in a vacuum environment is about 0.36 µN. However, according to the obtained experimental results, the van der Waals force in a vacuum environment is about 0.13 µN. Thus, the theoretical and experimental results are different. Because the amount of van der Waals force is affected by the surface roughness of the stylus tip and that of the measurement surface [
11], the surface roughness of the stylus tip and that of the measurement surface are, in turn, thought to be affected by the amount of van der Waals force.
4.3. Alternative Reduction Method for Surface Force
According to the above-mentioned experimental results, it is possible to reduce the liquid bridge force considerably by using a vacuum vessel. However, in scenarios where the use of a vacuum vessel is difficult, the stylus tip coated with a water-repellent coating has the potential to reduce the liquid bridge force. In order to reduce the van der Waals force, a stylus tip made of a material with a small Hamarker constant may be used. For example, the Hamaker constants of SiO2, Fe, Si, Cu, and Au are 8.55, 21.2, 25.6, 28.4, and 45.5 × 10−20 J, respectively. However, in practice, the use of a material with a small low Hamarker constant can be difficult. In such cases, a stylus tip coated with a material with a small Hamarker constant may be used. The effect of the material of the stylus tip can be made negligible by using a coating that is several nanometers thick. The influence of the electrostatic force on the surface force is small; however, it is believed that various methods of removal of electricity or antistatic agents could be useful in reducing the electrostatic force.