Simulation Model for Correction and Modeling of Probe Head Errors in Five-Axis Coordinate Systems
Abstract
:1. Introduction
- nx, ny, nz—approach direction cosines
- PEF—value of probe head error function
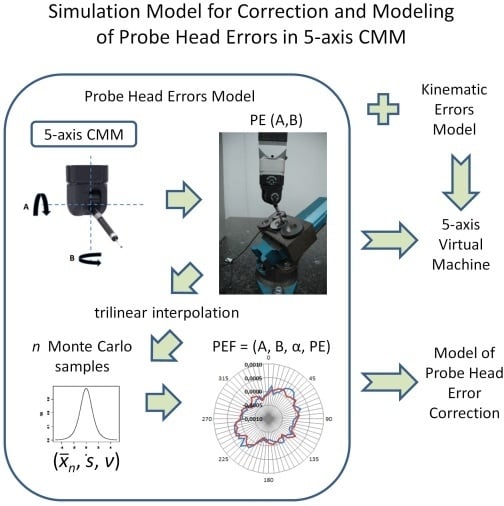
2. Developed Simulative Model and Steps to Its Implementation
2.1. Description of Simulative Model
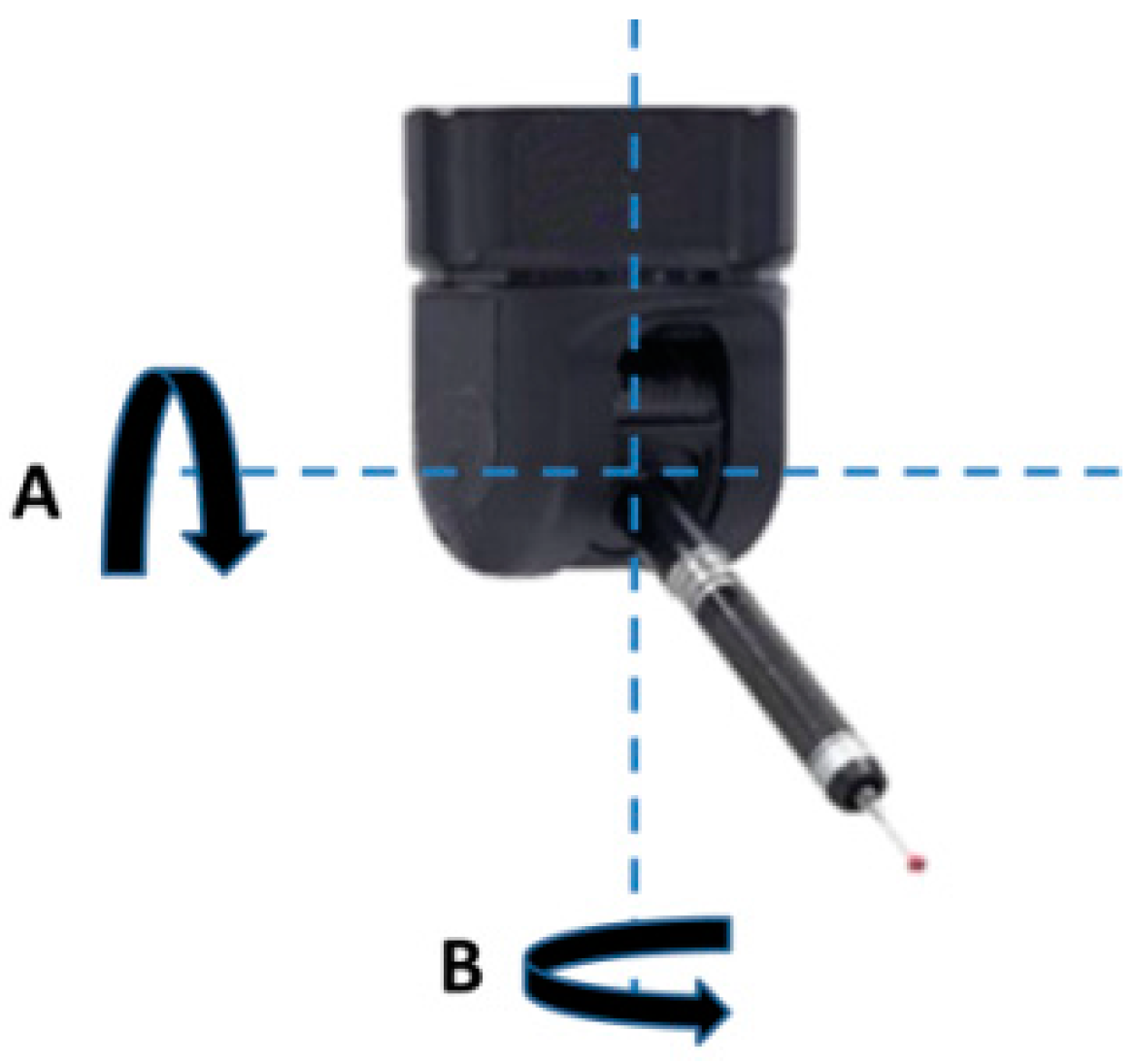
- A—rotation angle along the horizontal axis of the probe head,
- B—rotation angle along the vertical axis of the probe head,
- α—angle in which the touch-trigger module is working,
- PE—probe error given as a result of PEF usage for considered angles.
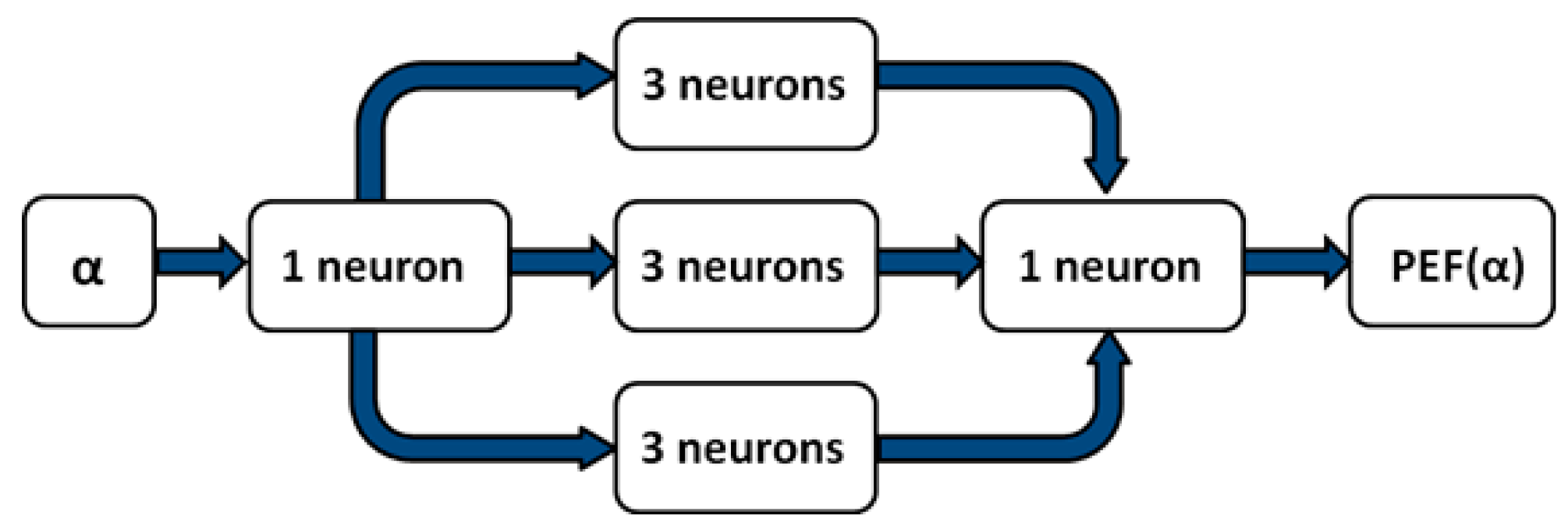
- P1 = (((αs+1 − αs)/(αs+1 − αs−1)) × PEF(As+1, Bs−1, αs−1)) + (((αs − αs−1)/(αs+1 − αs−1)) × PEF(As+1, Bs−1, αs+1))
- P2 = (((αs+1 − αs)/(αs+1 − αs−1)) × PEF(As−1, Bs−1, αs−1)) + (((αs − αs−1)/(αs+1 − αs−1)) × PEF(As−1, Bs−1, αs+1))
- P3 = (((αs+1 − αs)/(αs+1 − αs−1)) × PEF(As+1, Bs+1, αs−1)) + (((αs − αs−1)/(αs+1 − αs−1)) × PEF(As+1, Bs+1, αs+1))
- P4 = (((αs+1 − αs)/(αs+1 − αs−1)) × PEF(As−1, Bs+1, αs−1)) + (((αs − αs−1)/(αs+1 − αs−1)) × PEF(As−1, Bs+1, αs+1))
2.2. Implementation Measurements
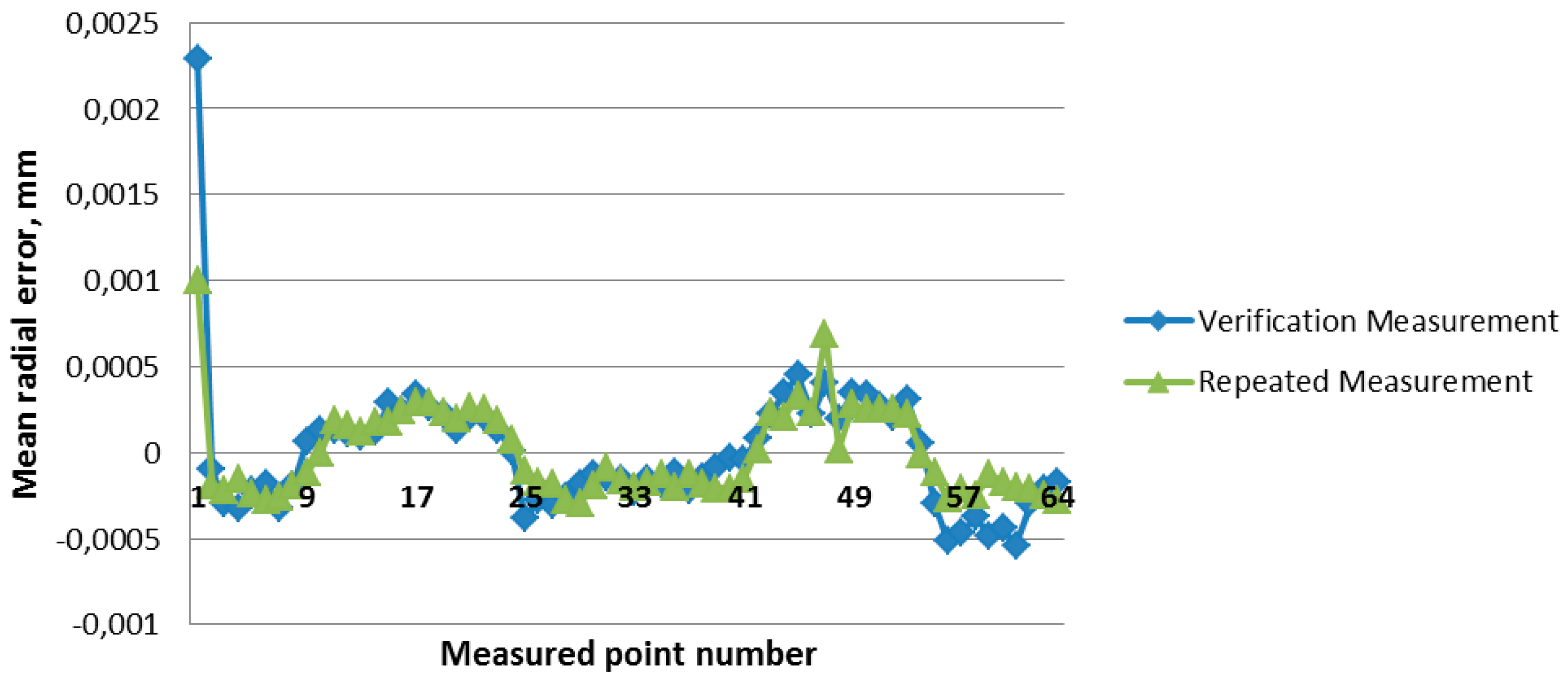
2.3. Verification Measurements
2.4. Correction of Probe Head Errors Using the Developed Model
3. Results
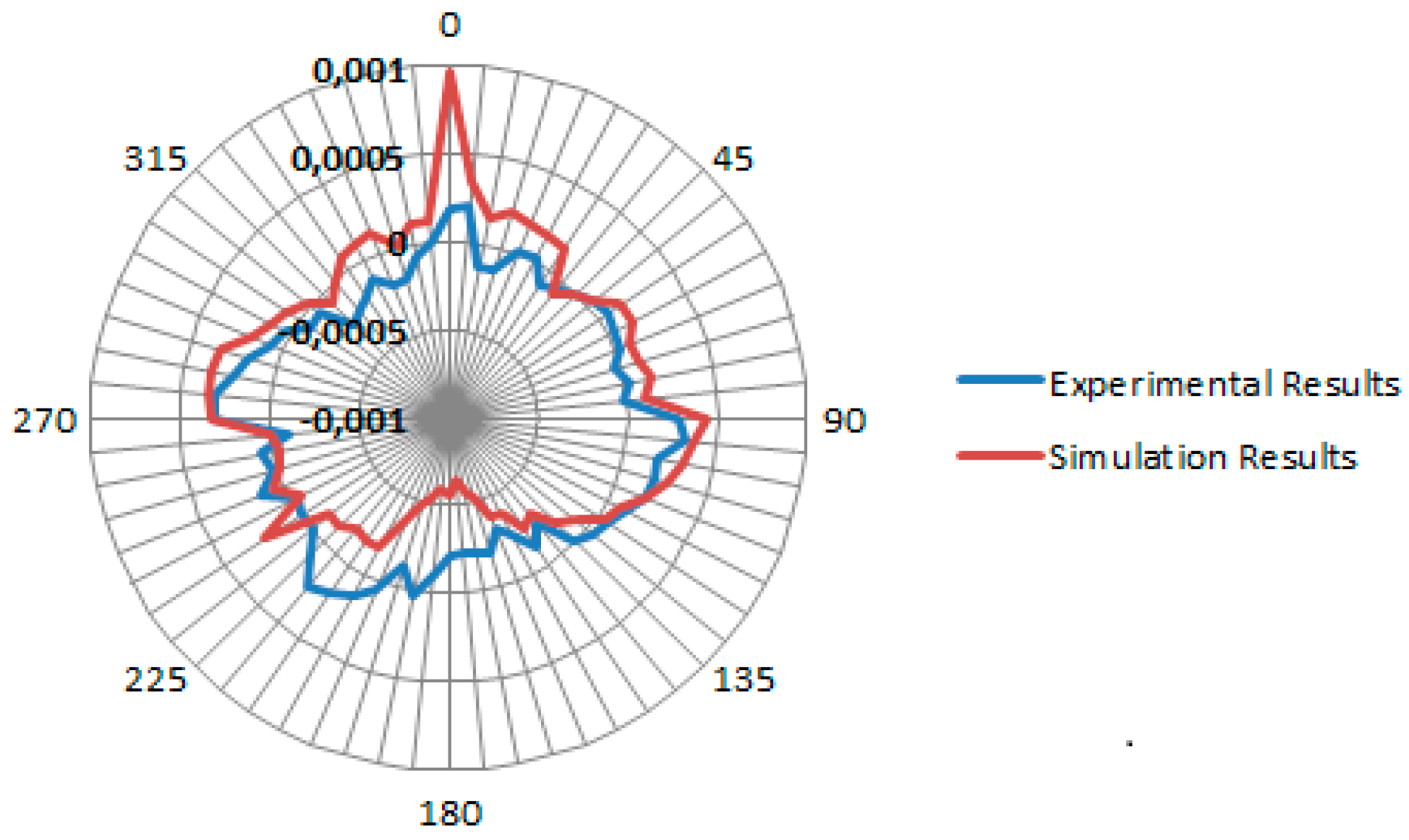
3.1. Results of Identification of Errors
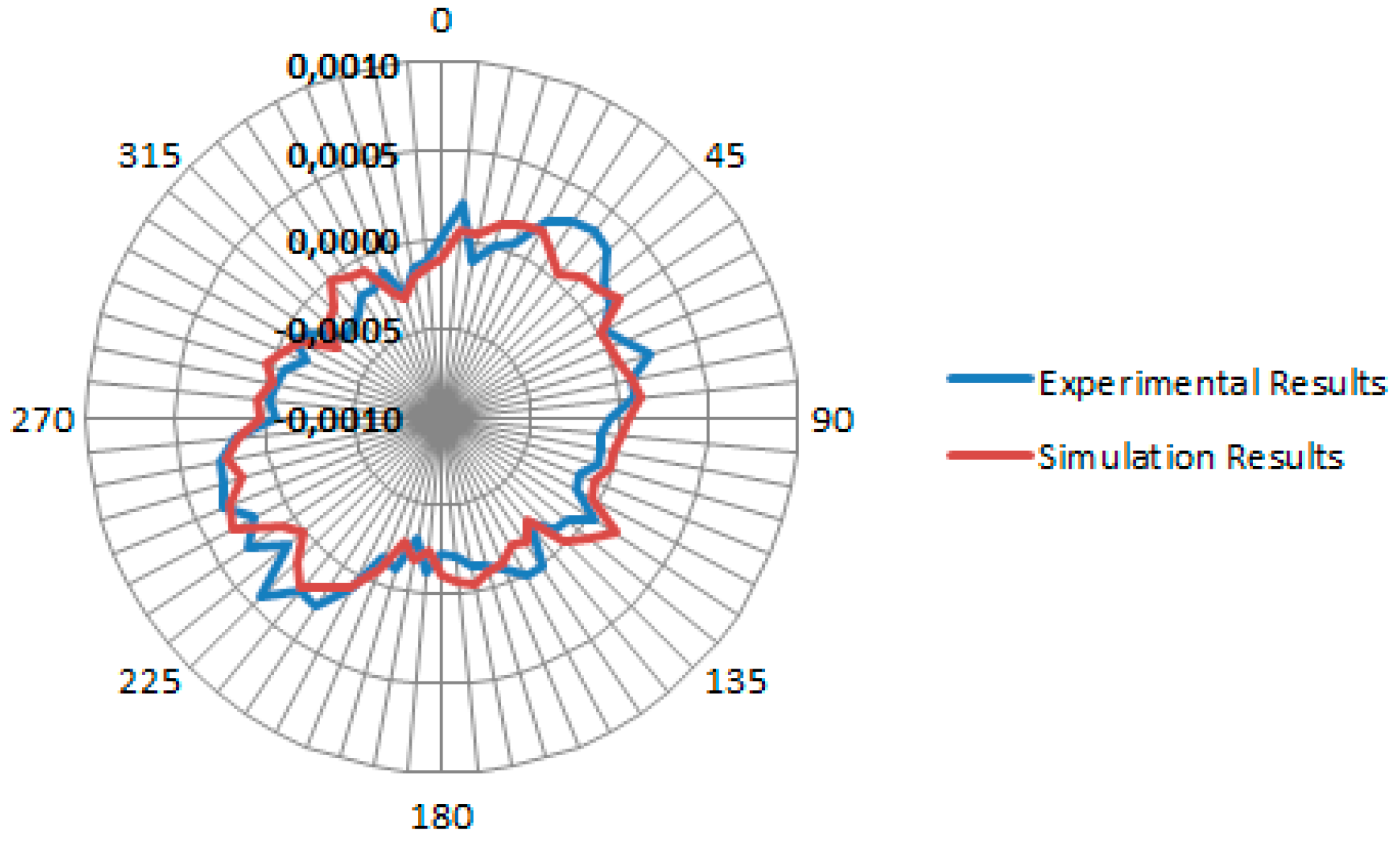
3.2. Results of Model Verification
3.3. Example of Probe Head Error Correction
4. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CMM | Coordinate Measuring Machine |
| LCM | Laboratory of Coordinate Metrology |
| PEF | Probe Error Function |
| PE | Probe Error |
References
- Kunzmann, H.; Pfeifer, T.; Schmitt, R.; Schwenke, H.; Weckenmann, A. Productive metrology-adding value to manufacture. CIRP Ann. Manuf. Technol. 2005, 54, 691–704. [Google Scholar] [CrossRef]
- Caja, J.; Gomez, E.; Maresca, P. Optical measuring equipments. Part I: Calibration model and uncertainty estimation. Precis. Eng. 2015, 40, 298–304. [Google Scholar] [CrossRef]
- Asano, Y.; Furutani, R.; Ozaki, M. Verification of interim check method of CMM. Int. J. Autom. Technol. 2011, 5, 115–119. [Google Scholar]
- Cuesta, E.; Alvarez, B.; Sanchez-Lasheras, F.; Gonzalez-Madruga, D. A statistical approach to prediction of the CMM drift behaviour using a calibrated mechanical artefact. Metrol. Meas. Syst. 2015, 22, 417–428. [Google Scholar] [CrossRef]
- Takamasu, K.; Takahashi, S.; Abbe, M.; Furutani, R. Uncertainty estimation for coordinate metrology with effects of calibration and form deviation in strategy of measurement. Meas. Sci. Technol. 2008, 19. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 15530-3:2011—Geometrical Product Specifications (GPS)—Coordinate Measuring Machines (CMM): Technique for Determining the Uncertainty of Measurement—Part 3: Use of Calibrated Workpieces or Measurement Standards; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- Weckenmann, A.; Lorz, J. Monitoring coordinate measuring machines by calibrated parts. J. Phys. Conf. Ser. 2005, 13, 190–193. [Google Scholar] [CrossRef]
- Sato, O.; Osawa, S.; Kondo, Y.; Komori, M.; Takatsuji, T. Calibration and uncertainty evaluation of single pitch deviation by multiple-measurement technique. Precis. Eng. 2010, 34, 156–163. [Google Scholar] [CrossRef]
- Osawa, S.; Busch, K.; Franke, M.; Schwenke, H. Multiple orientation technique for the calibration of cylindrical workpieces on CMMs. Precis. Eng. 2005, 29, 56–64. [Google Scholar] [CrossRef]
- Trapet, E.; Franke, M.; Hartig, F.; Schwenke, H.; Wadele, F.; Cox, M.; Forbers, A.; Delbressine, F.; Schnellkens, P.; Trenk, M.; et al. Traceability of Coordinate Measuring Machines According to the Method of the Virtual Measuring Machine; PTB: Braunschweig, Germany, 1999. [Google Scholar]
- Schwenke, H.; Siebert, B.R.L.; Wäldele, F.; Kunzmann, H. Assessment of uncertainties in dimensional metrology by Monte Carlo simulation: Proposal of a modular and visual software. CIRP Ann. Manuf. Technol. 2000, 49, 395–398. [Google Scholar] [CrossRef]
- Wilhelm, R.G.; Hocken, R.; Schwenke, H. Task specific uncertainty in coordinate measurement. CIRP Ann. Manuf. Technol. 2001, 50, 553–563. [Google Scholar] [CrossRef]
- Sładek, J.; Gąska, A. Evaluation of coordinate measurement uncertainty with use of virtual machine model based on Monte Carlo method. Measurement 2012, 45, 1564–1575. [Google Scholar] [CrossRef]
- Aggogeri, F.; Barbato, G.; Barini, E.M.; Genta, G.; Levi, R. Measurement uncertainty assessment of coordinate measuring machines by simulation and planned experimentation. CIRP J. Manuf. Sci. Technol. 2011, 4, 51–56. [Google Scholar] [CrossRef]
- Giusca, C.L.; Leach, R.K.; Forbes, A.B. A virtual machine-based uncertainty evaluation for a traceable areal surface texture measuring instrument. Measurement 2011, 44, 988–993. [Google Scholar] [CrossRef]
- Sładek, J. Coordinate Metrology: Accuracy of Systems and Measurements; Springer: Berlin, Germany, 2016. [Google Scholar]
- Maresca, P.; Gomez, E.; Caja, J.; Barajas, C. Virtual environment for the simulation of a horizontal coordinate measuring machine in the teaching of dimensional metrology. Procedia Eng. 2013, 63, 234–242. [Google Scholar] [CrossRef]
- Ostrowska, K.; Gąska, A.; Sładek, J. Determining the uncertainty of measurement with the use of a Virtual Coordinate Measuring Arm. Int. J. Adv. Manuf. Technol. 2014, 71, 529–537. [Google Scholar] [CrossRef]
- Cuesta, E.; Talenti, A.; Patino, H.; Gonzalez-Madruga, D.; Martínez-Pellitero, S. Sensor prototype to evaluate the contact force in measuring with coordinate measuring arms. Sensors 2015, 15, 13242–13257. [Google Scholar] [CrossRef] [PubMed]
- Nafi, A.; Mayer, J.R.R.; Wozniak, A. Novel CMM-based implementation of the multi-step method for the separation of machine and probe errors. Precis. Eng. 2011, 35, 318–328. [Google Scholar] [CrossRef]
- Gąska, A.; Krawczyk, M.; Kupiec, R.; Ostrowska, K.; Gąska, P.; Sładek, J. Modeling of the residual kinematic errors of coordinate measuring machines using Laser Tracer system. Int. J. Adv. Manuf. Technol. 2014, 73, 497–507. [Google Scholar] [CrossRef]
- Dobosz, M.; Woźniak, A. CMM touch trigger probes testing using a reference axis. Precis. Eng. 2005, 29, 281–289. [Google Scholar] [CrossRef]
- Gąska, A.; Harmatys, W.; Gąska, P.; Gruza, M.; Mathia, T.; Sładek, J. Optimization of probe head errors model used in Virtual CMM systems. In Proceedings of the 11th International Conference on Laser Metrology and Machine Performance (LAMDAMAP) 2015, Huddersfield, UK, 17–18 March 2015; Blunt, L., Hansen, H.N., Eds.; euspen: Cranfield, UK, 2015. [Google Scholar]

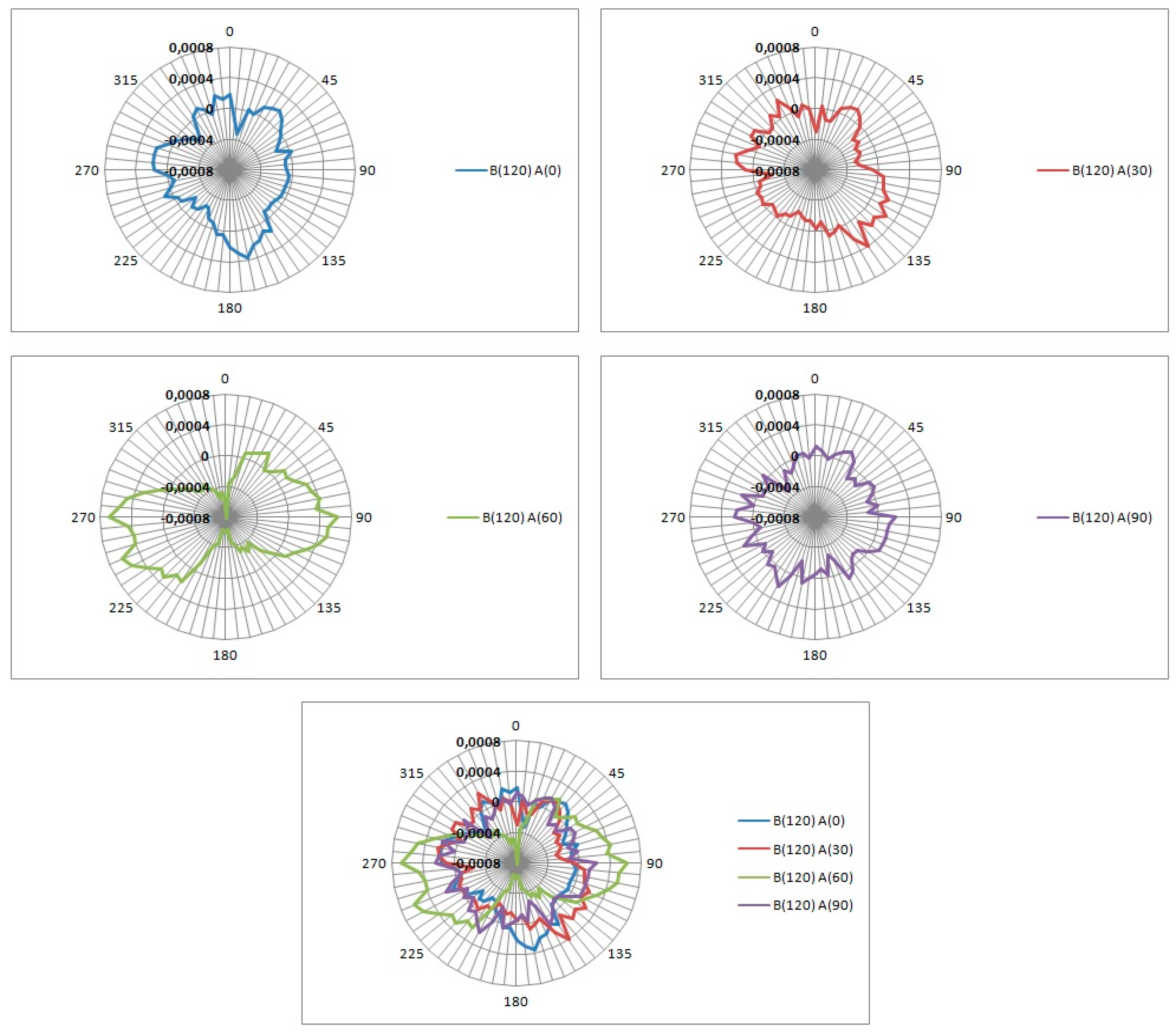
| A | B | α | s | A | B | α | s | ||
|---|---|---|---|---|---|---|---|---|---|
| 30 | −120 | 0.000 | −0.00072 | 0.00048 | 30 | −120 | 180.000 | −0.00017 | 0.00016 |
| 30 | −120 | 5.625 | 0.00007 | 0.00019 | 30 | −120 | 185.625 | −0.00034 | 0.00019 |
| 30 | −120 | 11.250 | 0.00007 | 0.00020 | 30 | −120 | 191.250 | −0.00024 | 0.00020 |
| 30 | −120 | 16.875 | 0.00015 | 0.00019 | 30 | −120 | 196.875 | −0.00034 | 0.00017 |
| 30 | −120 | 22.500 | 0.00022 | 0.00013 | 30 | −120 | 202.500 | −0.00010 | 0.00019 |
| 30 | −120 | 28.125 | 0.00029 | 0.00016 | 30 | −120 | 208.125 | 0.00005 | 0.00029 |
| 30 | −120 | 33.750 | 0.00015 | 0.00016 | 30 | −120 | 213.750 | 0.00016 | 0.00027 |
| 30 | −120 | 39.375 | 0.00010 | 0.00017 | 30 | −120 | 219.375 | 0.00032 | 0.00019 |
| 30 | −120 | 45.000 | 0.00020 | 0.00023 | 30 | −120 | 225.000 | 0.00018 | 0.00019 |
| 30 | −120 | 50.625 | 0.00019 | 0.00016 | 30 | −120 | 230.625 | 0.00010 | 0.00012 |
| 30 | −120 | 56.250 | 0.00029 | 0.00017 | 30 | −120 | 236.250 | 0.00012 | 0.00018 |
| 30 | −120 | 61.875 | 0.00009 | 0.00021 | 30 | −120 | 241.875 | 0.00039 | 0.00022 |
| 30 | −120 | 67.500 | 0.00010 | 0.00018 | 30 | −120 | 247.500 | 0.00035 | 0.00020 |
| 30 | −120 | 73.125 | 0.00012 | 0.00020 | 30 | −120 | 253.125 | 0.00026 | 0.00016 |
| 30 | −120 | 78.750 | 0.00012 | 0.00016 | 30 | −120 | 258.750 | 0.00036 | 0.00015 |
| 30 | −120 | 84.375 | 0.00016 | 0.00014 | 30 | −120 | 264.375 | 0.00027 | 0.00019 |
| 30 | −120 | 90.000 | 0.00014 | 0.00011 | 30 | −120 | 270.000 | 0.00009 | 0.00014 |
| 30 | −120 | 95.625 | 0.00004 | 0.00010 | 30 | −120 | 275.625 | 0.00012 | 0.00020 |
| 30 | −120 | 101.250 | −0.00001 | 0.00023 | 30 | −120 | 281.250 | −0.00003 | 0.00018 |
| 30 | −120 | 106.875 | 0.00000 | 0.00012 | 30 | −120 | 286.875 | 0.00003 | 0.00018 |
| 30 | −120 | 112.500 | −0.00003 | 0.00015 | 30 | −120 | 292.500 | −0.00001 | 0.00024 |
| 30 | −120 | 118.125 | −0.00007 | 0.00013 | 30 | −120 | 298.125 | −0.00004 | 0.00016 |
| 30 | −120 | 123.750 | 0.00019 | 0.00011 | 30 | −120 | 303.750 | −0.00037 | 0.00024 |
| 30 | −120 | 129.375 | 0.00004 | 0.00017 | 30 | −120 | 309.375 | −0.00020 | 0.00018 |
| 30 | −120 | 135.000 | −0.00004 | 0.00017 | 30 | −120 | 315.000 | −0.00016 | 0.00014 |
| 30 | −120 | 140.625 | −0.00030 | 0.00019 | 30 | −120 | 320.625 | −0.00006 | 0.00018 |
| 30 | −120 | 146.250 | −0.00021 | 0.00016 | 30 | −120 | 326.250 | −0.00007 | 0.00013 |
| 30 | −120 | 151.875 | −0.00023 | 0.00016 | 30 | −120 | 331.875 | −0.00010 | 0.00014 |
| 30 | −120 | 157.500 | −0.00019 | 0.00017 | 30 | −120 | 337.500 | −0.00032 | 0.00013 |
| 30 | −120 | 163.125 | −0.00014 | 0.00021 | 30 | −120 | 343.125 | −0.00033 | 0.00015 |
| 30 | −120 | 168.750 | −0.00009 | 0.00021 | 30 | −120 | 348.750 | −0.00027 | 0.00015 |
| 30 | −120 | 174.375 | −0.00011 | 0.00011 | 30 | −120 | 354.375 | −0.00021 | 0.00016 |
| Number of Points Used | Without Correction | With Correction | Calibration Certificate |
|---|---|---|---|
| 64 | 0.0013 | 0.0010 | 0.0004 |
| 16 | 0.0012 | 0.0008 | 0.0004 |
| 8 | 0.0010 | 0.0005 | 0.0004 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gąska, A.; Gąska, P.; Gruza, M. Simulation Model for Correction and Modeling of Probe Head Errors in Five-Axis Coordinate Systems. Appl. Sci. 2016, 6, 144. https://doi.org/10.3390/app6050144
Gąska A, Gąska P, Gruza M. Simulation Model for Correction and Modeling of Probe Head Errors in Five-Axis Coordinate Systems. Applied Sciences. 2016; 6(5):144. https://doi.org/10.3390/app6050144
Chicago/Turabian StyleGąska, Adam, Piotr Gąska, and Maciej Gruza. 2016. "Simulation Model for Correction and Modeling of Probe Head Errors in Five-Axis Coordinate Systems" Applied Sciences 6, no. 5: 144. https://doi.org/10.3390/app6050144
APA StyleGąska, A., Gąska, P., & Gruza, M. (2016). Simulation Model for Correction and Modeling of Probe Head Errors in Five-Axis Coordinate Systems. Applied Sciences, 6(5), 144. https://doi.org/10.3390/app6050144