1. Background
More than twenty years ago it was first discovered that even primitive single-celled organisms such as bacteria are able to communicate with each other and coordinate their behavior [
1,
2]. Bacterial communication is based on the exchange of signaling molecules, or autoinducers, which are produced and released in the surrounding space. At the same time, bacteria are able to measure the autoinducer concentration in the environment, and according to this, they can coordinate and even switch their behavior, adapting to environmental changes. The term “quorum sensing” was coined to summarize the cell-to-cell communication mechanism thanks to which single bacteria cells are able to measure (“sense”) the whole population density [
3]. Quorum sensing was first observed for the species
Vibrio fischeri [
2], which uses such a mechanism to regulate its bioluminescence. Nowadays, it is known that many bacterial species are able to use similar regulation systems, controlling biofilm formation, swarming motility, and the production of antibiotics or virulence factors [
4,
5,
6].
The basis for cell-to-cell communication is a gene regulatory network that not only controls certain target genes, but often also their own production, resulting in a positive feedback loop. Gram-positive bacteria use so-called two-component systems (see e.g., [
7]), whereas Gram-negative bacteria produce autoinducers directly in the cells, release them to and take them up from the extracellular space without any further modification or transformation.
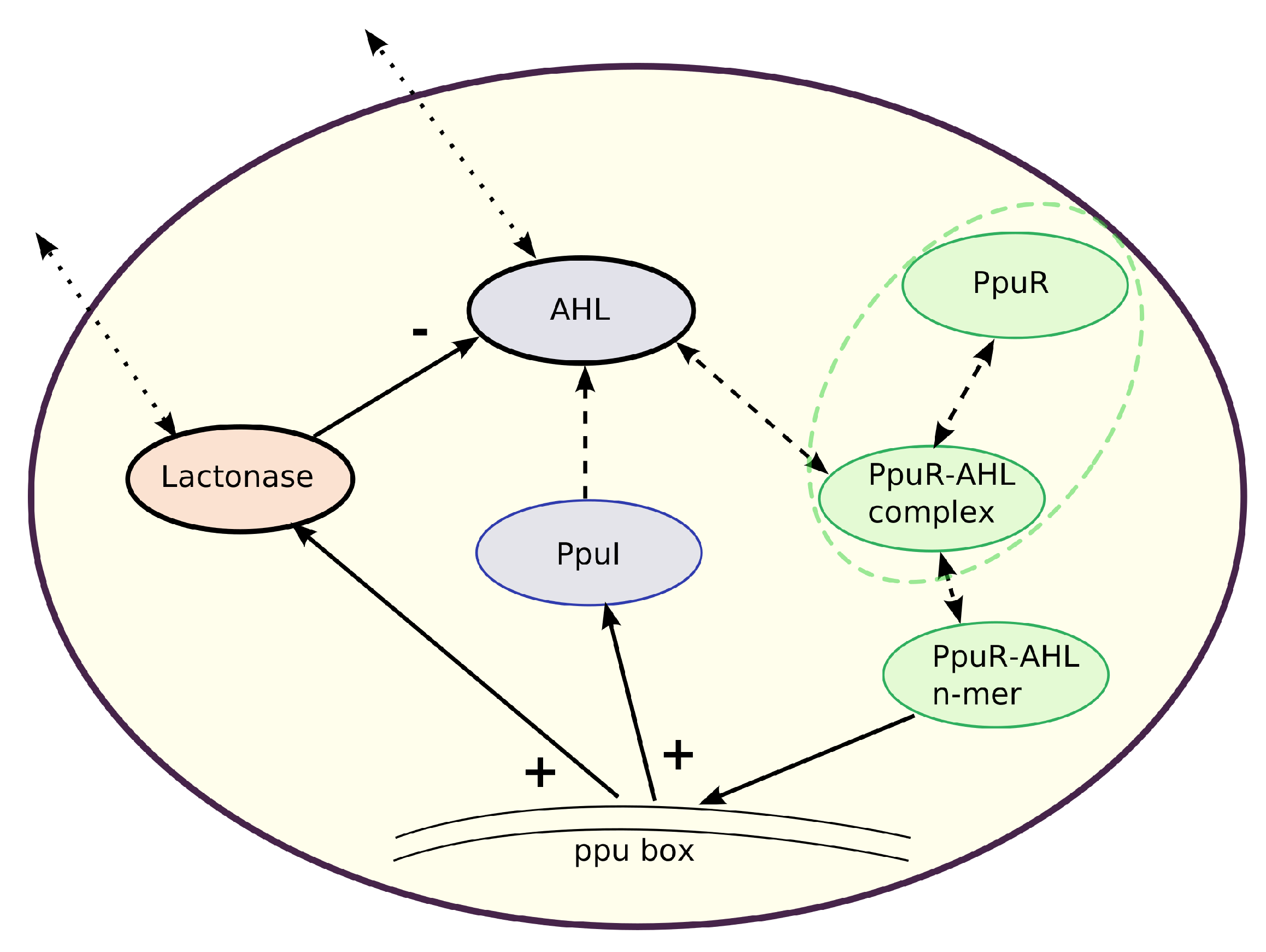
In the following, we focus on the architecture of a quorum sensing system in Gram-negative bacteria, which mainly communicate via
N-Acyl homoserine lactones (AHLs) [
3,
8], typically produced by a synthase. AHL molecules bind to receptors, which control the transcription of target genes. The receptor–AHL complex usually induces the expression of AHL synthases in a positive feedback loop.
We restrict our considerations to the bacteria species
Pseudomonas putida, a root colonizing, plant growth-promoting organism [
9]. Nevertheless, these basic principles may be easily transferred to related bacterial species.
Mathematical modeling of quorum sensing systems has developed in the last decade. Basic principles for a mathematical approach can be found, for example, in [
10], where quasi-steady state assumptions for mRNA and corresponding protein in
Pseudomonas aeruginosa were introduced, or in [
11], which focuses on the basic feedback system of
Vibrio fischeri and the resulting bistability. Alternative approaches for Gram-negative bacteria can be found in [
12] (focussing on population dynamics) and [
13] (including a further feedback loop). Classical mathematical models for Gram-positive bacteria were introduced, for example, for
Staphylococcus aureus in [
7,
14,
15].
Several model approaches have also been proposed for
Pseudomonas putida, in closed systems (batch) as well as in continuous cultures (chemostat) [
16,
17,
18]. The goal of this manuscript is to review such models, investigating mathematical properties and principles underlying the equations. The interesting component of quorum sensing models of
Pseudomonas putida is that beside a positive feedback for the autoinducer one also finds a negative feedback via an autoinducer-degrading enzyme, a Lactonase. This is initialized with a certain time lag, leading to a system of delay differential equations (DDEs).
The paper is organized as follows. In
Section 2 we provide a short overview of previous modeling approaches for quorum sensing of
Pseudomonas putida. Starting from ordinary differential equations (ODEs) for the regulatory network in one single cell, in a second step we extend to quorum sensing in populations, including signal exchange among cells and Lactonase activity. The latter component introduces delays into the system. The delay represents the activation time of the Lactonase-dependent negative feedback. Bacteria population might be considered in batch as well as in continuous cultures. It is our purpose to investigate the long term behavior of the presented dynamical systems, and this can be achieved via a reduced model of two delay equations. We explain in great detail how to obtain the two-equation system, maintaining key properties of the gene regulatory network.
In
Section 3 we present results concerning the existence and uniqueness of solutions to the reduced model. Moreover, we show that non-negative initial data yield non-negative solutions, a fundamental property of models in biology that is often violated when working with delay differential equations (
cf. [
19]). We compute stationary states of the dynamical system and investigate local stability properties. To this purpose, we compare the DDE system (with a constant delay,
) to the associated ODE system (
), studying delay-induced stability switches. In the last part of
Section 3, model parameters are fitted to experimental data from [
18], indicating that in the long run the reduced model is sufficient to explain and predict the general behavior of the system.
Everywhere in this manuscript, if not otherwise specified, we shall denote variables dependent on time by x or . First derivatives with respect to time are denoted by , respectively by .
3. Results
In this section we present analytical results concerning qualitative properties of the solution of the reduced model (8), as well as numerical simulations and data fit.
3.1. Existence of Solutions
Theorem 1. Let the system (8) hold for , and let initial data be given for , , with Lipschitz continuous. Then there is a unique solution to (8) in . Moreover, if are non-negative, the solution is also non-negative.
Proof. The proof follows from basic principles of DDE theory,
cf. [
19,
24,
25]. We provide here a sketch of the proof steps. For simplicity, we shall denote the right-hand side of the system (8) by
, where
and
.
Local existence.
For the construction of a local (maximal) solution on an interval
, it is sufficient to guarantee Lipschitz continuity of the initial data, as well as of
f with respect to both arguments,
cf. [
25] (Thm. 2.2.1). It is easy to verify that the right-hand side of (8) is continuously differentiable with respect to the delayed, as well as to the non-delayed argument, and that the partial derivatives are bounded (computation not shown).
Non-negativity.
Preservation of positivity is due to the fact that the delay only appears in the positive feedback term. Indeed, if for some , then , and remains non-negative. With this result it follows that also y stays non-negative. If for some , , then .
Global existence.
We show that the maximal solution is bounded. This follows with estimates on the right-hand side. Observe that
hence for all
we have
, where
Thus for all
we have
, with
The maximal solution is bounded, hence it exists on
,
cf. [
25] (Thm. 2.2.2).
3.2. Fixed Points
Fixed points of (8) are given by the solutions of
So we have
where
is given by the solutions of
Recall that for the biological motivation of the model, we are only interested in non-negative . In the following, for simplicity of notation, we shall omit the bars from .
In the general case
and
, solutions of (
9) are the zeros of the polynomial
where
Let us consider a special case which is relevant for our application, and assume
and
. Then, fixed points
satisfy
with
given by the solutions of a cubic equation
which has either three real zeros, or one real and two complex solutions. Thus, we might have up to three biologically-relevant fixed points.
3.3. The case
Consider the ODE system obtained from (8) by setting
:
It is important to know the dynamics of (12), because for small delays (
), the DDE system (8) will very likely behave as the ODE system (12),
cf. [
24].
Observe that the ODE system (12) and the DDE system (8) have exactly the same equilibrium points. In general, a DDE system and the associated ODE system have the same number of fixed points, but if the delay appears in the coefficients, the fixed points of the DDE system could be shifted with respect to those of the ODE system.
The presence of a negative feedback in (12) leads to the hypothesis that oscillatory solutions might show up. We investigate local properties of the steady states, looking for Hopf-bifurcations. For linear (local) stability analysis, we compute the Jacobian matrix of system (12),
In the special case
and
, we have
The trace and the determinant of (13) at a stationary point at
, with
in (10), are given by
If there was only one stationary point and this one is a repellor, one can use the fact that all solutions are bounded and stay positive, then the Poincare–Bendixson theorem yields the existence of periodic solutions. For a Hopf-bifurcation, necessary conditions are
and
. We choose
δ, the Lactonase activity, as bifurcation parameter. From the trace condition, we get
We solve for
δ and obtain
Note that, in turn, also depends on δ, cf. Equation (11). Neglecting this for a minute, we observe that , whereas . Due to the intermediate value theorem, there exists a , such that for . It is possible to choose as the smallest positive solution of . If a satisfies this condition, then at .
In the next step, we check the discriminant condition (
), or equivalently,
, as for the Hopf-bifurcation we need simultaneously
.
We solve
in dependence of the Lactonase decay rate
, and find the roots
(which does not provide further information), and
Hence
when
. We need to distinguish between two cases. If
,
i.e., a stationary state with high AHL concentration and activated bacteria, then we get
Thus, if , then . Analogously, we get if , in case of , i.e., with bacteria in a non-activated quorum sensing state. All in all, if the model parameters and the resulting stationary point satisfy the last condition yielding , and simultaneously according to (14), then a Hopf-bifurcation takes place.
3.4. The Case
We are interested in stability switches due to the presence of a delay
in (8). Consider the case
and
, and let
be one equilibrium point of (8). The linearized system about
is given by
with
and
The characteristic equation corresponding to (15) is given by
or equivalently,
Characteristic equations of this and more general type have been studied in [
24]. In the following, we report results from [
24], adapting them to our specific example. We apply standard methods for the analysis of characteristic equations and switches with respect to increasing delays, hence we consider purely imaginary roots,
. Separating real and imaginary parts in (17) we obtain
Now we square left- and right-hand sides and sum up the two equations, obtaining
It can be seen from (
18) that the parabola in
is open upwards and it has:
no positive intercept with the horizontal axis, if , i.e., if ;
one positive intercept () with the horizontal axis, if .
In the first case, there is no stability switch with respect to
τ; that is, the stability of the equilibrium point
remains the same for any
, and it is sufficient to study the ODE case (12). In the case
, there is one root (
) with positive imaginary part, hence one stability switch. In order to find out in which direction the stability switch occurs, we study the sign of the real part
in
, for
. From (17) we have
Roots cross the imaginary axis from the left to the right, indicating stability loss. If the solution
is asymptotically stable for
, then it is uniformly asymptotically stable for all
and unstable for
, where
with
implicitly defined by
All in all, we have shown the following result.
Theorem 2. Let be one equilibrium point of (8), with , and . Assume that , with given in (16). Then, the equilibrium point is uniformly asymptotically stable for all and unstable for , with defined by (19)–(20). 3.5. Numerical Simulations and Data Fitting
We consider experimental data published in [
18] and perform numerical simulations in MATLAB
and Wolfram Mathematica
. The reduced model (8) is obtained assuming the cell population to be in equilibrium, that is, for times
, where
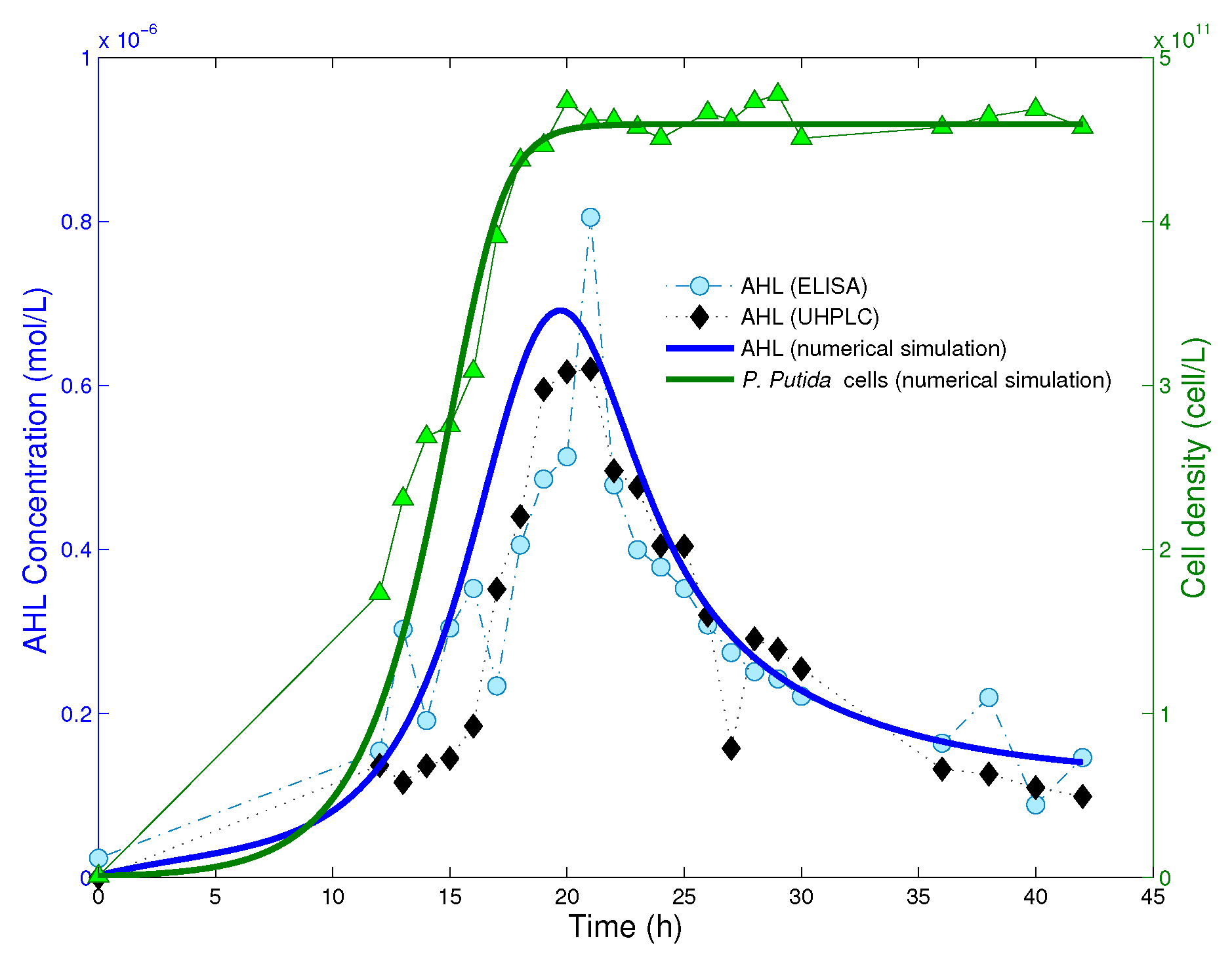
is the time at which bacteria have reached the saturation level. In
Figure 2, we read from experimental data that the cell population reaches the equilibrium after
ca. 20 h from the beginning of the experiment. Hence, we take
as the starting time point for numerical simulations of the reduced system (8), and define initial data on the time interval
.
For simplicity, we assume that initial data are constant functions on the definition interval, see also [
17,
18]. We fix the value of the delay,
h, as in [
18]. Then we take
, for
,
being the mean value of ELISA and UHPLC measurements at 19 h from the beginning of the experiment. Initial data for the Lactonase are estimated from simulations of the full model (4) in [
18]. To date, there is no experimental data available for Lactonase concentration, thus parameters associated with Lactonase production (
ρ), decay (
ω), and activity (
δ) can be only estimated from AHL experimental data. This means in turn that there are several plausible solutions for the estimation of
, and
δ. We choose to maintain parameter values as estimated in [
18].
It can be seen from the model reduction assumptions, as well as from the simplified parameters (
7) that we lack information on the receptor production (
) and decay (
); indeed, there is no equation for PpuR in (4). These parameters play a role for the critical threshold value,
, in the complex-regulated processes. We fit
and
, fixing all other parameter values as in [
18]. The results are summed up in
Table 1, with parameter values as provided by the fitting procedure, without rounding. In
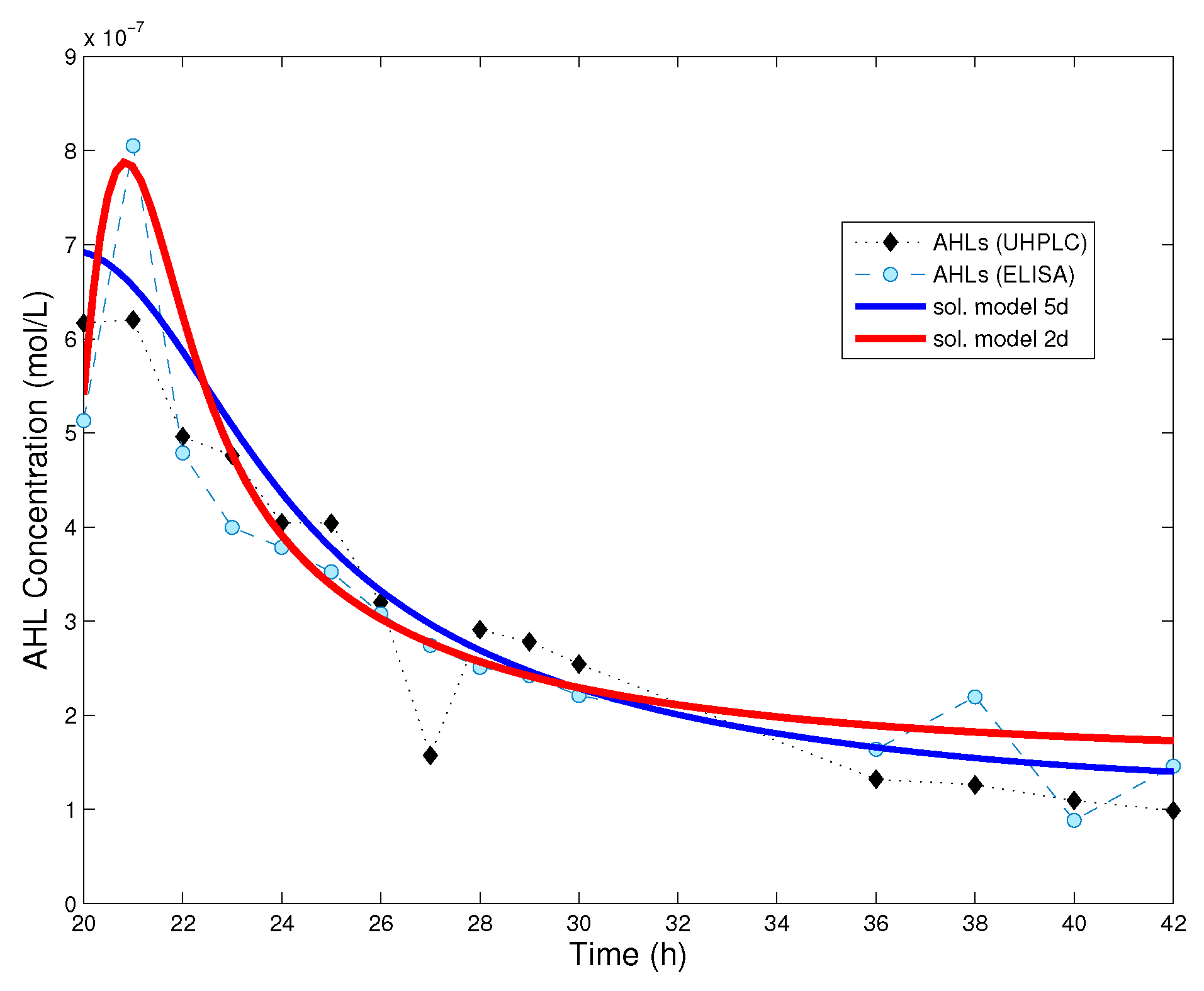
Figure 3 we show a comparison between the numerical solution of model (4), that of the simplified model (8) and experimental data for AHL time series.
With the estimated parameter values in
Table 1, we consider the analytical results in
Section 3.2 and
Section 3.4. The system has three equilibrium points
, but we only consider the stability properties of the largest one
, which corresponds to high AHL level and to an activated state of the bacteria population. Parameter values satisfy
, thus there is no stability switch with respect to
τ, and the system behaves as in the case
. We go back to
Section 3.3 and consider the Jacobian matrix (13), obtaining
and
. Hence, with the estimated parameter values, the system (8) has a locally asymptotically stable equilibrium
in which bacteria are activated.
4. Discussion
In this paper we have introduced a system of two delay differential Equation (8) for quorum sensing of
Pseudomonas putida in a continuous culture. Motivated by experimental data, a more detailed mathematical model (4) was previously proposed in [
18]. Though the system (4) describes the regulatory network in greater detail, in the long run, bacteria reach a saturation level and the model can be reduced to two governing Equation (8), as we have shown in
Section 2.1.
Surprisingly, even a simple model such as (8) can be used to explain experimental data (
Figure 3), maintaining parameter values from a previous fit [
18] for almost all model parameters. However, one should take into account that this is valid only from the moment the bacteria population has reached its saturation level. If one is interested in understanding quorum sensing in the initial phases (lag and exponential phase) of bacterial population, then it is convenient to use a more detailed model, such as (4) or (5).
The advantage of system (8) is that it can be investigated thoroughly thanks to well-established methods. We have shown existence and uniqueness of solutions and, more importantly, we could guarantee preservation of positivity. This property is often violated in systems of delay differential equations. We have studied linearized stability of non-negative equilibria and proved that the delay system (8) might show stability switches as the delay increases. On the other side, the Lactonase activity (δ) can induce Hopf-bifurcation in the associated ODE system (12).
For simplicity of computation in the analysis of the system, we have considered only the case of small Hill coefficients (
), which corresponds to a maximum of three biologically-relevant stationary states. This assumption is, however, not as restrictive as it seems. Three stationary states, with an intermediate unstable one, are the basis for the bistability situation already discovered in analogous regulatory networks [
11,
17]. Moreover, similar small values for the Hill coefficients were found to fit experimental data (
Table 1) and correspond well to the biological assumption of a dimer being relevant for the positive feedback in the quorum sensing system of
Pseudomonas putida [
16]. With the fitted parameter values, we do not find delay-induced stability switches. This is not a hint of the delay being not relevant. Though a positive time lag might not change the main qualitative behavior of the system, the DDE model still describes the experimentally-determined data and their time course quantitatively better than the associated ODE system, in particular when the bacteria population is in the lag or exponential phase. Stability switches and periodic oscillatory behavior might appear for a different choice of the parameters in system (8). As the main focus of this work was to provide a description for a real biological process, we decided to omit further numerical investigation on the qualitative behavior of (8).
Delay equations have been previously used in mathematical models of continuous cultures. Commonly, a time lag was included to describe the time necessary for the bacteria to convert nutrients in new biomass [
26,
27]. Being interested in the long term dynamics with bacteria being at an equilibrium, we have chosen not to consider such reproduction lags in our model. In our case, the time lag arises from the dynamics of the regulatory network, in particular from the initialization processes of the AHL-degrading enzyme.
Taken together, the presented simplified delay equation system is a good compromise between refined modeling for a well-known gene regulatory network with several players, and a system of equations which still allows explicit analysis of the basic qualitative behavior as well as parameter determination from few experimental data.