Abstract
Intraguild predation (IGP) is a widespread ecological phenomenon which occurs when one predator species attacks another predator species with which it competes for a shared prey species. The objective of this paper is to study the dynamical properties of a stochastic intraguild predation model. We analyze stochastic persistence and extinction of the stochastic IGP model containing five cases and establish the sufficient criteria for global asymptotic stability of the positive solutions. This study shows that it is possible for the coexistence of three species under the influence of environmental noise, and that the noise may have a positive effect for IGP species. A stationary distribution of the stochastic IGP model is established and it has the ergodic property, suggesting that the time average of population size with the development of time is equal to the stationary distribution in space. Finally, we show that our results may be extended to two well-known biological systems: food chains and exploitative competition.
Keywords:
intraguild predation; random perturbations; persistence; stationary distribution; global asymptotic stability MSC:
60H10; 92D25; 60H30
1. Introduction
Interactions among species can structure biological communities by affecting the identity, number and abundance of species present. Intraguild predation (IGP) has been playing an important role in structuring ecological communities, strongly influencing the structure and function of food webs. IGP describes an interaction in which one predator species consumes another predator species with whom it also competes for shared prey [1,2]. This suggests that IGP combines two important structuring forces in ecological communities: competition and predation. Accordingly, IGP is not only a taxonomically widespread interaction within communities which can occur at different trophic levels, but also a central force to forecast the stability of food webs and the maintenance of biodiversity.
The simplest form of IGP is depicted by a simple food web model in which IGP can occur: a top predator (IG predator P), an intermediate consumer (IG prey N), and a shared prey (R). The development of IGP model can be traced back to Holt and Polis [1] who initially introduce a three species model with the Lotka–Volterra type to study the species coexistence of IGP and point out that it is very difficult to achieve a stable three-species steady state. After that, there are some articles to consider an IGP model with different structures and forms, such as, IGP model with the Lotka–Volterra type [3,4,5], the IGP model with special forms of the functional and numerical responses [6,7,8], the IGP model with prey switching or adaptive prey behavior [9,10], and the IGP model with generalist predator or time delay [11,12,13].
The effect of the random variation of environment is an integral part of any realistic ecosystem. Stochastic models may be more important in characterizing population dynamics in contrast to the deterministic models. In essence, random factors can lead to complete extinction of populations even if the population size is relatively large. Previous studies have explored the dynamic properties for stochastic single species models [14,15,16], stochastic predator–prey models [17,18,19,20,21,22,23], stochastic competitive models [24,25,26,27], stochastic mutualism model [28,29,30,31]. Specially, Liu and Wang [32] investigated a two-prey one-predator model with random perturbations. However, there are few studies to investigate dynamics of a stochastic IGP model.
Motivated by the existing nice studies and the above considerations, we consider a following IGP model with the Lotka–Volterra type
where and are the densities of the shared prey, IG prey and IG predator, respectively; r is the per capita growth rate of the shared prey and is the death rate of species i; is the intraspecific competition rate of species i; and are the predation rates of IG predator to the shared prey and IG prey; is the predation rate of IG prey to the shared prey; is the conversion rates of resource consumption into reproduction for IG prey and IG predator. Here, is nonnegative constants and the remaining parameters are all positive constants. In view of the fact that the per capita growth rate and the death rate exhibit random fluctuation to a greater or lesser extent (see [33]), we assume that the environmental fluctuation mainly affects the parameters r, and and model these fluctuations by means of independent Gaussian white noises. Let be a three-dimensional Brownian motion defined on a complete probability space and
where are the intensity of the white noise. Thus we consider the Itô’s stochastic IGP model as follows:
The main aim of this paper is to study the dynamics of the model (3). Theoretical studies have suggested that it is very difficult to a achieve stable three-species steady state for the deterministic IGP model. Hence, the first interesting topic of the present paper is whether we can establish a criterion for three- species coexistence under the influence of environmental noise and give the sufficient conditions for global asymptotic stability of the positive solution of model (3). Another important and interesting problem is whether there is a stationary distribution of the stochastic IGP model (3) and if it has the ergodic property.
The rest of the paper is organized as follows. In the next section, we do some necessary preparations including some notations and several important lemmas. In Section 3, we explore stochastic persistence and the extinction of model (3) for five different cases and compare them with the corresponding results of the deterministic model (1).
Then, we establish global asymptotic stability of the positive solution of the model (3). In Section 4, we prove that there is a stationary distribution of model (3), and it has the ergodic property by using the theory of Has’minskii [34]. In the final section, according to the conclusions of previous sections, we first study dynamic properties of two well-known biological systems under random perturbations: food chains and exploitative competition. We state biological implications of our mathematical findings and present some figures to illustrate or complement our mathematical findings.
2. Preliminaries
In this section, we first introduce several important lemmas.
Lemma 1
(see [32]). Let , and .
- (i)
- If there exist two positive constants T and such thatfor all where , , are independent standard Brownian motions and , , are constants, then if or if
- (ii)
- If there exist three positive constants T, λ, and such thatfor all where , , are independent standard Browniam motions and , , are constants, then
Similar to Theorem 2.1, Lemma 3.1 and Lemma 3.4 in [25], we have the following lemma:
Lemma 2.
In order to obtain the conditions of global asymptotic stability of solutions for the stochastic model (3), we need the following two lemmas.
Lemma 3
(see [35]). If there exist positive constants and κ such that an n-dimensional stochastic process , satisfies
for , then there exists a continuous modification of such that for every there is a positive random variable such that
which implies that almost every sample path of is locally but uniformly Hölder continuous with exponent ω.
Lemma 4
(see [36]). If g is a non-negative function defined on such that g is integrable and is uniformly continuous, then
To establish the existence of a stationary distribution of model (3) in Section 4, we introduce the theory of Has’minskii [34] and let be a homogeneous Markov process in ( is an l-dimensional Euclidean space) described by the stochastic equation
Let the diffusion matrix be , .
Assumption 5.
There is a bounded domain with regular boundary Γ such that
- (H)
- In the domain U and some neighborhood thereof, the smallest eigenvalue of the diffusion matrix is bounded away from zero;
- (H)
- If , the mean time τ at which a path issuing from x reaches the set U is finite, and for every compact subset .
It is worth noting that we can use the following two stronger conditions to verify (H) and (H) in Assumption 5:
- (K)
- To obtain (H), we only need to show that T is uniformly elliptical in U, where , that is, there exists a such that , , (see [37,38]);
- (K)
- To obtain (H), we only need to prove that there exist a neighborhood U and a nonnegative -function such that for any , (see [39]).
Lemma 6
([34]). If Assumption 5 holds, then the Markov process has a stationary distribution . Moreover, if is a function integrable with respect to the measure μ, then
3. Stochastic Persistence and Stochastic Extinction
To illuminate the effect of the stochastic perturbations for population and compare the stochastic IGP model (3) with the deterministic IGP model (1), we first explore the existence and local stability of boundary and positive equilibria for model (1). The summary of conditions for the existence and local stability of equilibria are listed in Table 1.

Table 1.
Existence and local stability of equilibria for model (1).
Now, we analyze stochastic persistence and stochastic extinction of model (3).
Definition 7
(see [32]). Species is said to be persistent in the mean if .
Let
A direct calculation gives
Theorem 8.
The following five cases hold:
- (i)
- If , then all the populations are extinction a.s.
- (ii)
- If , then and are extinction a.s. and
- (iii)
- If , and , then is extinction a.s. and
- (iv)
- If , and , then is extinction a.s. and
- (v)
- If , , , then
Proof.
It follows from Itô’s formula that
By integrating from 0 to t on both sides of the above equation and dividing by t, we have
(i) It follows from the first equality of Equation (21) that
By Lemma 1, we have
since holds. Substituting Equation (23) into the second equality of Equation (21) yields
for sufficiently large t and sufficiently small ε such that . Applying Lemma 1 to Equation (24), we get
Similarly, in view of the third equality of Equation (21), Equation (23), Equation (25) and Lemma 1, we can conclude that This implies that (i) of Theorem 8 holds.
(ii) It follows from Equation (22) and Lemma 1 that
Combining the second equality of Equation (21) with Equation (26) gives
for sufficiently large t. Then
if and ε is sufficiently small such that . It follows from the third equality of Equation (21), Equation (26), Equation (28) and Lemma 1 that
since . From Equation (28) and Equation (29) and Lemma 1, we obtain
for sufficiently large t and
Combining Equation (26) with Equation (30) implies that (ii) holds.
(iii) Let
A direct calculation gives and . Multiplying both sides of three equalities of Equation (21) by , and , respectively, and then adding these three equalities, we have
We consider the following two cases:
- Case 1: if , then
- Case 2: if , then by Equation (7), for sufficiently large t, we getIt follows from Lemma 1 and the arbitrariness of ε thatOn the other hand, a direct calculation also shows thatwhere . For sufficiently large t, multiplying both sides of three equalities of Equation (21) by , and , respectively, and then adding these three equalities, we obtainHere, we have In fact, if , then , which implies that and This is a contradiction. By Equation (7), for sufficiently large t, we obtainFrom Lemma 1, we getsince ε is arbitrary. For the third equality of Equation (21) and sufficiently large t, combining Equation (33) with Equation (36) givesThen, if ε is sufficiently small.
Combining case 1 with case 2 gives The first equality of Equation (21) multiplied by plus the second equality of Equation (21) multiplied by gives
for sufficiently large t and sufficiently small ε since Equation (7) and hold. It follows from Lemma 1 and the arbitrariness of ε that
By applying the above inequality and into the first equality of Equation (21), we get
Then,
On the other hand, for sufficiently large t, substituting Equation (41) to the second equality of Equation (21) gives
which implies that
Combining Equation (39) with Equation (43) gives
It follows from Equation (43) and that
Then,
Combining Equation (41) with (46) gets
It follows from Equation (44) and (47) that (iii) holds.
(iv) Similar to the arguments of (iii), it follows from Equation (36) that if . The first equality of Equation (21) multiplied by plus the third equality of Equation (21) multiplied by gives
for sufficiently large t. By Lemma 1 and the arbitrariness of ε, we have
This implies that
for sufficiently large t. From Lemma 1, we get
It follows from and Equation (49) that
for sufficiently large t. Then,
Using Equation (53), we have
for sufficiently large t. Hence,
It follows from Equations (49)–(53) and Equation (55) that (iv) holds.
(v) By using Equation (37), we obtain
since . For sufficiently large t, it follows from (36) and Equation (56) that
which means
Similarly, we have
and
for sufficiently large t. Then,
By Equation (33), (36), (56), (58) and (61), (v) holds. The proof of the theorem is complete. ☐
Now, we establish the sufficient criteria for global asymptotic stability of the positive solutions for the stochastic model (3). This stochastic model (3) is said to be globally asymptotically stable (or globally attractive) if , where , are two arbitrary solutions of (3) with initial values , . By Lemma 3, similar to arguments as those of Lemma 15 in [32], we have the following lemma.
Lemma 9.
Theorem 10.
4. Stationary Distribution and Ergodicity
In this section, we establish the stationary distribution of the stochastic IGP model (3) and show that it has the ergodic property. It is clear that the diffusion matrix of (3) is . Let
Theorem 11.
Proof.
To obtain the conclusion, we need to show that (K) and (K) hold. It follows from (67) that the ellipsoid
lies entirely in . Let U be a neighborhood of the ellipsoid with . It is not difficult to show that there exists a such that
for and . This implies that (K) holds.
Let
Then,
where
Since is the positive equilibrium point of (1), we have
Then, for any , we get , which means that (K) holds. It follows from Lemma 6 that (3) has a stationary distribution , and it is ergodic.
On the other hand, for any , it follows from the dominated convergence theorem and Lemma 2 that
By the ergodic property, we have
Then, as . By Lemma 6, the first equality of Equation (68) holds. Similarly, we can conclude that the second and third equalities of Equation (68) hold. The proof of the theorem is completed. ☐
5. Conclusions
In this section, we first focus on the stochastic food chains model and the stochastic exploitative competition model. In the model (3), if we let or , then we get the stochastic food chains model
and the stochastic exploitative competition model
In view of the stochastic IGP model (3), Theorems 8, 10, 11 reduce the corresponding results of models (77) and (78), that is, we get the stochastic persistence and stochastic extinction, stationary distribution and ergodicity, and globally asymptotically stability of the positive solution for the stochastic food chains model (77), and the stochastic exploitative competition model (78), in the case of or .
In this paper, we have developed a stochastic IGP model (3) describing the interactions among a top predator (IG predator P), an intermediate consumer (IG prey N), and a shared prey (R) under the influence of environmental noise. We have analyzed the dynamic properties for the stochastic IGP model (3) and the deterministic IGP model (1). As applications, we show that our results may be extended to two well-known biological systems: food chains and exploitative competition.
Comparing the stochastic IGP model (3) with the deterministic IGP model (1) (see Theorems 8, 10, 11 and Table 1), we obtain the following conclusions:
- In the deterministic model (1), the total extinction of three populations is impossible since is unstable. However, this situation is possible for the stochastic model (3) when the noise intensity is large enough (see Figure 1a);
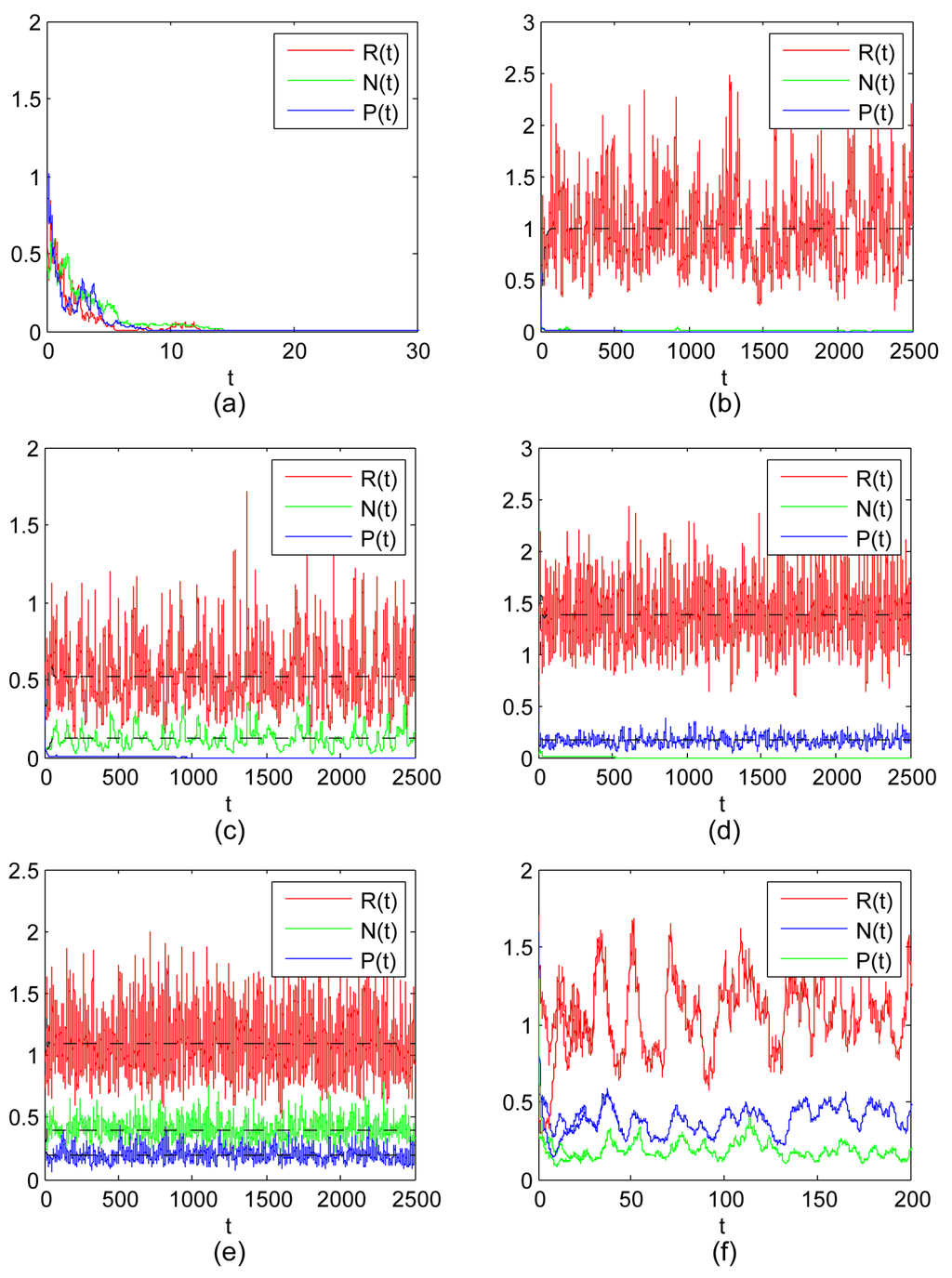 Figure 1. (a) = 0.9177, = 0.4472, = 0.6325, 0.8 = 2r < = 0.8422; (b) = 0.7750, = 0.6325, = 0.5477, = > 1 > = 0.9991, = , ; (c) = 0.7746, = 0.1414, = 0.1414, L= 0.1790, = 1.2088 > 1 and = = 0.0501, and ; (d) = 0.6, = 0.8, = 0.4, = 1.2 > 1 and = < = 0.0862, and ; (e) , and ; (f) = 0.7746, = 0.1414, = 0.2449, (0) = 1.7, (0) = 0.6, (0) = 0.3, (0) = 0.7, (0) = 1.6, (0) = 1.3. Here r = 0.4, = 0.1, = 0.2, = 0.1, = 0.4, = 0.5, = 0.75, = 0.4, = 0.3, = 0.6, = 0.5, = 0.8.
Figure 1. (a) = 0.9177, = 0.4472, = 0.6325, 0.8 = 2r < = 0.8422; (b) = 0.7750, = 0.6325, = 0.5477, = > 1 > = 0.9991, = , ; (c) = 0.7746, = 0.1414, = 0.1414, L= 0.1790, = 1.2088 > 1 and = = 0.0501, and ; (d) = 0.6, = 0.8, = 0.4, = 1.2 > 1 and = < = 0.0862, and ; (e) , and ; (f) = 0.7746, = 0.1414, = 0.2449, (0) = 1.7, (0) = 0.6, (0) = 0.3, (0) = 0.7, (0) = 1.6, (0) = 1.3. Here r = 0.4, = 0.1, = 0.2, = 0.1, = 0.4, = 0.5, = 0.75, = 0.4, = 0.3, = 0.6, = 0.5, = 0.8. - The existence of both the shared prey and IG prey with the extinction of IG predators, and the existence of both the shared prey and IG predators with the extinction of IG prey are both possible outcomes of the stochastic model (3) with different sets of parameters (see Figure 1c,d). Here, it is worth noting that the noise has a negative effect for IG prey and IG predators, and may also have a positive effect for the shared prey if the values of and grow larger (see (iii) and (iv) of Theorem 8). This also implies that stochastic fluctuation of N or P would help R to grow larger;
- This study suggests that the shared prey, IG prey and IG predators can coexist together for the stochastic model (3), which implies that it is possible for the coexistence of three species under the influence of environmental noise (see Figure 1e). There is recognition that the noise may be favorable to three-species coexistence if , (see (v) of Theorem 8). In addition, we also prove that three-species is stable coexistence for the influence of environmental noise (see Theorem 10 and Figure 1f);
- The study of Theorem 11 suggests that the time average of the population size of model (3) with the development of time is equal to the stationary distribution in space.
Acknowledgments
The authors are grateful to the anonymous referees for carefully reading the manuscript and for important suggestions and comments, which led to the improvement of their manuscript. This research is supported by National Natural Science Foundation of China (No.11201128,11302127) Natural Science Foundation of Heilongjiang Province (No.A201414,F2015032), The National High Technology Research and Development Program of China (No.2013AA122904), Science and Technology Innovation Team in Higher Education Institutions of Heilongjiang Province (No.2014TD005), and The Heilongjiang University Fund for Distinguished Young Scholars (No.201203).
Author Contributions
Zejing Xing and Jimin Zhang conceived the study and drafted the manuscript. Hongtao Cui participated in the design of the study and analysis of the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Holt, R.D.; Polis, G.A. A theoretical framework for intraguild predation. Am. Nat. 1997, 149, 745–764. [Google Scholar] [CrossRef]
- Polis, G.A.; Holt, R.D. Intraguild predation: The dynamics of complex trophic interactions. Trends Ecol. Evol. 1992, 7, 151–154. [Google Scholar] [CrossRef]
- Hsu, S.B.; Ruan, S.G.; Yang, T.H. Analysis of three species Lotka–Volterra food web models with omnivory. J. Math. Anal. Appl. 2015, 426, 659–687. [Google Scholar] [CrossRef]
- Shchekinova, E.Y.; Löder, M.G.J.; Boersma, M.; Wiltshire, K.H. Facilitation of intraguild prey by its intraguild predator in a three-species Lotka–Volterra model. Theor. Popul. Biol. 2014, 92, 55–61. [Google Scholar] [CrossRef] [PubMed]
- Velazquez, I.; Kaplan, D.; Velasco-Hernandez, J.X.; Navarrete, S.A. Multistability in an open recruitment food web model. Appl. Math. Comput. 2005, 163, 275–294. [Google Scholar] [CrossRef]
- Abrams, P.A.; Fung, S.R. Prey persistence and abundance in systems with intraguild predation and type-2 functional responses. J. Theor. Biol. 2010, 264, 1033–1042. [Google Scholar] [CrossRef] [PubMed]
- Freeze, M.; Chang, Y.; Feng, W. Analysis of dynamics in a complex food chain with ratio-dependent functional response. J. Appl. Anal. Comput. 2014, 4, 69–87. [Google Scholar]
- Verdy, A.; Amarasekare, P. Alternative stable states in communities with intraguild predation. J. Theor. Biol. 2010, 262, 116–128. [Google Scholar] [CrossRef] [PubMed]
- Urbani, P.; Ramos-Jiliberto, R. Adaptive prey behavior and the dynamics of intraguild predation systems. Ecol. Model. 2010, 221, 2628–2633. [Google Scholar] [CrossRef]
- Zabalo, J. Permanence in an intraguild predation model with prey switching. Bull. Math. Biol. 2012, 74, 1957–1984. [Google Scholar] [CrossRef] [PubMed]
- Fan, M.; Kuang, Y.; Feng, Z.L. Cats protecting birds revisited. Bull. Math. Biol. 2005, 67, 1081–1106. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Wedekin, L. Dynamics of a intraguild predation model with generalist or specialist predator. J. Math. Biol. 2013, 67, 1227–1259. [Google Scholar] [CrossRef] [PubMed]
- Shu, H.Y.; Hu, X.; Wang, L.; Watmough, J. Delay induced stability switch, multitype bistability and chaos in an intraguild predation model. J. Math. Biol. 2015, 71, 1269–1298. [Google Scholar] [CrossRef] [PubMed]
- Golec, J.; Sathananthan, S. Stability analysis of a stochastic logistic model. Math. Comput. Model. 2003, 38, 585–593. [Google Scholar] [CrossRef]
- Jiang, D.Q.; Shi, N.Z.; Li, X.Y. Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation. J. Math. Anal. Appl. 2008, 340, 588–597. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K.; Hong, Q. Stability of a stochastic logistic model with distributed delay. Math. Comput. Model. 2013, 57, 1112–1121. [Google Scholar] [CrossRef]
- Aguirre, P.; González-Olivares, E.; Torres, S. Stochastic predator–prey model with Allee effect on prey. Nonlinear Anal. RWA 2013, 14, 768–779. [Google Scholar] [CrossRef]
- Ji, C.Y.; Jiang, D.Q. Dynamics of a stochastic density dependent predator–prey system with Beddington-DeAngelis functional response. J. Math. Anal. Appl. 2011, 381, 441–453. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K. Global stability of a nonlinear stochastic predator–prey system with Beddington-DeAngelis functional response. Commun. Nonlinear Sci. 2011, 16, 1114–1121. [Google Scholar] [CrossRef]
- Mandal, P.S.; Banerjee, M. Stochastic persistence and stability analysis of a modified Holling-Tanner model. Math. Method. Appl. Sci. 2013, 36, 1263–1280. [Google Scholar] [CrossRef]
- Saha, T.; Chakrabarti, C. Stochastic analysis of prey-predator model with stage structure for prey. J. Appl. Math. Comput. 2011, 35, 195–209. [Google Scholar] [CrossRef]
- Vasilova, M. Asymptotic behavior of a stochastic Gilpin-Ayala predator–prey system with time-dependent delay. Math. Comput. Model. 2013, 57, 764–781. [Google Scholar] [CrossRef]
- Yagi, A.; Ton, T.V. Dynamic of a stochastic predator–prey population. Appl. Math. Comput. 2011, 218, 3100–3109. [Google Scholar] [CrossRef]
- Jovanović, M.; Vasilova, M. Dynamics of non-autonomous stochastic Gilpin-Ayala competition model with time-varying delays. Appl. Math. Comput. 2013, 219, 6946–6964. [Google Scholar] [CrossRef]
- Li, X.; Mao, X. Population dynamical behavior of non-autonomous Lotka–Volterra competitive system with random perturbation. Discrete Cont. Dyn. Syst. Ser. 2009, 24, 523–593. [Google Scholar]
- Lian, B.S.; Hu, S.G. Asymptotic behaviour of the stochastic Gilpin-Ayala competition models. J. Math. Anal. Appl. 2008, 339, 419–428. [Google Scholar] [CrossRef]
- Zhu, C.; Yin, G. On competitive Lotka–Volterra model in random environments. J. Math. Anal. Appl. 2009, 357, 154–170. [Google Scholar] [CrossRef]
- Ji, C.Y.; Jiang, D.Q.; Liu, H.; Yang, Q.S. Existence, uniqueness and ergodicity of positive solution of mutualism system with stochastic perturbation. Math. Probl. Eng. 2010, 2010. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K. Analysis of a stochastic autonomous mutualism model. J. Math. Anal. Appl. 2013, 402, 392–403. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K. Population dynamical behavior of Lotka–Volterra cooperative systems with random perturbations. Discrete Cont. Dyn. Syst. Ser. 2013, 33, 2495–2522. [Google Scholar] [CrossRef]
- Liu, Q. Analysis of a stochastic non-autonomous food-limited Lotka–Volterra cooperative model. Appl. Math. Comput. 2015, 254, 1–8. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K. Dynamics of a two-prey one-predator system in random environments. J. Nonlinear Sci. 2013, 23, 751–775. [Google Scholar] [CrossRef]
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Has’minskii, R.Z. Stochastic Stability of Differential Equations; Sijthoff & Noordhoff: Alphen aan den Rijn, the Netherlands, 1980. [Google Scholar]
- Karatzas, I.; Shreve, S. Brownian Motion and Stochastic Calculus; Springer: Berlin, Germany, 1991. [Google Scholar]
- Barbalat, I. Systems d’equations differentielles d’oscillations nonlineaires. Rev. Roum. Math. Pures Appl. 1959, 4, 267–270. [Google Scholar]
- Gard, T.C. Introduction to Stochastic Differential Equations; Marcel Dekker, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Strang, G. Linear Algebra and Its Applications; Wellesley-Cambridge Press: London, UK, 1988. [Google Scholar]
- Zhu, C.; Yin, G. Asymptotic properties of hybrid diffusion systems. SIAM J. Control Optim. 2007, 46, 1155–1179. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).