Investigation of the Machining Stability of a Milling Machine with Hybrid Guideway Systems
Abstract
:1. Introduction
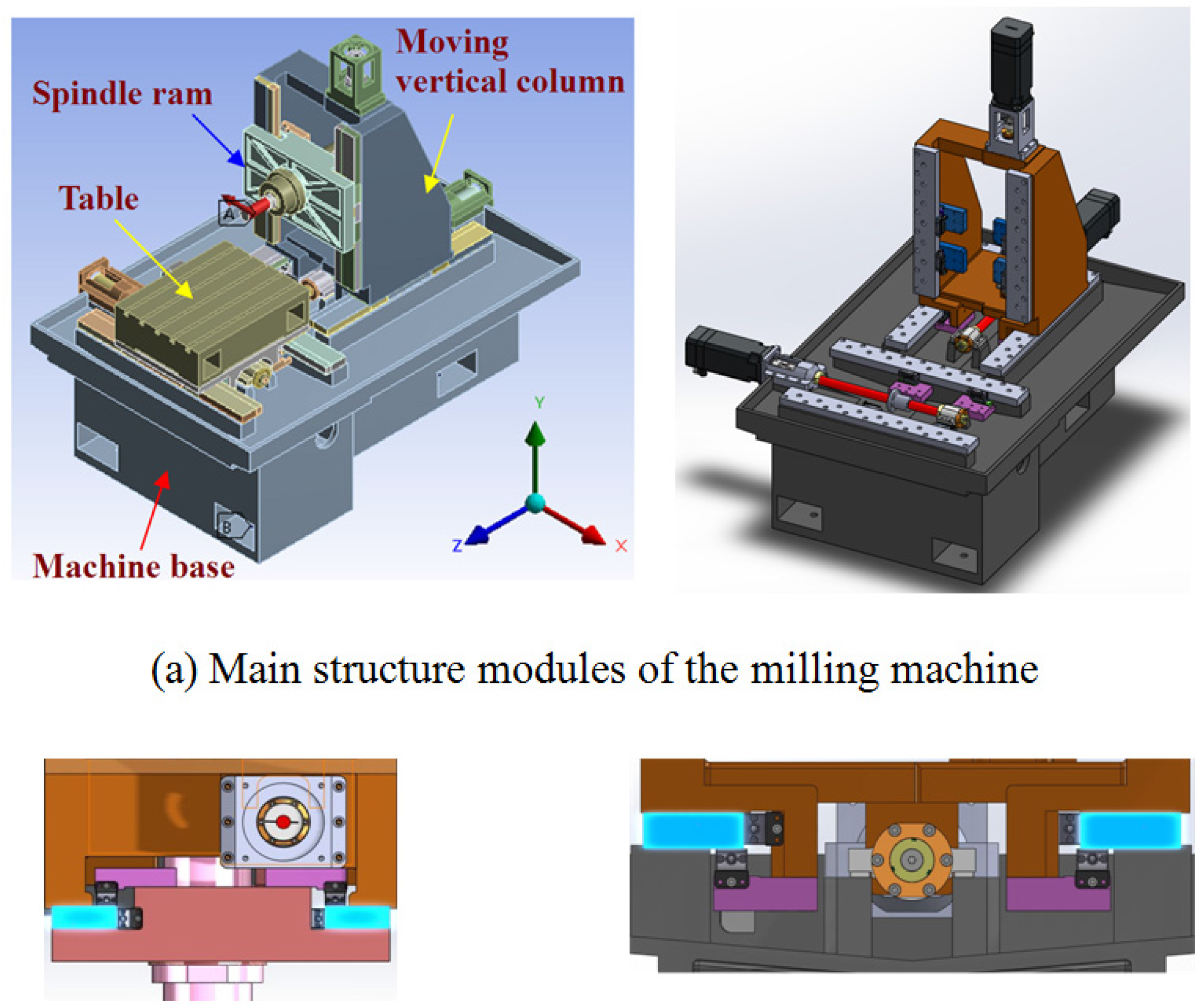
2. Construction of Milling Machine
3. Modeling of the Milling Machine
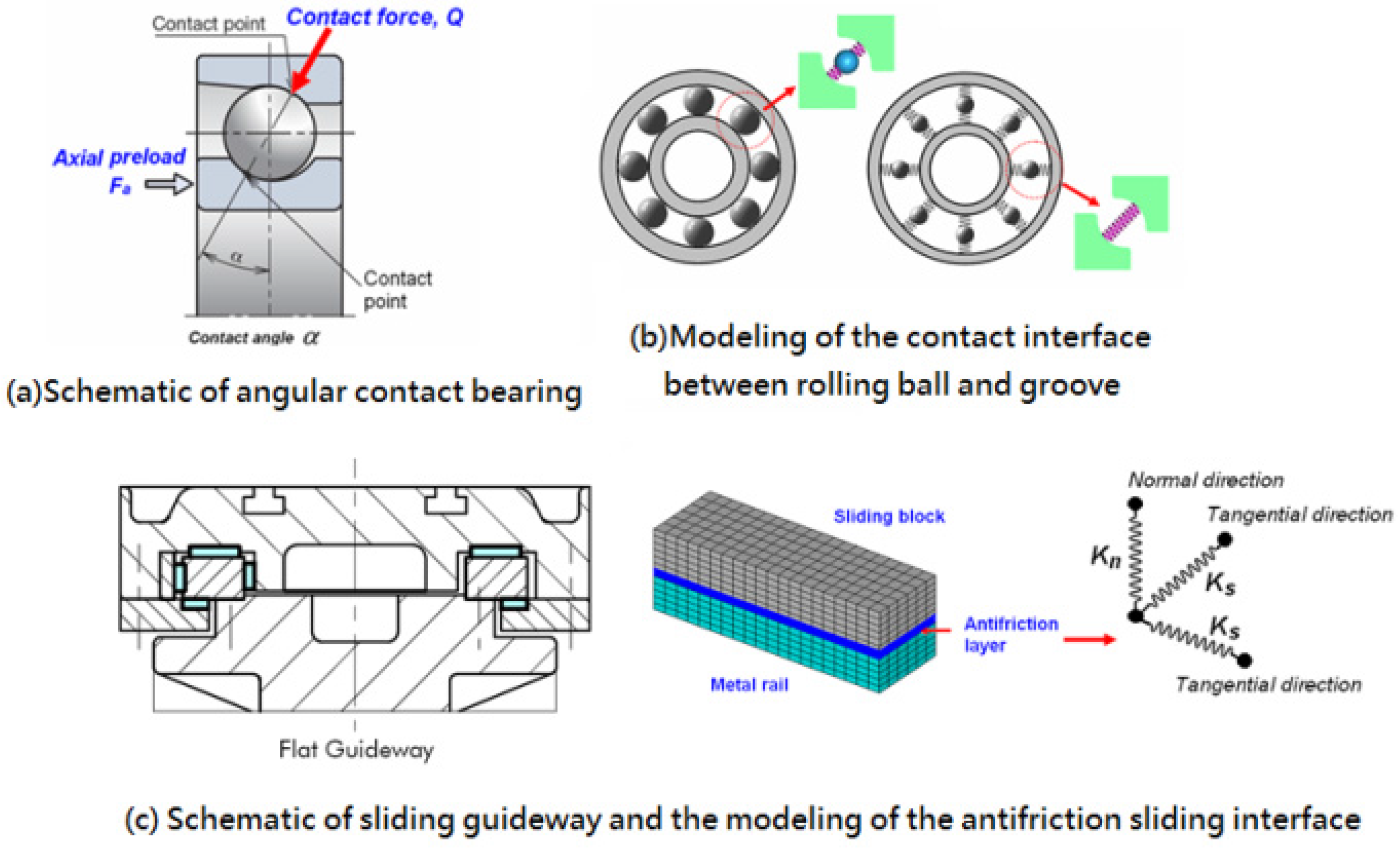
3.1. Modeling of the Joint/Interface
3.1.1. Rolling Interface
3.1.2. Sliding Interface
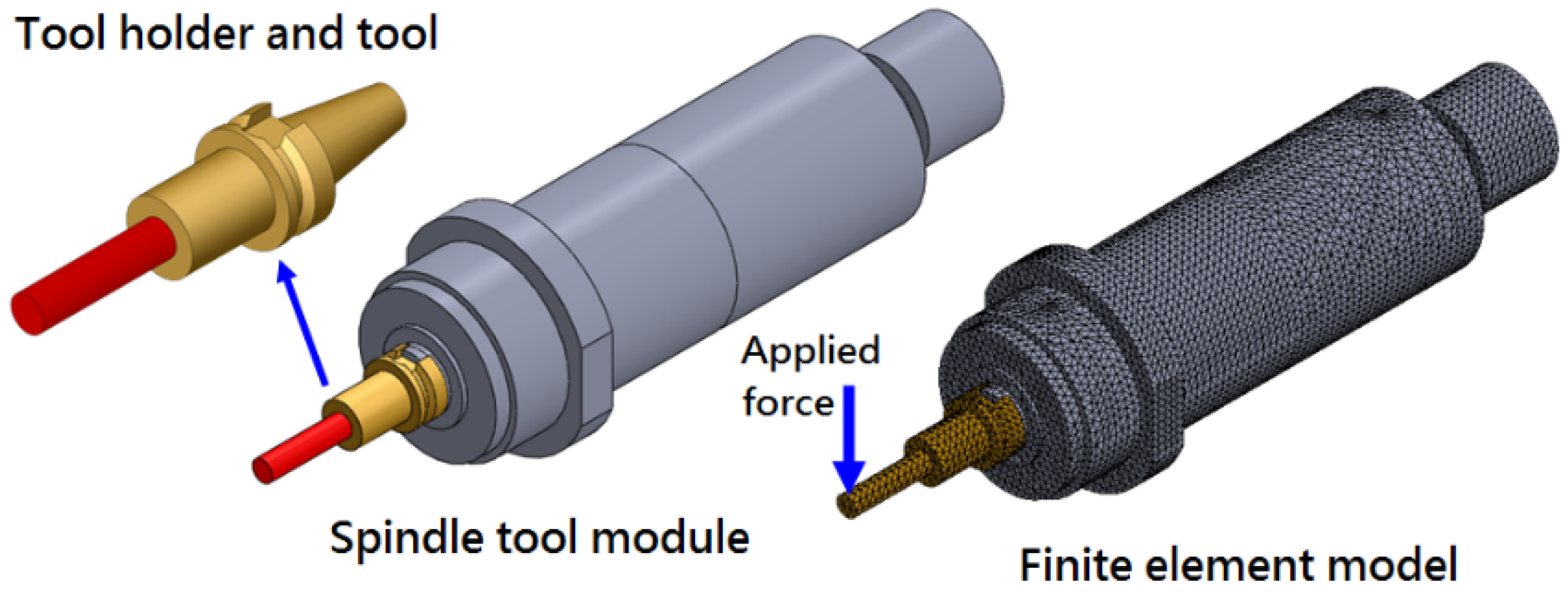
3.2. Modeling of Spindle Unit
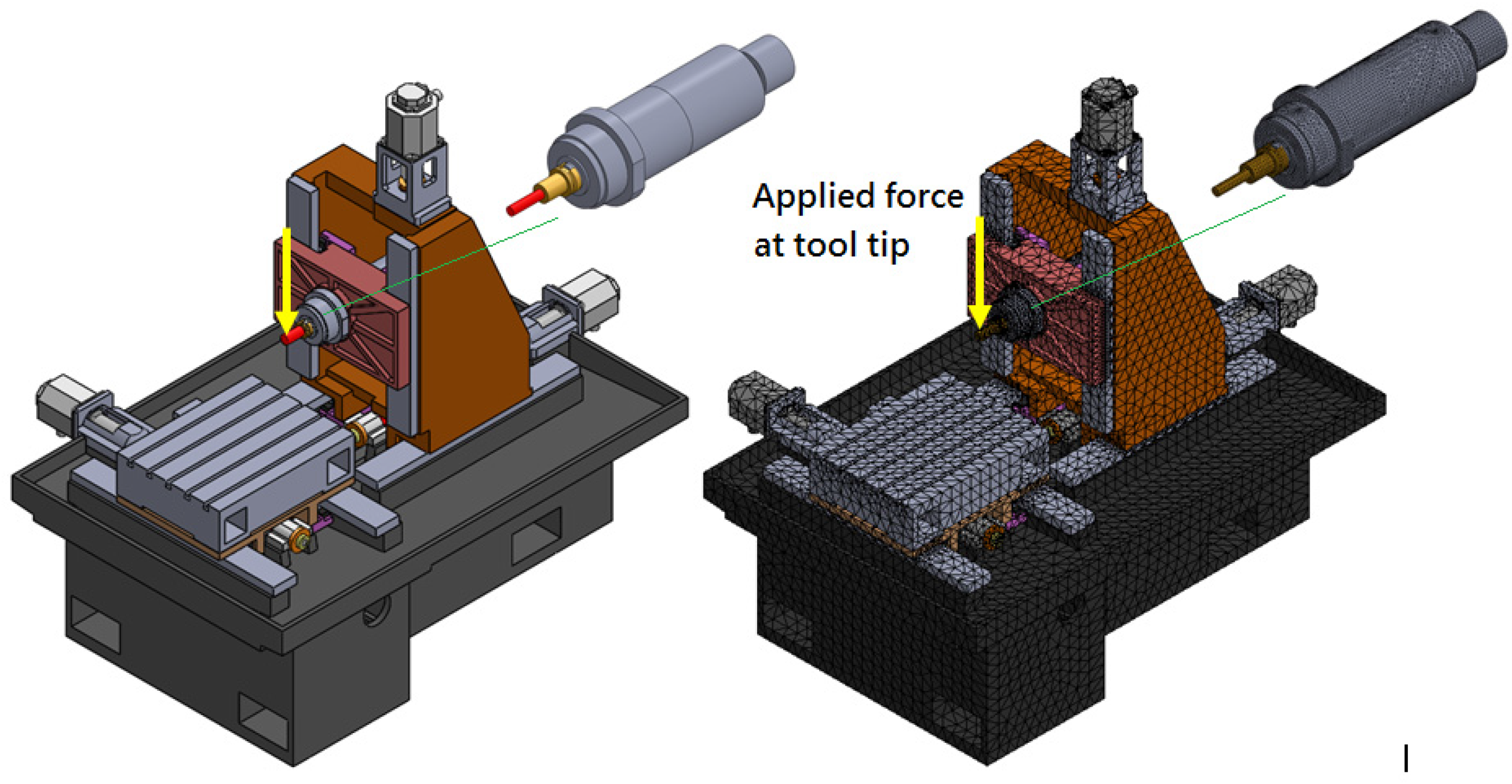
3.3. Finite Element Model of Milling Machine
4. Results and Discussions
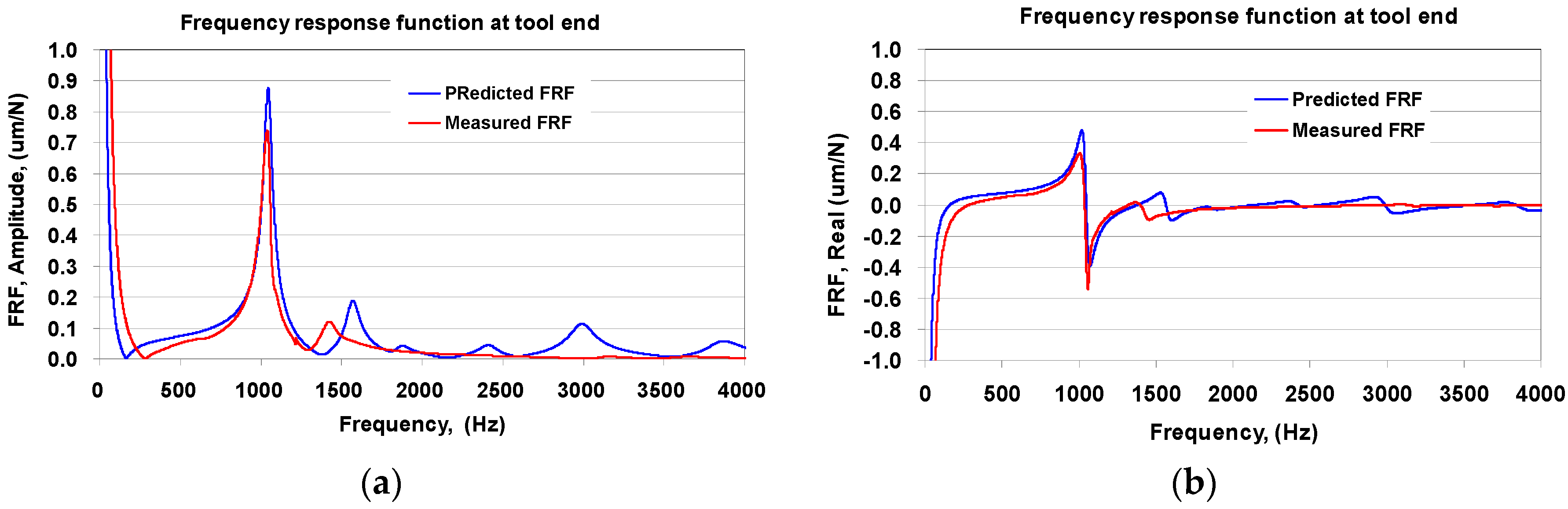
4.1. Frequency Response Function of Spindle Unit
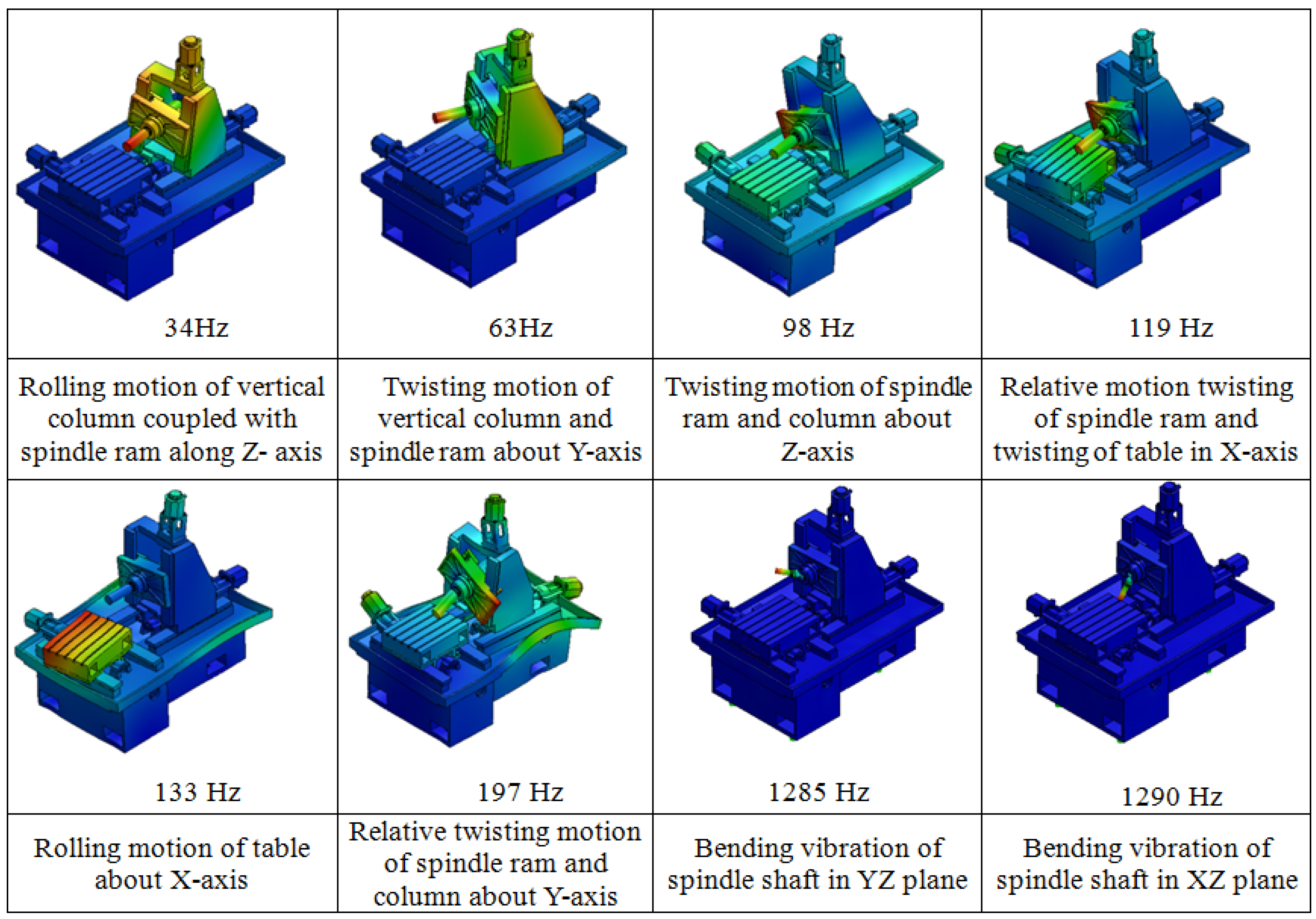
4.2. Natural Vibration Modes of Milling Machine
4.3. Frequency Response Functions of the Milling Machine
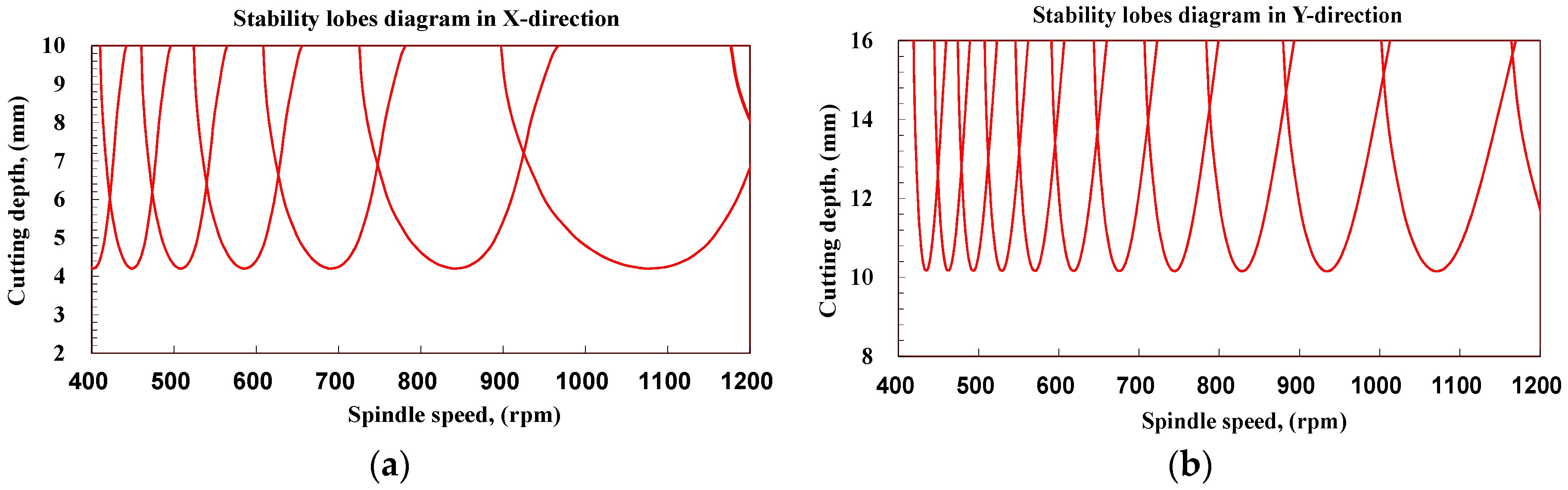
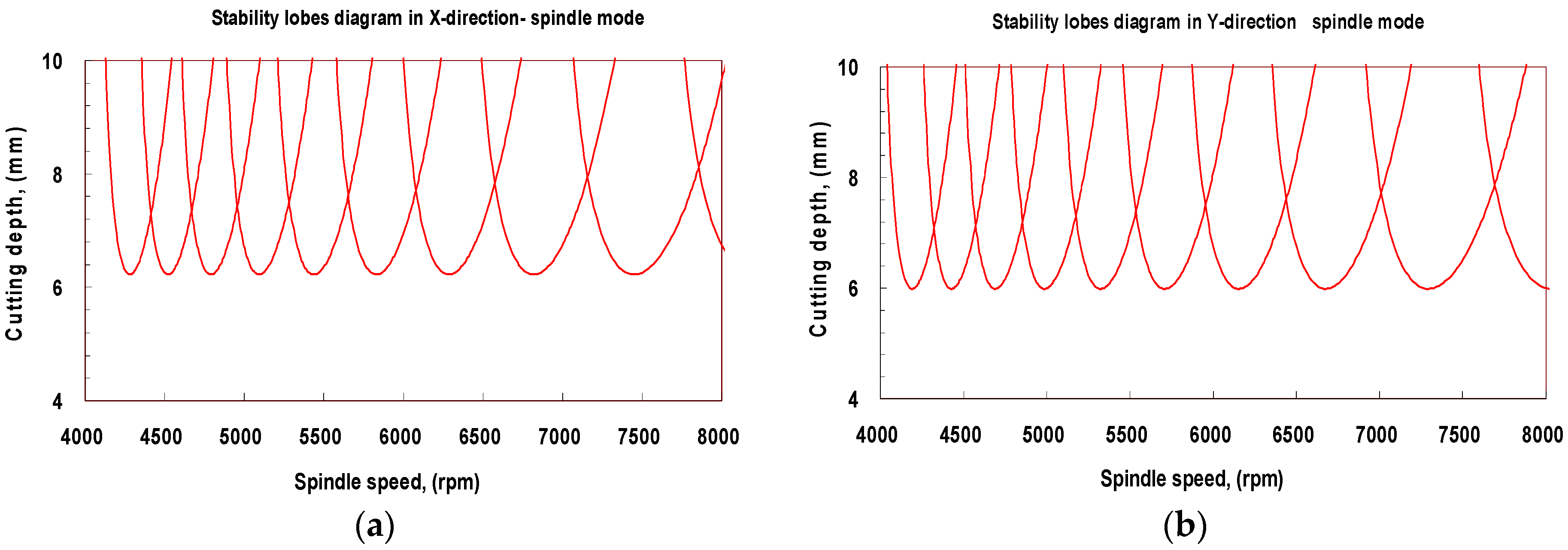
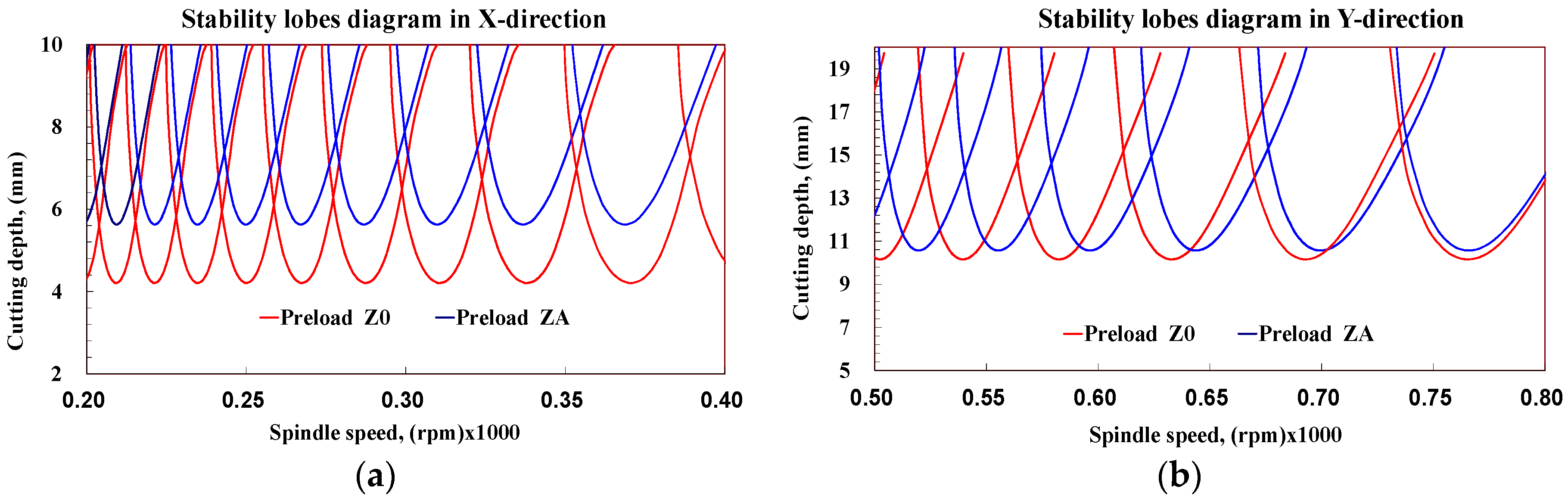
4.4. Machining Stability
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- To, Y. Modular Design for Machine Tools; McGraw Hill Professional: New York, NY, USA, 2008. [Google Scholar]
- Dhupia, J.S.; Powalka, B.; Ulsoy, A.G.; Katz, R. Effect of a nonlinear joint on the dynamic performance of a machine tool. J. Manuf. Sci. Eng. ASME 2007, 129, 943–950. [Google Scholar] [CrossRef]
- Dhupia, J.; Powalka, B.; Katz, R.; Ulsoy, A.G. Dynamics of the arch-type reconfigurable machine tool. Int. J. Mach. Tools Manuf. 2007, 47, 326–334. [Google Scholar] [CrossRef]
- Koren, Y.; Heisel, U.; Jovane, F.; Moriwaki, T.; Pritschow, G.; lsoy, G.; Brussel, H.V. Reconfigurable manufacturing systems. CIRP Ann. Manuf. Technol. 1999, 48, 527–540. [Google Scholar] [CrossRef]
- Koren, Y.; Ulsoy, A.G. Reconfigurable manufacturing system having a production capacity method for designing same and method for changing its production capacity. U.S. Patents 6,349,237, 19 February 2002. [Google Scholar]
- Seo, Y.; Hong, D.P.; Kim, I.; Kim, T.; Sheen, D.; Lee, G.B. Structure modeling of machine tools and internet-based implementation. In Proceedings of the 2005 Proceedings of the Winter Simulation Conference, Orlando, FL, USA, 4 December 2005; IEEE: New York, NY, USA, 2005; pp. 1699–1704. [Google Scholar]
- Yigit, A.S.; Ulsoy, A.G. Dynamic stiffness evaluation for reconfigurable machine tools including weakly non-linear joint characteristics. Proc. Inst. Mech. Eng. 2002, 216, 87–101. [Google Scholar] [CrossRef]
- Ravve, I.; Gottlieb, O.; Yarnitzky, Y. Nonlinear dynamics and stability of a machine tool traveling joint. Nonlinear Dynam. 1997, 13, 373–394. [Google Scholar] [CrossRef]
- Lin, C.Y.; Hung, J.P.; Lou, T.L. Effect of preload of linear guides on dynamic characteristics of a vertical column-spindle system. Int. J. Mach. Tools Manuf. 2010, 5, 741–746. [Google Scholar] [CrossRef]
- Hung, J.P. Load effect on the vibration characteristics of a stage with rolling guides. J. Mech. Sci. Technol. 2009, 23, 92–102. [Google Scholar] [CrossRef]
- Chlebus, E.; Dybala, B. Modelling and calculation of properties of sliding guideways. Int. J. Mach. Tools Manuf. 1999, 39, 1823–1839. [Google Scholar] [CrossRef]
- Fan, K.C.; Chen, H.M.; Kuo, T.H. Prediction of machining accuracy degradation of machine tools. Precis. Eng. 2012, 36, 288–298. [Google Scholar] [CrossRef]
- Bianchi, G.; Paolucci, F.; van den Braembussche, P.; van Brussel, H.; Jovane, F. Towards Virtual Engineering in Machine Tool Design. CIRP Ann. Manuf. Technol. 1996, 45, 381–384. [Google Scholar] [CrossRef]
- Altintas, Y.; Brecher, C.; Weck, M.; Witt, S. Virtual machine tool. CIRP Ann. Manuf. Technol. 2005, 54, 115–138. [Google Scholar] [CrossRef]
- Sulitka, M.; Kolar, P. Calculation of spindle compliance considering it′s interaction with machine frame. MM Sci. J. 2010, 6, 180–185. [Google Scholar] [CrossRef]
- Kolar, P.; Sulitka, M.; Janota, M. Simulation of dynamic properties of a spindle and tool system coupled with a machine tool frame. Int. J. Adv. Manuf. Technol. 2011, 54, 11–20. [Google Scholar] [CrossRef]
- Law, M.; Altintas, Y.; Phani, A.S. Rapid evaluation and optimization of machine tools with position-dependent stability. Int. J. Mach. Tools Manuf. 2013, 68, 81–90. [Google Scholar] [CrossRef]
- Hung, J.P.; Lai, Y.L.; Lou, T.L. Analysis of the machining stability of a milling machine considering the effect of machine frame structure and spindle bearings: Experimental and finite element approaches. Int. J. Adv. Manuf. Tech. 2013, 68, 2393–2405. [Google Scholar] [CrossRef]
- Zulaika, J.J.; Campa, F.J.; de Lacalle, L.N.L. An integrated process-machine approach for designing productive and lightweight milling machines. Int. J. Mach. Tools Manuf. 2011, 51, 591–604. [Google Scholar] [CrossRef]
- Huo, D.; Cheng, K.; Wardle, F. A holistic integrated dynamic design and modelling approach applied to the development of ultraprecision micro-milling machines. Int. J. Mach. Tools Manuf. 2010, 50, 335–343. [Google Scholar] [CrossRef]
- Mousseigne, M.; Landon, Y.; Seguy, S.; Dessein, G.; Redonnet, J.M. Predicting the dynamic behaviour of torus milling tools when climb milling using the stability lobes theory. Int. J. Mach. Tools Manuf. 2013, 65, 47–57. [Google Scholar] [CrossRef]
- Seguy, S.; Arnaud, L.; Insperger, T. Chatter in interrupted turning with geometrical defects: An industrial case study. Int. J. Adv. Manuf. Technol. 2014, 75, 45–56. [Google Scholar] [CrossRef]
- Aetna Plastics Corp. Turcite-B Slydway. Available online: http://www.aetnaplastics.com (accessed on 17 June 2013).
- Hiwin Technologies Corp. Ballscrews Technical Information. Available online: http://www.hiwin.com/online_cat (accessed on 11 June 2013).
- INA-Schaeffler Technologies Group UK. Flat Cage Guidance Systems. Available online: http:/www.ina.de (accessed on 14 May 2007).
- Brewe, D.E.; Hamrock, B.J. Simplified solution for elliptical-contact deformation between two elastic solid. ASME 1997, 99, 485–487. [Google Scholar] [CrossRef]
- Greenwood, J.A. Analysis of elliptical Herztian contacts. Tribol. Int. 1997, 30, 235–237. [Google Scholar] [CrossRef]
- Altintas, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- CUTPROV9.3, Advanced Machining Simulation Software. Available online: http://www.malinc.com (accessed on 1 March 2010).



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, J.-P.; Lin, W.-Z.; Chen, Y.-J.; Luo, T.-L. Investigation of the Machining Stability of a Milling Machine with Hybrid Guideway Systems. Appl. Sci. 2016, 6, 76. https://doi.org/10.3390/app6030076
Hung J-P, Lin W-Z, Chen Y-J, Luo T-L. Investigation of the Machining Stability of a Milling Machine with Hybrid Guideway Systems. Applied Sciences. 2016; 6(3):76. https://doi.org/10.3390/app6030076
Chicago/Turabian StyleHung, Jui-Pin, Wei-Zhu Lin, Yong-Jun Chen, and Tzou-Lung Luo. 2016. "Investigation of the Machining Stability of a Milling Machine with Hybrid Guideway Systems" Applied Sciences 6, no. 3: 76. https://doi.org/10.3390/app6030076
APA StyleHung, J.-P., Lin, W.-Z., Chen, Y.-J., & Luo, T.-L. (2016). Investigation of the Machining Stability of a Milling Machine with Hybrid Guideway Systems. Applied Sciences, 6(3), 76. https://doi.org/10.3390/app6030076





