Frequency-Dependent Amplitude Panning for the Stereophonic Image Enhancement of Audio Recorded Using Two Closely Spaced Microphones
Abstract
:1. Introduction
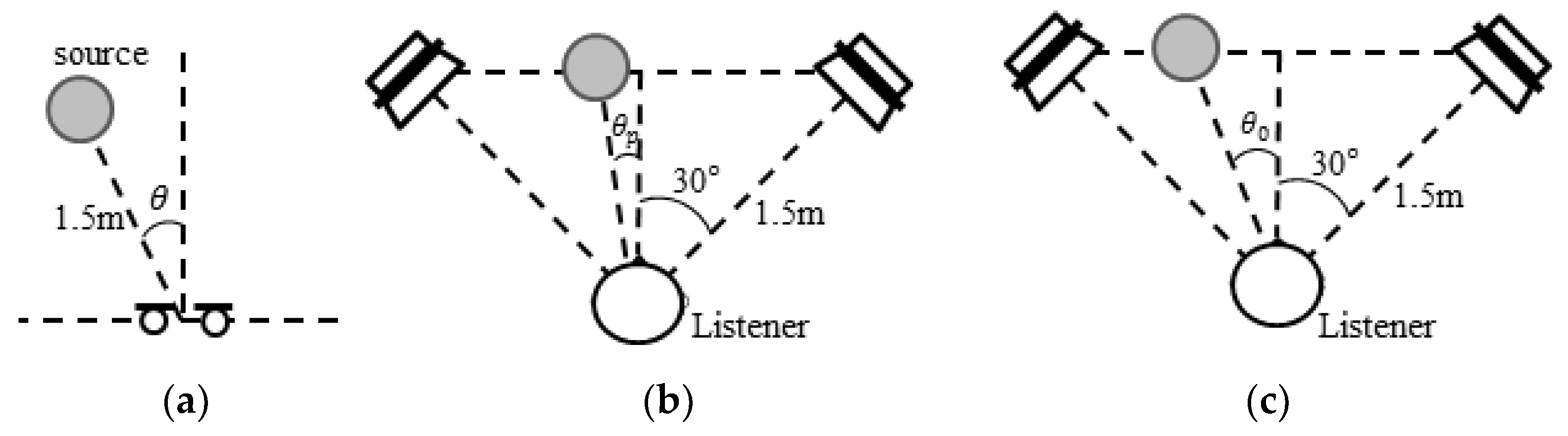
2. Conventional Stereophonic Image Enhancement
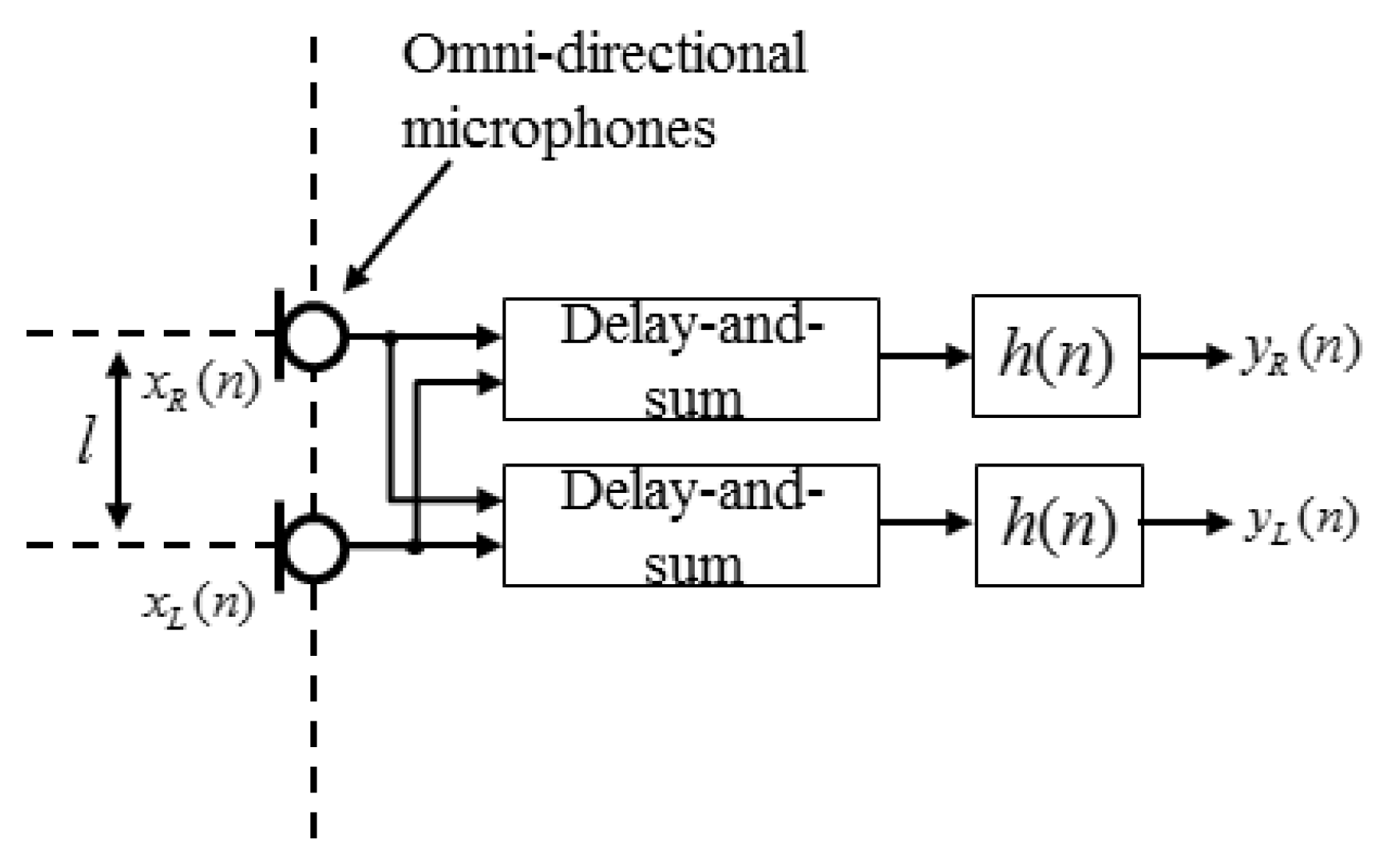
3. Proposed Frequency-Dependent Amplitude Panning for Stereophonic Image Enhancement
3.1. Overview
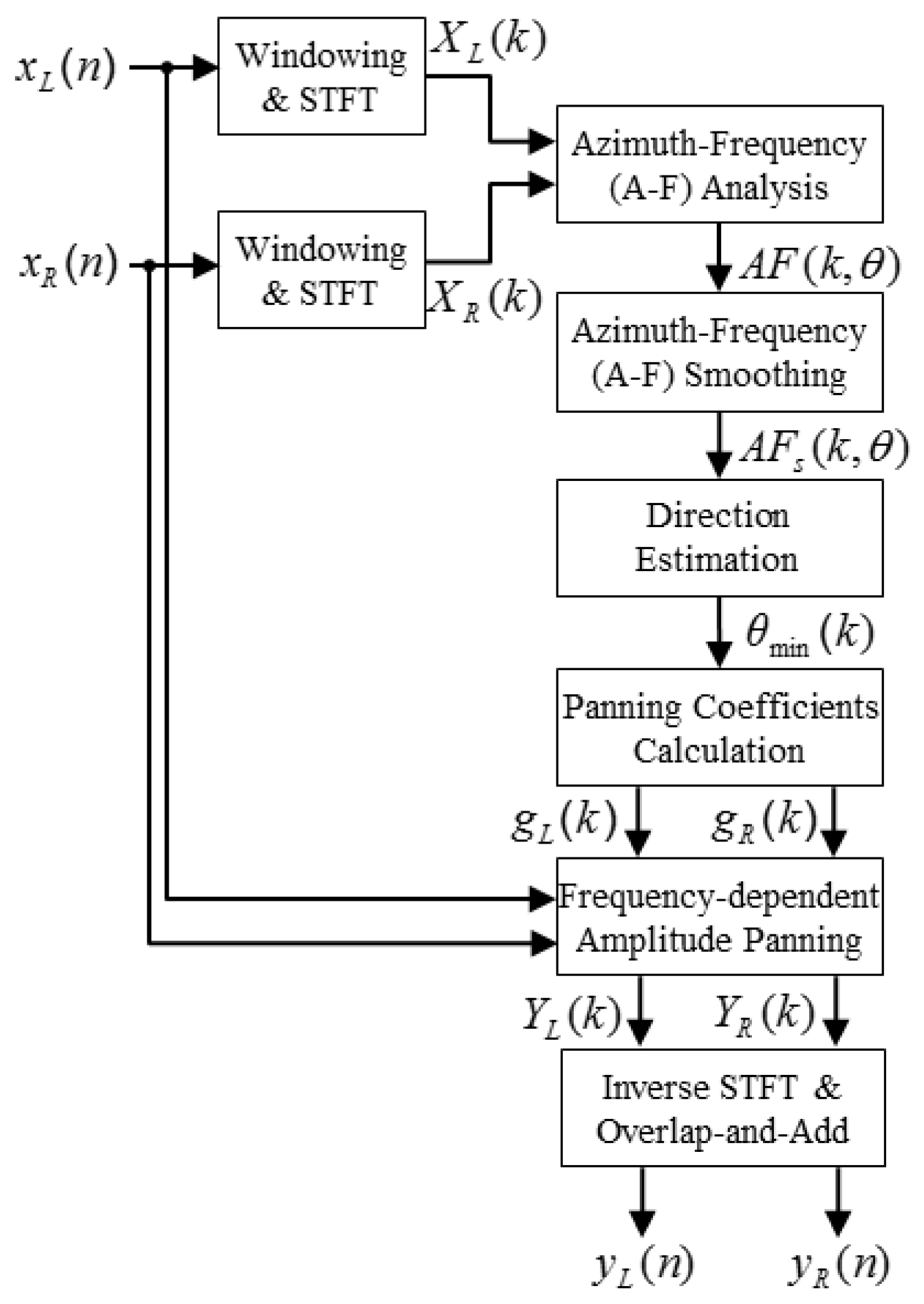
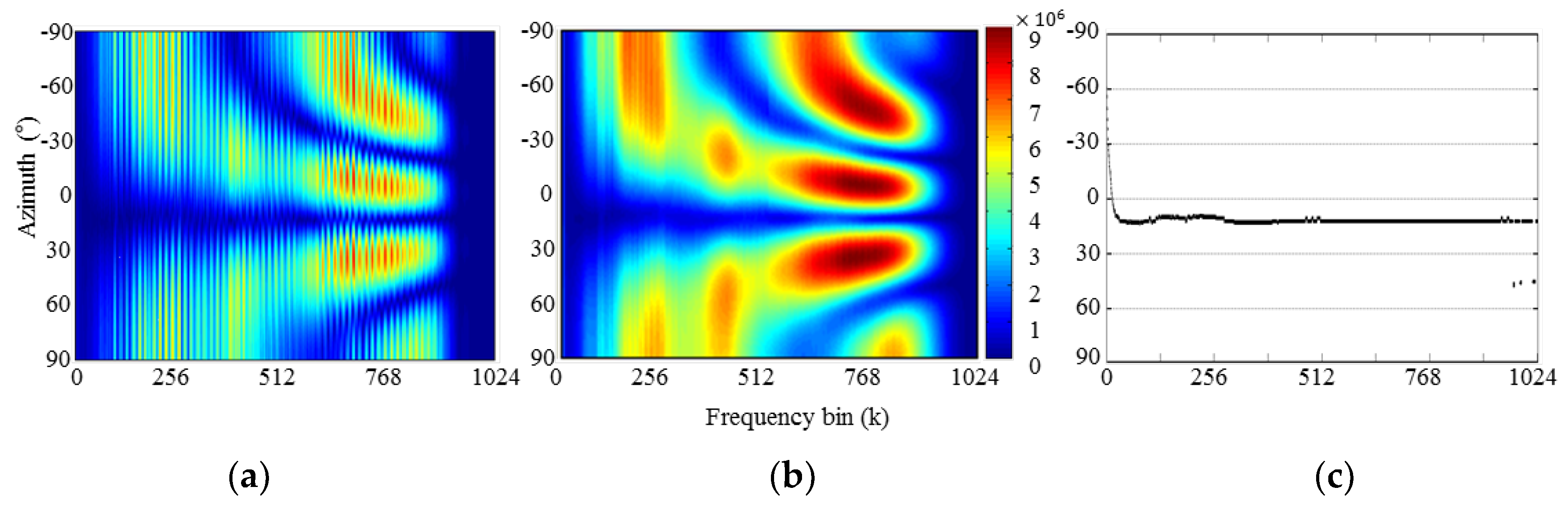
3.2. Azimuth-Frequency Analysis Using Time Delay
3.3. Frequency-Dependent Amplitude Panning
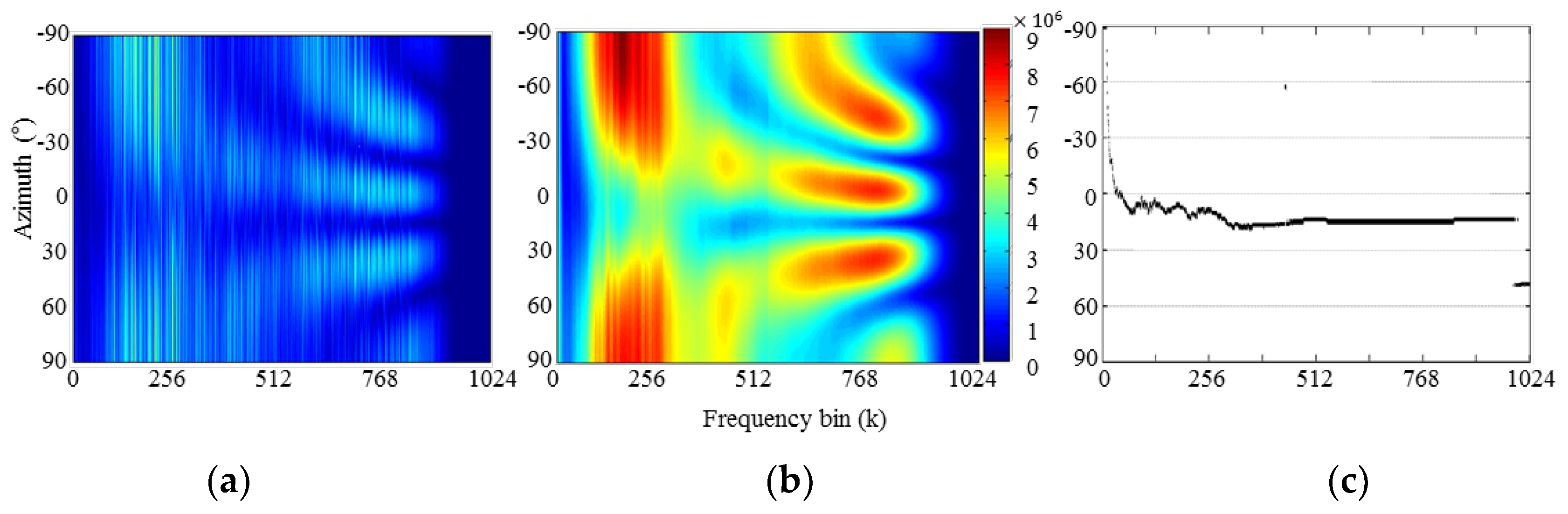
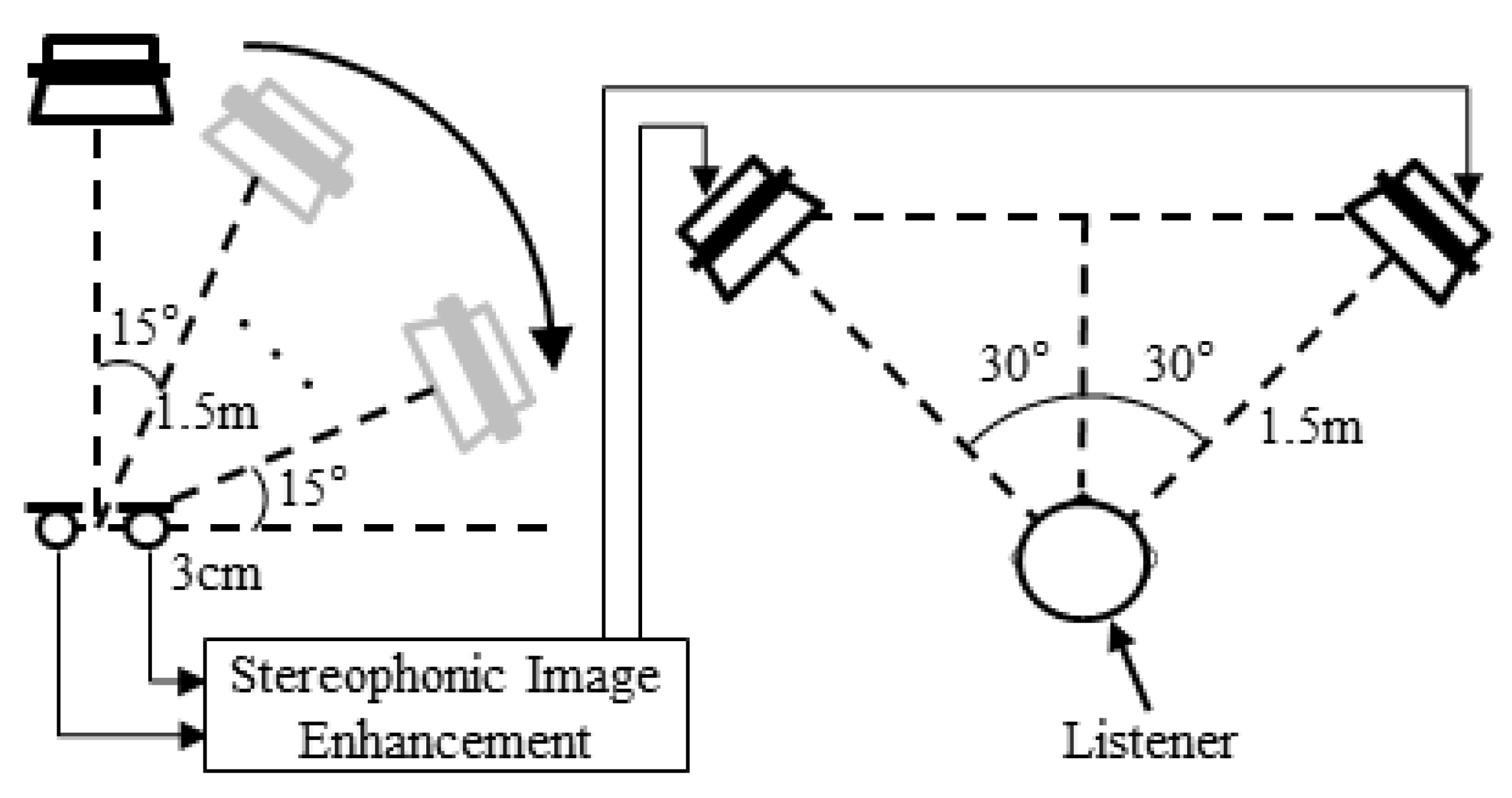
4. Performance Evaluation
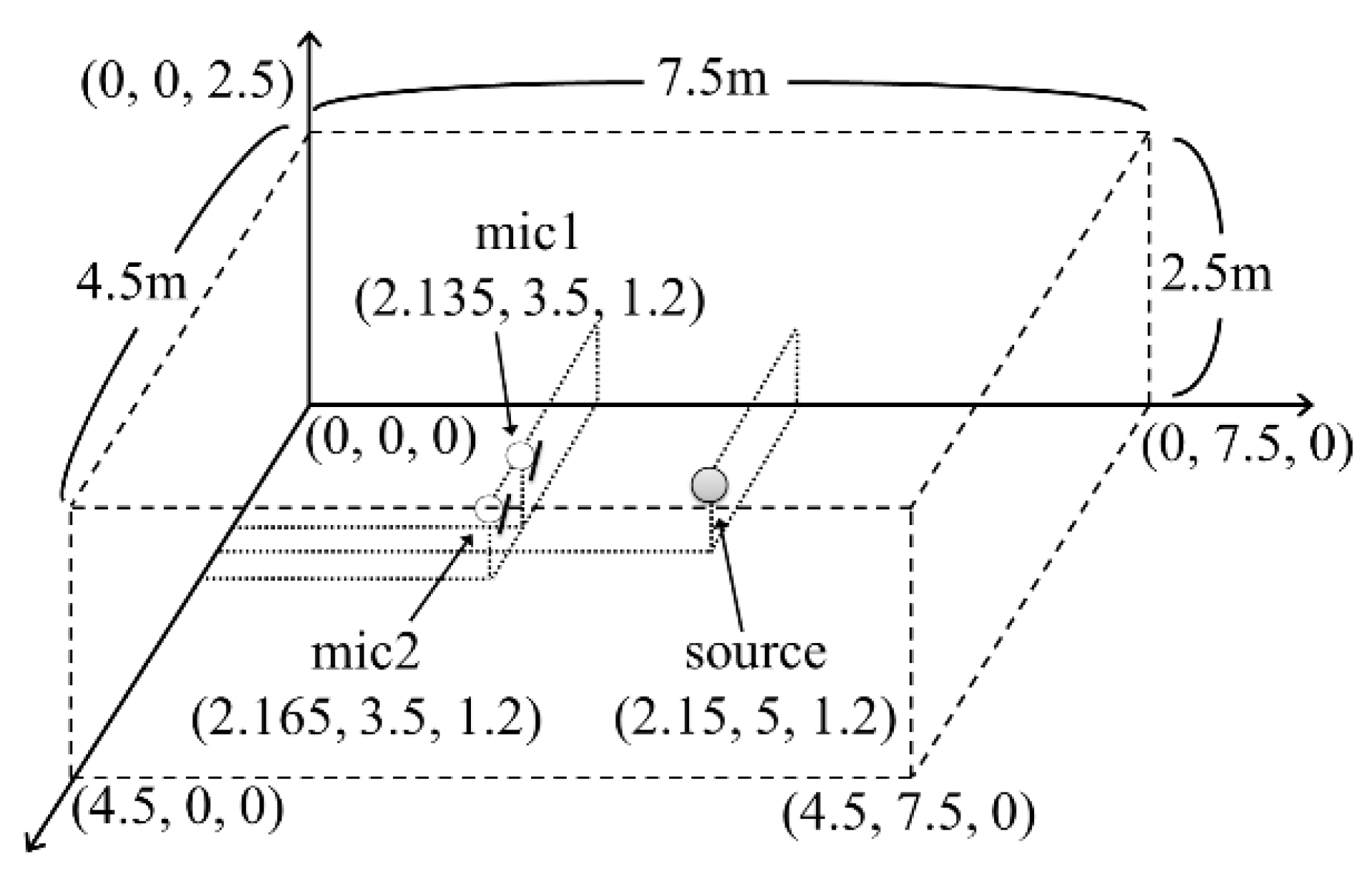
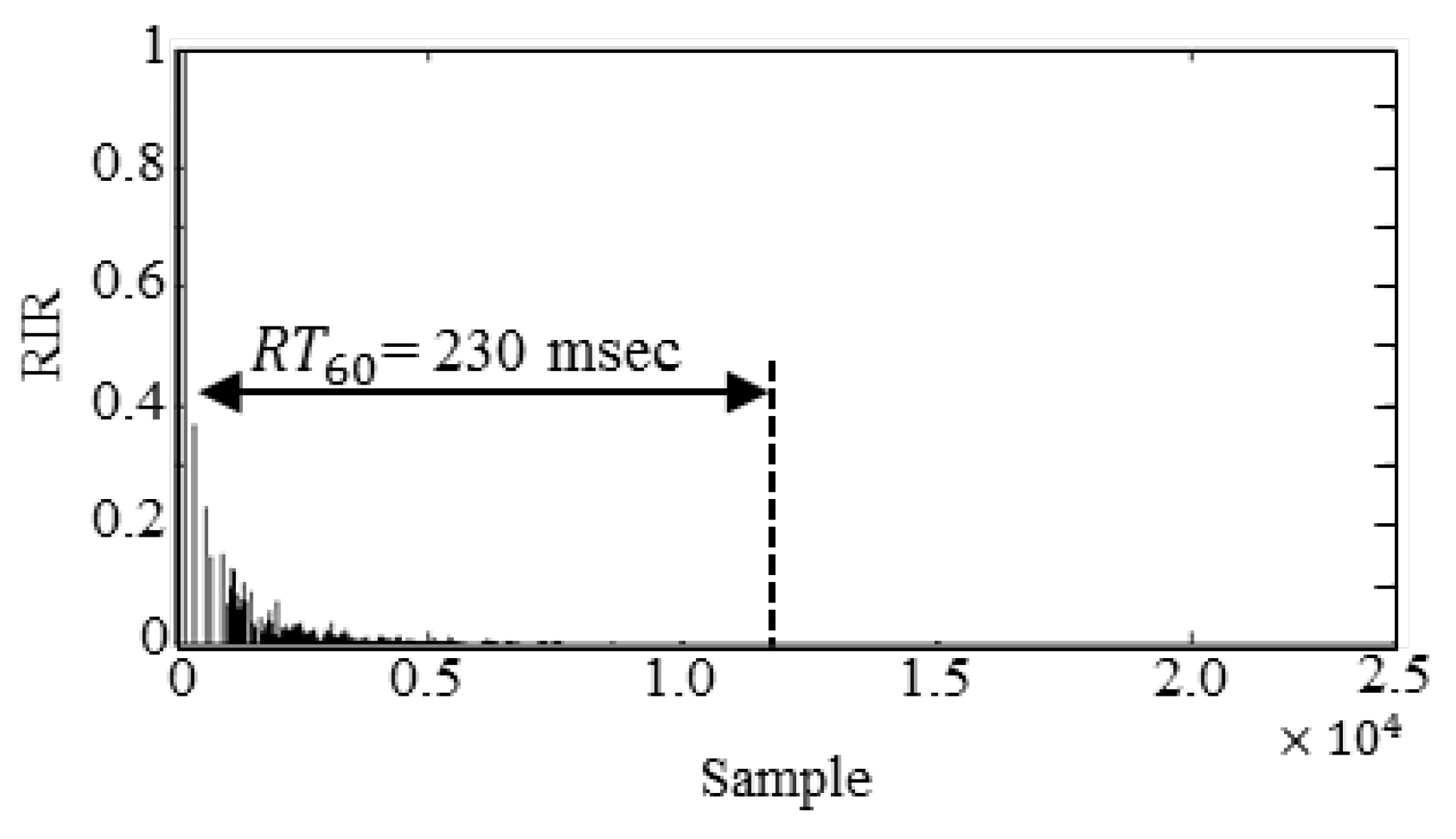
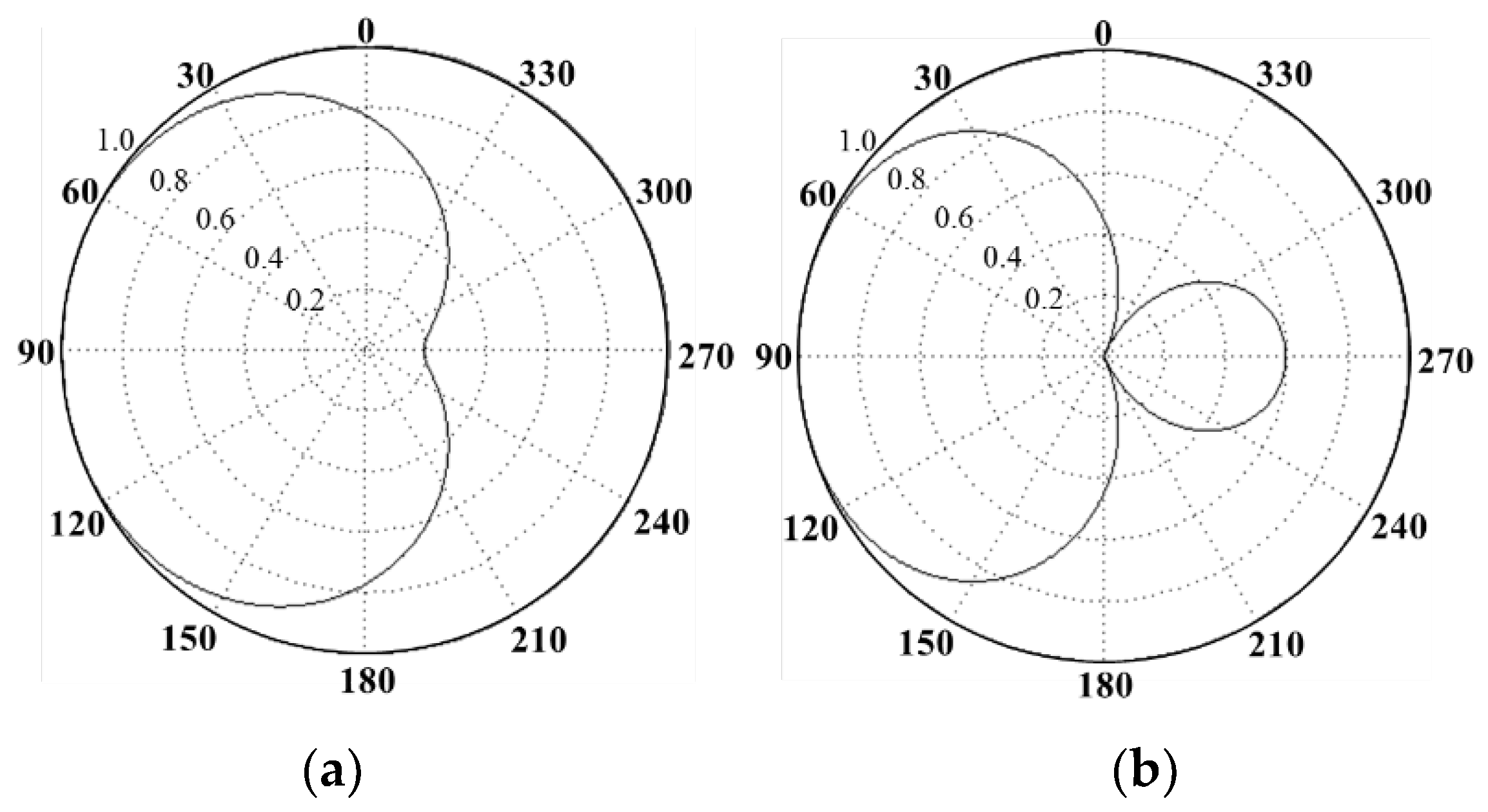
4.1. Directivity Pattern Performance
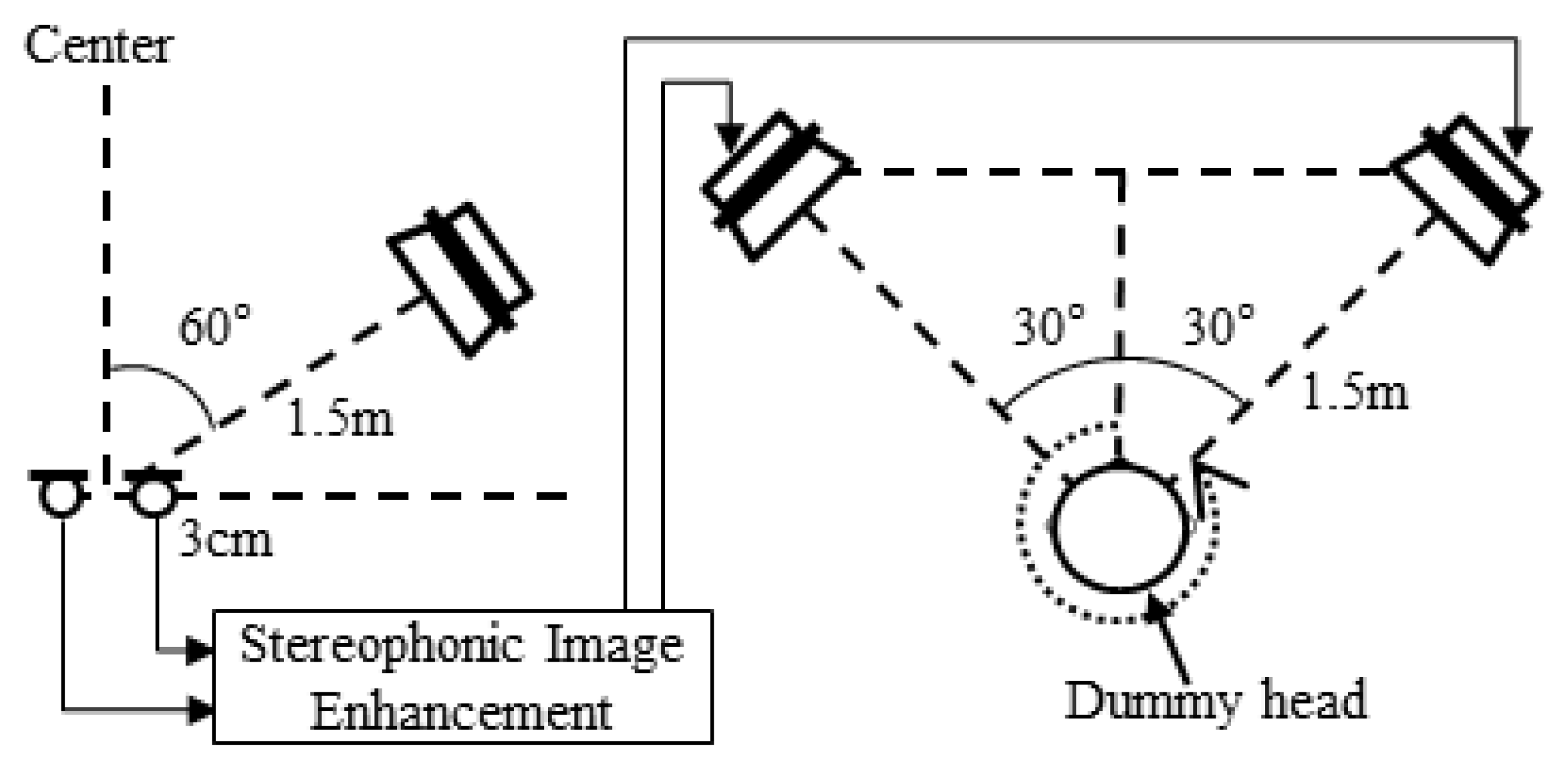
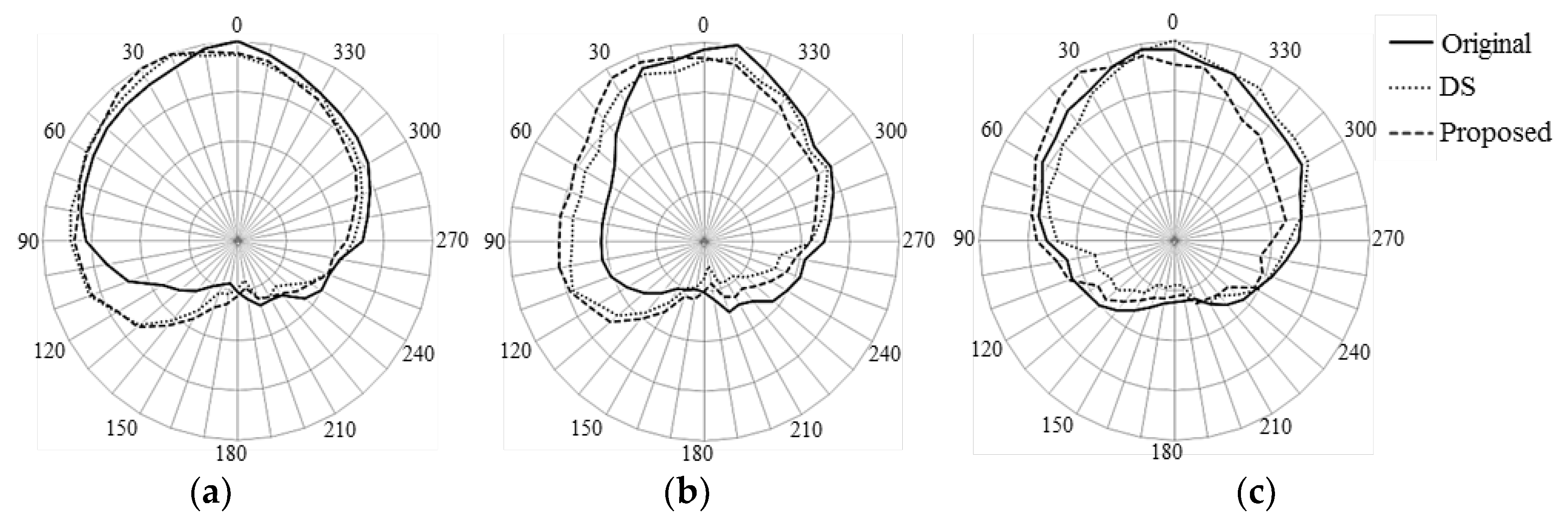
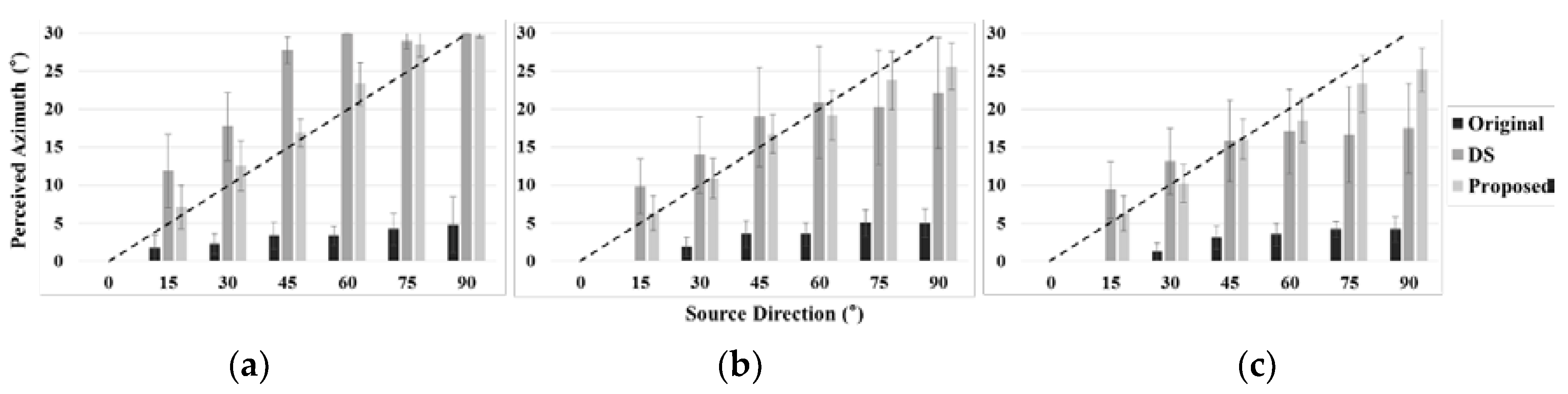
4.2. Perceived Direction Performance
| Track | Genre | Description |
|---|---|---|
| 49 | Speech | Female English speech |
| 66 | Orchestra | Wind ensemble, Stravinsky |
| 67 | Orchestra | Wind ensemble, Mozart |
| 69 | Pop music | Abba |
| 70 | Pop music | Eddie Rabbit |
4.3. Audio Quality Degradation
| Score | Description |
|---|---|
| 5 | Degradation is inaudible |
| 4 | Degradation is audible but not annoying |
| 3 | Degradation is slightly annoying |
| 2 | Degradation is annoying |
| 1 | Degradation is very annoying |
| Method | DS | Proposed | |
|---|---|---|---|
| Environment | |||
| Anechoic | 3.61 (0.2898) | 4.04 (0.2622) | |
| Convolutive | 3.31 (0.3147) | 3.97 (0.2581) | |
| Real Reverberant | 3.46 (0.2950) | 3.90 (0.2711) | |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Breebaart, J.; Faller, C. Spatial Audio Processing: MPEG Surround and Other Applications; John Wiley & Sons, Ltd.: Chichester, UK, 2007. [Google Scholar]
- Blauert, J. Spatial Hearing: The Psychophysics of Human Sound Localization; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Rumsey, F. Spatial quality evaluation for reproduced sound: Terminology, meaning, and a scene-based paradigm. J. Audio Eng. Soc. 2002, 50, 651–666. [Google Scholar]
- Rumsey, F. Spatial Audio; Focal Press: Woburn, MA, USA, 2001. [Google Scholar]
- Hibbing, M. XY and MS microphone techniques in comparison. J. Audio Eng. Soc. 1989, 37, 823–831. [Google Scholar]
- Bennett, J.C.; Barker, K.; Edeko, F.O. A new approach to the assessment of stereophonic sound system performance. J. Audio Eng. Soc. 1985, 33, 314–321. [Google Scholar]
- Kim, J.K.; Chun, C.J.; Kim, H.K. Design of a coincident microphone array for 5.1-channel audio recording using the mid-side recording technique. Adv. Sci. Technol. Lett. 2012, 14, 61–64. [Google Scholar]
- Dooley, W.; Streicher, T. MS stereo: A powerful technique for working in stereo. J. Audio Eng. Soc. 1982, 30, 707–718. [Google Scholar]
- Eargle, J. The Microphone Book; Focal Press: Oxford, UK, 2004. [Google Scholar]
- Menounou, P.; Papaefthymio, E.S. Shadowing of directional noise sources by finite noise barriers. Appl. Acoust. 2000, 71, 351–367. [Google Scholar] [CrossRef]
- Aarts, R.M. Phantom sources applied to stereo-base widening. J. Audio Eng. Soc. 2000, 48, 181–189. [Google Scholar]
- Umayahara, T.; Hokari, H.; Shimada, S. Stereo width control using interpolation and extrapolation of time-frequency representation. Audio Speech Lang. Process. IEEE Trans. 2006, 14, 1364–1377. [Google Scholar] [CrossRef]
- Faller, C. Conversion of two closely spaced omnidirectional microphone signals to an XY stereo signal. In Proceedings of the 129th AES Convention, San Francisco, CA, USA, 4–7 November 2010; p. 8188.
- Marsch, J.; Porschmann, C. Frequency dependent control of reverberation time for auditory virtual environments. Appl. Acoust. 2000, 61, 189–198. [Google Scholar] [CrossRef]
- Usher, J.; Woszczyk, W. Interaction of source and reverberance spatial imagery in multichannel loudspeaker audio. In Proceedings of the 118th AES Convention, Barcelona, Spain, 28–31 May 2005; p. 6370.
- Cobos, M.; Lopez, J.J. Method and Apparatus for Stereo Enhancement in Audio Recordings. PCT Patent PCT/ES2009/000409, 31 July 2009. [Google Scholar]
- Cobos, M.; Lopez, J.J. Interactive enhancement of stereo recordings using time-frequency selective panning. In Proceedings of the 40th Audio Engineering Society Conference, Tokyo, Japan, 8–10 October 2010; pp. 2–10.
- Barry, D.; Coyle, E.; Lawlor, B. Real-time sound source separation: Azimuth discrimination and resynthesis. In Proceedings of the 117th AES Convention, San Francisco, CA, USA, 28–31 October 2004; p. 6258.
- Bauer, B.B. Phasor analysis of some stereophonic phenomena. J. Acoust. Soc. Am. 1961, 33, 1536–1539. [Google Scholar] [CrossRef]
- P.800: Methods for Subjective Determination of Transmission Quality. Available online: https://www.itu.int/rec/T-REC-P.800-199608-I/en (accessed on 27 January 2016).
- Brandstein, M.; Ward, D.B. Microphone Arrays: Signal. Processing Techniques and Applications; Springer-Heidelberg: New York, NY, USA, 2001. [Google Scholar]
- Kennedy, R.A.; Abhayapala, P.T.D.; Ward, D.B.; Williamson, R.C. Nearfield broadband frequency invariant beamforming. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Atlanta, GA, USA, 7–10 May 1996; pp. 905–908.
- Duong, N.Q.K.; Vincent, E.; Gribonval, R. Under-determined reverberant audio source separation using local observed covariance and auditory-motivated time-frequency representation. Audio Speech Lang. Process. IEEE Trans. 2010, 18, 1830–1840. [Google Scholar] [CrossRef]
- Pulkki, V.; Karjalainen, M. Localization of amplitude-panned virtual sources I: Stereophonic panning. J. Audio Eng. Soc. 2001, 49, 739–752. [Google Scholar]
- Choi, T.S.; Park, Y.C.; Youn, D.H.; Lee, S.P. Virtual sound rendering in a stereophonic loudspeaker setup. Audio Speech Lang. Process. IEEE Trans. 2011, 19, 1962–1974. [Google Scholar]
- Pulkki, V. Virtual source positioning using vector base amplitude panning. J. Audio Eng. Soc. 1977, 45, 456–466. [Google Scholar]
- Allen, J.B.; Berkley, D.A. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 1979, 65, 943–951. [Google Scholar] [CrossRef]
- BS.775: Multichannel Stereophonic Sound System with and without Accompanying Picture. Available online: https://www.itu.int/rec/R-REC-BS.775/en (accessed on 27 January 2016).
- Product Information KU 100. Available online: http://www.coutant.org/ku100/ku100.pdf (accessed on 27 January 2016).
- Sound Quality Assessment Material Recordings for Subjective Tests—Users’ Handbook for the EBU-SQAM Compact Disc. Available online: https://tech.ebu.ch/docs/tech/tech3253.pdf (accessed on 27 January 2016).
- Chun, C.J.; Kim., H.K. Some Audio Samples Processed by Frequency-Dependent Amplitude Panning for the Stereophonic Image Enhancement. Available online: http://hucom.gist.ac.kr/2016ApplSci/sample.html (accessed on 27 January 2016).
- Spanias, A.; Painter, T.; Atti, V. Audio Signal. Processing and Coding; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chun, C.J.; Kim, H.K. Frequency-Dependent Amplitude Panning for the Stereophonic Image Enhancement of Audio Recorded Using Two Closely Spaced Microphones. Appl. Sci. 2016, 6, 39. https://doi.org/10.3390/app6020039
Chun CJ, Kim HK. Frequency-Dependent Amplitude Panning for the Stereophonic Image Enhancement of Audio Recorded Using Two Closely Spaced Microphones. Applied Sciences. 2016; 6(2):39. https://doi.org/10.3390/app6020039
Chicago/Turabian StyleChun, Chan Jun, and Hong Kook Kim. 2016. "Frequency-Dependent Amplitude Panning for the Stereophonic Image Enhancement of Audio Recorded Using Two Closely Spaced Microphones" Applied Sciences 6, no. 2: 39. https://doi.org/10.3390/app6020039
APA StyleChun, C. J., & Kim, H. K. (2016). Frequency-Dependent Amplitude Panning for the Stereophonic Image Enhancement of Audio Recorded Using Two Closely Spaced Microphones. Applied Sciences, 6(2), 39. https://doi.org/10.3390/app6020039







