Study on the Load Distribution and Dynamic Characteristics of a Thin-Walled Integrated Squirrel-Cage Supporting Roller Bearing
Abstract
:1. Introduction
2. Model Design
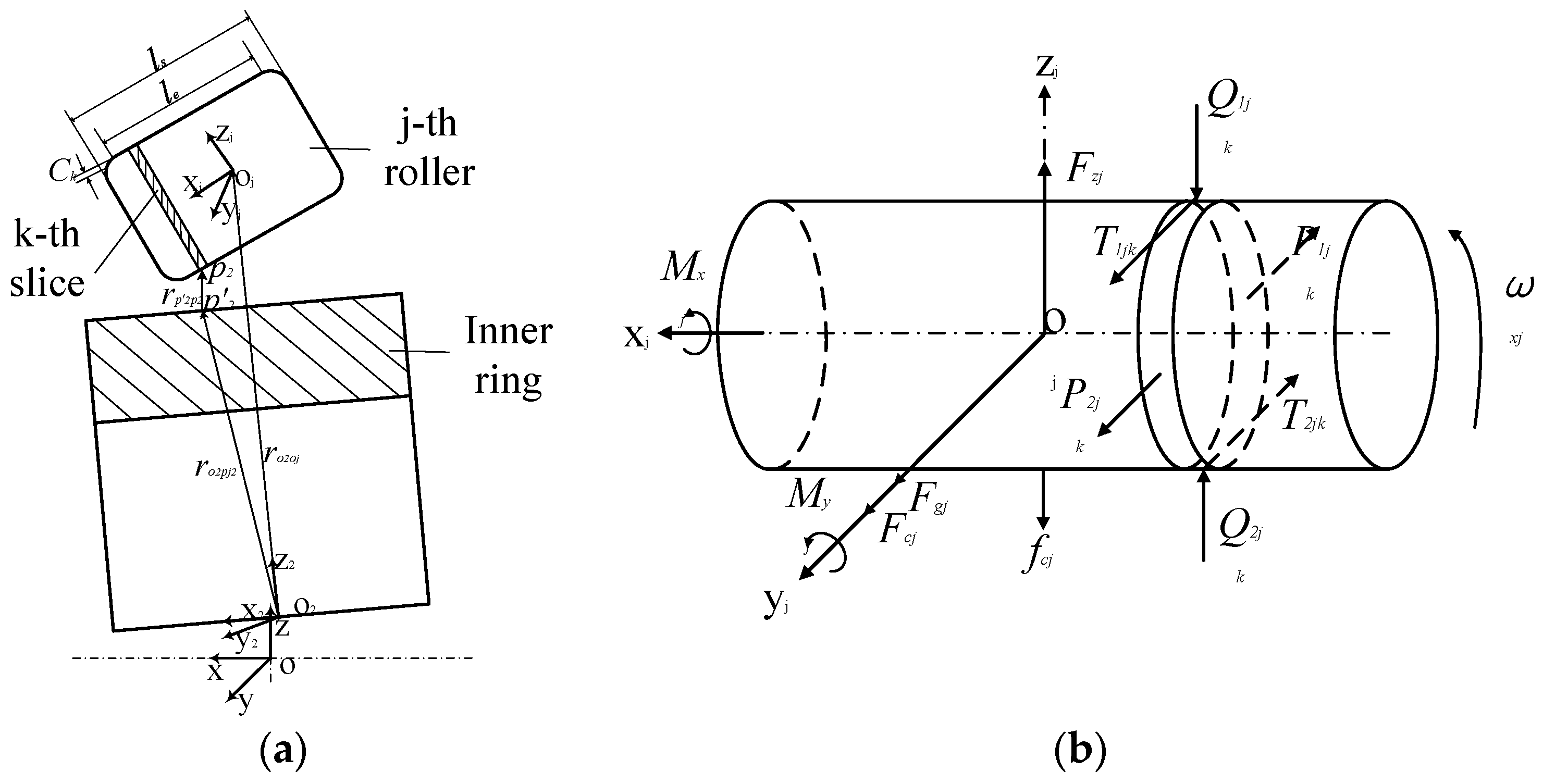
2.1. Modified Noncircular Rolling Bearing Quasi-Dynamic Model
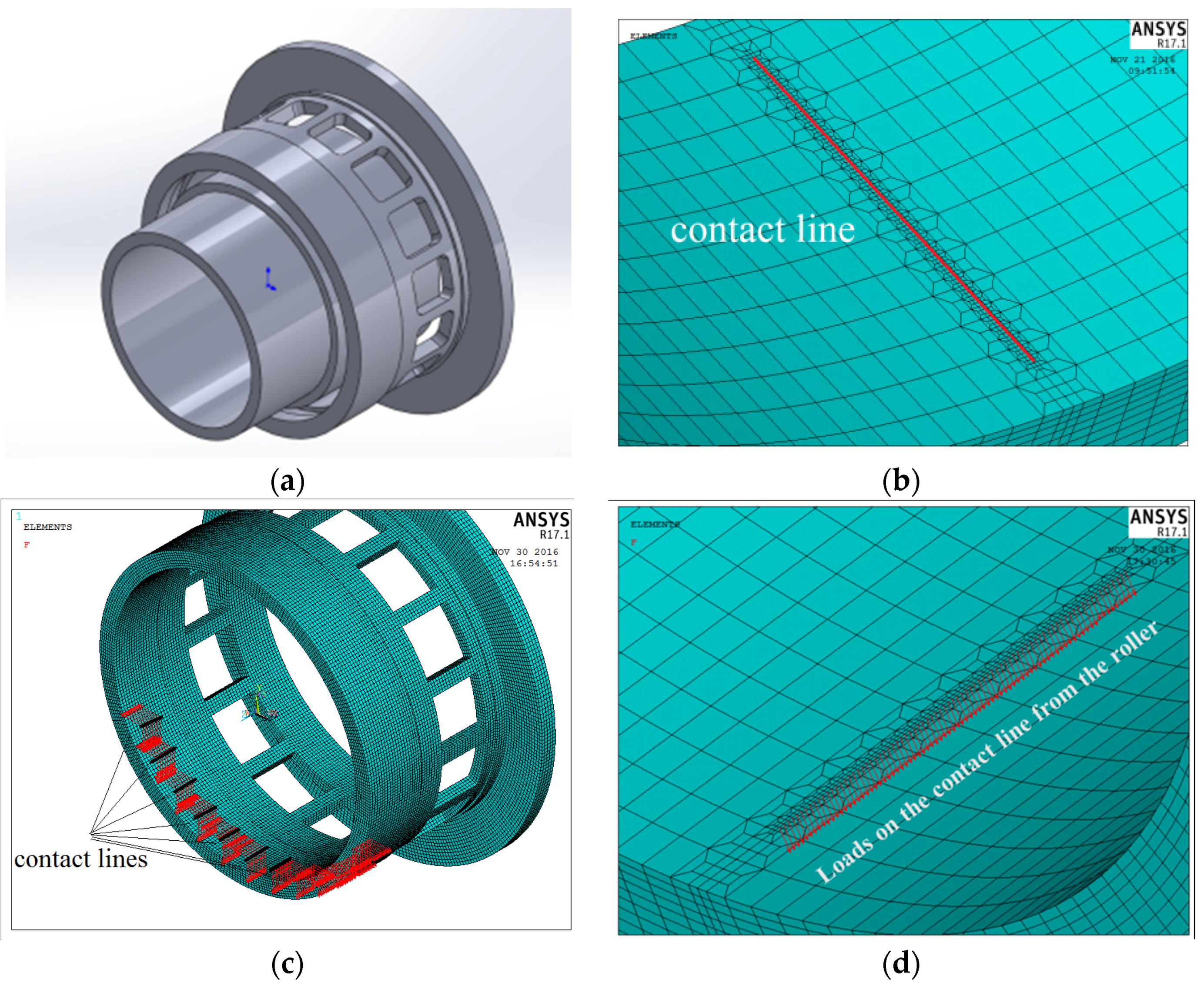
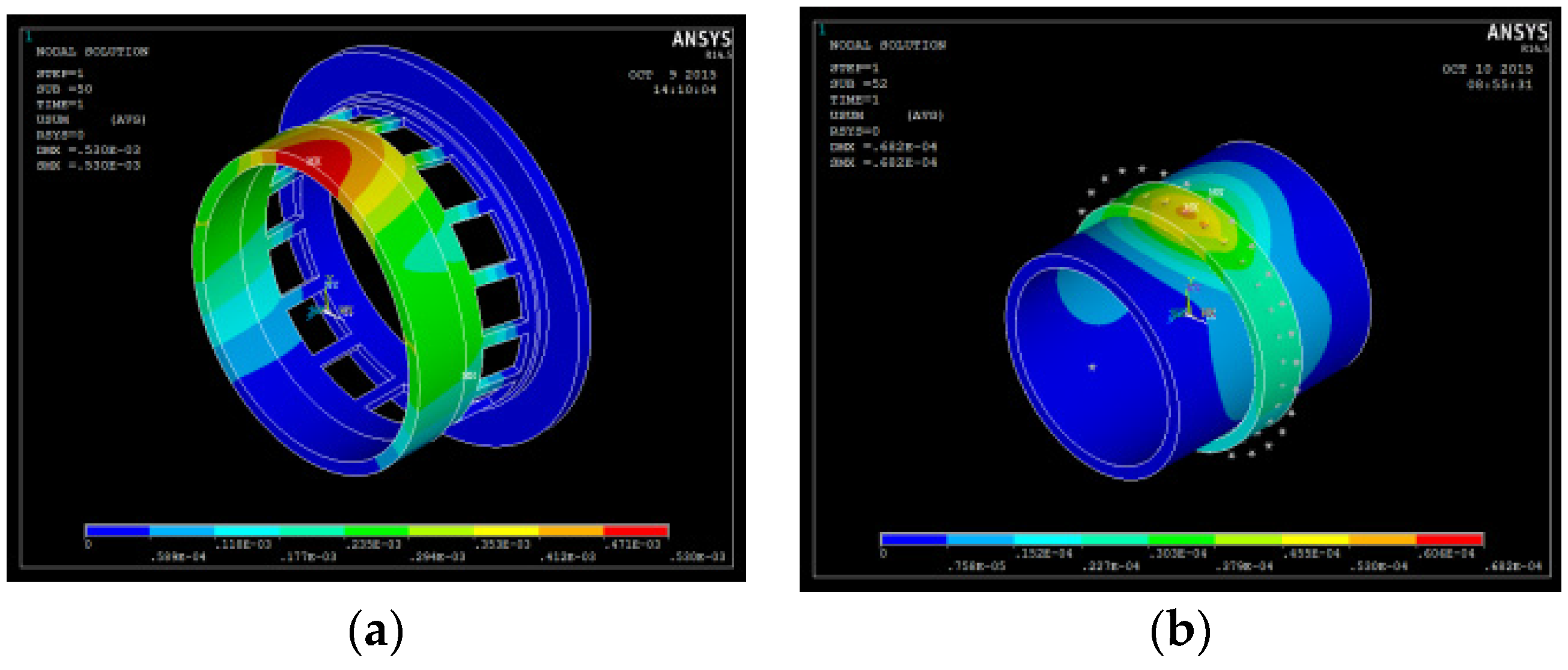
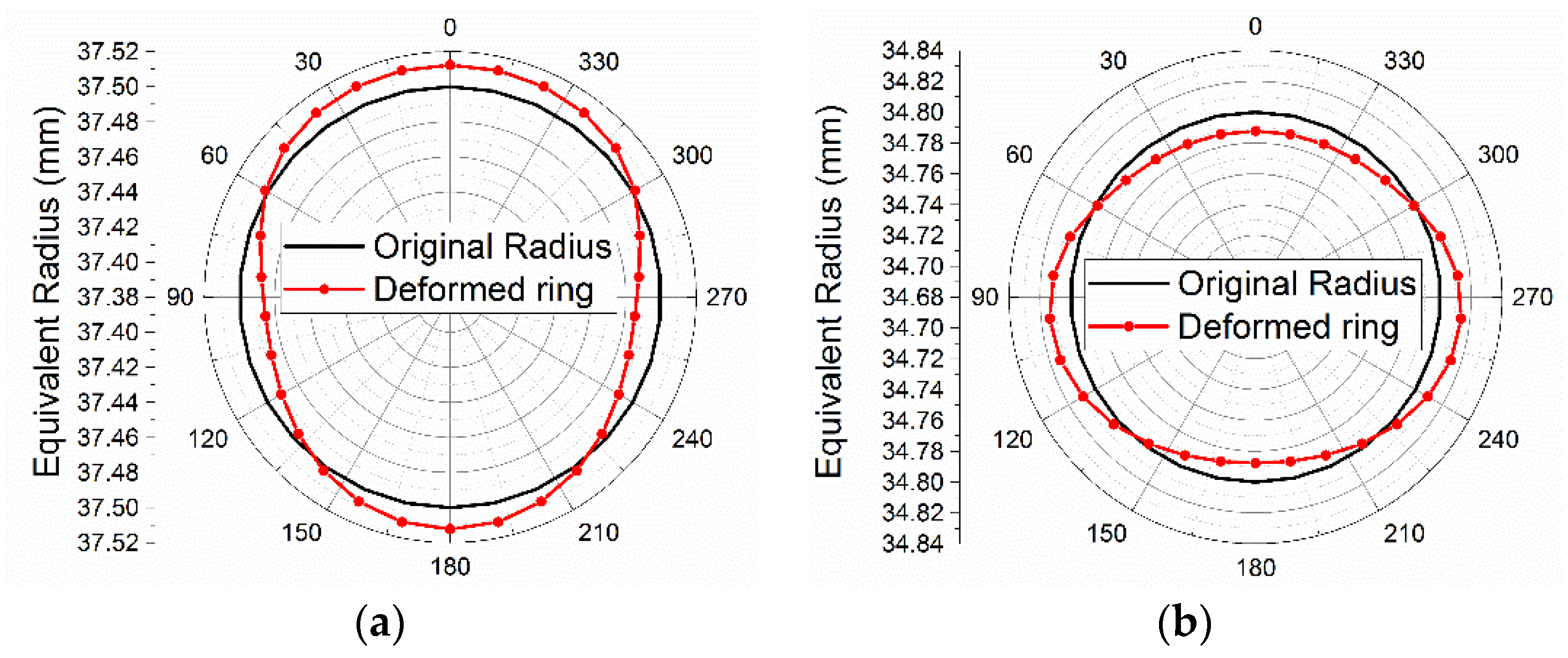
2.2. Finite Element Analysis of Integrated Squirrel-Cage Structural Deformation
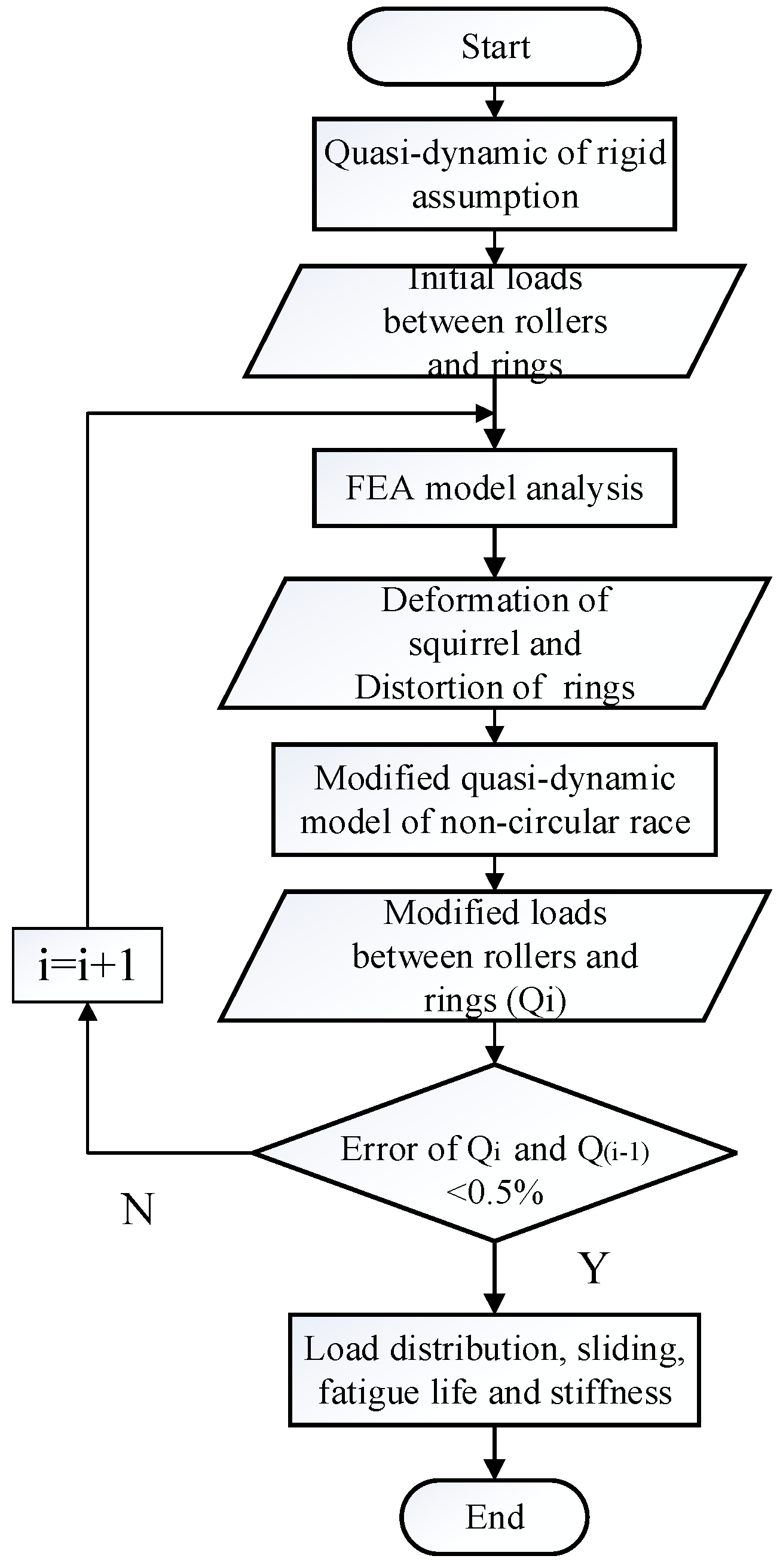
2.3. Iterative Quasi-Dynamic FEA Model
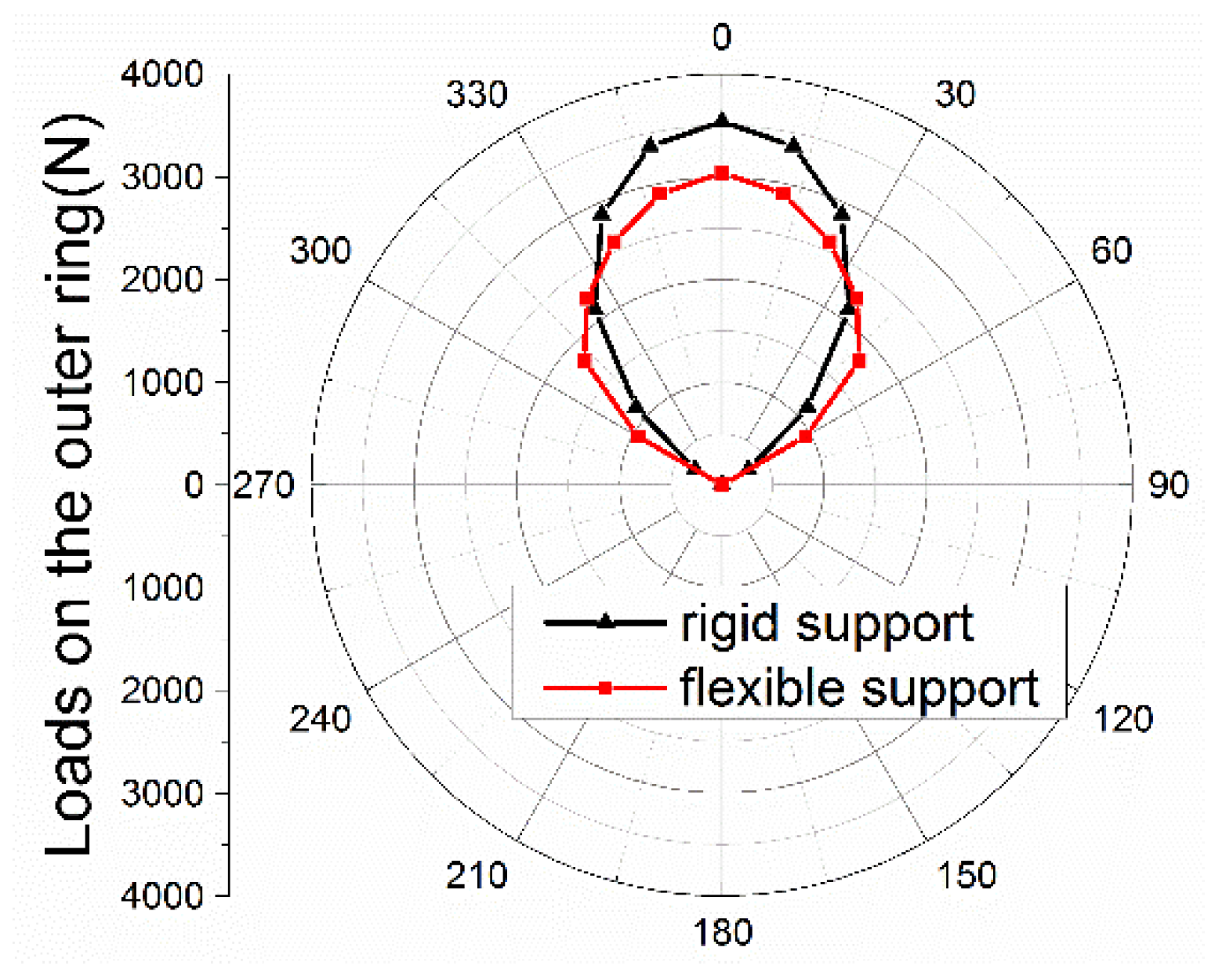
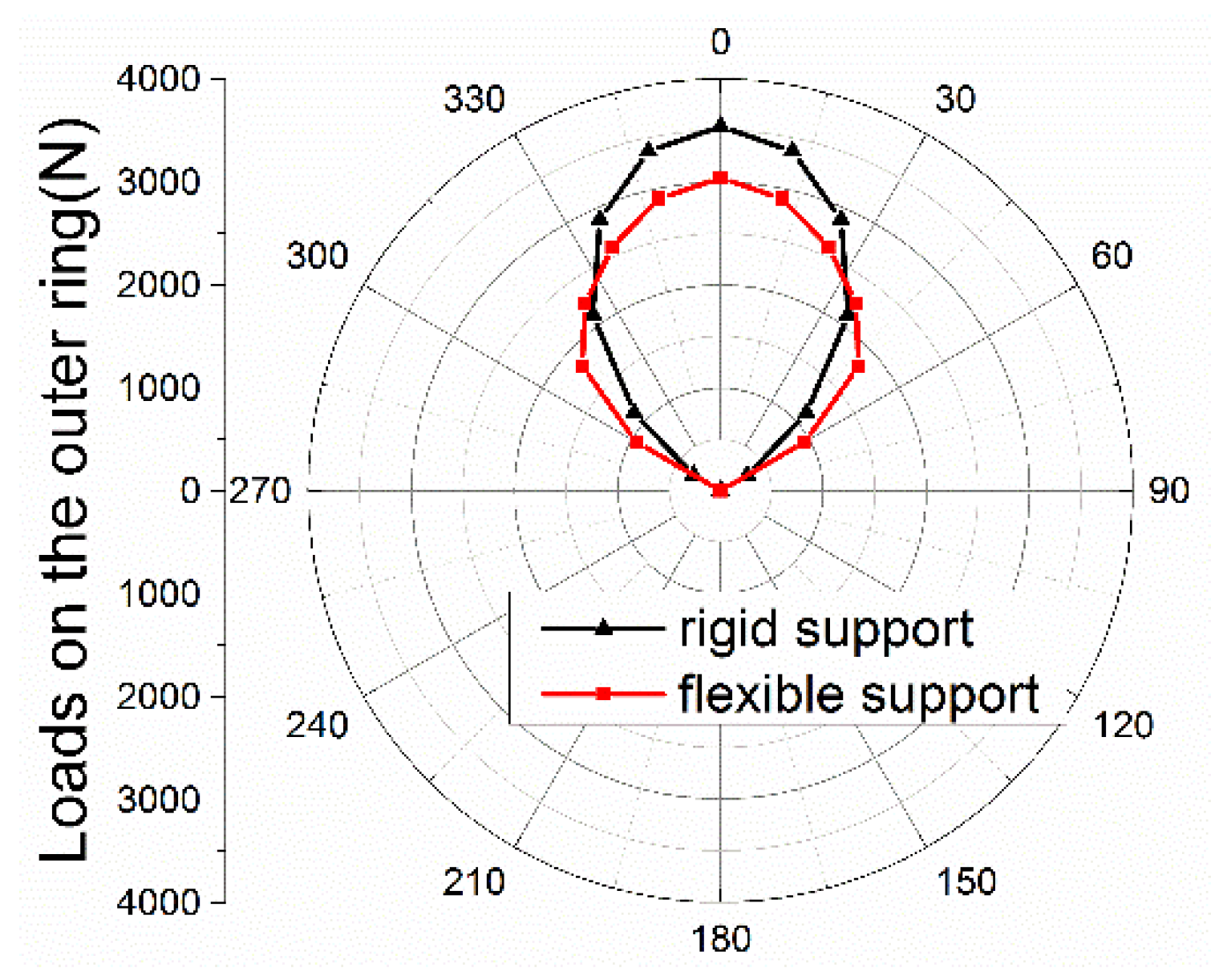
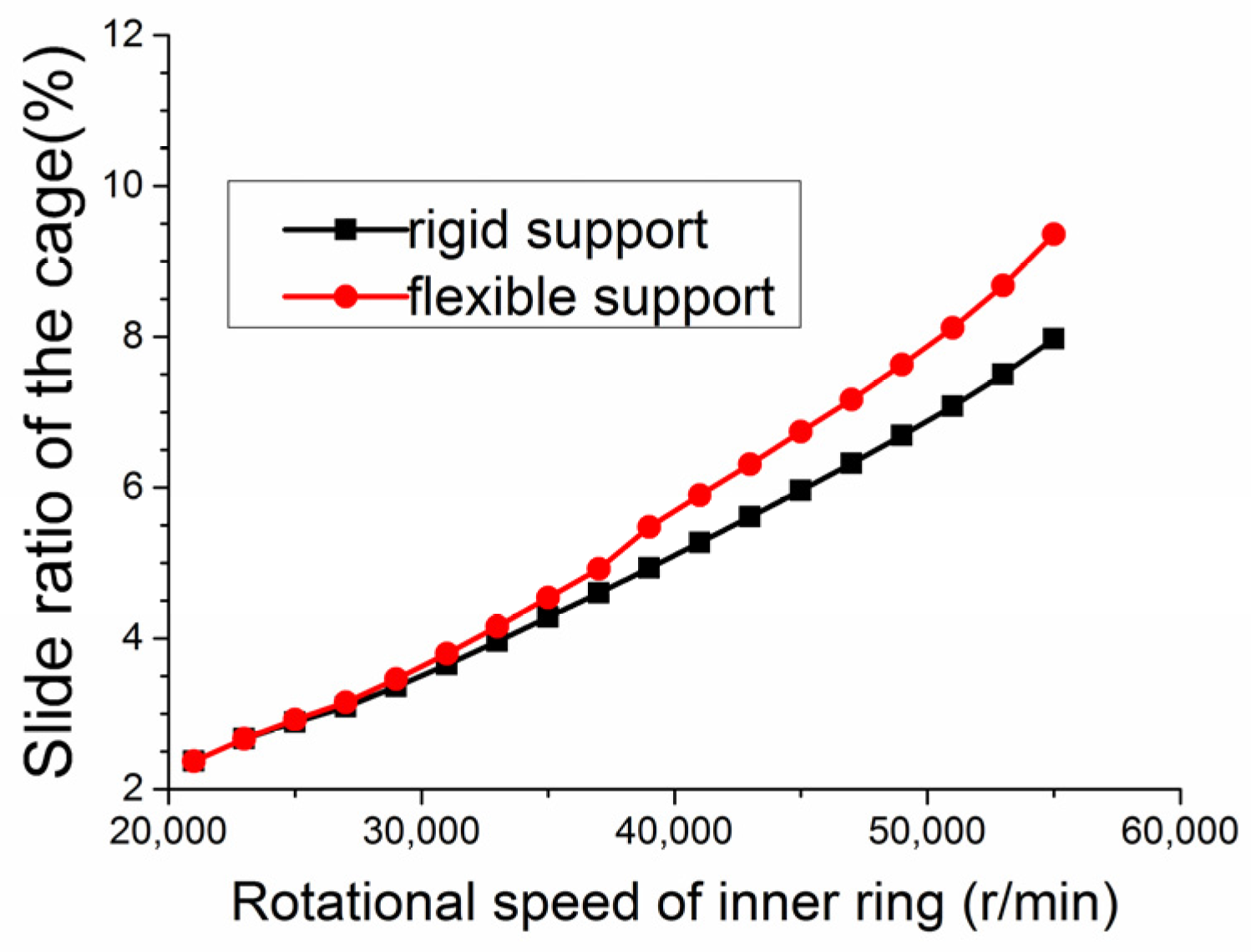
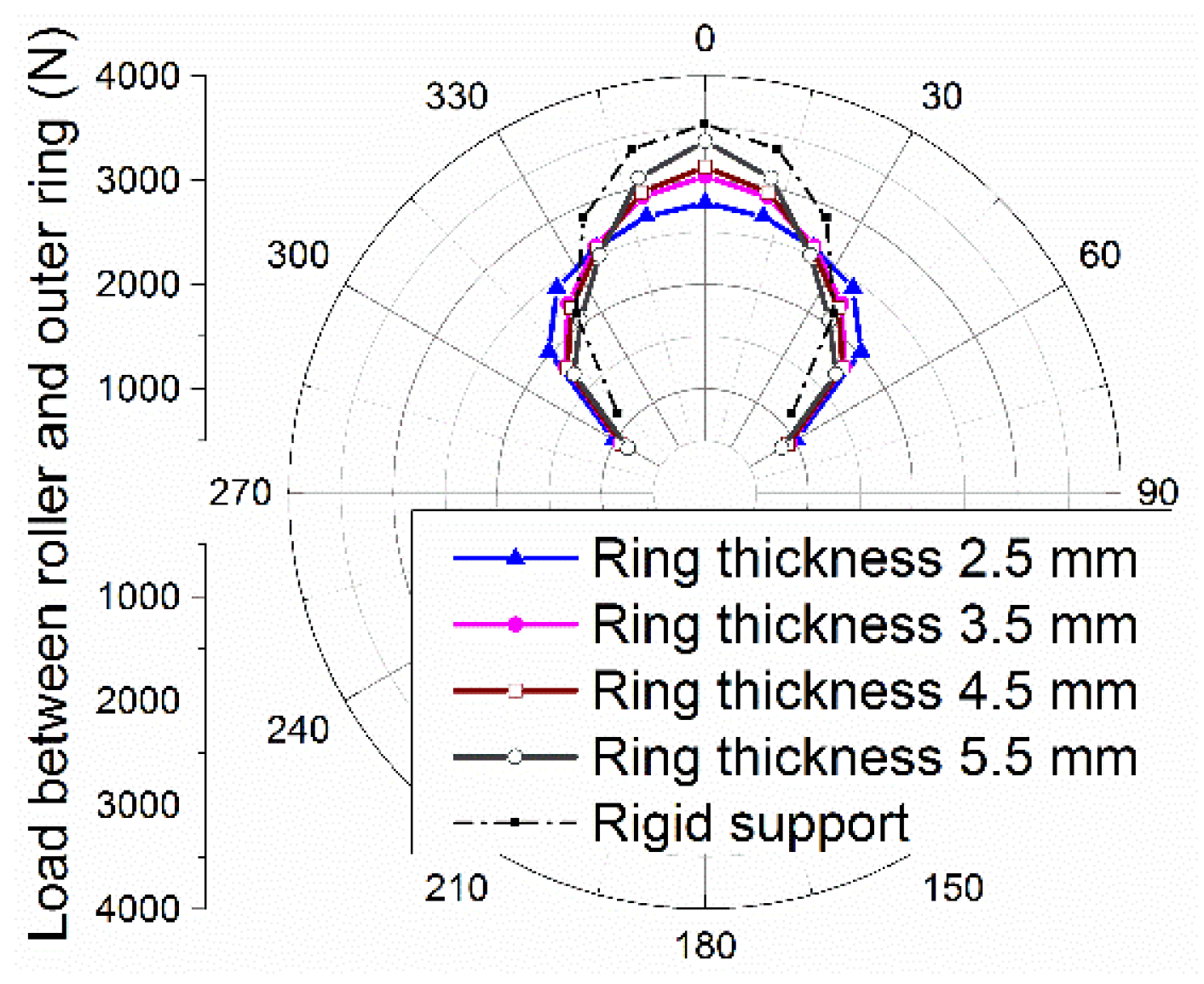
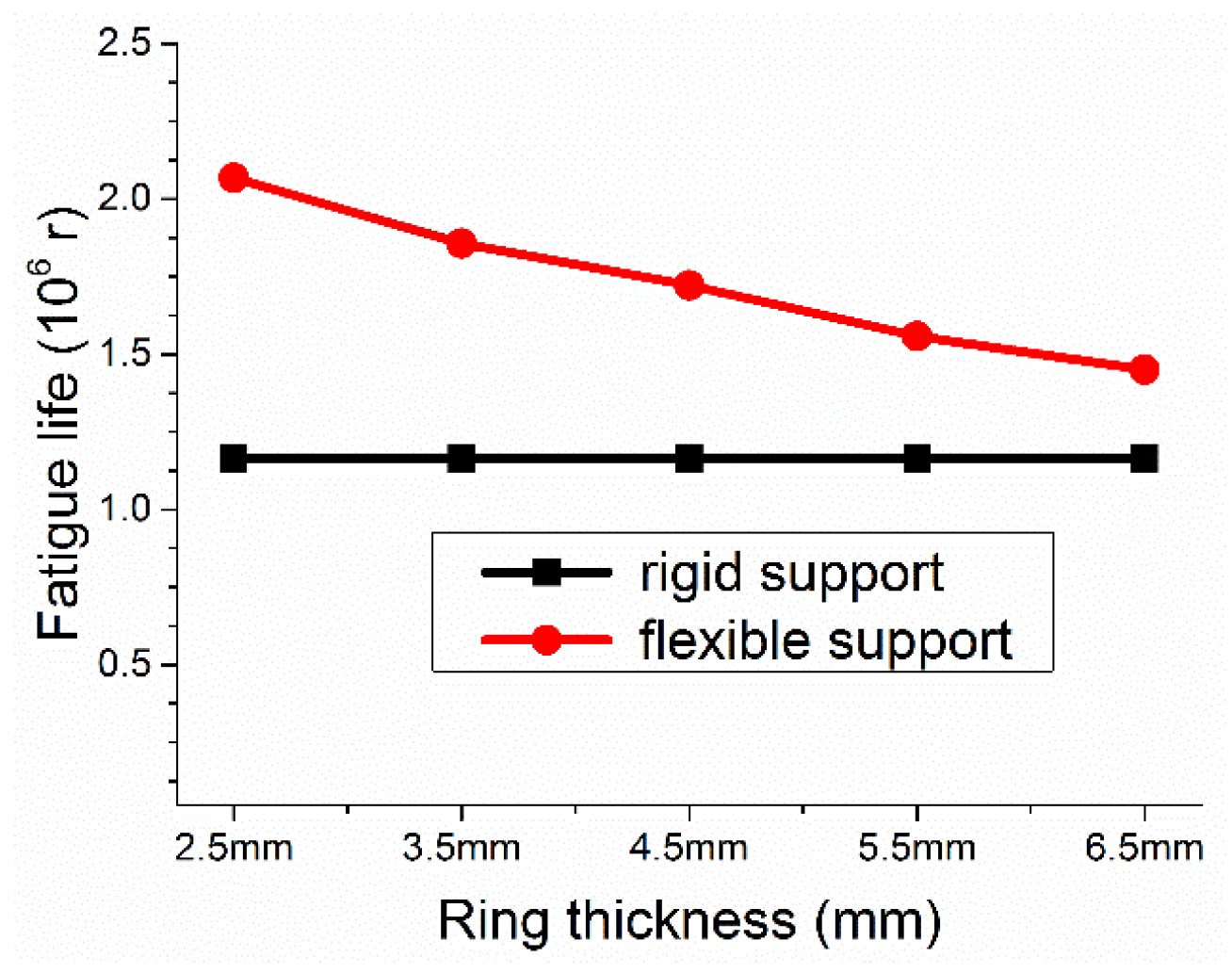
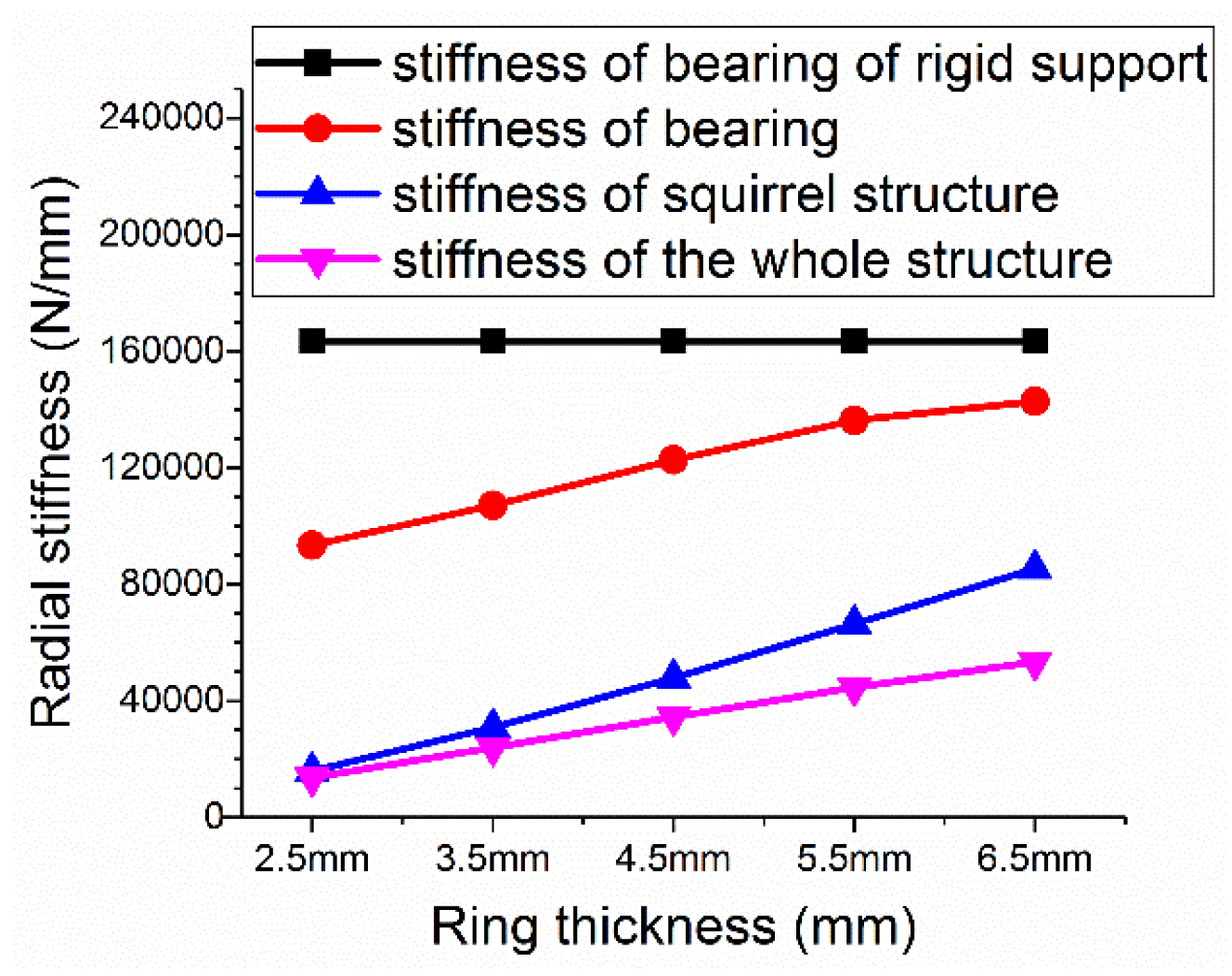
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhao, L.; Sun, Y. The fault diagnosis of aero-engine main shaft bearings. Aircr. Des. 2010, 4, 46–50. [Google Scholar]
- Harris, T.A. Rolling Bearing Anaysis; John Wiley & Sons. Inc.: New York, NY, USA, 2007. [Google Scholar]
- Ebert, F.-J. An Overview of Performance Characteristics, Experiences and Trends of Aerospace Engine Bearings Technologies. Chin. J. Aeronaut. 2007, 20, 378–384. [Google Scholar] [CrossRef]
- Hakan, A.; Aydin, B.; Hasan, S. An investigation of tribological behaviors of dynamically loaded non-grooved and micro-grooved journal bearings. Tribol. Int. 2013, 58, 12–19. [Google Scholar]
- Oswald, F.B.; Zaretsky, E.V.; Poplawski, J.V. Interference-Fit Life Factors for Ball Bearings. Tribol. Trans. 2010, 54, 1–20. [Google Scholar] [CrossRef]
- Broschard, J. Analysis of an improved planetary gear transmission bearing. ASME Trans. J. Basic Eng. 1964, 86, 457–461. [Google Scholar]
- Shen, Y.; Zhang, T. Vibration Analysis of Flexible Rolling Bearing. Mech. Sci. Technol. Aerosp. Eng. 1995, 5, 1–6. [Google Scholar]
- Yao, T.; Chi, Y.; Huang, Y. Research on flexibility of bearing rings for multibody contact dynamics of rolling bearings. Procedia Eng. 2012, 31, 586–594. [Google Scholar] [CrossRef]
- Lostado, R.; Martinez, R.F. Determination of the contact stresses in double-row tapered roller bearings using the finite element method, experimental analysis and analytical models. J. Mech. Sci. Technol. 2015, 29, 4645–4656. [Google Scholar] [CrossRef]
- Ignacio Amasorrain, J.; Sagartzazu, X.; Damian, J. Load distribution in a four contact-point slewing bearing. Mech. Mach. Theory 2003, 38, 479–496. [Google Scholar] [CrossRef]
- Kania, L. Modelling of rollers in calculation of slewing bearing with the use of finite elements. Mech. Mach. Theory 2006, 41, 1359–1376. [Google Scholar] [CrossRef]
- Olave, M.; Sagartzazu, X.; Damian, J.; Serna, A. Design of four contact-point slewing bearing with a new load distribution procedure to account for structural stiffness. J. Mech. Des. 2010, 132. [Google Scholar] [CrossRef]
- Shu, J.; Wang, L.; Mao, Y.; Ding, Y. Iterative FEA Method for Load Distribution of Flexible Supporting Thin-section Ball Bearing. J. Harbin Inst. Technol. 2015, 22, 9–14. [Google Scholar]
- Ni, Y.; Liu, W.; Deng, S.; Jiao, Y.; Liang, B. Performance analysis of thin wall angular contact ball bearings considering the ferrule deformation. J. Aerosp. Power 2010, 25, 1432–1436. [Google Scholar]
- Lostado, R.; Martínez-De-Pisón, F.J.; Pernía, A.; Alba, F.; Blanco, J. Combining regression trees and the finite element method to define stress models of highly non-linear mechanical systems. J. Strain Anal. Eng. Des. 2009, 44, 491–502. [Google Scholar] [CrossRef]
- Cui, L.; Wang, L.; Zheng, D. Analysis on dynamic characteristics of aero-engine high-speed roller bearings. Acta Aeronaut. Astronaut. Sin. 2008, 29, 492–498. [Google Scholar]
- Harris, T.A. An Analytical Investigation of Cylindrical Roller Bearings Having Annular Rollers. Tribol. Trans. 1967, 10, 235–242. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, B. Investigation into the Traction Coefficient in Elastohydro-dynamic Lubrication. Tribotest 2004, 11, 113–124. [Google Scholar] [CrossRef]
- Lostado, R.; García, R.E. Optimization of operating conditions for a double-row tapered roller bearing. Int. J. Mech. Mater. Des. 2016, 56, 1–21. [Google Scholar] [CrossRef]

| Parameter | Value/mm | Parameter | Value |
|---|---|---|---|
| Inner ring | 59.6 | inner ring thickness (mm) | 5 |
| Outer ring | 82.2 | outer ring thickness (mm) | 3.6 |
| Roller quantity | 30 | length of squirrel-cage (mm) | 10.25 |
| Roller diameter | 5 | shift thickness (mm) | 4 |
| Roller length | 5 | radial load (N) | 19,621.1 |
| clearance | 0.05 | Speed (r/min) | 38,000 |
| Component | Elastic Modulus (E)/GPa | Poisson Ratio (υ) | Density (ρ)/kg/m3 | Thermal Expansion Coefficient (α) |
|---|---|---|---|---|
| Shaft | 179 | 0.281 | 8240 | 0.0138 |
| Inner ring | 203 | 0.28 | 7850 | 0.0112 |
| Roller | 209 | 0.3 | 7860 | 0.0119 |
| Outer ring-squirrel Cage | 203 | 0.28 | 7850 | 0.0112 |
| Shaft | Inner Ring | Roller | Outer Ring and Squirrel-Cage |
|---|---|---|---|
| 230 °C | 220 °C | 226 °C | 218 °C |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Y.; Wang, L.; Zhang, C. Study on the Load Distribution and Dynamic Characteristics of a Thin-Walled Integrated Squirrel-Cage Supporting Roller Bearing. Appl. Sci. 2016, 6, 415. https://doi.org/10.3390/app6120415
Mao Y, Wang L, Zhang C. Study on the Load Distribution and Dynamic Characteristics of a Thin-Walled Integrated Squirrel-Cage Supporting Roller Bearing. Applied Sciences. 2016; 6(12):415. https://doi.org/10.3390/app6120415
Chicago/Turabian StyleMao, Yuze, Liqin Wang, and Chuanwei Zhang. 2016. "Study on the Load Distribution and Dynamic Characteristics of a Thin-Walled Integrated Squirrel-Cage Supporting Roller Bearing" Applied Sciences 6, no. 12: 415. https://doi.org/10.3390/app6120415
APA StyleMao, Y., Wang, L., & Zhang, C. (2016). Study on the Load Distribution and Dynamic Characteristics of a Thin-Walled Integrated Squirrel-Cage Supporting Roller Bearing. Applied Sciences, 6(12), 415. https://doi.org/10.3390/app6120415





