Seismic Responses of a Cable-Stayed Bridge with Consideration of Uniform Temperature Load
Abstract
:1. Introduction
2. Description of the Prototype Bridge
3. Finite Element Model
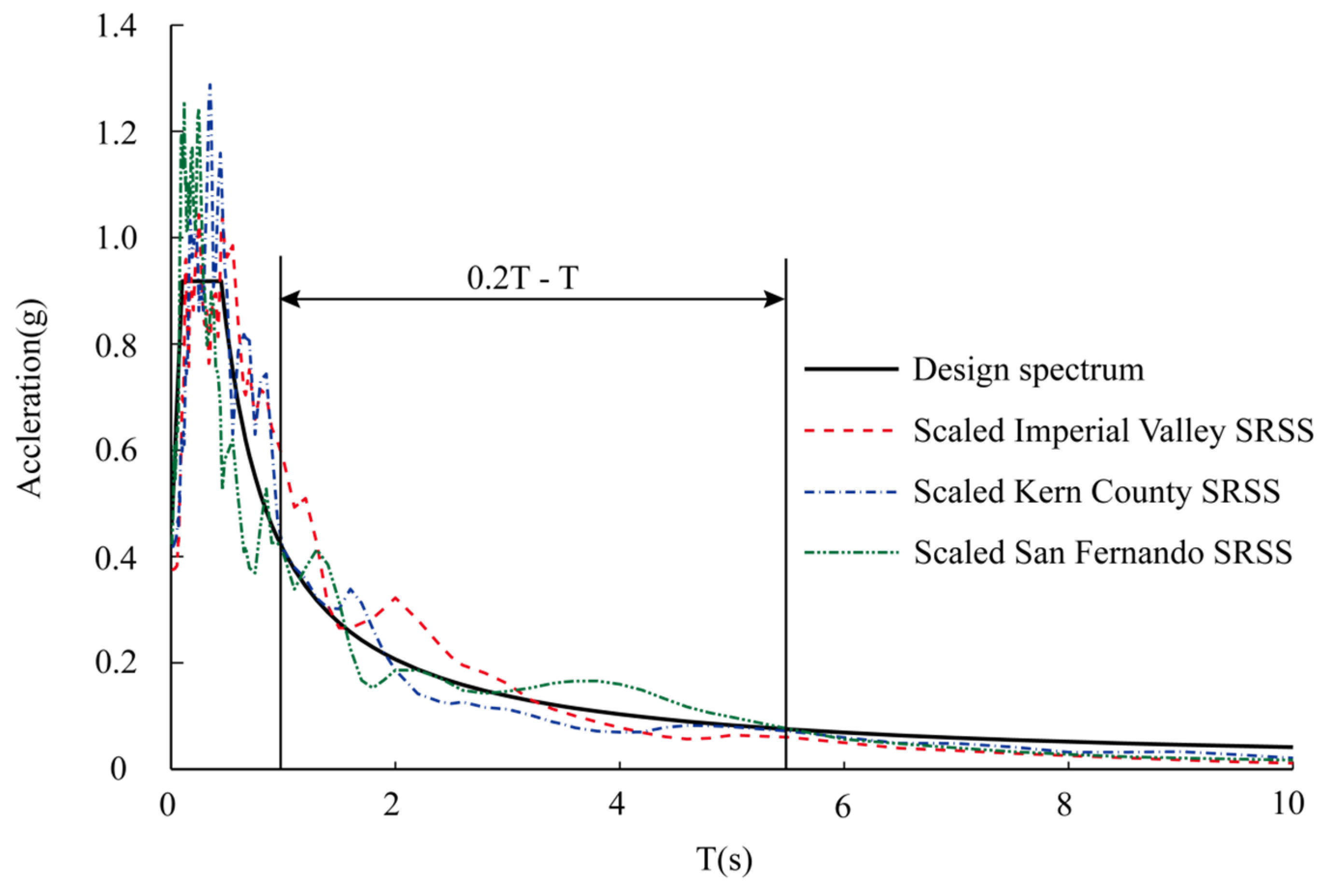
4. Thermal and Earthquake Loads
5. Case Study and Discussion
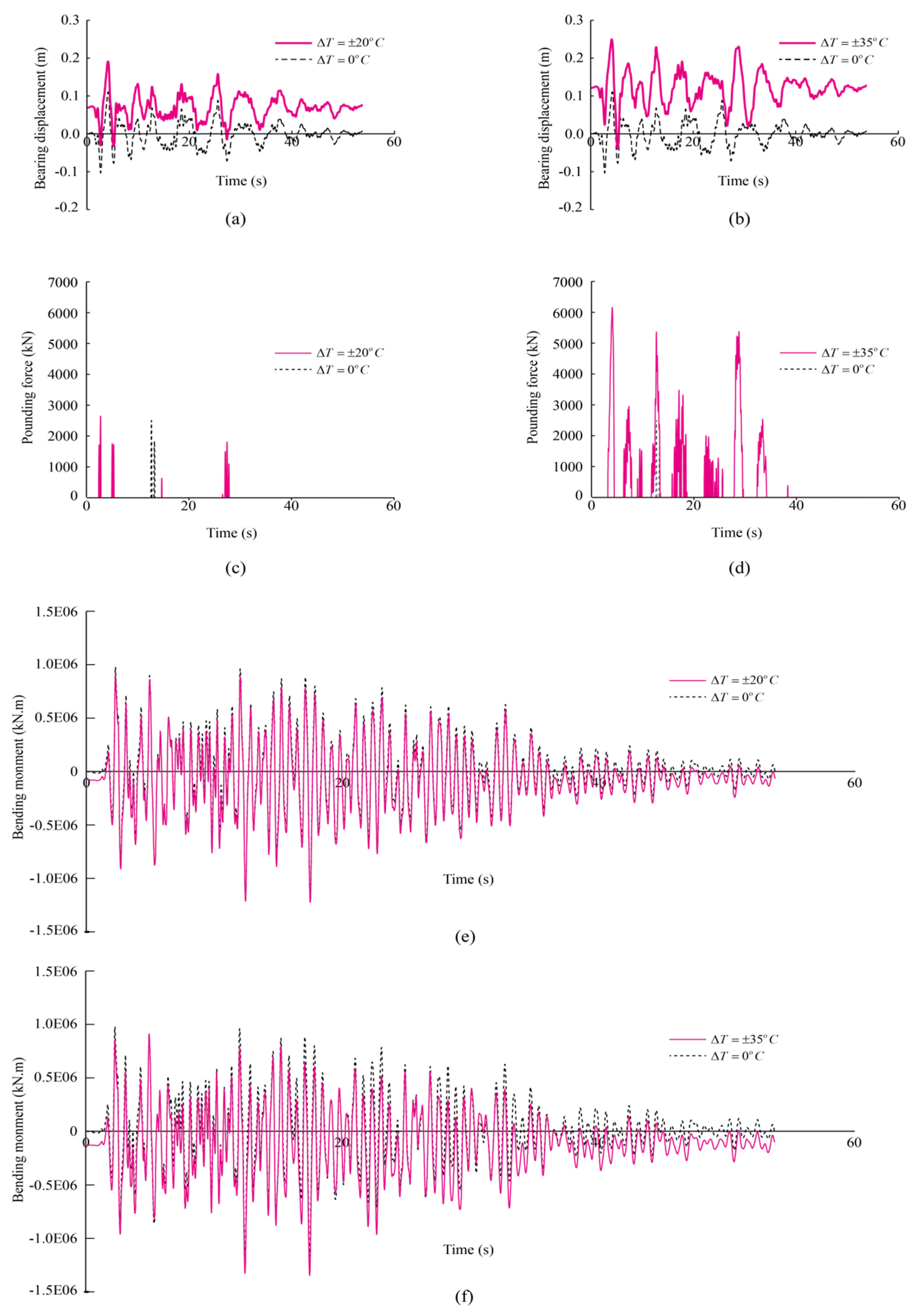
5.1. Changes of Uniform Temperature Load
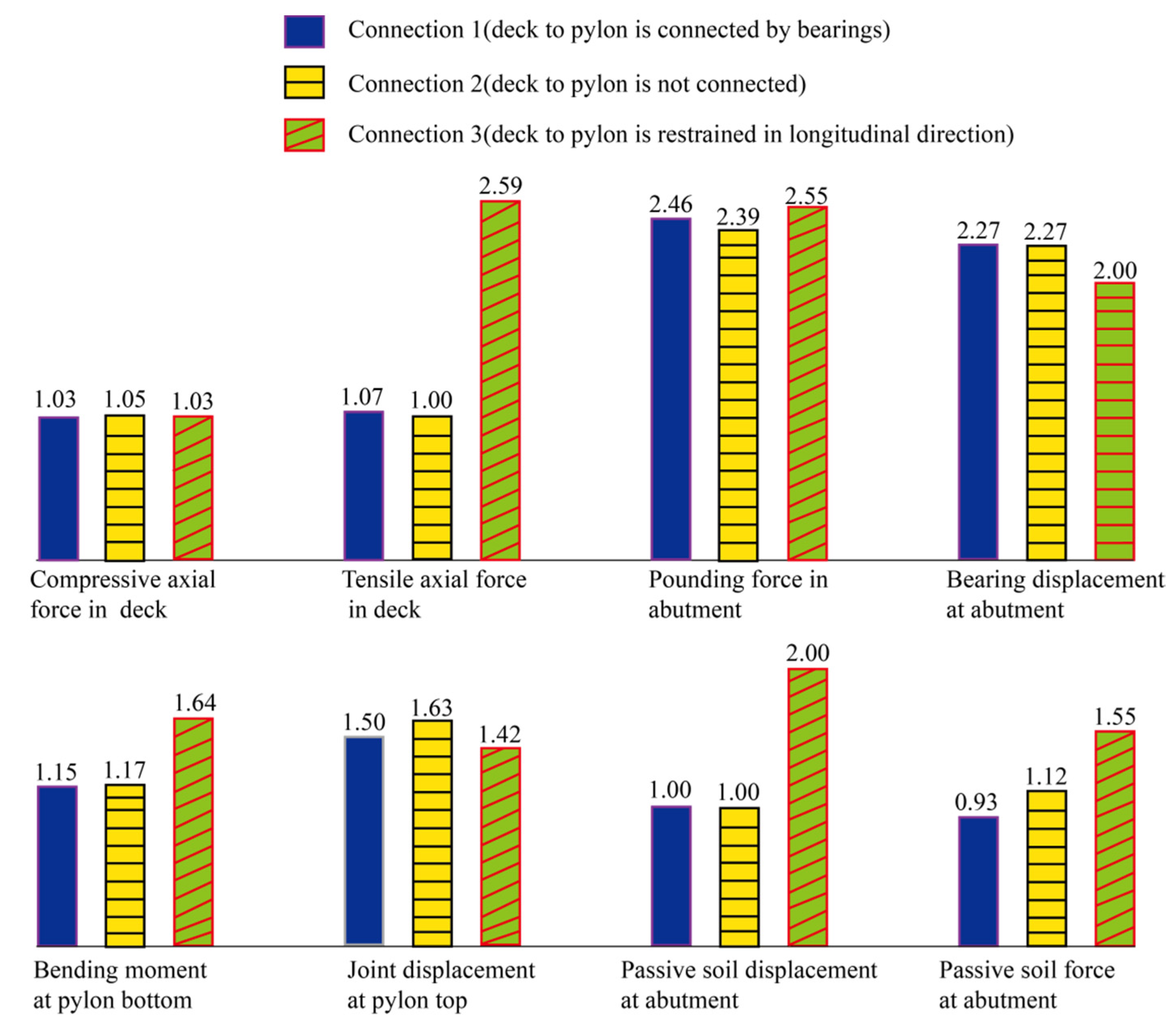
5.2. Deck to Pylon Connections
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, J.; Zou, X.; Yan, X.; Li, S. Integrated analysis model for the seismic responses of cable-stayed bridges near active faults. J. Earthq. Tsunami 2015, 9. [Google Scholar] [CrossRef]
- Shrestha, B. Seismic response of long span cable-stayed bridge to near-fault vertical ground motions. KSCE J. Civ. Eng. 2014, 19, 180–187. [Google Scholar] [CrossRef]
- Ismail, M.; Casas, J.R.; Rodellar, J. Near-fault isolation of cable-stayed bridges using RNC isolator. Eng. Struct. 2013, 56, 327–342. [Google Scholar] [CrossRef]
- Ismail, M.; Casas, J.R. Novel isolation device for protection of cable-stayed bridges against near-fault earthquakes. J. Bridge Eng. 2013, 19, A4013002. [Google Scholar] [CrossRef]
- Wesolowsky, M.J.; Wilson, J.C. Seismic isolation of cable-stayed bridges for near-field ground motions. Earthq. Eng. Struct. Dyn. 2003, 32, 2107–2126. [Google Scholar] [CrossRef]
- Atmaca, B.; Yurdakul, M.; Ateş, Ş. Nonlinear dynamic analysis of base isolated cable-stayed bridge under earthquake excitations. Soil Dyn. Earthq. Eng. 2014, 66, 314–318. [Google Scholar] [CrossRef]
- Seed, F.K.A.; Ahmed, H.H.; Raheem, S.E.A.; Shafy, Y.A. Dynamic non-linear behaviour of cable stayed bridges under seismic loadings. Life Sci. J. 2013, 4, 3725–3741. [Google Scholar]
- Raheem, S.E.A.; Hayashikawa, T. Soil-structure interaction modeling effects on seismic response of cable-stayed bridge tower. Int. J. Adv. Struct. Eng. 2013, 5, 1–17. [Google Scholar] [CrossRef]
- De, S.; Wojtkiewicz, S.F.; Johnson, E.A. Efficient optimal design and design-under-uncertainty of passive control devices with application to a cable-stayed bridge. Struct. Control Health Monit. 2016. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.; Li, J.Y.; Spencer, B.F., Jr. Dynamic behavior of stay cables with passive negative stiffness dampers. Smart Mater. Struct. 2016, 25, 1–14. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W.; Zheng, K.F.; Li, H.G. Seismic design of a long-span cable-stayed bridge with fluid viscous dampers. Pract. Period. Struct. Des. Constr. 2015, 21. [Google Scholar] [CrossRef]
- Martínez-Rodrigo, M.D.; Filiatrault, A. A case study on the application of passive control and seismic isolation techniques to cable-stayed bridges: A comparative investigation through non-linear dynamic analyses. Eng. Struct. 2015, 99, 232–252. [Google Scholar] [CrossRef]
- Sharabash, A.M.; Andrawes, B.O. Application of shape memory alloy dampers in the seismic control of cable-stayed bridges. Eng. Struct. 2009, 31, 607–616. [Google Scholar] [CrossRef]
- Domaneschi, M.; Martinelli, L. Extending the benchmark cable-stayed bridge for transverse response under seismic loading. J. Bridge Eng. 2014, 19, 165–184. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H. A Summary review of correlations between temperatures and vibration properties of long-span bridges. Math. Probl. Eng. 2014, 2014, 1–19. [Google Scholar] [CrossRef]
- Ding, Y.L.; Li, A.Q. Temperature-induced variations of measured modal frequencies of steel box girder for a long-span suspension bridge. Int. J. Steel Struct. 2011, 11, 145–155. [Google Scholar] [CrossRef]
- Cao, Y.; Yim, J.; Zhao, Y.; Wang, M.L. Temperature effects on cable stayed bridge using health monitoring system: A case study. Struct. Health Monit. 2010, 10, 523–537. [Google Scholar]
- Arena, A.; Pacitti, A.; Lacarbonara, W. Nonlinear response of elastic cables with flexural-torsional stiffness. Int. J. Solids Struct. 2015, 87, 267–277. [Google Scholar] [CrossRef]
- Lepidi, M.; Gattulli, V. Static and dynamic response of elastic suspended cables with thermal effects. Int. J. Solids Struct. 2012, 49, 1103–1116. [Google Scholar] [CrossRef]
- Qiu, W.L.; Zhe, Z. Research on combination of seismic and temperature action effects of bridge structures. Dalian Ligong Daxue Xue Bao J. Dalian Univ. Technol. 2011, 51, 540–544. [Google Scholar]
- Maleki, S.; Maghsoudi-Barmi, A. Effects of concurrent earthquake and temperature loadings on cable-stayed bridges. Int. J. Struct. Stab. Dyn. 2015, 16, 1550020. [Google Scholar] [CrossRef]
- Zhong, J.; Pang, Y.; Jeon, J.S.; Desroches, R.; Yuan, W. Seismic fragility assessment of long-span cable-stayed bridges in China. Adv. Struct. Eng. 2016. [Google Scholar] [CrossRef]
- Mckenna, F.; Scott, M.H.; Fenves, G.L. Nonlinear finite-element analysis software architecture using object composition. J. Comput. Civ. Eng. 2010, 24, 95–107. [Google Scholar] [CrossRef]
- Wilson, J.C.; Wayne, G. Modelling of cable-stayed bridge for dynamic analysis. Earthq. Eng. Struct. Dyn. 1991, 20, 707–721. [Google Scholar] [CrossRef]
- Elsa, C.; Alvaro, C.; Vincenzo, G.; Marco, L. Cable-deck dynamic interactions at the International Guadiana Bridge: On-site measurements and finite element modelling. Struct. Control Health Monit. 2008, 15, 237–264. [Google Scholar]
- Ernst, J.H. Der E-Modul von Seilen unter berucksichtigung des Durchhanges. Der Bauing. 1965, 40, 52–55. [Google Scholar]
- Caetano, E.; Cunha, A.; Taylor, C.A. Investigation of Dynamic Cable-deck Interaction in a Physical Model of a Cable-stayed Bridge. Part I: Modal Analysis. Earthq. Eng. Struct. Dyn. 2000, 29, 481–498. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Taylor, C.A. Investigation of dynamic cable–deck interaction in a physical model of a cable-stayed bridge. Part II: Seismic response. Earthq. Eng. Struct. Dyn. 2000, 29, 499–521. [Google Scholar] [CrossRef]
- Gattulli, V.; Lepidi, M. Localization and veering in the dynamics of cable-stayed bridges. Comput. Struct. 2007, 85, 1661–1678. [Google Scholar] [CrossRef]
- Yashinsky, M.; Ostrom, T. Caltrans new seismic design criteria for bridges. Earthq. Spectr. 2000, 1, 285–307. [Google Scholar] [CrossRef]
- Desroches, R.; Muthukumar, S. Effect of Pounding and restrainers on seismic response of multiple-frame bridges. J. Struct. Eng. 2002, 128, 860–869. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China (MOT). Guidelines for Seismic Design of Highway Bridges; MOT: Beijing, China, 2008.
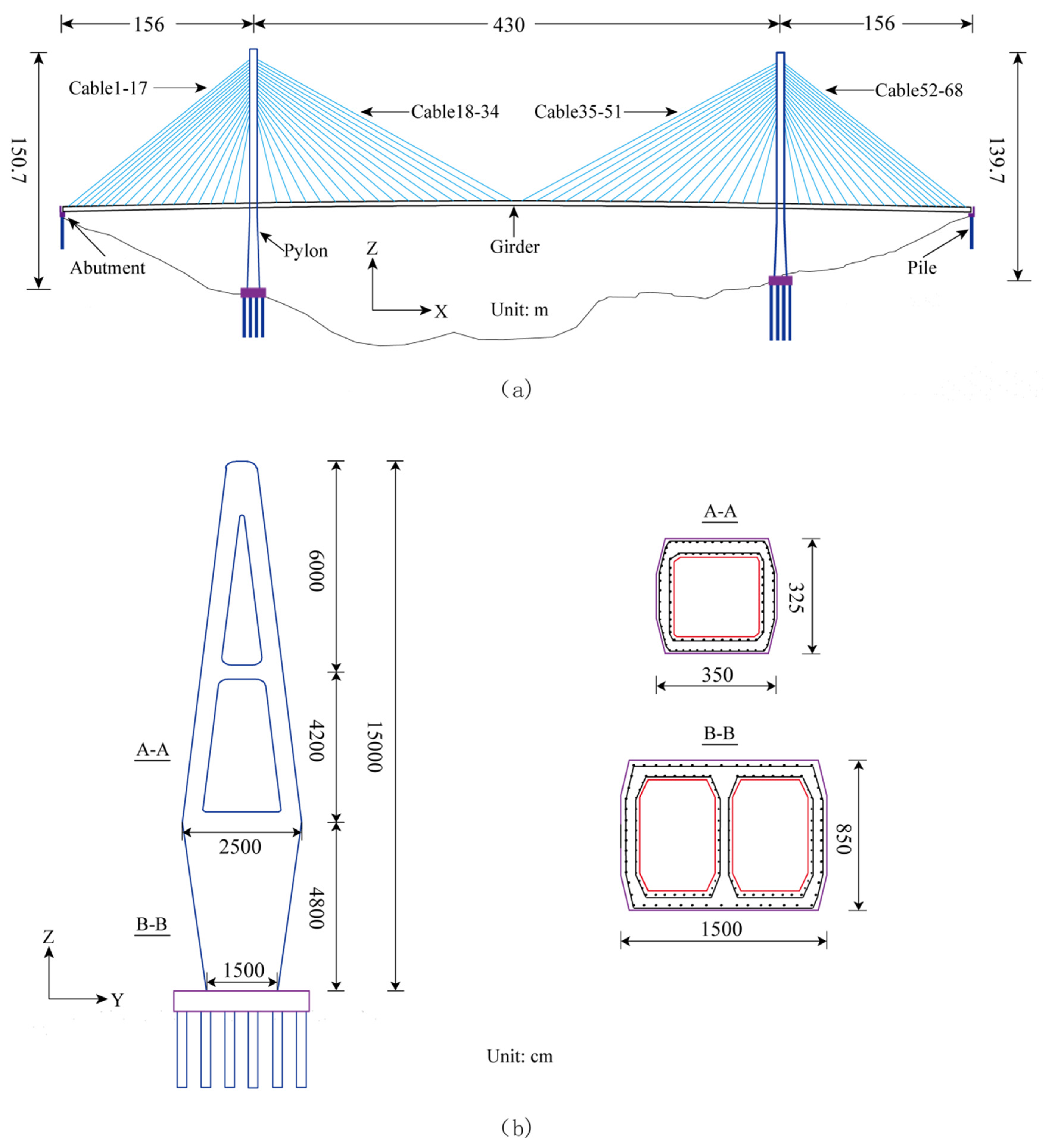
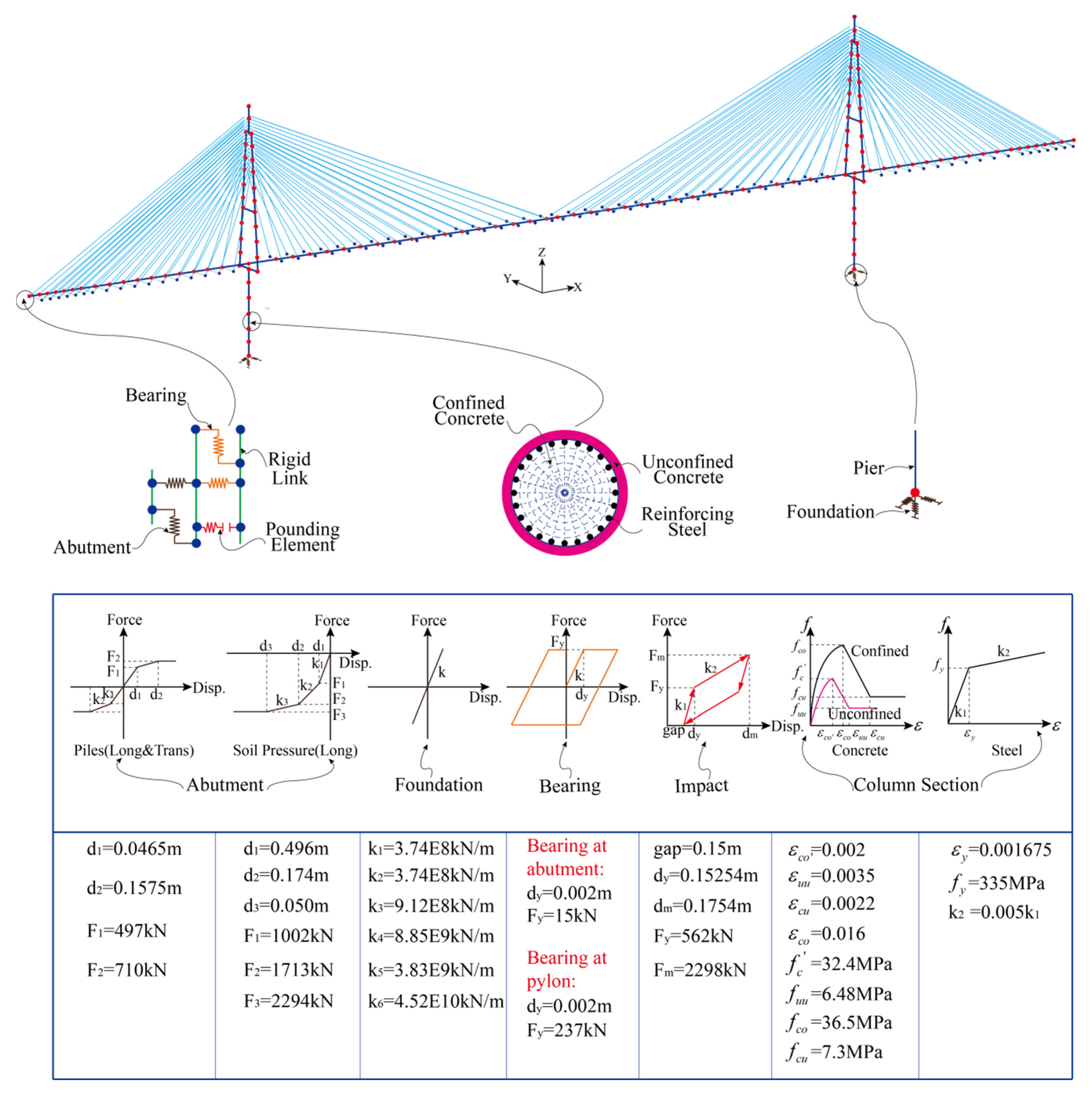
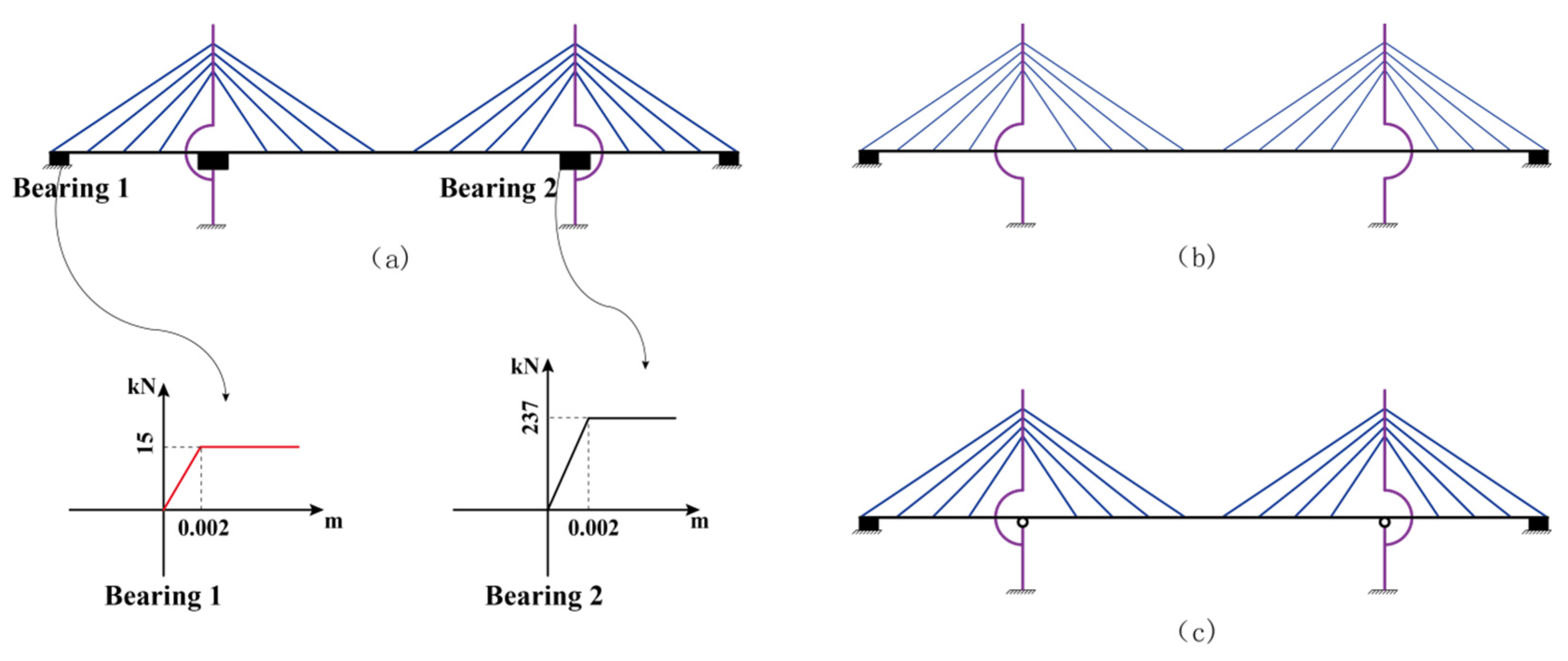
| Section | Area (m2) | Iy (m4) | Iz (m4) | J(m4) |
|---|---|---|---|---|
| Concrete | 11.546 | 7.512 | 352.221 | 4.287 |
| Steel | 1.850 | 0.858 | 36.282 | 0.0281 |
| No. | Record No. | Name | Time | Station | Magnitude | Scaling Factor |
|---|---|---|---|---|---|---|
| 1 | 6 | Imperial Valley | 1940 | EI Centro | 6.95 | 1.07 |
| 2 | 15 | Kern County | 1952 | Taft Lincoln | 7.36 | 1.73 |
| 3 | 68 | San Fernando | 1971 | LA-Holly wood | 6.61 | 1.38 |
| Responses | Earthquake | ΔT = 0 (°C) | ΔT = ±20 (°C) | Increase | ΔT = ±35 (°C) | Increase |
|---|---|---|---|---|---|---|
| No. | (%) | (%) | ||||
| Fx (comp.) in deck (kN) | 1 | 58,888 | 59,351 | 0.79 | 60,877 | 3.38 |
| 2 | 63,686 | 64,329 | 1.01 | 66,402 | 4.26 | |
| 3 | 62,965 | 69,969 | 11.12 | 73,354 | 16.50 | |
| Fx (tensile) in deck (kN) | 1 | 26,520 | 26,617 | 0.37 | 26,982 | 1.74 |
| 2 | 42,662 | 42,969 | 0.72 | 43,353 | 1.62 | |
| 3 | 27,409 | 27,494 | 0.31 | 30,616 | 11.70 | |
| Pounding force (kN) | 1 | 2501 | 3666 | 46.58 | 6155 | 146.10 |
| 2 | 11,892 | 17,951 | 50.95 | 15,846 | 33.25 | |
| 3 | 21,196 | 26,112 | 23.19 | 27,909 | 31.67 | |
| Bearing disp. at abutment (m) | 1 | 0.11 | 0.19 | 72.73 | 0.25 | 127.27 |
| 2 | 0.34 | 0.47 | 38.24 | 0.42 | 23.53 | |
| 3 | 0.55 | 0.68 | 23.64 | 0.76 | 38.18 | |
| My at pylon bottom (kN·m) | 1 | 1,176,896 | 1,224,878 | 4.08 | 1,347,783 | 14.52 |
| 2 | 1,929,557 | 2,000,932 | 3.70 | 2,045,541 | 6.01 | |
| 3 | 1,531,194 | 1,732,721 | 13.16 | 1,845,110 | 20.50 |
| Cable No. | 0 (°C) | ±20 (°C) | Increase (%) | ±35 (°C) | Increase (%) |
|---|---|---|---|---|---|
| 1 | 2827 | 2863 | 1.273 | 2872 | 1.592 |
| 18 | 2475 | 2485 | 0.404 | 2496 | 0.848 |
| Responses | Connection 1 | Connection 2 | Connection 3 | |||
|---|---|---|---|---|---|---|
| ΔT = 0 (°C) | ΔT = ±35 (°C) | ΔT = 0 (°C) | ΔT = ±35 (°C) | ΔT = 0 (°C) | ΔT = ±35 (°C) | |
| Pcomp. 1 (kN) | 58,888 | 60,877 | 60,213 | 63,193 | 77,877 | 79,850 |
| Ptensile 2 (kN) | 25,193 | 26,982 | 28,937 | 29,075 | 21,747 | 56,249 |
| Ppound 3 (kN) | 2501 | 6156 | 2621 | 6266 | 2600 | 6625 |
| Δbearing 4 (m) | 0.11 | 0.25 | 0.11 | 0.25 | 0.12 | 0.24 |
| Mpylon 5 (kN·m) | 1,176,896 | 1,347,783 | 1,295,675 | 1,513,304 | 2,390,025 | 3,918,211 |
| Δpylon 6 (m) | 0.16 | 0.24 | 0.16 | 0.26 | 0.24 | 0.34 |
| Δpassive 7 (m) | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.04 |
| Ppassive 8 (kN) | 7709 | 7169 | 7899 | 8866 | 7231 | 11,232 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Zhong, J.; Dang, X.; Yuan, W. Seismic Responses of a Cable-Stayed Bridge with Consideration of Uniform Temperature Load. Appl. Sci. 2016, 6, 408. https://doi.org/10.3390/app6120408
Guo J, Zhong J, Dang X, Yuan W. Seismic Responses of a Cable-Stayed Bridge with Consideration of Uniform Temperature Load. Applied Sciences. 2016; 6(12):408. https://doi.org/10.3390/app6120408
Chicago/Turabian StyleGuo, Junjun, Jian Zhong, Xinzhi Dang, and Wancheng Yuan. 2016. "Seismic Responses of a Cable-Stayed Bridge with Consideration of Uniform Temperature Load" Applied Sciences 6, no. 12: 408. https://doi.org/10.3390/app6120408
APA StyleGuo, J., Zhong, J., Dang, X., & Yuan, W. (2016). Seismic Responses of a Cable-Stayed Bridge with Consideration of Uniform Temperature Load. Applied Sciences, 6(12), 408. https://doi.org/10.3390/app6120408







