Three-Phase PV CHB Inverter for a Distributed Power Generation System
Abstract
:1. Introduction
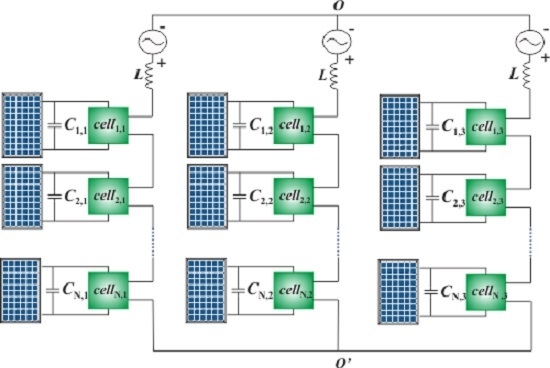
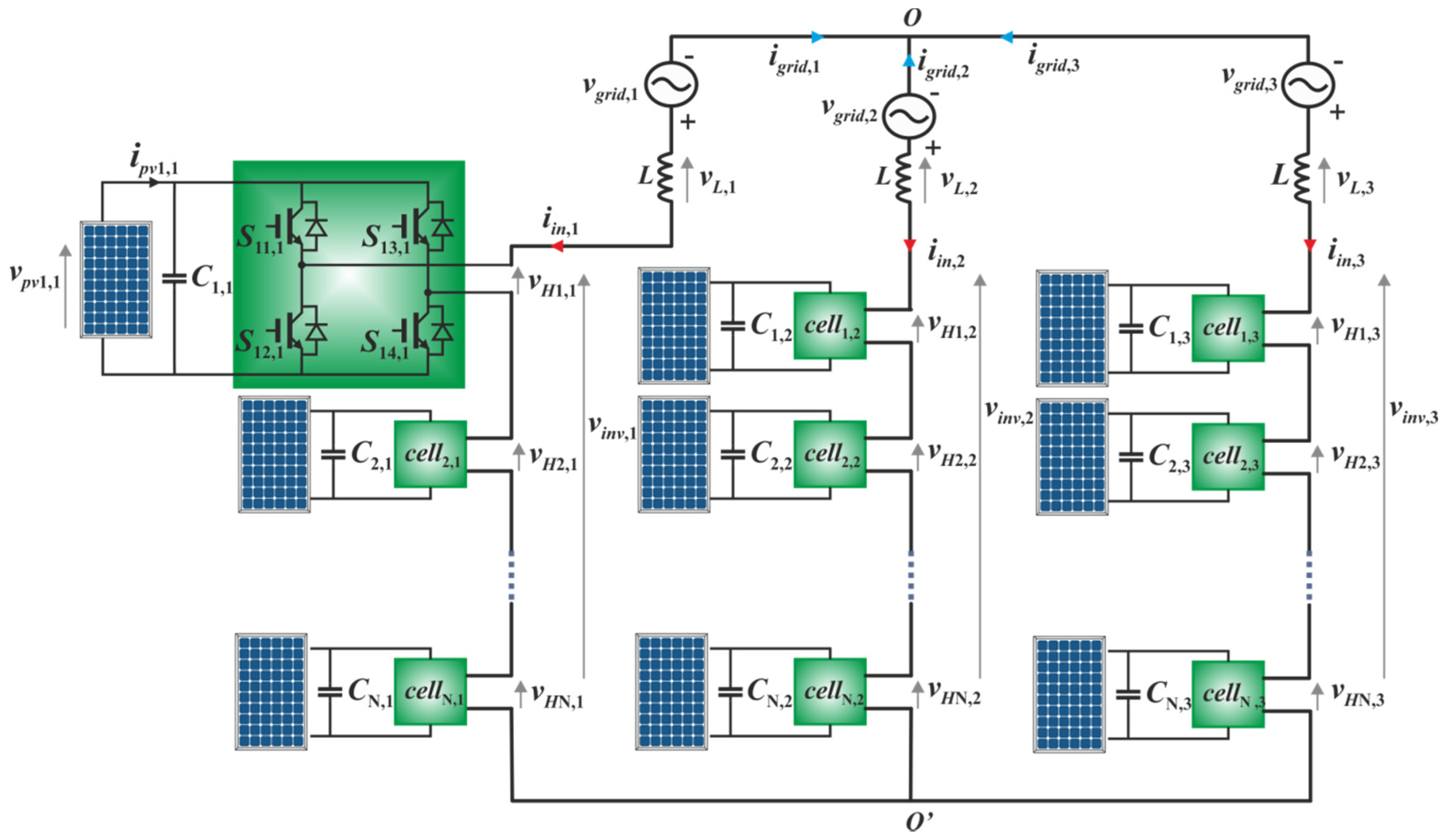
2. System Topology and Control Strategy
2.1. CHB Inverter Modeling
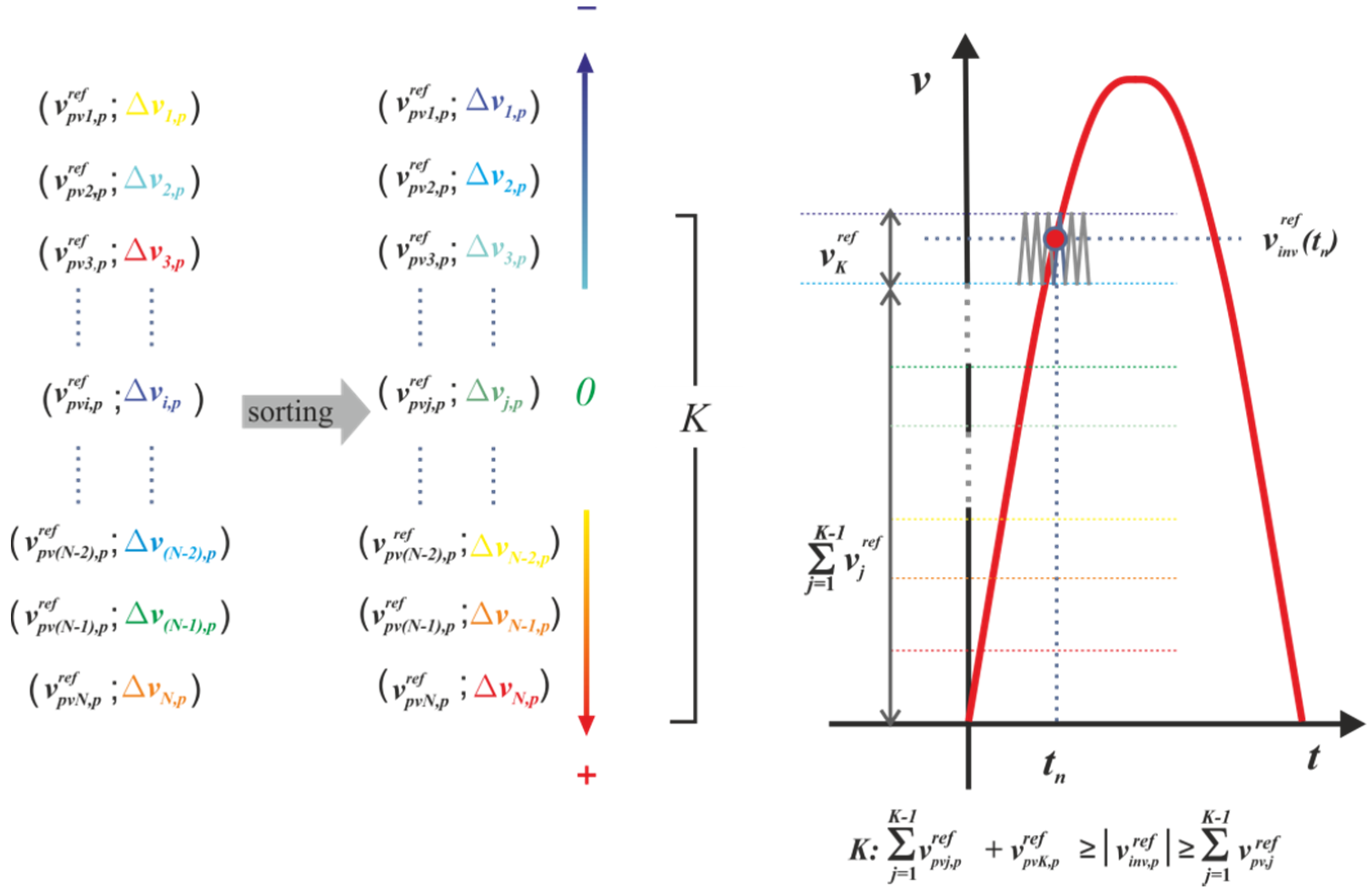
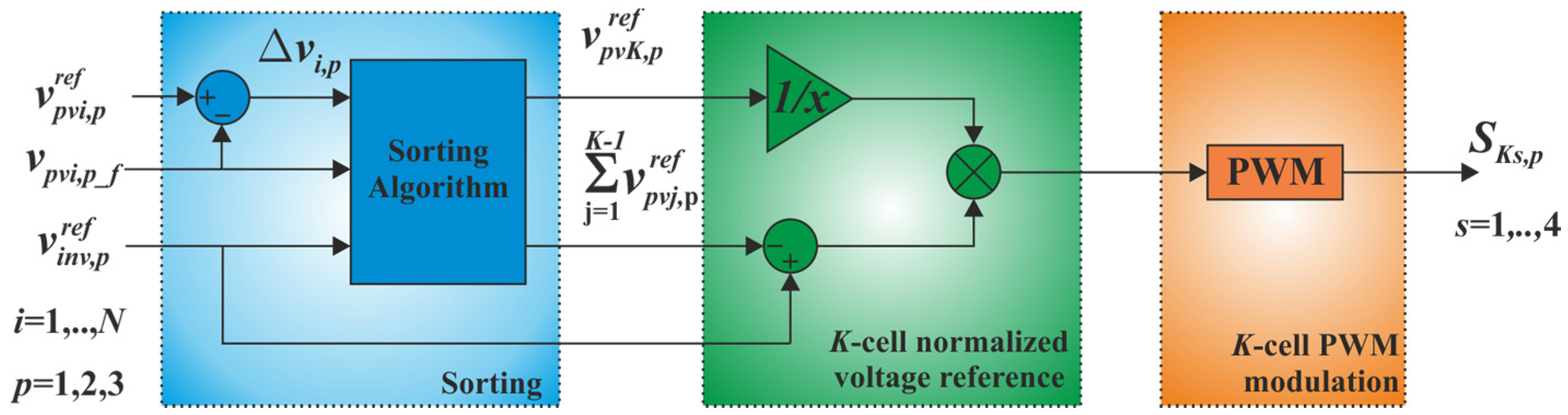
2.2. The Sorting Algorithm
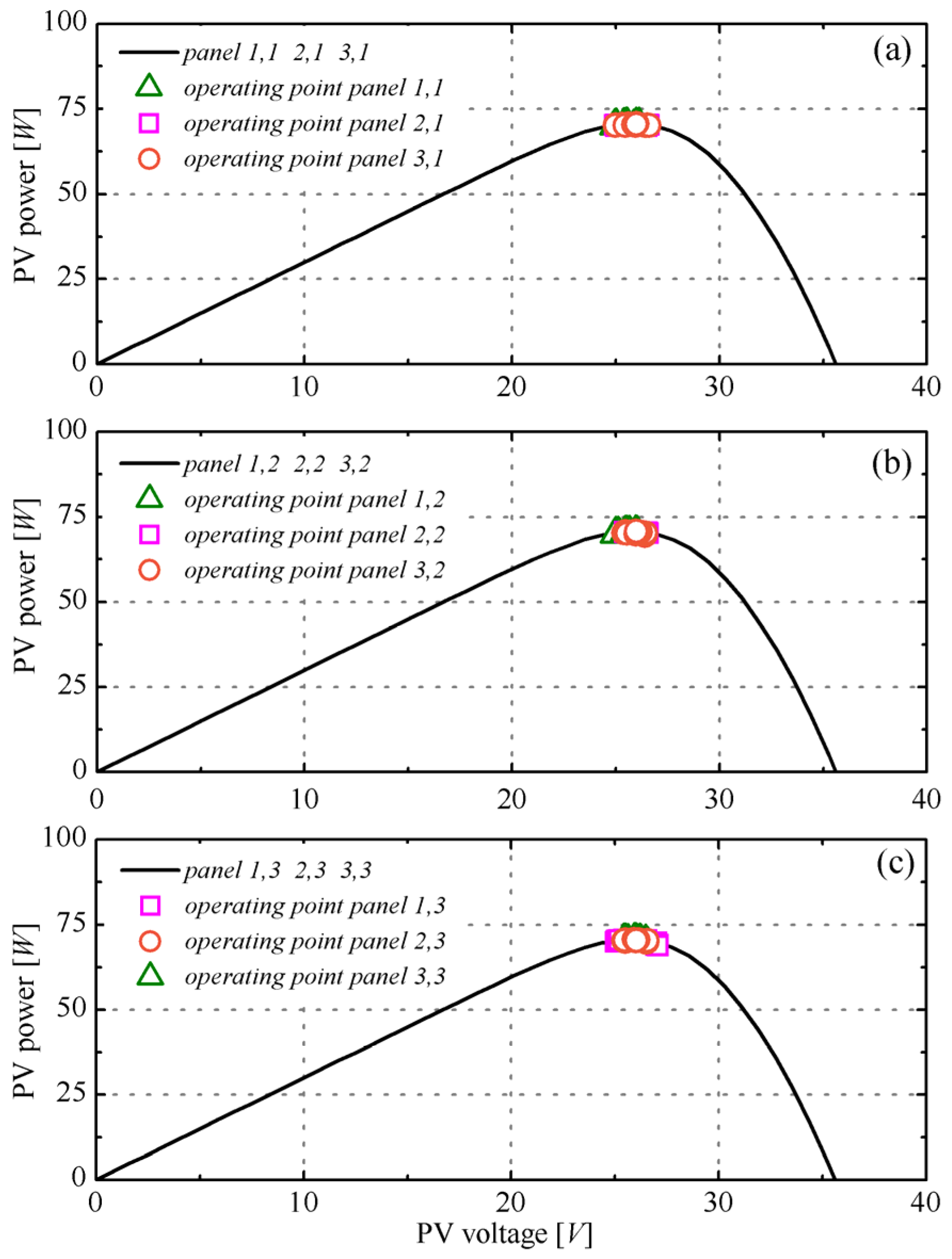
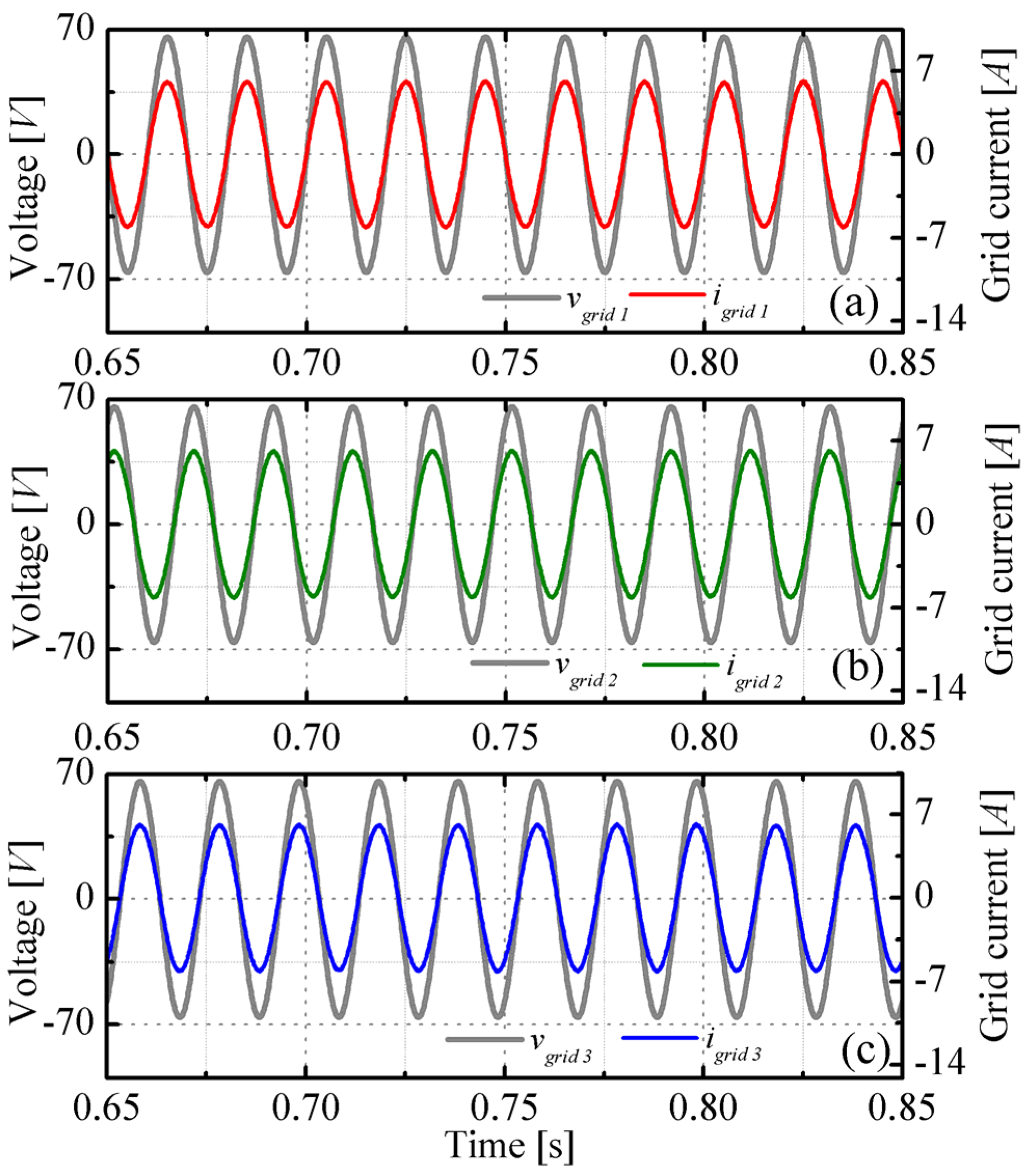
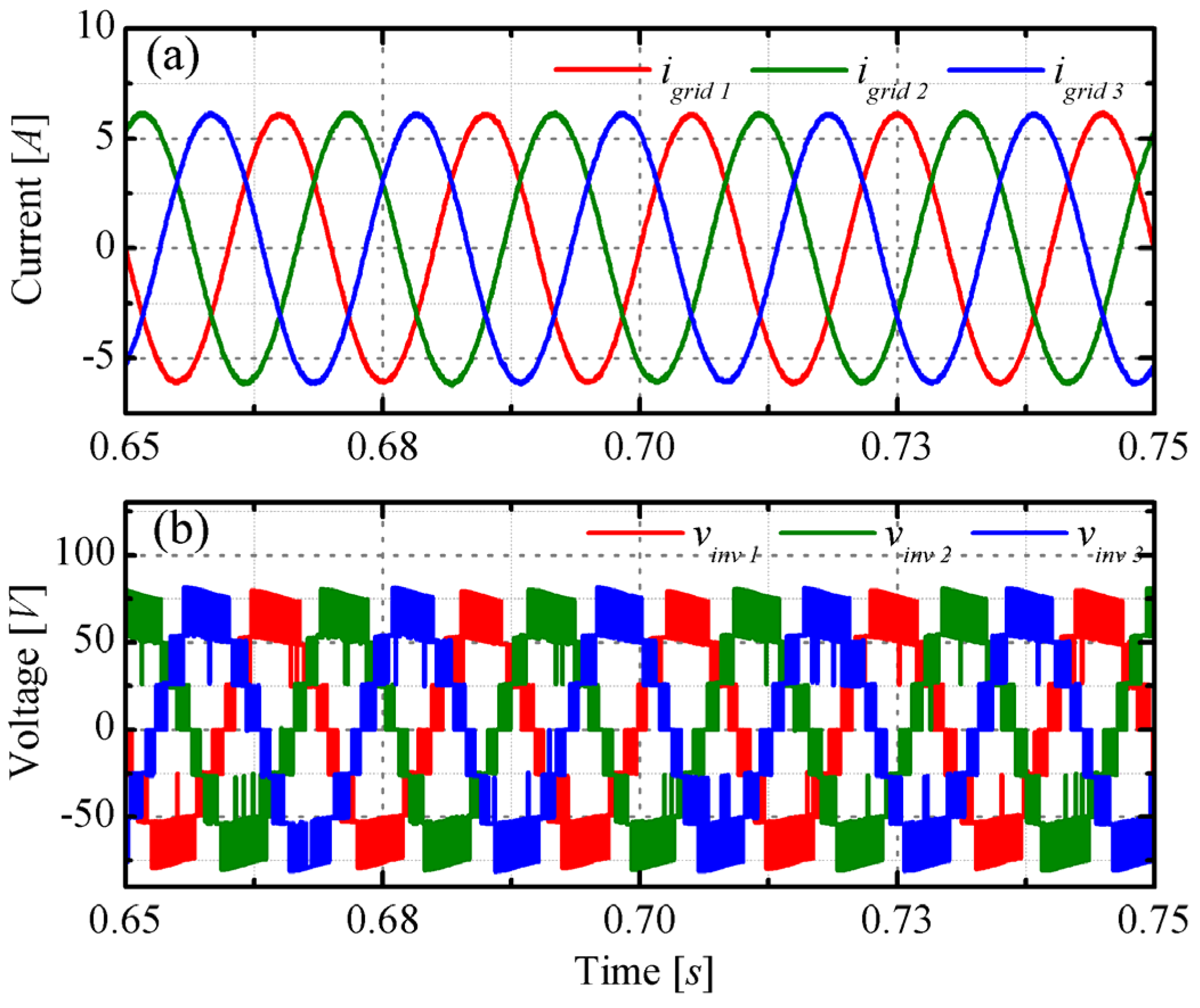
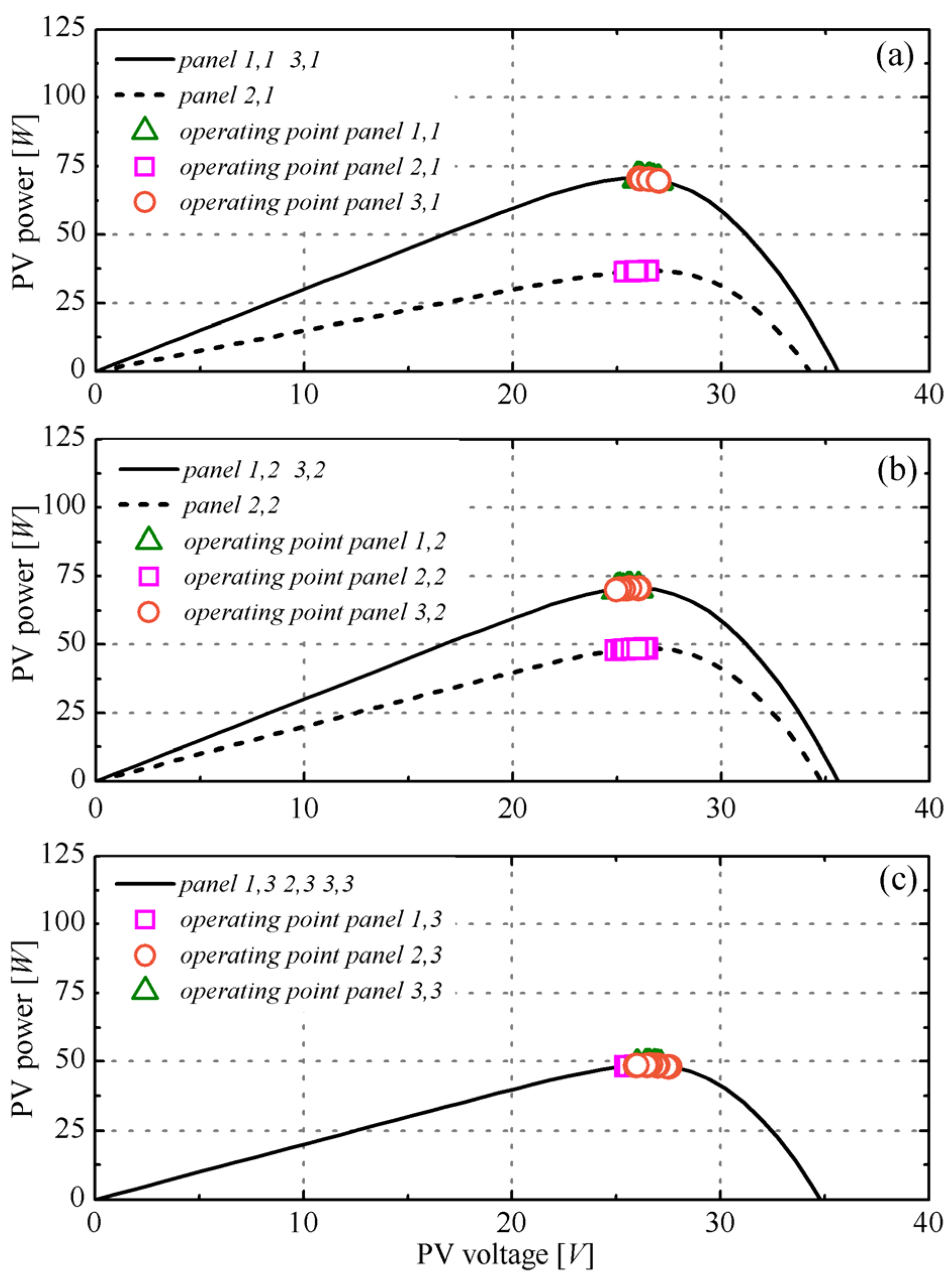
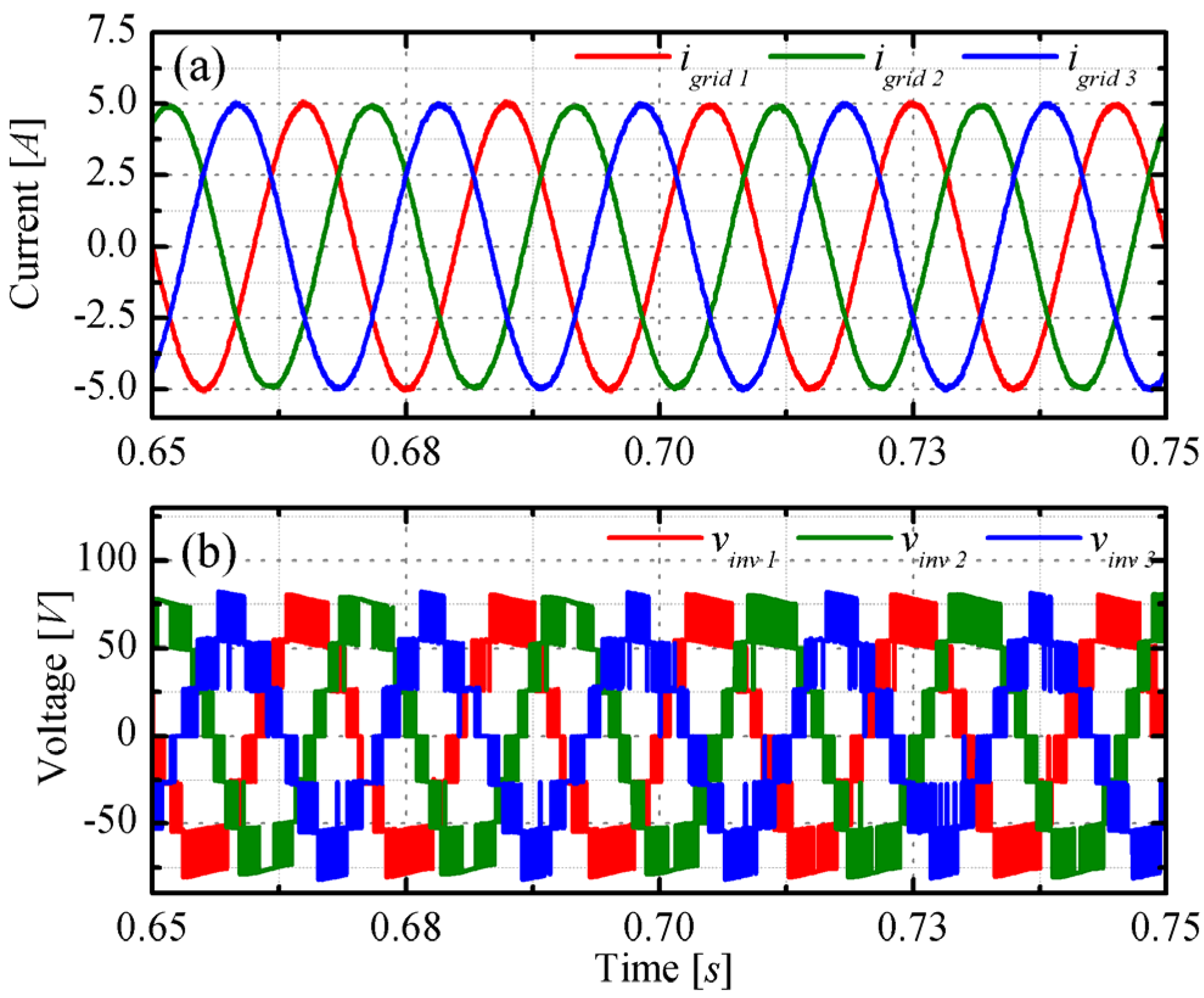
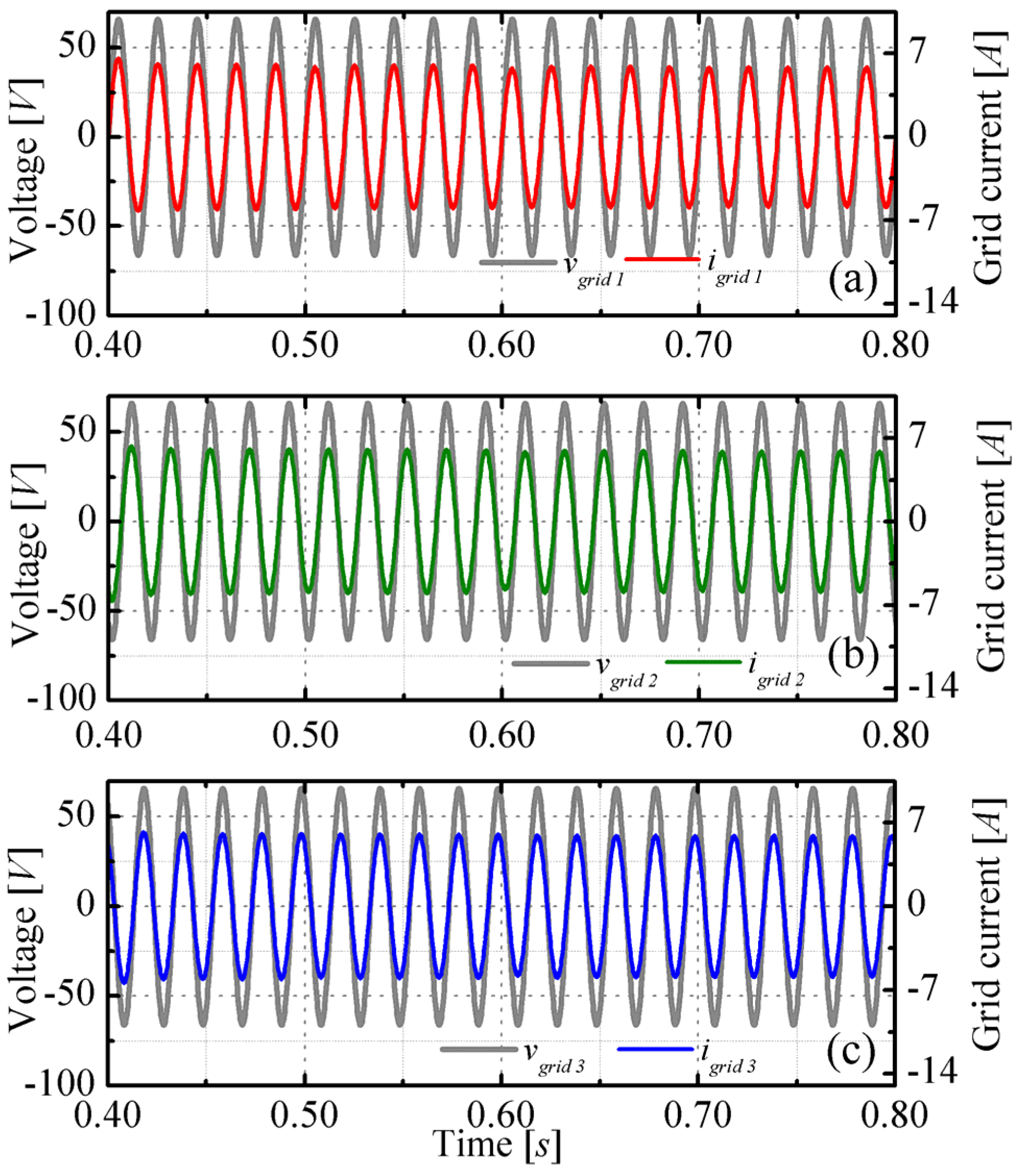
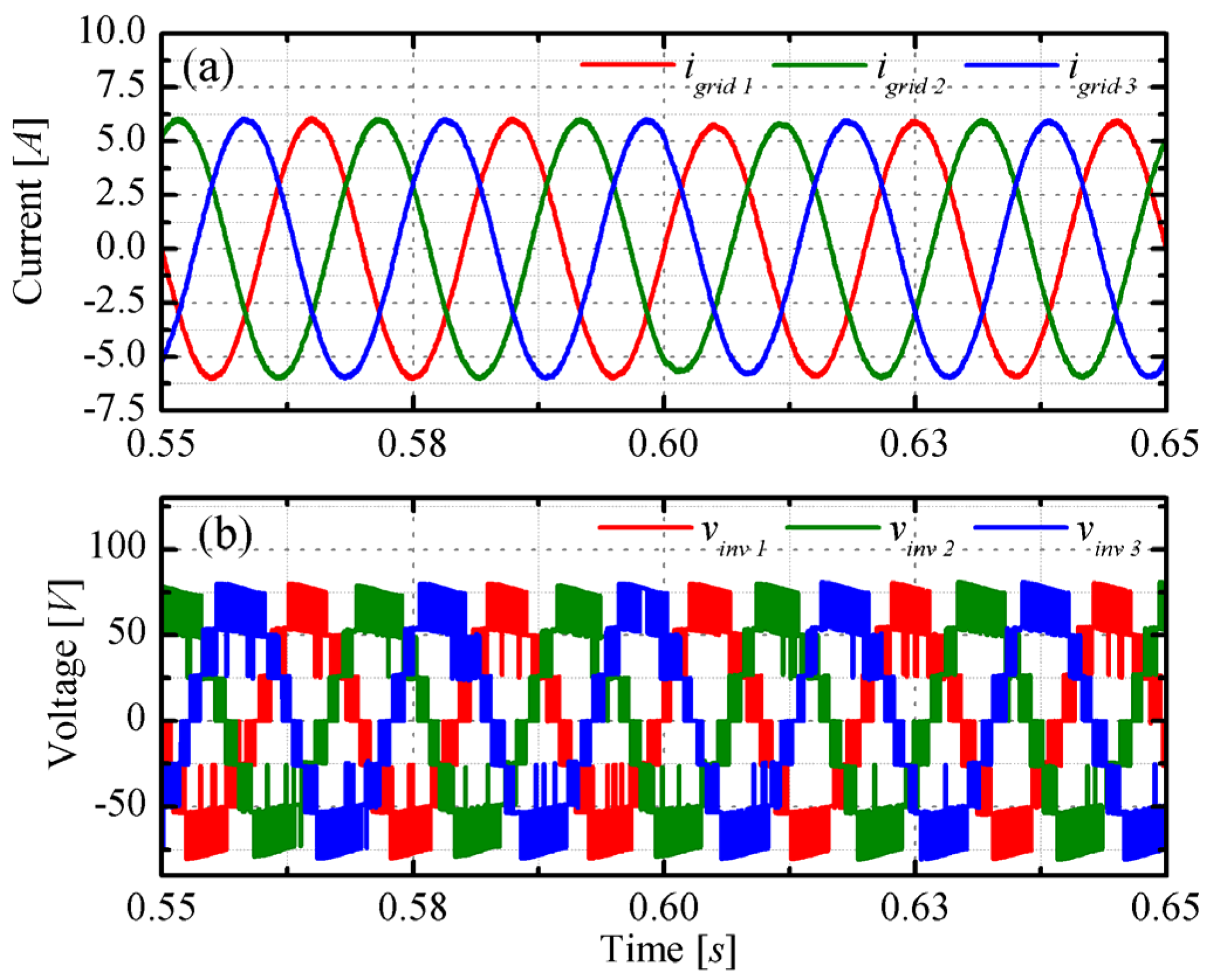
3. Numerical Analysis
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Calais, M.; Myrzik, J.; Spooner, T.; Agelidis, V.G. Inverters forsingle-phase grid connected photovoltaic systems—An overview. In Proceedings of the 33rd Annual IEEE Power Electronics Specialists Conference (PESC’02), Cairns, Australia, 23–27 June 2002; Volume 2, pp. 1995–2000.
- Lauria, D.; Coppola, M. Design and control of an advanced PV inverter. Sol. Energy 2014, 110, 533–542. [Google Scholar] [CrossRef]
- D’Alessandro, V.; Di Napoli, F.; Guerriero, P.; Daliento, S. An automated high-granularity tool for a fast evaluation of the yield of PV plants accounting for shading effects. Renew. Energy 2015, 83, 294–304. [Google Scholar] [CrossRef]
- Guerriero, P.; Di Napoli, F.; D’Alessandro, V.; Daliento, S. Accurate maximum power tracking in photovoltaic systems affected by partial shading. Int. J. Photoenergy 2015, 2015. [Google Scholar] [CrossRef]
- Petrone, G.; Spagnuolo, G.; Vitelli, M. An analog technique for distributed MPPT PV applications. IEEE Trans. Ind. Electron. 2012, 59, 4713–4722. [Google Scholar] [CrossRef]
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. Granular control of photovoltaic arrays by means of a multioutput Maximum Power Point Tracking algorithm. Prog. Photovolt. 2013, 21, 918–932. [Google Scholar]
- Spagnuolo, G.; Petrone, G.; Vitelli, M. Distributed Maximum Power Point Tracking: Challenges and Commercial Solutions. Automatika 2012, 53, 128–141. [Google Scholar]
- Piegari, L.; Rizzo, R.; Spina, I.; Tricoli, P. Optimized adaptive perturb and observe maximum power point tracking control for photovoltaic generation. Energies 2015, 8, 3418–3436. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Coppola, M.; Guerriero, P.; Di Napoli, F.; Daliento, S.; Lauria, D.; Del Pizzo, A. A PV AC-module based on coupled-inductors boost DC/AC converter. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 18–20 June 2014; pp. 1015–1020.
- Coppola, M.; Daliento, S.; Guerriero, P.; Lauria, D.; Napoli, E. On the design and the control of a coupled-inductors boost DC–AC converter for an individual PV panel. In Proceedings of the 2012 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 20–22 June 2012; pp. 1154–1159.
- Bandara, K.; Sweet, T.; Ekanayake, J. Photovoltaic applications for off-grid electrification using novel multi-level inverter technology with energy storage. Renew. Energy 2012, 37, 82–88. [Google Scholar] [CrossRef]
- Boulouiha, H.M.; Allali, A.; Laouer, M.; Tahri, A.; Denaï, M.; Draou, A. Direct torque control of multilevel SVPWM inverter in variable speed SCIG-based wind energy conversion system. Renew. Energy 2015, 80, 140–152. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Wu, B.; Pontt, J.O.; Kouro, S. Multilevel voltage-source-converter topologies for industrial medium-voltage drives. IEEE Trans. Ind. Electron. 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
- Vahedi, H.; Al-Haddad, K.; Ounejjar, Y.; Addoweesh, K. Crossover Switches Cell (CSC): A new multilevel inverter topology with maximum voltage levels and minimum DC sources. In Proceedings of the 39th IEEE Annual Conference on Industrial Electronics Society (IECON 2013), Vienna, Austria, 10–13 November 2013; pp. 54–59.
- Vahedi, H.; Labbé, P.A.; Al-Haddad, K. Sensor-Less Five-Level Packed U-Cell (PUC5) Inverter Operating in Stand-Alone and Grid-Connected Modes. IEEE Trans. Ind. Inform. 2016, 12, 361–370. [Google Scholar] [CrossRef]
- Leon, J.I.; Portillo, R.; Vazquez, S.; Padilla, J.J.; Franquelo, L.G.; Carrasco, J.M. Simple unified approach to develop a time-domain modulation strategy for single-phase multilevel converters. IEEE Trans. Ind. Electron. 2008, 55, 3239–3248. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef]
- Villanueva, E.; Correa, P.; Rodriguez, J.; Pacas, M. Control of a single-phase cascaded h-bridge multilevel inverter for grid-connected photovoltaic systems. IEEE Trans. Ind. Electron. 2009, 56, 4399–4406. [Google Scholar] [CrossRef]
- Chavarria, J.; Biel, D.; Guinjoan, F.; Meza, C.; Negroni, J.J. Energy-Balance Control of PV Cascaded Multilevel Grid-Connected Inverters Under Level-Shifted and Phase-Shifted PWMs. IEEE Trans. Ind. Electron. 2013, 60, 98–111. [Google Scholar] [CrossRef]
- Kouro, S.; Bin, W.; Moya, A.; Villanueva, E.; Correa, P.; Rodriguez, J. Control of a cascaded H-bridge multilevel converter for grid connection of photovoltaic systems. In Proceedings of the 35th IEEE Annual Conference on Industrial Electronics (IECON’09), Porto, Portugal, 3–5 November 2009; pp. 3976–3982.
- Rahim, N.A.; Selvaraj, J. Multistring five-level inverter with novel PWM control scheme for PV Application. IEEE Trans. Ind. Electron. 2010, 57, 2111–2123. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Operation of cascaded h-bridge multilevel converters for large-scale photovoltaic power plants under bridge failures. IEEE Trans. Ind. Electron. 2015, 62, 7228–7236. [Google Scholar] [CrossRef]
- Calais, M.; Agelidis, V.G.; Dymond, M.S. A cascaded inverter for transformerless single-phase grid-connected photovoltaic systems. Renew. Energy 2001, 22, 255–262. [Google Scholar] [CrossRef]
- Rahim, N.A.; Selvaraj, J.; Krismadinata, C. Five-level inverter with dual reference modulation technique for grid-connected PV system. Renew. Energy 2010, 35, 712–720. [Google Scholar] [CrossRef]
- Daliento, S.; Mele, L.; Spirito, P.; Carta, R.; Merlin, L. Experimental study on power consumption in lifetime engineered power diodes. IEEE Trans. Electron Devices 2009, 56, 2819–2824. [Google Scholar] [CrossRef]
- Coppola, M.; Di Napoli, F.; Guerriero, P.; Iannuzzi, D.; Daliento, S.; Del Pizzo, A. An FPGA-based advanced control strategy of a grid-tied PV CHB Inverter. IEEE Trans. Power Electron. 2016, 31, 806–816. [Google Scholar] [CrossRef]
- Coppola, M.; Di Napoli, F.; Guerriero, P.; Dannier, A.; Iannuzzi, D.; Daliento, S.; Del Pizzo, A. MPPT algorithm for grid-tied PV cascaded H-bridge inverter. Electr. Power Compon. Syst. 2015, 43, 8–10, 951–963. [Google Scholar]
- Coppola, M.; Di Napoli, F.; Guerriero, P.; Dannier, A.; Iannuzzi, D.; Daliento, S.; Del Pizzo, A. FPGA implementation of an adaptive modulation method for a three-phase grid-tied PV CHB inverter. In Proceedings of the Electrical Systems for Aircraft, Railway and Ship Propulsion (ESARS), Aachen, Germany, 3–5 March 2015.
- Iman-Eini, H.; Schanen, J.-L.; Farhangi, S.; Roudet, J. A modular strategy for control and voltage balancing of cascaded h-bridge rectifiers. IEEE Trans Power Electron. 2008, 23, 2428–2442. [Google Scholar] [CrossRef]
- Sepahvand, H.; Jingsheng, L.; Ferdowsi, M.; Corzine, K.A. Capacitor Voltage Regulation in Single-DC-Source Cascaded H-Bridge Multilevel Converters Using Phase-Shift Modulation. IEEE Trans. Ind. Electron. 2013, 60, 3619–3626. [Google Scholar] [CrossRef]
- Kang, F.S.; Park, S.J.; Cho, S.E.; Kim, C.U.; Ise, T. Multilevel PWM inverters suitable for the use of stand-alone photovoltaic power systems. IEEE Trans. Energy Convers. 2005, 20, 906–915. [Google Scholar] [CrossRef]
- Bahrani, B.; Kenzelmann, S.; Rufer, A. Multivariable-PI-based dq current control of voltage source converters with superior axis decoupling capability. IEEE Trans. Ind. Electron. 2011, 58, 3016–3026. [Google Scholar] [CrossRef]
- Townsend, C.D.; Summers, T.J.; Betz, R.E. Control and modulation scheme for a cascaded H-bridge multi-level converter in large scale photovoltaic systems. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3707–3714.
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Power balance of cascaded H-bridge multilevel converters for large-scale photovoltaic integration. IEEE Trans. Power Electron. 2016, 31, 292–303. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Power balance optimization of cascaded H-bridge multilevel converters for large-scale photovoltaic integration. IEEE Trans. Power Electron. 2016, 31, 1108–1120. [Google Scholar] [CrossRef]
- Alonso, O.; Sanchis, P.; Gubia, E.; Marroyo, L. Cascaded H-bridge multilevel converter for grid connected photovoltaic generators with independent maximum power point tracking of each solar array. In Proceedings of the 34th IEEE Annual PESC, Acapulco, Mexico, 15–19 June 2003; pp. 731–735.
- Negroni, J.; Guinjoan, F.; Meza, C.; Biel, D.; Sanchis, P. Energy-Sampled Data Modeling of a Cascade H-Bridge Multilevel Converter for Grid-connected PV Systems. In Proceedings of the 10th IEEE International Power Electronics Congress, Puebla, Mexico, 16–18 October 2006; pp. 1–6.
- Xiao, B.; Filho, F.; Tolbert, L.M. Single-phase cascaded H-bridge multilevel inverter with nonactive power compensation for grid-connected photovoltaic generators. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 17–22 September 2011; pp. 2733–2737.
- Rezaei, M.A.; Farhangi, S.; Iman-Eini, H. Enhancing the reliability of single-phase CHB-based grid-connected photovoltaic energy systems. In Proceedings of the 2nd Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Tehran, Iran, 16–17 February 2011; pp. 117–122.
- Eskandari, A.; Javadian, V.; Iman-Eini, H.; Yadollahi, M. Stable operation of grid connected Cascaded H-Bridge inverter under unbalanced insolation conditions. In Proceedings of the 3rd International Conference on Electric Power and Energy Conversion Systems (EPECS), Istanbul, Turkey, 2–4 October 2013.
- Iannuzzi, D.; Pagano, M.; Piegari, L.; Tricoli, P. A star-configured cascade H-bridge converter for building integrated photovoltaics. In Proceedings of the Ninth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 25–27 March 2014.
- Xilinx. Available online: http://www.xilinx.com/ (accessed on 1 May 2016).
- The Institute of Electrical and Electronics Engineers, Inc. IEEE Standard for Verilog Hardware Description Language; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar]
- Shell Solar. Sheet Shell SQ150-PC Photovoltaic Solar Module. Shell Solar: Camarillo, CA, USA, 2008. Available online: www.shell.com/solar (accessed on 1 May 2016).



| Parameter Description | Value |
|---|---|
| Line inductance L (mH) | 5 |
| DC-link capacitance Ci,j (mF) | 4.32 |
| Carrier frequency (kHz) | 5 |
| Parameter Description | Value |
|---|---|
| Inherent diode saturation current (A) | 1e-9 |
| Series resistance (Ω) | 2 |
| Shunt resistance (kΩ) | 7 |
| Ideality factor | 1.06 |
| Photogenerated current (A) | 4.8 |
| Number of cells | 72 |
| Phase | 1 | 2 | 3 |
|---|---|---|---|
| cell 1 | 625 W/m2 | 625 W/m2 | 425 W/m2 |
| cell 2 | 300 W/m2 | 425 W/m2 | 425 W/m2 |
| cell 3 | 625 W/m2 | 625 W/m2 | 425 W/m2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerriero, P.; Coppola, M.; Di Napoli, F.; Brando, G.; Dannier, A.; Iannuzzi, D.; Daliento, S. Three-Phase PV CHB Inverter for a Distributed Power Generation System. Appl. Sci. 2016, 6, 287. https://doi.org/10.3390/app6100287
Guerriero P, Coppola M, Di Napoli F, Brando G, Dannier A, Iannuzzi D, Daliento S. Three-Phase PV CHB Inverter for a Distributed Power Generation System. Applied Sciences. 2016; 6(10):287. https://doi.org/10.3390/app6100287
Chicago/Turabian StyleGuerriero, Pierluigi, Marino Coppola, Fabio Di Napoli, Gianluca Brando, Adolfo Dannier, Diego Iannuzzi, and Santolo Daliento. 2016. "Three-Phase PV CHB Inverter for a Distributed Power Generation System" Applied Sciences 6, no. 10: 287. https://doi.org/10.3390/app6100287
APA StyleGuerriero, P., Coppola, M., Di Napoli, F., Brando, G., Dannier, A., Iannuzzi, D., & Daliento, S. (2016). Three-Phase PV CHB Inverter for a Distributed Power Generation System. Applied Sciences, 6(10), 287. https://doi.org/10.3390/app6100287