Carrier-Envelope Offset Stabilized Ultrafast Diode-Pumped Solid-State Lasers
Abstract
:1. Introduction
2. Optical Frequency Comb Self-Referencing
2.1. Nonlinear Interferometry for fCEO Detection
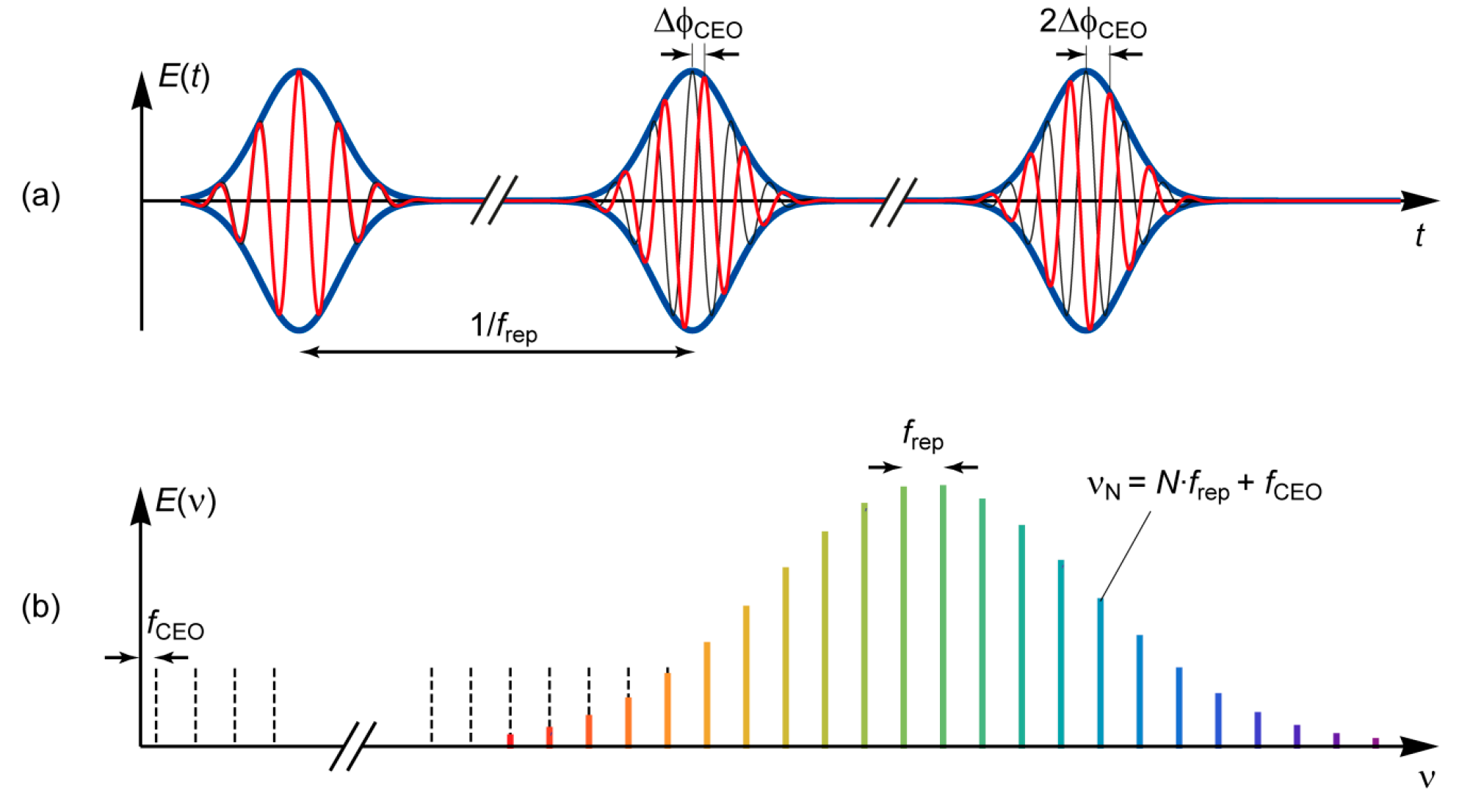
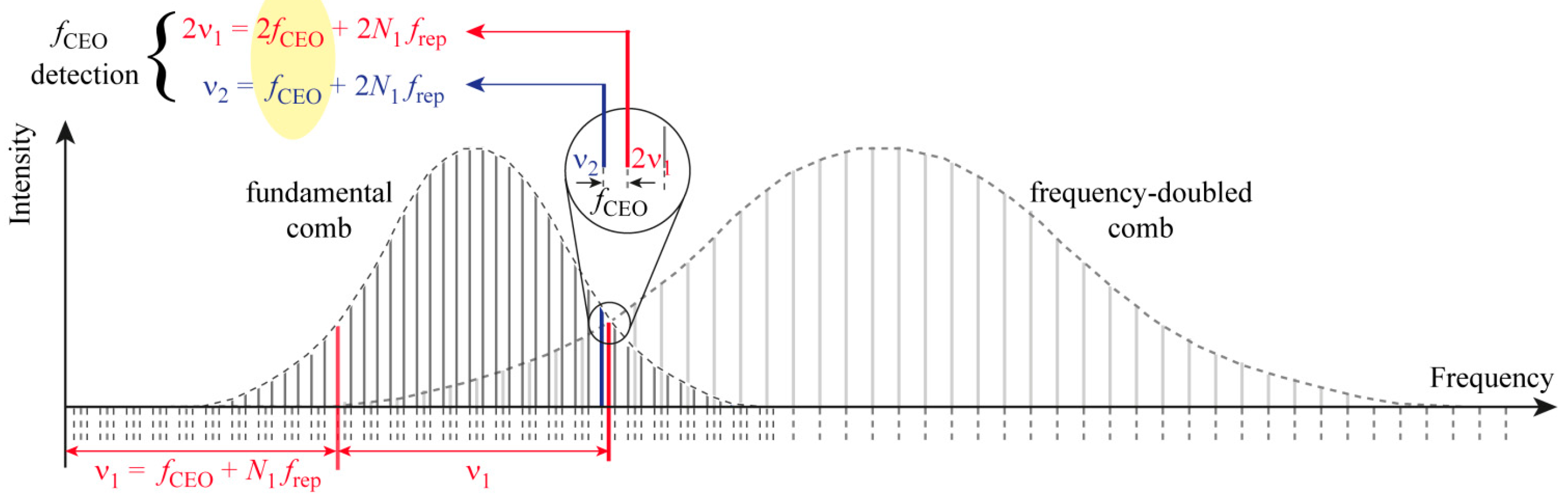
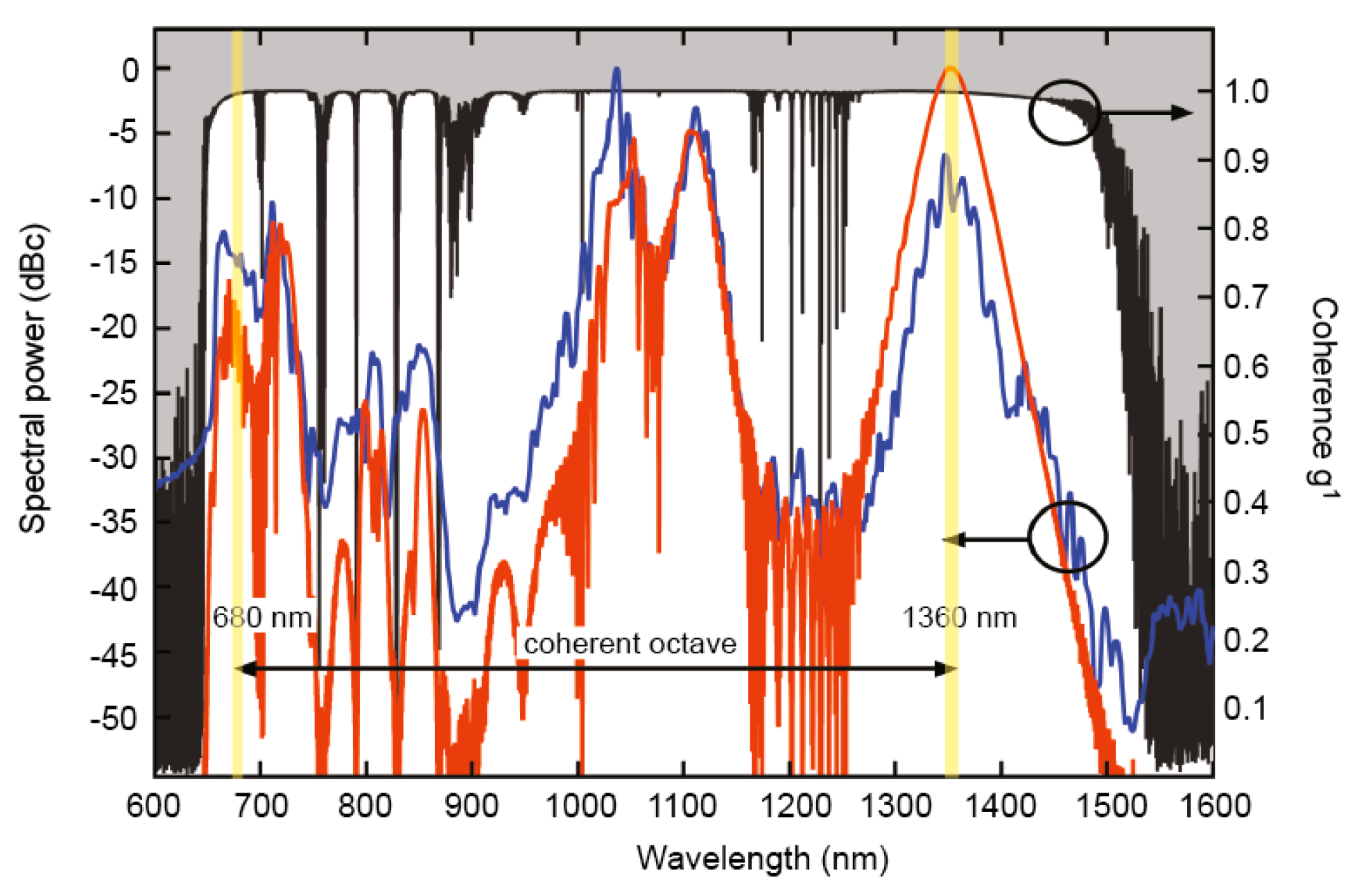
2.2. Coherent Supercontinuum Spectrum Generation
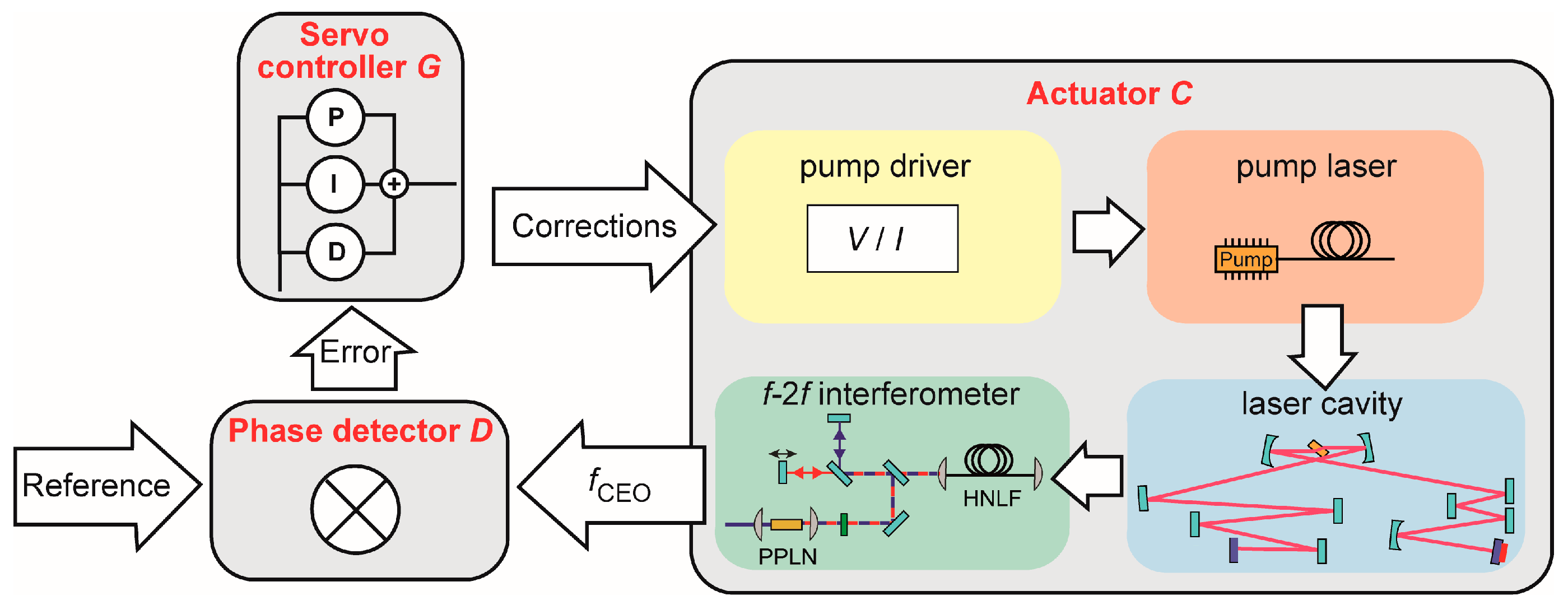
2.3. CEO Stabilization Loop

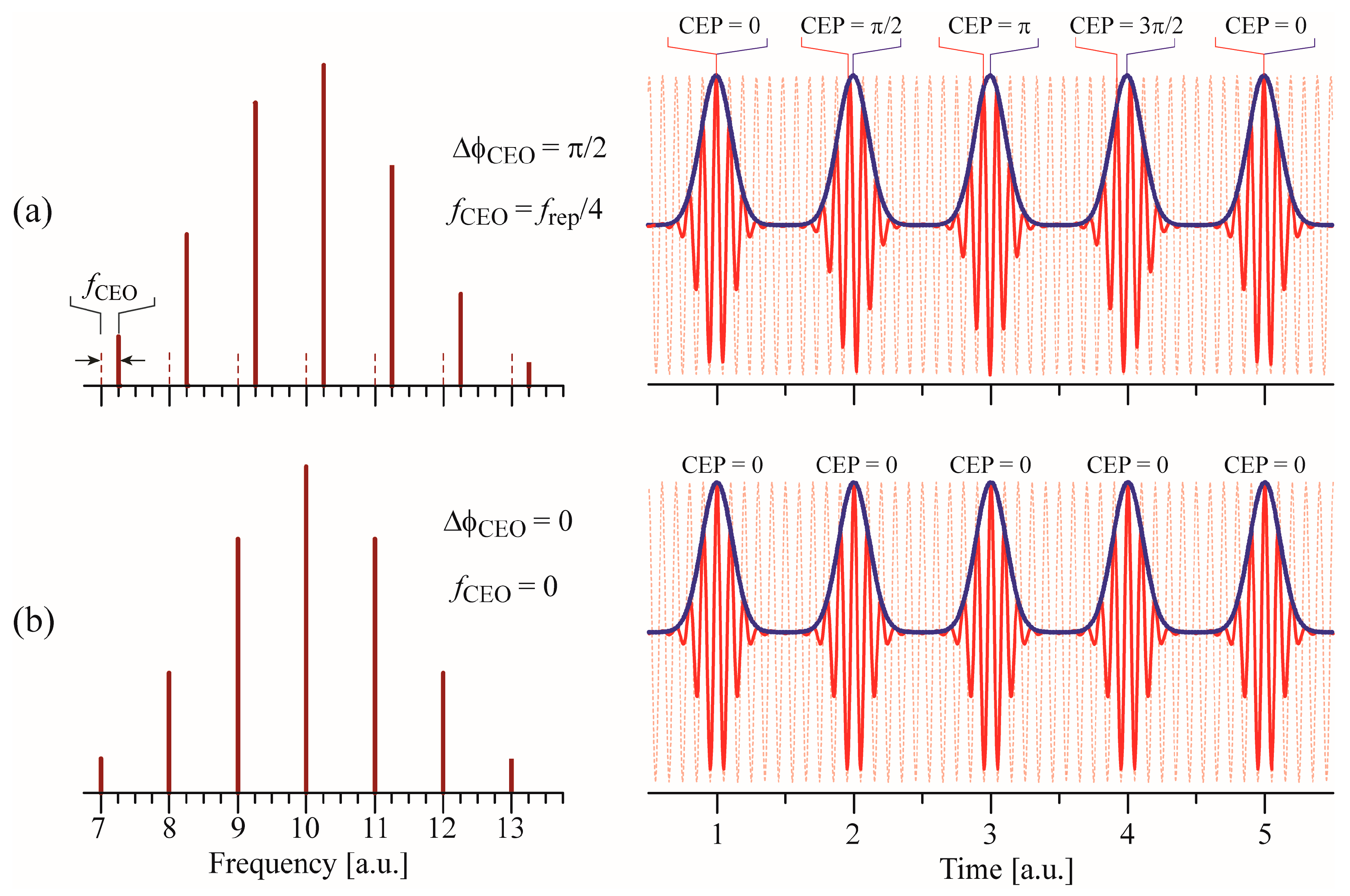
2.4. CEO vs. CEP Stabilization
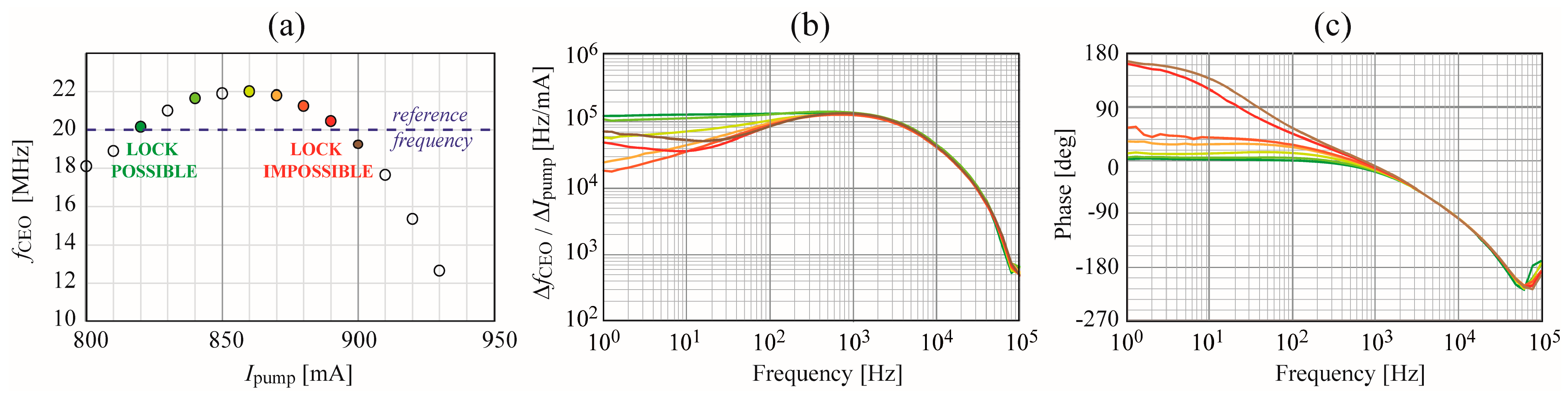
3. Self-Referenced DPSSLs with Bulk Gain Material
3.1. Chromium-Doped Lasers
| Type | Gain | λ (nm) | Pav (W) | frep (GHz) | Δτ (fs) | ML | Pump | CEO Control | CEO Lock BW (kHz) | CEO Integr. Noise (mrad) | Other | Refs. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bulk DPSSLs | Cr:LiSAF | 894 | 0.115 | 0.093 | ~60 | KLM | STM | not stabilized | - | [55] | ||
| Yb:KYW | 1033 | 0.250 | 0.16 | ~300 | SESAM | FBG-STM | Ipump | 100 | 300 [[0.1 Hz–1 MHz] | External amplification + compression | [25,26] | |
| Yb:KGW | 1042 | 2.2 | 1.0 | ~290 | SESAM | STM | not stabilized | External compression | [19] | |||
| Yb:KGW | 1047 | 3.4 | 1.06 | 125 | SESAM | MTM | not stabilized | - | [20] | |||
| Yb:KGW | 1040 | 0.6 | 0.133 | 100 | SESAM | MTM | Ipump | ~300 | 407 [[1 Hz–5 MHz] | - | [56] | |
| Yb:CALGO | 1062 | 1.7 | 1.0 | ~60 | SESAM | MTM | Ipump | ~300 | 744 [[1 Hz–5 MHz] | - | [21] | |
| Yb:CALGO | 1055 | 1.7 | 1.0 | 63 | SESAM | VHG-MTM | Ipump | <200 | 339 [[1 Hz–5 MHz] | - | [57] | |
| Yb | 1047 | 0.205 | 0.1 | 111 | SESAM | FBG-STM | Ipump | ~130 | 83 [[1 Hz–1 MHz] | - | [29] | |
| Yb:KGW | 1031 | 0.215 | 0.1 | 155 | SESAM | Ipump | ~100 | 1100 [ 1 Hz; 1 MHz] | External compression | [58] | ||
| Er:Yb:glass | 1558 | 0.11 | 0.075 | 170 | SESAM | FBG-STM | Ipump | 5.5 | 720 [[1 Hz–100 kHz] | - | [27,28] | |
| Er:Yb:glass | 1558 | 0.11 | 0.075 | 170 | SESAM | FBG-STM | OOM | 40–50 | 65 (30 *) [[1 Hz–100 kHz] | - | [44] | |
| Er:Yb:glass | 1560 | 0.115 | 0.1 | 190 | SESAM | FBG-STM | AOFS-FB | not reported | 118 | - | [59] | |
| Thin Disk Lasers | Yb:Lu2O3 | 1035 | 7 | 0.064 | 142 | SESAM | VHG-MTM | not stabilized | - | [60] | ||
| Yb:YAG | 1030 | 17 | 0.038 | 250 | KLM | MTM | Ipump IC-AOM | not reported | 250 100/200 (ool **) [[1 Hz–500 kHz] | External compression | [61] | |
| Yb:YAG | 1030 | 40 | 0.038 | 250 | KLM | MTM | IC-AOM | not reported | 180/270 (ool **) [[1 Hz–500 kHz] | External compression | [62] | |
| Yb:CALGO | 1052 | 2.1 | 0.065 | 70 | SESAM | VHG-MTM | Ipump | 30–40 | 120 [[1 Hz–1 MHz] | - | [30] | |
| Yb:YAG | 1030 | 140 | 0.0095 | ~950 | SESAM | MTM | not stabilized | External compression | [31,63] | |||
3.2. One-Micrometer Ytterbium-Doped Lasers
3.3. 1.5-μm Erbium-Doped Lasers
4. Self-Referenced DPSSLs in Thin Disk Geometry
5. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
References
- Hänsch, T.W. Nobel lecture: Passion for precision. Rev. Mod. Phys. 2006, 78, 1297–1309. [Google Scholar] [CrossRef]
- Ye, J.; Schnatz, H.; Hollberg, L.W. Optical frequency combs: From frequency metrology to optical phase control. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1041–1058. [Google Scholar]
- Diddams, S.A.; Udem, T.; Bergquist, J.C.; Curtis, E.A.; Drullinger, R.E.; Hollberg, L.; Itano, W.M.; Lee, W.D.; Oates, C.W.; Vogel, K.R.; et al. An Optical Clock Based on a Single Trapped 199Hg+ Ion. Science 2001, 293, 825–828. [Google Scholar] [CrossRef] [PubMed]
- Sterr, U.; Degenhardt, C.; Stoehr, H.; Lisdat, C.; Schnatz, H.; Helmcke, J.; Riehle, F.; Wilpers, G.; Oates, C.; Hollberg, L. The optical calcium frequency standards of PTB and NIST. C. R. Phys. 2004, 5, 845–855. [Google Scholar] [CrossRef]
- Quinlan, F.; Fortier, T.M.; Kirchner, M.S.; Taylor, J.A.; Thorpe, M.J.; Lemke, N.; Ludlow, A.D.; Jiang, Y.; Diddams, S.A. Ultralow phase noise microwave generation with an Er:fiber-based optical frequency divider. Opt. Lett. 2011, 36, 3260–3262. [Google Scholar] [CrossRef] [PubMed]
- Diddams, S.A.; Hollberg, L.; Mbele, V. Molecular fingerprinting with the resolved modes of a femtosecond laser frequency comb. Nature 2007, 445, 627–630. [Google Scholar] [CrossRef] [PubMed]
- Schiller, S. Spectrometry with frequency combs. Opt. Lett. 2002, 27, 766–768. [Google Scholar] [CrossRef] [PubMed]
- Diddams, S.A. The evolving optical frequency comb. J. Opt. Soc. Am. B 2010, 27, B51–B62. [Google Scholar] [CrossRef]
- Ma, L.S.; Zucco, M.; Picard, S.; Robertsson, L.; Windeler, R.S. A new method to determine the absolute mode number of a mode-locked femtosecond-laser comb used for absolute optical frequency measurements. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1066–1071. [Google Scholar]
- Hall, J.L. Nobel lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 778, 1279–1295. [Google Scholar] [CrossRef]
- Telle, H.R.; Steinmeyer, G.; Dunlop, A.E.; Stenger, J.; Sutter, D.H.; Keller, U. Carrier-envelope offset phase control: A novel concept for absolute optical frequency measurement and ultrashort pulse generation. Appl. Phys. B 1999, 69, 327–332. [Google Scholar] [CrossRef]
- Holzwarth, R.; Udem, T.; Hänsch, T.W.; Knight, J.C.; Wadsworth, W.J.; Russell, P.S. Optical frequency synthesizer for precision spectroscopy. Phys. Rev. Lett. 2000, 85, 2264–2267. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.J.; Diddams, S.A.; Ranka, J.K.; Stentz, A.; Windeler, R.S.; Hall, J.L.; Cundiff, S.T. Carrier envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 2000, 288, 635–639. [Google Scholar] [CrossRef] [PubMed]
- Predehl, K.; Grosche, G.; Raupach, S.M.F.; Droste, S.; Terra, O.; Alnis, J.; Legero, T.; Hänsch, T.W.; Udem, T.; Holzwarth, R.; et al. A 920-Kilometer Optical Fiber Link for Frequency Metrology at the 19th Decimal Place. Science 2012, 336, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Hartl, I.; McKay, H.A.; Thapa, R.; Thomas, B.K.; Ruehl, A.; Dong, L.; Fermann, M.E. Fully Stabilized GHz Yb-Fiber Laser Frequency Comb. In Proceedings of the Advanced Solid-State Photonics, Denver, CO, USA, 1–4 February 2009.
- Lee, C.-C.; Mohr, C.; Bethge, J.; Suzuki, S.; Fermann, M.E.; Hartl, I.; Schibli, T.R. Frequency comb stabilization with bandwidth beyond the limit of gain lifetime by an intracavity graphene electro-optic modulator. Opt. Lett. 2012, 37, 3084–3086. [Google Scholar] [CrossRef] [PubMed]
- Klenner, A.; Golling, M.; Keller, U. High peak power gigahertz Yb:CALGO laser. Opt. Express 2014, 22, 11884–11891. [Google Scholar] [CrossRef] [PubMed]
- Pekarek, S.; Klenner, A.; Südmeyer, T.; Fiebig, C.; Paschke, K.; Erbert, G.; Keller, U. Femtosecond diode-pumped solid-state laser with a repetition rate of 4.8 GHz. Opt. Express 2012, 20, 4248–4253. [Google Scholar] [CrossRef] [PubMed]
- Pekarek, S.; Südmeyer, T.; Lecomte, S.; Kundermann, S.; Dudley, J.M.; Keller, U. Self-referenceable frequency comb from a gigahertz diode-pumped solid-state laser. Opt. Express 2011, 19, 16491–16497. [Google Scholar] [CrossRef] [PubMed]
- Klenner, A.; Golling, M.; Keller, U. A gigahertz multimode-diode-pumped Yb:KGW enables a strong frequency comb offset beat signal. Opt. Express 2013, 21, 10351–10357. [Google Scholar] [CrossRef] [PubMed]
- Klenner, A.; Schilt, S.; Südmeyer, T.; Keller, U. Gigahertz frequency comb from a diode-pumped solid-state laser. Opt. Express 2014, 22, 31008–31019. [Google Scholar] [CrossRef] [PubMed]
- Fortier, T.M.; Kirchner, M.S.; Quinlan, F.; Taylor, J.; Bergquist, J.C.; Rosenband, T.; Lemke, N.; Ludlow, A.; Jiang, Y.; Oates, C.W.; et al. Generation of Ultrastable Microwaves via Optical Frequency Division. Nat. Photonics 2011, 5, 425–429. [Google Scholar] [CrossRef]
- Steinmetz, T.; Wilken, T.; Araujo-Hauck, C.; Holzwarth, R.; Hänsch, T.W.; Pasquini, L.; Manescau, A.; D’Odorico, S.; Murphy, M.T.; Kentischer, T.; et al. Laser Frequency Combs for Astronomical Observations. Science 2008, 321, 1335–1337. [Google Scholar] [CrossRef] [PubMed]
- Rauschenberger, J.; Fortier, T.; Jones, D.; Ye, J.; Cundiff, S. Control of the frequency comb from a modelocked Erbium-doped fiber laser. Opt. Express 2002, 10, 1404–1410. [Google Scholar] [CrossRef] [PubMed]
- Meyer, S.A.; Squier, J.A.; Diddams, S.A. Diode-pumped Yb:KYW femtosecond laser frequency comb with stabilized carrier envelope offset frequency. Eur. Phys. J. D 2008, 48, 19–26. [Google Scholar] [CrossRef]
- Meyer, S.A.; Fortier, T.M.; Lecomte, S.; Diddams, S.A. A frequency-stabilized Yb:KYW femtosecond laser frequency comb and its application to low-phase-noise microwave generation. Appl. Phys. B 2013, 112, 565–570. [Google Scholar] [CrossRef]
- Schilt, S.; Bucalovic, N.; Dolgovskiy, V.; Schori, C.; Stumpf, M.C.; di Domenico, G.; Pekarek, S.; Oehler, A.E.H.; Südmeyer, T.; Keller, U.; et al. Fully stabilized optical frequency comb with sub-radian CEO phase noise from a SESAM modelocked 1.5-μm solid-state laser. Opt. Express 2011, 19, 24171–24181. [Google Scholar] [CrossRef] [PubMed]
- Schilt, S.; Dolgovski, V.; Bucalovic, N.; Schori, C.; Stumpf, M.C.; Di Domenico, G.; Pekarek, S.; Oehler, A.E.H.; Südmeyer, T.; Keller, U.; et al. Noise properties of an optical frequency comb from a SESAM-modelocked 1.5-µm solid-state laser stabilized to the 10−13 level. Appl. Phys. B 2012, 109, 391–402. [Google Scholar]
- Kundermann, S.; Portuondo-Campa, E.; Lecomte, S. Ultra-low-noise 1 μm optical frequency comb. IEEE Electron. Lett. 2014, 50, 1231–1232. [Google Scholar] [CrossRef]
- Klenner, A.; Emaury, F.; Schriber, C.; Diebold, A.; Saraceno, C.J.; Schilt, S.; Keller, U.; Südmeyer, T. Phase-Stabilization of the Carrier-Envelope-Offset Frequency of a SESAM modelocked Thin Disk Laser. Opt. Express 2013, 21, 24770–24780. [Google Scholar] [CrossRef] [PubMed]
- Emaury, F.; Diebold, A.; Klenner, A.; Saraceno, C.J.; Schilt, S.; Südmeyer, T.; Keller, U. Frequency comb offset dynamics of SESAM modelocked thin disk lasers. Opt. Express 2015, 23, 21836–21856. [Google Scholar] [CrossRef] [PubMed]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-based optical frequency combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Del’Haye, P.; Arcizet, O.; Schliesser, A.; Holzwarth, R.; Kippenberg, T.J. Full Stabilization of a Microresonator-Based Optical Frequency Comb. Phys. Rev. Lett. 2008, 101, 053903. [Google Scholar] [CrossRef] [PubMed]
- Hou, D.; Ning, B.; Wu, J.; Wang, Z.; Zhao, J. Demonstration of a stable erbium-fiber-laser-based frequency comb based on a single rubidium atomic resonator. Appl. Phys. Lett. 2013, 102, 151104. [Google Scholar] [CrossRef]
- Schratwieser, T.C.; Balskus, K.; McCracken, R.A.; Farrell, C.; Leburn, C.G.; Zhang, Z.; Lamour, T.P.; Ferreiro, T.I.; Marandi, A.; Arnold, A.S.; et al. 87Rb-stabilized 375-MHz Yb:fiber femtosecond frequency comb. Opt. Express 2014, 22, 10494–10499. [Google Scholar] [CrossRef] [PubMed]
- Saraceno, C.J.; Emaury, F.; Heckl, O.H.; Baer, C.R.E.; Hoffmann, M.; Schriber, C.; Golling, M.; Südmeyer, T.; Keller, U. 275 W average output power from a femtosecond thin disk oscillator operated in a vacuum environment. Opt. Express 2012, 20, 23535–23541. [Google Scholar] [CrossRef] [PubMed]
- Ferray, M.; L’Huillier, A.; Li, X.F.; Lompré, L.A.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B 1988, 21, L31–L35. [Google Scholar] [CrossRef]
- Apolonski, A.; Poppe, A.; Tempea, G.; Spielmann, C.; Udem, T.; Holzwarth, R.; Hänsch, T.W.; Krausz, F. Controlling the Phase Evolution of Few-Cycle Light Pulses. Phys. Rev. Lett. 2000, 85, 740–743. [Google Scholar] [CrossRef] [PubMed]
- Ramond, T.M.; Diddams, S.A.; Hollberg, L.; Bartels, A. Phase coherent link from optical to microwave frequencies via the broadband continuum from a 1 GHz Ti:Sapphire femtosecond oscillator. Opt. Lett. 2002, 27, 1842–1844. [Google Scholar] [CrossRef] [PubMed]
- Ell, R.; Morgner, U.; Kärtner, F.X.; Fujimoto, J.G.; Ippen, E.P.; Scheuer, V.; Angelow, G.; Tschudi, T.; Lederer, M.J.; Boiko, A.; et al. Generation of 5 fs pulses and octave-spanning spectra directly from a Ti:Sapphire laser. Opt. Lett. 2001, 26, 373–375. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Genty, G.; Cohen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Meyer, A.S.; Klenner, A.; Johnson, A.R.; Luke, K.; Lamont, M.R.E.; Okawachi, Y.; Lipson, M.; Gaeta, A.L.; Keller, U. Frequency comb offset detection using supercontinuum generation in silicon nitride waveguides. Opt. Express 2015, 23, 15440–15451. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Washburn, B.R.; Wilpers, G.; Oates, C.W.; Hollberg, L.; Newbury, N.R.; Diddams, S.A.; Nicholson, J.W.; Yan, M.F. Stabilized frequency comb with a self-referenced femtosecond Cr:forsterite laser. Opt. Lett. 2005, 30, 932–934. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.; Schilt, S.; Südmeyer, T. CEO stabilization of a femtosecond laser using a SESAM as fast opto-optical modulator. Opt. Express 2013, 21, 30054–30064. [Google Scholar] [CrossRef] [PubMed]
- Schilt, S.; Bucalovic, N.; Tombez, L.; Dolgovskiy, V.; Schori, C.; Di Domenico, G.; Zaffalon, M.; Thomann, P. Frequency discriminators for the characterization of narrow-spectrum heterodyne beat signals: Application to the measurement of a sub-hertz carrier-envelope-offset beat in an optical frequency comb. Rev. Sci. Instrum. 2011, 82, 123116. [Google Scholar] [CrossRef] [PubMed]
- Riehle, F. Frequency Standards, Basics and Applications; WILEY-VCH Verlag GmbH & Co.: Weinheim, Germany, 2004; Chapter 3. [Google Scholar]
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple approach to the relation between laser frequency noise and laser lineshape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef] [PubMed]
- Bucalovic, N.; Dolgovskiy, V.; Schori, C.; Thomann, P.; Di Domenico, G.; Schilt, S. Experimental Validation of a Simple Approximation to Determine the Linewidth of a Laser from Its Frequency Noise Spectrum. Appl. Opt. 2012, 51, 4582–4588. [Google Scholar] [CrossRef] [PubMed]
- Bucalovic, N.; Dolgovskiy, V.; Stumpf, M.C.; Schori, C.; di Domenico, G.; Keller, U.; Schilt, S.; Südmeyer, T. Effect of the Carrier-Envelope-Offset Dynamics on the Stabilization of a Diode-Pumped Solid-State Frequency Comb. Opt. Lett. 2012, 37, 4428–4430. [Google Scholar] [CrossRef] [PubMed]
- Fox, R.W.; Oates, C.W.; Hollberg, L.W. Stabilizing diode lasers to high-finesse cavities. In Experimental Methods in the Physical Sciences;Cavity-Enhanced Spectroscopies; van Zee, R.D., Looney, J.P., Eds.; Academic Press: Waltham, MA, USA, 2003; Volume 40, pp. 1–46. [Google Scholar]
- Cundiff, S.T. Phase stabilization of ultrashort optical pulses. J. Phys. D Appl. Phys. 2002, 35, R43–R57. [Google Scholar] [CrossRef]
- Koke, S.; Grebing, C.; Frei, H.; Anderson, A.; Assion, A.; Steinmeyer, G. Direct frequency comb synthesis with arbitrary offset and shot-noise-limited phase noise. Nat. Photonics 2010, 4, 462–465. [Google Scholar] [CrossRef]
- Krauss, G.; Fehrenbacher, D.; Brida, D.; Riek, C.; Sell, A.; Huber, R.; Leitenstorfer, A. All-passive phase locking of a compact Er:fiber laser system. Opt. Lett. 2011, 36, 540–542. [Google Scholar] [CrossRef] [PubMed]
- Keller, U.; Weingarten, K.J.; Kärtner, F.X.; Kopf, D.; Braun, B.; Jung, I.D.; Fluck, R.; Hönninger, C.; Matuschek, N.; Aus der Au, J. Semiconductor saturable absorber mirrors (SESAMs) for femtosecond tonanosecond pulse generation in solid-state lasers. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 435–453. [Google Scholar] [CrossRef]
- Holzwarth, R.; Zimmermann, M.; Udem, T.; Hänsch, T.W.; Russbüldt, P.; Gäbel, K.; Poprawe, R.; Knight, J.C.; Wadsworth, W.J.; Russell, P.S.J. White-light frequency comb generation with a diode-pumped Cr:LiSAF laser. Opt. Lett. 2001, 26, 1376–1378. [Google Scholar] [CrossRef] [PubMed]
- Klenner, A.; Emaury, F.; Diebold, A.; Schriber, C.; Saraceno, C.J.; Schilt, S.; Südmeyer, T.; Keller, U. Harnessing frequency combs pumped by multimode high-power diodes. In Proceedings of the EPS-QEOD Europhoton Conference, Neuchatel, Switzerland, 24–29 August 2014.
- Meyer, A.S.; Klenner, A.; Johnson, A.R.; Luke, K.; Lamont, M.R.E.; Okawachi, Y.; Lipson, M.; Gaeta, A.L.; Keller, U. Low-noise Gigahertz Frequency Comb from diode-Pumped Solid-State Laser using Silicon Nitride Waveguides. In Proceedings of the Advanced Solid State Lasers Conference and Exhibition (ASSL), Berlin, Germany, 4–8 October 2015.
- Buchs, G.; Kundermann, S.; Portuondo-Campa, E.; Lecomte, S. Radiation hard mode-locked laser suitable as a spaceborne frequency comb. Opt. Express 2015, 23, 9890–9900. [Google Scholar] [CrossRef] [PubMed]
- Kundermann, S.; Lecomte, S. Comparison of different carrier-envelope frequency stabilization methods for a high performance DPSSL frequency comb. In Proceedings of the 2015 Joint Conference of the IEEE International Frequency Control Symposium & European Frequency and Time Forum (FCS), Denver, CO, USA, 12–16 April 2015; pp. 594–598.
- Saraceno, C.J.; Pekarek, S.; Heckl, O.H.; Baer, C.R.E.; Schriber, C.; Golling, M.; Beil, K.; Kränkel, C.; Huber, G.; Keller, U.; et al. Self-referenceable frequency comb from an ultrafast thin disk laser. Opt. Express 2012, 20, 9650–9656. [Google Scholar] [CrossRef] [PubMed]
- Pronin, O.; Seidel, M.; Brons, J.; Lücking, F.; Pervak, V.; Apolonski, A.; Udem, T.; Krausz, F. Carrier-envelope phase stabilized thin-disk oscillator. In Proceedings of the Advanced Solid-State Lasers conference, Paris, France, 27 October–1 November 2013.
- Pronin, O.; Seidel, M.; Lücking, F.; Brons, J.; Fedulova, E.; Trubetskov, M.; Pervak, V.; Apolonski, A.; Udem, T.; Krausz, F. High-power multi-megahertz source of waveform-stabilized few-cycle light. Nat. Commun. 2015, 6, 6988. [Google Scholar] [CrossRef] [PubMed]
- Diebold, A.; Emaury, F.; Schriber, C.; Saraceno, C.J.; Südmeyer, T.; Keller, U. Self-referenceable frequency comb with 140 W of average power. In Proceedings of the 6th EPS-QEOD Europhoton Conference, Neuchatel, Switzerland, 24–29 August 2014.
- Hönninger, C.; Paschotta, R.; Morier-Genoud, F.; Moser, M.; Keller, U. Q-switching stability limits of continuous-wave passive mode locking. J. Opt. Soc. Am. B 1999, 16, 46–56. [Google Scholar] [CrossRef]
- Chin, A.K.; Bertaska, R.K. Catastrophic Optical Damage in High-Power, Broad-Area Laser Diodes. In Materials and Reliability Handbook for Semiconductor Optical and Electron Devices; Ueda, O., Pearton, S.J., Eds.; Springer: New York, NY, USA, 2013; pp. 123–147. [Google Scholar]
- Link, S.M.; Klenner, A.; Mangold, M.; Zaugg, C.A.; Mayer, A.S.; Gini, E.; Tilma, B.W.; Keller, U. Passive linewidth reduction of the carrier-envelope-offset frequency. In Proceedings of the 6th EPS-QEOD Europhoton Conference, Neuchatel, Switzerland, 24–29 August 2014.
- Dolgovskiy, V.; Bucalovic, N.; Thomann, P.; Schori, C.; Di Domenico, G.; Schilt, S. Cross-influence between the two servo-loops of a fully-stabilized Er:fiber optical frequency comb. J. Opt. Soc. Am. B 2012, 29, 2944–2957. [Google Scholar] [CrossRef]
- Mulder, T.D.; Scott, R.P.; Kolner, B.H. Amplitude and envelope phase noise of a modelocked laser predicted from its noise transfer function and the pump noise power spectrum. Opt. Express 2008, 16, 14186–14191. [Google Scholar] [CrossRef] [PubMed]
- McFerran, J.J.; Swann, W.C.; Washburn, B.R.; Newbury, N.R. Suppression of pump-induced frequency noise in fiber-laser frequency combs leading to sub-radion fceo phase excursion. Appl. Phys. B 2007, 86, 219–227. [Google Scholar] [CrossRef]
- Petit, J.; Goldner, P.; Viana, B. Laser emission with low quantum defect in Yb:CaGdAlO4. Opt. Lett. 2005, 30, 1345–1347. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Lee, K.; Jang, Y.-S.; Jang, H.; Han, S.; Lee, S.-H.; Kang, K.-I.; Lim, C.-W.; Kim, Y.-J.; Kim, S.-W. Testing of a femtosecond pulse laser in outer space. Sci. Rep. 2014, 4, 5134. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, M.; Pekarek, S.; Oehler, A.E.H.; Südmeyer, T.; Dudley, J.M.; Keller, U. Self-referencable frequency comb from a 170-fs, 1.5-μm solid-state laser oscillator. Appl. Phys. B 2010, 99, 401–408. [Google Scholar] [CrossRef]
- Dolgovskiy, V.; Schilt, S.; Bucalovic, N.; Di Domenico, G.; Grop, S.; Dubois, B.; Giordano, V.; Südmeyer, T. Ultra-stable microwave generation with a diode-pumped solid-state laser in the 1.5-µm range. Appl. Phys. B 2014, 116, 593–601. [Google Scholar] [CrossRef]
- Portuondo-Campa, E.; Paschotta, R.; Lecomte, S. Sub-100 attosecond timing jitter from low-noise passively mode-locked solid-state laser at telecom wavelength. Opt. Lett. 2013, 38, 2650–2653. [Google Scholar]
- Portuondo-Campa, E.; Buchs, G.; Kundermann, S.; Lecomte, S. Ultra-low phase noise microwave generation from a diode-pumped solid-state laser. In Proceedings of the 2015 Joint Conference of the IEEE International Frequency Control Symposium & European Frequency and Time Forum (FCS), Denver, CO, USA, 12–16 April 2015.
- Portuondo-Campa, E.; Bennès, J.; Kundermann, S.; Lecomte, S. Dual frequency comb interferometer for fast and high resolution optical spectroscopy. In Proceedings of the CLEO/Europe-EQEC 2015, Munich, Germany, 21–25 June 2015.
- Giesen, A.; Hügel, H.; Voss, A.; Wittig, K.; Brauch, U.; Opower, H. Scalable concept for diode-pumped high-power solid-state lasers. Appl. Phys. B 1994, 58, 365–372. [Google Scholar] [CrossRef]
- Saraceno, C.J.; Emaury, F.; Schriber, C.; Hoffmann, M.; Golling, M.; Südmeyer, T.; Keller, U. Ultrafast thin-disk laser with 80 μJ pulse energy and 242 W of average power. Opt. Lett. 2014, 39, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Matos, L.; Mücke, O.D.; Chen, J.; Kärtner, F.X. Carrier-envelope phase dynamics and noise analysis in octave-spanning Ti:Sapphire lasers. Opt. Express 2006, 14, 2497–2511. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schilt, S.; Südmeyer, T. Carrier-Envelope Offset Stabilized Ultrafast Diode-Pumped Solid-State Lasers. Appl. Sci. 2015, 5, 787-816. https://doi.org/10.3390/app5040787
Schilt S, Südmeyer T. Carrier-Envelope Offset Stabilized Ultrafast Diode-Pumped Solid-State Lasers. Applied Sciences. 2015; 5(4):787-816. https://doi.org/10.3390/app5040787
Chicago/Turabian StyleSchilt, Stéphane, and Thomas Südmeyer. 2015. "Carrier-Envelope Offset Stabilized Ultrafast Diode-Pumped Solid-State Lasers" Applied Sciences 5, no. 4: 787-816. https://doi.org/10.3390/app5040787
APA StyleSchilt, S., & Südmeyer, T. (2015). Carrier-Envelope Offset Stabilized Ultrafast Diode-Pumped Solid-State Lasers. Applied Sciences, 5(4), 787-816. https://doi.org/10.3390/app5040787





