Abstract
We report on a possibility of efficient engineering of the acoustic phonon energy spectrum in multishell tubular structures produced by a novel high-tech method of self-organization of micro- and nano-architectures. The strain-driven roll-up procedure paved the way for novel classes of metamaterials such as single semiconductor radial micro- and nano-crystals and multi-layer spiral micro- and nano-superlattices. The acoustic phonon dispersion is determined by solving the equations of elastodynamics for InAs and GaAs material systems. It is shown that the number of shells is an important control parameter of the phonon dispersion together with the structure dimensions and acoustic impedance mismatch between the superlattice layers. The obtained results suggest that rolled up nano-architectures are promising for thermoelectric applications owing to a possibility of significant reduction of the thermal conductivity without degradation of the electronic transport.
1. Introduction
Spatial confinement of acoustic and optical phonons in semiconductor thin films, superlattices, and nanowires changes their properties in comparison with bulk materials [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Phonon confinement in nanostructures leads to emergence of the quantized energy sub-bands with corresponding modification of the phonon density of states [1,2,3,4,10,11,12,13,14,15]. The changes in the phonon dispersion give rise to changes in the electron-phonon scattering rates [15,16,17,18,19,20,21], optical properties of the nanostructured materials [5,22,23,24,25,26,27,28], and phonon scattering on defects, boundaries, and other phonons [10,12,13,29,30,31]. It was predicted that the electron mobility can be increased in the phonon engineered core-shell nanowires and planar heterostructures with the barrier shell materials, which are acoustically harder than the core materials [32,33]. The experimentally-measured reduction of the phonon thermal conductivity in thin films and nanowires usually results from the increased phonon-rough boundary scattering. Another mechanism of the thermal conductivity reduction is related to the phonon spectrum modification and decrease of the phonon group velocity in thin films [10,29,34] and nanowires [12,13,14,30,31,34]. The predicted decrease of two orders of magnitude of the thermal conductivity in silicon nanowires at room temperature [31] has recently found experimental confirmation [35]. It has been determined that the thermal conductivity of the sub-20 nm diameter nanowires is suppressed by the phonon confinement effects beyond the diffusive boundary scattering limit [35]. The acoustic phonon confinement effects theoretically predicted for thin films and nanowires [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] have been directly observed experimentally using the Brillouin light scattering technique using suspended silicon thin films with the thickness H ≈ 7 nm [36] and gallium nitride nanowires with the diameters D ≈ 150 nm [37].
The initial work on the phonon confinement effects in thin films and nanowires was performed using the elastic continuum approximation [10,11,14,29,30,31,38]. The results obtained with the elastic continuum approach have been confirmed using other techniques such as lattice dynamics [34,39] and molecular dynamics (MD) [40,41,42]. All computational approaches proved that the acoustic impedance η = ρ × v of the barrier shells of nanostructures presents an important tuning parameter for phonon transport, which can be used together with the lateral dimensions and shape for phonon engineering of material properties (ρ is the mass density and v is the sound velocity of the material). In the core-shell nanostructures with the acoustically mismatched barrier shells new types of phonon modes appear. Some of them are mainly concentrated in the nanostructure core while others are localized in the shell layers [11,14,34,38,39]. Controlling the acoustic impedance mismatch and thickness of the shell layers one can tune the electron-phonon interaction and the electron mobility [32,33]. Similarly, one can engineer the phonon group velocity and thermal conductivity in such nanostructures [11,14,34,38,39].
Further progress in phonon engineering of material properties depends on availability of nanostructures with layered structures and substantial acoustic impedance mismatch. Multilayer tubes have attracted a special attention in newly developed acoustic metamaterials and phononic crystals at the micro- and nanoscale [43,44]. In particular, a cylindrical structure from 40 alternating layers of 0.36 mm thick natural latex rubber film and 0.38 mm thick silicone elastomers containing boron nitride particles serves as a thermal shield [45]. In a two-layered tube with the weak interfaces between the layers, the dispersion characteristics of longitudinal guided acoustic wave provide a tool for detecting and exploring defects [46]. The microstructures are shown to play a decisive role in the dispersion of both flexural and longitudinal waves in single- and multiwall carbon nanotubes [47].
Acoustic metamaterials and phononic crystals are formed by periodic variation of the acoustic properties of the materials (elasticity and/or density), what leads to the occurrence of the phononic band gaps and provides powerful tools to control the phonon velocity spectra. The phonon crystals were proposed theoretically for elastic waves propagating in a composite material consisting of identical spheres [48] and infinite cylinders [49,50] with parallel axes embedded in a periodic way within a host. First, sonic materials with effective negative elastic constants were fabricated as lead-coated spheres arranged in a simple cubic crystal [51]. They acted as total wave reflectors within certain adjustable acoustic frequency ranges. Split-ring resonator periodic arrays [52] and double-negative (with the negative effective bulk modulus and the negative effective density) acoustic metamaterials [53] were suggested in a close analogy with electromagnetic metamaterials. For diverse experimental realizations of phononic crystals and their applications, see [44].
A novel method of self-assembly of micro- and nanoarchitectures was designed on the base of the strain-driven roll-up procedure [54,55]. It paved the way for novel classes of metamaterials: single semiconductor micro- and nanotubes (or radial crystals) [56] and multilayer spiral micro- and nanotubes (or radial superlattices) [57]. A comprehensive structural study was provided for semiconductor/oxide, semiconductor/organic, as well as semiconductor/metal hybrid radial superlattices [58]. A combined “roll-up press-back” technology has been recently presented to fabricate novel acoustic metamaterials/mechanically-joined nanomembrane superlattices [59], which reveal a significant reduction of the measured cross-sectional phonon transport compared to a single nanomembrane layer.
The optical phonon spectra in multilayer cylindrical quantum wires manifest a geometric structural effect [4], which is of immanent importance for understanding of the pairing of charge carries in quantum wires [60], as well as the electron-phonon phenomena in multilayer coaxial cylindrical AlxG1−xAs/GaAs quantum cables [61] and double-coupled nanoshell systems [62]. The aim of the present work is to investigate the feasibility of controlling the acoustic phonon energy spectra and corresponding phonon velocity dispersion in rolled-up micro- and nanoarchitectures. Of fundamental importance in this context is the experimental evidence [63], that due to oxide formation during fabrication, a single period of a radial superlattice is represented by a semiconductor/amorphous oxide/polycrystalline metal/amorphous oxide layer rather than a semiconductor/metal layer. This implies a necessity to investigate multilayer tubes. The elastodynamic boundary conditions on spiral interfaces of a rolled-up microtube with multiple windings or on cylindrical interfaces of a multilayer tube, which consists of coaxial cylindrical shells, (multishell) immediately affect the acoustic phonon energy spectrum and, hence, phonon group velocities for propagation along the tube. Since the effect of these boundary conditions depends on the number of shells along with the geometric parameters, multishells are qualified into acoustic metamaterials. This introduces, in particular, extra capability for tuning the phonon spectrum, engineering the phonon transport and advancement of thermoelectric materials [9].
2. Theoretical Model
Spiral interfaces of a rolled-up microtube with multiple windings (Figure 1a,b) are modelled by cylindrical interfaces of a multilayer tube that consists of coaxial shells (multishell) as shown schematically in Figure 1c. We use the elastic continuum model because it works well for the considered dimensions of the structures. It was shown previously that such a model gives results in good agreement with the lattice dynamics and MD simulations [34,39,40,41,42]. Moreover, we are primarily interested in the acoustic phonon confinement energies near the Brillouin zone (BZ) center. These phonon modes are primarily responsible for heat transfer and can be directly studied with Brillouin spectroscopy. The elastic continuum model is particularly accurate for the BZ center phonons. We consider theoretically infinitely long structures because, practically, the length of micro- and nano-tubes is much larger than their diameter. The effect of the finite length on the phonon energies is negligible in our case.
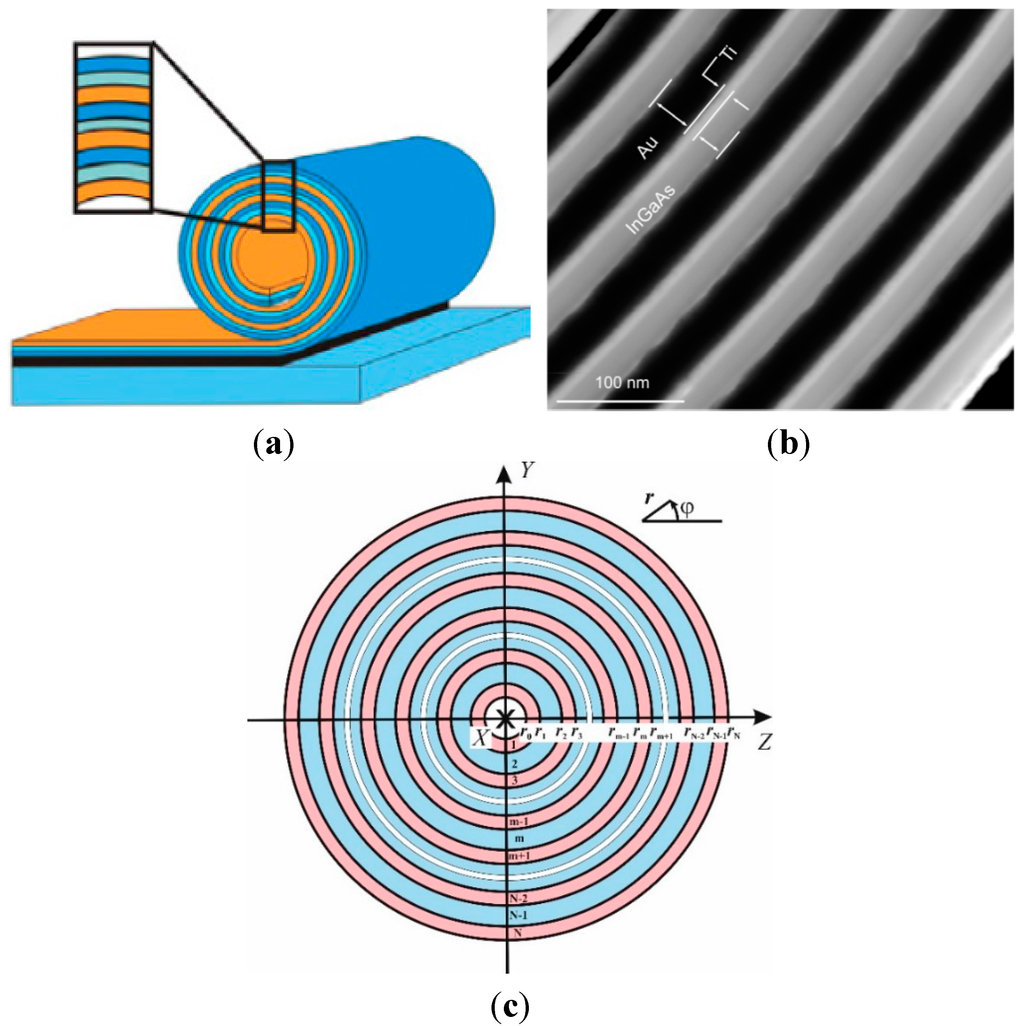
Figure 1.
Microtube with multiple windings fabricated using roll-up technology, a scheme (a) and a STEM image of a radial superlattice from a rolled-up 20 nm InGaAs/10 nm Ti/46 nm Au layer (b) (From Ref. [58] © IOP Publishing. Reproduced with permission. All rights reserved). Cross-section in the plane orthogonal to the X-axis of a multilayer tube consisting of coaxial shells (multishell) (c). The tube core and the outer medium are vacuum. The axis of the structure is selected as the X-axis. The polar coordinates in the YZ-plane are (r,φ). The picture corresponds to a multishell with a periodic alternation of two materials.
The displacement vector um in each layer (m = 1,…, N), treated as an elastic continuum, obeys the equations of elastodynamics [64]:
At every intershell boundary rm, (m = 1,…, N−1) the following six boundary conditions represent continuity of the stress tensor components:
and of the displacement vector components:
At the internal boundary r0, the following three boundary conditions represent vanishing of the stress tensor components:
Similarly, at the external boundary rN, the following three boundary conditions represent vanishing of the stress tensor components:
In total, there are 6N boundary conditions. The boundary problem described by the Equation (1) and the boundary conditions (2) to (5) for an arbitrary number of the shell pairs satisfies the correspondence principle with respect to the case of a two-shell composite coaxial tube [65,66].
The solutions to the equations of elastodynamics are sought in the form of a combination of dilatational waves and shear (equivoluminal) waves:
Here the scalar potential of the dilatational motion and the vector potential of the shear motion along the axis of the structure (which has only two independent components) satisfy the equations:
The velocities ν1m and ν2m correspond to dilatational and shear waves in the material of the m-th layer. The solutions to the wave equations are sought as plane waves traveling along the axis of the structure.
Every neighboring layers are assumed to be perfectly bonded. Therefore, the eigenwaves in all layers will have the same longitudinal wave vector ζ and circular frequency ω:
A multishell with a periodic alternation of two materials is further assumed (see Figure 1, lower panel) with r0 = 100 nm. All odd shells (m = 2k + 1) consist of one and the same material with elastic properties λ1, μ1, density ρ1 and have the same thickness: Δr1. All even shells (m = 2k) consist of the same material with elastic properties λ2, μ2, density ρ2 and have the same thickness: Δr2. They are represented in Table 1. In what follows, the number of layers is denoted by NL.

Table 1.
Geometric and materials parameters of the multishell.
| Parity i of the layer number m | 1 | 2 |
|---|---|---|
| Material | InAs | GaAs |
| λi, dyn/cm2 | 4.54 × 1011 | 5.34 × 1011 |
| μi, dyn/cm2 | 1.90 × 1011 | 3.285 × 1011 |
| ρi, g/cm3 | 5.68 | 5.317 |
| Δri, nm | 5 | 5 |
The wave characteristics in the materials are defined in Table 2.

Table 2.
Definitions of the wave characteristics in the materials.
| Characteristic of the layer with parity i of the number m | Denotation |
|---|---|
| Velocity of a dilatational wave | v1i = [(λi + 2μi)/ ρi]1/2 |
| Velocity of a shear wave | v2i = [μi/ ρi]1/2 |
| Squared radial wave number for a dilatational wave | αi2 = ω2/v1i2 − ζ2 |
| Squared radial wave number for a shear wave | βi2 = ω2/v2i2 − ζ 2 |
| Dispersion of the Rayleigh waves αi2 = 0 | ω = v1iζ |
| Dispersion of the Rayleigh waves βi2 = 0 | ω = v2iζ |
The further procedure is a generalization of that in [65] for a two-shell tube onto an arbitrary number of shells. Substituting the eigenwaves of Equation (8) into the differential equations of motion (7), we exclude three coordinates (t, x, and φ) and arrive at a set of differential equations with respect to the radial coordinate r for the amplitude functions fm(r) and hxm(r) at m = 1, 2,…, NL:
and two similar equations for the amplitude functions hrm(r) and hφm(r). Due to gauge invariance of the vector potential, one of the functions hrm(r), hφm(r), hxm(r) can be selected arbitrarily; we use, like in [65], the calibration hrm(r) = −hφm(r) ≡ h1m(r). The differential Equations (9) are Bessel equations (see Chapter 9 in [67]). Their solutions can be represented in the general form:
where Zn (Wn) are the Bessel functions of the first kind Jn (second kind Yn) (p. 358 of [67]) for the real radial wave numbers αm and βm and the modified Bessel functions In (Kn) (p. 374 of [67]) for the imaginary wave numbers αm and βm. In the set of solutions (10), there are in total 6NL unknown coefficients, which can be represented as a 6NL-dimensional vector . After substituting the solutions (10) in the set of 6NL boundary conditions (2) to (5), we arrive at a homogeneous system of 6NL linear algebraic equations with respect to 6NL components Ξj (j = 1,…, NL) of the vector Ξ:
A non-trivial solution to this system exists under the condition that its determinant vanishes:
A numerical solution to the secular Equation (12) is found using Intel® Visual Fortran with Microsoft Visual Studio 2008 [68]. It provides phonon eigenfrequencies as a function of the longitudinal wave vector ζ. The resulting phonon dispersion curves are represented below in the non-dimensional form, using the units, which are defined in Table 3.

Table 3.
Units for wave characteristics
| Physical quantity | Unit |
|---|---|
| Longitudinal wave vector ζ | 1/Δr2 |
| Frequency ω | πv22/Δr2 |
| Group velocity dω/dζ | πv22 |
3. Results for NL = 2
The lowest phonon dispersion curves (in the window of eigenfrequencies [0, 1.5]) are shown for axially-symmetric waves n = 0, NL = 2 in Figure 2. (More time-consuming calculations for flexural waves with n = 1,… are ongoing.) There are anticrossings of torsional or non-torsional modes, but there might occur crossings of torsional (ux = ur = 0, uθ ≠ 0) and non-torsional (associated with the displacement components ux and ur, uθ = 0) modes. Dispersion of the phonon group velocity for the dispersion curves in Figure 2 is represented in Figure 3 (see Figure A1 for a detailed graph). A group velocity dispersion curves stops when the eigenfrequency ω goes beyond the window [0, 1.5].
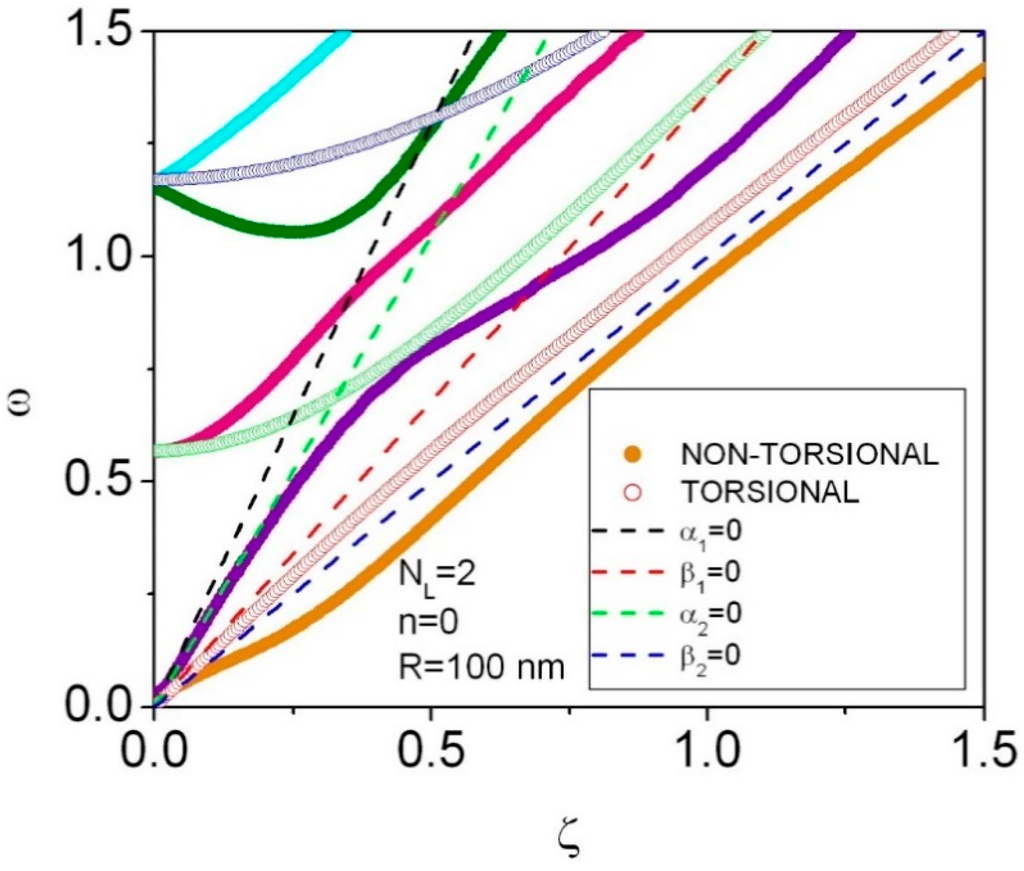
Figure 2.
Phonon dispersion curves for n = 0, NL = 2. The inner and outer radii of a multishell are r0 = 100 nm and r2 = 110 nm, respectively. Non-torsional and torsional modes are represented with filled and empty circles, correspondingly. Dashed lines indicate the dispersion curves for dilatational (αI = 0) ans shear (βI = 0) waves in the material with parity i of the number m.
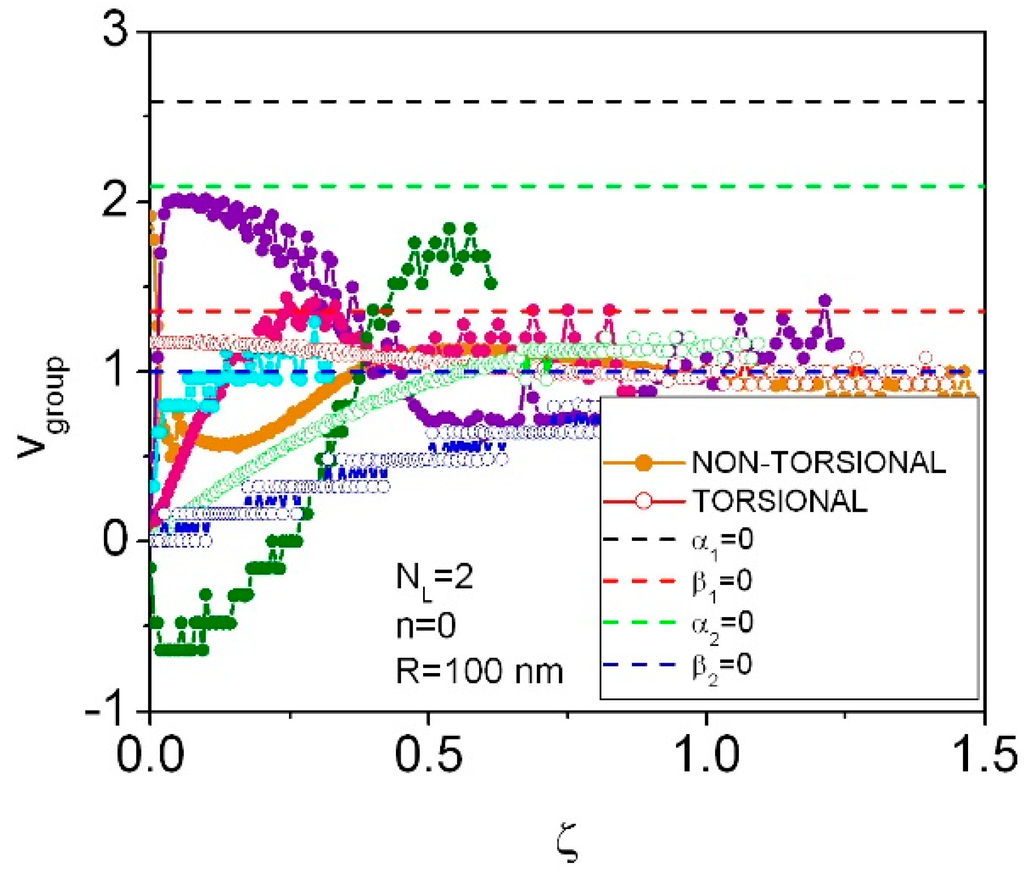
Figure 3.
Phonon group velocity dispersion curves for n = 0, NL = 2. Denotations of non-torsional and torsional modes are the same as in Figure 2.
4. Results for NL = 4 and NL =6
The lowest phonon dispersion curves are shown for axially symmetric waves n = 0, NL = 4 in Figure 4. For clarity, dispersion curves for non-torsional and torsional waves are represented also separately.
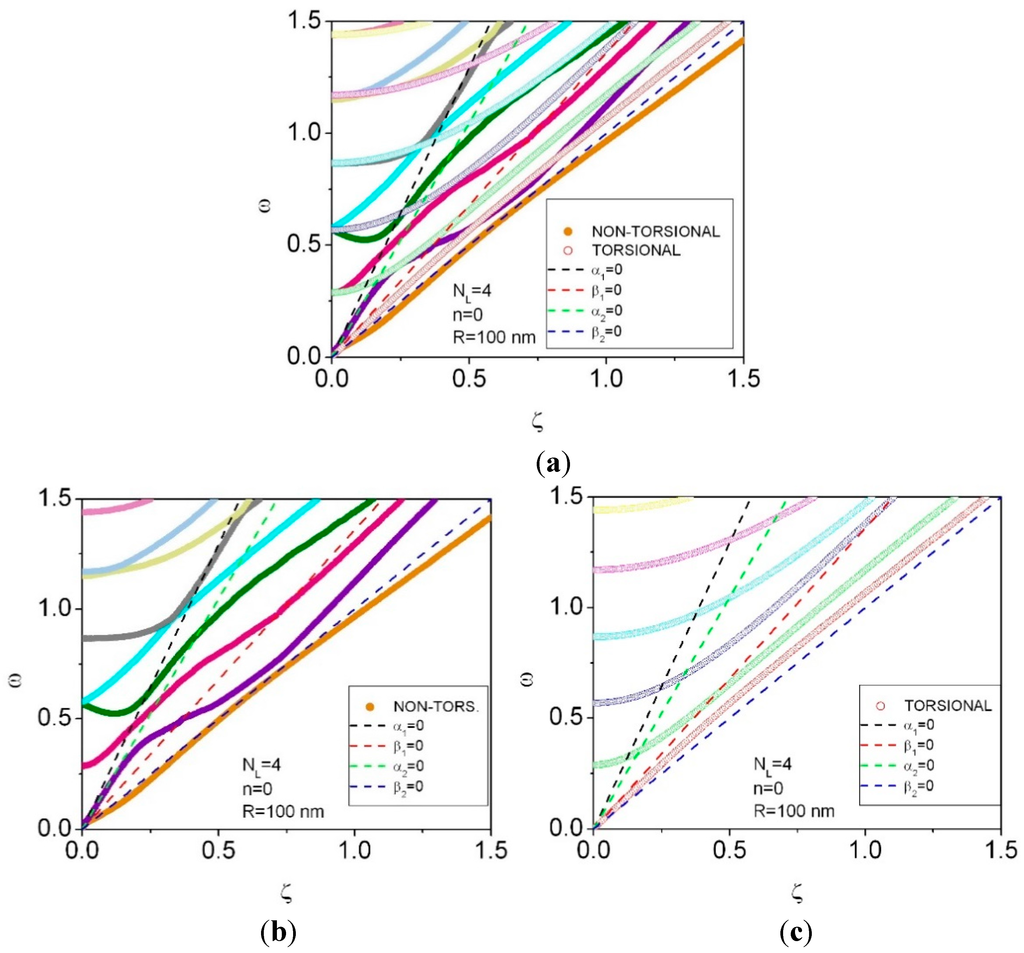
Figure 4.
Phonon dispersion curves for n = 0, NL = 4 (a). The inner and outer radii of a multishell are r0 = 100 nm and r4 = 120 nm, respectively. Phonon dispersion curves for non-torsional (b) and torsional (c) waves.
A larger number of dispersion curves in multishells with four shells emerge within the same interval of energies and wave vectors as for multishells with two shells in Figure 2. Dispersion of the phonon group velocity for the lowest dispersion curves in Figure 4 is represented in Figure 5 (see Figure A2 for a detailed graph).
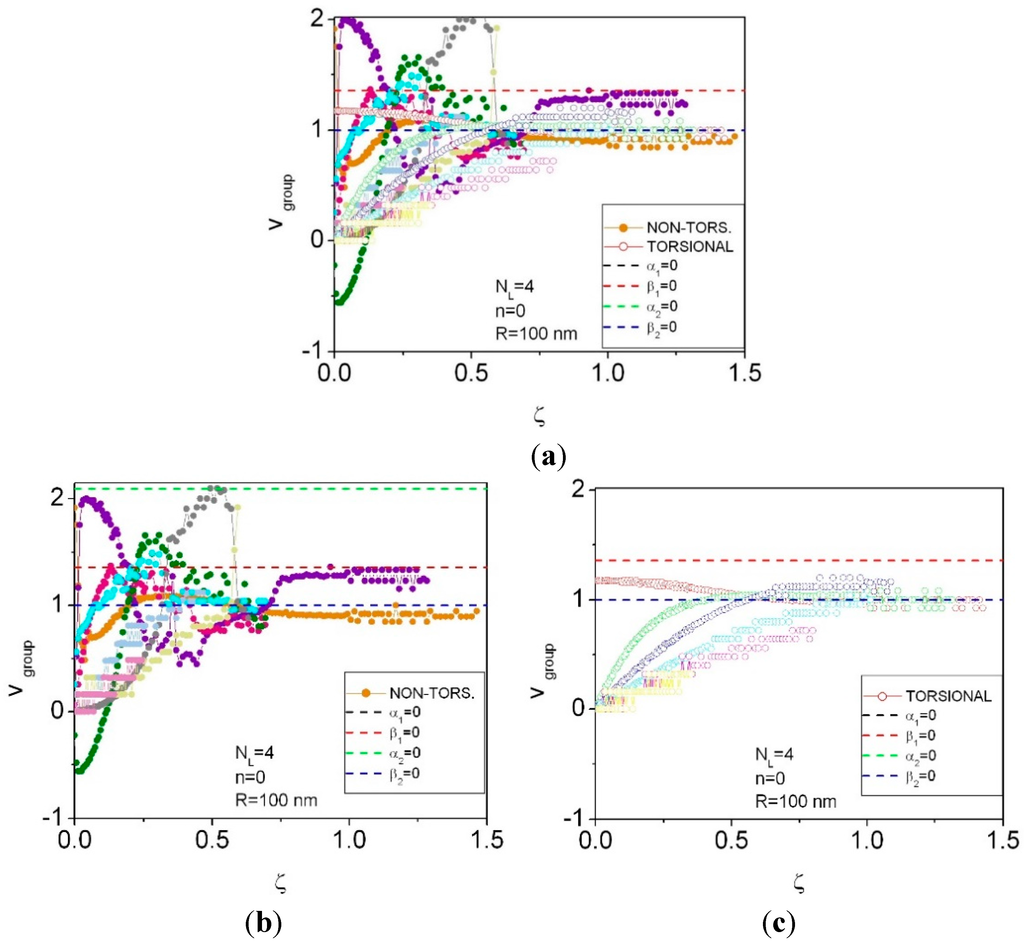
Figure 5.
Phonon group velocity dispersion curves for n = 0, NL = 4 (a). Phonon group velocity dispersion curves for non-torsional (b) and torsional (c) waves.
The lowest phonon dispersion curves are shown for axially symmetric waves n = 0, NL = 6 in Figure 6.
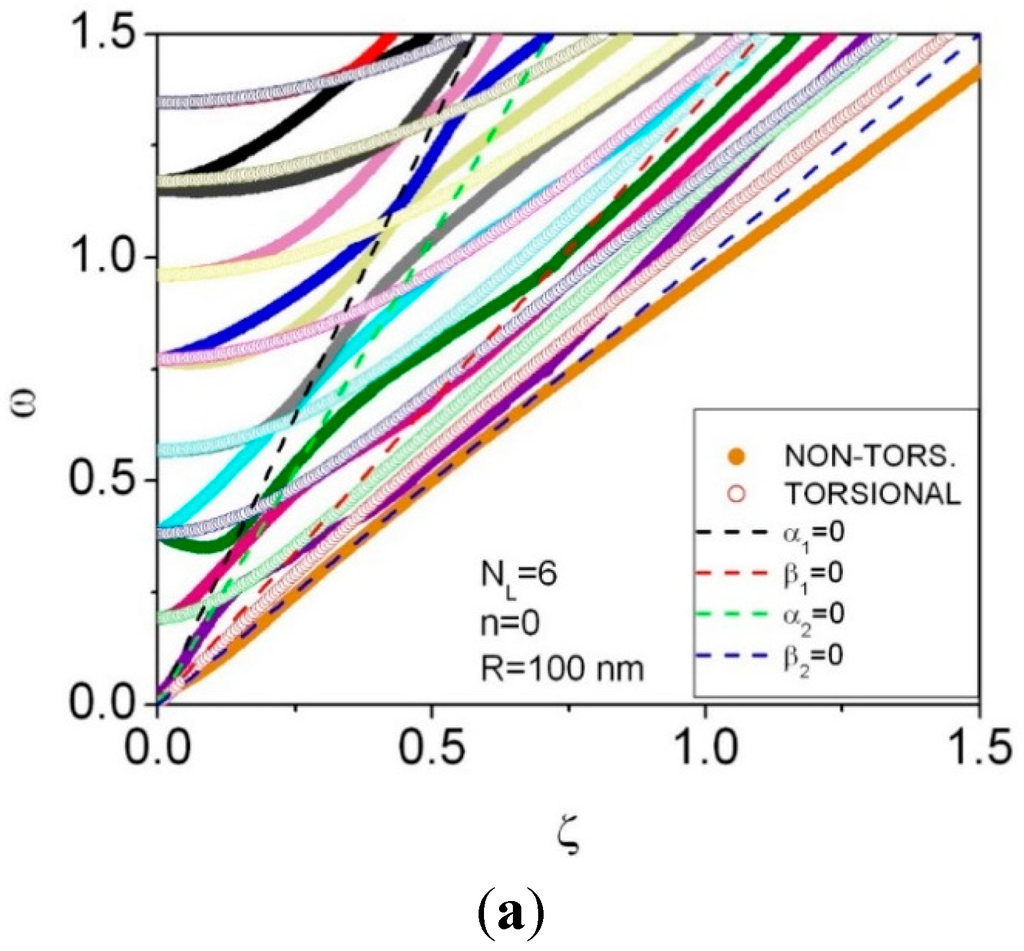
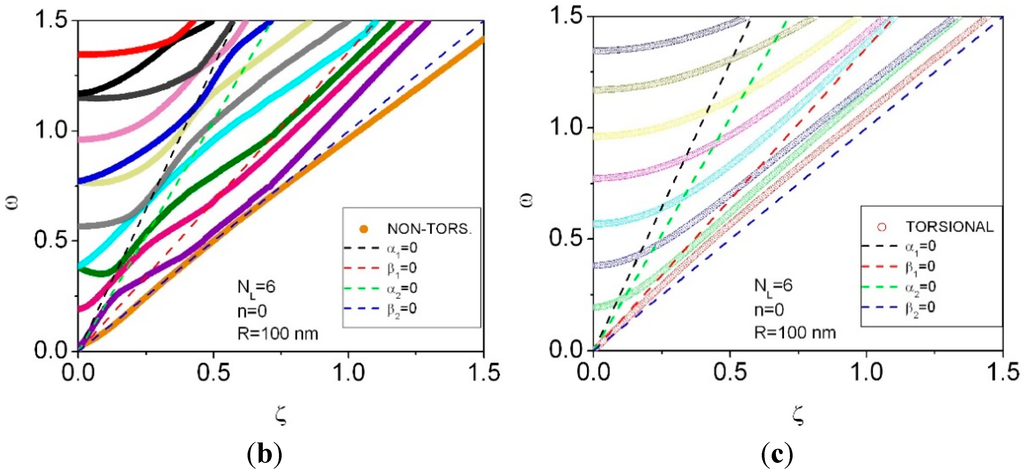
Figure 6.
Phonon dispersion curves for n = 0, NL = 6 (a). The inner and outer radii of a multishell are r0 = 100 nm and r6 = 130 nm, respectively. Phonon dispersion curves for non-torsional (b) and torsional (c) waves.
A larger number of dispersion curves in multishells with six shells emerge within the same interval of energies and wave vectors as for multishells with four shells in Figure 4 and even more so for multishells with two shells in Figure 2. Dispersion of the phonon group velocity for the lowest dispersion curves in Figure 6 is represented in Figure 7 (see Figure A3 for a detailed graph).
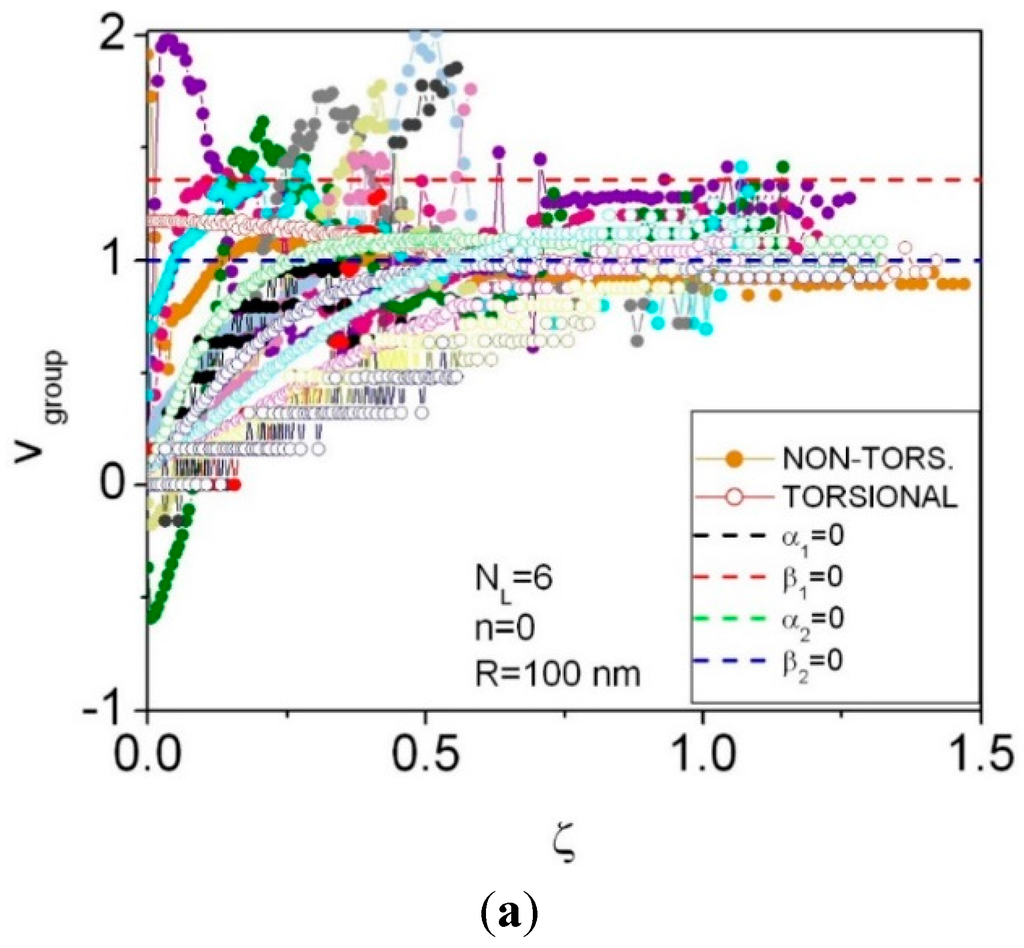
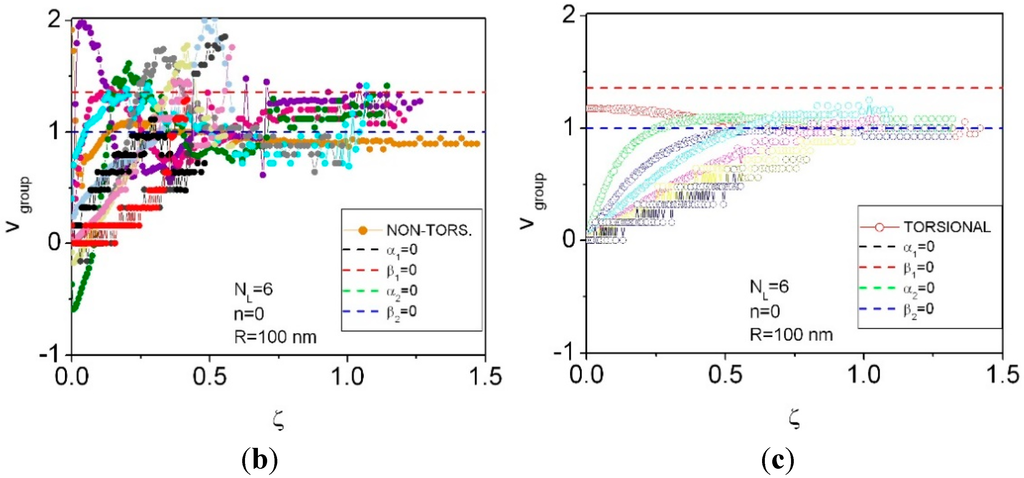
Figure 7.
Phonon group velocity dispersion curves for n = 0, NL = 6 (a). Phonon group velocity dispersion curves for non-torsional (b) and torsional (c) waves.
5. Geometric Effects in the Phonon Dispersion and Group Velocities for Different Numbers of Layers
For the axially-symmetric waves (n = 0), as follows from Figure 2, Figure 4 and Figure 6, the lowest group of the phonon dispersion curves, containing one torsional and two non-torsional modes, at the small wave vectors ζ is only slightly changed by the number of layers NL. In the same region of wave vectors, the second, consisting of one torsional and one non-torsional modes (the third, consisting of one torsional and two non-torsional modes) group of the phonon frequencies ω significantly decreases from 0.57 (1.17) for NL = 2 to 0.29 (0.57) for NL = 4 and 0.19 (0.38) for NL = 6. Within the numerical accuracy, the decrease of the phonon frequencies in the long-wave limit is inversely proportional to NL. Away from the long-wave limit, a general trend of “compression” of the phonon energy spectrum towards lower values of phonon frequencies persists.
As seen from Figure 3, Figure 5 and Figure 7, the phonon group velocity related to the fundamental (lowest) torsional mode is a weakly varying function of the wave vector ζ, while for the higher torsional modes it monotonously increases with the wave vector ζ, apparently towards a saturation. For a fixed value ζ = 0.05, the phonon group velocity related to the lowest (second lowest) torsional mode depends on the number of layers NL as follows: 1.17 (0.13) for NL = 2; 1.17 (0.27) for NL = 4; 1.17 (0.37) for NL = 6. Within the numerical accuracy, the increase of the phonon group velocity for the second lowest torsional mode is directly propotional to NL.
The phonon group velocity related to the lowest two non-torsional modes is a weak function of the wave vector ζ, while for higher torsional modes it always strongly depends on ζ. For the same fixed value ζ = 0.05 as above, the phonon group velocity related to the lowest (second lowest and third lowest) non-torsional mode depends on the number of layers NL as follows: 0.75 (2.02 and 0.43) for NL = 2; 0.75 (1.98 and 0.82) for NL = 4; and 0.78 (1.94 and 1.06) for NL = 6. Within the numerical accuracy, the phonon group velocity for the third lowest torsional mode reveals a sublinear dependence on NL.
Finally, in order to clearly vizualize the overall impact of the number of layers in a multishell on the group velocity dispersion, the average and rms phonon group velocities are calculated for the branches available from the results of the previous section. The results, shown in Figure 8, demonstrate that an increase of NL from two to four leads to an appreciable decrease of the average and rms phonon group velocities. A further increase of NL from four to six has a smaller impact on the average and RMS phonon group velocities. For the wave vector ζ = 0.05, the average phonon group velocity decreases from 0.82 for NL = 2 to 0.54 for NL = 4 and further to 0.53 for NL = 6. At the same time, the RMS phonon group velocity is reduced from 0.95 for NL = 2 to 0.71 for NL = 4 and further to to 0.65 for NL = 6. At small wave vectors the trend persists: the average and RMS phonon group velocities decrease with increasing NL.
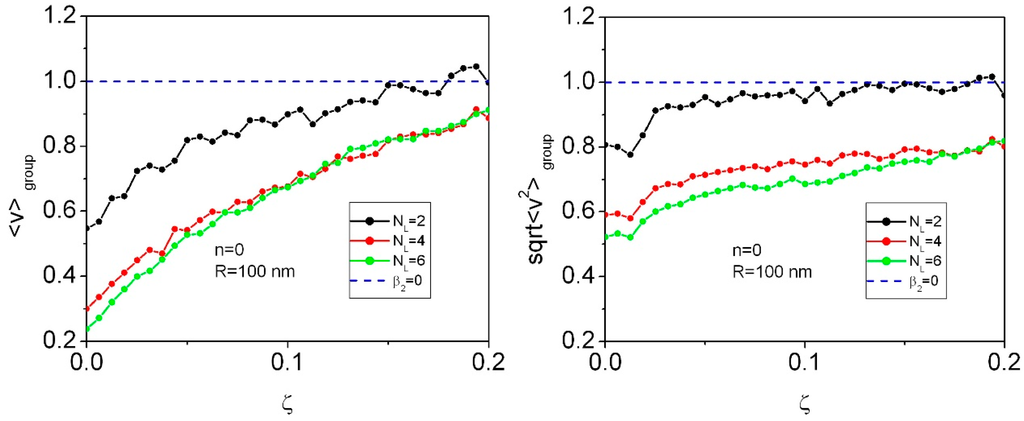
Figure 8.
Average (left) and rms (right panel) phonon group velocity dispersion curves for n = 0 at NL = 2, 4, and 6.
6. Conclusions
We established a possibility of efficient engineering of the acoustic phonon energy dispersion in multishell tubular structures produced by a novel method of self-assembly of micro- and nano-architectures. A dependence on the number of layers in a multishell structure is a manifestation of geometric effects on phonon energy spectrum. Such geometric effects are features pertinent to acoustic metamaterials and phonon crystals. Based on the calculated energies, the phonon confinement effects should be directly observable using Brillouin spectrometry. The changes in the acoustic phonon spectrum affect phonon transport and can be experimentally detected in thermal conductivity measurements. The reduction of the phonon group velocity and phonon thermal conductivity can be achieved without significant roughness scattering and degradation of electron transport. Our results suggest that arrays of rolled-up multishell tubular structures are prospective candidates for advancement in thermoelectric materials and devices.
Acknowledgments
Discussions with O. G. Schmidt are gratefully acknowledged. The work at the IIN IFW Dresden was partly supported by the Deutsche Forschungsgemeinschaft (DFG) under Grant # FO 956/2-1. The work at UC Riverside was supported as part of the Spins and Heat in Nanoscale Electronic Systems (SHINES), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences (BES) under Award # SC0012670.
Author Contributions
The authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Figure A1, Figure A2 and Figure A3 represent the detailed phonon group velocity for the wavevector window [0, 0.5]. Step-like features provide a measure of precision for the exploited numerical procedure of solving the boundary problem of Equations (1–5).
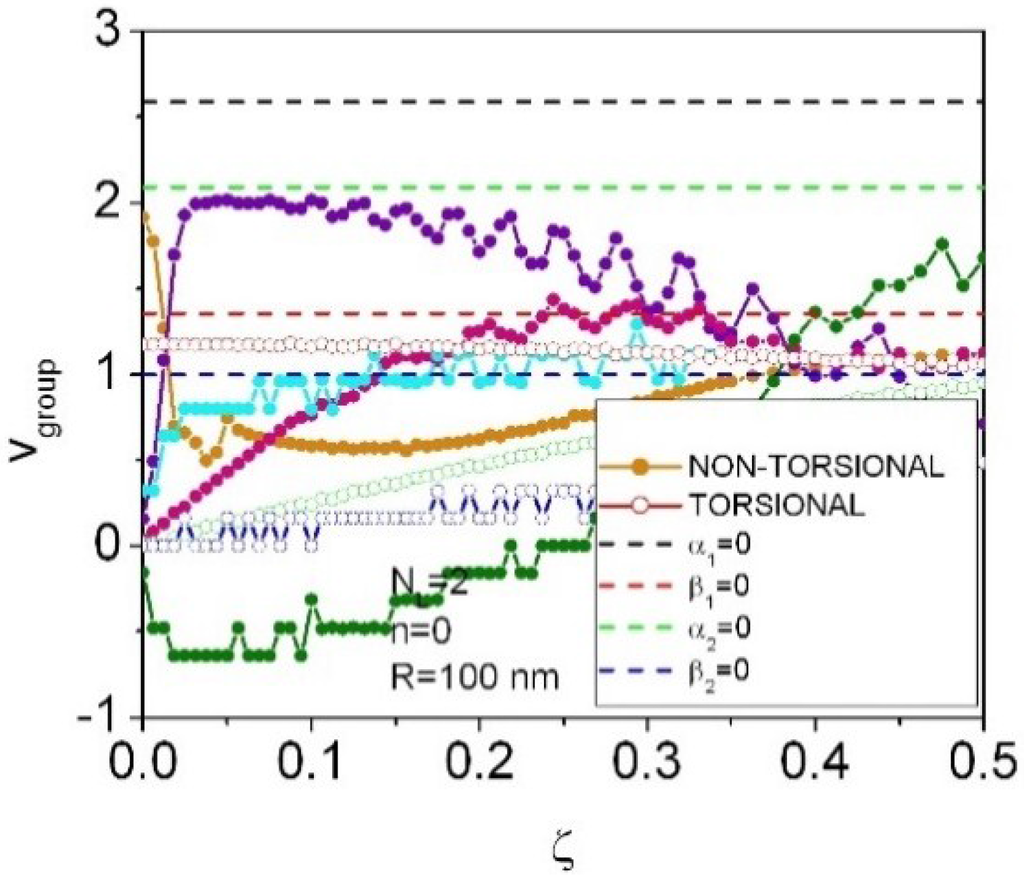
Figure A1.
Detailed phonon group velocity dispersion curves for n = 0, NL = 2. Denotations of non-torsional and torsional modes are the same as in Figure 2.
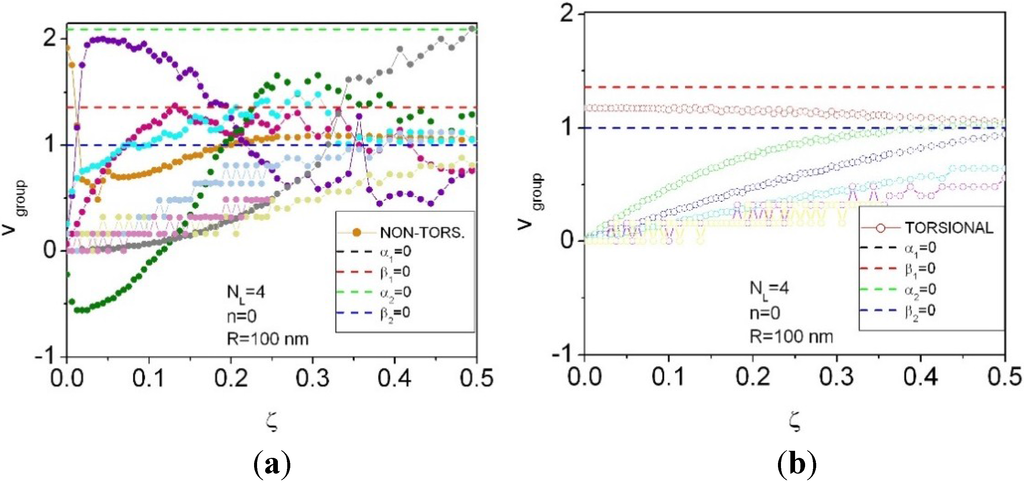
Figure A2.
Detailed phonon group velocity dispersion curves for n = 0, NL = 4 for non-torsional (a) and torsional (b) waves.
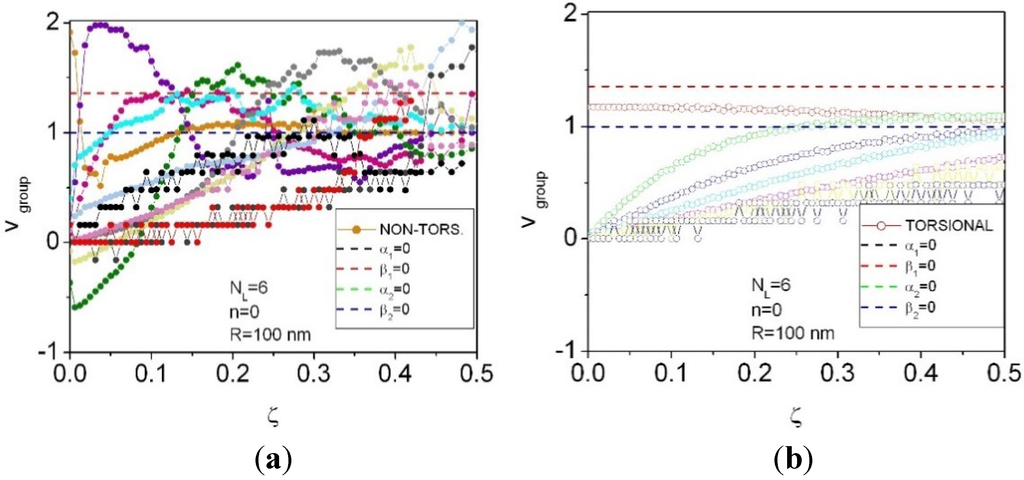
Figure A3.
Detailed phonon group velocity dispersion curves for n = 0, NL = 6 for non-torsional (a) and torsional (b) waves.
References
- Fomin, V.M.; Pokatilov, E.P. Phonons and the electron-phonon interaction in multi-layer systems. Phys. Stat. Sol. 1985, 132, 69–82. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Fomin, V.M.; Beril, S.I. Vibrational excitations, polarons and excitons in multi-layer structures and superlattices; Shtiintsa: Kishinev, USSR, 1990; pp. 1–280. [Google Scholar]
- Pokatilov, E.P.; Fomin, V.M.; Semenovskaya, N.N.; Beril, S.I. Interaction Hamiltonian between an electron and polar surface vibrations in a symmetrical three-layer structure. Phys. Rev. B 1993, 47, 16597–16600. [Google Scholar] [CrossRef]
- Klimin, S.N.; Pokatilov, E.P.; Fomin, V.M. Bulk and interface polarons in quantum wires and dots. Phys. Stat. Sol. 1994, 184, 373–383. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Fomin, V.M.; Klimin, S.N.; Balaban, S.N. Characterization of nanostructures by virtue of the phenomena due to the electron-phonon interaction. Appl. Surf. Sci. 1996, 104–105, 546–551. [Google Scholar] [CrossRef]
- Stroscio, M.A.; Dutta, M. Phonons in Nanostructures; Cambridge University Press: Cambridge, UK, 2001; pp. 1–282. [Google Scholar]
- Balandin, A.A. Nanophononics: Phonon engineering in nanostructures and nanodevices. J. Nanosci. Nanotechnol. 2005, 5, 1015–1022. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Pokatilov, E.P.; Nika, D.L. Phonon engineering in hetero- and nanostructures. J. Nanoelectron. Optoelectron. 2007, 2, 140–170. [Google Scholar] [CrossRef]
- Balandin, A.A.; Nika, D.L. Phononics in low-dimensional materials. Mater. Today 2012, 15, 266–275. [Google Scholar] [CrossRef]
- Balandin, A.; Wang, K.L. Significant decrease of the lattice thermal conductivity due to phonon confinement in a free-standing semiconductor quantum well. Phys. Rev. B 1998, 58, 1544–1549. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. Phonon spectrum and group velocities in AlN/GaN/AlN and related heterostructures. Superlatt. Microstruct. 2003, 33, 155–171. [Google Scholar] [CrossRef]
- Mingo, N.; Yang, L.; Li, D.; Majumdar, A. Predicting the thermal conductivity of Si and Ge nanowires. Nano Lett. 2003, 3, 1713–1716. [Google Scholar] [CrossRef]
- Mingo, N. Calculation of Si nanowire thermal conductivity using complete phonon dispersion relations. Phys. Rev. B 2003, 68, 113308. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. Acoustic-phonon propagation in rectangular semiconductor nanowires with elastically dissimilar barriers. Phys. Rev. B 2005, 72, 113311. [Google Scholar] [CrossRef]
- Bannov, N.; Aristov, V.; Mitin, V.; Stroscio, M.A. Electron relaxation times due to the deformation-potential interaction of electrons with confined acoustic phonons in a free-standing quantum well. Phys. Rev. B 1995, 51, 9930–9942. [Google Scholar] [CrossRef]
- Stroscio, M.A. Interaction between longitudinal-optical-phonon modes of a rectangular quantum wire and charge carriers of a one-dimensional electron gas. Phys. Rev. B 1989, 40, 6428–6431. [Google Scholar] [CrossRef]
- Mickevičius, R.; Mitin, V. Acoustic-phonon scattering in a rectangular quantum wire. Phys. Rev. B 1993, 48, 17194–17201. [Google Scholar] [CrossRef]
- Mickevičius, R.; Mitin, V.; Harithsa, U.K.; Jovanovic, D.; Leburton, J.P. Superlinear electron transport and noise in quantum wires. J. Appl. Phys. 1994, 75, 973–978. [Google Scholar] [CrossRef]
- Svizhenko, A.; Balandin, A.; Bandyopadhyay, S.; Stroscio, M.A. Electron interaction with confined acoustic phonons in quantum wires subjected to a magnetic field. Phys. Rev. B 1998, 57, 4687–4693. [Google Scholar] [CrossRef]
- Svizhenko, A.; Bandyopadhyay, S.; Stroscio, M.A. The effect of acoustic phonon confinement on the momentum and energy relaxation of hot carriers in quantum wires. J. Phys. Cond. Matter 1998, 10, 6091–6094. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. Confined electron-confined phonon scattering rates in wurtzite AlN/GaN/AlN heterostructures. J. Appl. Phys. 2004, 95, 5626–5632. [Google Scholar] [CrossRef]
- Fomin, V.M.; Pokatilov, E.P.; Devreese, J.T.; Klimin, S.N.; Gladilin, V.N.; Balaban, S.N. Multiquantum optical processes in semiconductor quantum dots. Phys. Stat. Sol. 1997, 164, 417–420. [Google Scholar] [CrossRef]
- Fomin, V.M.; Gladilin, V.N.; Devreese, J.T.; Pokatilov, E.P.; Balaban, S.N.; Klimin, S.N. Photoluminescence of spherical quantum dots. Phys. Rev. B 1998, 57, 2415–2425. [Google Scholar] [CrossRef]
- Fomin, V.M.; Klimin, S.N.; Gladilin, V.N.; Devreese, J.T. Characterization of self-assembled quantum dots using the phonon-induced features of PL spectra. J. Lumin. 2000, 87–89, 330–332. [Google Scholar] [CrossRef]
- Fomin, V.M.; Devreese, J.T. Theory of excitons in semiconductor quantum dots. Nonlinear Opt. 2002, 29, 321–327. [Google Scholar]
- Fonoberov, V.A.; Pokatilov, E.P.; Fomin, V.M.; Devreese, J.T. Photoluminescence of tetrahedral quantum-dot quantum wells. Phys. Rev. Lett. 2004, 92, 127402. [Google Scholar] [CrossRef] [PubMed]
- Klimin, S.N.; Fomin, V.M.; Devreese, J.T.; Bimberg, D. Model of Raman scattering in self-assembled InAs/GaAs quantum dots. Phys. Rev. B 2008, 77, 045307. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Sun, G. Enhancement of light absorption in a quantum well by surface plasmon polariton. Appl. Phys. Lett. 2009, 94, 191106. [Google Scholar] [CrossRef]
- Balandin, A.; Wang, K.L. Effect of phonon confinement on the thermoelectric figure of merit of quantum wells. J. Appl. Phys. 1998, 84, 6149–6153. [Google Scholar] [CrossRef]
- Khitun, A.; Balandin, A.; Wang, K.L. Modification of the lattice thermal conductivity in silicon quantum wires due to spatial confinement of acoustic phonons. Superlatt. Microstruct. 1999, 26, 181–193. [Google Scholar] [CrossRef]
- Zou, J.; Balandin, A. Phonon heat conduction in a semiconductor nanowire. J. Appl. Phys. 2001, 89, 2932–2938. [Google Scholar] [CrossRef]
- Fonoberov, V.A.; Balandin, A.A. Giant enhancement of the carrier mobility in Silicon nanowires with diamond coating. Nano Lett. 2006, 6, 2442–2446. [Google Scholar] [CrossRef] [PubMed]
- Nika, D.L.; Pokatilov, E.P.; Balandin, A.A. Phonon-engineered mobility enhancement in the acoustically mismatched silicon/diamond transistor channels. Appl. Phys. Lett. 2009, 93, 173111. [Google Scholar] [CrossRef]
- Zincenco, N.D.; Nika, D.L.; Pokatilov, E.P.; Balandin, A.A. Acoustic phonon engineering of thermal properties of silicon-based nanostructures. J. Phys. Conf. Ser. 2007. [Google Scholar] [CrossRef]
- Wingert, M.C.; Chen, Z.C.Y.; Dechaumphai, E.; Moon, J.; Kim, J.-H.; Xiang, J.; Chen, R. Thermal conductivity of Ge and Ge-Si core-shell nanowires in the phonon confinement regime. Nano Lett. 2011, 11, 5507–5513. [Google Scholar] [CrossRef] [PubMed]
- Cuffe, J.; Chávez, E.; Shchepetov, A.; Chapuis, P.-O.; El Boudouti, E.H.; Alzina, F.; Kehoe, T.; Gomis-Bresco, J.; Dudek, D.; Pennec, Y.; et al. Phonons in slow motion: Dispersion relations in ultrathin Si membranes. Nano Lett. 2012, 12, 3569–3573. [Google Scholar] [PubMed]
- Johnson, W.L.; Kim, S.A.; Geiss, R.; Flannery, C.M.; Bertness, K.A.; Heyliger, P.R. Vibrational modes of GaN nanowires in the gigahertz range. Nanotechnology 2012, 23, 495709. [Google Scholar] [CrossRef] [PubMed]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. A phonon depletion effect in ultrathin heterostructures with acoustically mismatched layers. Appl. Phys. Lett. 2004, 85, 825–827. [Google Scholar] [CrossRef]
- Nika, D.L.; Zincenco, N.D.; Pokatilov, E.P. Engineering of thermal fluxes in phonon mismatched heterostructures. J. Nanoelect. Optoelect. 2009, 4, 180–185. [Google Scholar] [CrossRef]
- Hu, M.; Giapis, K.P.; Goicochea, J.V.; Zhang, X.; Poulikakos, D. Significant reduction of thermal conductivity in Si/Ge core-shell nanowires. Nano Lett. 2011, 11, 618–623. [Google Scholar] [CrossRef] [PubMed]
- Bi, K.; Wang, J.; Wang, Y.; Sha, J.; Wang, Z.; Chen, M.; Chen, Y. The thermal conductivity of SiGe heterostructure nanowires with different cores and shells. Phys. Lett. A 2012, 376, 2668–2671. [Google Scholar] [CrossRef]
- He, Y.; Galli, G. Microscopic origin of the reduced thermal conductivity of Silicon nanowires. Phys. Rev. Lett. 2012, 108, 215901. [Google Scholar] [CrossRef] [PubMed]
- Wave Propagation in Materials for Modern Applications; Petrin, A. (Ed.) InTech: Rijeka, Croatia, 2010; pp. 1–552.
- Acoustic Metamaterials and Phononic Crystals; Deymier, P.A. (Ed.) Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–378.
- Narayana, S.; Sato, Y. Heat flux manipulation by engineered thermal materials. Phys. Rev. Lett. 2012, 108, 214303. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Yang, S.; Gan, C.; Lei, H. A new procedure for exploring the dispersion characteristics of longitudinal guided waves in a multi-layered tube with a weak interface. J. Nondestruct. Eval. 2013, 32, 263–276. [Google Scholar] [CrossRef]
- Wang, L.; Hu, H.; Guo, W. Wave Propagation in Carbon Nanotubes. In Wave Propagation in Materials for Modern Applications; Petrin, A., Ed.; InTech: Rijeka, Croatia, 2010; pp. 225–252. [Google Scholar]
- Sigalas, M.M.; Economou, M.N. Elastic and acoustic wave band structure. J. Sound Vibr. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Economou, M.N. Band structure of elastic waves in two dimensional systems. Solid State Communs. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Movchan, A.B.; Guenneau, S. Split-ring resonators and localized modes. Phys. Rev. B 2004, 70, 125116. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602(R). [Google Scholar] [CrossRef]
- Prinz, V.Y.; Seleznev, V.A.; Gutakovsky, A.K.; Chehovskiy, A.V.; Preobrazhenskii, V.V.; Putyato, M.A.; Gavrilova, T.A. Free-standing and overgrown InGaAs/GaAs nanotubes, nanohelices and their arrays. Physica E: Low-dimension. Syst. Nanostruct. 2000, 6, 828–831. [Google Scholar] [CrossRef]
- Schmidt, O.G.; Eberl, K. Nanotechnology—Thin solid films roll up into nanotubes. Nature 2001, 410, 168. [Google Scholar] [CrossRef] [PubMed]
- Krause, B.; Mocuta, C.; Metzger, T.H.; Deneke, C.; Schmidt, O.G. Local structure of a rolled-up single crystal: An X-ray microdiffraction study of individual semiconductor nanotubes. Phys. Rev. Lett. 2006, 96, 165502. [Google Scholar] [CrossRef] [PubMed]
- Deneke, C.; Jin-Phillipp, N.-Y.; Loa, I.; Schmidt, O.G. Radial superlattices and single nanoreactors. Appl. Phys. Lett. 2004, 84, 4475–4477. [Google Scholar] [CrossRef]
- Deneke, C.; Songmuang, R.; Jin-Phillipp, N.Y.; Schmidt, O.G. The structure of hybrid radial superlattices. J. Phys. D Appl. Phys. 2009, 42, 103001. [Google Scholar] [CrossRef]
- Grimm, D.; Wilson, R.B.; Teshome, B.; Gorantla, S.; Rümmeli, M.H.; Bublat, T.; Zallo, E.; Li, G.; Cahill, D.G.; Schmidt, O.G. Thermal conductivity of mechanically joined semiconducting/metal nanomembrane superlattices. Nano Lett. 2014, 14, 2387–2393. [Google Scholar] [CrossRef] [PubMed]
- Pokatilov, E.P.; Fomin, V.M.; Devreese, J.T.; Balaban, S.N.; Klimin, S.N. Bipolaron binding in quantum wires. Phys. Rev. B 2000, 61, 2721–2728. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, H.-J. Fröhlich electron-interface and -surface optical phonon interaction Hamiltonian in multilayer coaxial cylindrical AlxGa1−xAs/GaAs quantum cables. J. Phys. Condens. Matter 2003, 15, 5871–5879. [Google Scholar]
- Kanyinda-Malu, C.; Clares, F.J.; de la Cruz, R.M. Axial interface optical phonon modes in a double-nanoshell system. Nanotechnology 2008, 19, 285713. [Google Scholar] [CrossRef] [PubMed]
- Deneke, C.; Sigle, W.; Eigenthaler, U.; van Aken, P.A.; Schütz, G.; Schmidt, O.G. Interfaces in semiconductor/metal radial superlattices. Appl. Phys. Lett. 2007, 90, 263107. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Dover: New York, NY, USA, 1991; pp. 1–688. [Google Scholar]
- Armenàkas, A.E. Propagation of Harmonic Waves in Composite Circular Cylindrical Shells. I: Theoretical investigation. Am. Inst. Aeronaut. Astronautics (AIAA) J. 1966, 5, 740–744. [Google Scholar] [CrossRef]
- Armenàkas, A.E. Propagation of Harmonic Waves in Composite Circular Cylindrical Shells. Part II: Numerical Analysis. Am. Inst. Aeronaut. Astronautics (AIAA) J. 1971, 9, 599–605. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 10th ed.National Bureau of Standards: Washington, DC, USA, 1972; pp. 1–1046.
- Intel® Visual Fortran with Microsoft Visual Studio 2008. Available online: https://www.visualstudio.com/ (accessed on 29 September 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).