1. Introduction
Thin-film solar cells with Cu(In,Ga)Se
2 (CIGS) absorber layer are one of the most promising photovoltaic technologies, with reported highest efficiency over 21% [
1]. A crucial factor that determines the efficiency of CIGS thin-film devices are the optical properties of the absorber material [
2]. This chalcopyrite compound possesses an excellent absorbing ability in the wide range of electromagnetic spectrum (typically 400–1200 nm, depending on the precise gallium amount within the material), making it ideal for the application in thin-film photovoltaics, despite its polycrystalline nature.
To reduce the fabrication costs and deposition time, there is a need to reduce the thickness of the absorbing CIGS layer from current widely used 2 μm to several hundreds of nm. However, in sub-micrometer thin CIGS solar cells additional efficiency issues emerge, such as back-contact recombination and decrease of optical path which reduces the absorption of the incoming photons [
3]. Back-contact recombination can be limited by the choice of the back-contact material, surface modification or grading of gallium concentration throughout the absorber layer [
4]. In order to improve the harvesting of the available photons that reach the cell, the employment of light management methods are of a great importance.
Two groups of methods are the most commonly used for enhancing the absorption within the solar cell’s absorber layer: texturing and use of nanoparticles embedded within the device. Texturing of solar cell layers causes a change in optical paths of the incoming light, which can modify the reflection on the cell’s surface as well as on the interface between the cell’s layers [
5,
6]. Texturing of the front side of the device is commonly used for reduction of overall reflectance of the cell, thus increasing the number of photons reaching the absorber material [
7].
The use of both metal and dielectric nanoparticles in light trapping applications have been extensively studied recently [
8,
9]. With a proper choice of size (within the visible spectrum range) and material, the employment of metallic and dielectric nanoparticles may exhibit light scattering properties through effect of plasmon resonance or dielectric scattering.
Regarding the CIGS based solar cells, there are already some promising works published using scattering on the embedded dielectric nanoparticles [
10], and texturing of the transparent front electrode [
11]. The difficulty of stable integration of plasmonic metal nanoparticles was recently published [
12], which makes the achieving of the proposed structures such as in [
13] more plausible.
In this simulation work we explore the possibilities of light-trapping effects achieved by texturing of the back (molybdenum) electrode of the CIGS thin-film solar cell. Similar techniques have been used for the efficiency improvement in thin film silicon solar cells [
14,
15,
16]. These simulations should give an insight in the range of the texturing features’ sizes, thus reducing the need for costly experimental works, giving the experimental focus to the best-resulting configurations.
2. Simulation Description
There are several models commonly used for the optical simulation of absorption and reflectance in thin-film photovoltaic devices. Depending on the dimensions of the structures (layer thicknesses, texture feature size,
etc.) compared to the wavelength of the excitation light, these models can be classified as ray tracing model [
17], models based on light scattering effects [
18] and finally, rigorous methods which are based on solving Maxwell’s equation describing the interaction of electro-magnetic waves with the material. Resolving the system of partial differential Maxwell’s equations can be completed analytically only for problems with simple geometry. Since the geometry of the textured thin-films is usually complex, some type of numerical methods must be employed. The most frequently used numerical methods for this purpose are finite difference time domain [
19] and finite element method [
20].
Based on the numbers of spatial dimensions there are 1-D, 2-D and 3-D models. While for a number of thin-film photovoltaic simulations the application of 1-D models is sufficient [
21], the simulation of non-flat cell layers requires the use of 2-D or 3-D models. In some simulations a combination of models can be used to simulate the cells with higher dimensions [
22].
The simulations in this work were based upon finite element method with 2-D geometry. The simulations were carried out using the RF module of COMSOL Multiphysics software package (COMSOL Inc, Burlington, MA, USA) [
23]. Since the model geometry is 2-D, with reasonable number of degrees of freedom, a direct solver was used. The simulated thin-film cell based on CIGS absorber material has the following layer structure: Mo (800 nm)/CIGS (500 nm)/CdS (70 nm)/ITO (indium tin oxide) (330 nm). The whole geometry domain was meshed, keeping in mind that the maximum mesh element size does not exceed 1/10 of the wavelength of the excitation electromagnetic wave. The optical properties of materials were described by complex wavelength-dependent refraction index (ε). The values of the refraction indexes of all materials used in the simulation were taken from the literature [
24,
25]. The simulation was carried out at wavelengths in the range of absorption of CIGS material (400–1200 nm). The software calculates the vector of electric field in all nodes of the mesh. The absorption of light in a geometric domain was calculated based on the integration of the electric field strength values within the boundaries of the respective domain. The absorbed power in a node within the domain excited by a single wavelength (λ) can be calculated using the following equation
where ω is angular frequency equal to 2π
/λ, ε′′ is imaginary component of complex permittivity of the respective material, while
E(λ) denotes electric field strength at the respective excitation wavelength.
The presented texturing is based on introduction of a 2-D periodic texture on the substrate material, and subsequent growth of the solar cell layer stack on such a substrate. The model geometry was simplified assuming the conformal growth of all the layers, causing the angles of the texture in each layer to remain conserved. Although in literature exist more complex models describing the thin-film solar cell layer growth, such as those considering the combination of isotropic and conformal growth [
26], they are optimized for silicon based thin-film solar cells.
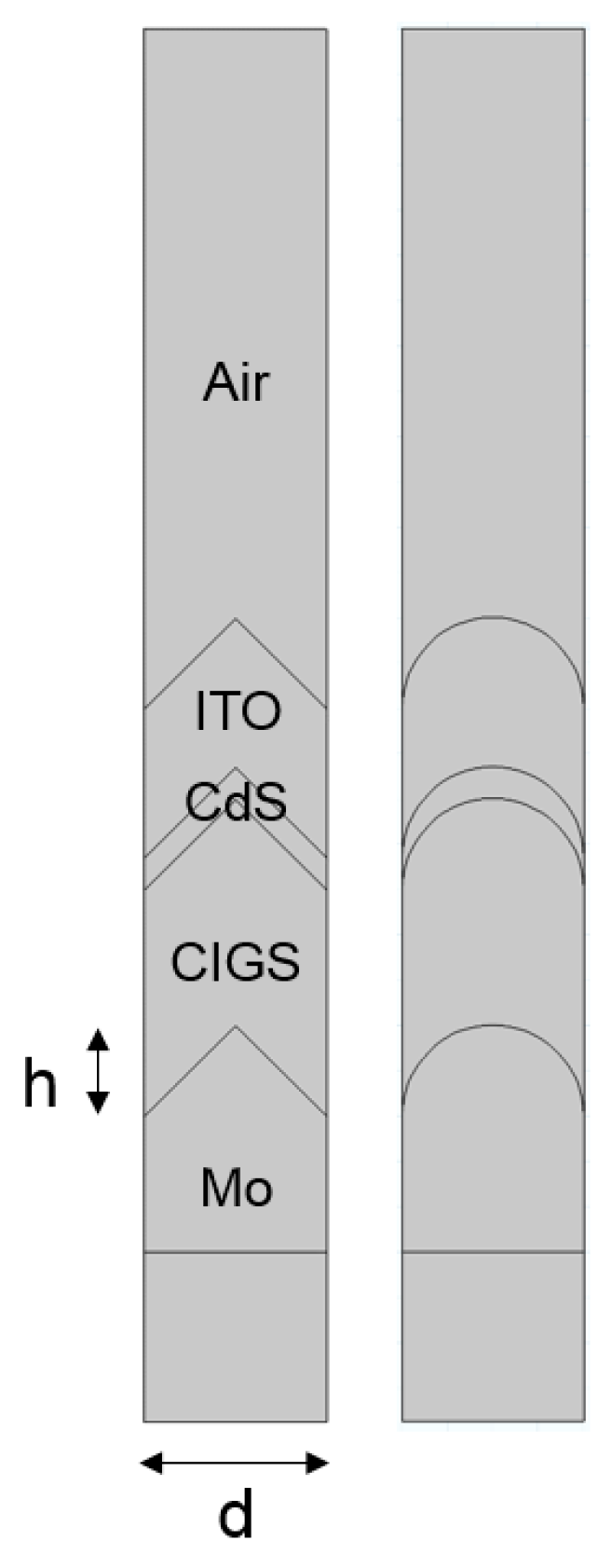
Two different structuring geometries have been explored: triangular (with sharp edges) and convex (with smooth upper edges). The dimensions of the texture period and height have been varied in the range of hundreds of nanometers, which is comparable to the visible light spectrum wavelengths, in order to enable the light scattering within the layers of the solar cell. The preliminarily carried-out simulations had shown that the absorption enhancement is observable for the texture widths in the range 50–500 nm, which was used as a reference for the dimension range in this work. The geometries of the model used in the simulations are presented in
Figure 1.
The top edge of the air domain was set-up with “port” boundary condition, which has the possibility to produce excitation waves. The excitation was set-up in the form of a vertically incident plane wave with the constant irradiation power, swept in the range of wavelengths from 400 to 1200 nm. The used “port” boundary condition has the properties of an absorbing boundary, suppressing the multiple reflections from the simulated device. The width of the model was set to match the width of the texture (d). Thus, the periodic Floquet boundary condition could be established on the corresponding left and right boundaries of the model. The power of the incident irradiation was kept constant while the model width was varied, in order to normalize the levels of absorption and reflection for the variable texture dimension. Thus, the results of models with different widths can be directly compared.
Figure 1.
Used model geometry; (left) triangular and (right) convex texture features, with two variable parameters: texture height (h) and width (d).
Figure 1.
Used model geometry; (left) triangular and (right) convex texture features, with two variable parameters: texture height (h) and width (d).
Since the natural sunlight that reaches the Earth’s surface is not polarized, the cases of both TE (transverse-electric) and TM (transverse-magnetic) polarized irradiation have been simulated and the average value has been calculated. Finally, the calculated absorption was scaled to AM1.5 standard solar irradiance spectrum [
27] in order to assess the contribution of light-trapping to the absorption enhancement depending on the real-life spectral distribution of the incident light.
3. Results and Discussion
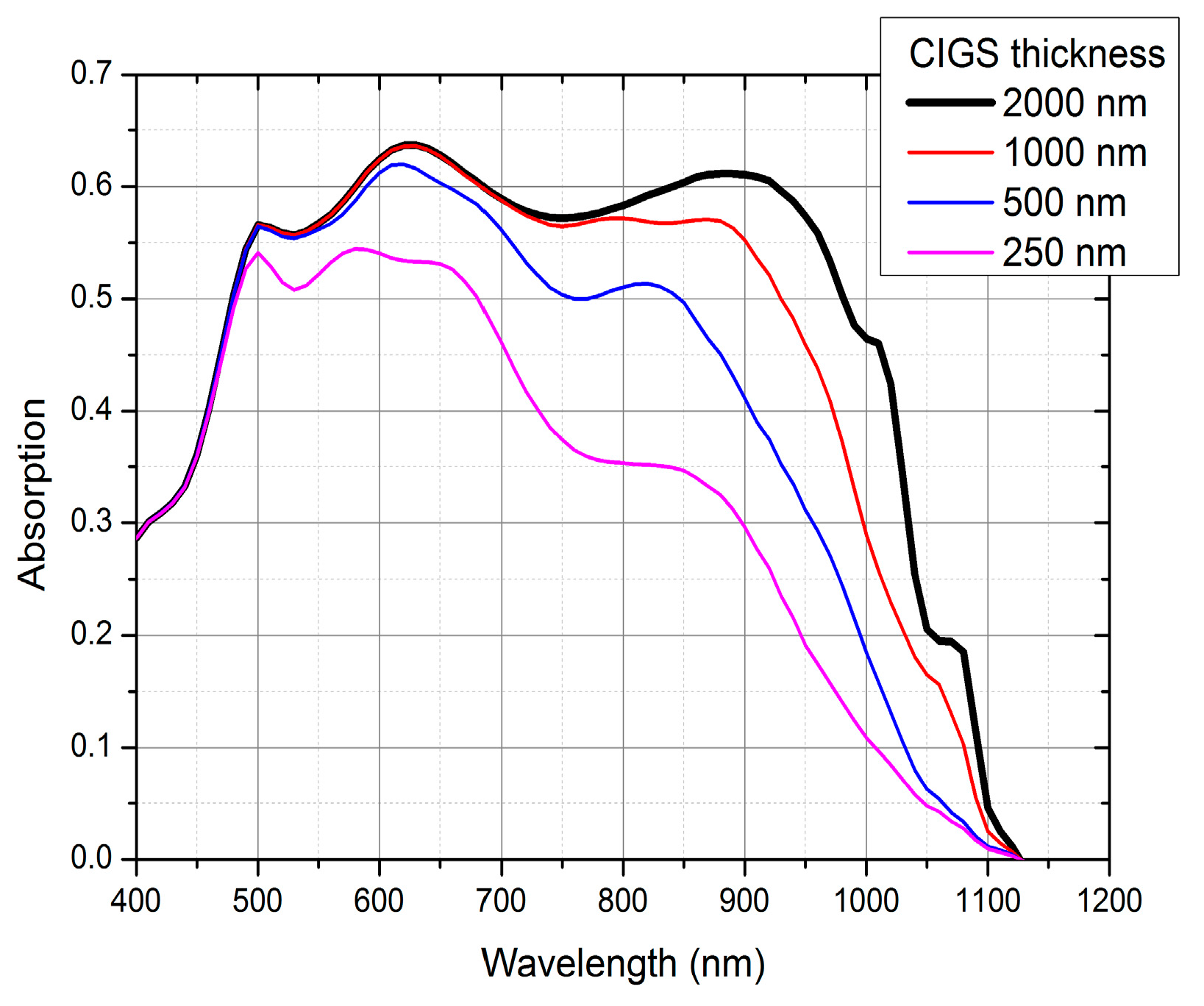
Before the simulation of the textured layers, the flat-layered solar cells with different thicknesses of CIGS absorbers were simulated. The decrease of the optical absorption in the absorbers with thicknesses ranging from standard 2000 nm to ultra-thin 250 nm is presented in
Figure 2. As expected, the largest absorption decrease is present in the higher wavelength region, since the absorption of the CIGS material is the lowest in this spectral region.
Figure 2.
Absorption in the Cu(In,Ga)Se2 (CIGS) absorber layer with the varying thickness.
Figure 2.
Absorption in the Cu(In,Ga)Se2 (CIGS) absorber layer with the varying thickness.
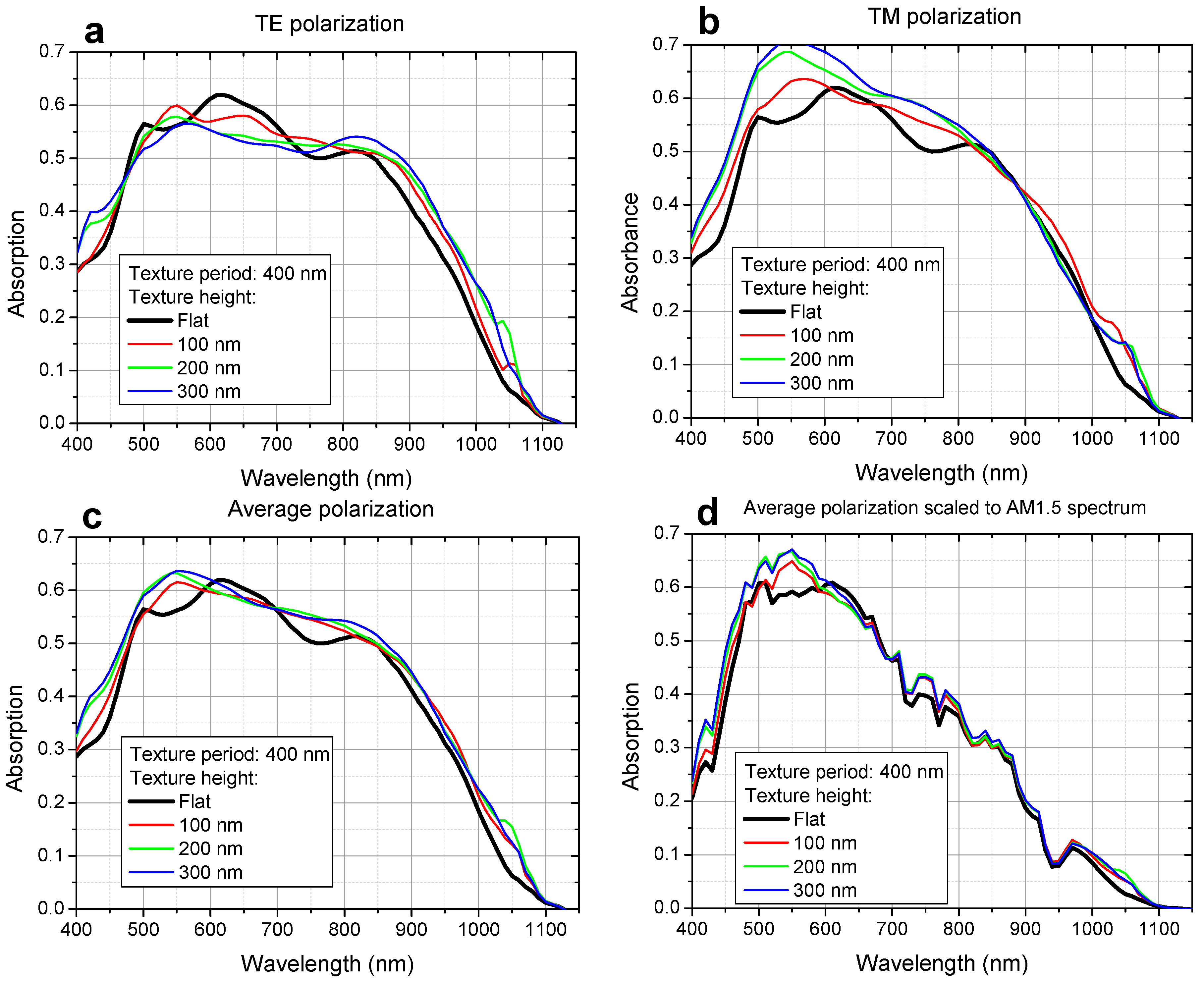
In all of the following simulations a 500 nm thick absorber layer was considered. An example of triangular texturing, with the texture period
d = 400 and variable height
h is presented in
Figure 3. Based on Equation (1) the absorption within the CIGS layer was calculated and presented in
Figure 3a,b for TE and TM polarized excitations, respectfully. It can be observed that the absorption was significantly increased over the majority of the wavelength spectrum in the case of TM polarization. Especially high is the enhancement at 550 nm. The absorption increases with the rise of texture aspect ratio. For the wavelengths in the range between 830 and 1000 nm there is no visible change of absorption. In the case of TE polarization the enhancement was observed for the longer wavelengths in the range of 800–1050 nm, as well as in the narrow window between 400 and 470 nm. In the wavelength range between 470–750 nm a decrease of the absorption can be observed. This may be contributed to the increased absorption within the transparent conductive oxide (TCO) layer due to the elevated interference in that specific wavelength range. While the absorption rises with the aspect ratio also in the case of TE polarization, in the window of 470–750 nm the decrease of the absorption is more prominent at the higher aspect ratios.
Figure 3.
Absorption of the CIGS absorber layer with the use of triangular structuring, with texture period of 400 nm and variable height. (a) transverse-electric (TE) polarization; (b) transverse-magnetic (TM) polarization; (c) average polarization; (d) average polarization scaled to AM1.5 solar irradiance spectrum.
Figure 3.
Absorption of the CIGS absorber layer with the use of triangular structuring, with texture period of 400 nm and variable height. (a) transverse-electric (TE) polarization; (b) transverse-magnetic (TM) polarization; (c) average polarization; (d) average polarization scaled to AM1.5 solar irradiance spectrum.
The average value of the absorption was calculated as
PabsAVG = (
PabsTE +
PabsTM)/2.
Figure 3c shows the average absorption in the absorber layer of the considered textured device. The practical contribution of the light trapping can be seen on the absorption enhancement diagram scaled to the referent AM1.5 solar irradiance spectrum presented in
Figure 3d. It can be seen that the highest impact of the textured layers is on the absorption within the range of 400–600 nm. Large absorption enhancement is also present in the high wavelength range 1000–1100 nm. However, due to the poor absorption capabilities of CIGS material in these wavelengths, the contribution of the absorption enhancement in this range does not have such significant effect on the total enhancement of absorption.
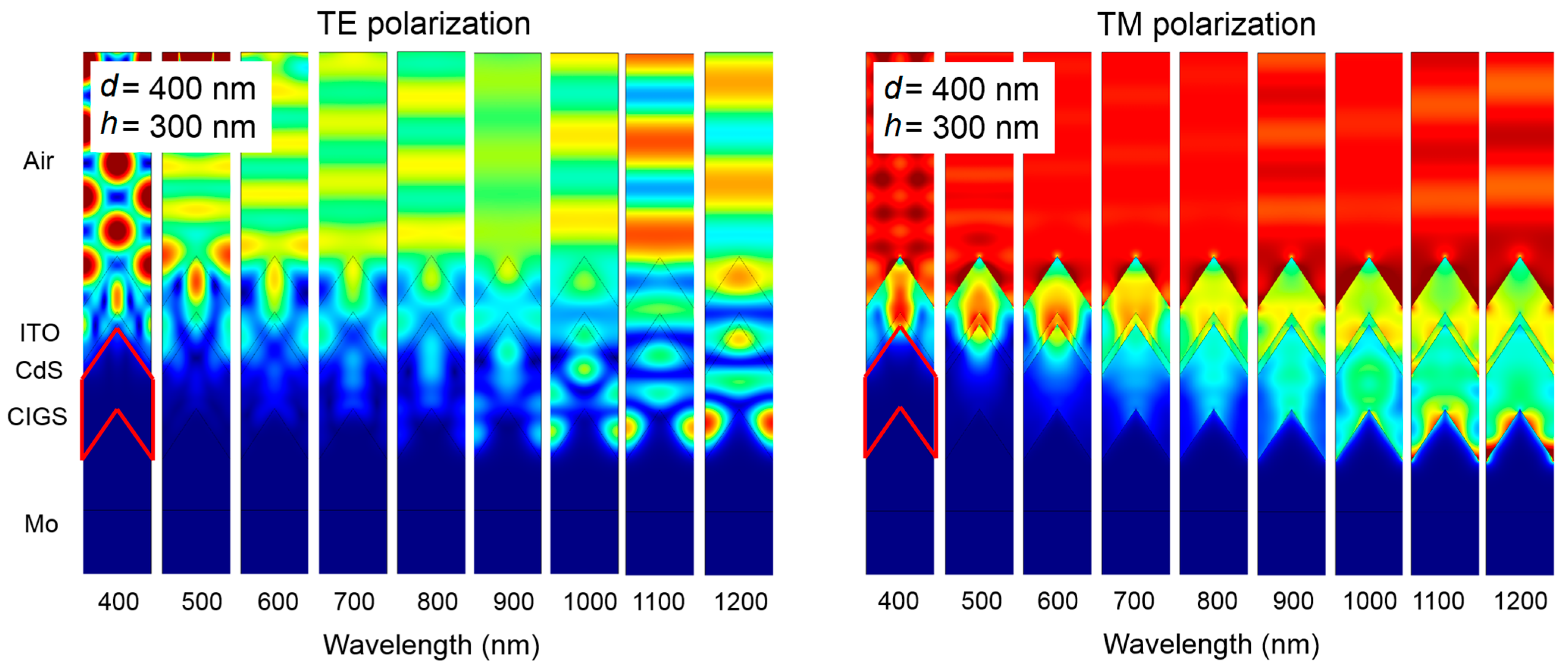
Figure 4 presents the electric field strength within the layers of the cell with the texture dimensions
h = 300 nm and
d = 400 nm.
Figure 4.
Simulation results of the triangular structuring with texture height and period of h = 300 nm and d = 400 nm, for both TE and TM polarizations.
Figure 4.
Simulation results of the triangular structuring with texture height and period of h = 300 nm and d = 400 nm, for both TE and TM polarizations.
In order to better assess the origin of absorption enhancement in the CIGS layer, the absorption in the other layers was also investigated.
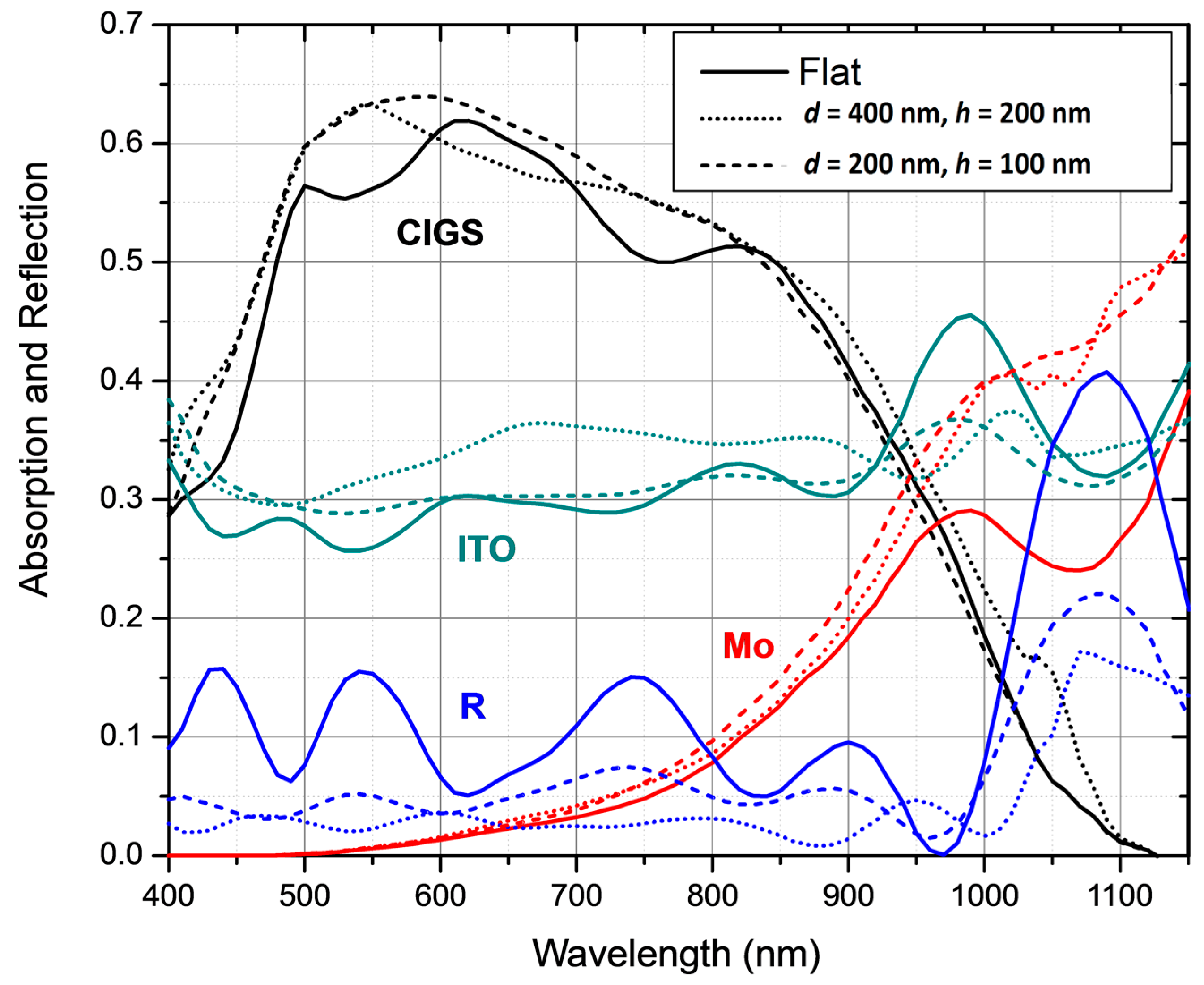
Figure 5 presents absorption in all device’s layers, excluding the buffer layer since it was observed that the texturing of the device does not have a noticeable effect on the absorption within this layer. The total device’s reflection was comparatively presented in the same figure. Besides the flat device, two textured devices’ layers absorption properties were shown:
d = 400 nm and
h = 200 nm, and
d = 200 nm and
h = 100 nm. Both of these devices possess the same texture aspect ratio.
The most prominent effect caused by the texturing of the cell layers is the decrease of the cell’s total reflection, similarly to the texturing of TCO layer to minimize the reflection [
28] or introduction of antireflection layer on top of the cell stack [
29]. The significant decrease of reflection is observable over the entire simulated spectrum. It can be also seen that all the interference fringes get lowered and almost extinct. The effect of reflection decrease is more visible for the texture with period of 200 nm.
Texturing causes a rise of the absorption within the ITO layer in the range of 400–930 nm. The rise is more prominent in the case of the 400 nm texture period. For the wavelengths above 930 nm there is an equal decrease of absorption within ITO layer for the both presented cases of the texturing.
The increase of the absorption within Mo back electrode layer is also observable in the textured layers stack. This increase is observable at 700 nm and gradually rising as the wavelength increases. This shows that the light trapping mechanism is not achieved in the back of the absorber layer in the case of the presented configuration.
Based on these results it can be concluded that the light management introduced by the back texturing of the solar cell stack has led to considerable decrease of reflection, which lead to the overall enhancement of the absorption in the absorber layer. Although the parasitic absorption in the Mo layer is not reduced, the enhancement achieved in the short wavelengths is much more prominent considering the distribution of the AM1.5 spectrum.
In order to directly compare the effects of texturing on the absorption increase within the absorber layer for all simulated cases (with both triangular and convex textures), the absorption was integrated over the whole range of wavelengths and divided with the absorption in the flat reference cell. The increase of the absorption within the absorber (CIGS) layer is presented in
Figure 6. The results show that the best enhancement was achieved using triangular features with 100–200 nm texture periods with high aspect ratios. The enhancement in the small wavelengths range can be attributed to the reduction of reflectance of the solar cell’s surface. The enhancement of the absorption is more prominent with the further reduction of absorber’s thickness.
Figure 5.
Absorption in individual solar cell layers (ITO, CIGS and Mo) as well as total reflection from the surface of the cell. The results are shown for flat cell, and two textured cells with different texture size (d = 400 nm and h = 200 nm; d = 200 nm and h = 100 nm). Absorption within the buffer layer (CdS) is not displayed since its change with the variation of texturing dimensions is very small.
Figure 5.
Absorption in individual solar cell layers (ITO, CIGS and Mo) as well as total reflection from the surface of the cell. The results are shown for flat cell, and two textured cells with different texture size (d = 400 nm and h = 200 nm; d = 200 nm and h = 100 nm). Absorption within the buffer layer (CdS) is not displayed since its change with the variation of texturing dimensions is very small.
Figure 6.
Absorption enhancement in CIGS absorber layer with reference to the flat, non-structured cell.
Figure 6.
Absorption enhancement in CIGS absorber layer with reference to the flat, non-structured cell.