Synthesis of Cascadable DDCC-Based Universal Filter Using NAM
Abstract
:1. Introduction
2. Description of the Proposed Method
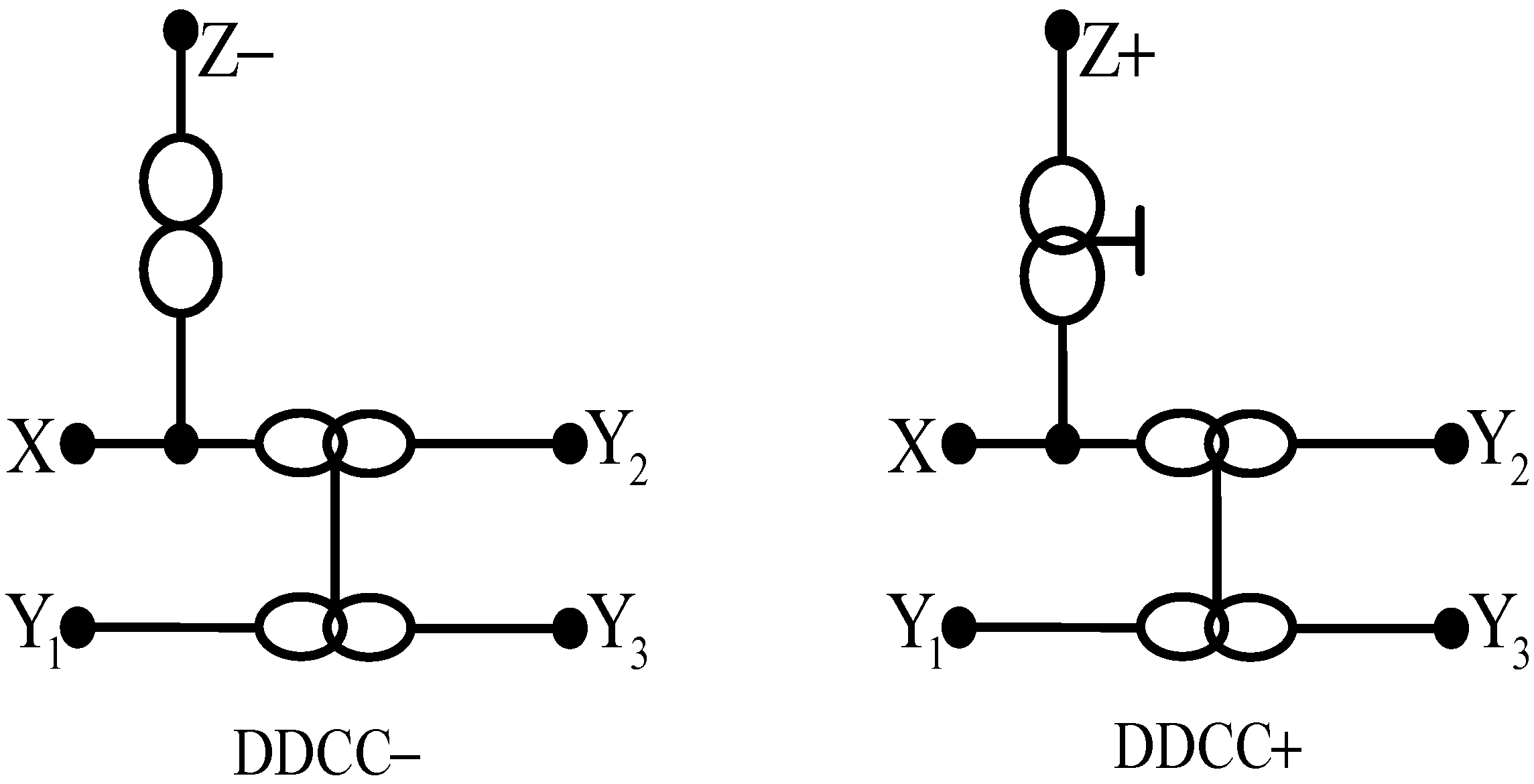

- Step 1:
- Of the desired transfer function of the synthesized filter in the form of the Matrix (4). It must be noted that each capacitor in the denominator must be arranged to have only a single position on the primary diagonal to obtain circuits with grounded capacitors.
- Step 2:
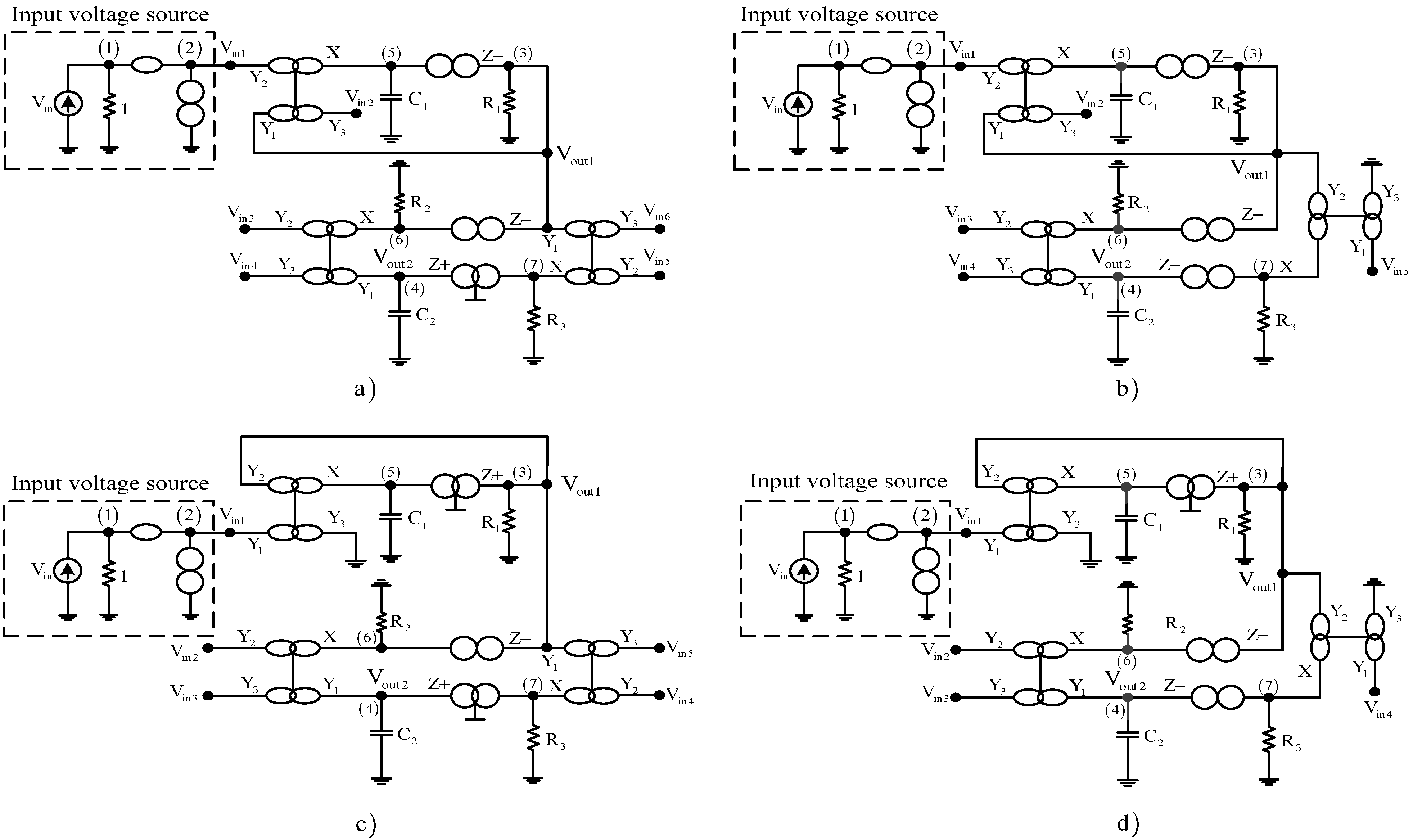
- Introduce a row and a column of zeros to row 1 and column 1 and place a unity resistor to position (1,1) of (4). The existing columns and rows are moved to the right and to the bottom, as given by (5). Then add infinity variables and zero terms to realize a nullator between column 1 and column 2 and a norator between row 2 and ground. The Step 2 corresponds to the adding of the equivalent circuit of voltage source in Figure 2 [19]. So, Matrix (5) becomes (6).
- Step 3:
- Step 4:
- Add pair of infinity-variables of remained Yi-terminals represented by (2) or (3) to the suitable positions in column 2 of the Matrix (7) to realize the infinity-variables notation of a DDCC+ or DDCC−. This operation will duplicate the existing admittance terms to the first column of (5), so the numerator of the desired transfer function is obtained. For example, by adding a pair of ± ∞i to the second column of (7), the term y1,2 will be duplicated in the first column of (5) to obtain the desired numerator, as shown in (8). The addition of infinity-variable pairs to column 2 corresponds to applying input voltage signal to the added Yi-terminals at node 2. This operation will not affect the denominator of the transfer function. The obtained matrix represents the full matrix of the synthesized circuit.
3. Application Examples
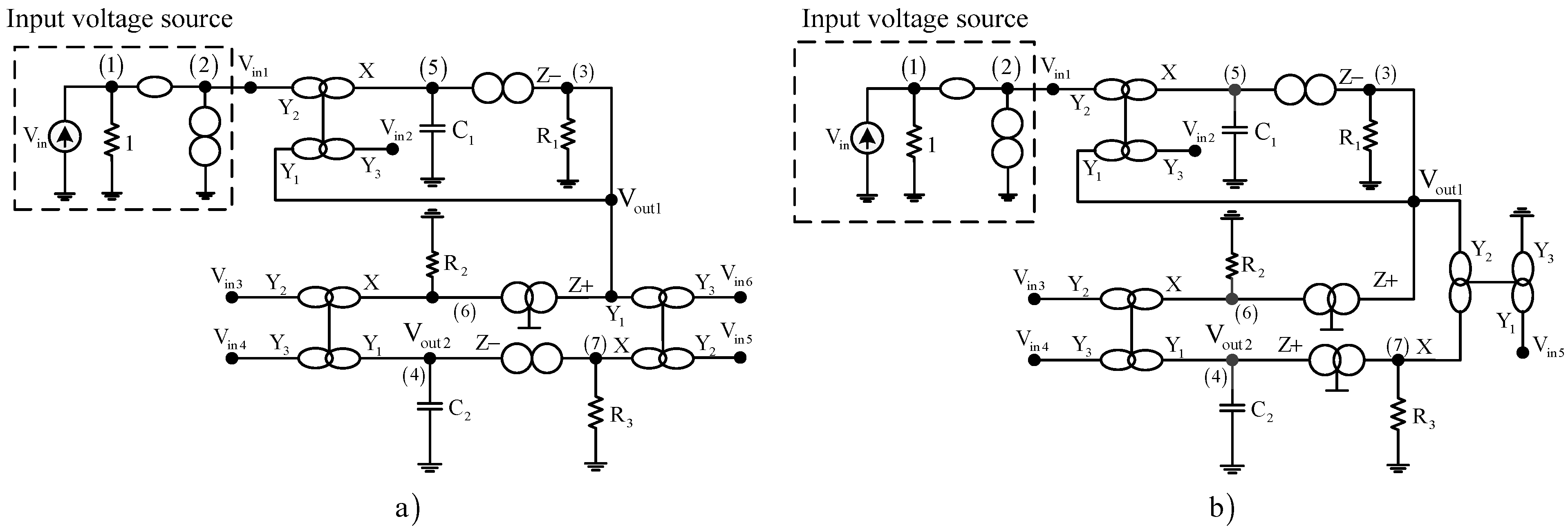
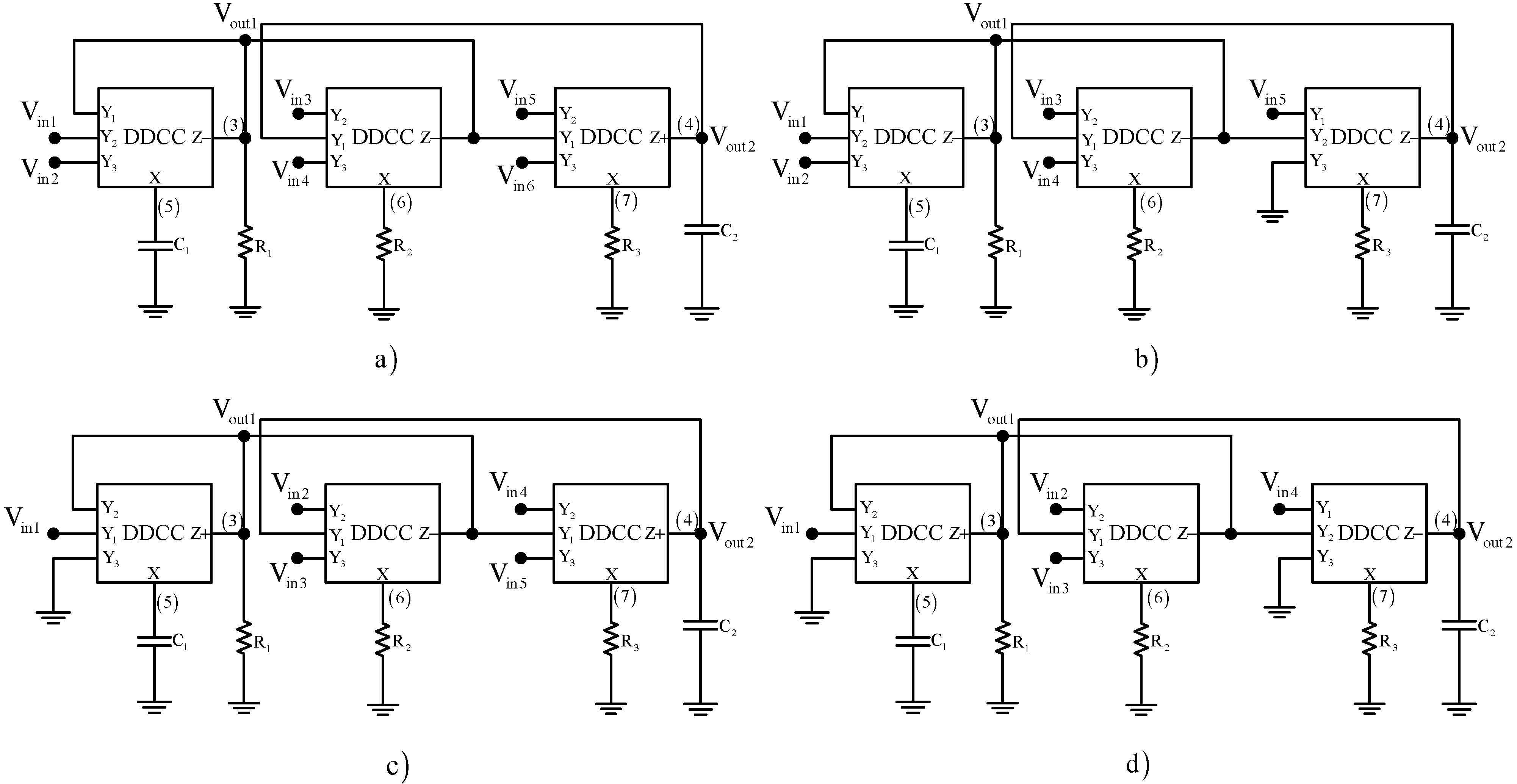
3.1. Synthesis of Type-A Universal Filters
| NAM Type-A (Case 1) | NAM Type-A (Case 2) |
| NAM Type-A (Case 3) | NAM Type-A (Case 4) |
| NAM Type-A (Case 5) | NAM Type-A (Case 6) |
| NAM Type-A (Case 7) | NAM Type-A (Case 8) |
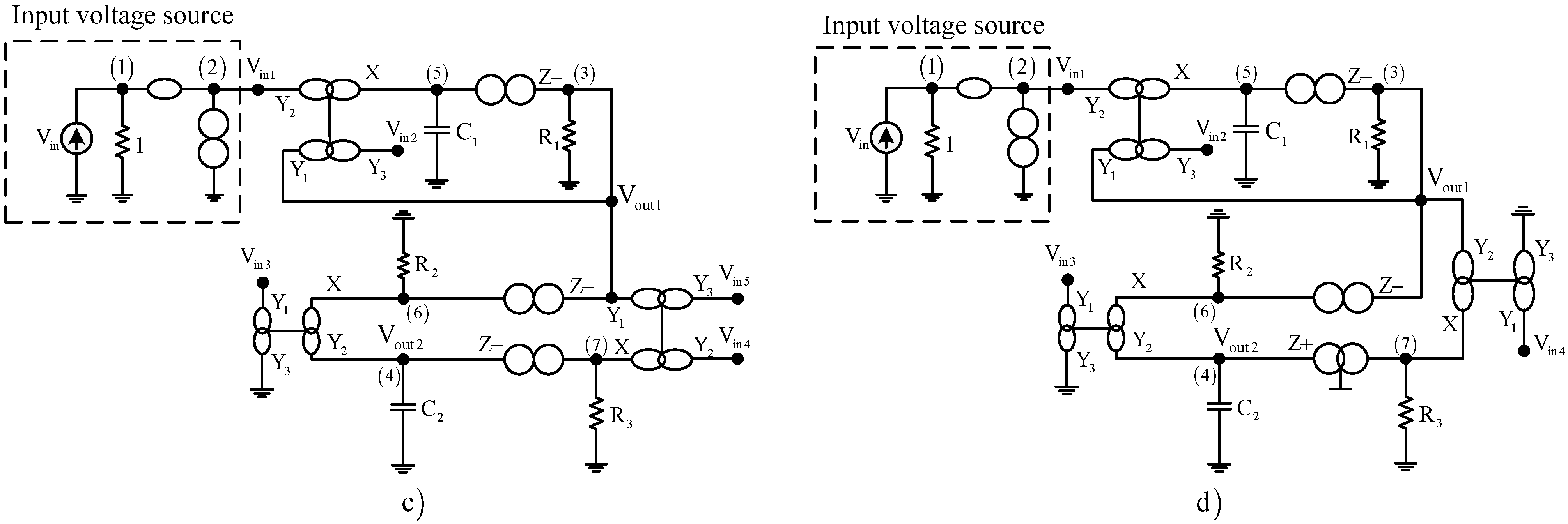
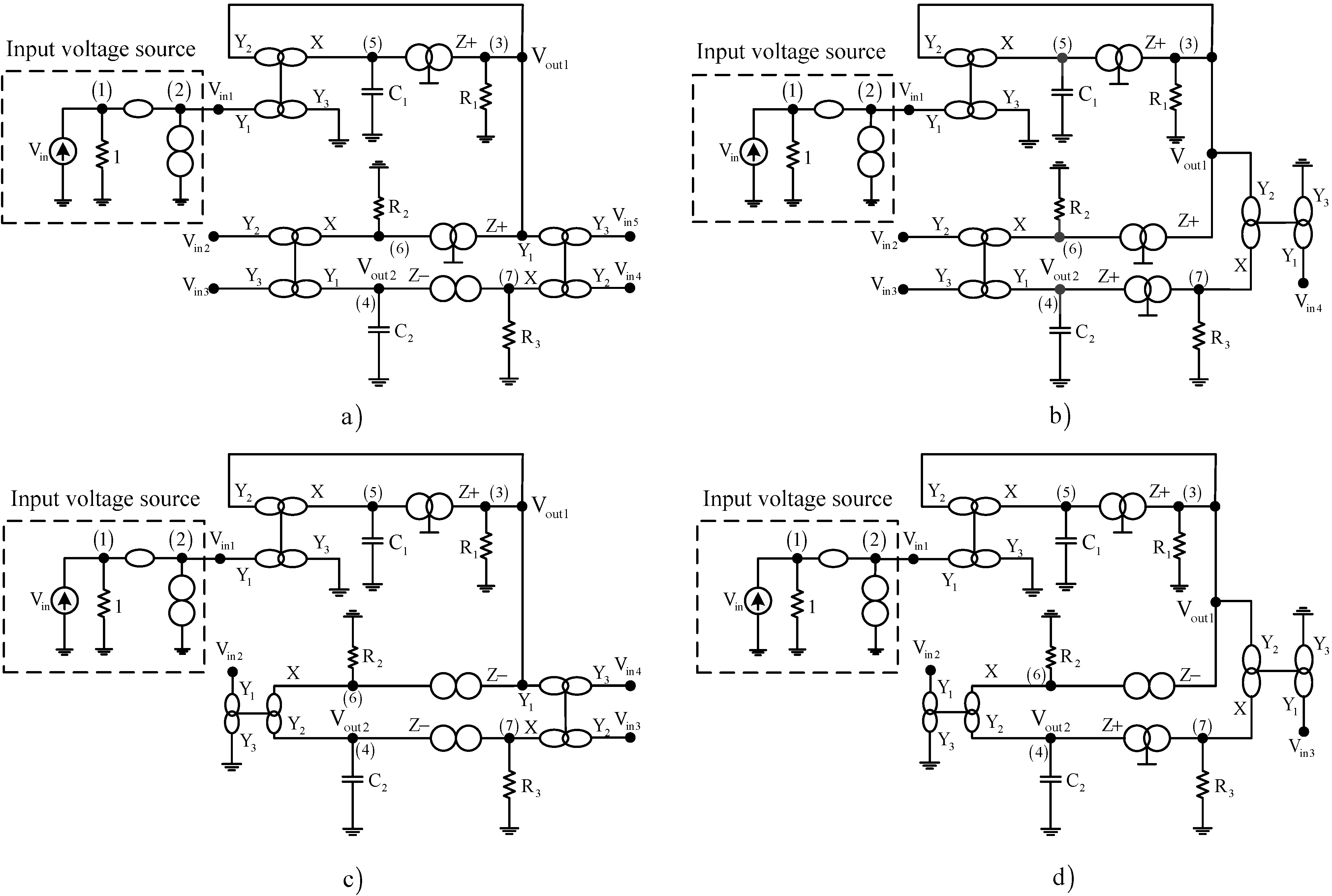
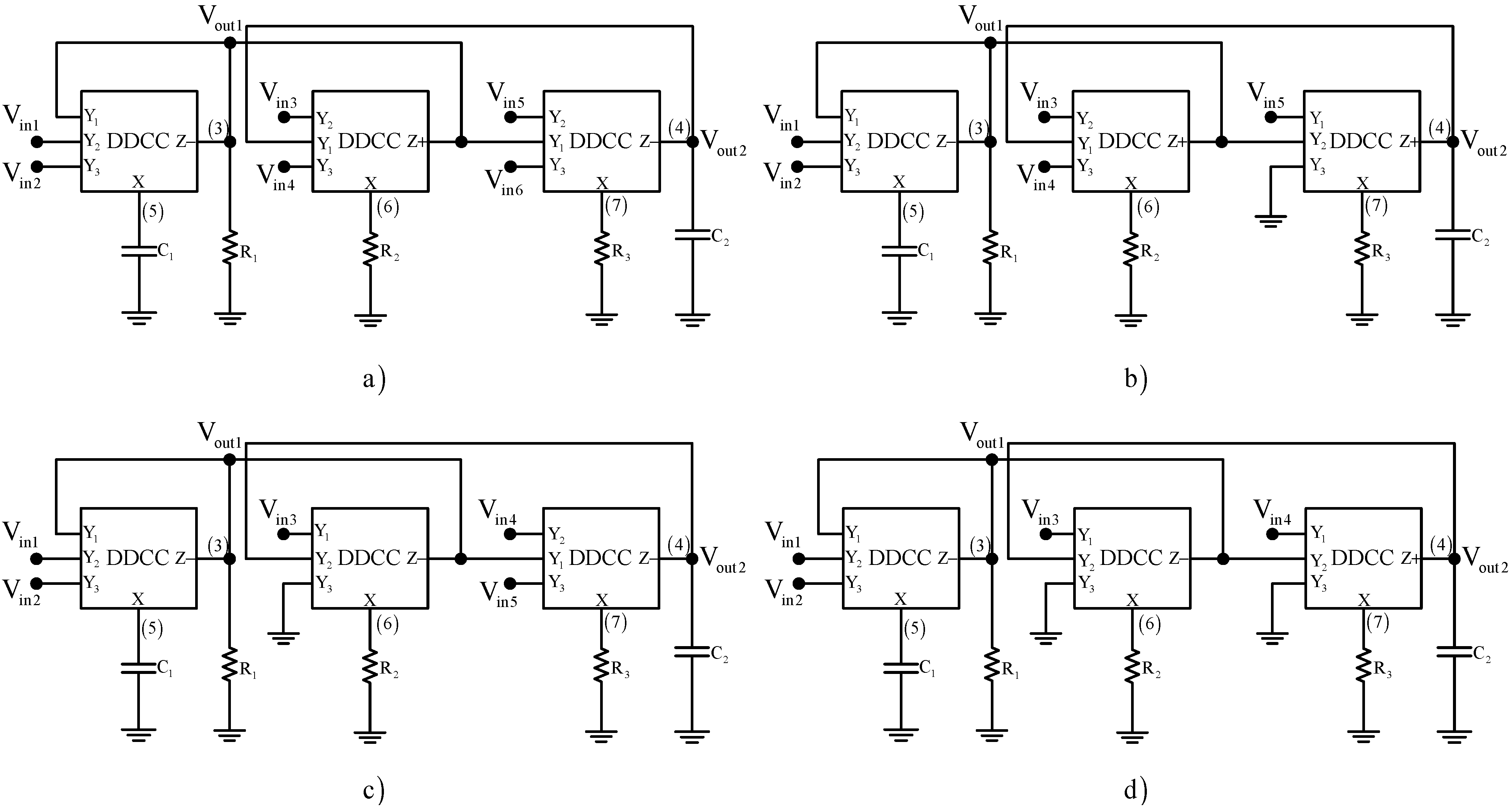
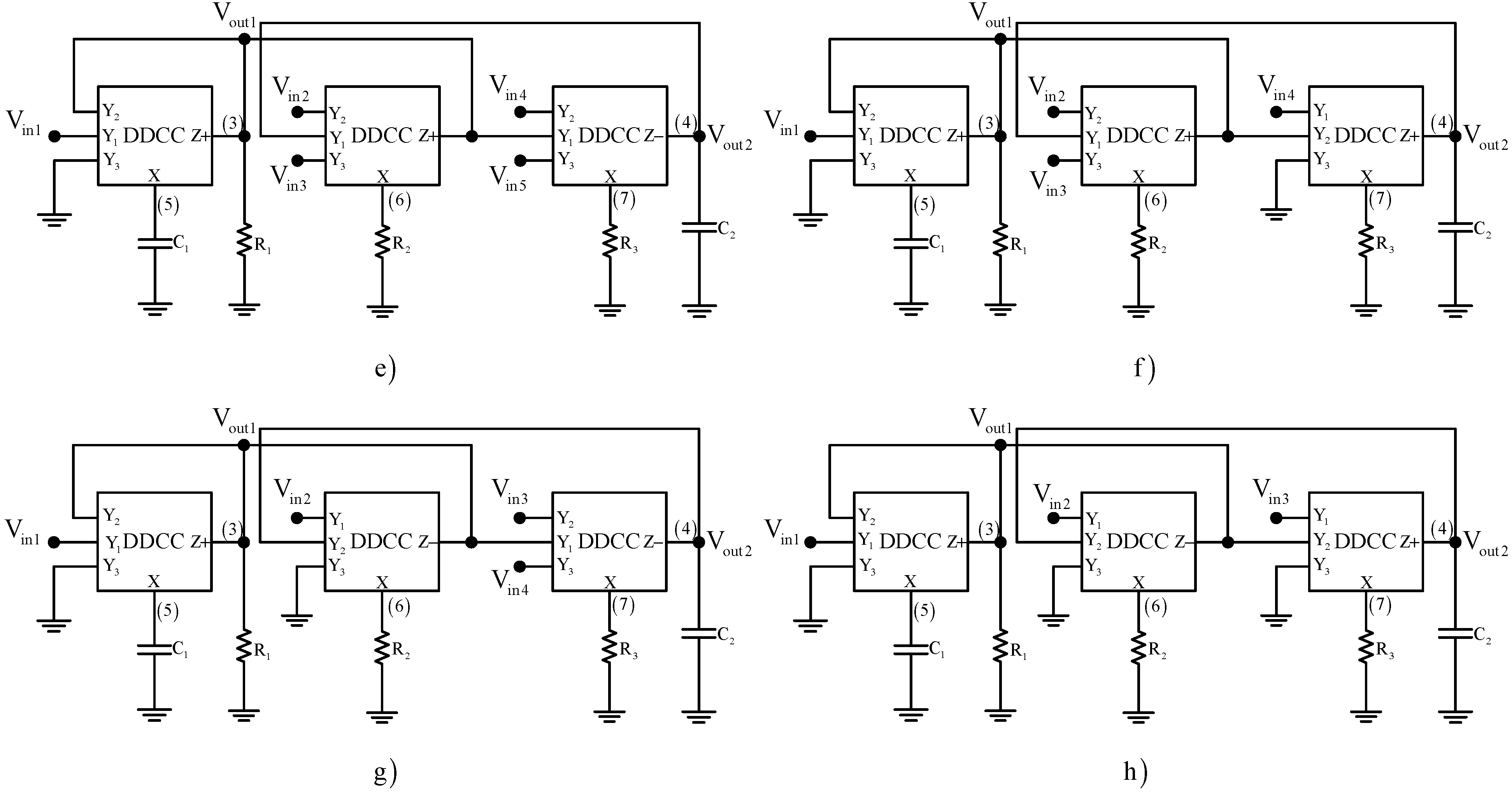
3.2. Synthesis of Type-B Universal Filters
| NAM Type-B (Case 1) | NAM Type-B (Case 2) |
| NAM Type-B (Case 3) | NAM Type-B (Case 4) |
| Related work | Operating mode | Filter type | Using grounded capacitors | Number of active elements | Cascadable property |
|---|---|---|---|---|---|
| [16] | Current | Universal | Yes | 4 | Yes |
| [17] | Transimpedance | Single function | No | 1 or 2 | Yes |
| [19] | Voltage | Notch | No | 3 | No |
| [21] | Voltage | Lowpass and bandpass | Yes | 2 | Yes |
| This work | Voltage | Universal | Yes | 3 | Yes |
3.3. Non-Ideal Effect of Active Elements
4. Simulation Results
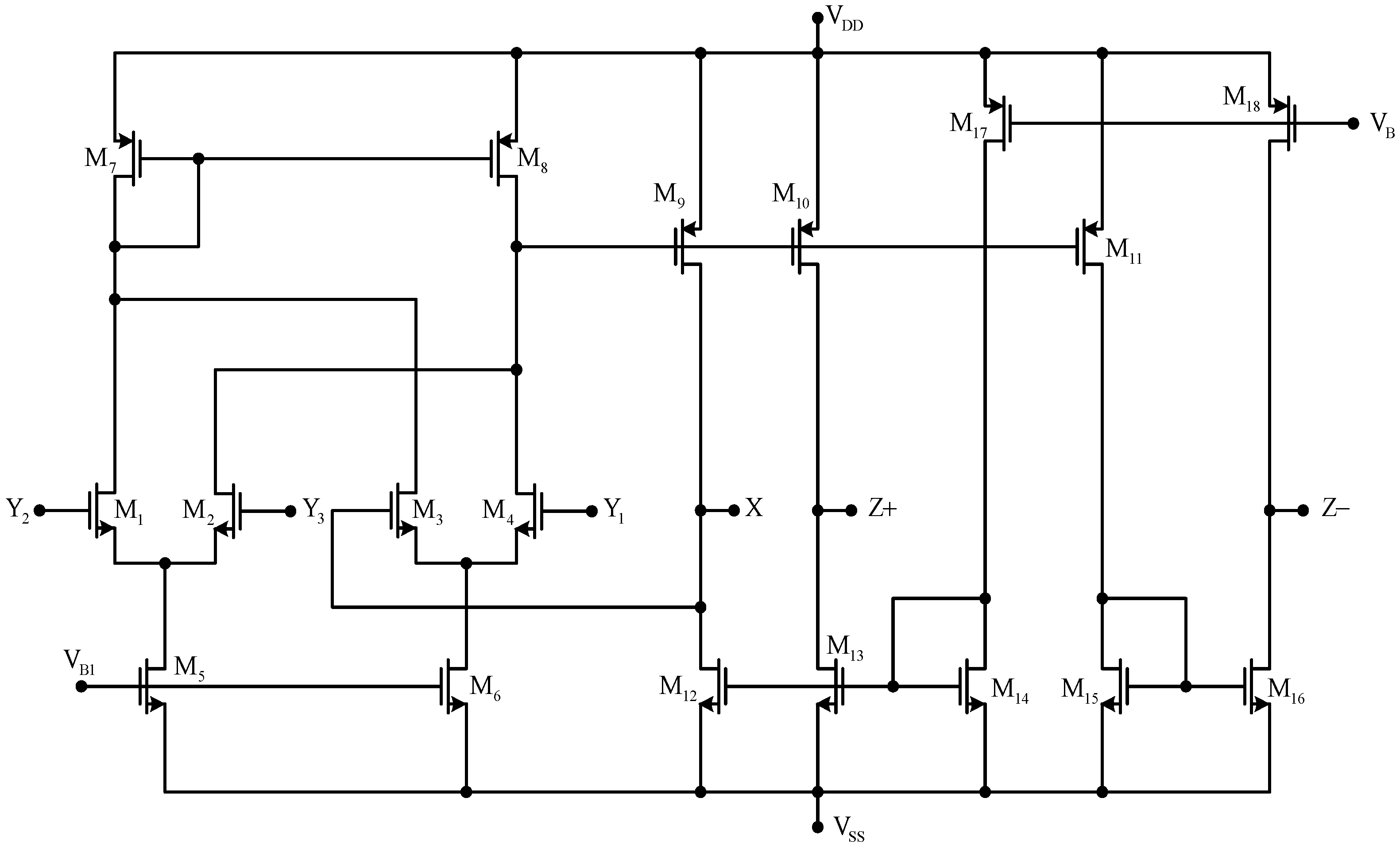
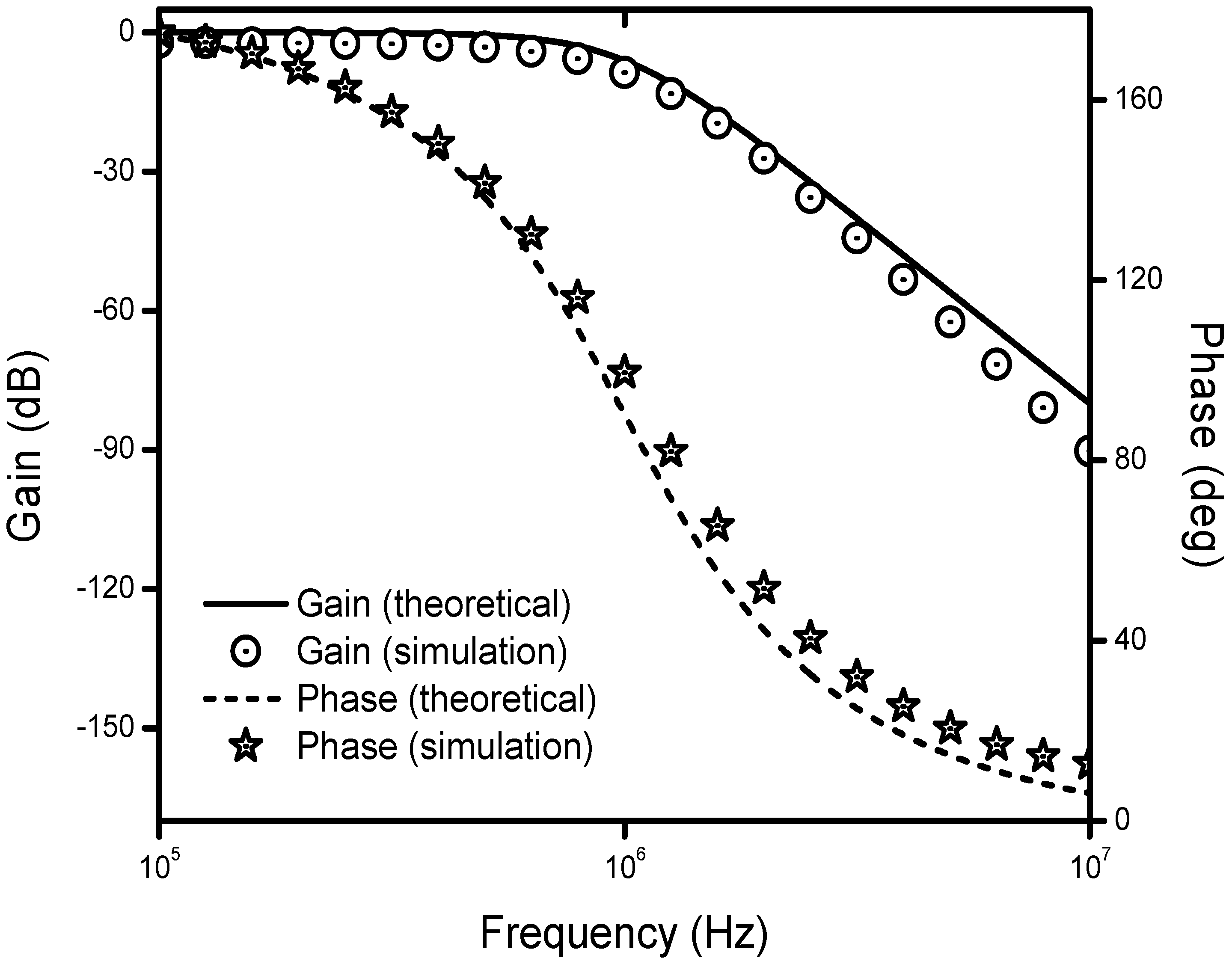
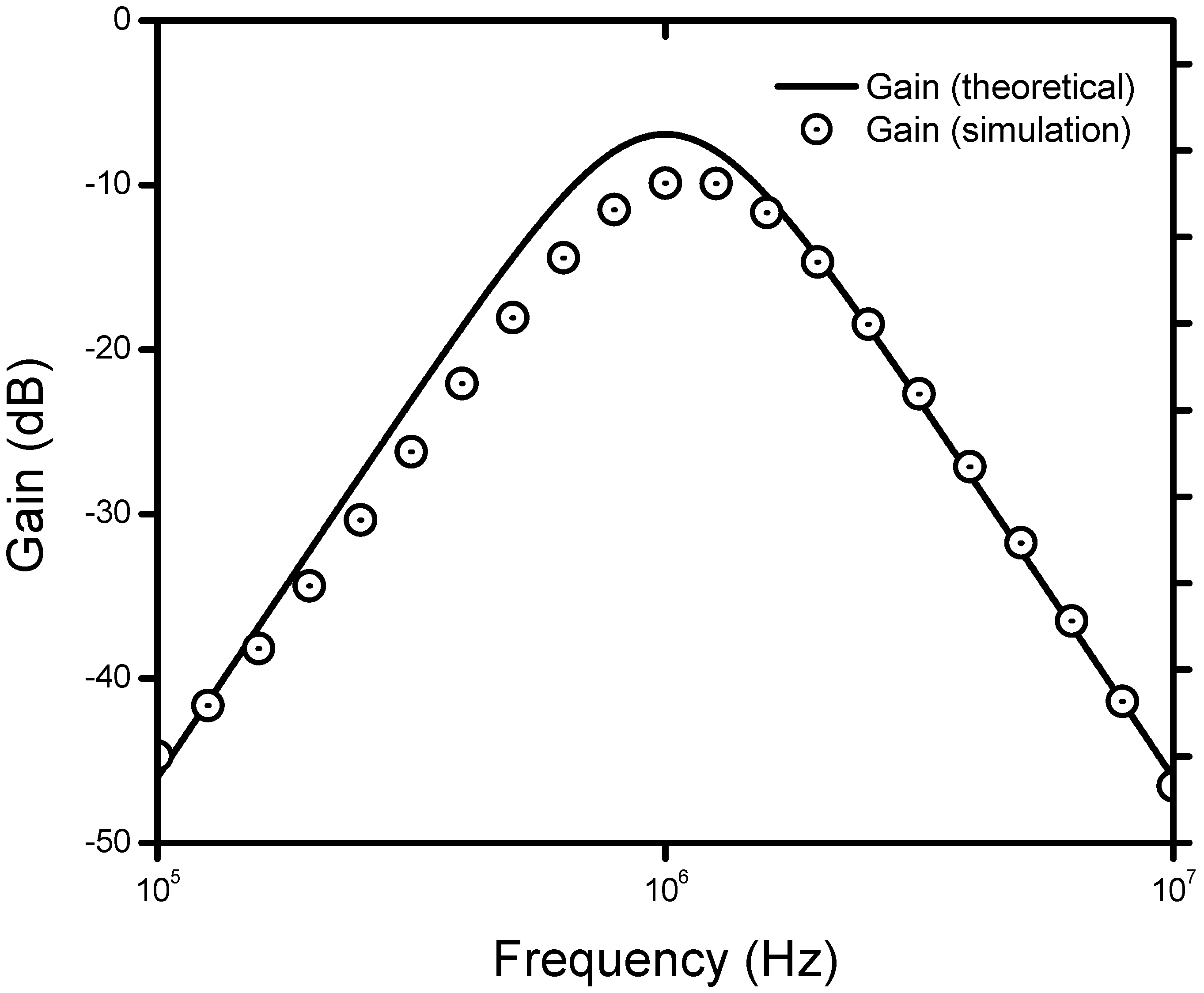
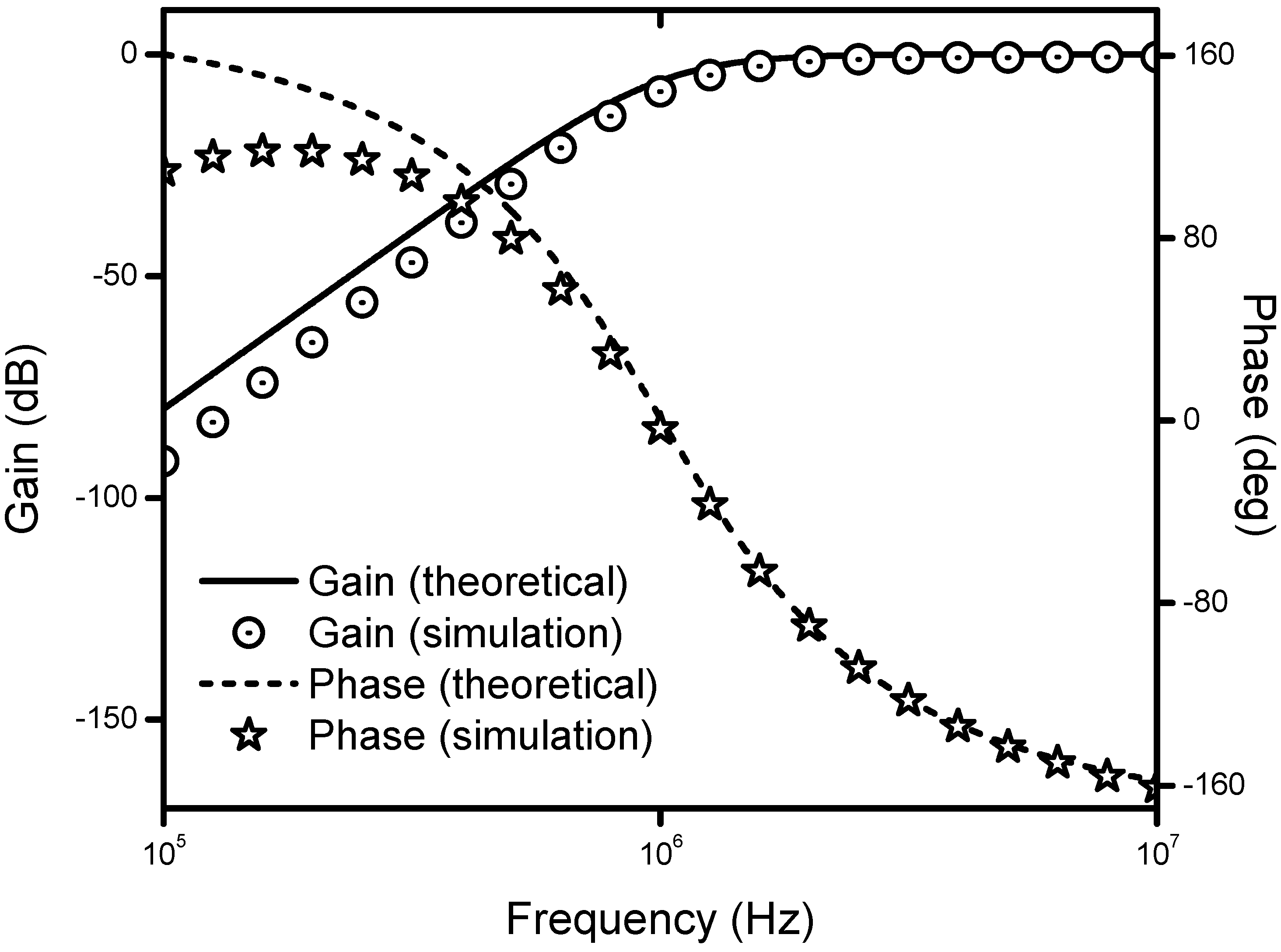
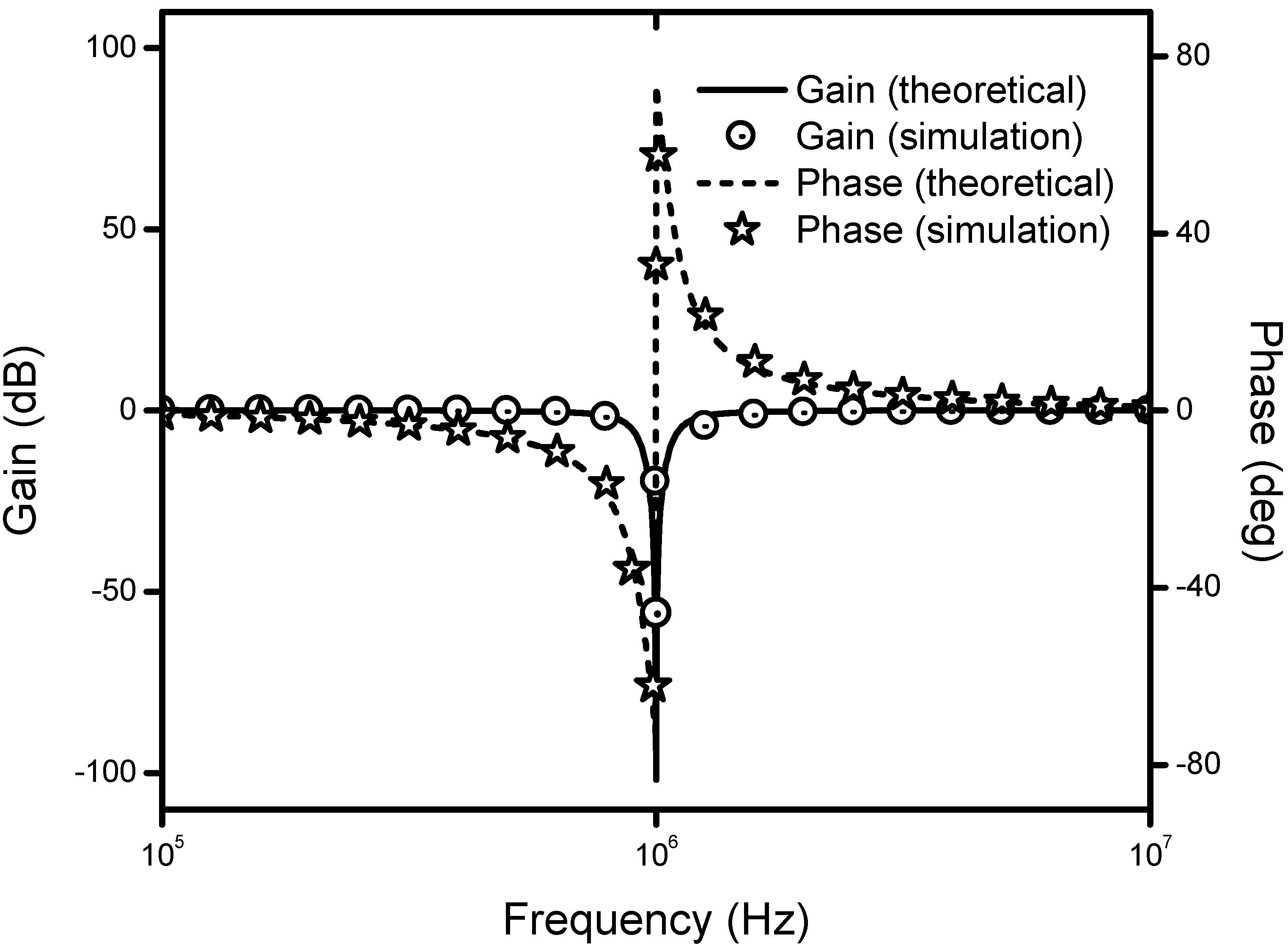
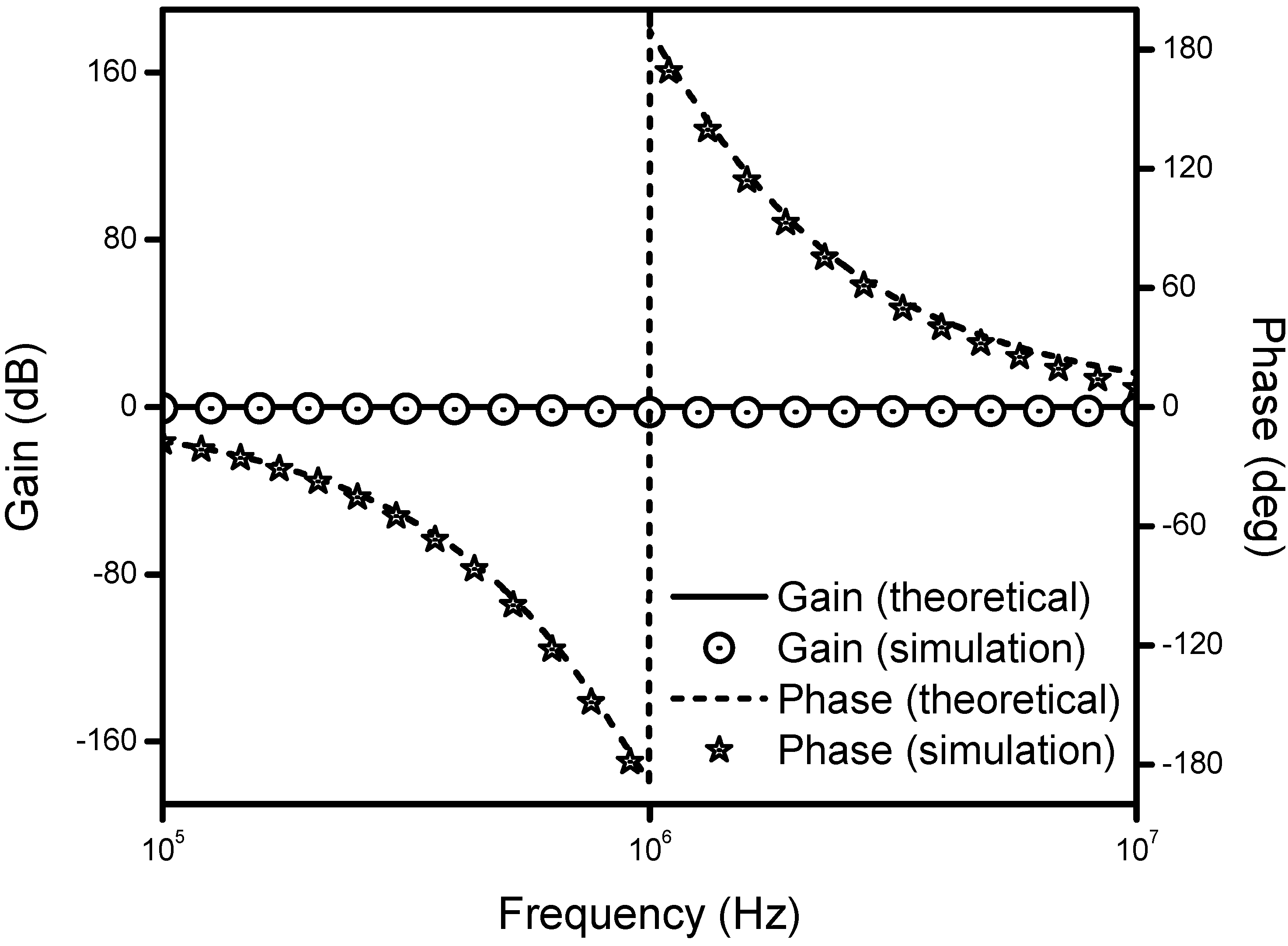
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fabre, F.; Dayoub, L.; Duruisseau, L.; Kamoun, M. High-input impedance insensitive second-order filters implemented from current conveyors. IEEE Trans. Circuits Syst. I 1994, 41, 918–921. [Google Scholar]
- Chen, H.P. Single CCII-based voltage-mode universal filter. Analog Integr. Circuits Signal Process. 2010, 62, 259–262. [Google Scholar]
- Horng, J.W. High-input impedance voltage-mode universal biquadratic filters with three inputs using plus-type CCIIs. Int. J. Electron. 2004, 91, 465–475. [Google Scholar]
- Chen, H.P. Single FDCCII-based universal voltage-mode filter. AEU-Int. J. Electron. Commun. 2009, 63, 713–719. [Google Scholar]
- Horng, J.W. High-input impedance voltage-mode universal biquadratic filters using three plus-type CCIIs. IEEE Trans. Circuits Syst. II 2001, 48, 996–997. [Google Scholar]
- Chen, H.P. Voltage-mode FDCCII-based universal filter. AEU-Int. J. Electron. Commun. 2008, 62, 320–323. [Google Scholar]
- Horng, J.W.; Hou, C.L.; Chang, C.M.; Chou, H.P.; Lin, C.T. High-input impedance voltage-mode universal biquadratic filter with one input and five outputs using current conveyors. Circuits Syst. Signal Process. 2006, 25, 767–777. [Google Scholar] [CrossRef]
- Horng, J.W.; Hou, C.L.; Chang, C.M.; Chung, W.Y.; Wei, H.Y. Voltage-mode universal biquadratic filters with one input five outputs using MOCCIIs. Comput. Electr. Eng. 2005, 31, 190–202. [Google Scholar] [CrossRef]
- Chang, C.M.; Tu, S.H. Universal voltage mode filter with four inputs and one output using two CCII+s. Int. J. Electron. 1999, 86, 305–309. [Google Scholar] [CrossRef]
- Chang, C.M. Multifunction biquadratic filters using current conveyors. IEEE Trans. Circuits Syst. II 1997, 44, 956–958. [Google Scholar] [CrossRef]
- Haigh, D.G.; Clarke, T.J.W.; Radmore, P.M. Symbolic framework for linear active circuits based on port equivalence using limit variables. IEEE Trans. Circuits Syst. I 2006, 53, 2011–2024. [Google Scholar] [CrossRef] [Green Version]
- Haigh, D.G. A method of transformation from symbolic transfer function to active-RC circuit by admittance matrix expansion. IEEE Trans. Circuits Syst. I 2006, 53, 2715–2728. [Google Scholar] [CrossRef]
- Haigh, D.G.; Tan, F.Q.; Papavassiliou, C. Systematic synthesis of active-RC circuit building-blocks. Analog Integr. Circuits Signal Process. 2005, 43, 297–315. [Google Scholar] [CrossRef]
- Haigh, D.G.; Radmore, P.M. Admittance matrix models for the nullor using limit variables and their application to circuit design. IEEE Trans. Circuits Syst. I 2006, 53, 2214–2223. [Google Scholar] [CrossRef]
- Saad, R.A.; Soliman, A.M. Use of mirror elements in the active device synthesis by admittance matrix expansion. IEEE Trans. Circuits Syst. I 2008, 55, 2726–2735. [Google Scholar] [CrossRef]
- Soliman, A.M. Generation of current mode filters using NAM expansion. Int. J. Circuit Theory Appl. 2011, 39, 1087–1103. [Google Scholar] [CrossRef]
- Tan, L.; Bai, Y.; Teng, J.; Liu, K.; Meng, W. Trans-impedance filter synthesis based on nodal admittance matrix expansion. Circuits Syst. Signal Process. 2013, 32, 1467–1476. [Google Scholar] [CrossRef]
- Li, Y.A. NAM expansion method for systematic synthesis of floating gyrators using CCCCTAs. Analog Integr. Circuits Signal Process. 2015, 82, 733–743. [Google Scholar] [CrossRef]
- Tran, H.D.; Wang, H.Y.; Nguyen, Q.M.; Chiang, N.H.; Lin, W.C.; Lee, T.F. High-Q biquadratic notch filter synthesis using nodal admittance matrix expansion. AEU-Int. J. Electron. Commun. 2015, 69, 981–987. [Google Scholar] [CrossRef]
- Li, Y.A. On the systematic synthesis of OTA-based Wien Oscillators. AEU-Int. J. Electron. Commun. 2013, 67, 754–760. [Google Scholar] [CrossRef]
- Soliman, A.M. Two integrator loop filters: Generation using NAM expansion and review. J. Electri. Comput. Eng. 2010. [CrossRef]
- Chiu, W.; Liu, S.I.; Tsao, H.W.; Chen, J.J. CMOS differential difference current conveyors and their applications. IEE Proc. Circuits Devices Syst. 1996, 143, 91–96. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Horng, J.W. High-input and low-output impedance voltage-mode universal biquadratic filter using DDCCs. IEEE Trans. Circuits Syst. II 2007, 54, 649–652. [Google Scholar] [CrossRef]
- Chen, H.P. Universal voltage-mode filter using only plus-type DDCCs. Analog Integr. Circuits Signal Process. 2007, 50, 137–139. [Google Scholar] [CrossRef]
- Horng, J.W. High input impedance voltage-mode universal biquadratic filter with three inputs using DDCCs. Circuits Syst. Signal Process. 2008, 27, 553–562. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Horng, J.W. High input impedance voltage-mode biquadratic filter with three inputs and six outputs using three DDCCs. Circuits Syst. Signal Process. 2012, 31, 19–30. [Google Scholar] [CrossRef]
- Elwan, H.O.; Soliman, A.M. Novel CMOS differential voltage current conveyor and its applications. IEE Proc. Circuits Devices Syst. 1997, 144, 195–200. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, H.-D.; Wang, H.-Y.; Lin, M.-C.; Nguyen, Q.-M. Synthesis of Cascadable DDCC-Based Universal Filter Using NAM. Appl. Sci. 2015, 5, 320-343. https://doi.org/10.3390/app5030320
Tran H-D, Wang H-Y, Lin M-C, Nguyen Q-M. Synthesis of Cascadable DDCC-Based Universal Filter Using NAM. Applied Sciences. 2015; 5(3):320-343. https://doi.org/10.3390/app5030320
Chicago/Turabian StyleTran, Huu-Duy, Hung-Yu Wang, Min-Chuan Lin, and Quoc-Minh Nguyen. 2015. "Synthesis of Cascadable DDCC-Based Universal Filter Using NAM" Applied Sciences 5, no. 3: 320-343. https://doi.org/10.3390/app5030320
APA StyleTran, H.-D., Wang, H.-Y., Lin, M.-C., & Nguyen, Q.-M. (2015). Synthesis of Cascadable DDCC-Based Universal Filter Using NAM. Applied Sciences, 5(3), 320-343. https://doi.org/10.3390/app5030320






