Abstract
We present the current development of an injector for a high-contrast, ultrashort laser system devoted to relativistic laser-plasma interaction in the few-cycle regime. The front-end is based on CEP-stabilized Ti:Sa CPA followed by XPW filter designed at the mJ level for temporal cleaning and shortening. Accurate characterization highlights the fidelity of the proposed injector. Measured CEP drift is 170 mrad rms.
1. Introduction
A recent breakthrough of ultrafast laser science has been the ability to produce laser pulses with duration close to the optical cycle (2.7 fs at 800 nm) with controlled waveform, i.e., controlled carrier-envelope phase (CEP). The availability of such pulses has provided new insight into attosecond electronic processes in matter [1]. CEP-controlled few-cycle pulses are routinely used at moderate intensities to probe attosecond electronic dynamics in atoms or molecules. More recently, few-cycle pulses with relativistic intensities (above 1018 W/cm2 at 800 nm) have been used to study collective electronic dynamics in laser-driven plasmas, such as few-fs electron bunch acceleration from gas jets [2,3] or high-harmonic generation from solid targets [4]. Unfortunately, all these pioneering experiments were performed without CEP control.
Recent experiments at Laboratoire d’Optique Appliquée have demonstrated, for the first time, attosecond time-scale control over plasma electron dynamics using a CEP-controlled few-cycle laser system at 1 kHz (Salle Noire), as well as the ability to isolate single attosecond pulses from the harmonic emission via spatio-temporal gating of the laser-plasma interaction [5,6]. Moreover, few-cycle laser-driven energetic particle acceleration was also demonstrated using the same experimental set-up [7]. These pioneer experiments were performed with the Salle Noire laser, delivering 1.2 mJ, 5 fs pulses and a relative CEP drift of 250 mrad rms [8]. Reaching the relativistic regime with few-cycle pulses, especially on solid targets, requires both an increase in the pulse energy and temporal contrast. As a consequence, we are in the process of upgrading our laser system to produce CEP-controlled, 5 mJ, 5 fs pulses with a temporal contrast ratio better than 1010.
Nowadays, two major techniques are widely used to efficiently enhance the final pulse contrast: plasma mirrors at the end of the laser chain [9,10] and nonlinear temporal filters in a double-CPA scheme [11]. In the past few years, we have developed and qualified a nonlinear filtering device relying on cross-polarized wave (XPW) generation [12]. XPW generation is an achromatic and degenerated four wave mixing process relying on the anisotropy of the χ3 tensor in isotropic crystals [13]. When an intense, linearly polarized input beam (fundamental) illuminates a nonlinear crystal placed between crossed polarizers, it gives rise to an orthogonally polarized wave (XPW). The cubic dependence between output and input intensities provides an improvement in temporal contrast that is limited only by the extinction ratio of the crossed polarizers. Nowadays, XPW-based contrast enhancement has become widespread in high peak-power laser systems [10,14–17].
The planned upgraded Salle Noire laser will first consist of a Ti:Sa double-CPA system, providing 1 kHz, 10 mJ, 25 fs pulses. The first CPA is a commercial CEP-stabilized laser system. The compressed pulses are then temporally filtered by an XPW setup and stretched to about 50 ps during propagation through a SF57 bulk and an AOPDF (Dazzler). Further amplification will occur in two multipass amplifiers. Pulse compression will be achieved in a specially designed, high-energy, grism compressor [18]. It has been shown that XPW process and compression in grisms both preserve CEP stability [19]. The double-CPA is therefore expected to produce high-contrast, multi-mJ, CEP-stabilized pulses. Further post-compression in a hollow-core fiber setup to the few-cycle regime will aim at providing around 5 mJ, 5 fs pulses for relativistic laser-plasma interaction [8,20].
In this paper, we present a detailed characterization of the CEP-controlled, high-contrast injector for the second CPA, consisting of a Ti:Sa CPA followed by a high-efficiency XPW contrast filter at the mJ level. We demonstrate that this injector fulfills all the critical requirements in order to seed the second CPA stage: high-contrast, high spatio-temporal quality and high fidelity in terms of stability. The added benefit of XPW filtering is the significant spectral broadening that ensues, which will allow us to obtain very short pulses at the output of the future second CPA stage. The current front-end light source routinely delivers 300 μJ pulses, with a Gaussian spectrum with more than 100 nm bandwidth (FWHM). Temporal compression of the XPW pulse to 9.3 fs is demonstrated. The results show that XPW filtering can be used as a simple and efficient pulse shortener.
2. Experimental Setup
The proposed laser system, described on Figure 1, consists of a commercial 1 kHz CEP-stabilized amplifier (Femtopower Compact Pro CE Phase, Femtolasers GmbH) followed by an XPW contrast filter. The oscillator pulses (Rainbow) are CEP locked via pump-laser amplitude modulation and stretched in a 20 cm-long SF57 block before amplification up to 1.9 mJ in a ten-pass titanium-sapphire amplifier. The amplification stage is pumped by 11 W from a 1 kHz frequency-doubled Q-switched Nd:YLF laser (JADE, Thales). An AOPDF (low-jitter Dazzler HR800, Fastlite) is inserted between the fourth and fifth passes in the amplifier in order to optimize the spectral amplitude and phase. Finally, the 7 ps long amplified pulses are then compressed through a transmission-grating compressor (TGC) with an overall efficiency of 85%. The TGC consists of a pair of 1280 g/mm gratings used at the Littrow incidence angle (30.8°) and separated by 10 mm. We have already shown that this compression setup is fully compatible with CEP stabilization [21]. The compressed pulse duration is slightly below 30 fs and the Gaussian output beam has a diameter of 10 mm (1/e2). Self-referenced spectral interferometry (Wizzler device [22]) (Figure 2) enables the fine-tuning of the residual spectral phase of the compressed pulses, which is critical before they are sent into the XPW filtering stage [23]. Typical energy stability at this stage is around 1% RMS over hours.
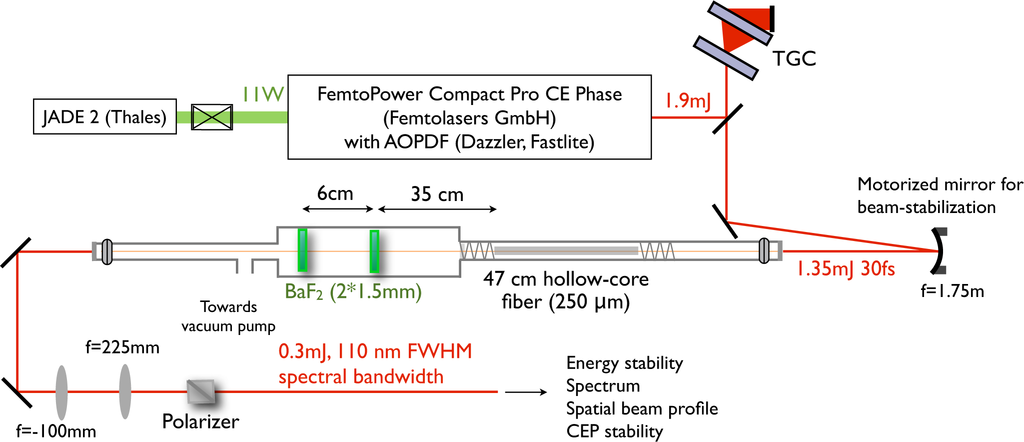
Figure 1.
Experimental scheme of the 1 kHz CEP-stable CPA system and waveguide-XPW filter (TGC: Transmission Gratings Compressor).
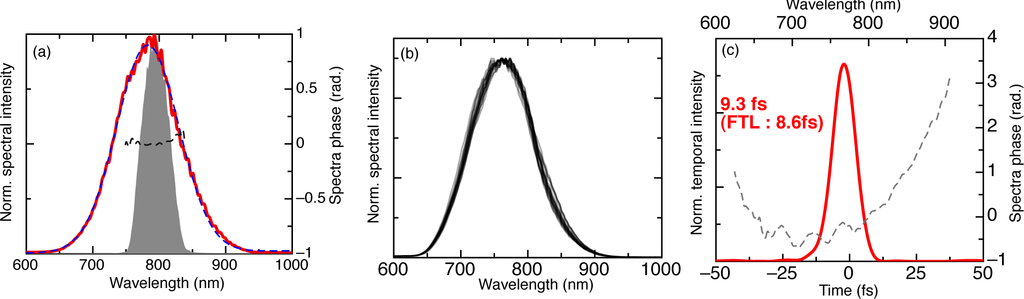
Figure 2.
(a) Initial fundamental spectral amplitude (shaded area) and phase (dashed black line), measured after the TGC. XPW spectrum (red line) with a Gaussian fit (dashed blue line, 105 nm FWHM); (b) Density plot of XPW spectra (averaged over 500 shots) recorded every 5 nm over 90 nm. Lower spread corresponds to higher stability; (c) Temporal intensity profile and residual spectral phase of the compressed XPW pulse measured by SRSI.
In our current setup, the XPW filter is an optimized version of that described in [24]. Thanks to the TGC providing pure polarization and thanks to little propagation between the TGC and the XPW filter, the use of an input polarizer is not necessary. The XPW setup consists of a 47 cm, 250 μm inner diameter hollow-core waveguide providing efficient (75% transmission) spatial filtering, followed by two nonlinear BaF2 crystals, all under vacuum. Coupling of the beam into the hollow-core fiber is achieved using a 1.75 m focal length mirror. Slow drift of the input beam pointing is corrected using a home-built beam stabilization system, ensuring constant long-term fiber transmission. Two thin, 1.5 mm thick, BaF2 crystals with holographic crystallographic orientation are employed for XPW conversion, situated 35 cm and 41 cm respectively after the fiber output. The position of the first crystal corresponds to a fundamental beam diameter of 1.7 mm (1/e2), adapted to the incident 1 mJ. This scheme does not correspond to the standard two-crystal scheme described in [25], where phase-matched XPW generation is ensured by Kerr focusing of the fundamental beam between the two crystals. In this scheme, the fundamental beam diverges out of the fiber and thus self-focusing in the first crystal mainly collimates the fundamental beam. However, we noticed that using two thin crystals instead of a thicker one leads to a slightly higher output energy and improved pulse-to-pulse stability. Because the XPW is driven closer into saturation, the pump spatial profile is depleted during XPW conversion and free-space propagation enables to optimize the fundamental spatial beam profile and improve the XPW conversion efficiency in the second crystal. A direct consequence of the improved efficiency XPW close to saturation is the enhanced pulse-to-pulse stability of the device. The advantage of this approach is that it is scalable to higher energies [24]. Here, the output beam is then expanded to go through the output Glan polarizer enabling XPW pulse selection. 300 μJ pulses are routinely generated, corresponding to a XPW internal efficiency as high as 33% (fiber transmission and reflection losses on crystals deduced) and a global energy transmission of 22%.
3. Characterization of Front-End Light Source Performance
3.1. Spectro-Temporal Characterization
The pulse contrast improvement cannot be measured precisely with enough dynamic range at this energy level. However, as previously demonstrated [26], the extinction ratio of the polarization management is the only limit to the overall contrast enhancement. In the current system, we measured an extinction ratio of 4 orders of magnitude, which, starting from a contrast ratio of the order of 108 [24], leads us to infer the temporal contrast of front-end system to be of the order of 1012.
The initial fundamental and XPW spectra are compared in Figure 2(a). The initial laser spectrum is shaped into a perfectly Gaussian spectrum during the nonlinear process. This feature is a direct consequence of the XPW temporal cleaning properties [27–29]. This is an essential point for the final spatio-temporal quality of the output pulses.
Moreover, extensive spectral broadening is measured. The calculated FWHM spectral bandwidth is increased by a factor of 2.4. The expected temporal shortening (the ratio of input laser pulse duration over output XPW pulse duration using Fourier-transform limited values) is around 3. The discrepancy comes from the differing spectral intensity profiles. The output spectrum supports sub-10 fs duration (8.6 fs Fourier transform limited). At lower efficiencies, for an unchirped pulse, spectral broadening following XPW is a direct consequence of the shortening of the pulse duration by a factor of 1.7 [23]. Here, the higher XPW efficiency is associated with important self-phase modulation (SPM) on the fundamental beam, and thus significant spectral broadening, a feature that is transferred onto the XPW wave. Simultaneous pulse shortening during the process prevents the XPW pulse from spectral and temporal distortions [30]. The higher the XPW efficiency, the more pronounced the broadening. This is illustrated in Figure 3, displaying the spectral evolution of the fundamental and XPW waves with respect to input pulse energy. While the fundamental spectrum exhibits features typical of SPM, the process provides smooth and homogeneous broadening of the XPW spectrum. These clean spectral features indicate that SPM on the XPW beam is negligible. Although significant spectral broadening and reshaping during XPW have already been observed before [27], they are particularly emphasized here. This results from the combination of high efficiency and perfect spectral phase correction thanks to the spectral phase-loop optimization of the Wizzler device (Figure 2(a)).
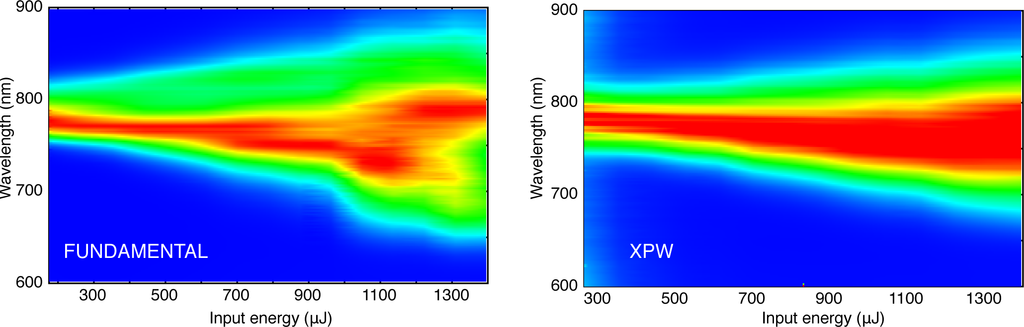
Figure 3.
Fundamental (measured after the nonlinear interaction) and XPW normalized spectra as a function of laser input energy. Each spectrum is averaged over 500 shots.
In order to characterize pulse fidelity of the front-end, we then verified the spectral repeatability. The short-term stability is measured by the acquisition of 500 consecutive spectra of the amplified and XPW pulses. Despite the fact that broadening is due to nonlinear effects, spectral stability is not degraded after XPW and remains below 2% RMS across the entire spectrum. The long-term stability was monitored by recording the spectrum at regular intervals over 90 nm, showing only minor variations (Figure 2(b)). The available spectral bandwidth for further amplification will therefore not be significantly affected by the weak energy fluctuations of the input amplifier beam.
For temporal compression and characterization, the XPW pulse is discriminated by a reflective Ga polarizer to minimize the propagation in dispersive elements. The dispersion introduced by the crystals and chamber output window is compensated by chirped mirrors. Temporal measurement is provided by SRSI (self-referenced spectral interferometry, Wizzler) adapted to ultrashort pulses [31]. The result indicate a pulse duration of 9.3 fs (Figure 2(c)), confirming a compression factor of 3 during the XPW process. Spectral phase oscillations are typical of chirped mirrors, ultimately limiting the spectro-temporal quality of the XPW pulse.
3.2. Spectro-Spatial Characterization
The creation of new frequencies by SPM, beyond the typical 1.7 spectral broadening factor, is intensity-dependent and therefore varies across the Gaussian input beam profile. This feature affects the spatial homogeneity of the XPW pulse spectrum, as shown in Figure 4(a), representing the measured XPW spectrum through a 0.2 mm pinhole translated across the beam, 15 cm after the second crystal. The spectral FWHM varies between 60 nm at the edges and 110 nm at the center (Fourier transform limited durations: 15 fs and 8.5 fs, respectively). However, the same measurement performed on the beam after 2 m propagation (far-field) exhibits a broad and homogeneous spectrum across the beam (Figure 4(b)). The complex spatio-temporal dynamics of this process is currently under study. In first approximation, it can be explained by cross-phase modulation of the XPW beam by the intense pump beam. It has recently been demonstrated that wavelength-dependent nonlinear focusing follows nonlinear spectral phase [32]. Consequently, extreme wavelengths, created at the highest beam intensity, may experience stronger self-focusing, leading to nonlinear wavelength-dependent propagation after the crystal that compensates the initial spatio-spectral inhomogeneity. The final spectro-spatial homogeneity is not a particular feature of the double-crystal scheme and the same results are obtained with a single crystal.
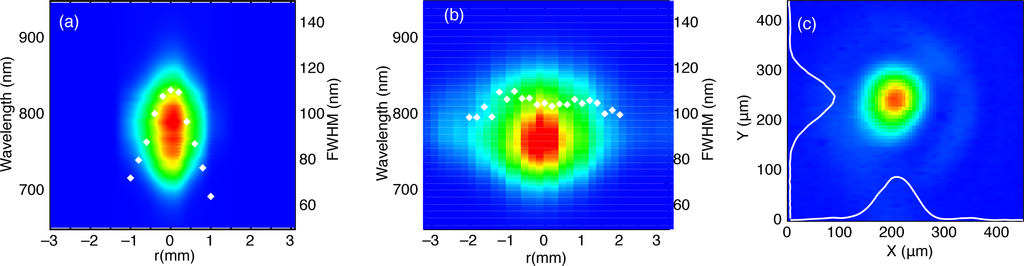
Figure 4.
Spectro-spatial distribution of the XPW beam, 15 cm after the second crystal (a) and propagated over 2 m (b). Spectral FWHM measured across the beam profile are indicated with white diamonds; (c) Spatial intensity distribution of the XPW beam at the focus of a 500 mm lens.
To summarize, although nonlinear self-action is negligible for the XPW beam, SPM and Kerr focusing undergone by the pump beam confer to the XPW pulse a broad, spatially uniform, Gaussian spectrum, optimal for further amplification. The measurements presented in Figure 4 underscore the excellent spatial quality of the output beam in the far field. Figure 4(c) shows the intensity profile of the pulses measured at the focus of a 500 mm lens. The spatial profile is Gaussian with a beam Strehl ratio of about 0.9. The measured shot-to-shot beam pointing stability of the beam after XPW is 30 μrad (8 μrad rms). This is yet another direct advantage of the wave guided XPW setup.
This simple and efficient XPW setup can consequently be used as a pulse shortener device, providing excellent spatial and spectro-temporal quality.
4. Fidelity of the Front-End
To further quantify the fidelity of the front-end system, long-term energy stability is monitored continuously and is usually below 2% rms after XPW. Figure 5(a) is an illustration of typical energy fluctuations over a few minutes of the pump laser, amplified and filtered pulses.
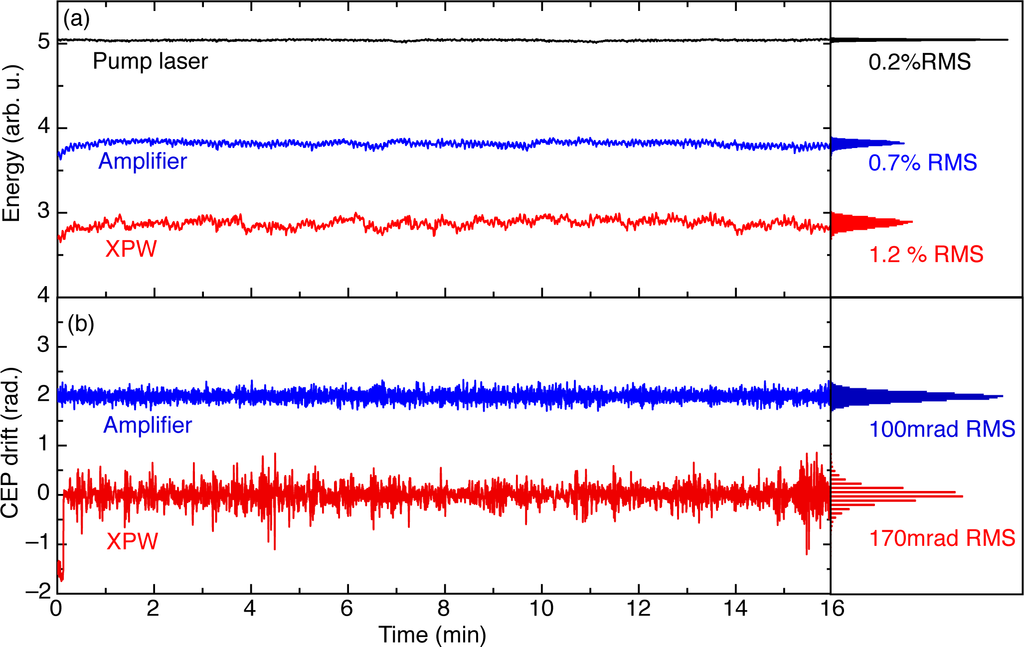
Figure 5.
(a) Simultaneous measurements of energy fluctuations of the pump laser, amplified and filtered pulses over 16 min. Over one hour, typical rms energy deviations of the pump, amplifier and XPW pulses are 0.3%, 1% and 1.6% respectively; (b) Relative CEP drift with feedback control on the oscillator of the amplifier (measured after the XPW setup with no BaF2 crystal) and XPW pulses. Energy and CEP stability measurements have been done on the same day under similar experimental conditions.
CEP stability of the front-end system is the last critical feature to be characterized. To estimate it, a few microjoules of the XPW pulse are split off, compressed with chirped mirrors and sent into a collinear f-to-2f interferometer (APS 800, Menlo Systems). The slow CEP drift of the output pulses at 1 kHz is pre-compensated by a feedback loop to the oscillator locking electronics. For the measurement, the spectrometer acquisition time is 1 ms and the cycle loop time of the APS software is 100 ms. Results are shown in Figure 5(b). The rms phase error is 170 mrad over 16 min. Although slightly higher than the amplifier (typically 100 mrad rms), this value confirms the robustness of the XPW filter. We estimate the degradation of the CEP stability to be partly due to the measurement itself, which is affected both by the input pulse-to-pulse stability and by the limited ability of the APS device to handle such short (spectrally broad) pulses.
5. Conclusions
To conclude, we have described a front-end light source featuring high contrast and high spatial and spectral quality pulses of potential sub-10 fs duration. The overall CEP fluctuations of the system can be reliably kept well under 200 mrad rms. We expect this excellent pulse fidelity to be improved or at least preserved thanks to careful management of saturation effects in any further amplification stages. Although the effect of a second CPA on the overall CEP stability is unknown, its measurement should benefit from an improved pulse-to-pulse energy stability and accurate compression of the laser pulse. This work also shows that XPW acts as a temporal post-compression device, producing sub-10 fs pulses with exceptional spatio-temporal fidelity. Previous validation of this setup with an input energy as high as 11 mJ [33] demonstrates that XPW can be configured as an efficient multi-mJ post-compression device.
Acknowledgments
The authors acknowledge financial support from the Agence Nationale pour la Recherche through program ANR-09-JC-JC-0063 (UBICUIL) and the RTRATriangle de la Physique through program 2011-024T -NewXPW. Thomas Oksenhendler (Fastlite) is also gratefully acknowledged for the loan of the Wizzler-USP and reflective polarizer.
References
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar]
- Schmid, K.; Veisz, L.; Tavella, F.; Benavides, S.; Tautz, R.; Herrmann, D.; Buck, A.; Hidding, B.; Marcinkevicius, A.; Schramm, U.; et al. Few-cycle laser-driven electron acceleration. Phys. Rev. Lett. 2009, 102. [Google Scholar] [CrossRef]
- Buck, A.; Nicolai, M.; Schmid, K.; Sears, C.M.S.; Savert, A.; Mikhailova, J.M.; Krausz, F.; Kaulza, M.C.; Veisz, L. Real-time observation of laser-driven electron acceleration. Nat. Phys. 2011, 7, 543–548. [Google Scholar]
- Heissler, P.; Hörlein, R.; Mikhailova, J.M.; Waldecker, L.; Tzallas, P.; Buck, A.; Schmid, K.; Sears, C.M.S.; Krausz, F.; Veisz, L.; et al. Few-cycle driven relativistically oscillating plasma mirrors: A source of intense isolated attosecond pulses. Phys. Rev. Lett. 2012, 108, 235003. [Google Scholar]
- Borot, A.; Malvache, A.; Chen, X.; Jullien, A.; Geindre, J.-P.; Audebert, P.; Mourou, G.; Quéré, F.; Lopez-Martens, R. Attosecond control of collective electron motion in plasmas. Nat. Phys. 2012, 8. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Borot, A.; Monchoce, S.; Vincenti, H.; Ricci, A.; Malvache, A.; Lopez-Martens, R.; Quere, F. Attosecond lighthouses from plasma mirrors. Nat. Photonics 2013, in press. [Google Scholar]
- Veltcheva, M.; Borot, A.; Thaury, C.; Malvache, A.; Lefebvre, E.; Flacco, A.; Lopez-Martens, R.; Malka, V. Brunel-dominated proton acceleration with a few-cycle laser pulse. Phys. Rev. Lett. 2012, 108, 075004. [Google Scholar]
- Chen, X.; Malvache, A.; Ricci, A.; Jullien, A.; Lopez-Martens, R. Efficient hollow fiber compression scheme for generating multi-mJ, carrier-envelope phase stable, sub-5 fs pulses. Laser Phys 2011, 21, 1–4. [Google Scholar]
- Doumy, G.; Quere, F.; Gobert, O.; Perdrix, M.; Martin, P.; Audebert, P.; Gauthier, J.C.; Geindre, J.-P.; Wittmann, T. Complete characterization of a plasma mirror for the production of high-contrast ultraintense laser pulse. Phys. Rev. E. 2004, 69, 026402. [Google Scholar]
- Mikhailova, J.M.; Buck, A.; Borot, A.; Schmid, K.; Sears, C.; Tsakiris, G.D.; Krausz, F.; Veisz, L. Ultra-high-contrast few-cycle pulses for multipetawatt-class laser technology. Opt. Lett. 2011, 36, 3145–3147. [Google Scholar]
- Kalashnikov, M.P.; Risse, E.; Schönnagel, H.; Sandner, W. Double chirped-pulse-amplification laser: A way to clean pulses temporally. Opt. Lett. 2005, 30, 923–925. [Google Scholar]
- Jullien, A.; Albert, O.; Burgy, F.; Hamoniaux, G.; Rousseau, J.-P.; Chambaret, J.-P.; Augé-Rochereau, F.; Chériaux, G.; Etchepare, J.; Minkovski, N.; et al. 10−10 temporal contrast for femtosecond ultraintense lasers by cross-polarized wave generation. Opt. Lett. 2005, 30, 920–922. [Google Scholar]
- Minkovski, N.; Petrov, G.I.; Saltiel, S.M.; Albert, O.; Etchepare, J. Nonlinear polarization rotation and orthogonal polarization generation experienced in a single-beam configuration. J. Opt. Soc. Am. B. 2004, 21, 1659–1664. [Google Scholar]
- Chvykov, V.; Rousseau, P.; Reed, S.; Kalinchenko, G.; Yanovsky, V. Generation of 1011 contrast 50 TW laser pulses. Opt. Lett. 2006, 31, 1456. [Google Scholar]
- Flacco, A.; Sylla, F.; Veltcheva, M.; Carrié, M.; Nuter, R.; Lefebvre, E.; Batani, D.; Malka, V. Dependence on pulse duration and foil thickness in high-contrast-laser proton acceleration. Phys. Rev. E. 2010, 81, 036405. [Google Scholar]
- Plateau, G.R.; Matlis, N.H.; Albert, O.; Toth, C.; Geddes, C.G.R.; Schroeder, C.B.; van Tilborg, J.; Esarey, E.; Leemans, W.P. Optimization of Thz Radiation Generation From a Laser Wakefield Accelerator, Proceedings of the AIP Conference Proceedings, Santa Cruz, CA, USA, 27 uly–2 August 2008.
- Leemans, W.P.; Simon-Boisson, C. The BELLA System and Facility, Proceedings of the Conference of the International Committee on Ultra-High Intensity Lasers, Mamaia, Romania, 16–21 September 2012.
- Ricci, A.; Jullien, A.; Forget, N.; Crozatier, V.; Tournois, P.; Lopez-Martens, R. Grism compressor for carrier-envelope phase-stable millijoule-energy chirped pulse amplifier lasers featuring bulk material stretcher. Opt. Lett. 2012, 37, 1196–1198. [Google Scholar]
- Osvay, K.; Canova, L.; Durfee, C.; Kovács, A.P.; Börzsönyi, A.; Albert, O.; Martens, R.L. Preservation of the carrier envelope phase during cross-polarized wave generation. Opt. Express. 2009, 17, 22358–22365. [Google Scholar]
- Bohman, S.; Suda, A.; Kanai, T.; Yamaguchi, S.; Midorikawa, K. Generation of 5.0 fs, 5.0 mJ pulses at 1 kHz using hollow-fiber pulse compression. Opt. Lett. 2010, 35, 1887–1889. [Google Scholar]
- Canova, L.; Chen, X.; Trisorio, A.; Jullien, A.; Assion, A.; Tempea, G.; Forget, N.; Oksenhendler, T.; Lopez-Martens, R. Carrier-envelope phase stabilization and control using a transmission grating compressor and an aopdf. Opt. Lett. 2009, 34, 1333–1335. [Google Scholar]
- Moulet, A.; Grabielle, S.; Cornaggia, C.; Forget, N.; Oksenhendler, T. Single-shot, high-dynamic-range measurement of sub-15 fs pulses by self-referenced spectral interferometry. Opt. Lett. 2010, 35, 3856–3858. [Google Scholar]
- Canova, L.; Albert, O.; Forget, N.; Mercier, B.; Kourtev, S.; Minkovski, N.; Saltiel, S.; Lopez-Martens, R. Influence of spectral phase on cross-polarized wave generation with short femtosecond pulses. App. Phys. B. 2008, 93, 443–453. [Google Scholar]
- Ramirez, L.P.; Papadopoulos, D.N.; Pellegrina, A.; Georges, P.; Druon, F.; Monot, P.; Ricci, A.; Jullien, A.; Chen, X.; Rousseau, J.P.; et al. Efficient cross polarized wave generation for compact, energy-scalable, ultrashort laser sources. Opt. Express. 2011, 19, 93–98. [Google Scholar]
- Jullien, A.; Albert, O.; Chériaux, G.; Etchepare, J.; Kourtev, S.; Minkovski, N.; Saltiel, S.M. A two crystal arrangement to fight efficiency saturation in cross-polarized wave generation. Opt. Express. 2006, 14, 2760–2769. [Google Scholar]
- Jullien, A.; Kourtev, S.; Albert, O.; Cheriaux, G.; Etchepare, J.; Minkovski, N.; Saltiel, S. Highly efficient temporal cleaner for femtosecond pulses based on cross-polarized wave generation in a dual crystal scheme. App. Phys. B. 2006, 84, 409–414. [Google Scholar]
- Jullien, A.; Rousseau, J.-P.; Mercier, B.; Antonucci, L.; Albert, O.; Chériaux, G.; Kourtev, S.; Minkovski, N.; Saltiel, S.M. Highly efficient nonlinear filter for femtosecond pulse contrast enhancement and pulse shortening. Opt. Lett. 2008, 33, 2353–2355. [Google Scholar]
- Jullien, A.; Durfee, C.G.; Trisorio, A.; Canova, L.; Rousseau, J.P.; Mercier, B.; Antonucci, L.; Cheriaux, G.; Albert, O.; Lopez-Martens, R. Nonlinear spectral cleaning of few-cycle pulses via cross-polarized wave (xpw) generation. App. Phys. B. 2009, 96, 293. [Google Scholar]
- Jullien, A.; Chen, X.; Ricci, A.; Rousseau, J.P.; Lopez-Martens, R.; Ramirez, L.P.; Papadopoulos, D.; Pellegrina, A.; Druon, F.; Georges, P. High-fidelity front-end for high-power, high temporal quality few-cycle lasers. App. Phys. B. 2011, 102, 769. [Google Scholar]
- Adams, D.E.; Planchon, T.A.; Squier, J.A.; Durfee, C.G. Spatiotemporal dynamics of cross-polarized wave generation. Opt. Lett. 2010, 35, 1115–1117. [Google Scholar]
- Grabielle, S.; Moulet, A.; Forget, N.; Crozatier, V.; Coudreau, S.; Gobert, O.; Cornaggia, C.; Oksenhendler, T. Sub-12fs Pulses Characterization by Self-Referenced Spectral Interferometry, Proceedings of The European Conference on Lasers and Electro-Optics, Munich, Germany, 22 May 2011.
- Adams, D.E.; Planchon, T.A.; Hrin, A.; Squier, J.A.; Durfee, C.G. Characterization of coupled nonlinear spatiospectral phase following an ultrafast self-focusing interaction. Opt. Lett. 2009, 34, 1294–1296. [Google Scholar]
- Ricci, A.; Ramirez, L.P.; Papadopoulos, D.; Pellegrina, A.; Georges, P.; Druon, F.; Monot, P.; Jullien, A.; Chen, X.; Rousseau, J.-P.; et al. High Energy and Efficient Cross Polarized Wave Generation for High Contrast Ultrashort Laser Sources, Proceedings of The European Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 1–6 May 2011.
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).