Abstract
We perform first-principles calculations to study the high-order harmonic generation induced in graphene nanostructures by the laser field. Three distinct signals are noticed: the integer higher-order harmonic generation (HHG), the shifted fractional order peaks from the integer order harmonics, and the intrinsic emissions. Due to the small gap between HOMO and LUMO of graphene molecule, the HHG can be generated for the infrared laser pulse with the photon energy ranging from 20 meV to ~1 eV. The intrinsic emission corresponds to the electron excitation between eigenstates. Using a laser pulse with a photon energy of 0.042 eV and amplitude of 0.2 V/Å, HHGs up to 19th order are identified. Unsaturated graphene molecule is an excellent medium for HHG. Moreover, the HHG signals are very sensitive to the hydrogen passivation. Our results also indicate that HHG can be a promising method for detecting the product in the fabrication of graphene molecules.
1. Introduction
Atoms and molecules exposed in an intense laser field show several fascinating effects, such as high harmonic generation (HHG), above threshold ionization (ATI), multiphoton ionization, etc. [1,2]. Most of these are nonlinear processes and are beyond the conventional perturbation theory. HHG is attractive due to its potential application in functional devices [3] and for measuring novel states in biological systems [4] or even traditional materials like water [5]. It is such a general phenomenon that can be emitted even from the two dimensional metallic system [6]. Recently, with the development of ultra-intense laser pulses, the efficiency and control of HHG have been remarkably improved [7].
The graphene system, which has drawn intensive investigations due to its massless Dirac Fermions, is a two dimensional conductor. It is a promising material for the next generation of electronic and spintronic devices. For instance, graphene nanoribbons (GNR) can be half-metallic under an external field [8,9], and GNRs with hydrogen-passivated edges have been shown to behave as a metal or semiconductor, depending on the spin on each edge [10]. It is interesting to see the multiphoton processes in this system under a high intensity laser field. Some efforts have been made to explore the nonlinear effects in graphene [11–18]. With an electron-hole model, Mikhailov theoretically predicted the strongly nonlinear response to the external electric field in graphene [11]. Later on Dean et al. reported experimental probe of the second harmonic generation (SHG) in graphene. Distinct symmetries between graphene and graphite are observed in the anisotropy of SHG [14]. Recently, the nonlinearity is examined under a strong magnetic field up to 3 Tesla [18].
In this article, we examine the higher harmonic generation in graphene molecules using first-principles calculations. Harmonics up to the 19th order are identified. Three types of signals are noticed in the spectrum. The first one is the HHG, the frequency of which is always an integer multiple (harmonic order) of that of the laser pulse. The second signal is a shift of the HHG due to the limited duration of the laser field. The last one is the intrinsic emission, which corresponds to the optical transition between eigenstates. We explain the difference and the origin of the signals of these three types. We have compared the graphene molecules with and without hydrogen passivation, and found that the dangling bonds at graphene edge will enhance the HHG signal. Therefore HHG is very sensitive to the passivation situation of graphene nano-molecules.
2. Theory
The underlying mechanism of the HHG for an atomic system has been well understood both experimentally and theoretically [19,20]. HHG originates from the higher order Fourier components of the electric dipole. In other words, it is highly nonlinear. Compared with the isolated atoms, the nano-clusters, e.g., C60 [21], require a much weaker laser field to generate HHG. This is due to the increase of the electron densities and delocalization of the electron. Graphene is an excellent candidate.
2.1. Formalism of the HHG Calculation
The interaction between the laser field and the graphene is depicted as
where
is the time-dependent electric field of the laser pulse. –e,
, τ and t are the electron charge, laser field amplitude, pulse duration, and time, respectively. c† and c are the electron creation and annihilation operators.
is the dipole operator, whose matrix elements are computed from the single-electron momentum operator through [22]
where pij is the electron momentum matrix element between states i and j, m is the electron mass, Ei and Ej are the eigen-energies of states i and j. The momentum matrix elements are calculated with the Furthmüller’s method [23].
In this work we consider a laser pulse with 32 laser field cycles, and the electric field is polarized in the z-direction. When a laser impinges on the graphene, the time evolution of the density matrix obeys the Liouville Equation:
where
is the density operator. H = H0 + HI, and H0 is the system’s Hamiltonian,
.
By solving the Liouville equation, we find the density matrix. The time evolution of the electron dipole is obtained from
. Then it is Fourier transformed to the frequency domain, FT[d(t)] ⇒ D(ω).
2.2. Simulation Details
We investigate two rectangularly-cut graphene molecules (see Figure 1). Both molecules contain two carbon rings in the x-direction and three carbon rings in the y-direction. Previous studies indicated that the edge states are crucial to the graphene nanoribbon (GNR), which may even induce the half metallicity into the graphene system [8]. In order to examine the effect of the edge states, we compare the graphene molecules without (Figure 1(a)) and with (Figure 1(b)) saturation of the dangling bonds.
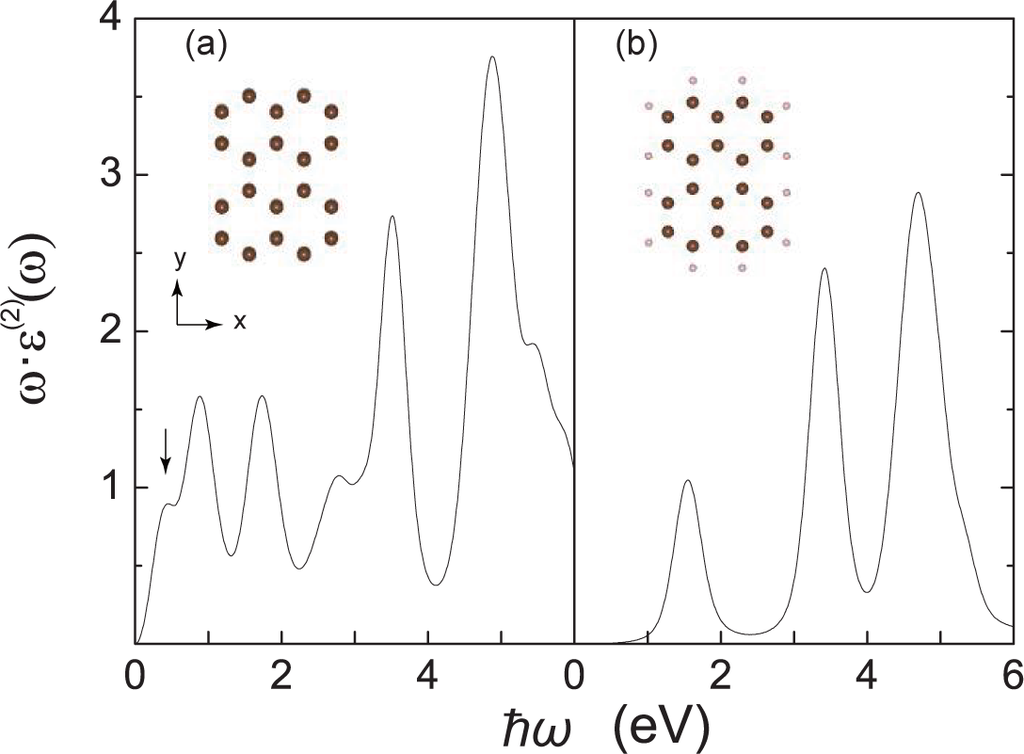
Figure 1.
Optical absorption spectra for (a) non-passivated and (b) passivated graphene molecules. Insets: molecular structures. Carbon and hydrogen atoms are shown in brown and pink spheres, respectively. The arrow denotes the absorption peak corresponding to the first allowed optical transition.
We use the Vienna ab initio simulation package (VASP) [24] to compute our models. The energy cut-off for the plane-wave basis set is 500 eV, which is sufficient to converge our results. The projector augmented wave (PAW) method is used to treat the valence-core interaction. The calculations are performed using the supercells with a vacuum layer of 15 Å along the x, y and z directions. The C–C bond length is fixed at the theoretical value of 1.42 Å while the C–H bond is optimized to find the energy minimum (~ 1.09 Å). The energy eigenstates are shown in Figure 2. In our calculation 40 states, with 20 empty and 20 occupied states, are included, which have a span of ~12 eV in the energy spectrum.
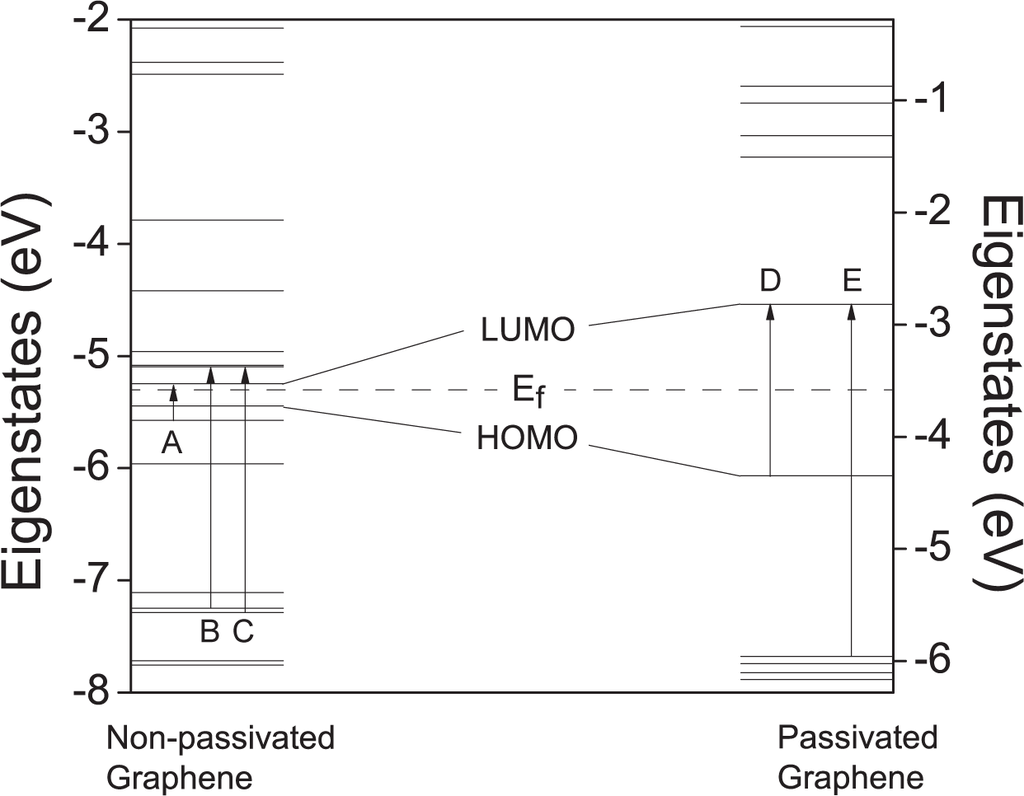
Figure 2.
The eigenstates of two graphene molecules. Fermi energy is denoted with the dashed line. A–E denote the electron transitions between eigenstates.
3. Results and Discussions
The electronic and optical properties of these two structures are different due to the existence of dangling bonds. It leads to the differences in the HHG emissions. We will investigate these two structures in the following.
3.1. Graphene Molecules without/with Hydrogen Passivation
The optical absorption spectra for the graphene molecules without and with passivation are shown in Figure 1. We first check the graphene molecule without hydrogen passivation. We notice that the first absorption peak is at ~ 0.3 eV. The absorption of such low energy indicates that the gap between LUMO and HOMO is small. We plot the eigenstates of the molecules in Figure 2. The energy gap of ~0.197 eV is found from the energy spectrum. The first absorption peak (denoted in Figure 1(a)) corresponds to the electron excitation from the HOMO-1 to the LUMO, rather than HOMO-LUMO excitation. This is because the HOMO is formed by the pz orbital (π-electron), while the LUMO is composed with the hybridized sp2 orbital (σ-electron). That is to say, the optical transition between HOMO and LUMO is forbidden due to symmetry. We carefully choose the pulse photon energy to be ~ 0.042 eV, which is approximately one seventh of the transition energy from the HOMO-1 to LUMO.
The results with a laser amplitude of 0.2 V/Å are shown in Figure 3(a). Harmonic generations up to the 19th order are identified. The plateau of the HHG intensity is observed. There is a peak with the order number of ~7.8, denoted with the empty square in Figure 3(a). This peak corresponds to the electron excitation from HOMO-1 to LUMO, which we attribute to the intrinsic emission, rather than the HHG (see discussions in Section 3.2). Sub-peaks near the major harmonic peaks are also identified (denoted by triangles in Figure 3(a)). The positions of these sub-peaks are not exactly at the integer orders, however the neighboring orders differ by one. In our case, each integer major peak with order of n has one sub-peak at the order of (n − 0.59375). The existence of these peaks is interesting and consistent with the previous works on benzene and other ring-shaped molecules [25,26]. The shifted peaks may originate from the limited duration of the laser pulse [27], which will be further discussed in Section 3.2.
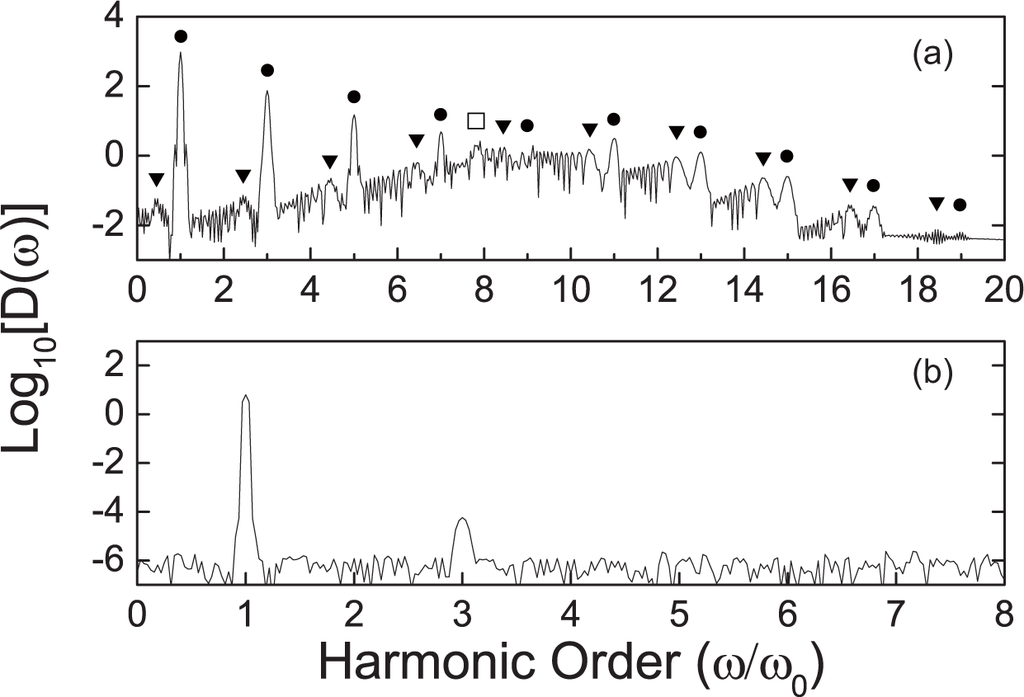
Figure 3.
HHG spectra for the non-passivated (a) and passivated (b) graphene molecules. The parameters for the laser field are: ħω = 0.042 eV, A = 0.2 V/Å. The intensity of the passivated graphene is much smaller than that of the non-passivated one. The integer-order harmonics are denoted by circles, while the shifted peaks are denoted by triangles. The empty square denotes the intrinsic emission for HOMO-1 to LUMO.
If we select a laser pulse with a higher frequency, the total number of HHG is reduced. For instance, for ω = 0.28 eV the highest harmonic order is only 5th. A larger laser amplitude is required for the other higher order peaks to occur. This is governed by the law for the harmonic cutoff of Ip + 3.17Up [28–30], where Ip is the ionization potential and Up is the ponderomotive energy that Up = E2/4ω2. Since the laser frequency is higher, the laser amplitude should be increased accordingly to obtain the same HHG order.
When the dangling bonds are saturated by hydrogen atoms, the excessive electrons at the edge form the C–H covalent bonds. The electrons in the system become localized. This is revealed by the narrow absorption peaks in Figure 1(b). The LUMO–HOMO gap is 1.53 eV, much larger than that of the one without passivation. The HHG spectrum is plotted in Figure 3(b). Above all, the harmonic intensity is highly suppressed compared with the non-passivated one, and a reduction of more than two orders is found. This shows that the unpaired electrons on the edge of the non-passivated graphene enhance the non-linear optical response due to the weak localization [31].
Furthermore, the total number of higher harmonics is also suppressed. Only the 3rd order peak can be identified with the same laser pulse parameter (ω = 0.042 eV, A = 0.2 V/Å). This reveals that the ionization energy for this structure is much higher than the non-passivated one. That is to say, the HHG is very sensitive to the passivation of the graphene system. Accordingly, HHG can be used as a detector to probe the passivation during the growth of graphene.
3.2. Peaks with Fractional Harmonic Orders
Besides the integer order harmonics, the fractional peaks are intricate. Two types of optical responses with fractional order are observed: the companion peaks of the major HHG peaks and the intrinsic optical emission peaks (denoted in Figure 3(a)). The first one originates from the degeneracy of the quasi-energy Floquet states. Since the lifetime of the non-degenerate states is usually different, the interference between these states tends to shift the integer harmonic to a fractional order. It has been noticed before in benzene by TDDFT calculation [25]. We find that these peaks exist when the applied laser field has a large amplitude and short duration time, and will be suppressed when the laser duration is increased.
The other type of fractional peak is from the intrinsic emission of the graphene molecule. The peak at the 7.8 harmonic order in Figure 3(a) is a good example. The intensity of this peak is high and comparable to the integer-order HHG peaks, since it represents the first dipole-allowed excitation. However other intrinsic emission peaks can be usually observed when the laser amplitude is small or the frequency is high, in other words, only when the nonlinear effect is small. Otherwise when the amplitude of the laser is large, the signals of the intrinsic emissions are concealed by the HHG signals. We plot the spectra with a small laser amplitude of only 0.002 V/Å, see Figure 4. Since these peaks are intrinsic to the graphene molecule itself, their frequencies do not shift with respect to the applied field. By changing the unit of the x-axis in Figure 4 from harmonic order into eV, one can easily find the one-to-one correspondence between these intrinsic peaks and the energy difference of eigenstates. For example, the peaks a–e carry photon energies for the optical transitions A–E denoted in Figure 2.
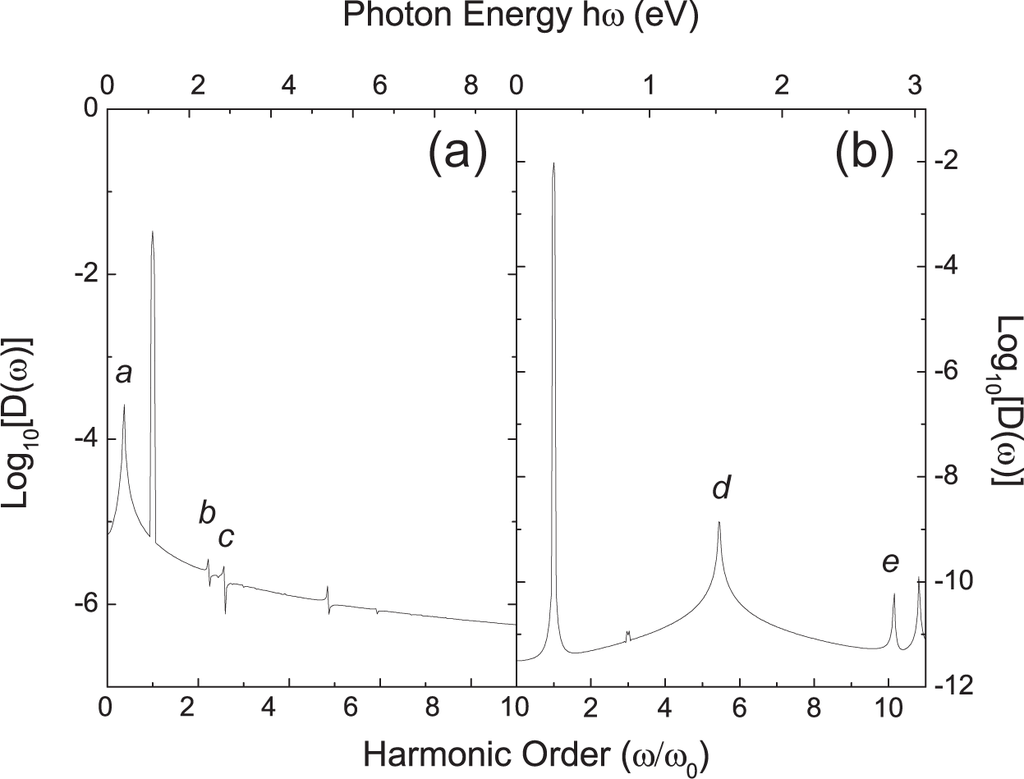
Figure 4.
HHG spectra of the non-passivated (a) and passivated (b) graphene molecules with a weaker laser pulse. The laser field parameters are: ħω = 0.9 eV, A = 0.002 V/Åfor the non-passivated one and ħω = 0.28 eV, A = 0.002 V/Å for the passivated one. The photon energies of the peaks a-e correspond well to the optical transitions A–E denoted in Figure 2.
To further distinguish the integer order and the two types of fractional order signals, we examine the intensity of the HHG signal as a function of the field amplitude A (Figure 5). The intensities of the n-th order HHG peaks are of n-th order polynomials of the amplitude, shown in Figure 5(a). It clearly shows the nonlinear properties of the integer order harmonics. This is governed by the relationship [32]:
, where Ḏ is the electric displacement, ε(n) is the n-th order dielectric constant, and E is the electric field. The companion peaks near the integer order harmonics do not show clear relationship with the laser field amplitude (Figure 5(b)). Their intensities generally increase but with high fluctuations. On the other hand, the signal from the intrinsic excitation is easily distinguished from the others, since it reveals a linear dependence (Figure 5(c,d)). The intensity is proportional to the number of photons. The difference between intrinsic emission and the HHG also explains why the intrinsic emissions can be observed when the laser amplitude is small: When the laser amplitude decreases, the decay of the n-th order HHG peak is much faster than that of the intrinsic emission.
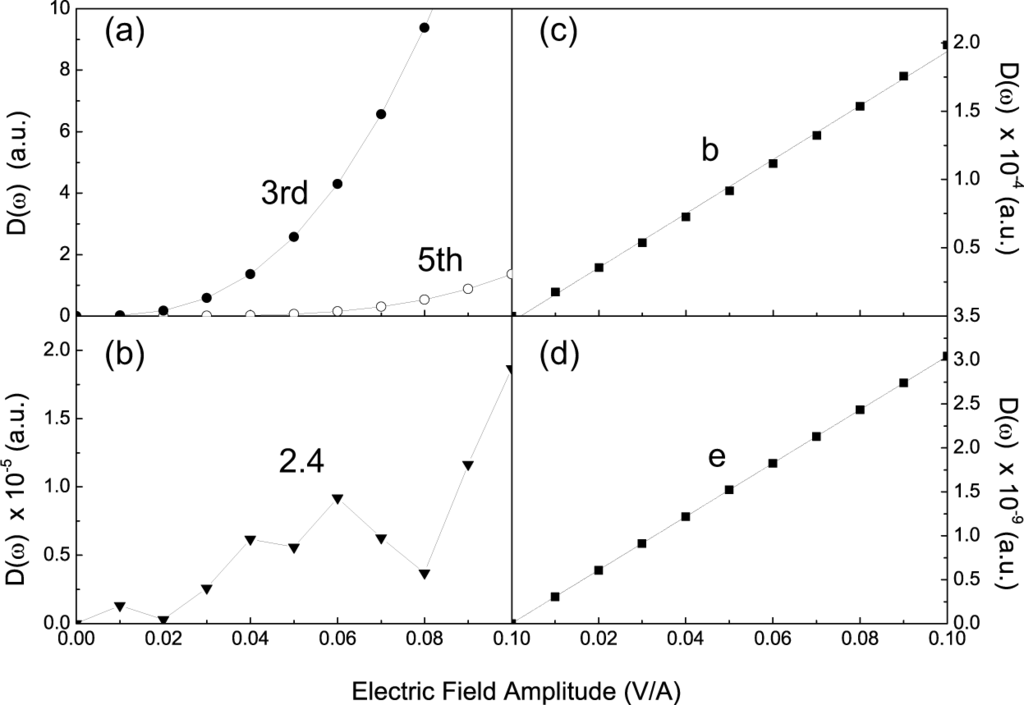
Figure 5.
(a) Intensity of peaks with harmonic order of 3 and 5 in Figure 2(a) as functions of laser field amplitude. A cubic- and a fifth-order dependence are noticed, respectively. These peaks directly result from the multiphoton process; (b) Intensity of the peak with a harmonic order of 2.4 in Figure 3(a). No clear dependence is found; (c) and (d) Intensities for peaks b in Figure 3(a) and e in Figure 3(b). Here the dependence is linear and reveals that the emissions are from the intrinsic excitation.
4. Conclusions
In this work, we have presented a theoretical approach to investigate the HHG in the nano-graphene molecules. Graphene molecules both with and without hydrogen passivation reveal the ability to emit HHG under the laser radiation. There are signals of three distinct types. One is the integer order generations, which is directly caused by the high-order interactions with the laser field. Due to the limited duration of the laser pulse, companion peaks near the integer order peaks emerge. The remaining one is the fractional order generations, which is contributed by the intrinsic electron transitions between eigenstates. The intensity of the HHG and the existence of the integer order generations are sensitive to the hydrogen passivation. This shows that HHG can be a promising way to probe the passivation during growth. Since our method is not limited to the graphene system, it is in principle applicable to all nanostructures with dangling bonds saturated or unsaturated by hydrogen atoms. Our results agree well with the previous model calculation [11]. We expect such effects to be examined by experiments or further theories like quantum chemistry code or TDDFT calculation.
Acknowledgments
This work has been supported by the U.S. Department of Energy under Contract No. DE-FG02-06ER46304 and DE-AC02-06CH11357 (MG, GPZ), and NKPBRC (2010CB923404) and NNSFC (10974081, 10979017, 11274153). We also acknowledge part of the work as done on Indiana State University’s high-performance computers. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We are grateful to the High Performance Computing Center of Nanjing University, for the award of CPU hours to accomplish this work. MG thanks China Scholarship Council and Indiana State University for all the resources provided during the exchange period.
References
- Bucksbaum, P.H.; Bashkansky, M.; Freeman, R.R.; McIlrath, T.J.; DiMauro, L.F. Suppression of multiphoton ionization with circularly polarized coherent light. Phys. Rev. Lett. 1986, 56, 2590–2593. [Google Scholar]
- Johann, U.; Luk, T.S.; Egger, H.; Rhodes, C.K. Rare-gas electron-energy spectra produced by collision-free multiquantum processes. Phys. Rev. A. 1986, 34, 1084–1103. [Google Scholar]
- Van der Zwan, E.V.; Lein, M. Molecular imaging using high-order harmonic generation and above-threshold ionization. Phys. Rev. Lett. 2012, 108, 043004:1–043004:5. [Google Scholar]
- Squirrel, J.M.; Wokosin, D.L.; White, J.G.; Barister, B.D. Long-term two-photon fluorescence imaging of mammalian embryos without compromising viability. Nat. Biotechnol. 1999, 17, 763–767. [Google Scholar]
- Farrell, J.P.; Petretti, S.; Förster, J.; McFarland, B.K.; Spector, L.S.; Vanne, Y.V.; Decleva, P.; Bucksbaum, P.H.; Saenz, A.; Gühr, M. Strong field ionization to multiple electronic states in water. Phys. Rev. Lett. 2011, 107, 083001:1–083001:4. [Google Scholar]
- Varró, S.; Ehlotzky, F. Higher-harmonic generation from a metal surface in a powerful laser field. Phys. Rev. A. 1994, 49, 3106–3109. [Google Scholar]
- Kim, I.J.; Kim, C.M.; Kim, H.T.; Lee, G.H.; Lee, Y.S.; Park, J.Y.; Cho, D.J.; Nam, C.H. Highly efficient high-harmonic generation in an orthogonally polarized two-color laser field. Phys. Rev. Lett. 2005, 94, 243901:1–243901:4. [Google Scholar]
- Son, Y.-W.; Cohen, M.L.; Louie, S.G. Half-metallic graphene nanoribbons. Nature 2006, 444, 347–349. [Google Scholar]
- Longo, R.C.; Carrete, J.; Gallego, L.J. Ab initio study of 3d, 4d, and 5d transition metal adatoms and dimers adsorbed on hydrogen-passivated zigzag graphene nanoribbons. Phys. Rev. B. 2011, 83, 235415:1–235415:9. [Google Scholar]
- Martins, T.B.; Miwa, R.H.; da Silva, A.J.R.; Fazzio, A. Electronic and transport properties of boron-doped graphene nanoribbons. Phys. Rev. Lett. 2007, 98, 196803:1–196803:4. [Google Scholar]
- Mikhailov, S.A. Non-linear electromagnetic response of graphene. Europhys. Lett. 2007, 79. [Google Scholar] [CrossRef]
- Mikhailov, S.A.; Ziegler, K. Nonlinear electromagnetic response of graphene: Frequency multiplication and the self-consistent-field effects. J. Phys. Condens. Matt. 2008, 20. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Electromagnetic response of electrons in graphene: Non-linear effects. Physica E 2008, 40, 2626–2629. [Google Scholar]
- Dean, J.J.; van Driel, H.M. Second harmonic generation from graphene and graphitic films. Appl. Phys. Lett. 2009, 95, 261910–261913. [Google Scholar]
- Dean, J.J.; van Driel, H.M. Graphene and few-layer graphite probed by second-harmonic generation: Theory and experiment. Phys. Rev. B. 2010, 82, 125411:1–125411:10. [Google Scholar]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent nonlinear optical response of graphene. Phys. Rev. Lett. 2010, 105, 097401:1–097401:4. [Google Scholar]
- Jafari, S.A. Nonlinear optical response in gapped graphene. J. Phys. Condens. Matt. 2012, 24. [Google Scholar] [CrossRef]
- Yao, X.; Belyanin, A. Giant optical nonlinearity of graphene in a strong magnetic field. Phys. Rev. Lett. 2012, 108, 255503:1–255503:4. [Google Scholar]
- Atoms in Intense Laser Fields; Gavrila, M. (Ed.) Academic: New York, NY, USA, 1992.
- Eberly, J.H.; Javanainen, J. Rzążewski. Above-threshold ionization. Phys. Rep. 1991, 204, 331–383. [Google Scholar]
- Zhang, G.P. Optical high harmonic generation in C60. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Sharma, S.; Dewhurst, J.K.; Ambrosch-Draxl, C. Linear and second-order optical response of III-V monolayer superlattices. Phys. Rev. B. 2003, 67. [Google Scholar] [CrossRef]
- Adolph, B.; Furthmüller, J.; Bechstedt, F. Optical properties of semiconductors using projector-augmented waves. Phys. Rev. B. 2001, 63. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar]
- Baer, R.; Neuhauser, D.; Ždánská, P.R.; Moiseyev, N. Ionization and high-order harmonic generation in aligned benzene by a short intense circularly polarized laser pulse. Phys. Rev. A. 2003, 68, 043406:1–043406:8. [Google Scholar]
- Ceccherini, F.; Bauer, D. Harmonic generation in ring-shaped molecules. Phys. Rev. A. 2001, 64. [Google Scholar] [CrossRef]
- Moiseyev, N.; Lein, M. Non-hermitian quantum mechanics for high-order harmonic generation spectra. J. Phys. Chem. A. 2003, 107, 7181–7188. [Google Scholar]
- Krause, J.L.; Schafer, K.J.; Kulander, K.C. High-order harmonic generation from atoms and ions in the high intensity regime. Phys. Rev. Lett. 1992, 68, 3535–3538. [Google Scholar]
- Becker, W.; Long, S.; McIver, J.K. Modeling harmonic generation by a zero-range potential. Phys. Rev. A. 1994, 50, 1540–1560. [Google Scholar]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A. 1994, 49, 2117–2132. [Google Scholar]
- Morozov, S.V.; Novoselov, K.S.; Katsnelson, M.I.; Schedin, F.; Ponomarenko, L.A.; Jiang, D.; Geim, A.K. Strong suppression of weak localization in graphene. Phys. Rev. Lett. 2006, 97, 016801:1–016801:4. [Google Scholar]
- Nonlinear Optics in Metals; Bennemann, K.H. (Ed.) Clarendon Press: Oxford, UK, 1998.
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).