Abstract
High-order harmonic generation (HHG) is a nonlinear nonperturbative process in ultrashort intense laser-matter interaction. It is the main source of coherent attosecond (1 as = 10−18 s) laser pulses to investigate ultrafast electron dynamics. HHG has become an important table-top source covering a spectral range from infrared to extreme ultraviolet (XUV). One way to extend the cutoff energy of HHG is to increase the intensity of the laser pulses. A consequence of HHG in such intense short laser fields is the characteristic nonadiabatic red and blue shifts of the spectrum, which are reviewed in the present work. An example of this nonperturbative light-matter interaction is presented for the one-electron nonsymmetric molecular ion HeH2+, as molecular systems allow for the study of the laser-molecule orientation dependence of such new effects including a four-step model of MHOHG (Molecular High-order Harmonic Generation).
1. Introduction
Atomic high-order harmonic generation (HHG) was discovered in 1980s [1,2]. It is a nonlinear nonperturbative process, which converts low-frequency fundamental femtosecond (1 fs = 10−15 s) laser fields to coherent high-energy attosecond (1 as = 10−18 s) pulse trains or an isolated attosecond laser pulse [3]. The typical laser intensity I used for HHG is around 1014 W/cm2. The general feature of atomic HHG which also appears in molecular high-order harmonic generation (MHOHG) is a fast decay of the lower order harmonics, then a long plateau, and a short cutoff [4]. The mechanism of HHG is interpreted by a three-step model [5,6,7] neglecting the role of excited states due to their short lifetime in strong laser field. First, the bound state electron is freed by tunnel ionization through the static barrier created by the instantaneous laser field and Coulomb potential. Then, the electron oscillates in the laser field and acquires kinetic energy. It may finally return to the parent ion and recombine to the ground state to emit HHG photons. The maximal kinetic energy Ek of electrons returning to the origin is 3.17 Up, where 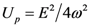 is the ponderomotive energy of the electrons oscillating in the laser field, E and ω are the amplitude and frequency of the laser field, respectively (atomic units e = me = ћ = 1 are used throughout the paper unless otherwise specified). As a consequence, the cutoff energy of HHG, i.e., maximal kinetic energy Ek plus ionization potential Ip, is:
is the ponderomotive energy of the electrons oscillating in the laser field, E and ω are the amplitude and frequency of the laser field, respectively (atomic units e = me = ћ = 1 are used throughout the paper unless otherwise specified). As a consequence, the cutoff energy of HHG, i.e., maximal kinetic energy Ek plus ionization potential Ip, is:
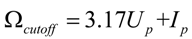
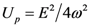 is the ponderomotive energy of the electrons oscillating in the laser field, E and ω are the amplitude and frequency of the laser field, respectively (atomic units e = me = ћ = 1 are used throughout the paper unless otherwise specified). As a consequence, the cutoff energy of HHG, i.e., maximal kinetic energy Ek plus ionization potential Ip, is:
is the ponderomotive energy of the electrons oscillating in the laser field, E and ω are the amplitude and frequency of the laser field, respectively (atomic units e = me = ћ = 1 are used throughout the paper unless otherwise specified). As a consequence, the cutoff energy of HHG, i.e., maximal kinetic energy Ek plus ionization potential Ip, is:
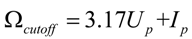
In MHOHG, the ionized electron can recombine with neighboring ions in the same molecule leading to a much larger cutoff energy depending on the internuclear distance R [8,9,10]. This larger cutoff energy comes from longer acceleration distance in the above process.
From Equation (1), one has to increase the ionization potential Ip, laser intensity I and wavelength λ to extend the cutoff energy 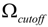 of the HHG spectrum. In short laser fields with very high intensity, the depletion of the ground state and rapid change of intensity I(t) will lead to nonadiabatic effects in HHG, such as red [11] and blue [12] shifts of HHG. We review the recent progress in these nonadiabatic spectral shifts of HHG and in particular MHOHG in this article.
of the HHG spectrum. In short laser fields with very high intensity, the depletion of the ground state and rapid change of intensity I(t) will lead to nonadiabatic effects in HHG, such as red [11] and blue [12] shifts of HHG. We review the recent progress in these nonadiabatic spectral shifts of HHG and in particular MHOHG in this article.
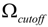 of the HHG spectrum. In short laser fields with very high intensity, the depletion of the ground state and rapid change of intensity I(t) will lead to nonadiabatic effects in HHG, such as red [11] and blue [12] shifts of HHG. We review the recent progress in these nonadiabatic spectral shifts of HHG and in particular MHOHG in this article.
of the HHG spectrum. In short laser fields with very high intensity, the depletion of the ground state and rapid change of intensity I(t) will lead to nonadiabatic effects in HHG, such as red [11] and blue [12] shifts of HHG. We review the recent progress in these nonadiabatic spectral shifts of HHG and in particular MHOHG in this article.2. Blue Shift in HHG
Earlier work has studied the blue shift of HHG. It is the result of mainly two mechanisms. One is the propagation effect of a fundamental laser pulse in an ionized medium [13,14]. The other is the nonadiabatic response of the electronic dipole to the rapid change of laser fields [15,16,17].
2.1. Blue Shift by Propagating Effect
Free electrons created during the laser pulse induce a change of the refractive index [13],
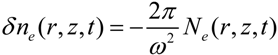 where
where 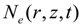 denotes the electron density. The variation of the refractive index leads to a blue shift of the fundamental laser field. The shift can be estimated by the following expression (CGS units) [18],
denotes the electron density. The variation of the refractive index leads to a blue shift of the fundamental laser field. The shift can be estimated by the following expression (CGS units) [18],
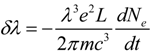 where L is the propagation length. For HHG with order n, the total blue shift comes from two contributions: a shift δλ1 induced by the shift of the fundamental field and the other shift δλ2 caused by the generated harmonics propagating in the medium. δλ1 is proportional δλ/n, while δλ2 is propational to δλ/n3.
where L is the propagation length. For HHG with order n, the total blue shift comes from two contributions: a shift δλ1 induced by the shift of the fundamental field and the other shift δλ2 caused by the generated harmonics propagating in the medium. δλ1 is proportional δλ/n, while δλ2 is propational to δλ/n3.
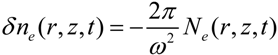
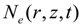 denotes the electron density. The variation of the refractive index leads to a blue shift of the fundamental laser field. The shift can be estimated by the following expression (CGS units) [18],
denotes the electron density. The variation of the refractive index leads to a blue shift of the fundamental laser field. The shift can be estimated by the following expression (CGS units) [18],
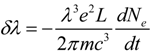
2.2. Nonadiabatic Blue Shift in HHG
Rapid change of a laser pulse shape will lead to a chirp of HHG. The electronic dipole response to the external laser field is nonadiabatic. This effect is intuitive in the above three-step model. As shown in Figure 1, the laser intensity is rising in the first half of the pulse. The effective amplitude of the successive laser cycle is higher than the previous one. The electron gains more energy from the latter laser field compared to the previous cycle. In other words, the rising laser envelope (RLE) with t < 0 induces a positive-chirp role in HHG, thus leading to a blue shift in HHG [16]. In contrast, a negative chirp of HHG occurs on the falling laser envelope (FLE) with t > 0. This causes a red shift of HHG. However, no net shift of HHG is observed with low laser intensity since the blue shift generated on the RLE and the red shift produced on the FLE will result in broadening of the harmonics, but no net change in the central frequency. When the laser intensity is above the ionization saturation threshold, the depletion of the ground state has to be included. Especially for long intense laser pulses, the sample is highly ionized on the RLE, little HHG is emitted on the FLE. This imbalance of HHG will lead to a net blue shift in HHG. This has been experimentally confirmed in [12,19].
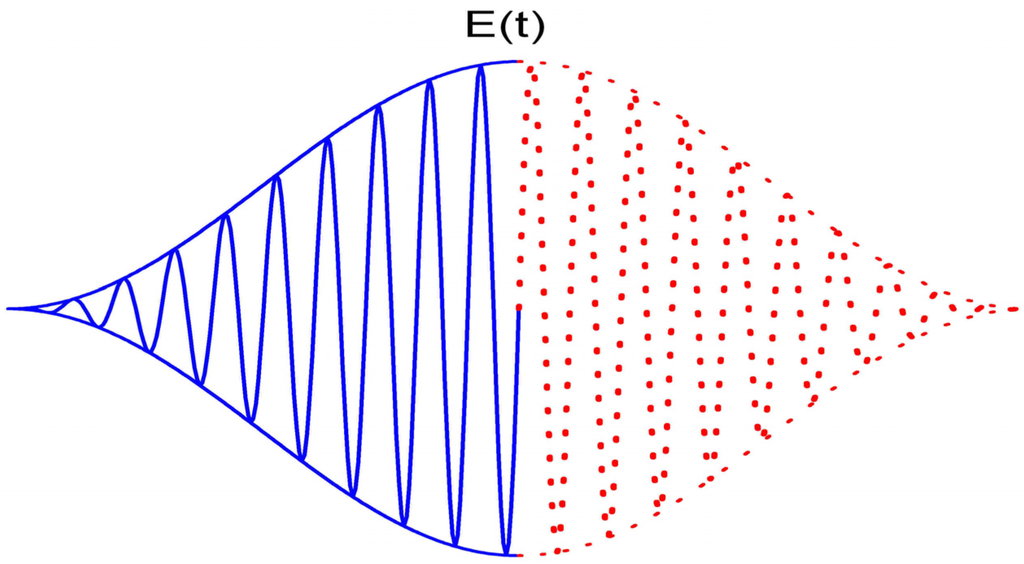
Figure 1.
Illustration of the positive (solid line) and negative (dotted line) chirp of High-order harmonic generation (HHG) by the rapid change of the electric field E(t) (Equation (5)). The total pulse duration τ is 20 optical cycles.
3. Red Shift of HHG in Resonant Systems
From the discussion in the above section, the depletion of the ground state on the RLE will prevent the HHG emission on the FLE. It is therefore hard to observe a noticeable red shift of HHG directly in such a case. However, enhanced excitation (EE) in resonant systems will change the above three-step model to a four-step model. We take the resonant nonsymmetric system HeH2+ as an example to explore the nonadiabatic red shift in MHOHG [11,20,21]. This one-electron model also emphasizes the importance of laser-induced electron transfer, LIET [20], in molecular spectra.
3.1. Four-Step Model of MHOHG in Resonant Systems
We study numerically the following time-dependent Schrödinger equation (TDSE):
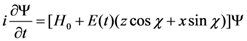 where H0 is the field-free Hamiltionian [22], χ is the angle between the laser polarization and the molecular axis z in the xz plane. The electric field E(t) of the laser pulse is given by:
where H0 is the field-free Hamiltionian [22], χ is the angle between the laser polarization and the molecular axis z in the xz plane. The electric field E(t) of the laser pulse is given by:
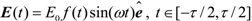
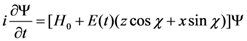
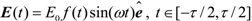
where the pulse shape 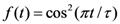 , τ is the total duration of the laser pulses.
, τ is the total duration of the laser pulses.
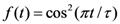 , τ is the total duration of the laser pulses.
, τ is the total duration of the laser pulses.The molecular ion HeH2+ has a large ionization potential (Ip =2.25 a.u. (61.2 eV)) and a long-life excited state  (the life time is around 4 ns [23].) resonant with the ground state. The MHOHG spectra of HeH2+ are obtained by numerically solving the TDSE. For the computational details of this one-electron system, we refer to reference [21]. The internuclear distance R is fixed at 4 a.u. (near the excited state minimum R =3.89 a.u.). The energy of the first excited state
(the life time is around 4 ns [23].) resonant with the ground state. The MHOHG spectra of HeH2+ are obtained by numerically solving the TDSE. For the computational details of this one-electron system, we refer to reference [21]. The internuclear distance R is fixed at 4 a.u. (near the excited state minimum R =3.89 a.u.). The energy of the first excited state  is −1.03 a.u. (28 eV). The initial state for time evolution is the ground state
is −1.03 a.u. (28 eV). The initial state for time evolution is the ground state 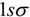 . The laser polarization is along the z molecular axis. The power spectra of MHOHG is calculated by a Fourier transformation of the dipole momentum in the acceleration form
. The laser polarization is along the z molecular axis. The power spectra of MHOHG is calculated by a Fourier transformation of the dipole momentum in the acceleration form 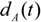 , as it is the most reliable numerical method for strong field interactions avoiding after pulse transient effects such as in the dipole form [24]. To further probe the temporal structures of MHOHG, we perform a time profile analysis of the harmonic spectra. The time profile of harmonic ωq is obtained by a wavelet analysis as in signal processing [25,26,27]:
, as it is the most reliable numerical method for strong field interactions avoiding after pulse transient effects such as in the dipole form [24]. To further probe the temporal structures of MHOHG, we perform a time profile analysis of the harmonic spectra. The time profile of harmonic ωq is obtained by a wavelet analysis as in signal processing [25,26,27]:
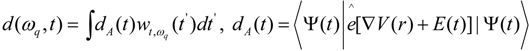 with the wavelet kernel
with the wavelet kernel 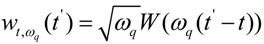 . The mother wavelet we use is a Morlet wavelet:
. The mother wavelet we use is a Morlet wavelet:
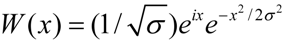
 (the life time is around 4 ns [23].) resonant with the ground state. The MHOHG spectra of HeH2+ are obtained by numerically solving the TDSE. For the computational details of this one-electron system, we refer to reference [21]. The internuclear distance R is fixed at 4 a.u. (near the excited state minimum R =3.89 a.u.). The energy of the first excited state
(the life time is around 4 ns [23].) resonant with the ground state. The MHOHG spectra of HeH2+ are obtained by numerically solving the TDSE. For the computational details of this one-electron system, we refer to reference [21]. The internuclear distance R is fixed at 4 a.u. (near the excited state minimum R =3.89 a.u.). The energy of the first excited state  is −1.03 a.u. (28 eV). The initial state for time evolution is the ground state
is −1.03 a.u. (28 eV). The initial state for time evolution is the ground state 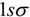 . The laser polarization is along the z molecular axis. The power spectra of MHOHG is calculated by a Fourier transformation of the dipole momentum in the acceleration form
. The laser polarization is along the z molecular axis. The power spectra of MHOHG is calculated by a Fourier transformation of the dipole momentum in the acceleration form 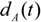 , as it is the most reliable numerical method for strong field interactions avoiding after pulse transient effects such as in the dipole form [24]. To further probe the temporal structures of MHOHG, we perform a time profile analysis of the harmonic spectra. The time profile of harmonic ωq is obtained by a wavelet analysis as in signal processing [25,26,27]:
, as it is the most reliable numerical method for strong field interactions avoiding after pulse transient effects such as in the dipole form [24]. To further probe the temporal structures of MHOHG, we perform a time profile analysis of the harmonic spectra. The time profile of harmonic ωq is obtained by a wavelet analysis as in signal processing [25,26,27]:
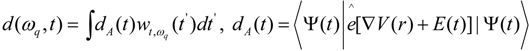
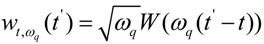 . The mother wavelet we use is a Morlet wavelet:
. The mother wavelet we use is a Morlet wavelet:
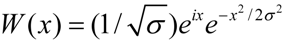
The MHOHG spectrum of HeH2+ in a laser field at wavelength 400 nm and intensity I = 3.5 ×1015 W/cm2 with a duration of 15 optical cycles is shown in Figure 2a. The corresponding time profile of the spectrum is presented in Figure 2b. Due to the break of the symmetry of the system, both odd and even order harmonics are generated as illustrated in Figure 2a. A typical difference from the usual HHG spectra of neutral atoms and molecules is a strong resonance around harmonic order 15 in Figure 2a which agrees well with the dressed energy difference between the first excited state and the ground state [20]. One can also observe a strong resonance range around harmonic order 15 in the time profile analysis in Figure 2b. The conversion efficiency of the resonant harmonics is about 3 orders higher than the harmonics in the long plateau, which can be used to generate bright attosecond pulses (trains). The strong resonance in MHOHG (Figure 2a) cannot be explained consistently by the three-step model [5].
We take the resonant EE of long lifetime excited states into account explicitly and generalize the three-step model to a four-step model as presented in Figure 3. The electron is preexcited to a localized long lifetime resonant bound state, tunnel ionized from the resonant excited state, driven by the laser field, followed by a recombination to the ground state to emit MHOHG. This four-step model is different from the four-step mechanism proposed by Strelkov [28]. In the latter model, the resonant state is an autoionizing state embedded in the continuum. The sequence of the above two models is also different. In the latter, the electron is ionized from the ground state first, then oscillation in the laser field, transition the resonant state, and recombination to the ground state finally.
Resonant MHOHG described by the above four-step model have novel features [20,21], which do not occur in the three-step model of atomic HHG. For example, resonance enhanced harmonic generation, multiple frequency harmonic series, double plateau, and a larger cutoff energy. Another important feature presented in the inset of Figure 2 is the redshift of MHOHG above the ionization threshold. No such shift appears in the lower-order MHOHG in the perturbative regime with photon energy less than the ionization potential Ip since it is of pure molecular bound state character [29]. It clearly shows that the red shift is a nonadiabatic effect.
To understand the red shift in detail, we explore the role of EE and enhanced ionization (EI) [30,31] in MHOHG. The latter is a nonlinear characteristic effect of molecules in intense laser fields. We present the population of the resonant  state and the total ionization rate Г(t) as a function of time in Figure 4, from which one concludes that EE and EI are not synchronous. For laser intensity below the saturation threshold, the excitation to the localized resonant state
state and the total ionization rate Г(t) as a function of time in Figure 4, from which one concludes that EE and EI are not synchronous. For laser intensity below the saturation threshold, the excitation to the localized resonant state  on the RLE will strongly enhance the ionization rate of the system on the FLE. In this way, the red shift generated on the FLE will be larger than the blue shift on the RLE. An overall noticeable red shift can be observed in the MHOHG process. The time delay between EE and subsequent EI plays an important role in producing a noticeable “redshift” in MHOHG for very short pulses.
on the RLE will strongly enhance the ionization rate of the system on the FLE. In this way, the red shift generated on the FLE will be larger than the blue shift on the RLE. An overall noticeable red shift can be observed in the MHOHG process. The time delay between EE and subsequent EI plays an important role in producing a noticeable “redshift” in MHOHG for very short pulses.
 state and the total ionization rate Г(t) as a function of time in Figure 4, from which one concludes that EE and EI are not synchronous. For laser intensity below the saturation threshold, the excitation to the localized resonant state
state and the total ionization rate Г(t) as a function of time in Figure 4, from which one concludes that EE and EI are not synchronous. For laser intensity below the saturation threshold, the excitation to the localized resonant state  on the RLE will strongly enhance the ionization rate of the system on the FLE. In this way, the red shift generated on the FLE will be larger than the blue shift on the RLE. An overall noticeable red shift can be observed in the MHOHG process. The time delay between EE and subsequent EI plays an important role in producing a noticeable “redshift” in MHOHG for very short pulses.
on the RLE will strongly enhance the ionization rate of the system on the FLE. In this way, the red shift generated on the FLE will be larger than the blue shift on the RLE. An overall noticeable red shift can be observed in the MHOHG process. The time delay between EE and subsequent EI plays an important role in producing a noticeable “redshift” in MHOHG for very short pulses.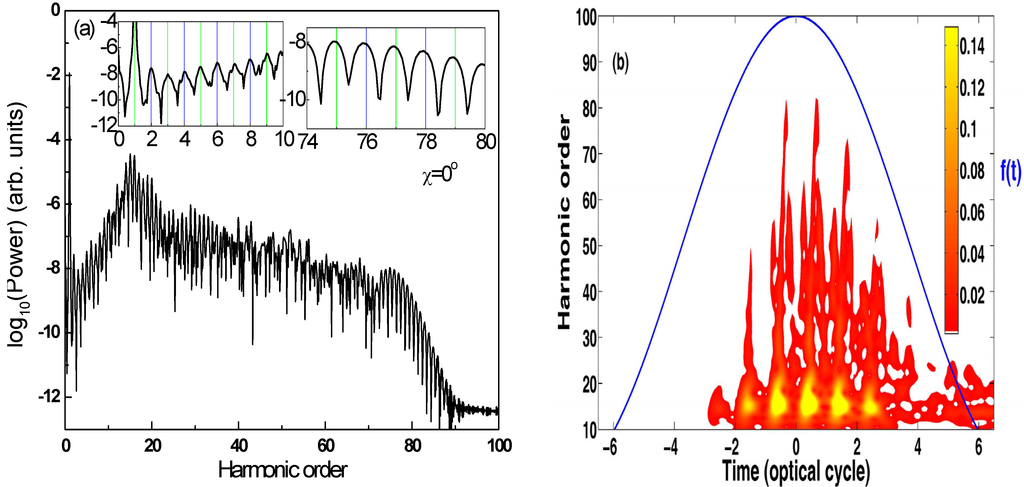
Figure 2.
(a) Molecular high-order harmonic generation (MHOHG) spectra of HeH2+ in linearly polarized laser fields; (b) wavelet analysis of the harmonic generation. The insets in (a) are the enlarged areas of the MHOHG spectrum. The left inset shows the harmonics in the purtabative regime without shift. The right inset presents the harmonics near the cutoff with noticable red shift. The internuclear distance R = 4 a.u. is fixed. The initial state is the ground  state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).
state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).
 state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).
state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).
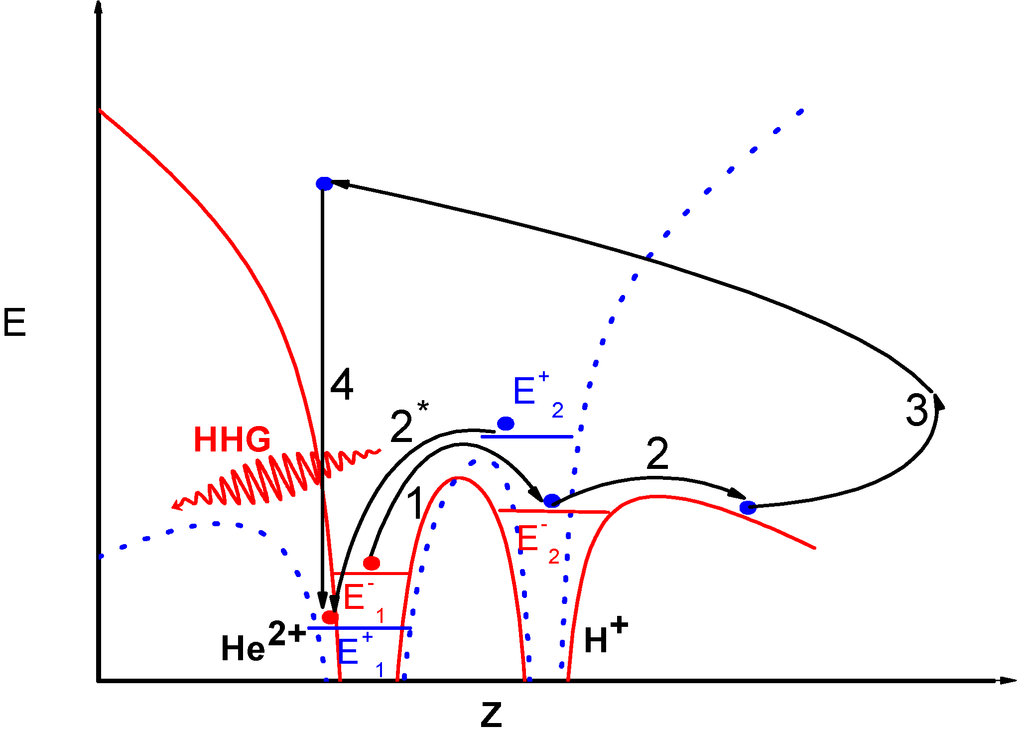
Figure 3.
Four-step model for MHOHG in the resonant molecular ion system HeH2+. Step (1): the laser field pumps the electron from the ground  state to the localized long lifetime
state to the localized long lifetime  excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
 state to the localized long lifetime
state to the localized long lifetime  excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
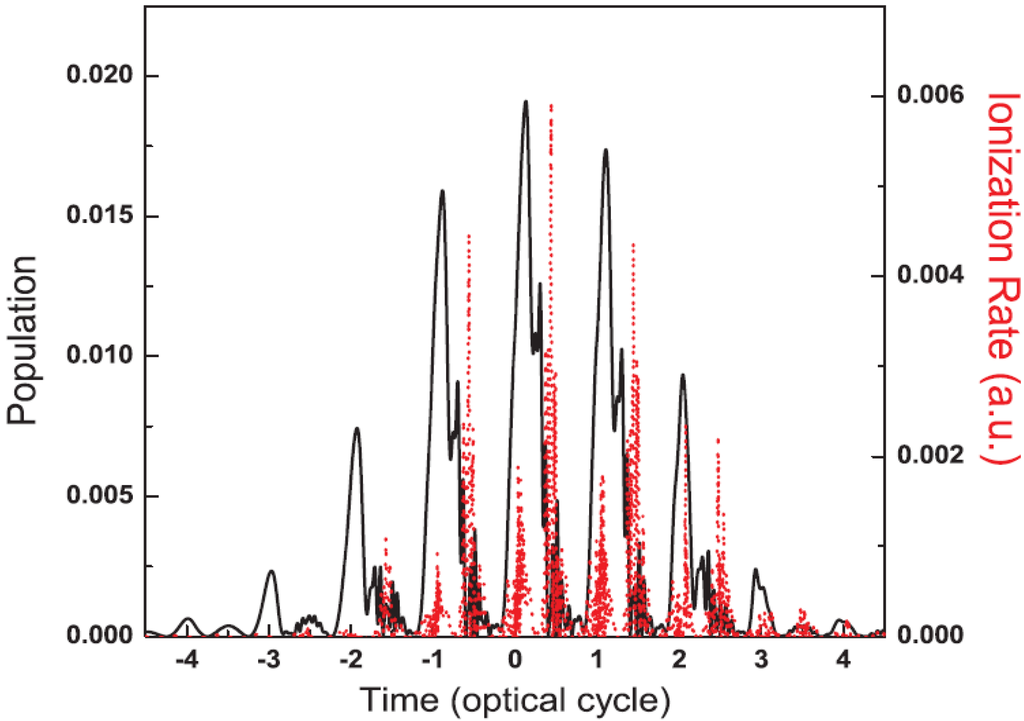
Figure 4.
Population of the first excited state  (solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.
(solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.
 (solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.
(solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.
3.2. Pulse Duration Dependence of Red Shift in MHOHG
The red shift in MHOHG is a nonadiabatic process as it depends on the pulse shape ƒ(t) in Figure 2b. An important parameter in this process is the pulse duration in addition to the laser intensity. This nonadiabatic effect is strongly related to 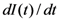 . Shorter pulses enhance this effect, while this nonadiabatic effect will be less noticeable for longer pulses. To emphasize this effect, MHOHG spectra for harmonic order 40 to 42 in the plateau produced by different duration of laser pulses are illustrated in Figure 5a. The laser intensity and wavelength are kept the same as those in Figure 2. The corresponding time profiles of harmonic with order 40 are presented in Figure 5b. The nonadiabatic spectral red shift of MHOHG gradually decreases as the laser-pulse duration increases from 10 to 20 optical cycles. From the time profile analysis, the harmonic generation process is gradually shifted from the falling part of the pulse to the rising part in agreement with the above prediction.
. Shorter pulses enhance this effect, while this nonadiabatic effect will be less noticeable for longer pulses. To emphasize this effect, MHOHG spectra for harmonic order 40 to 42 in the plateau produced by different duration of laser pulses are illustrated in Figure 5a. The laser intensity and wavelength are kept the same as those in Figure 2. The corresponding time profiles of harmonic with order 40 are presented in Figure 5b. The nonadiabatic spectral red shift of MHOHG gradually decreases as the laser-pulse duration increases from 10 to 20 optical cycles. From the time profile analysis, the harmonic generation process is gradually shifted from the falling part of the pulse to the rising part in agreement with the above prediction.
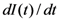 . Shorter pulses enhance this effect, while this nonadiabatic effect will be less noticeable for longer pulses. To emphasize this effect, MHOHG spectra for harmonic order 40 to 42 in the plateau produced by different duration of laser pulses are illustrated in Figure 5a. The laser intensity and wavelength are kept the same as those in Figure 2. The corresponding time profiles of harmonic with order 40 are presented in Figure 5b. The nonadiabatic spectral red shift of MHOHG gradually decreases as the laser-pulse duration increases from 10 to 20 optical cycles. From the time profile analysis, the harmonic generation process is gradually shifted from the falling part of the pulse to the rising part in agreement with the above prediction.
. Shorter pulses enhance this effect, while this nonadiabatic effect will be less noticeable for longer pulses. To emphasize this effect, MHOHG spectra for harmonic order 40 to 42 in the plateau produced by different duration of laser pulses are illustrated in Figure 5a. The laser intensity and wavelength are kept the same as those in Figure 2. The corresponding time profiles of harmonic with order 40 are presented in Figure 5b. The nonadiabatic spectral red shift of MHOHG gradually decreases as the laser-pulse duration increases from 10 to 20 optical cycles. From the time profile analysis, the harmonic generation process is gradually shifted from the falling part of the pulse to the rising part in agreement with the above prediction.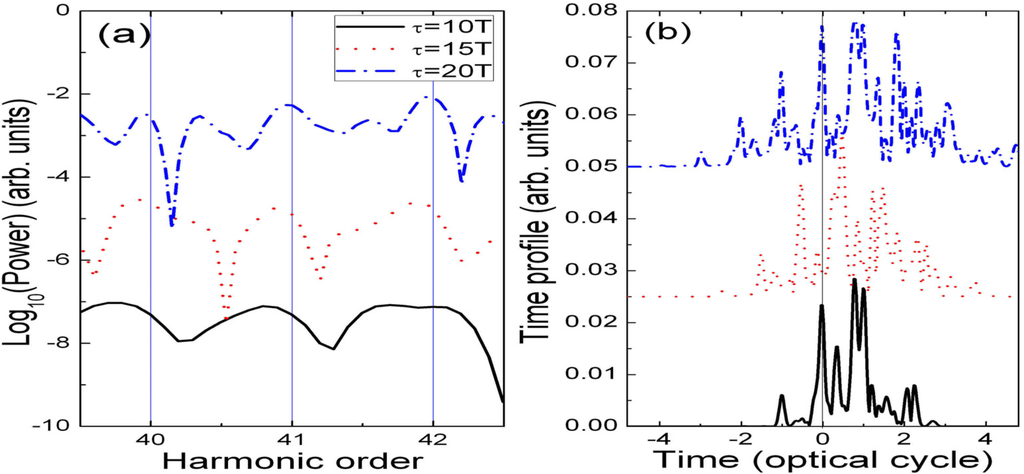
Figure 5.
(a) Red shifted harmonics in the plateau with order N = 40–42 at different laser pulse durations τ. With increasing the pulse duration, the nonadiabatic effect is reducing and the redshift of the harmonics becomes smaller. (b) The corresponding time profiles of harmonic order N = 40. When the laser pulse duartion is increased, more harmonics generated with t < 0, and the asymmetry between t < 0 and t > 0 is less, which reduces the red shift of the harmonics. The curves have been shifted vertically for clarity.
3.3. Orientation Dependence of Red Shift in MHOHG
From the above discussion, the resonance of  state with long life time plays a key role in the red shift of MHOHG. The radiative transition from the ground
state with long life time plays a key role in the red shift of MHOHG. The radiative transition from the ground 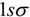 state to the resonant
state to the resonant  state is however restricted to the parallel component of the laser field. In this subsection, we explore the orientation dependence of the red shift in MHOHG [22]. The numerical results of MHOHG spectra with different orientation angles χ and the corresponding time profiles are presented in Figure 6a,b, respectively.
state is however restricted to the parallel component of the laser field. In this subsection, we explore the orientation dependence of the red shift in MHOHG [22]. The numerical results of MHOHG spectra with different orientation angles χ and the corresponding time profiles are presented in Figure 6a,b, respectively.
 state with long life time plays a key role in the red shift of MHOHG. The radiative transition from the ground
state with long life time plays a key role in the red shift of MHOHG. The radiative transition from the ground 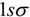 state to the resonant
state to the resonant  state is however restricted to the parallel component of the laser field. In this subsection, we explore the orientation dependence of the red shift in MHOHG [22]. The numerical results of MHOHG spectra with different orientation angles χ and the corresponding time profiles are presented in Figure 6a,b, respectively.
state is however restricted to the parallel component of the laser field. In this subsection, we explore the orientation dependence of the red shift in MHOHG [22]. The numerical results of MHOHG spectra with different orientation angles χ and the corresponding time profiles are presented in Figure 6a,b, respectively.An obvious feature in Figure 6a is that the overall intensity of MHOHG is strongly dependent on the resonance of the excited state  . The intensity of MHOHG in the plateau with orientation angle χ=0° (parallel) is more than two orders higher than that with orientation angle χ=90° (perpendicular). The reason is that the direct ionization rate from the ground state
. The intensity of MHOHG in the plateau with orientation angle χ=0° (parallel) is more than two orders higher than that with orientation angle χ=90° (perpendicular). The reason is that the direct ionization rate from the ground state 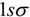 is very low due to the large ionization potential. However, the EE to the resonant excited state
is very low due to the large ionization potential. However, the EE to the resonant excited state  will lead to EI, which greatly increases the ionization rate of the system. For the parallel orientation, the amplitude of radiative transition to the
will lead to EI, which greatly increases the ionization rate of the system. For the parallel orientation, the amplitude of radiative transition to the  state is maximal. This corresponds to an efficient laser-induced electron transfer (LIET) in a nonsymmetric system [20]. One can observe a strong resonance in the MHOHG spectra. When we gradually increase the orientation angle χ between the molecular axis and laser polarization, the transition amplitude along the molecular axis direction diminishes, and the intensity of the resonance and the plateau in MHOHG decreases. It can be observed in the corresponding time profiles in Figure 6b. For perpendicular orientation with χ=90°, the transition from the
state is maximal. This corresponds to an efficient laser-induced electron transfer (LIET) in a nonsymmetric system [20]. One can observe a strong resonance in the MHOHG spectra. When we gradually increase the orientation angle χ between the molecular axis and laser polarization, the transition amplitude along the molecular axis direction diminishes, and the intensity of the resonance and the plateau in MHOHG decreases. It can be observed in the corresponding time profiles in Figure 6b. For perpendicular orientation with χ=90°, the transition from the 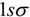 state to
state to  state is forbidden by selection rules. The electron may transit from the
state is forbidden by selection rules. The electron may transit from the 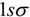 state to 2pπ state (−0.7388 a.u. (20.1 eV)). However, the 2pπ state is not a resonant state with long life time. Its role in the MHOHG is therefore negligible. As a consequence, the above four-step model gradually changes to a three-step model with increasing angle χ, and the time profiles of higher-order harmonics illustrated in Figure 6b becomes more symmetric with respect to the time when the laser pulse reaches its peak intensity, i.e., t = 0. The red shift of MHOHG decreases with the increase of the orientation angle χ. No noticeable red shift occurs in the MHOHG spectra when χ=90° as illustrated in the calculations presented in Figure 6a for the intensities and in Figure 6b for the time profiles. One may expect only odd-order harmonic generation due to the symmetry of the system with χ=90°. However, a little population on the 2pπ state will break the symmetry of the system, which will lead to even-order harmonic generation [22].
state to 2pπ state (−0.7388 a.u. (20.1 eV)). However, the 2pπ state is not a resonant state with long life time. Its role in the MHOHG is therefore negligible. As a consequence, the above four-step model gradually changes to a three-step model with increasing angle χ, and the time profiles of higher-order harmonics illustrated in Figure 6b becomes more symmetric with respect to the time when the laser pulse reaches its peak intensity, i.e., t = 0. The red shift of MHOHG decreases with the increase of the orientation angle χ. No noticeable red shift occurs in the MHOHG spectra when χ=90° as illustrated in the calculations presented in Figure 6a for the intensities and in Figure 6b for the time profiles. One may expect only odd-order harmonic generation due to the symmetry of the system with χ=90°. However, a little population on the 2pπ state will break the symmetry of the system, which will lead to even-order harmonic generation [22].
 . The intensity of MHOHG in the plateau with orientation angle χ=0° (parallel) is more than two orders higher than that with orientation angle χ=90° (perpendicular). The reason is that the direct ionization rate from the ground state
. The intensity of MHOHG in the plateau with orientation angle χ=0° (parallel) is more than two orders higher than that with orientation angle χ=90° (perpendicular). The reason is that the direct ionization rate from the ground state 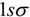 is very low due to the large ionization potential. However, the EE to the resonant excited state
is very low due to the large ionization potential. However, the EE to the resonant excited state  will lead to EI, which greatly increases the ionization rate of the system. For the parallel orientation, the amplitude of radiative transition to the
will lead to EI, which greatly increases the ionization rate of the system. For the parallel orientation, the amplitude of radiative transition to the  state is maximal. This corresponds to an efficient laser-induced electron transfer (LIET) in a nonsymmetric system [20]. One can observe a strong resonance in the MHOHG spectra. When we gradually increase the orientation angle χ between the molecular axis and laser polarization, the transition amplitude along the molecular axis direction diminishes, and the intensity of the resonance and the plateau in MHOHG decreases. It can be observed in the corresponding time profiles in Figure 6b. For perpendicular orientation with χ=90°, the transition from the
state is maximal. This corresponds to an efficient laser-induced electron transfer (LIET) in a nonsymmetric system [20]. One can observe a strong resonance in the MHOHG spectra. When we gradually increase the orientation angle χ between the molecular axis and laser polarization, the transition amplitude along the molecular axis direction diminishes, and the intensity of the resonance and the plateau in MHOHG decreases. It can be observed in the corresponding time profiles in Figure 6b. For perpendicular orientation with χ=90°, the transition from the 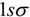 state to
state to  state is forbidden by selection rules. The electron may transit from the
state is forbidden by selection rules. The electron may transit from the 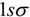 state to 2pπ state (−0.7388 a.u. (20.1 eV)). However, the 2pπ state is not a resonant state with long life time. Its role in the MHOHG is therefore negligible. As a consequence, the above four-step model gradually changes to a three-step model with increasing angle χ, and the time profiles of higher-order harmonics illustrated in Figure 6b becomes more symmetric with respect to the time when the laser pulse reaches its peak intensity, i.e., t = 0. The red shift of MHOHG decreases with the increase of the orientation angle χ. No noticeable red shift occurs in the MHOHG spectra when χ=90° as illustrated in the calculations presented in Figure 6a for the intensities and in Figure 6b for the time profiles. One may expect only odd-order harmonic generation due to the symmetry of the system with χ=90°. However, a little population on the 2pπ state will break the symmetry of the system, which will lead to even-order harmonic generation [22].
state to 2pπ state (−0.7388 a.u. (20.1 eV)). However, the 2pπ state is not a resonant state with long life time. Its role in the MHOHG is therefore negligible. As a consequence, the above four-step model gradually changes to a three-step model with increasing angle χ, and the time profiles of higher-order harmonics illustrated in Figure 6b becomes more symmetric with respect to the time when the laser pulse reaches its peak intensity, i.e., t = 0. The red shift of MHOHG decreases with the increase of the orientation angle χ. No noticeable red shift occurs in the MHOHG spectra when χ=90° as illustrated in the calculations presented in Figure 6a for the intensities and in Figure 6b for the time profiles. One may expect only odd-order harmonic generation due to the symmetry of the system with χ=90°. However, a little population on the 2pπ state will break the symmetry of the system, which will lead to even-order harmonic generation [22].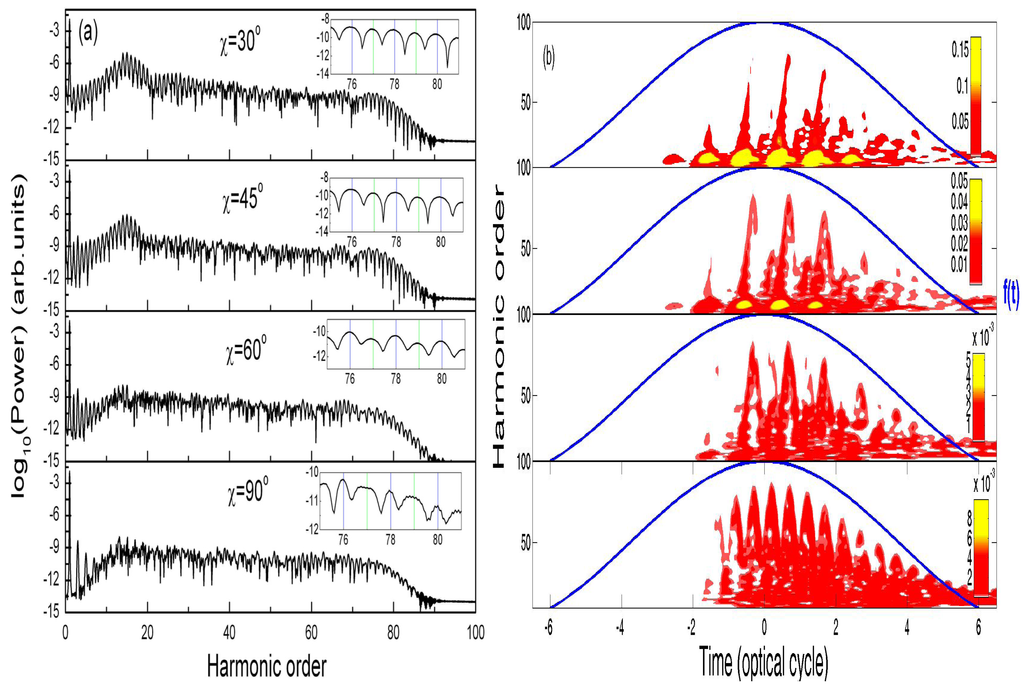
Figure 6.
(a) Orientation dependence of MHOHG in linearly polarized laser fields. (b) The corresponding time profile analysis. With increasing orientation angle, the intensity of the resonance in MHOHG around order 18 becomes weaker and weaker. The redshift in the inset of (a) is becoming less noticeable. For higher order MHOHG (larger than 40), the time-profile analysis in (b) shows increasing symmetry with increasing orientation angle.
4. Conclusions
We have reviewed in the presented work the nonadiabatic spectral shift of atomic HHG and MHOHG in intense laser fields. The blue shift in HHG has been well studied in theories and confirmed by experiments. In the present work, red shifts of harmonic generation are described and predicted theoretically by a four-step model in resonant systems, thus confirming that the principle of nonadiabatic red shifts is general at high intensities. Since resonant HHG in laser plasma interaction systems [28,32,33] has been theoretically studied and experimentally reported, we predict that the appearance of a red shift in HHG should be observed experimentally in such media. The principle mechanism for such an effect is the time delay between EE and EI. Red shifts in MHOHG open a way to measure this delay in photoemission [34,35,36].
Acknowledgments
We thank RQCHP and Compute Canada for access to massively parallel computer clusters and useful discussion with T. Ozaki at INRS on laser-plasma interactions.
Conflict of Interest
The authors declare no conflict of interest.
References
- McPherson, A.; Gibson, G.; Jara, H.; Johann, U.; Luk, T.S.; McIntyre, I.A.; Boyer, K.; Rhodes, C.K. Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Opt. Soc. Am. B 1987, 4, 595–601. [Google Scholar]
- Ferray, M.; Huillier, A.L.; Li, X.F.; Lompre, L.A.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B 1988, 21, L31–L35. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar]
- Bandrauk, A.D.; Chelkowski, S.; Goudreau, S. Control of harmonic generation using two-colour femtosecond-attosecond laser fields: Quantum and classical perspectives. J. Mod. Opt. 2005, 52, 411–428. [Google Scholar]
- Bandrauk, A.D.; Barmaki, S.; Kamta, G.L. Laser phase control of high-order harmonic generation at large internuclear distance: the h+-h2+ system. Phys. Rev. Lett. 2007, 98, 013001–1. [Google Scholar]
- Bandrauk, A.D.; Barmaki, S.; Cheklowski, S.; Kamta, G.L. Progress in Ultrafast Intense Laser Science III; Yamanouchi, K., Chin, S.L., Agostini, P., Ferrante, G., Eds.; Springer: Berlin, Germany, 2008; Volume 3, p. 171. [Google Scholar]
- Moreno, P.; Plaja, L.; Roso, L. Ultrahigh harmonic generation from diatomic molecular ions in highly excited vibrational states. Phys. Rev. A 1997, 55, R1593–R1596. [Google Scholar] [CrossRef]
- Bian, X.B.; Bandrauk, A.D. Nonadiabatic molecular high-order harmonic generation from polar molecules: Spectral redshift. Phys. Rev. A 2011, 83, 041403:1–041403:4. [Google Scholar]
- Shin, H.J.; Lee, D.G.; Cha, Y.H.; Hong, K.H.; Nam, C.H. Generation of nonadiabatic blueshift of high harmonics in an intense femtosecond laser field. Phys. Rev. Lett. 1999, 83, 2544–2547. [Google Scholar]
- Wahlström, C.G.; Larsson, J.; Persson, A.; Starczewski, T.; Svanberg, S.; Salières, P.; Balcou, P.; L’Huillier, A. High-order harmonic generation in rare gases with an intense short-pulse laser. Phys. Rev. A 1993, 48, 4709–4720. [Google Scholar] [CrossRef]
- Singhal, H.; Arora, V.; Naik, P.A.; Gupta, P.D. Spectral blueshifts in laser light scattered from argon-gas-cluster plasmas. Phys. Rev. A 2005, 72, 043201:1–043201:7. [Google Scholar]
- Geissler, M.; Tempea, G.; Brabec, T. Phase-matched high-order harmonic generation in the nonadiabatic limit. Phys. Rev. A 2000, 62, 033817:1–033817:8. [Google Scholar]
- Watson, J.B.; Sanpera, A.; Burnett, K. Pulse-shape effects and blueshifting in the single-atom harmonic generation from neutral species and ions. Phys. Rev. A 1995, 51, 1458–1463. [Google Scholar] [CrossRef]
- Kan, C.; Capjack, C.E.; Rankin, R.; Burnett, N.H. Spectral and temporal structure in high harmonic emission from ionizing atomic gases. Phys. Rev. A 1995, 52, R4336–R4339. [Google Scholar]
- Rae, S.C.; Burnett, K. Detailed simulations of plasma-induced spectral blueshifting. Phys. Rev. A 1992, 46, 1084–1090. [Google Scholar]
- Shin, H.J.; Lee, D.G.; Cha, Y.H.; Kim, J.H.; Hong, K.H.; Nam, C.H. Nonadiabatic blueshift of high-order harmonics from Ar and Ne atoms in an intense femtosecond laser field. Phys. Rev. A 2001, 63, 053407:1–053407:9. [Google Scholar]
- Bian, X.B.; Bandrauk, A.D. Multichannel molecular high-order harmonic generation from asymmetric diatomic molecules. Phys. Rev. Lett. 2010, 105, 093903:1–093903:4. [Google Scholar]
- Bian, X.B.; Bandrauk, A.D. Phase control of multichannel molecular high-order harmonic generation by the asymmetric diatomic molecule HeH2+ in two-color laser fields. Phys. Rev. A 2011, 83, 023414:1–023414:7. [Google Scholar]
- Bian, X.-B.; Bandrauk, A.D. Orientation dependence of nonadiabatic molecular high-order-harmonic generation from resonant polar molecules. Phys. Rev. A 2012, 86, 053417:1–053417:5. [Google Scholar]
- Ben-Itzhak, I.; Gertner, I.; Heber, O.; Rosner, B. Experimental evidence for the existence of the 2pσ bound state of HeH2+ and its decay mechanism. Phys. Rev. Lett. 1993, 71, 1347–1350. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Chelkowski, S.; Diestler, D.J.; Manz, J.; Yuan, K.J. Quantum simulation of high-order harmonic spectra of the hydrogen atom. Phys. Rev. A 2009, 79, 023403:1–023403:14. [Google Scholar]
- Antoine, P.; Piraux, B.; Maquet, A. Time profile of harmonics generated by a single atom in a strong electromagnetic field. Phys. Rev. A 1995, 51, R1750–R1753. [Google Scholar]
- Chandre, C.; Wiggins, S.; Uzer, T. Time–frequency analysis of chaotic systems. Physica D 2003, 181, 171–196. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Witting, T.; Hutchison, C.; Frank, F.; Tudorovskaya, M.; Lein, M.; Okell, W.A.; Zaïr, A.; Marangos, J.P.; Tisch, J.W.G. Isolated sub-fs XUV pulse generation in Mn plasma ablation. Opt. Express 2012, 20, 25239–25248. [Google Scholar] [CrossRef]
- Strelkov, V. Role of autoionizing state in resonant high-order harmonic generation and attosecond pulse production. Phys. Rev. Lett. 2010, 104, 123901:1–123901:4. [Google Scholar] [CrossRef]
- Hostetter, J.A.; Tate, J.L.; Schafer, K.J.; Gaarde, M.B. Semiclassical approaches to below-threshold harmonics. Phys. Rev. A 2010, 82, 023401:1–023401:8. [Google Scholar]
- Kamta, G.L.; Bandrauk, A.D. Effects of molecular symmetry on enhanced ionization by intense laser pulses. Phys. Rev. A 2007, 75, 041401:1–041401:4. [Google Scholar]
- Kamta, G.L.; Bandrauk, A.D. Nonsymmetric molecules driven by intense few-cycle laser pulses: Phase and orientation dependence of enhanced ionization. Phys. Rev. A 2007, 76, 053409:1–053409:15. [Google Scholar]
- Milošević, D.B. Resonant high-order harmonic generation from plasma ablation: Laser intensity dependence of the harmonic intensity and phase. Phys. Rev. A 2010, 81, 023802:1–023802:7. [Google Scholar]
- Ganeev, R.A.; Suzuki, M.; Baba, M.; Kuroda, H.; Ozaki, T. Strong resonance enhancement of a single harmonic generated in the extreme ultraviolet range. Opt. Lett. 2006, 31, 1699–1701. [Google Scholar]
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef]
- Klünder, K.; Dahlström, J.M.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guénot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A.; et al. Probing single-photon ionization on the attosecond time scale. Phys. Rev. Lett. 2011, 106, 143002:1–143002:4. [Google Scholar]
- Neppl, S.; Ernstorfer, R.; Bothschafter, E.M.; Cavalieri, A.L.; Menzel, D.; Barth, J.V.; Krausz, F.; Kienberger, R.; Feulner, P. Attosecond time-resolved photoemission from core and valence states of magnesium. Phys. Rev. Lett. 2012, 109, 087401:1–087401:5. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).