1. Introduction
For nonlinear optics and time resolved spectroscopic studies of atoms, molecules and biological processes there is a rising need for ultrashort light pulses in the UV and deep UV spectral domain. Straightforward frequency upconversion of short visible pulses in non-linear crystals already allows for the generation of sub-20 fs UV pulses [
1] and 30 fs pulses down to 189 nm [
2]. The phase-matching bandwidth can be increased by advanced angular dispersion methods leading to sub-10 fs pulses [
3,
4]. Other important techniques capable of generating UV pulses are four wave mixing in a gas filled hollow wave guide providing sub-10 fs pulses at 270 nm [
5]. Third harmonic generation of the fundamental pulses at around 800 nm provide sub-30 fs pulses in air [
6] or even 3-fs pulses in a Neon filled gas cell [
7]. These techniques are characterized by a low conversion efficiency and require an elaborate experimental implementation.
Pulse shortening can also be achieved through spectral broadening of longer UV pulses typically generated by frequency up conversion. Spectral broadening can be achieved by nonlinear phase modulation of the UV pulse in an optically transparent medium. In cross phase modulation the nonlinearity is induced by an auxiliary high intensity laser pulse. To increase the interaction length, gas filled hollow waveguides are often used. With this approach cross phase modulation between the fundamental and the third harmonic of a Ti:sapphire laser amplifier allows to compress the 266 nm pulses by a factor of 2 down to 23 fs [
8]. For a 35 fs Ti:sapphire laser system this process helps to further broaden the intense 266 nm pulses originating from four-wave-mixing of blue and red pulses down to a length of 8-fs [
9].
Efficient spectral pulse broadening in gas-filled hollow fibers or gas cells has also been achieved by self-phase modulation (SPM). With input pulse lengths of around 100 fs, deep UV pulses with an pulse energy of several hundred μJ as short as 20 fs centered at 268 nm [
10] and 25 fs centered at 248 nm [
11] were obtained. This technique however needs high input UV pulse energies up to several hundred μJ due to the low nonlinearity of the gas. Such high energy pulses are typically not available in spectroscopic setups, particularly at high repetition rates, and therefore the practical use of spectral broadening in gases is limited.
Bulk materials and fibers in contrast offer medium to high nonlinearities and are suitable candidates for nonlinear phase modulation. In single-mode fibers the pulse power is typically limited to tens of nJ. Fibers are therefore best suited for high repetition laser systems [
12]. Bulk materials can be operated at any input energy as the thickness of the material can be suitably adjusted so that self-focusing in the crystal is controlled and any serious beam distortion or material destruction can be avoided. Spectral broadening by SPM in bulk material has been first observed in the visible by Alfano
et al. [
13] and later in the UV by Hata
et al. [
14]. Theoretically, it was shown that in bulk material cross phase modulation should be capable of generating chirp free nearly-single cycle pulses [
15]. The shortening of IR and VIS pulses by SPM in bulk materials has been realized successfully in the 1980s [
16,
17] and it was envisioned that this approach can be extended into the UV spectral domain [
17].
In this paper we demonstrate that SPM can indeed be used to shorten UV pulses below their input Fourier limit. Taking into account the nonlinear processes of self-focusing and SPM we use simulations to find the optimal conditions for UV spectral broadening in common crystals. We then describe our experimental results on spectral broadening of UV pulses in a CaF2 plate and describe the way to achieve shorter pulses by incorporating a few supplemental parts into the setup. Compression of the pulses to nearly their Fourier limit is demonstrated by implementing an acousto-optical pulse shaper not necessary if the residual higher order chirp is of no concern.
Finally we apply the broadened UV pulses as pump and probe in a collinear two-dimensional experiment that allows us to resolve the spectral correlations of two vibrational bands of pyrene due to the enlarged spectral window of the pulses.
2. Parameter Optimization for Spectral Broadening
SPM modifies the spectral content of a laser pulse. The result of this modification is influenced by several experimental factors such as the pulse intensity, the wavelength and the nonlinear material properties. When an intense laser pulse propagates through a medium it induces a dynamic refractive index change
n(
t) =
n0 +
n2I(
t) due to the third-order Kerr nonlinearity
n2. This leads to self-focusing, self-steepening and SPM. In the case of SPM,
n2 causes a change of the phase of the electric field in the pulse itself. For an input pulse with spatial and temporal intensity profile
I(
r,t), this nonlinear phase variation accumulates over the propagation direction
z in a medium with thickness
l according to the
B integral:
Here ω0 is the initial circular frequency, c the speed of light and r parameterizes the spatial intensity distribution perpendicular to the propagation direction. The accumulated phase shift results in a corresponding frequency shift and thus a broadening or narrowing of the pulse spectrum.
A quantification of the maximum frequency shift due to SPM is given by
where the maximum frequency shift
∆ωmax is typically located at the maximum slope of the leading and trailing edge of the pulse intensity.
From Equations (1) and (2) one can conclude that high intensities and a long propagation distance in a material with a large positive
n2 is favorable to maximize spectral broadening through SPM. However, in bulk materials the large dispersion experienced by a UV pulse has to be taken into account. This leads to a reduction of the pulse intensity and thus the accumulated phase. A further limiting factor is the nonlinear process of self-focusing. As often mentioned in the literature, if the self-focus lies within the crystal length, severe beam distortions, beam breakup [
14] or ultimately filamentation occurs [
10,
18].
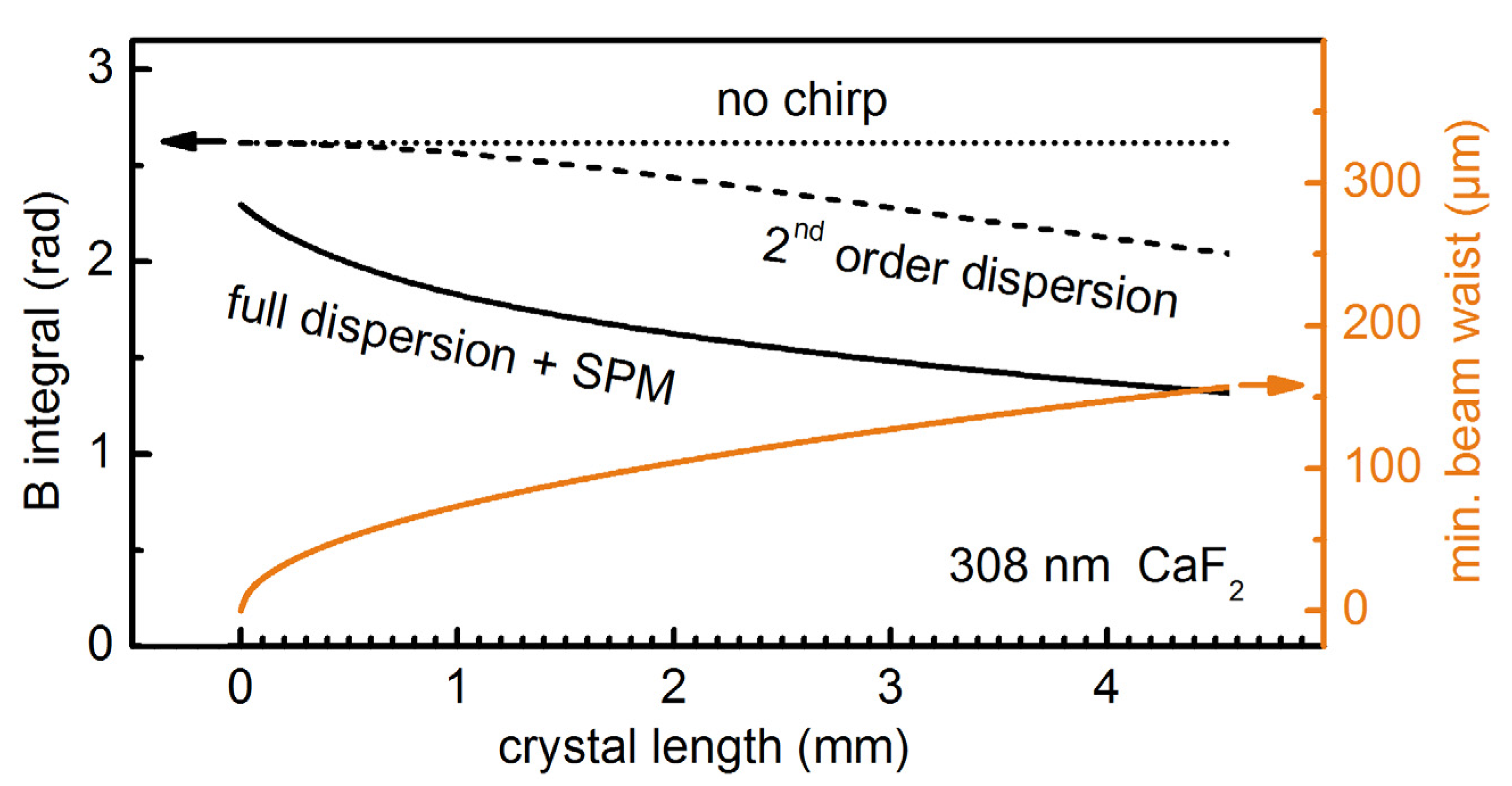
To illustrate the influence of the material's dispersion on SPM we calculated the
B integral (Equation (1)) for different thicknesses of a CaF
2 crystal (
n2 = 1.92 × 10
−16 cm
2/W [
19]). The results for a 25 fs long UV pulse centered at 308 nm with a pulse energy of 3μJ are shown in
Figure 1. One should note, that for a given crystal thickness we optimize the beam focusing to a minimal beam waist radius
w for which the self-focal length is 1.25 times the crystal length (see orange line in
Figure 1). This puts the self-focus outside the crystal and ensures that beam distortions do not occur. The self-focal length for a pulse with a power
P focused to a beam waist
w can be calculated according to Equation (3).
with
ρ0 being the Rayleigh length and
Pcr the critical self-focusing power threshold [
20,
21]. In the simulations, the change in the peak intensity due to self-focusing and self-steepening is neglected. The spatial intensity distribution is assumed to be Gaussian and the input pulses are Fourier limited. For the calculation of the
B integral we integrate over the whole beam profile.
Figure 1.
Amount of self-phase modulation (SPM) for 25 fs, 308 nm, 3 μJ UV pulses broadened in a CaF2 crystal. Calculated B-integral at increasing levels of theory for varied crystal length. The input beam waist is set to a value for which the self-focal length is 1.25 × the crystal length.
Figure 1.
Amount of self-phase modulation (SPM) for 25 fs, 308 nm, 3 μJ UV pulses broadened in a CaF2 crystal. Calculated B-integral at increasing levels of theory for varied crystal length. The input beam waist is set to a value for which the self-focal length is 1.25 × the crystal length.
The B integral does not vary with the crystal length when no material dispersion is included in the simulation (
Figure 1, dotted line) as the self-focal length is kept 1.25 times the crystal length for the different crystal thicknesses. As soon as 2nd order dispersion is considered (for a formula see, e.g., [
20]), the
B integral starts dropping steadily when the crystal thickness exceeds 1 mm and converges to zero for long crystals (
Figure 1, dashed line). The effect is even more dramatic when the full material dispersion is introduced by using virtual femtosecond laboratory software Lab2 [
22]. The resulting
B integral (
Figure 1, continuous line) shows a pronounced decrease even for crystals thinner than a few mm.
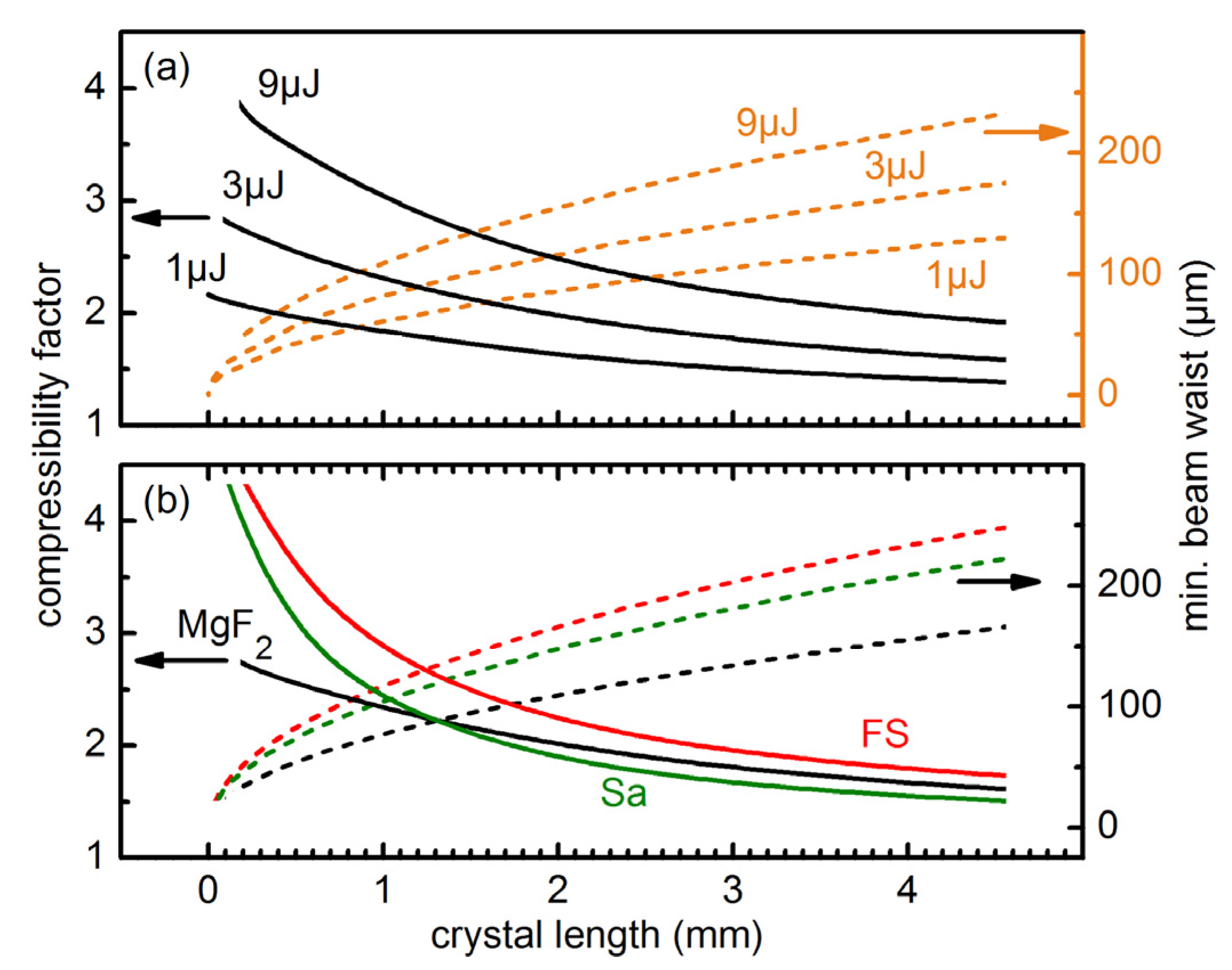
To find the optimal experimental conditions for a specific crystal thickness and a given minimal beam waist, we varied the input pulse energies and the type of bulk materials (
Figure 2). To get direct information on the achieved broadening we calculated the compressibility factor, which is the Fourier limit of the broadened pulse spectrum after propagating through the material divided by the initial Fourier limited pulse length (25 fs for all simulations).
Figure 2a shows, that for a fixed crystal length an increase of the input pulse energy increases the achievable compressibility factor. This behavior can be understood from Equations (1) and (3). The self-focal length scales roughly inversely with the square root of the pulse power
P, while the pulse intensity is directly proportional to the power. Therefore, the compressibility factor can be estimated to roughly scale with
![Applsci 03 00153 i004]()
.
Figure 2.
Compressibility factor (ratio between input and output Fourier limit) for a 25 fs pulse. Results for varied input energies, pulses centered at 308 nm, and a CaF2 crystal (a) and for different crystals with 266 nm pulses of 3 μJ energy (b). The input beam waist is set to a value for which the calculated self-focal length is 1.25 × the crystal length.
Figure 2.
Compressibility factor (ratio between input and output Fourier limit) for a 25 fs pulse. Results for varied input energies, pulses centered at 308 nm, and a CaF2 crystal (a) and for different crystals with 266 nm pulses of 3 μJ energy (b). The input beam waist is set to a value for which the calculated self-focal length is 1.25 × the crystal length.
In
Figure 2b the simulation results for different materials are shown. The
n2 values of MgF
2 (1.5 × 10
−16 cm
2/W), fused silica (7.8 × 10
−16 cm
2/W) and Sapphire (6.0 × 10
−16 cm
2/W) at 266 nm were taken from the literature [
19,
23]. The simulations show that a larger
n2 generally leads to an increase of the compressibility factor. However, the differing dispersion of the materials can change this general trend (see crossing of MgF
2 and Sa curves in
Figure 2b).
The simulations show that due to the pronounced dispersion in the UV, it is favorable to use short crystals with tight focusing. This is unlike spectral broadening in gases, where meter-long propagations are needed due to the much lower n2 values. 1 mm thick crystals lead to compressibility factors between 2 to 2.5 for Fourier limited Gaussian pulses with energies of a few μJ. The required beam waist radius lies in the order of 100 μm. These parameters are experimentally sensible.
3. Experimental Setup
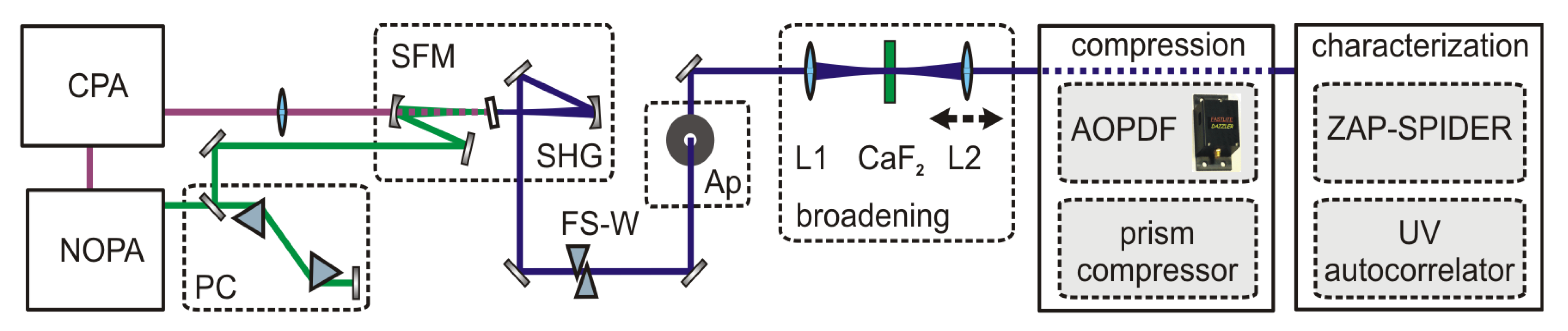
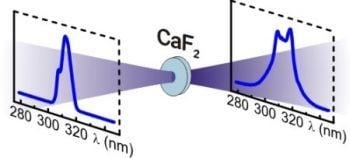
A schematic of the setup, which comprises the generation, broadening and characterization of UV pulses, is shown in
Figure 3. Tunable visible pulses were generated from a single-stage noncollinear parametric amplifier (NOPA) pumped by a 1-kHz Ti:Sa amplifier system (CPA 2001; Clark MXR) and optimally compressed by a pair of fused silica Brewster prisms. UV pulses with a typical pulse length of 25 fs were generated by frequency doubling or sum frequency mixing the NOPA pulses with the CPA fundamental in BBO crystals with a thickness of 53 μm. For the frequency doubling we typically obtain < 1 μJ which corresponds to an efficiency of < 15%. For the sum frequency mixing both beams were collinearly overlapped and the CPA fundamental was focused with a fused silica lens to match the focal size of the beam of the visible pulse in the BBO. Typical energies of 4 μJ are achieved with a visible to UV efficiency of 50 %.
To introduce a variable positive chirp the UV pulses pass through a set of UV antireflection coated movable fused silica wedges (apex angel 45°) with counter oriented apexes [
24]. To obtain a clean and spatially symmetric beam profile, which is advantageous for SPM, we introduce an aperture accepting a minimal loss of energy. The UV beam is then focused with the f = 150 mm antireflection coated fused silica lens L1 into a few mm thick crystal which spectrally broadens the pulses due to SPM. The position of the crystal relative to the soft focus of the UV beam can be adjusted to obtain maximum broadening without impairing the spatial mode due to self-focusing inside the crystal. A second fused silica lens L2 (f = 100 mm), that can be translated along the beam axis, recollimates the spectrally broadened UV pulse. This not only accounts for the change in divergence caused by the partial self-focusing in the crystal but also adjusts the collimation of the beam such that the specific requirements for pulse shaping with an acousto-optic programmable dispersive filter (AOPDF) are met [
1]. Specifically, the intermediate beam waist of the broadened UV pulse after the AOPDF has to be located one focusing length in front of the focusing element which is used to focus the beam into the interaction region, e.g., the sample.
Figure 3.
Setup for the generation, compression and characterization of UV pulses spectrally broadened by SPM. PC: prism compressor; SFM (SHG): sum frequency (second harmonic) generation; FS-W: Fused silica wedges; Ap: aperture; L1, L2 lenses.
Figure 3.
Setup for the generation, compression and characterization of UV pulses spectrally broadened by SPM. PC: prism compressor; SFM (SHG): sum frequency (second harmonic) generation; FS-W: Fused silica wedges; Ap: aperture; L1, L2 lenses.
The compression of the positively chirped broadened UV pulses is achieved by either a second UV prism compressor or a combination of a UV prism compressor and an AOPDF (DAZZLER
TM model T-UV-250-400; Fastlite) [
25] for higher order chirp correction. The prisms are UV antireflection coated and have an apex angle of 45°. The throughput of the UV PC is roughly 93%. In the PC-AOPDF combination the precompression with the UV PC permits a larger bandwidth of the AOPDF because the acoustic wave is less chirped and thus less elongated within the shaper crystal.
To measure the pulse lengths obtained in the simple setup where only a UV-PC is used to compress the broadened pulses, we employ a newly developed UV autocorrelator [
26] based on two photon absorption in a 173 μm thick BBO crystal. To check if the higher order chirp contributions of the UV-broadened pulses can be compensated for by the PC-AOPDF combination, we characterized the spectral phase with a ZAP-SPIDER [
27].
5. Application: Collinear Two-Dimensional Spectroscopy on Pyrene
Two-dimensional electronic spectroscopy can be regarded as an excitation frequency resolved pump-probe experiment. The measurable excitation window is determined by the spectral bandwidth of the excitation. Pulses with a spectral width large enough to cover the transitions to a multitude of vibronic or even electronic states are therefore an essential requirement. In contrast to 2D-Vis [
32,
33], where a bandwidth up to 150 nm can be reached, experimental realizations in the UV are so far limited to about 5 nm [
34,
35,
36].
We therefore introduce SPM broadened pulses in our collinear 2D-UV experiment. The central wavelength is set to 312 nm to excited the S
2 1B
2u←S
0 electronic transition of the test molecule pyrene. We use the same experimental parameters as determined above (1 mm CaF
2 and 2.5 μJ input energy) and achieve a FWHM bandwidth of 13 nm. This pulse spectrum is large enough to cover two vibronic bands of the absorption spectrum (see
Figure 8c, black line).
The 2D experiment is carried out in a pulse shaper assisted pump-probe geometry, as described in refs. [
34,
37]. After the SPM stage the UV beam is compressed with a UV prism compressor and then split into a pump and a probe beam. The pump passes through the AOPDF, which is used to resolve the excitation frequency by generating phase locked double pulses and scanning their interpulse delay. Additionally the shaper compensates for the higher order chirp. Both pump and probe are focused inside a 120 μm thick flow cell as described in ref. [
38]. The energy of the pump pulse in the cell is 63 nJ at a duration of the sub-pulses of 22 fs and the probe energy is about 2 nJ. After the sample cell the probe is spectrally resolved in a prism based CCD spectrometer. To increase the signal‑to‑noise ratio a fraction of the probe beam is used as a reference in a second prism based spectrometer [
39].
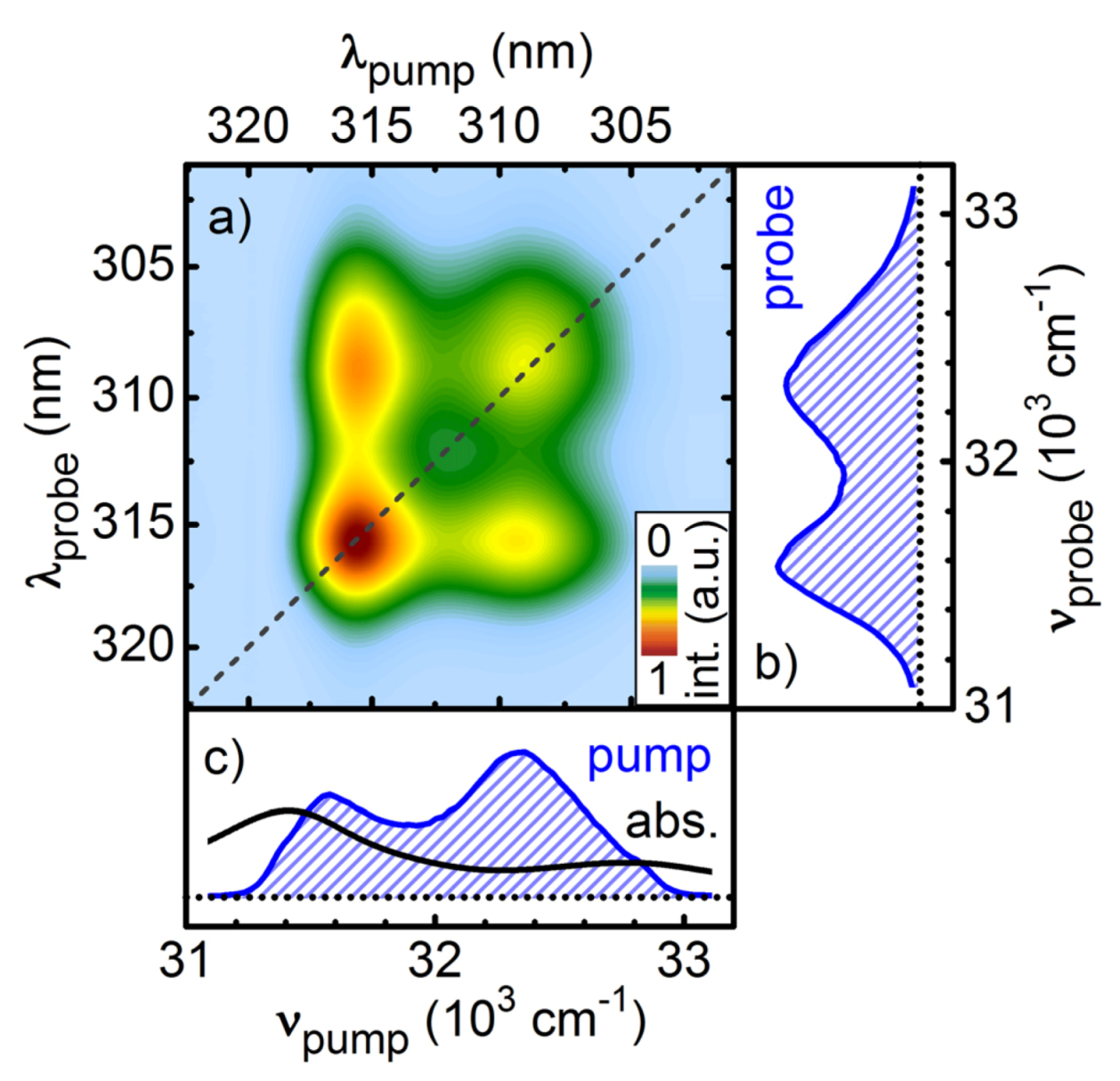
Figure 8.
SPM broadened UV pulses in collinear two-dimensional spectroscopy as pump and probe pulses. The absorptive signal resolves the pump-probe frequency correlation of the ground-state bleach of Pyrene in methanol for a population delay of 100 ps (a). The spectral intensity of the pulses (blue hashed areas) and the absorption spectrum of Pyrene (black line) are shown in the right (b) and lower side panel (c).
Figure 8.
SPM broadened UV pulses in collinear two-dimensional spectroscopy as pump and probe pulses. The absorptive signal resolves the pump-probe frequency correlation of the ground-state bleach of Pyrene in methanol for a population delay of 100 ps (a). The spectral intensity of the pulses (blue hashed areas) and the absorption spectrum of Pyrene (black line) are shown in the right (b) and lower side panel (c).
In
Figure 8a the absorptive part of the 2D-UV measurement of pyrene dissolved in methanol is shown for a pump-probe delay of 100 ps. All signals in the 2D spectrum are positive and are assigned to ground state bleach contributions of pyrene. The two diagonal peaks correspond to the two vibronic bands in the absorption spectrum. In addition, due to the large spectral bandwidth of the pump pulses, the off-diagonal peaks describing the correlation between the vibronic bands are clearly resolved for the first time.
6. Summary and Perspectives
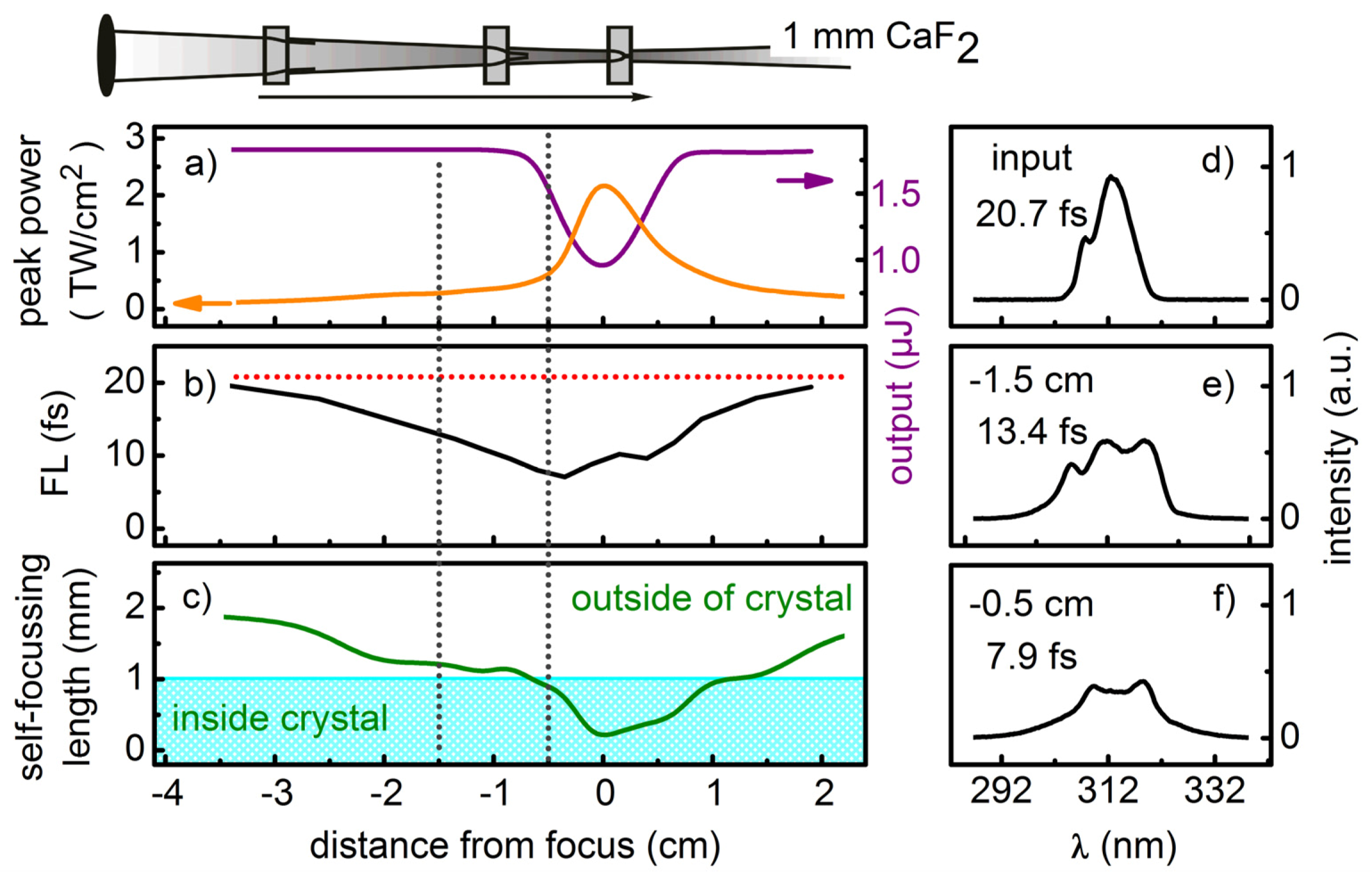
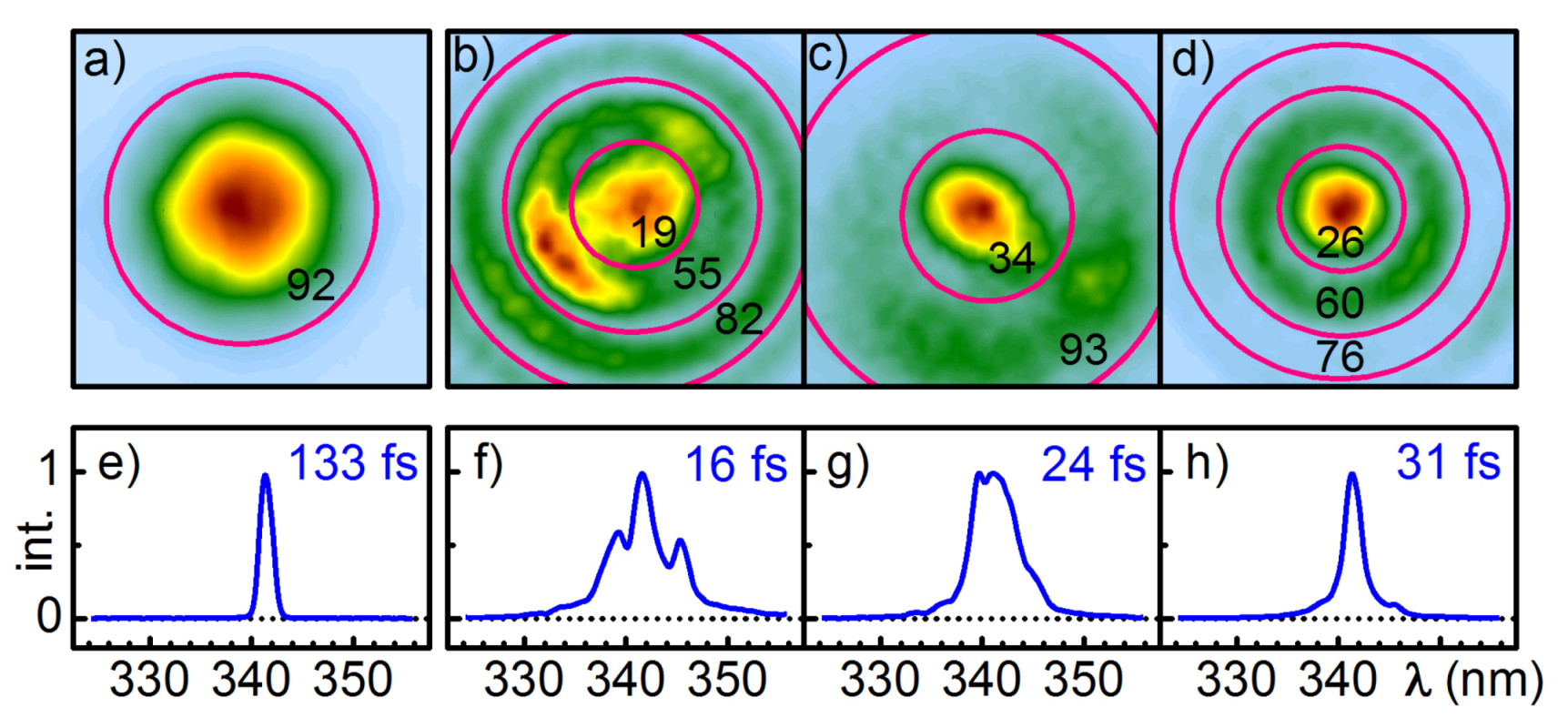
In this work we have shown that SPM in bulk materials can be readily used to broaden the spectrum of μJ femtosecond UV pulses and to reduce the pulse length. The broadening stage is most conveniently incorporated into an optical setup by using two lenses or spherical mirrors with a slight off-axis geometry and a crystal plate and thus relies only on components present in most ultrafast spectroscopy laboratories. There is no need for a specially designed fiber or meter long gas cells.
By focusing the UV beam into the crystal the high pulse intensity leads to self-phase modulation and self-focusing. In contrast to techniques using gas filled cells [
10] where self-focusing induced filamentation is a prerequisite for broadening, we find that the self-focus should be kept just outside the crystal, about 25% of the crystal thickness. This leads to broadening without serious beam distortions and to no beam break-up. Under this condition the pulse energy is nearly conserved as multi-photon absorption is minimized. It allows a maximum achievable broadening of up to a factor of three. Thin crystals with high nonlinearity in conjunction with reasonably tight focusing are found optimal as this keeps the negative influence of the strong group delay dispersion in the UV and the associated pulse lengthening to a minimum. A slight up chirp of the input pulse helps to enhance the broadening. Experimentally we find that a few millimeter thick CaF
2 crystal delivers the best results in terms of broadening and transmission efficiency. Once the pulse energy and length, and the crystal thickness is known, the beam size at the plate can be determined from the well known formula for the self-focal length.
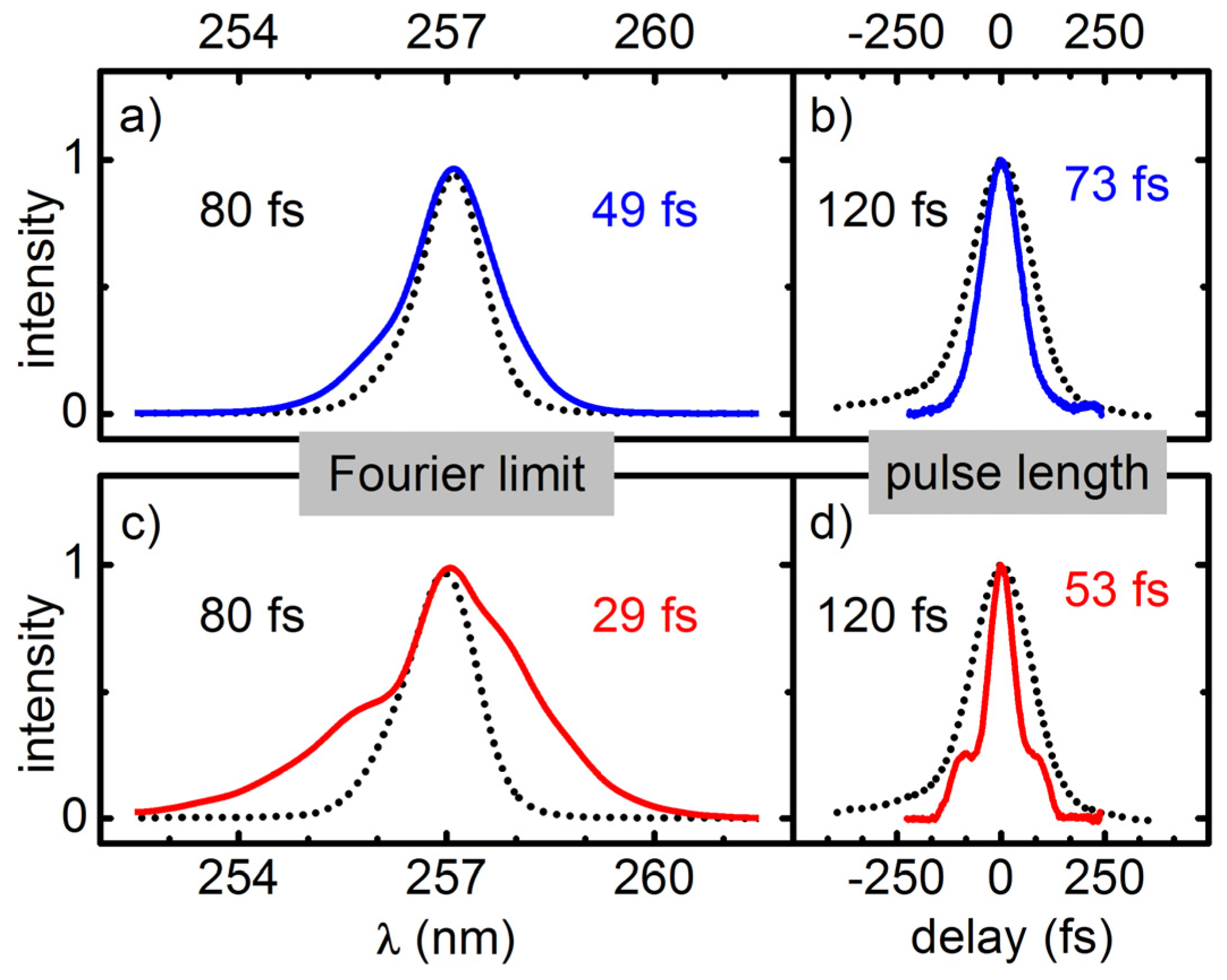
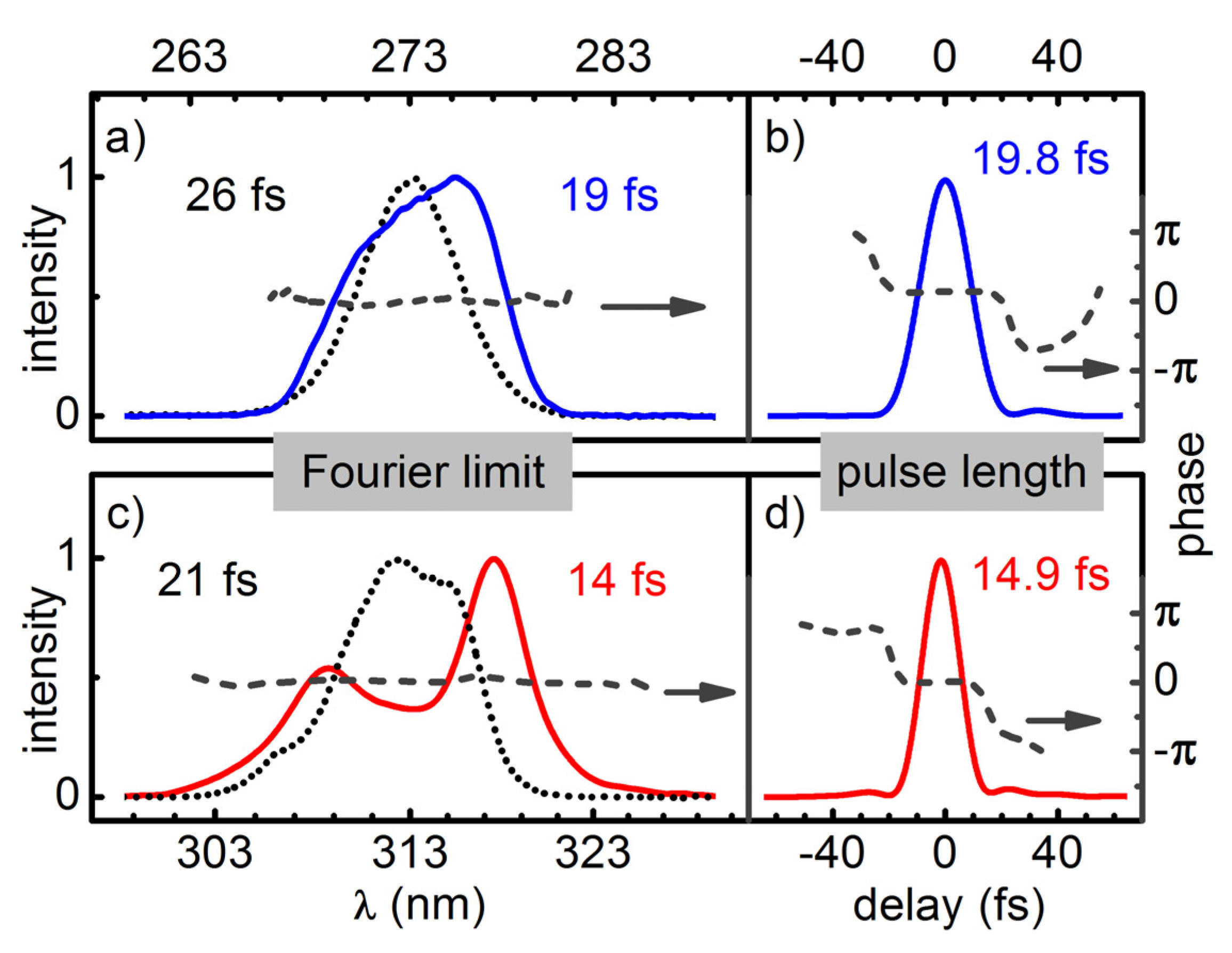
Temporal compression of the broadened pulses is done with a simple prism compressor for the regime down to about 50 fs. A compression by a factor of two to three is demonstrated. For even shorter pulses an AOPDF (DAZZLER) is added for the compensation of higher order chirp components. For pulses at 312 nm and 273 nm this allowed for a near Fourier limited compression down to 15 fs and 20 fs. If the pulses do not have to be perfectly compressed, even larger spectral broadening can be achieved.
The beam profile is quite acceptable for spectroscopic applications. The use of a circular aperture to select the central part of beam is often helpful. Still many tens of percent of the pulse energy can be utilized with the resulting new-Gaussian transversal profile.
We expect that SPM in bulk material can be employed for a large range of energies as the focusing conditions can be adapted for pulses less than a μJ to tens of μJ. Although here we only investigated the broadening of 120 and 25 fs input pulses, we envision that pulses at various pulse length can be broadened and compressed. The method likely will be best suited to situations where just an extra factor around two is needed for a successful experiment. This is, to our own experience, quite often the case.
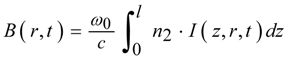
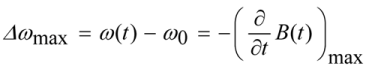
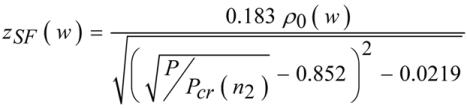
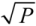 .
.