Adaptive Generation and Diagnostics of Linear Few-Cycle Light Bullets

Abstract

Recently we introduced the class of highly localized wavepackets (HLWs) as a generalization of optical Bessel-like needle beams. Here we report on the progress in this field. In contrast to pulsed Bessel beams and Airy beams, ultrashort-pulsed HLWs propagate with high stability in both spatial and temporal domain, are nearly paraxial (supercollimated), have fringe-less spatial profiles and thus represent the best possible approximation to linear “light bullets”. Like Bessel beams and Airy beams, HLWs show self-reconstructing behavior. Adaptive HLWs can be shaped by ultraflat three-dimensional phase profiles (generalized axicons) which are programmed via calibrated grayscale maps of liquid-crystal-on-silicon spatial light modulators (LCoS-SLMs). Light bullets of even higher complexity can either be freely formed from quasi-continuous phase maps or discretely composed from addressable arrays of identical nondiffracting beams. The characterization of few-cycle light bullets requires spatially resolved measuring techniques. In our experiments, wavefront, pulse and phase were detected with a Shack-Hartmann wavefront sensor, 2D-autocorrelation and spectral phase interferometry for direct electric-field reconstruction (SPIDER). The combination of the unique propagation properties of light bullets with the flexibility of adaptive optics opens new prospects for applications of structured light like optical tweezers, microscopy, data transfer and storage, laser fusion, plasmon control or nonlinear spectroscopy.

1. Introduction

The localization of ultrashort and ultrabroadband pulses in spatial and temporal domain is a challenge for ultrashort pulse laser physics because of the fundamental aspects as well as the enormous application potential, e.g., in microscopy, spectroscopy or optical communication, to mention only a few. In particular, a stable propagation of localized wavepackets over large distances requires an appropriate mechanism to continually compensate for the divergence. This can be obtained by balancing dispersion and diffraction effects as known from soliton formation [1,2,3,4].

In 1990, Silberberg predicted the possibility of simultaneous spatial and temporal self-focusing in a homogeneous medium leading to the existence of nondispersing, nondiffracting optical pulses which he referred to as “light bullets” [5]. During the recent years, the conditions for the formation of certain types of light bullets were studied theoretically and experimentally (for an extensive review on the state of the art, see ref. [6]). Most of these papers were focused on the specific interactions of light and a medium and can be separated in two basically different approaches: (a) nonlinear light bullets and (b) linear light bullets. While this main stream of works evolved from nonlinear optics (preferentially of fibers and waveguides), a quite other approach to linear light bullets already existed in the frame of general wave physics and provided, in reverse direction, new impetus straight back to the soliton theory. The essential difference to abovementioned methods is that no medium is required, i.e., the light bullets can be shaped and propagated also in vacuum without complicated constraints with respect to dispersion functions, and their features are therefore found to be much more distinct and stable in propagation. Here we will discuss this particular new class of linear optical bullets more in detail. We present our most recent results including the adaptive generation, characterization and application of near infrared ultrashort-pulsed Bessel-like needle beams, highly localized wavepackets and complex nondiffracting patterns at pulse durations corresponding to just a few cycles of the optical field.

2. Linear Light Bullets

2.1. Medium-Free Generation of Linear Light Bullets

The search for stable, non-spreading solutions of wave equations for electromagnetic waves like those of Maxwell, Schroedinger or Helmholtz type, quantum mechanic wave functions and acoustic waves resulted in wave phenomena called “undistorted progressive” [7], “diffraction-less” [8,9,10] or “localized waves” [11]. Among the propagation-invariant solutions is the important Bessel beam which is characterized by a radially symmetric intensity profile following the square of a zero-order first kind Bessel function. The perfect theoretical monochromatic Bessel beam has an unlimited depth of focus (DOF) and consists of an infinite number of concentric rings surrounding a central maximum in all transversal planes. Practical realizations, however, work with conical phase elements (axicons) of finite diameter. In this case, the DOF and the number of fringes is limited. In frame of ultrasound studies it was found that the spatio-spectral interference of pulsed conical waves with large spectral bandwidths leads to the formation of X-shaped waves (X-waves) [12,13]. In their maximum, Bessel-X-pulses can reach giant intensities by focusing the energy in space and time. Optical Bessel-X-waves were first shaped with high pressure lamps of few-fs coherence time with conical axicons and indicated by cross correlation experiments [14]. Ultrashort-pulsed Bessel-X-pulses were demonstrated by shaping pulses of a Ti:sapphire laser with transparent and reflective thin-film axicons and detecting the characteristic features by spatially resolved autocorrelation [11,15,16].

In contrast to other types of linear light bullets, the generation of optical X-pulses does not require a dispersive medium. The bullet structure, i.e., the spatial and temporal confinement and propagation invariance, is the result of a linear superposition and constructive interference of many contributing spectral modes with approximately identical angular spectra. It has to be noticed that an analogous effect might contribute to the spontaneous generation of extreme water waves (rogue or monster waves), in regions of deep ocean water which can not simply be explained by shallow water models (the similarity was addressed in [17], p. 193). Conti et al. extended the X-wave concept to the nonlinear regime [18,19]. The spontaneous generation of nonlinear X-waves was first experimentally demonstrated in [20]. For linear, normally dispersive media, a certain class of finite energy light bullets was identified which allows arbitrary spatio-temporal profiles [21]. Recently, several variations of linear and nonlinear light bullets emerged in the literature, most of which are close relatives of Bessel beams, e.g., Mathieu [22], Airy [23], Pearsey [24], Weber [25], or Helmholtz beams [26]. It was found that such beams are self-healing after distortion (for the self-reconstruction of Bessel-X-pulses, see [11]). This results from the subsequent constructive interference of conical waves which continues again behind a shadow zone. The detailed theoretical interpretation of nondiffracting wave phenomena is still a subject of discussion.

2.2. Ambiguity of the Poynting Vector Maps of Nondiffracting Beams

Free-space light bullets raise the question about an adequate definition of “propagation” and “beam” in the Fresnel domain. The use of both terms is not trivial here because in most cases the detected spatial patterns represent time-integrated photon density distributions instead of Poynting vector maps or wavefronts. If the propagation is analyzed on the basis of energy flux, the description has a close relationship to such measuring conditions [27,28]. A Poynting vector, however, indicates the directional energy flux density per unit area. The local wavefront of a Bessel-like beam results from the interference of two or more partial waves. If one places a Shack-Hartmann wavefront sensor in a Bessel beam, the conical shape of the wavefront [29] and, in combination with a diffractive grating, the spectral phase [30] can be reconstructed. The focal spot of each microlens splits into a ring, as follows from the analysis in [31]. In other words, the sensor which normally delivers a Poynting vector at each position resolves the local ambiguous structure of the wavefront which is more realistic than a formal but physically meaningless vector addition. To illustrate this specific ambiguity in comparison to other types of beams, one can imagine a simplified ray representation in Fresnel domain as schematically drawn in Figure 1. It has to be mentioned that in the extreme near-paraxial case of ultra-small conical angles, the different vectors in WS₂ tend to become nearly identical again so that a wavefront-division based detection technique can be well applied to characterize the beams. This is of relevance to the experiments we will report on.

Particular types of beams like Airy beams are often described as accelerating light bullets propagating on “curved trajectories”. Airy beams were originally introduced by Berry and Balazs as a particular nonspreading solution of the 1D-Schroedinger equation [32,33] and later extended to the 3D-case [34]. They have to be interpreted as caustics [32] rather than as propagating along a bended pathway. Vectorial, nonparaxial types of accelerating beams as recently discussed [35] are sometimes believed to be able to go around a corner (see Figure 2 of ref. [36]) or even to propagate along a circle [37]. To establish bended beams, however, the straight trajectories of all constituting partial beams are necessary (compare [38]) whereas the obstruction by a shading edge distorts the field pattern behind (except in a medium with a gradient index). In medium-free case, the physical significance of this statement can directly be proved by detecting the far field which separates the directional components of the partial waves. The same should apply to Airy-type and other nondiffracting beams. To stay in concordance with the conservation laws of energy and momentum, one has to carefully examine the unambiguity of the Poynting vector maps of accelerating beams (e.g., in [35]) in a similar way as shown for Bessel beams (for a theoretical treatment of the Poynting vector maps of Airy beams, see [39,40,41]). We agree with the related comment in ref. [42]: “As with the Bessel beam's diffraction -free “propagation”, light doesn't actually propagate along the curved path.”

Figure 1. Ambiguity of local wavefronts of nondiffracting beams in comparison to a convergent beam (simplified ray representation): (a) Gaussian-type beam with unambiguous Poynting vectors (red arrows) as detected by a Shack-Hartmann wavefront sensor at a certain plane WS₁ (gray); (b) Bessel beam with an ambiguity in the superposition zone WS₂ (gray) and a ring-shaped unambiguous angular distribution at a distance WS₃ behind the superposition zone (gray). Linear light bullets in absence of a medium are created by constructive interference in superposition zones like shown in (b).

Figure 1. Ambiguity of local wavefronts of nondiffracting beams in comparison to a convergent beam (simplified ray representation): (a) Gaussian-type beam with unambiguous Poynting vectors (red arrows) as detected by a Shack-Hartmann wavefront sensor at a certain plane WS₁ (gray); (b) Bessel beam with an ambiguity in the superposition zone WS₂ (gray) and a ring-shaped unambiguous angular distribution at a distance WS₃ behind the superposition zone (gray). Linear light bullets in absence of a medium are created by constructive interference in superposition zones like shown in (b).

Figure 2. Intensity profiles of (a) a Bessel and (b) a needle beam schematically represented for an arbitrary plane perpendicular to the propagation axis (color-coded, red = maximum intensity, green = minimum intensity). Needle beams correspond to Bessel beams which are truncated exactly at the first zero (self-apodized truncation).

Figure 2. Intensity profiles of (a) a Bessel and (b) a needle beam schematically represented for an arbitrary plane perpendicular to the propagation axis (color-coded, red = maximum intensity, green = minimum intensity). Needle beams correspond to Bessel beams which are truncated exactly at the first zero (self-apodized truncation).

Irrespective of their continuous recreation along curved envelope surfaces of caustics, all kinds of accelerating light bullets promise novel and intriguing applications. A key problem to be solved, however, is the limited spatial localization of Bessel- and Airy-type beams because of their fringe structure. We will return to this issue soon in section 2.4.

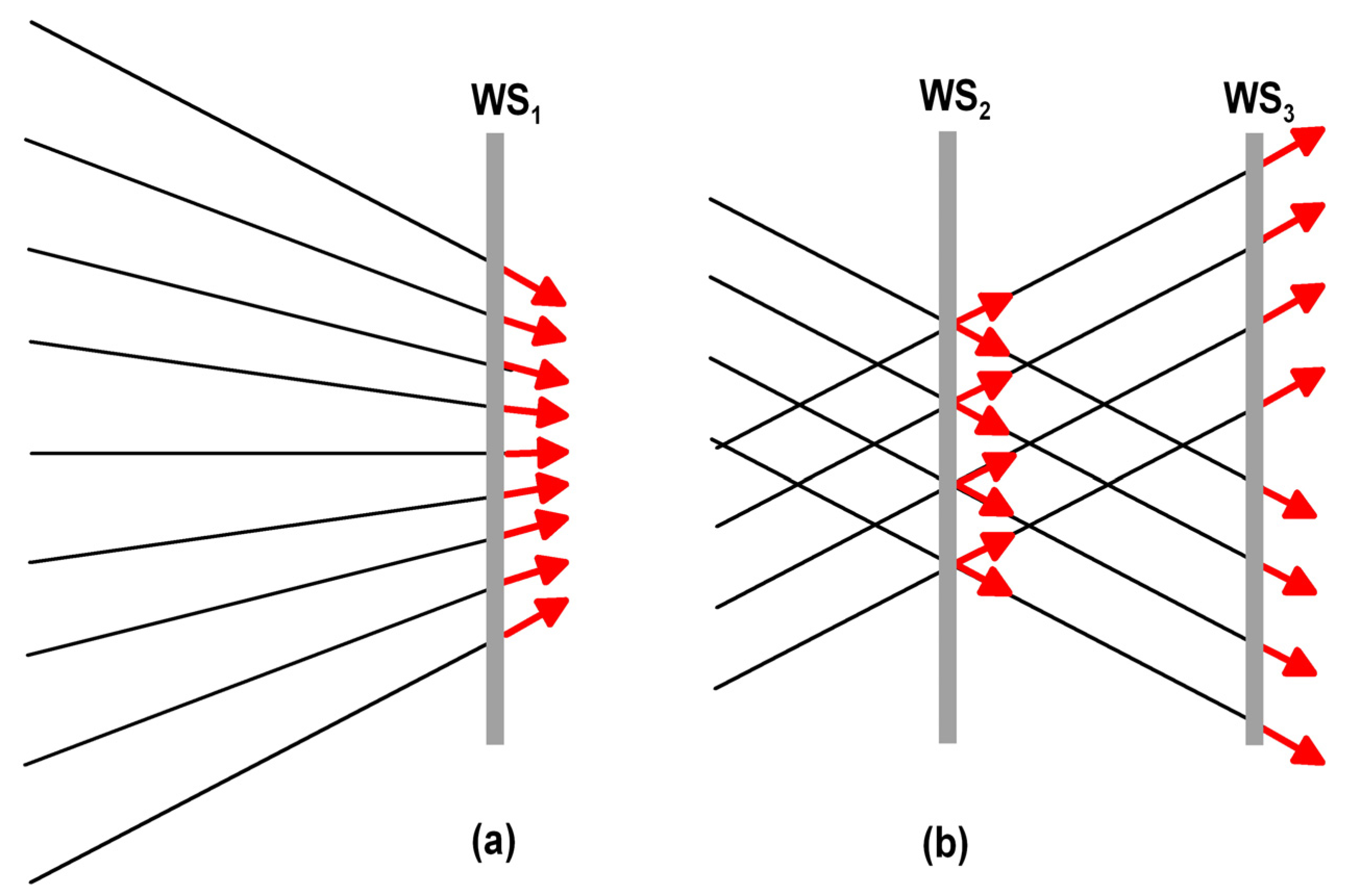
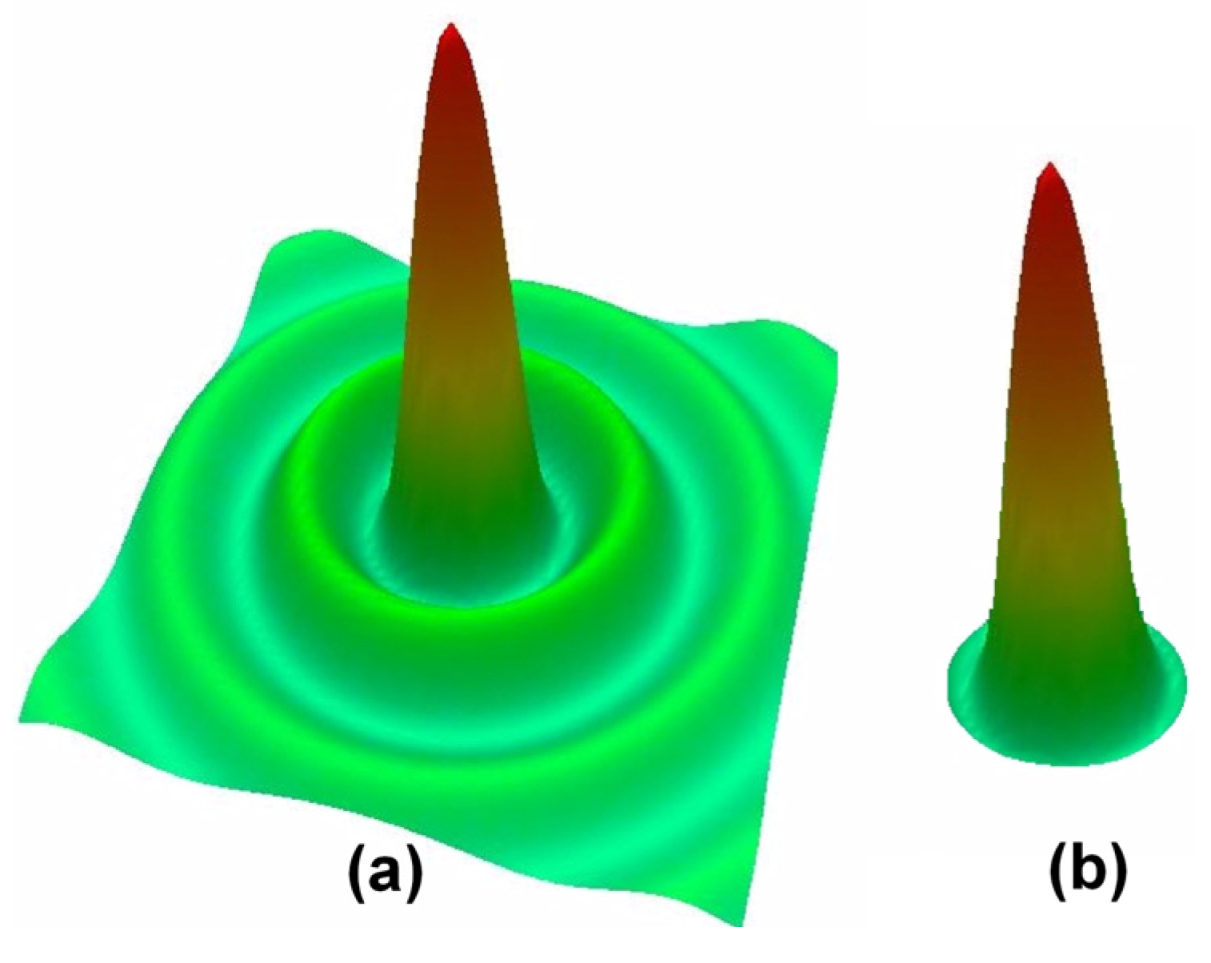
2.3. Nonlinear and Linear Light Bullets: Brief Remark on the Terminology

Further confusion is caused by the double application of the term “nonlinear” (i) for media with nonlinear optical constants (e.g., in [18]) and (ii) for a mathematically nonlinear (e.g., parabolic) phase distribution function as programmed into spatial light modulators to generate Airy beams (e.g., in [23]). In our case, the term “linear bullets” simply implies the absence of a nonlinear medium within the nondiffracting propagation zone whereas the generating phase functions are flexible and can (but does not have to) approximate conical shapes.

2.4. Pulsed Needle Beams and Highly Localized Wavepackets

The vast majority of free-space nondiffracting beams including Bessel beams and Airy beams still contains a considerable part of their energy in the outer fringes. In case of Bessel beams, this can be circumvented in two ways: (A) by downstream spatial filtering in a self-apodizing truncation setup, i.e., matching a diaphragm to the first zero of the intensity distribution so that the central lobe passes without diffraction (but wasting the energy of the fringes) [17,43], or (B) in aperture-less setup by optimizing the parameters (conical angle, waist radius of the input profile) to only generate this central lobe exactly to the first zero (fulfilling a self-apodizing condition [43,44]). Because of the distinct needle-shape, this particular type of paraxial single-maximum Bessel-like beams was referred to by us as “needle beams” [17,43,44]. To illustrate that, Figure 2b show the intensity distribution functions of a Bessel beam and a needle beam in a transversal plane, respectively. The aperture-less case for self-apodizing geometrical boundary conditions (B) can be found in Figure 3.

Figure 3. Self-apodized truncation condition for the aperture-less Bessel-like needle pulses (schematically, after ref. [44]). Curve on the separated blue plane: radial Bessel intensity profile, red area: central lobe, white area: not generated outer parts (Λ = diameter of central lobe, z = propagation axis, D = axicon diameter, θ_max = maximum allowed half conical angle, Δz_min = minimum extension of the needle-shaped nondiffracting zone, J₀ = zero order first kind Bessel function).

Figure 3. Self-apodized truncation condition for the aperture-less Bessel-like needle pulses (schematically, after ref. [44]). Curve on the separated blue plane: radial Bessel intensity profile, red area: central lobe, white area: not generated outer parts (Λ = diameter of central lobe, z = propagation axis, D = axicon diameter, θ_max = maximum allowed half conical angle, Δz_min = minimum extension of the needle-shaped nondiffracting zone, J₀ = zero order first kind Bessel function).

The length of the interference zone z_max is determined by the finite diameter D of the initial transversal field under self-apodized conditions [44]. For a wavelength λ, it amounts roughly to

z_max = D²/4λ

(1)

For ultrashort pulses it is an enormous benefit if the spectral and temporal corruption of the outer Bessel fringes (resulting from different delay times of the locally interfering conical waves) is minimized. Special kinds of pulsed Bessel beams were discussed as temporally propagation-invariant localized waves [45,46]. After equation (7) in [45], the field amplitude U_NB of the pulsed needle beam can be represented (after some transformation) by the following Equations (2)–(7):

(2)

with

(3)

(4)

(5)

(6)

(7)

where t, r and k are the time, the radial coordinate and the wave number, θ and λ are the cone angle and the wavelength, q is an integration variable, c is the speed of light in vacuum, J₀(r,k_r) represents a wavelength-dependent Bessel distribution function in radial direction, Φ(r,t) is a complex phase term, τ_a a radial-dependent time separation between two interfering pulses and τ₀ an input pulse duration (standard deviation). In good approximation, one can replace the integral in Equation (3) by the expression

(8)

In our case of a free-space (dispersion-free), axicon-generated Bessel-like beam with an extremely narrow angular spectrum, the temporal invariance results from approximately equal optical path of all contributing conical parts at all distances. Therefore, pulsed needle beams can justifiably be called not only spatially nondiffracting but temporally nondiffracting as well. This makes them interesting for applications where a stable pulse transfer is required. For example, we demonstrated the undistorted ultrafast cross-talk-free transfer of image information (“flying images”) which was encoded into arrays of needle beams [46,47].

Starting from this fundamental finding we generalized the spatially oscillation-free structure of rotationally symmetric pulsed needle beams to non-symmetric geometries by geometrical transforms (linear magnification, eccentric rotations [48,49]). The main target of these studies was to find a set of non-circular light bullets which also remain their temporal pulse shape during the propagation so that they can be used as building blocks for flying images of higher complexity in comparison to 2D arrays of needle beams. In the previous experiments, we studied the spatio-temporal propagation of tubular and line-shaped linear light bullets and simple composed nondiffracting images at pulse durations between 10 and 20 fs at laser wavelengths around 800 nm. Here we extend the approach to even more complicated spatially structured wavepackets with pulse durations down to the sub-3-cycle range (6 fs).

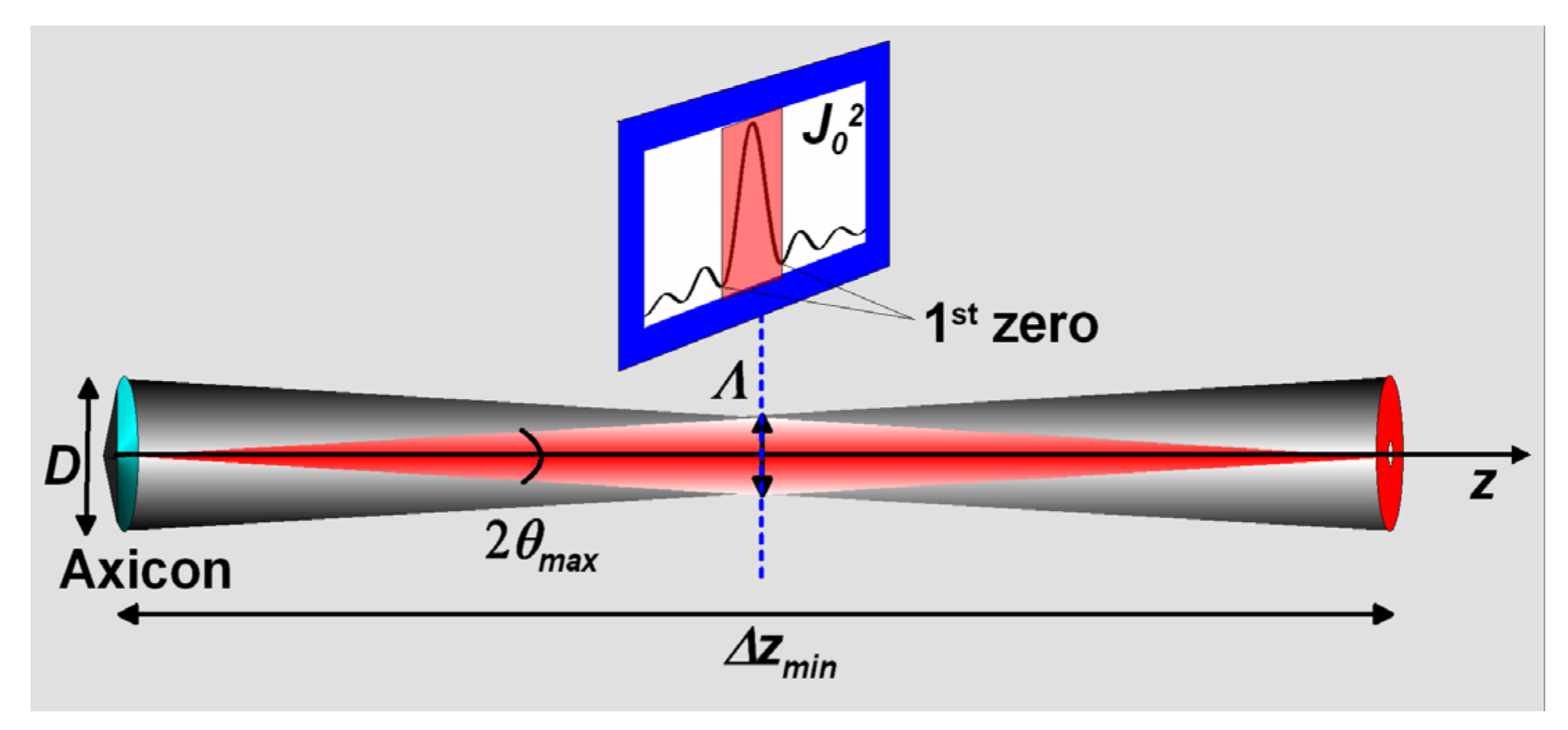
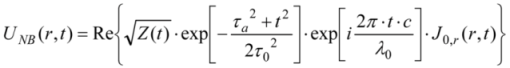
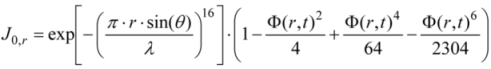
3. Experimental Section

In the literature it was pointed out that the generation of X waves in a linear system “requires non-trivial input shaping techniques that involve the use of dispersive elements such as the axicon” ([4]). Our experiments were performed with a Ti:sapphire laser oscillator (Venteon PULSE: ONE PE, pulse duration around 6.5 fs, FWHM bandwidth 300 nm, center wavelength 800 nm, repetition rate 80 MHz, pulse energy > 7 nJ, linearly polarized) as light source and a programmable liquid-crystal-on-silicon spatial light modulator (LCoS-SLM, HoloEye, 1920 × 1200 pixels, pixel size 8.1 μm) as flexible beam shaper. It was found that few-cycle pulses of Ti:sapphire laser oscillators are transferred by the low-dispersion SLMs with only marginal temporal distortions [50]. The SLM can flexibly emulate the phase maps of axicons via calibrated grayscale patterns and works in reflection. We demonstrated that an adaptive correction of tilt-induced spatial aberrations can be obtained by programming linear transformations. In this way, tilt-induced beam ellipticity was compensated at angles of incidence up to 50°. The setup is schematically drawn in Figure 4. Single and multiple light bullets were generated with the SLM. For the spatial and temporal characterization of the light bullets, the combination of a Shack-Hartmann geometry (based on the division of the wavefront into separated channels) and a collinear nonlinear autocorrelator is used. In this case, a primary light bullet can be decomposed into an array of sub-bullets to ensure a clear separation of local parameters by avoiding an overlap during the propagation. The basic approach of such a time-wavefront sensor was recently described in detail in [51].

The light bullets were analyzed by combining the shaper with a 2D second order nonlinear autocorrelator consisting of a balanced interferometer, a nonlinear crystal and a matrix camera with zoom lens. The spectral phase was measured with few-cycle spectral phase interferometry for direct electric field reconstruction (FC-SPIDER, APE). To enable for working at low intensities down to the single-photon level, intensity profiles were analyzed with a highly sensitive electron-multiplying charge coupled device (EMCCD) camera (iXon, Andor). Second harmonic generation (SHG) was performed in thin BBO crystals (thickness 10–20 μm). The long effective lever arms formed by the extended needle-shaped nondiffracting zones lead to a high angular sensitivity of the system. Therefore, the setup enables not only to extract spatially resolved pulse duration via image autocorrelation but also wavefront curvature and vortex characterization [52]. Furthermore it was demonstrated that a time delay mapping with sub-fs resolution is possible by a relative measurement of the arrival times of light bullets in spatially separated channels [39].

Figure 4. Experimental setup for adaptive shaping and detection of paraxial linear few-cycle light bullets (schematically). For collinear autocorrelation, a balanced interferometer generates two identical replica of the pulse. The variable time delay (Δτ) is induced by the length variation (Δz) of the interferometer arm with a piezo actuator. The SLM shapes the light bullets in finite but extended zones of stable nondiffracting propagation. The combination with second order nonlinear conversion and 2D detection enables to extract spatially resolved pulse duration via image autocorrelation, as well as wavefront curvature, vortex characterization, and highly resolved time delay mapping.

Figure 4. Experimental setup for adaptive shaping and detection of paraxial linear few-cycle light bullets (schematically). For collinear autocorrelation, a balanced interferometer generates two identical replica of the pulse. The variable time delay (Δτ) is induced by the length variation (Δz) of the interferometer arm with a piezo actuator. The SLM shapes the light bullets in finite but extended zones of stable nondiffracting propagation. The combination with second order nonlinear conversion and 2D detection enables to extract spatially resolved pulse duration via image autocorrelation, as well as wavefront curvature, vortex characterization, and highly resolved time delay mapping.

4. Results and Discussion

By adaptively programming phase maps via calibrated gray value maps of symmetric and non-symmetric axicons into the LCoS-SLM, corresponding types of linear light bullets were generated and their spatio-temporal features were analyzed. The solitary or multiple light bullets are of radially symmetric and non-symmetric structure belong to the classes of above discussed pulsed needle beams and highly localized wavepackets (HLWs). Figure 5 shows the gray value distributions corresponding to the phase maps of the axicons (left) and the resulting, measured time-integrated intensity maps (right) of a set of simultaneously formed light bullets of different spatial structures (here: disks, rings, lines and stadiums). All of these light bullets have two important properties in common which are the main benchmarks of HLWs: (1) They are non-oscillating in space (i.e., they have no side wings), and (2) they preserve the temporal properties during the nondiffracting propagation.

Figure 5. Flexible generation of few-cycle light bullets with the characteristics of spatially oscillation-free, temporally nondiffracting highly localized wavepackets (HLWs): (a) gray value distributions corresponding to the phase maps of axicons; (b) measured time-integrated intensity maps of a set of simultaneously formed light bullets of different spatial structures in a transversal plane (disks, lines, rings and stadiums). Both the new types of shaping phase elements and the HLWs represent generalizations of the conventional approaches of axicons and nondiffracting beams, respectively. Arrays of programmable HLWs enable to realize time-wavefront sensors with spatially encoded spots and flexible array geometries.

Figure 5. Flexible generation of few-cycle light bullets with the characteristics of spatially oscillation-free, temporally nondiffracting highly localized wavepackets (HLWs): (a) gray value distributions corresponding to the phase maps of axicons; (b) measured time-integrated intensity maps of a set of simultaneously formed light bullets of different spatial structures in a transversal plane (disks, lines, rings and stadiums). Both the new types of shaping phase elements and the HLWs represent generalizations of the conventional approaches of axicons and nondiffracting beams, respectively. Arrays of programmable HLWs enable to realize time-wavefront sensors with spatially encoded spots and flexible array geometries.

Figure 6. Nondiffracting intensity propagation of a stadium-shaped light bullet (time integrated, field of view 2.7 × 2.7 mm², detected after SHG at 400 nm, initial pulse duration 6.5 fs).

Figure 6. Nondiffracting intensity propagation of a stadium-shaped light bullet (time integrated, field of view 2.7 × 2.7 mm², detected after SHG at 400 nm, initial pulse duration 6.5 fs).

The propagation invariance can be well recognized for a stadium-shaped 6-fs light bullet (smaller and larger diameter: 700 μm and 1500 μm, respectively) in Figure 6. From an axial distance of 80 mm to 130 mm, only a slight enhancement of the local cross-section of the light ring is observed. The basic geometrical structure, however, propagates unchanged and the outer dimensions are stable.

In Figure 7, the spatially resolved second order autocorrelation function measured by imaging autocorrelation is shown for two planar cuts through the long and short axes of the stadium-shaped bullet. The maxima clearly indicate the few-cycle field oscillation in time. The autocorrelation at three different propagation distances (80 mm, 100 mm and 120 mm) is compared in Figure 8.

Figure 7. Temporal autocorrelation function of a stadium-shaped few-cycle light bullet at a distance of 80 mm; left: cut through the major (long) axis; right: cut through the minor (short) axis.

Figure 7. Temporal autocorrelation function of a stadium-shaped few-cycle light bullet at a distance of 80 mm; left: cut through the major (long) axis; right: cut through the minor (short) axis.

Figure 8. Temporal autocorrelation function of a stadium-shaped light bullet measured at three different axial distances (80 mm, 100 mm and 120 mm). For a sech²-pulse shape, one can estimate a nearly constant pulse duration of about 6.6 fs for the propagating light bullet.

Figure 8. Temporal autocorrelation function of a stadium-shaped light bullet measured at three different axial distances (80 mm, 100 mm and 120 mm). For a sech²-pulse shape, one can estimate a nearly constant pulse duration of about 6.6 fs for the propagating light bullet.

The FWHM width of the autocorrelation function was found to be about 10.1 fs. Assuming a sech²-pulse shape, the corresponding final pulse duration is 6.6 fs at an input pulse duration of 6.5 fs. Thus, the results indicate a very stable propagation behavior also in temporal domain within the fluctuations (the estimated error bar was about 0.1 fs). In another experiment, the spectral phase of a circular light bullet (pulsed needle beam, depth of the nondiffracting zone 1 m) was characterized with few-cycle spatially integrated spectral phase interferometry for direct electric field reconstruction (FC-SPIDER, Figure 9). The retrieved final pulse duration (τ_M = 6.4 fs) was found to be within the error bar as well.

Figure 9. Phase transfer in a circular nondiffracting light bullet (pulsed needle beam, length of the nondiffracting zone about 1 m), measured with an FC-SPIDER (APE); black curve: temporal phase, dashed red curve: pulse calculated for the Fourier transform limited case, blue curve: pulse retrieved from measuring data. τ_FL and τ_M are the corresponding pulse durations, respectively. The distance of the entrance window of the SPIDER from the SLM was about 20 cm (the effective distance was higher because of the additional internal path in the SPIDER system). The diameter of the light bullet at the entrance of the SPIDER was 1 mm.

Figure 9. Phase transfer in a circular nondiffracting light bullet (pulsed needle beam, length of the nondiffracting zone about 1 m), measured with an FC-SPIDER (APE); black curve: temporal phase, dashed red curve: pulse calculated for the Fourier transform limited case, blue curve: pulse retrieved from measuring data. τ_FL and τ_M are the corresponding pulse durations, respectively. The distance of the entrance window of the SPIDER from the SLM was about 20 cm (the effective distance was higher because of the additional internal path in the SPIDER system). The diameter of the light bullet at the entrance of the SPIDER was 1 mm.

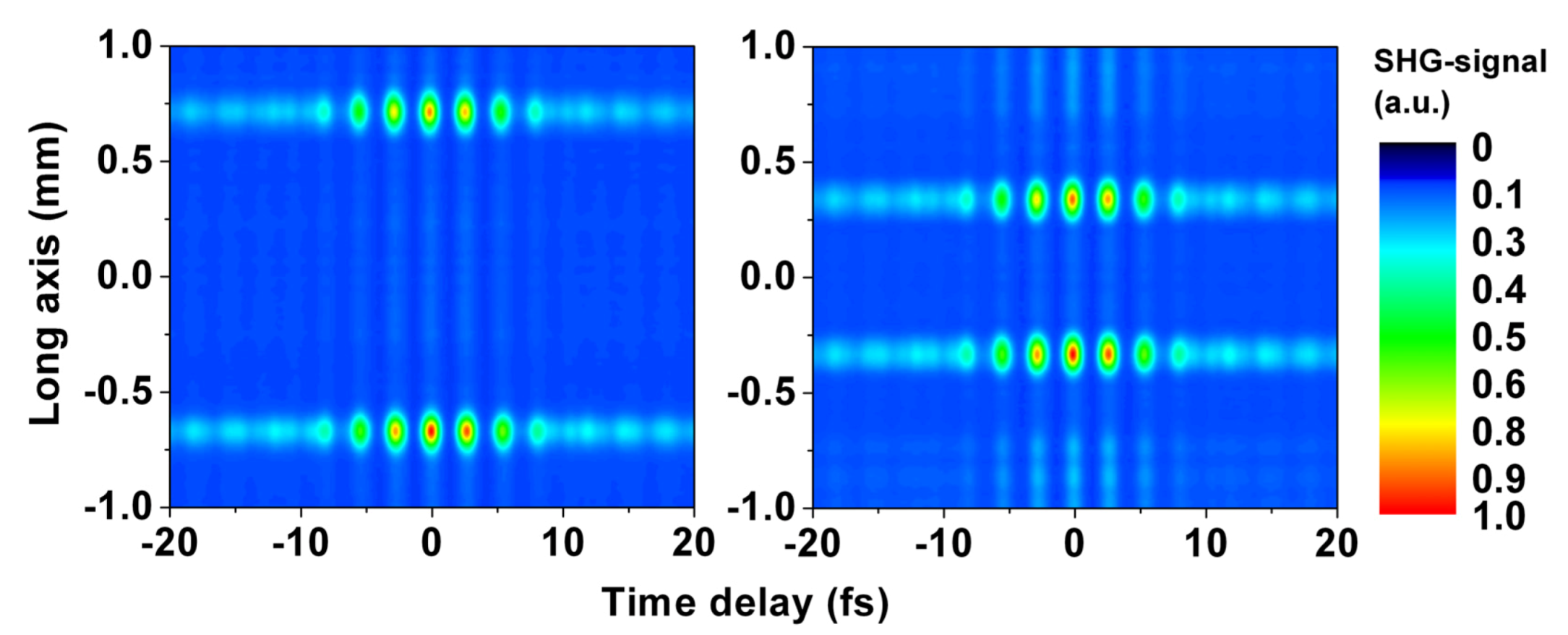
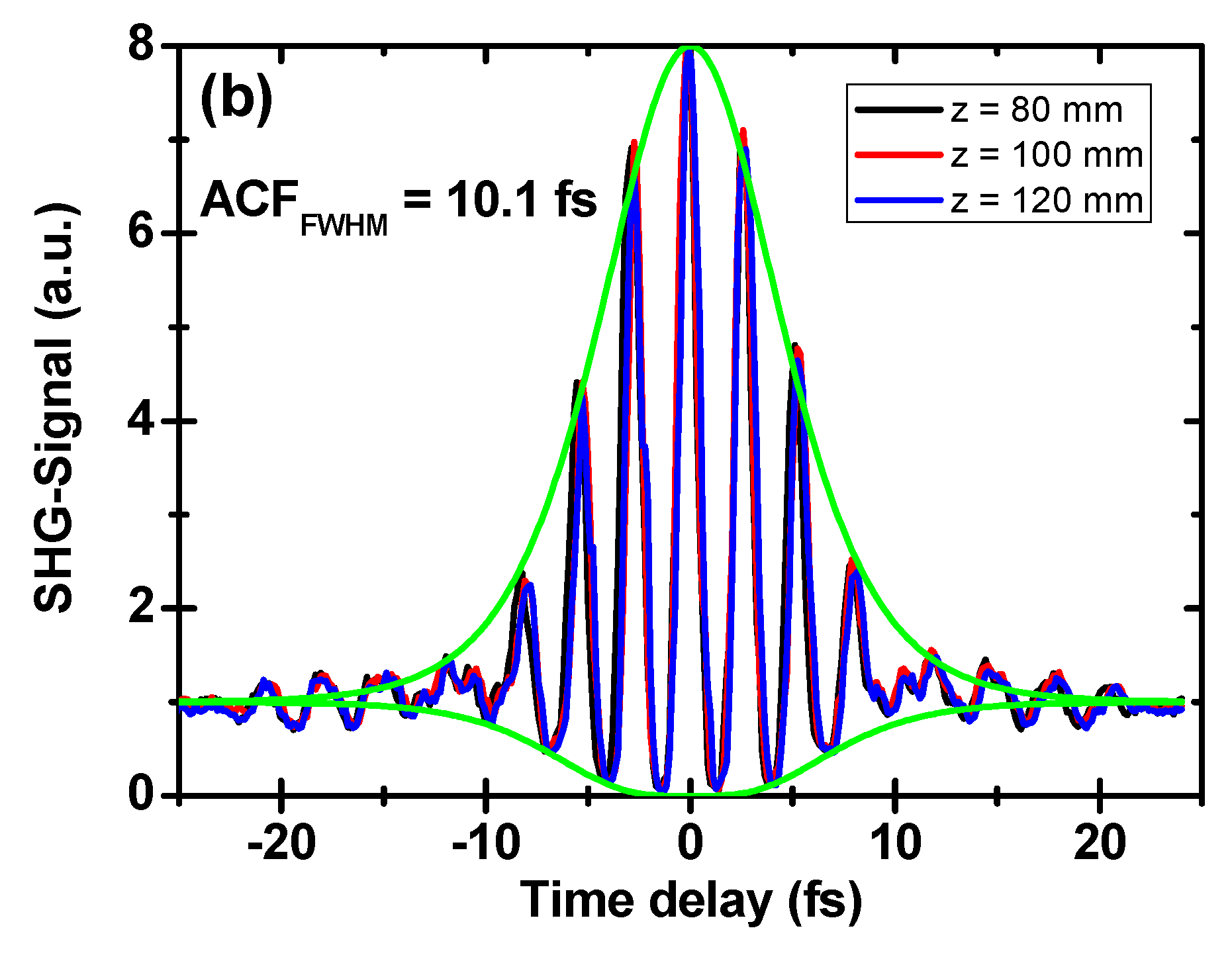
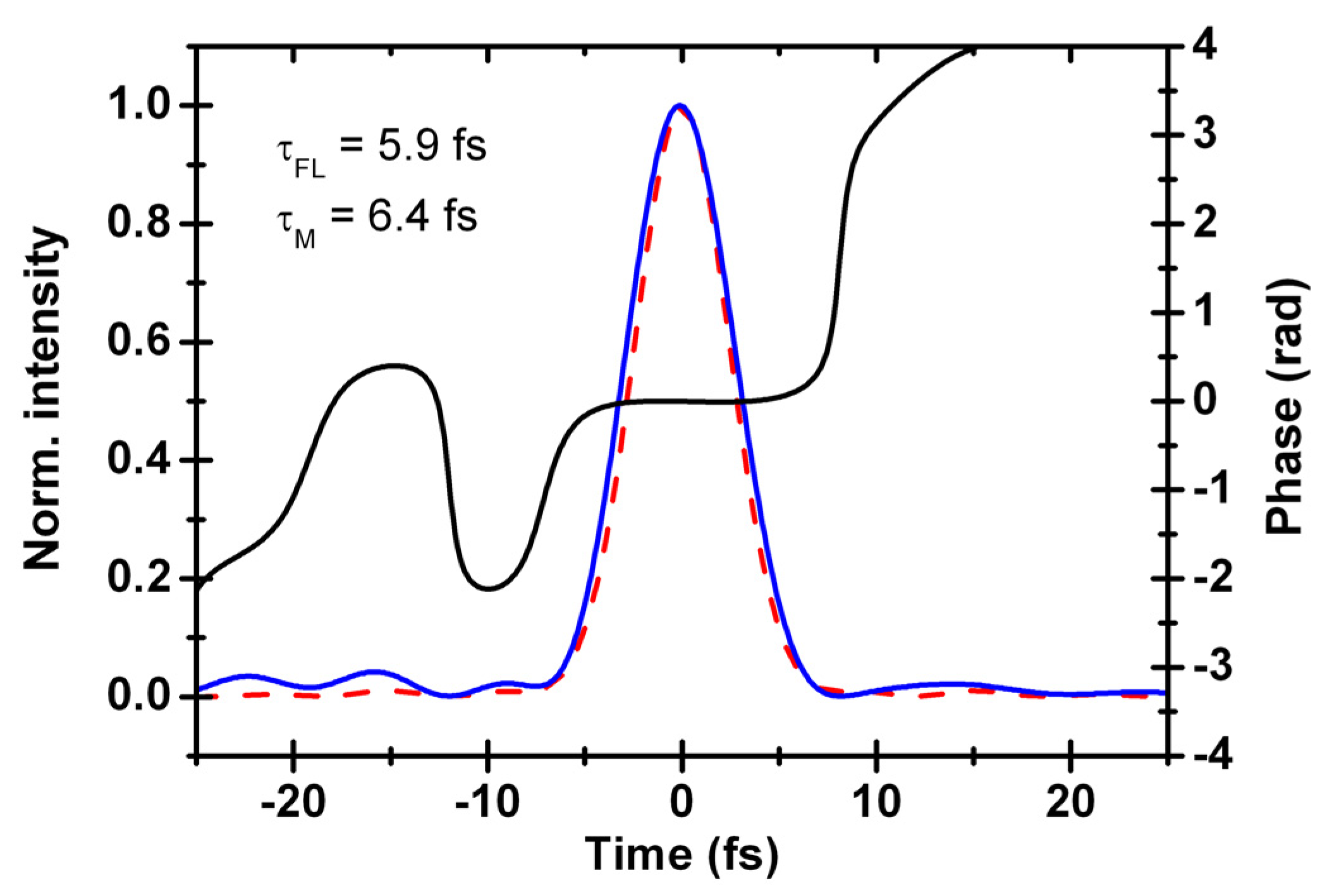
5. Conclusions

To conclude, we have shown that a particular type of linear light bullets representing generalized pulsed Bessel-like needle beams or “highly localized wavepackets” (HLWs) [41] can be generated from few-cycle pulses without the need of a dispersive medium. Therefore, the shaping procedure is basically very straight forward because it has not to take into account a time-variant optical system and thus reduces to an optimization of the linear space-time coupling effects. Typical instabilities of nonlinear processes (as known, e.g., from filaments) are avoided. The use of programmable high-fidelity SLMs enables to adaptively correct for distortions as well as for a spatial and phase-related encoding of individual light bullets. Purely reflective techniques with MEMS axicons show promise to be capable of handling even shorter pulses with pulse durations down to the attosecond scale. Thus, the shaping of carrier-envelope stabilized single-cycle pulses opens the possibility to obtain the ultimate kind of light bullets without parasitic spatial and temporal oscillations. Further future activities will be directed on the adaptive control of optical angular momenta of linear light bullets.