Adaptive Generation and Diagnostics of Linear Few-Cycle Light Bullets
Abstract
:1. Introduction
2. Linear Light Bullets
2.1. Medium-Free Generation of Linear Light Bullets
2.2. Ambiguity of the Poynting Vector Maps of Nondiffracting Beams
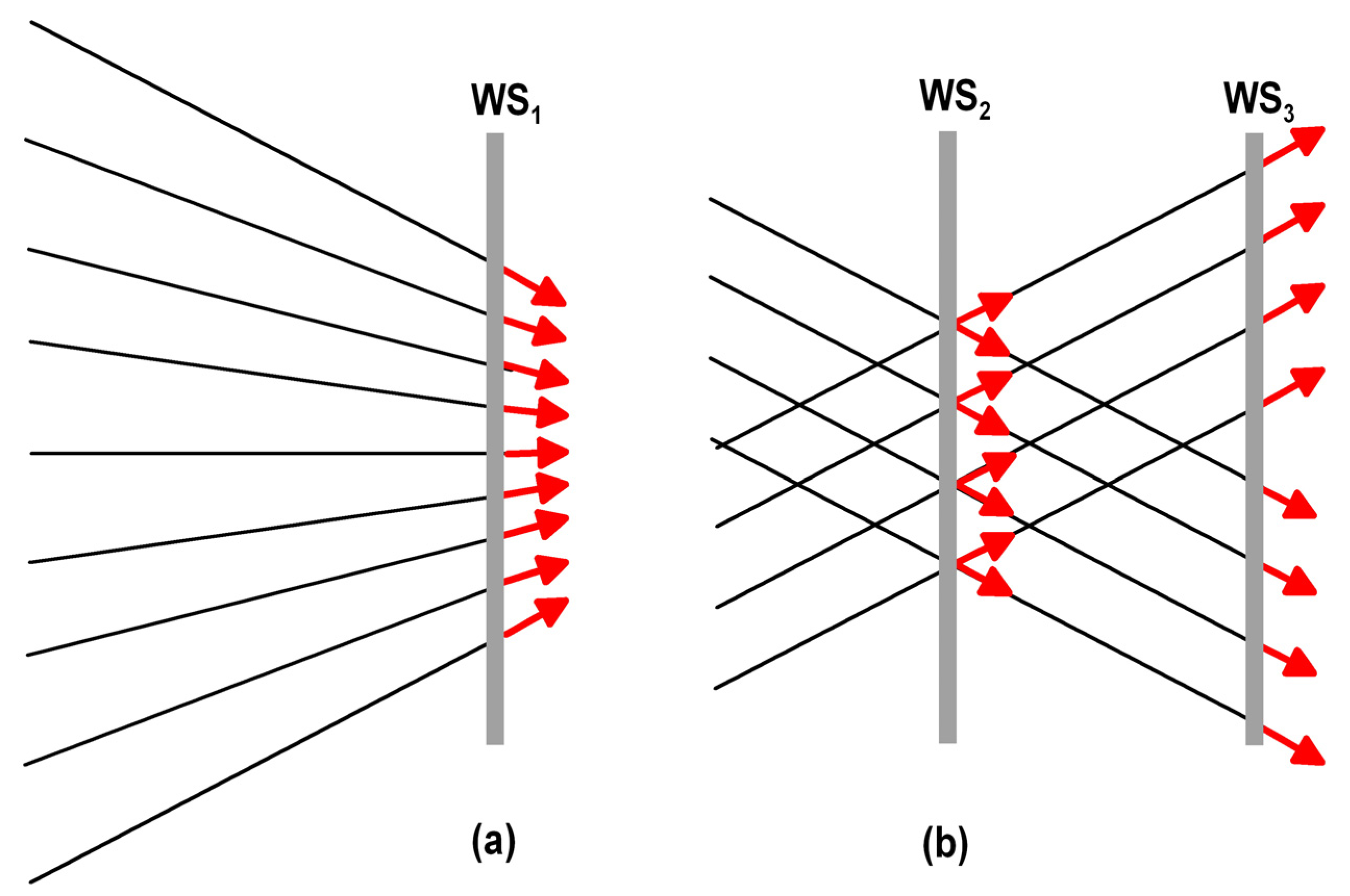
2.3. Nonlinear and Linear Light Bullets: Brief Remark on the Terminology
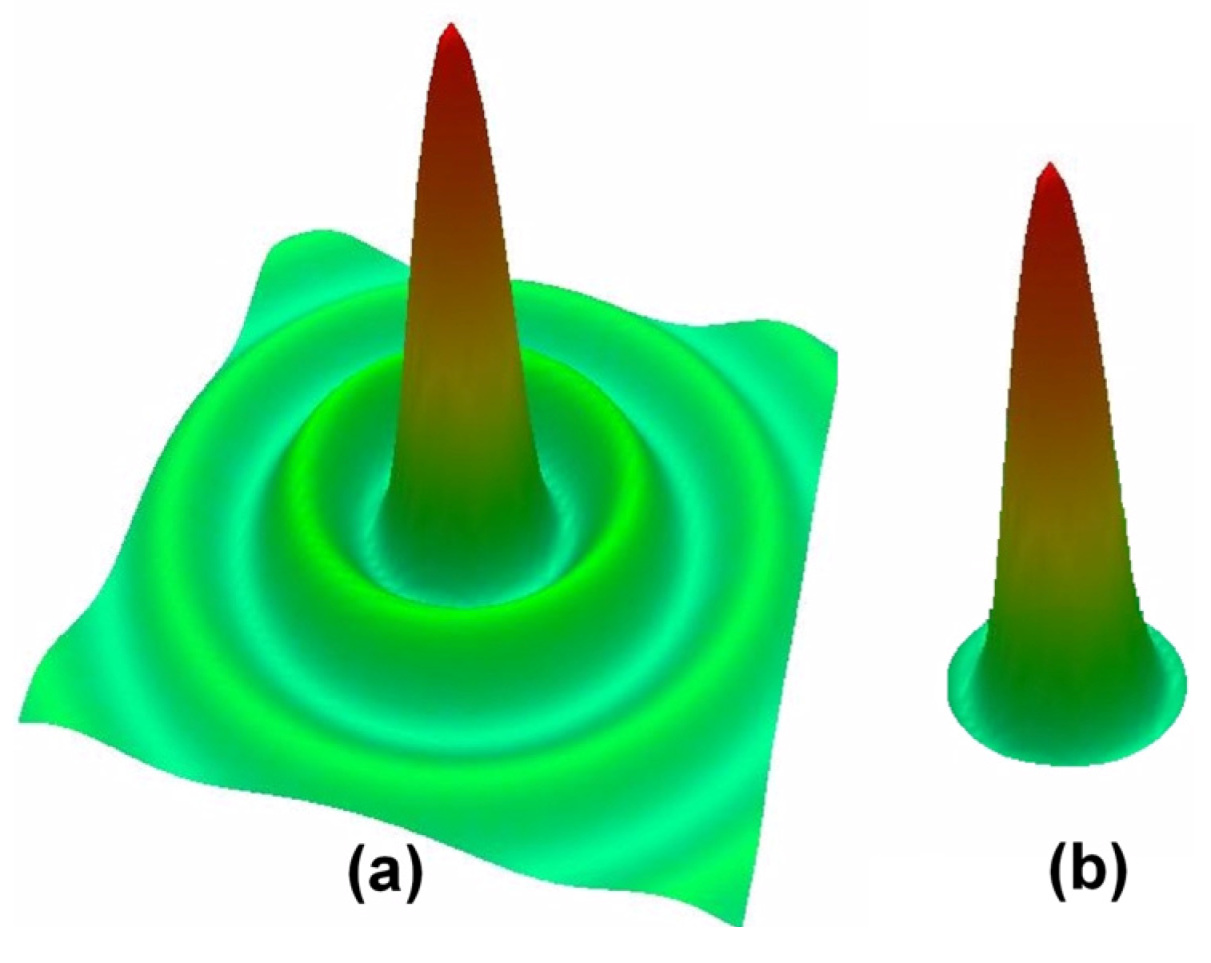
2.4. Pulsed Needle Beams and Highly Localized Wavepackets
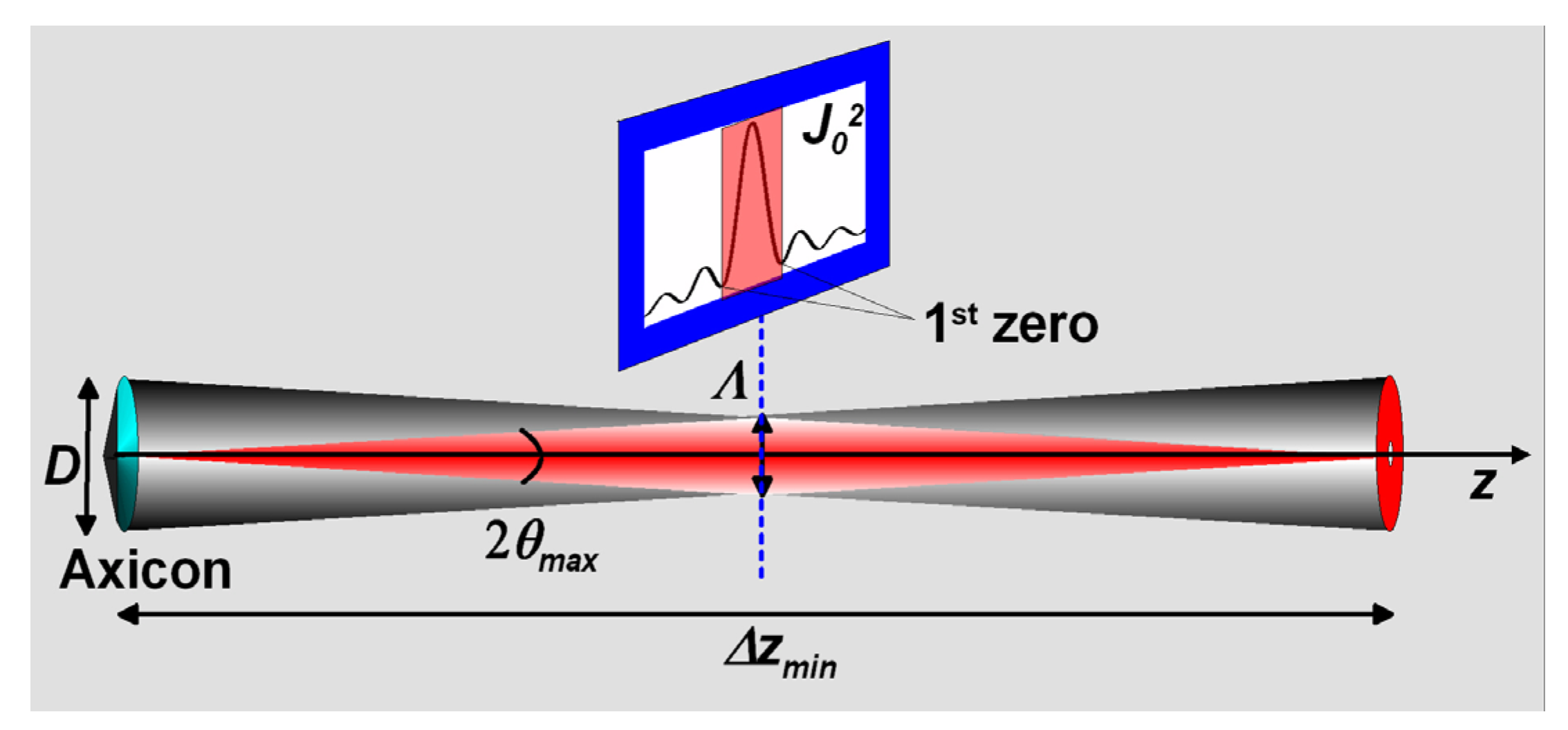
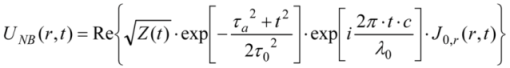
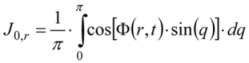
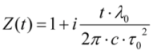
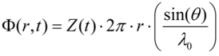
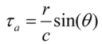

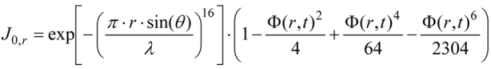
3. Experimental Section

4. Results and Discussion


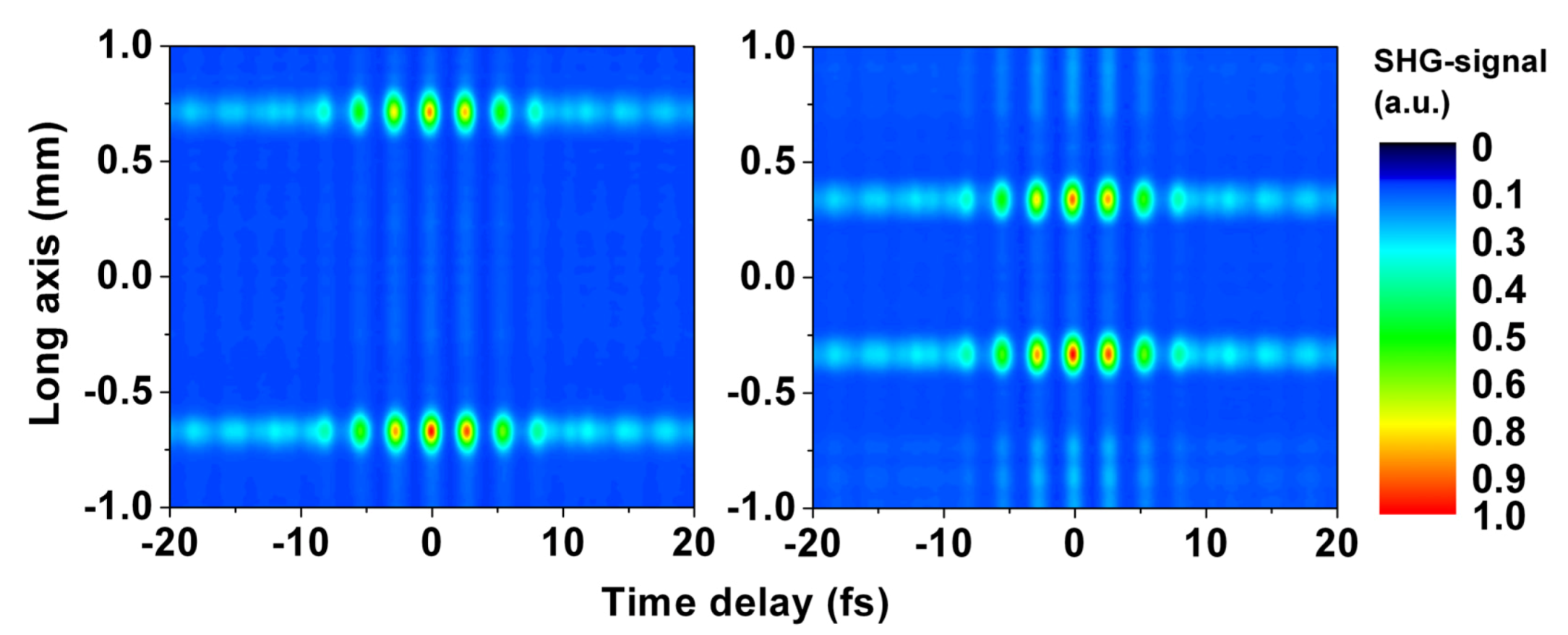
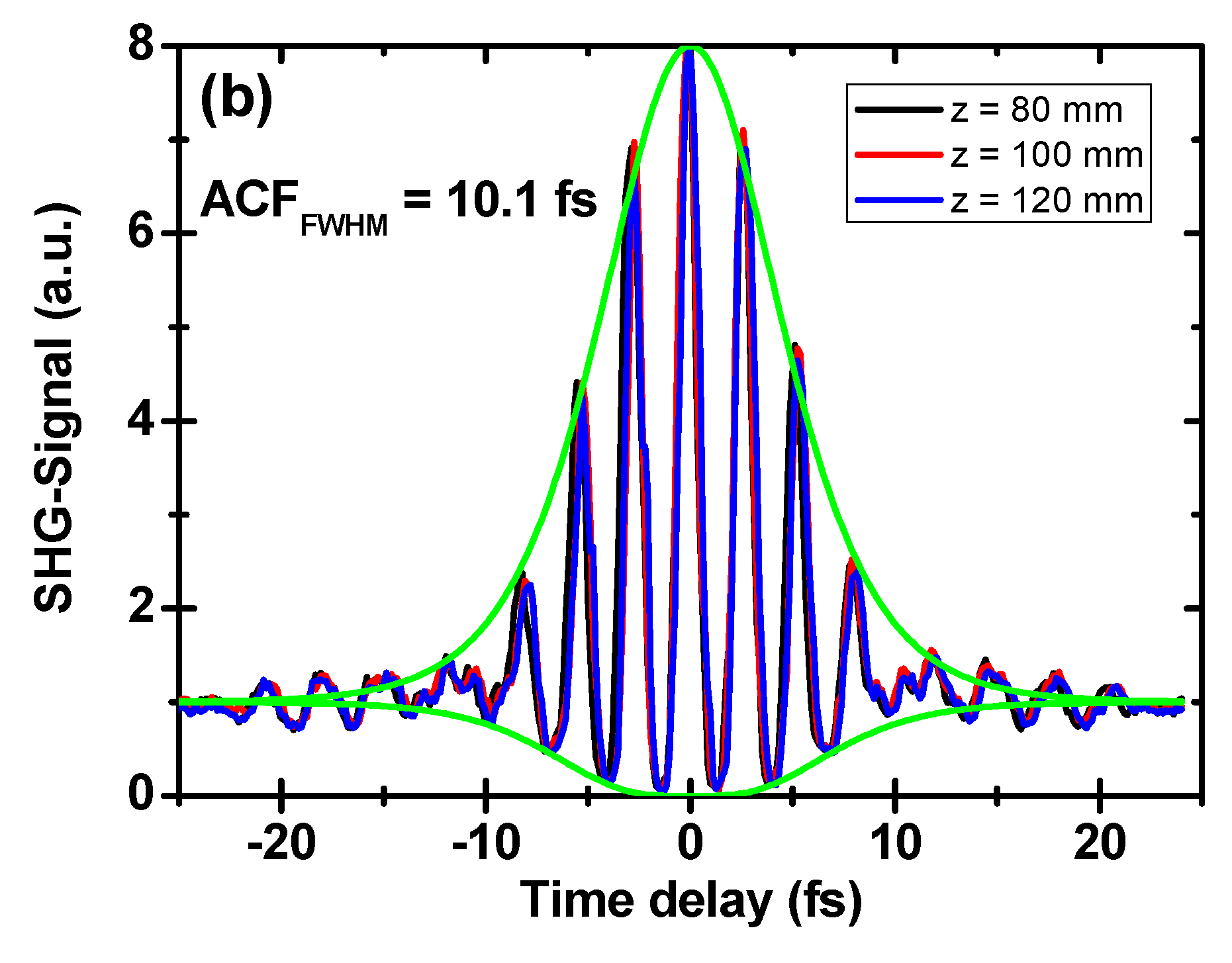
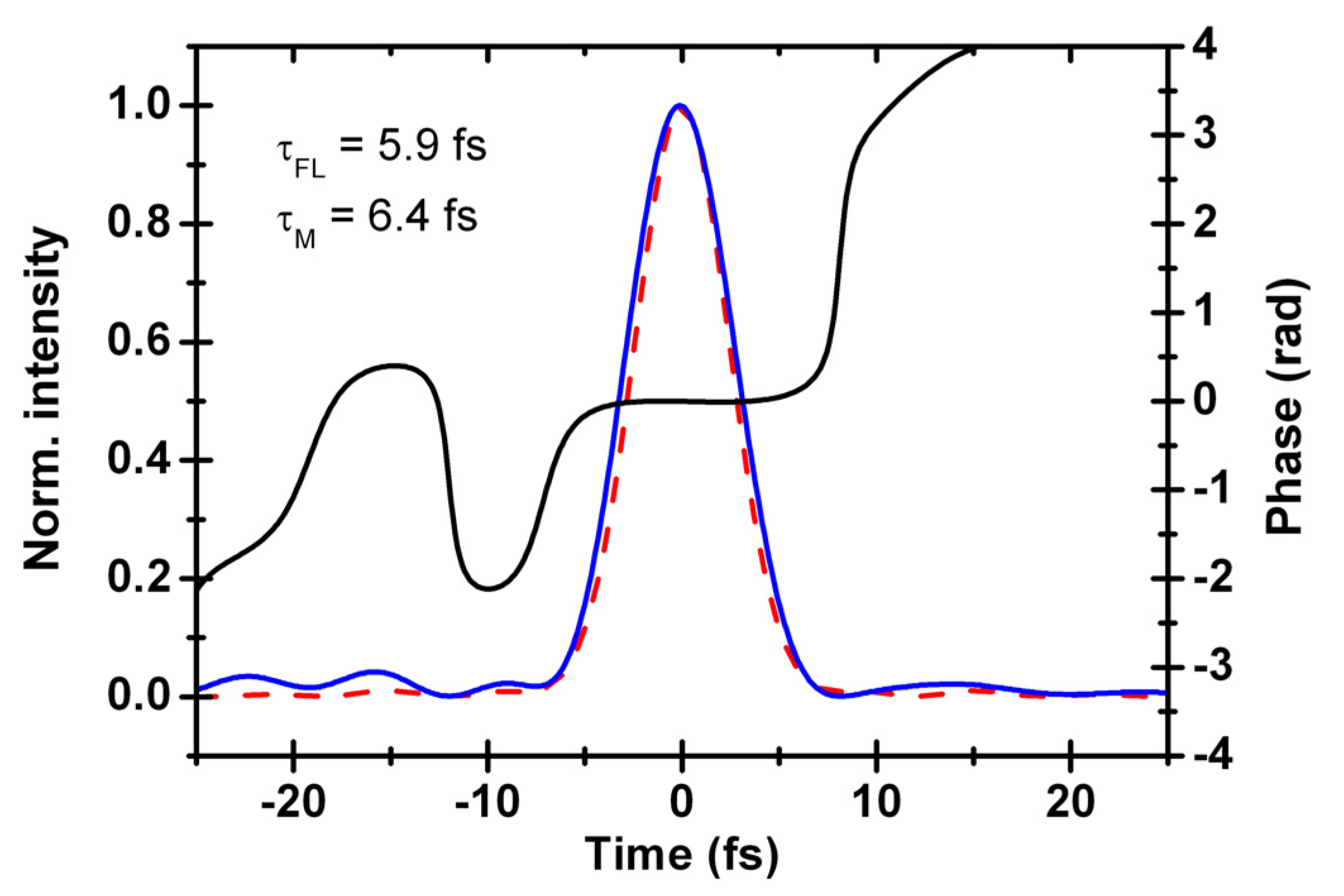
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Mollenauer, L.F.; Gordon, J.P. Solitons in Optical Fibers: Fundamentals and Applications; Elsevier-Academic Press: Amsterdam, The Netherland, 2006. [Google Scholar]
- Spatial Solitons; Trillo, S.; Torruellas, W. (Eds.) Springer-Verlag: Berlin, Germany, 2001.
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons—From Fibers to Photonic Crystals; Elsevier-Academic Press: Amsterdam, The Netherland, 2003. [Google Scholar]
- Boyd, R.W.; Lukishova, S.G.; Shen, Y.R. Self-Focusing: Past and Present; Springer Science and Business Media: New York, NY, USA, 2009; p. 451. [Google Scholar]
- Silberberg, Y. Collapse of optical pulses. Opt. Lett. 1990, 15, 1282–1284. [Google Scholar] [CrossRef]
- Mihalache, D. Linear and nonlinear light bullets: Recent theoretical and experimental studies. Rom. J. Phys. 2012, 57, 352–371. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; McGraw Hill: New York, NY, USA, 1941. [Google Scholar]
- Durnin, J. Exact solution for nondiffracting beams I—The scalar theory. J. Opt. Soc. Am. A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar]
- Turunen, J.; Friberg, A.T. Propagation-Invariant Optical Fields. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherland, 2009; Volume 54, pp. 1–88. [Google Scholar]
- Localized Waves, Theory and Experiments; Zamboni-Rached, M.; Recami, E.; Hernández-Figueroa, H.E. (Eds.) Wiley & Sons: New York, NY, USA, 2008.
- Lu, J.Y.; Greenleaf, J.F. Nondiffracting X-waves. Exact solutions to free space scalar wave equation and their finite aperture realizations. IEEE Trans. Ultrason. Ferroelec. Freq. Control 1992, 39, 19–31. [Google Scholar] [CrossRef]
- Lu, J.Y.; Greenleaf, J.F. Experimental verification of nondiffracting X waves. IEEE Trans. Ultrason. Ferroelec. Freq. Control 1992, 39, 441–446. [Google Scholar] [CrossRef]
- Saari, P.; Reivelt, K. Evidence of X-shaped propagation-invariant localized light waves. Phys. Rev. Lett. 1997, 79, 4135–4138. [Google Scholar] [CrossRef]
- Grunwald, R.; Griebner, U.; Neumann, U.; Kummrow, A.; Nibbering, E.T.J.; Piché, M.; Rousseau, G.; Fortin, M.; Kebbel, V. Generation of Ultrashort-Pulse Nondiffracting Beams and X-waves with Thin-Film Axicons. In Ultrafast Phenomena XIII; Murnane, M., Scherer, N.F., Weiner, A.M., Eds.; Springer-Verlag: New York, NY, USA, 2002; pp. 247–249. [Google Scholar]
- Grunwald, R.; Kebbel, V.; Griebner, U.; Neumann, U.; Kummrow, A.; Rini, M.; Nibbering, M.T.J.; Piché, M.; Rousseau, G.; Fortin, M. Generation and characterization of spatially and temporally localized few-cycle optical wavepackets. Phys. Rev. A 2003, 67, 063820. [Google Scholar] [CrossRef]
- Grunwald, R. Thin-Film Microoptics—New Frontiers of Spatio-Temporal Beam Shaping; Elsevier: Amsterdam, The Netherland, 2007. [Google Scholar]
- Conti, C.; Trillo, S.; di Trapani, P.; Valiulis, G.; Jedrkiewicz, O.; Trull, J. Electromagnetic nonlinear X-waves. arXiv:physics/0204066 2002. [Google Scholar]
- Porras, M.A.; Trillo, S.; Conti, C.; di Trapani, P. Paraxial envelope X waves. Opt. Lett. 2003, 28, 1090–1092. [Google Scholar] [CrossRef]
- Di Trapani, P.; Valiulis, G.; Piskarskas, A.; Jedrkiewicz, O.; Trull, J.; Conti, C.; Trillo, S. Spontaneously generated X-shaped light bullets. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef]
- Ponomarenko, S.A.; Agrawal, G.P. Linear optical bullets. Opt. Commun. 2006, 261, 1–4. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.D.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef]
- Ring, J.D.; Lindberg, J.; Mourka, A.; Mazilu, M.; Dholakia, K.; Dennis, M.R. Auto-focusing and self-healing of Pearcey beams. Opt. Express 2012, 20, 18955–18966. [Google Scholar]
- Zhang, P.; Hu, Y.; Li, T.; Cannan, D.; Yin, X.; Morandotti, R.; Chen, Z.; Zhang, X. Nonparaxial Mathieu and Weber Accelerating beams. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Aleahmad, P.; Miri, M.-A.; Mills, M.S.; Kaminer, I.; Segev, M.; Christodoulides, D.N. Fully vectorial accelerating diffraction-free Helmholtz beams. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Lotti, A.; Couairon, A.; Faccio, D.; di Trapani, P. Energy-flux characterization of conical and space-time coupled wave packets. Phys. Rev. A 2010, 81. [Google Scholar] [CrossRef]
- Faccio, D.; Lotti, A.; Matijosius, A.; Bragheri, F.; Degiorgio, V.; Couairon, A.; di Trapani, P. Experimental energy-density flux characterization of ultrashort laser pulse filaments. Opt. Express. 2009, 17, 8193–8200. [Google Scholar]
- Bonaretti, F.; Faccio, D.; Clerici, M.; Biegert, J.; di Trapani, P. Spatiotemporal amplitude and phase retrieval of Bessel-X pulses using a Hartmann-Shack sensor. Opt. Express 2009, 17, 9804–9809. [Google Scholar] [CrossRef]
- Rubino, E.; Faccio, D.; Tartara, L.; Bates, P.K.; Chalus, O.; Clerici, M.; Bonaretti, F.; Biegert, J.; di Trapani, P. Spatiotemporal amplitude and phase retrieval of space-time coupled ultrashort pulses using the Shackled-FROG technique. Opt. Lett. 2009, 34, 3854–3856. [Google Scholar]
- Lü, B.; Huang, W.; Zhang, B.; Kong, F.; Zhai, Q. Focusing properties of Bessel beams. Opt. Commun. 1996, 131, 223–228. [Google Scholar] [CrossRef]
- Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Greenberger, D.M. Comment on nonspreading wave packets. Am. J. Phys. 1980, 48, 256. [Google Scholar] [CrossRef]
- Besieris, I.M.; Shaarawi, A.M.; Ziolkowski, R.W. Nondispersive accelerating wave packets. Am. J. Phys. 1994, 62, 519–521. [Google Scholar] [CrossRef]
- Kaminer, I.; Bekenstein, R.; Nemirovsky, J.; Segev, M. Nondiffracting accelerating wave packets of Maxwell’s equations. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef]
- Chen, Z. Viewpoint: Light bends itself into an arc. Physics 2012, 5, 44. [Google Scholar] [CrossRef]
- Courvoisier, F.; Mathis, L.; Froehly, A.; Giust, R.; Furfaro, L.; Lacourt, P.A.; Jacquot, M.; Dudley, J.M. Sending femtosecond pulses in circles: Highly nonparaxial accelerating beams. Opt. Lett. 2012, 37, 736–738. [Google Scholar]
- Chremmos, Ch.; Chen, Z.; Christodoulides, D.N.; Efremidis, N.K. Abruptly autofocusing and autodefocusing optical beams with arbitrary caustics. Phys. Rev. A 2012, 85. [Google Scholar] [CrossRef]
- Sztul, H.I.; Alfano, R.R. The Poynting vector and angular momentum of Airy beams. Opt. Express 2008, 16, 9411–9416. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, G. The far field divergent properties of an Airy beam. Opt. Laser Technol. 2012, 44, 1318–1323. [Google Scholar]
- Deng, D.; Du, S.; Guo, Q. Energy flow and angular momentum density of nonparaxial Airy beams. Opt. Commun. 2013, 289, 6–9. [Google Scholar] [CrossRef]
- Wofsey, M. Focus: Light beam with a curve. Phys. Rev. Focus 2007, 20, 19. [Google Scholar] [CrossRef]
- Grunwald, R.; Bock, M.; Kebbel, V.; Huferath, S.; Neumann, U.; Steinmeyer, G.; Stibenz, G.; Néron, J.-L.; Piché, M. Ultrashort-pulsed truncated polychromatic Bessel-Gauss beams. Opt. Express 2008, 16, 1077–1089. [Google Scholar]
- Bock, M.; Das, S.K.; Grunwald, R. Programmable ultrashort-pulsed flying images. Opt. Express 2009, 17, 7465–7478. [Google Scholar]
- Saari, P.; Sõnajalg, H. Pulsed Bessel beams. Laser Phys. 1997, 7, 32–39. [Google Scholar]
- Porras, M.; Valiulis, G.; di Trapani, P. Unified description of Bessel X waves with cone dispersion and tilted pulses. Phys. Rev. E 2003, 68. [Google Scholar] [CrossRef]
- Grunwald, R.; Bock, M. Spatially encoded localized wavepackets for ultrafast optical data transfer. J. Eur. Opt. Soc. Rap. Public. 2012, 7. [Google Scholar] [CrossRef]
- Grunwald, R.; Bock, M.; Das, S.K. Light bullets, light rings and flying images: Adaptive spatial modulation of ultrashort laser pulses. KIRAN 2010, 21, 21–23. [Google Scholar]
- Bock, M.; Das, S.K.; Grunwald, R. Ultrashort highly localized wavepackets. Opt. Express 2012, 20, 12563–12578. [Google Scholar] [CrossRef]
- Bock, M.; Das, S.K.; Grunwald, R.; Osten, S.; Staudt, P.; Stibenz, G. Spectral and temporal response of liquid-crystal-on-silicon spatial light modulators. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
- Bock, M.; Das, S.K.; Fischer, C.; Diehl, M.; Börner, P.; Grunwald, R. Reconfigurable wavefront sensor for ultrashort pulses. Opt. Lett. 2012, 37, 1154–1156. [Google Scholar]
- Bock, M.; Jahns, J.; Grunwald, R. Few-cycle high-contrast vortex pulses. Opt. Lett. 2012, 37, 3804–3806. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bock, M.; Grunwald, R. Adaptive Generation and Diagnostics of Linear Few-Cycle Light Bullets. Appl. Sci. 2013, 3, 139-152. https://doi.org/10.3390/app3010139
Bock M, Grunwald R. Adaptive Generation and Diagnostics of Linear Few-Cycle Light Bullets. Applied Sciences. 2013; 3(1):139-152. https://doi.org/10.3390/app3010139
Chicago/Turabian StyleBock, Martin, and Ruediger Grunwald. 2013. "Adaptive Generation and Diagnostics of Linear Few-Cycle Light Bullets" Applied Sciences 3, no. 1: 139-152. https://doi.org/10.3390/app3010139
APA StyleBock, M., & Grunwald, R. (2013). Adaptive Generation and Diagnostics of Linear Few-Cycle Light Bullets. Applied Sciences, 3(1), 139-152. https://doi.org/10.3390/app3010139





