Redundantly Actuated Hydraulic Shaking Tables via Dual-Loop Fuzzy Control

Abstract

The vertical actuation of multi-axis seismic simulators usually requires a redundant parallel scheme for high load capacity. Due to geometric over-constraints, the internal force coupling and the nonlinear hysteresis are high; thus, waveform reproduction quality and structural fatigue may result. A displacement–force dual closed loop cooperative control mechanism can address these problems. First, a real-time kinematic model is developed to overcome the platform pose via actuator extension, and second, a dynamic force balance loop is introduced to actively redistribute the load components. In addition, a fuzzy PID controller is incorporated to optimize gain scheduling online, compensating for hydraulic nonlinearities and time-varying structural parameters. In the experiment on a 3 × 3 m 6-DOF shaking table, the presented method performs very favorably compared to traditional methods. Under broadband random excitation, the THD of acceleration waveform drops from 15.2% (single-loop control) to 3.2%, and the internal momentum oscillation amplitude is suppressed by over 70%. The results show that our proposed method eliminates internal force dependence while maintaining high precision trajectory tracking for seismic simulation.

1. Introduction

Hydraulic shaking tables are used in structural seismic testing due to their large output force, long stroke, and high velocity [1]. In 6-degree-of-freedom shaking table systems, four redundant actuators are often employed in the horizontal direction to fulfill high load capacities and stability. However, in these coupled systems, manufacturing/installation errors, asymmetric load distribution, uneven actuation forces, and the inherent nonlinear hysteresis could add extra stresses to the platform [2,3]. This results in fatigue damage of crucial parts, weak system tracking accuracy, and severely complicates the table’s ability to reproduce complex excitation waveforms [4].

The control system for shaking tables presents a number of challenges. First, the system’s multivariable highly coupled dynamics, particularly the inherent internal force couplings resulting from the Z-axis redundant actuator, impact platform posture and tracking accuracy [5]. Second, the intrinsic nonlinearity and phase lag in hydraulic systems severely impair the efficiency of traditional linear controllers under broadband excitation [6]. Finally, the time-dependent loads and the requirement for broadband excitations require the control system to be robust to these requirements.

To address these challenges, various control strategies have been developed. The Three-Variable Control (TVC) [7] is the industry standard, utilizing feedback of acceleration, velocity, and displacement to extend bandwidth. However, as a linear fixed-gain strategy, TVC lacks the adaptability to handle the strong coupling in redundant mechanisms. Iterative Learning Control (ILC) [8] excels in improving tracking for repetitive waveforms but fails to suppress instantaneous internal force coupling in non-repetitive seismic tests. Other approaches, such as the kinematic-based strategy by Guan [9] and the deformation-coupling model by Wei [10], have made progress in theoretical decoupling. Liao Yang [11] utilized sliding mode control and adaptive inverse control techniques to eliminate alien disturbance forces and compensate for system uncertainties, thereby achieving random vibration control for acceleration. To further enhance the fidelity of seismic reproduction, researchers have extensively explored advanced compensation strategies. Ren et al. [12] investigated a dual-loop hybrid control method for electro-hydraulic shaking tables, demonstrating that combining pressure feedback with displacement control can effectively improve system damping and stability. In terms of frequency-domain compensation, Ji et al. [13] developed a power-exponent feedforward method, which significantly reduces the amplitude and phase tracking errors in the high-frequency band. Similarly, Li et al. [14] introduced a jerk-based control technique, utilizing the derivative of acceleration to smooth the trajectory and reduce mechanical impact during seismic reproduction. Furthermore, intelligent optimization algorithms have been applied to controller tuning; for instance, Gao et al. [15] employed a Particle Swarm Optimization (PSO) algorithm to auto-tune the PID parameters, achieving better transient response than manual tuning. Zhang et al. [16] also proposed a hybrid control strategy for dual-shaking tables, emphasizing the importance of synchronized optimization. While they have advanced the state of the art in single-axis or decoupled control, they often treat kinematic errors and force tracking as separate problems. Consequently, they rarely address the specific ‘fighting’ issue caused by redundant actuation in multi-DOF systems, nor do they fully resolve the fundamental conflict between rigid position constraints and flexible force distribution under the influence of hydraulic nonlinearities [17].

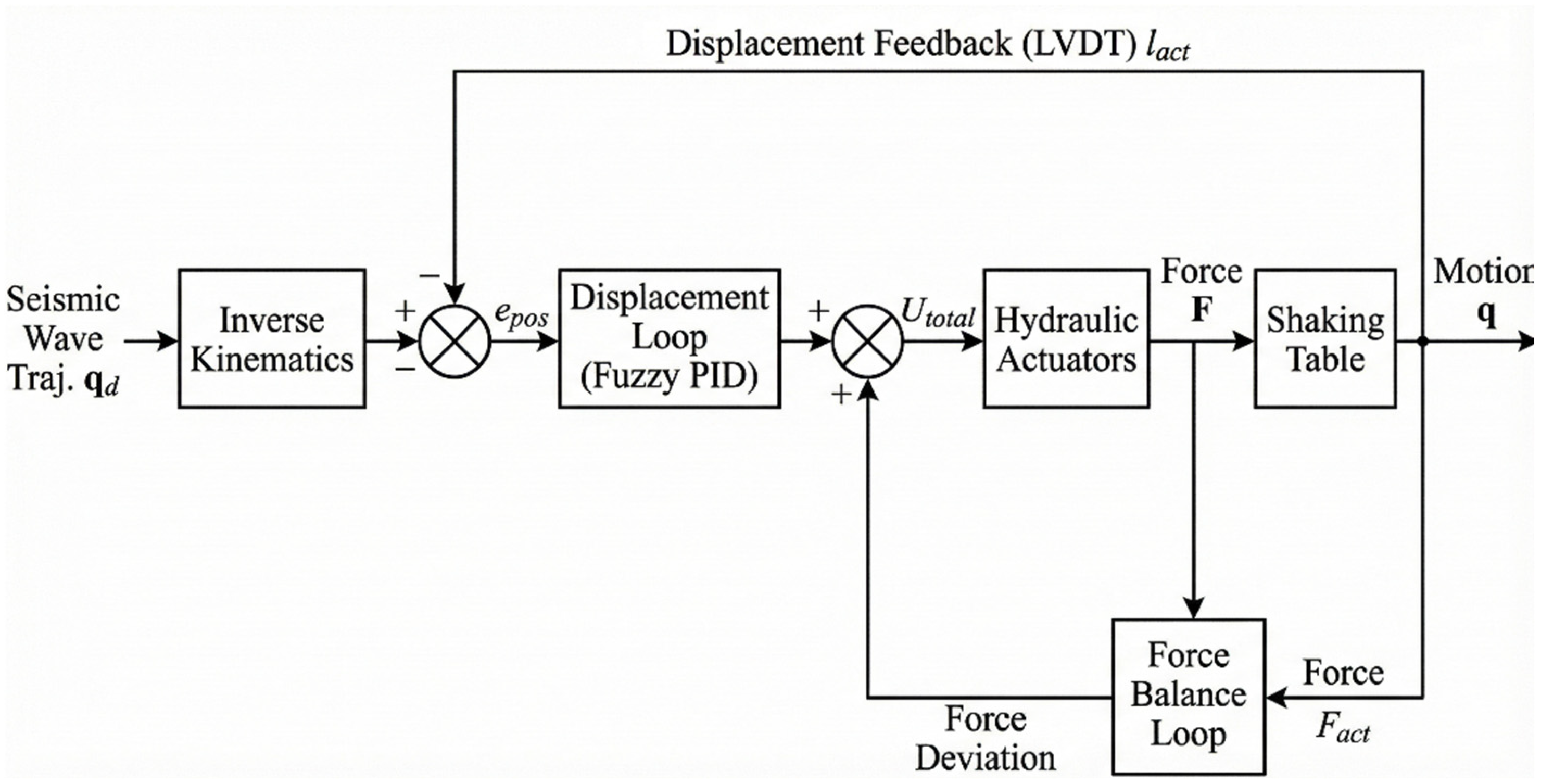
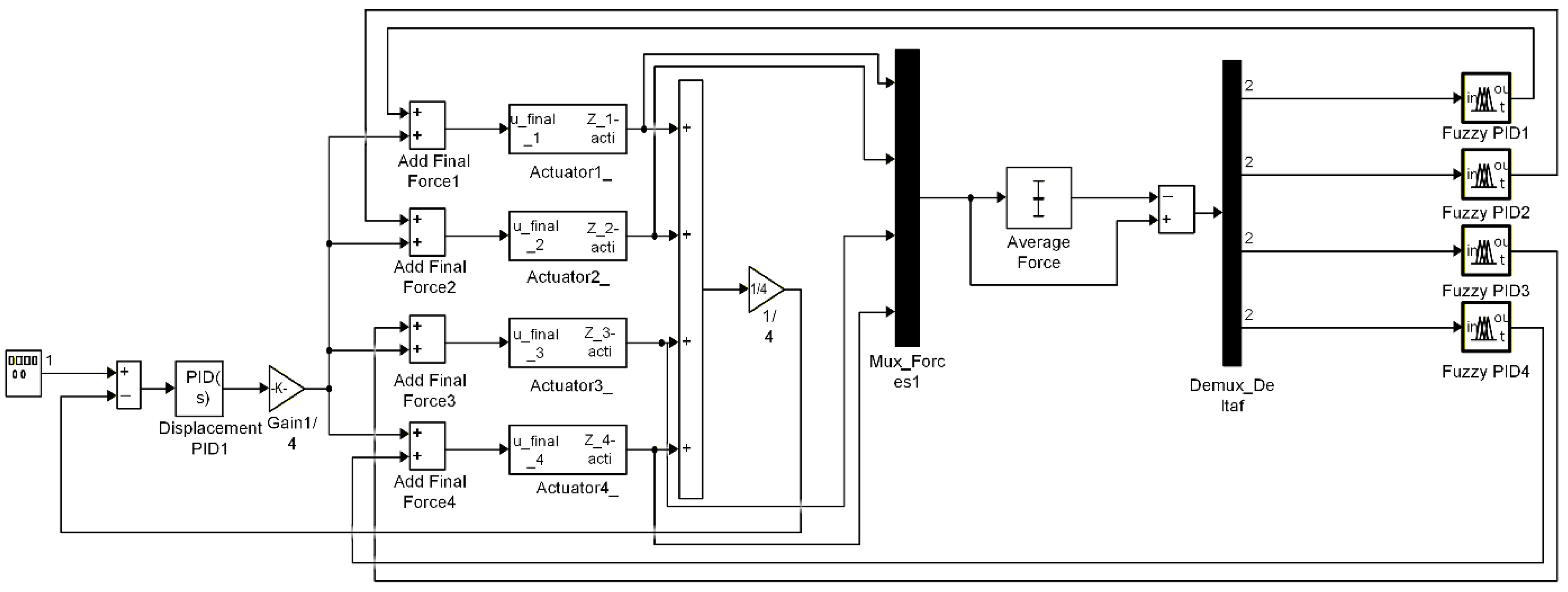
To bridge this gap, this paper proposes a displacement–force dual closed-loop cooperative control method. Unlike previous approaches that prioritize either position accuracy or force equalization, our strategy integrates a Fuzzy PID controller within a dual-loop architecture. This allows for real-time kinematic decoupling for trajectory tracking, and active compliance control for internal force minimization, thereby achieving a trade-off optimization between tracking precision and structural safety.

2. Model Construction of the Seismic Simulation Shaking Table

2.1. System Configuration and Modeling Assumptions

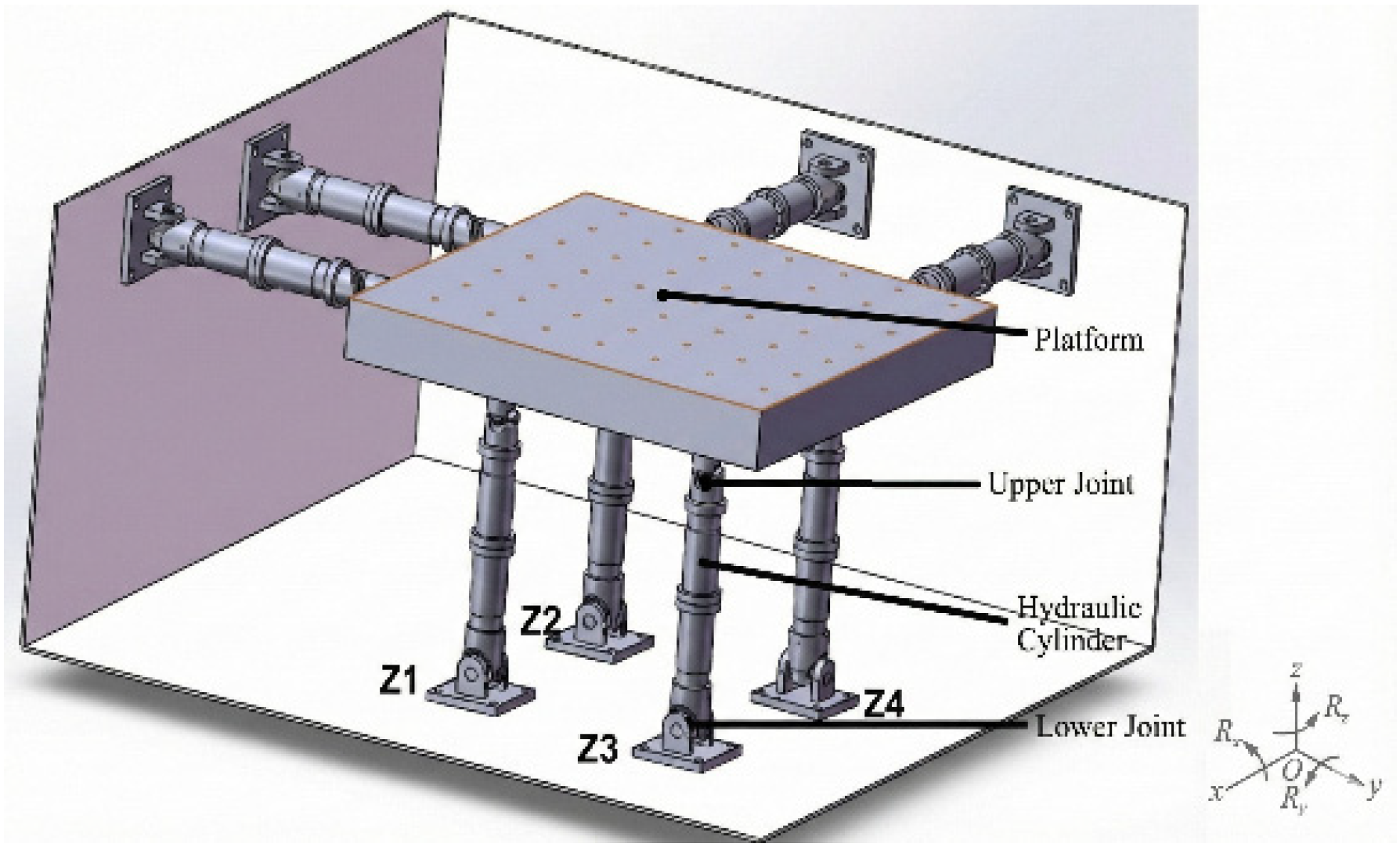
The experimental platform utilized in this study is a custom-developed 3 × 3 m 6-DOF hydraulic shaking table prototype, designed and constructed by the authors’ research group at Taiyuan University of Science and Technology. This prototype serves as a testbed for validating the proposed control strategies. The earthquake simulation system studied in this paper employs a spatially redundant parallel mechanism specifically designed for high-fidelity payload reproduction. Unlike the widely used Stewart platform (hexapod), which utilizes six inclined actuators to realize 6-DOF motion, this study adopts an orthogonal redundant actuation layout (n = 8 inputs driving m = 6 DOFs). The rationale for selecting this orthogonal configuration lies in its superior kinematic decoupling and load-carrying capacity. In a standard Stewart platform, the inclined orientation of the actuators results in strong coupling between vertical and horizontal forces. Conversely, the proposed orthogonal design allows the four vertical actuators ($Z_1-Z_4$) to directly bear the gravitational load without inducing parasitic horizontal components, thereby significantly enhancing the vertical payload capacity. Additionally, the redundant arrangement of these actuators at the four corners provides a larger resisting moment arm against overturning, which is critical for testing tall, heavy civil engineering structures that generate high overturning moments. However, this redundancy inherently introduces static indeterminacy (over-constraint), necessitating the specialized dual-loop control proposed in this study to actively manage the internal force distribution. As illustrated in the system schematic (refer to Figure 1), the actuation architecture is categorized into two decoupled functional groups. The Vertical Group consists of four actuators ($Z_1-Z_4$) symmetrically mounted underneath the table corners; these actuators support the gravitational load and govern the vertical translation ($z$), roll ($\alpha$), and pitch ($\beta$) motions. Complementing this, the Horizontal Group comprises four actuators arranged orthogonally, with two attached to Side-A (X-axis) and two to Side-B (Y-axis), which collaboratively drive the horizontal translations ($x,y$) and yaw rotation ($\gamma$).

To facilitate the mathematical derivation and ensure the tractability of the control design, several standard assumptions are adopted regarding the system dynamics. First, both the moving platform and the base are modeled as ideal rigid bodies, neglecting any elastic deformation during operation. Second, the mechanical connections between the actuators and the platform are assumed to utilize frictionless spherical joints to simplify the kinematic constraints. Finally, the bulk modulus of the hydraulic fluid and the hydraulic supply pressure are considered constant parameters throughout the dynamic analysis.

An inertial coordinate frame $O_b-X_b{Y}_b{Z}_b$ is established at the foundation center, while a moving coordinate frame is attached to the geometric center of the platform. The generalized pose vector describing the platform’s motion is explicitly defined as $q={[x,y,z,\alpha ,\beta ,\gamma ]}^T$, where $x,y,z$ denote the translational displacements along the three axes, and $\alpha ,\beta ,\gamma$ represent the rotational angles (roll, pitch, yaw) about the X, Y, and Z axes, respectively. The system is driven by eight hydraulic actuators, indexed by $i(i=1,2,\dots ,8)$, where actuators $i=1\dots 4$ constitute the vertical group and $i=5\dots 8$ constitute the horizontal group. This redundant configuration (n = 8 inputs driving m = 6 DOFs) is specifically adopted to enhance the vertical load-carrying capacity and the resistance to overturning moments compared to standard 6-actuator Stewart platforms, thereby meeting the rigorous requirements of heavy-duty seismic simulation.

2.2. Kinematic Formulation

To achieve precise mapping from the platform’s desired pose to individual actuator extensions—thereby providing setpoints for the displacement control loop—the inverse kinematics of the system must be formulated. Based on the closed-loop vector chain method, the length vector $l_i$ of the i-th actuator is expressed as:

$$l_i=t+R{p}_i-b_i,(i=1,\dots ,8)$$

(1)

where $t$ denotes the translation vector of {$O_p$}, $R$ represents the rotation matrix derived from the $Z-Y-X$ Euler angle sequence; and $p_i$ and $b_i$ are the position vectors of the upper and lower hinge points, respectively. The scalar control input is given by the Euclidean norm $l_i=‖l_i‖$.

Differentiating Equation (1) with respect to time yields the differential kinematic relationship:

$$\dot{I}=J(q)\dot{q}$$

(2)

where $J(q)\in {ℝ}^{8\times 6}$ is the system Jacobian matrix. A critical characteristic of this orthogonal configuration is that $J$ is a non-square matrix with full column rank. This geometric over-constraint (8 inputs driving 6 outputs) implies that strictly coupled constraints exist among the actuators. Theoretically, the inverse kinematic solution is unique for a rigid body; however, in practice, manufacturing tolerances and installation errors disrupt this geometric consistency, necessitating the consideration of force–level coupling.

2.3. Dynamic Modeling and Force Indeterminacy

The dynamic behavior of the platform is governed by the rigid-body equations of motion derived via the Newton–Euler formulation [18]. While the general formulation follows the standard Newton–Euler approach adapted from robotic dynamics literature, the specific force distribution model for this orthogonal redundant configuration is derived as follows. Considering the platform mass and inertia, the dynamic equilibrium in the task space is:

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)={\tau }_{gen}+{\tau }_{ext}$$

(3)

where $M(q)\in {ℝ}^{6\times 6}$ is the symmetric positive-definite inertia matrix, $C(q,\dot{q})\in {ℝ}^{6\times 1}$ represents the vector of Coriolis and centrifugal forces, $G(q)\in {ℝ}^{6\times 1}$ is the gravity vector, and $\tau \in {ℝ}^{6\times 1}$ is the generalized driving force vector acting on the DOFs.

According to the principle of virtual work, the mapping between the actuator output forces $F\in {ℝ}^{8\times 1}$ (where components $F_i$ correspond to the i-th actuator) and the generalized force ${\tau }_{gen}\in {ℝ}^6$ is established as:

$${\tau }_{gen}=J_{T}F$$

(4)

Substituting Equation (4) into Equation (3) yields the relationship between the actuator forces and the platform motion. The physical utility of this formulation is to reveal the fundamental indeterminacy of the redundant system. Since the Jacobian matrix $J^T$ is non-square ($6\times 8$), the inverse mapping from the required generalized force $\tau$ to the actuator driving forces $F$ is not unique. This mathematical property allows the actuator force vector to be decomposed into two orthogonal components: the motion-inducing force and the internal null-space force. Equation (5) below provides the mathematical basis for this decomposition, which is the theoretical foundation of the proposed dual-loop control strategy.

$$F=F_{motion}+F_{\mathrm{int}}={(J^T)}^{+}{D}_{dyn}+(I-J^T{(J^T)}^{+})\lambda$$

(5)

where ${(J^T)}^{+}$ denotes the Moore–Penrose pseudoinverse, and $D_{dyn}$ represents the total dynamic load. The first term $(F_{motion})$ represents the minimum-norm force required to drive the motion. The second term ($F_{\mathrm{int}}$) resides in the null space of $J^T$ and represents the internal forces. The vector $\lambda$ is arbitrary, indicating that infinite force combinations can produce the same motion. Without active regulation, $F_{\mathrm{int}}$ is determined uncontrolledly by structural stiffness and geometric errors, leading to the “fighting” phenomenon between actuators.

2.4. Mechanism of Z-Axis Internal Force Coupling

This study specifically targets the coupling within the Vertical Group ($Z_1\dots Z_4$). Due to the static indeterminacy described in Equation (5), the four vertical actuators form a hyperstatic structure. Ideally, the load should be distributed symmetrically. However, physical inconsistencies (e.g., sensor drift, mounting errors $\Delta l_{\mathrm{err}}$) violate the ideal constraint surface. To quantify the mechanism of ‘actuator fighting’, we establish the relationship between kinematic error and internal force.

Based on the geometric compatibility condition and Hooke’s law, the antagonistic internal force induced by a kinematic mismatch $\Delta l$ can be approximated by:

$$F_{\mathrm{int},z}\approx k_{\mathrm{oil}}\Delta l_{\mathrm{err}}$$

(6)

where $K_{oil}$ represents the equivalent stiffness of the hydraulic oil column. The utility of this formulation extends beyond physical modeling, it reveals the fundamental limitation of single-loop control. Given the high bulk modulus of hydraulic fluid, the equivalent stiffness $k_{\mathrm{oil}}$ is typically very large (>10⁷ N/m). 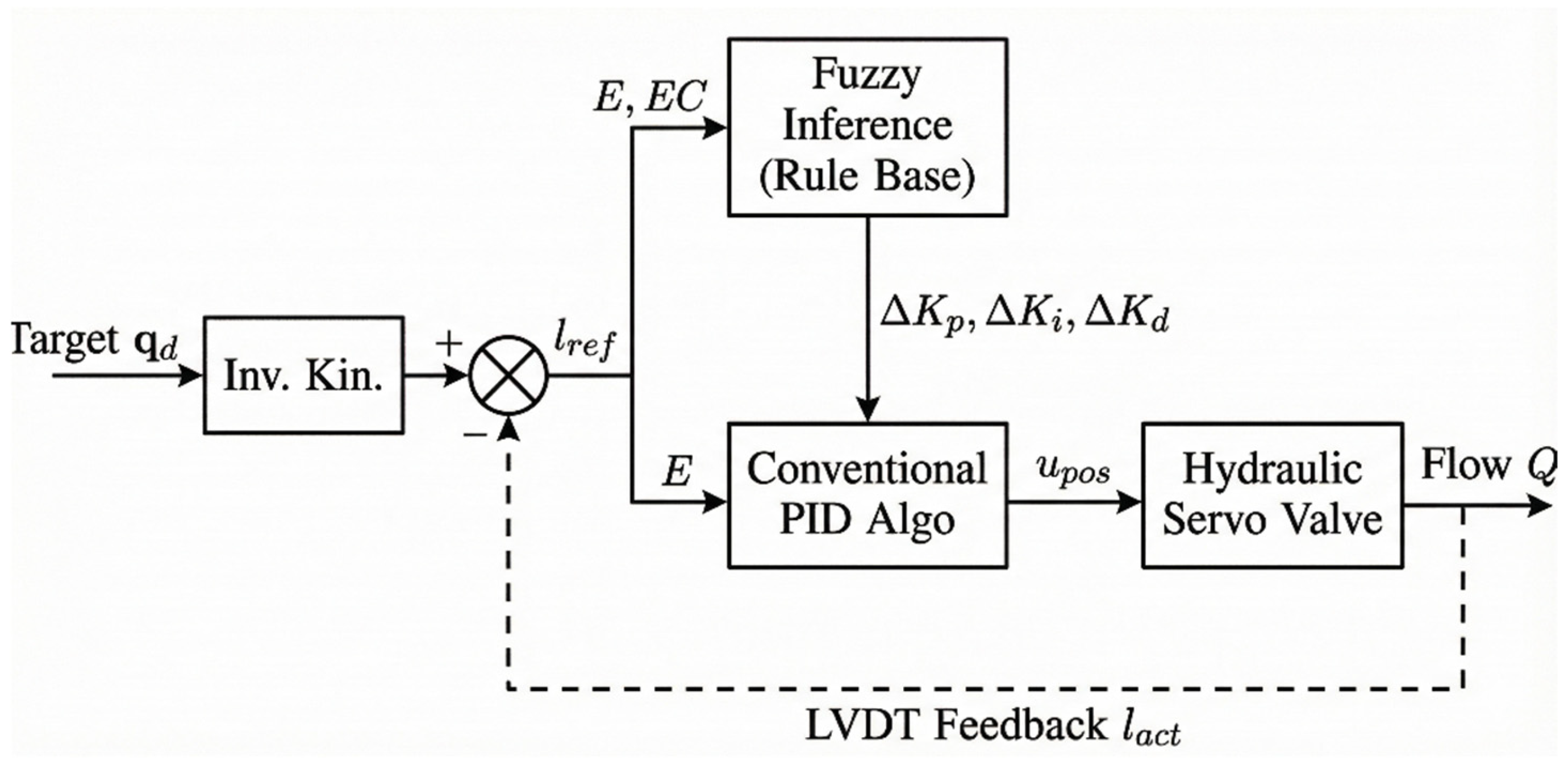Consequently, even a sub-millimeter geometric error ($\Delta l_{\mathrm{err}}$) is amplified into a significant internal force distortion. This parasitic force does not contribute to the platform motion but generates structural stress, consumes hydraulic energy, and accelerates seal wear. It is important to note that Equation (6) represents a linearized model of the force–structure interaction. In actual operation, the system exhibits complex structural non-linearities (e.g., joint friction and time-varying stiffness). Instead of establishing a high-order complex model which is difficult to identify in real-time, this study treats these unmodeled structural non-linearities as lumped disturbances. The proposed control strategy relies on the adaptive capability of the Fuzzy logic (Section 3.4) to compensate for these uncertainties online, ensuring the control robustness without requiring an explicit non-linear structural model. Therefore, the proposed dual-loop control strategy is essential to actively regulate the null-space component $F_{\mathrm{int}}$ toward zero.

2.5. Linearized Model of Hydraulic Actuator

To facilitate the control system design, the dynamics of the valve-controlled hydraulic cylinder are modeled. Each actuator is driven by a critical-center servo valve. Neglecting minor leakage and assuming the dynamic response of the servo valve is significantly faster than the hydraulic natural frequency, the linearized flow equation for the i-th actuator is given by:

$$Q_{L,i}=K_q{x}_{v,i}-K_c{P}_{L,i}$$

(7)

where $Q_{L,i}$ is the load flow, $x_{v,i}$ is the valve spool displacement, $P_{L,i}$ is the load pressure difference, $K_q$ is the flow gain, and $K_c$ is the flow-pressure coefficient.

Applying the continuity equation to the cylinder chambers yields:

$$Q_{L,i}=A_p{\dot{l}}_i+C_{tp}{P}_{L,i}+{\displaystyle \frac{V_t}{4{\beta }_e}}{\dot{P}}_{L,i}$$

(8)

where $A_p$ is the effective piston area, $C_{tp}$ is the total leakage coefficient, $V_t$ is the total control volume, and ${\beta }_e$ is the effective bulk modulus.

Finally, the force balance equation for the piston rod is:

$$A_p{P}_{L,i}=F_i+m_p{\ddot{l}}_i+B_p{\dot{l}}_i$$

(9)

where $m_p$ is the equivalent mass of the piston rod and $B_p$ is the viscous damping coefficient. Combining Equations (7)–(9), the plant model relating the valve input $x_{v,i}$ to the output force $F_i$ and displacement $l_i$ is established. This third-order hydraulic dynamics, coupled with the rigid-body dynamics derived in Section 2.3, constitutes the complete plant model for the subsequent controller design.

3. Dual-Loop Cooperative Control Strategy

3.1. Hierarchical Control Architecture

In selecting the specific non-linear compensation algorithm, we evaluated advanced data-driven approaches alongside model-free strategies. As highlighted in recent literature [19], Gaussian Process Regression (GPR) has demonstrated a high capacity to represent coupled behaviors in complex physical systems. Specifically, it enables the online estimation of hydraulic dynamics and force–structure interactions, effectively handling multi-variable dependent parameters even in the presence of experimental noise. These characteristics make GPR a powerful theoretical alternative for redundant seismic platforms. However, GPR algorithms typically involve matrix inversion operations with cubic computational complexity ($O(N^3)$), which imposes a significant burden on real-time processors. Given the hardware constraints of the experimental dSPACE DS1104 system (operating at a 1 kHz sampling rate), this study adopts the Adaptive Fuzzy PID strategy. Fuzzy logic offers a computationally efficient, ‘model-free’ mechanism to compensate for the hydraulic nonlinearities and internal force couplings derived in Section 2, achieving robust performance without the latency risks associated with heavy probabilistic learning models.

As demonstrated by the dynamic modeling in Section 2.3, the orthogonal redundant actuation system presents a fundamental challenge: the generalized solution for actuator forces comprises a motion-driving component and a redundant internal force component lying in the null space of the Jacobian transpose. Consequently, the control objective is twofold: to ensure rigorous tracking of the reference trajectory while simultaneously minimizing the antagonistic internal forces. To resolve this conflict, a displacement–force dual-loop cooperative control architecture is developed, as schematically illustrated in Figure 2.

The strategy adopts a decoupled parallel structure where the system is divided into two cooperative layers. The primary displacement loop (outer loop) operates in the task space to enforce kinematic consistency, ensuring that the platform follows the seismic waveform. Simultaneously, the secondary force balance loop (inner loop) operates in the null space to regulate force distribution. By synthesizing the control efforts from both loops, the system achieves an optimized trade-off between geometric precision and structural load equilibrium. Furthermore, to accommodate the time-varying hydraulic dynamics and structural stiffness uncertainties derived in Equation (6), an adaptive Fuzzy PID algorithm is integrated to perform real-time gain scheduling, thereby ensuring robustness across the broadband frequency range.

The stability of this dual-loop cooperative architecture is fundamentally guaranteed by the bandwidth separation principle. In the controller design, the inner force balance loop is tuned to have a significantly higher bandwidth (typically 5–10 times) compared to the outer displacement loop. This spectral separation ensures that the fast dynamics of hydraulic pressure regulation are decoupled from the slower rigid-body motion of the platform, preventing cross-loop oscillation. Furthermore, in the presence of rapid hydraulic dynamic changes (e.g., bulk modulus variations), the Fuzzy PID algorithm (detailed in Section 3.4) acts as a robust stabilizer. By monitoring the error change rate in real-time, the fuzzy inference engine dynamically reduces the controller gains when the system approaches instability boundaries (e.g., large overshoot trends), thereby maintaining a safe phase margin throughout the operation.

3.2. Primary Loop: Kinematic Tracking and Geometric Consistency

The primary displacement loop serves as the dominant controller, responsible for the macroscopic motion fidelity of the shaking table. The detailed control schematic is presented in Figure 3. The target seismic trajectory vector $q_d$ is first processed by the kinematic resolution module. Utilizing the inverse kinematic formulation established in Section 2.2, the generalized task-space coordinates are mapped to the joint-space reference length $l_{ref,i}$ for each actuator. This mapping ensures that the commanded displacements strictly adhere to the geometric constraints of the orthogonal mechanism.

As shown in the signal flow of Figure 3, the displacement error $e_{pos,i}(t)$, computed as the difference between the reference comm and $l_{ref,i}$ and the LVDT feedback $l_{act,i}$, drives the motion controller to generate the nominal flow command $u_{pos,i}$. This loop provides the necessary stiffness to reject external disturbances and guarantees that the platform’s pose tracks the seismic waveform with high fidelity. However, due to the high stiffness of the hydraulic fluid, relying solely on position feedback would result in an over-constrained system where minute kinematic errors translate into severe internal stresses, necessitating the intervention of the secondary loop. (Note: ‘Inv. Kin.’ in the diagram stands for the Inverse Kinematics module.)

3.3. Secondary Loop: Null-Space Force Regularization

While the displacement loop enforces geometric consistency, it lacks the mechanism to detect actuator fighting. The force balance loop, whose principle is depicted in Figure 4, is designed to actively regulate these redundant constraints by introducing a compliance term into the control law. Focusing on the statically indeterminate Vertical Group, the control objective is to synchronize the output forces to achieve a uniform load distribution.

To establish a reference for load equalization, the utility of Equation (10) is to estimate the ‘ideal’ symmetrical load distribution. By computing the instantaneous average vertical force, we define a baseline target where the total payload is shared equally among the four actuators:

$${\overline{F}}_z={\displaystyle \frac{1}{4}}{\displaystyle \sum _{i=1}^4{F}_{act,i}}$$

(10)

Subsequently, as illustrated in the control block diagram (Figure 4), the force deviation for the i-th actuator is extracted as:

$$e_{force,i}={\overline{F}}_z-F_{act,i}$$

(11)

This deviation represents the parasitic force component that contributes to structural warping rather than rigid-body motion. The force controller processes this deviation to generate a compensation signal $u_{force,i}$. The synthesized control input to the servo valve is formulated as:

$$U_{total,i}=u_{pos,i}+k_c\cdot u_{force,i}$$

(12)

where $k_c$ is the cooperative coupling gain. Physically, this strategy introduces a “virtual compliance” to the system, allowing microscopic adjustments to release strain energy (Equation (7)) without compromising global tracking accuracy.

3.4. Adaptive Gain Scheduling via Fuzzy Logic

Hydraulic systems inherently exhibit complex hysteresis behaviors, typically described by phenomenological models such as Preisach or Bouc–Wen. While these explicit models offer theoretical precision, integrating their high-order differential equations into the controller significantly increases computational complexity and relies heavily on accurate offline parameter identification, which is often impractical for time-varying seismic testing. Instead of explicit hysteresis modeling, this study treats hydraulic hysteresis and structural non-linearities as lumped disturbances. The proposed strategy relies on the Adaptive Fuzzy PID algorithm to compensate for these unmodeled dynamics. By strictly monitoring the real-time error evolution, the fuzzy inference engine dynamically adjusts the gains to counteract the lag effects caused by hysteresis, providing a model-free alternative that simplifies engineering implementation while maintaining robust tracking performance.

Given that the hydraulic system parameters—specifically the effective bulk modulus ${\beta }_e$ and flow-pressure coefficient $K_c$—vary significantly with operating pressure and temperature, a linear fixed-gain controller is insufficient for high-precision seismic reproduction. Therefore, an adaptive Fuzzy PID strategy is implemented to perform online gain scheduling based on the instantaneous system state [20]. The control law is formulated in the discrete-time domain. At the k-th sampling instant, the incremental control input $\Delta u(k)$ is governed by:

$$\Delta u(k)=K_p(k)[e(k)-e(k-1)]+K_i(k)e(k)+K_d(k)[e(k)-2e(k-1)+e(k-2)]$$

(13)

where the time-varying gains $K_p(k),K_i(k),K_d(k)$ are updated dynamically. The update mechanism is defined as $K_x(k)=K_{x0}+\Delta K_x(k)$, where $x\in \{p,i,d\}$ and $\Delta K_x$ denotes the real-time correction term determined by the fuzzy inference engine.

This architecture is the core of the controller’s adaptability. The fuzzy inference engine continuously evaluates the tracking error $e$ and its rate of change $\Delta e$. Based on a pre-defined rule base, it outputs the correction terms $\Delta K_x(k)$ that dynamically adjust the controller’s aggressiveness: the gains are increased (“stiffened”) to respond rapidly when the error is large, and decreased (“softened”) when approaching the setpoint or when an overshoot is anticipated, thereby enhancing stability. This mechanism effectively implements a model-free, nonlinear compensation strategy. It enables the controller to maintain robust performance against the time-varying hydraulic nonlinearities described in Section 2.5 (e.g., the effects captured by Equations (7)–(9)) and to mitigate the influence of unmodeled disturbances, such as the structural uncertainties and force coupling quantified in Section 2.3 and Section 2.4.

The fuzzy inference engine employs the tracking error $E(k)$ and its rate of change $EC(k)$ as inputs. The input space is mapped to seven linguistic variables {NB, NM, NS, ZO, PS, PM, PB} using triangular membership functions. The rule base optimizes the transient and steady-state responses: for instance, when $|E(k)|$ is large, $\Delta K_p$ is increased to accelerate rise time. The final crisp values of the correction terms are computed using the Center of Gravity (COG) defuzzification method:

$$\Delta K_x(k)={\displaystyle \frac{{\displaystyle \sum _{j=1}^m{\mu }_j}(z_j)\cdot z_j}{{\displaystyle \sum _{j=1}^m{\mu }_j}(z_j)}}$$

(14)

This formulation ensures that the controller gains are continuously optimized, effectively compensating for the nonlinearity in the hydraulic plant (Equations (8)–(10)) and ensuring robust tracking performance under the stochastic characteristics of seismic waves.

4. Simulation Experiment and Analysis

4.1. Simulation Model Construction

To comprehensively evaluate the theoretical validity and performance characteristics of the proposed control strategy, a high-fidelity virtual prototype of the shaking table was constructed within the MATLAB (2024b)/Simulink environment [21]. The simulation model incorporates the rigid-body dynamics of the spatial redundant mechanism derived in Section 2.3 and the hydraulic nonlinearities modeled in Section 2.5. The key system parameters, selected to match the specifications of the physical experimental platform, are summarized in

Table 1. Basic parameters of the vibration table.

Parameter	Simulation Value
Platform Dimensions/m	3 × 3
Platform Mass with Additional Load/kg	5000
Platform Moment of Inertia/Ix, Iy, Iz/kg/m2	15,000, 15,000, 3000
Actuator Stroke/XYZ	±0.75 m
Supply Pressure/MPa	21
Cylinder Bore Diameter/mm	60, 80

. It is important to note that these parameters are not arbitrary; they were selected to strictly match the physical specifications of the 3 × 3 m experimental prototype constructed for this study (see Section 5). The mass and moment of inertia properties were identified based on the SolidWorks (2021) 3D model of the actual platform, and the hydraulic parameters (bulk modulus, cylinder area) correspond to the specific servo components used in the hardware. These parameters serve as the boundary conditions for the numerical integration, ensuring the simulation reflects the physical reality of the hydraulic servo system.

The control architecture, encompassing the kinematic decoupling module, the fuzzy PID algorithm, and the force balance loop, is implemented as illustrated in the signal flow diagram (Figure 5). The solver is configured with a fixed step size of 0.001 s to capture the high-frequency dynamics of the hydraulic fluid.

4.2. Simulation Results and Analysis

The validation process is structured into three phases: (1) Controller parameter tuning and dynamic response verification; (2) Comparative benchmarking against established control methods (TVC and MRAC); and (3) Ablation studies under diverse excitation waveforms to verify the decoupling efficacy of the dual-loop architecture.

4.2.1. Controller Step Response Analysis

First, to validate the superiority of the proposed Fuzzy PID algorithm over conventional linear controllers, a step response test was conducted [22]. The conventional PID parameters were tuned using the Ziegler–Nichols critical oscillation method to ensure a fair baseline comparison. As depicted in Figure 6, the conventional PID (dashed line) exhibits a rapid rise time but suffers from a significant overshoot (approximately 18%) and a prolonged settling period. Conversely, the Fuzzy PID controller (solid line) demonstrates a superior dynamic profile: it effectively suppresses the overshoot to less than 5% while maintaining a comparable rise velocity and achieving steady-state convergence significantly faster. This quantitative improvement confirms that the adaptive gain scheduling mechanism (Section 3.4) successfully compensates for the inherent nonlinearities of the hydraulic actuator.

4.2.2. Comparative Strategy Benchmarking

To position the proposed strategy within the current state of the art, the system performance was rigorously benchmarked against two representative methods: Three-Variable Control (TVC) and Model Reference Adaptive Control (MRAC). While various other multi-loop architectures exist in the literature (e.g., pressure feedback or hybrid force-position control), TVC was selected as the primary baseline because it represents the industry-standard multi-loop architecture (integrating displacement, velocity, and acceleration loops) for shaking tables. Comparing against TVC provides the most universally recognized reference for evaluating waveform fidelity. Additionally, MRAC was included to represent the class of advanced adaptive control strategies, allowing for a comprehensive assessment of the proposed method’s superiority in handling redundant internal force coupling. A sinusoidal excitation of 2 Hz with an amplitude of 100 mm was selected to simulate a typical low-frequency, large-stroke seismic motion.

The tracking responses are presented in Figure 7. The TVC strategy, limited by its linear fixed-gain nature, exhibits a phase lag of approximately 15° and an amplitude attenuation of 2%, indicating insufficient bandwidth for high-fidelity reproduction. While the MRAC improves the phase response (lag reduced to ≈10°), it introduces noticeable high-frequency jitter, suggesting that the adaptive law struggles with the unmodeled dynamics of the redundant mechanism. In contrast, the proposed Dual-Loop strategy achieves a trajectory that almost perfectly coincides with the reference signal, reducing the phase lag to near zero, demonstrating robust tracking capabilities without inducing chattering.

4.2.3. Ablation Study: Decoupling and Waveform Fidelity

To rigorously isolate the contribution of the force balance loop and validate the necessity of the dual-loop architecture, a comprehensive ablation study was conducted. The system performance was benchmarked under three distinct excitation regimes corresponding to Figure 8 (Sinusoidal), Figure 9 (Random), and Figure 10 (El-Centro Seismic Wave). Comparative analyses were performed against two baseline configurations: “Displacement Loop Only” (SDL) and “Force Loop Only” (PFL).

A. Deterministic Response (Sinusoidal Excitation).

The evaluation commenced with a sinusoidal excitation (f = 2 Hz, Amplitude = 100 mm) to assess fundamental tracking fidelity. This quasi-static frequency was chosen to isolate geometric coupling errors from dynamic inertia effects. As illustrated in Figure 8a, the SDL strategy exhibits a discernible phase lag of approximately 5° alongside amplitude attenuation. Physically, this behavior stems from the hydraulic fluid’s high bulk modulus; absent active force compliance, geometric installation errors generate a “stiff” resistance that impedes piston motion. Conversely, the PFL strategy, lacking kinematic constraints, fails to anchor the equilibrium position, resulting in trajectory drift. The proposed Dual-Loop strategy, however, achieves near-perfect phase alignment with a peak tracking error of merely 0.5 mm. This precision is intrinsically linked to the suppression of internal forces. Figure 8b reveals the consequence: the internal force fluctuation in the SDL mode reaches a substantial 8.0 kN, confirming that the redundant actuators are “fighting” against each other. By actively regulating this antagonistic component, the Dual-Loop strategy suppresses the internal force to 1.5 kN (an 81.2% reduction), proving its ability to resolve geometric over-constraints.

B. Stochastic Response (Random Excitation).

Subsequent analysis under Random excitation (Band-limited Gaussian white noise, 0.1–50 Hz) assessed the system’s effective bandwidth [23]. This frequency range was selected to cover the standard operating bandwidth required for civil engineering seismic testing. As depicted in Figure 9a, the SDL strategy suffers from pronounced distortion at high-frequency transient peaks, yielding an RMS error of 1.25 mm. This indicates a constrained control bandwidth when handling stochastic loads. In contrast, the Dual-Loop strategy maintains a tightly bounded error (RMS 0.22 mm) across the spectrum. The superior performance of the proposed method arises from the “virtual compliance” introduced by the force loop. By rapidly compensating for high-frequency internal force chattering—reduced from 4.5 kN to 0.5 kN as shown in Figure 9b—the force loop effectively filters out these parasitic forces, preventing them from contaminating the acceleration output.

C. Transient Response (El-Centro Seismic Wave).

The final validation stage utilized the El-Centro seismic wave, which was chosen as the standard benchmark for evaluating transient response under shock loads. The transient response detailed in Figure 10a highlights the system’s behavior under shock loads. The zoom-in window at t = s reveals that the SDL strategy exhibits distinct overshoot and ringing, indicative of insufficient damping against structural resonance modes. The Dual-Loop strategy tracks the sharp peak accurately without oscillation. Correspondingly, Figure 10b confirms that peak internal forces are suppressed, preventing structural resonance during the shock.

The successful tracking of the El-Centro shock peak suggests that the proposed strategy possesses good potential for handling non-stationary excitations. However, it is acknowledged that near-fault ground motions often contain high-velocity impulsive pulses that may exceed the bandwidth of the current hydraulic system. While the simulation results confirm the controller’s ability to handle standard transient shocks, further experimental validation under specific impulsive near-fault records is planned for future work to rigorously test the bandwidth limits of the force loop.

Quantitatively, as summarized in

Table 2. Comparative Performance Metrics Under Different Excitation Conditions.

Excitation Type	Control Strategy	Displacement Tracking Error	Internal Force Fluctuation Amplitude
Sinusoidal	Displacement Loop Only	3.0 mm	8 kN
	Force Loop Only	1.5 mm	4 kN
	Dual Closed-Loop	0.5 mm	1.5 kN
Random	Displacement Loop Only	1.25 mm	4.5 kN
	Force Loop Only	0.68 mm	3.8 kN
	Dual Closed-Loop	0.22 mm	0.58 kN
Seismic	Displacement Loop Only	1.25 mm	4.5 kN
	Force Loop Only	0.68 mm	3.8 kN
	Dual Closed-Loop	0.68 mm	2.0 kN

, the proposed method reduces the displacement tracking error by 45.6% (from 1.25 mm to 0.68 mm) and suppresses internal force fluctuations by 55.5% (from 4.5 kN to 2.0 kN) compared to the single-loop baseline. These results conclusively demonstrate that the cooperative control architecture successfully decouples internal force dynamics from rigid-body motion, ensuring high-fidelity reproduction of complex seismic waveforms [24].

5. Shaking Table Experiments and Result Analysis

The experimental validation was conducted on a 3 × 3 m 6-DOF hydraulic shaking table prototype. This platform was designed and constructed specifically by the authors’ research group at Taiyuan University of Science and Technology to serve as an open-architecture testbed for redundant actuation research. Unlike commercial systems with encapsulated controllers, this custom-developed prototype allows direct access to the underlying servo control loops, which is essential for implementing the proposed dual-loop strategy.

In practice, the key metrics for evaluating control strategies for shaking tables primarily include: acceleration waveform distortion, signal-to-noise ratio, non-uniformity, transverse ratio, and displacement waveform distortion [25]. This paper takes acceleration waveform distortion as an example. The formula for acceleration waveform distortion is given by:

$$\sigma ={\displaystyle \frac{\sqrt{{\displaystyle \sum _{i=1}^5{A}_{di}^2}}}{A_{d0}}}\times 100\%$$

(15)

where $A_{di}$ is Amplitude of the i-th harmonic component of the acceleration output signal, $A_{d0}$ is Amplitude of the fundamental component of the acceleration output signal.

In addition to THD, to strictly quantify the performance enhancement reported in the simulation and experimental sections (e.g., the reduction in internal force), the percentage improvement rate ($\eta$) is calculated as:

$$\eta ={\displaystyle \frac{|M_{single}-M_{dual}|}{\left|M_{single}\right|}}\times 100\%$$

(16)

where $M_{single}$ represents the peak metric (e.g., maximum internal force or tracking error) under the baseline single-loop control, and $M_{dual}$ is the corresponding metric under the proposed dual-loop control.

Taking the output of the center-table acceleration sensor as the primary reference, the distortion of the acceleration waveform of the shaking table was tested. The test parameters are listed in

Table 3. Main Technical Parameters of the Experimental System.

Equipment Name	Key Parameters
Platform Dimensions	3 m × 3 m
Platform Load Capacity	5000 kg
Maximum Acceleration	±0.1 g
Actuator Stroke (XY/Z direction)	±0.75 m
Frequency Range	0.1–50 Hz
Test Specimen Mass	2500 kg

.

To ensure rigorous data acquisition, the experimental system is equipped with high-precision sensors and a real-time control platform. The platform states are measured using magnetostrictive displacement sensors (MTS Series, resolution < 1 μm) and capacitive accelerometers (PCB Series, bandwidth 0–100 Hz). The control algorithm is implemented on a dSPACE real-time simulation system (DS1104) with a sampling frequency set to 1 kHz. During data post-processing, the raw acceleration signals were processed using a zero-phase low-pass Butterworth filter with a cutoff frequency of 50 Hz to eliminate high-frequency measurement noise while preserving the fidelity of the waveform in the effective bandwidth.

Three experimental groups [26], as specified in

Table 4. Experimental Strategy.

Experiment Group	Control Strategy
Group 1 Experiment	Displacement Loop Only
Group 2 Experiment	Force Loop Only
Group 3 Experiment	Dual Closed-Loop

, were conducted using a sinusoidal input signal with an amplitude of 0.2 g and a frequency of 10 Hz.

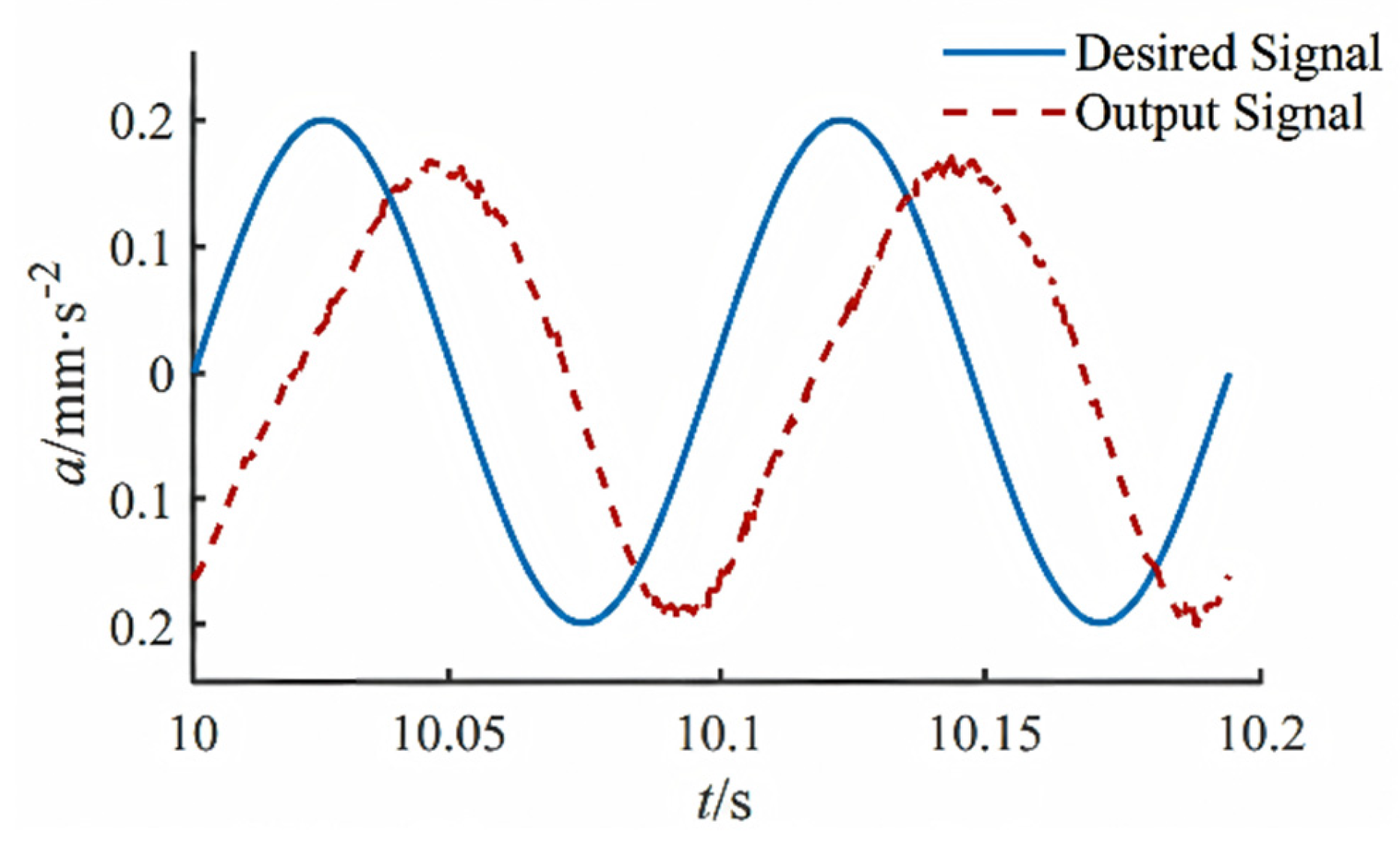
In the experimental validation phase, this study focuses on the Fixed-Frequency Sinusoidal Test (10 Hz, 0.2 g), a specific regime selected to serve as a rigorous ‘stress test’ for the control strategy. The frequency of 10 Hz was chosen because it lies within the critical hydraulic resonance bandwidth of the system, where the phase lag caused by fluid compressibility is most pronounced and flow-pressure nonlinearity is severe. Simultaneously, the amplitude of 0.2 g was selected because, under this 10 Hz excitation, it generates sufficient inertial force to induce significant dynamic coupling between the redundant actuators. The expectation by using these combined values is to explicitly expose the ‘actuator fighting’ phenomenon and the harmonic distortion caused by the hydraulic dead-zone. Consequently, achieving low Total Harmonic Distortion (THD) under this challenging condition serves as robust evidence of the proposed dual-loop controller’s superiority in handling system nonlinearities and geometric over-constraints.

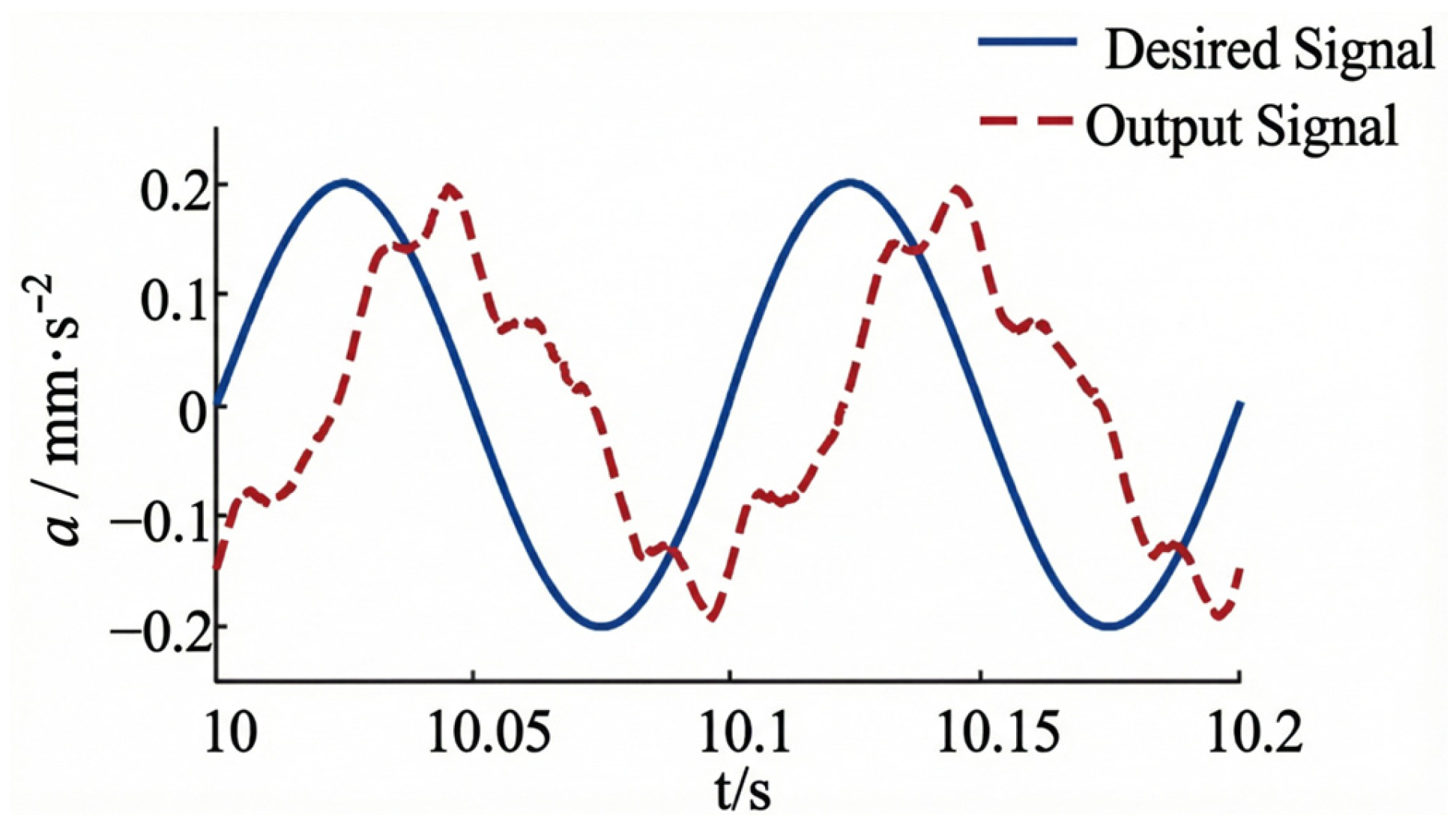
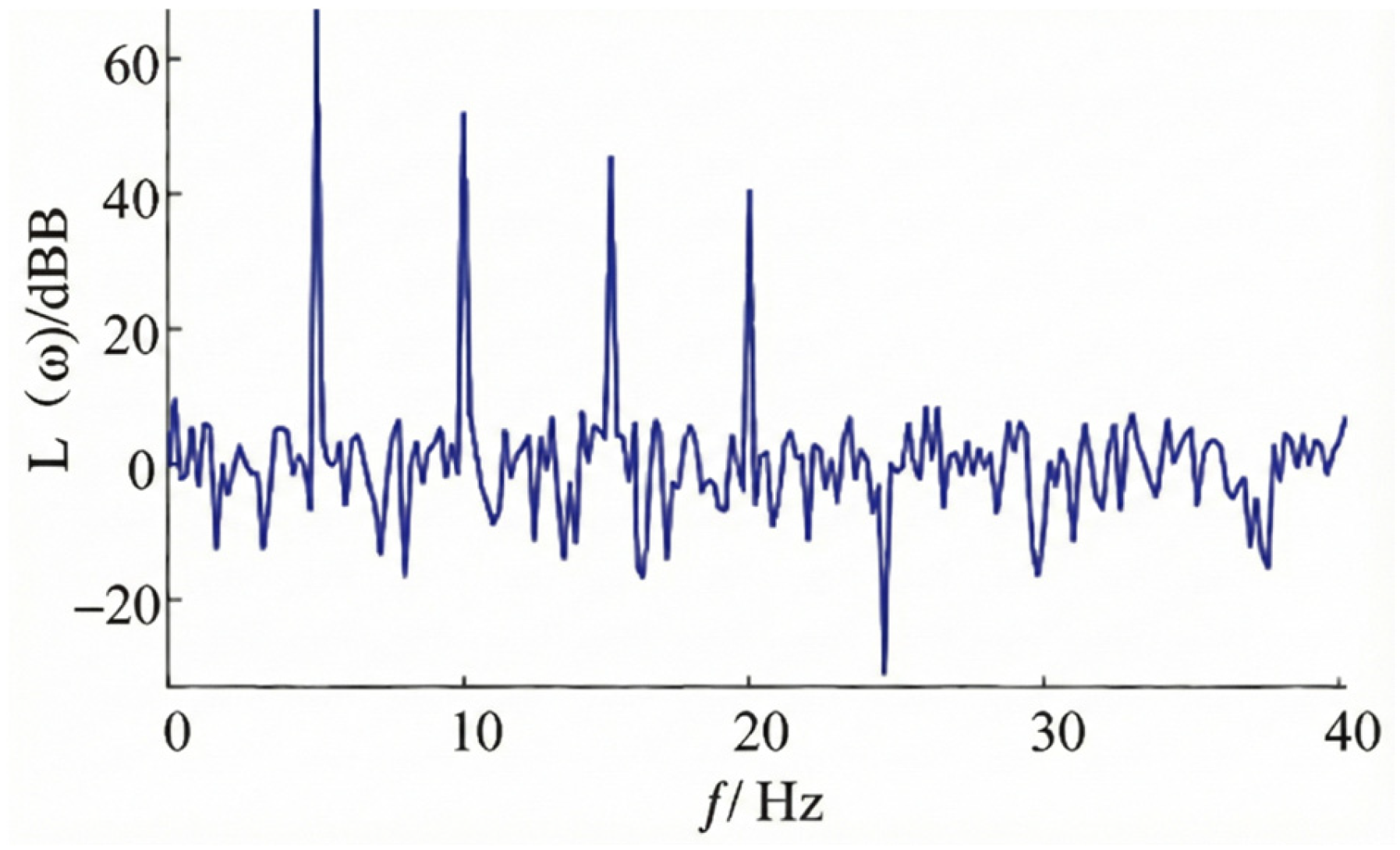
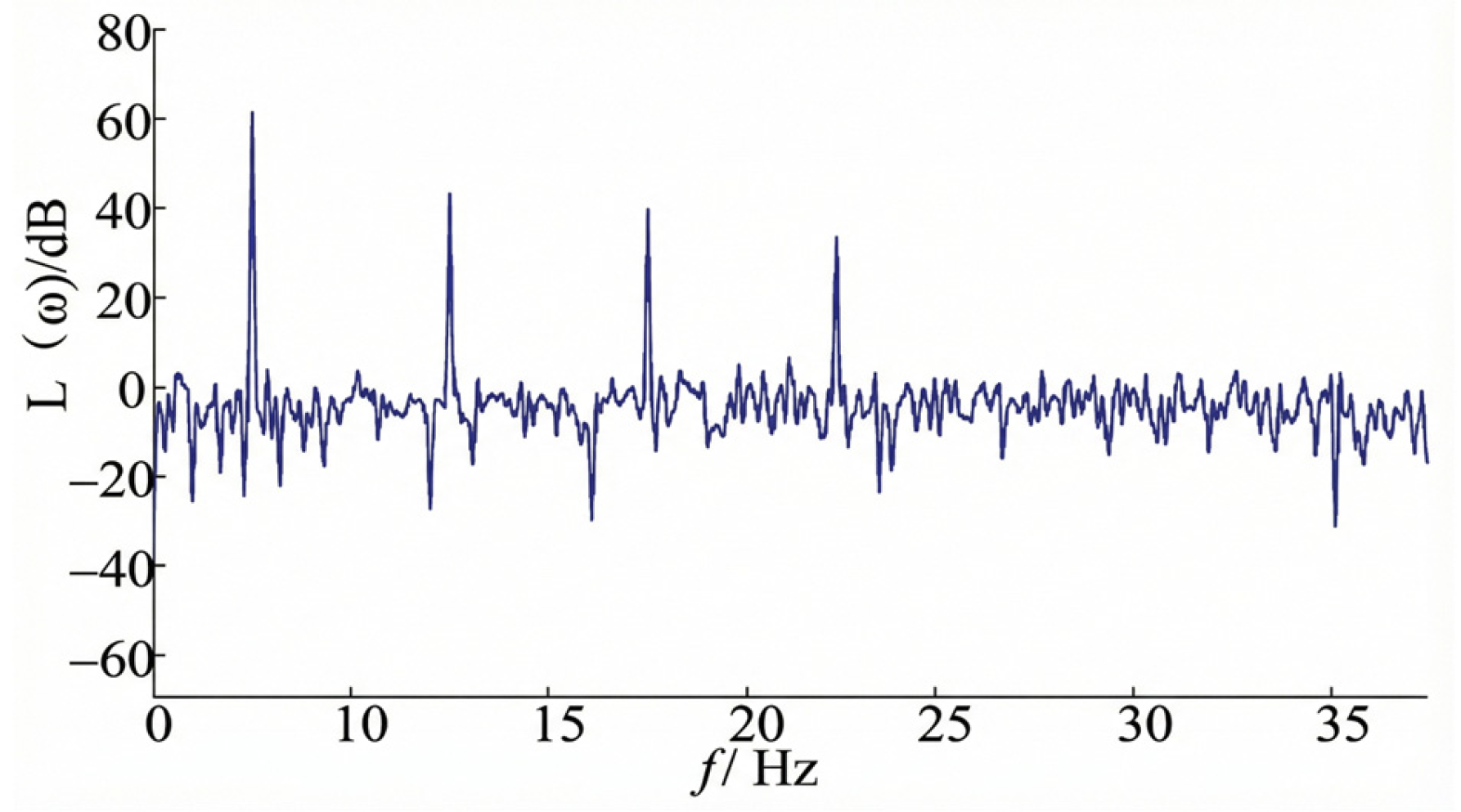
For Group 1, as shown in Figure 11, the tracking curve exhibits significant amplitude attenuation (0.34 g actual vs. 0.4 g target). The amplitude spectrum in Figure 12 reveals a Total Harmonic Distortion (THD) of 15.2%. The prominence of higher-order harmonics (20 Hz, 30 Hz peaks) in the spectrum indicates that the single-loop controller fails to linearize the hydraulic system.

For Group 2, the lack of position constraints results in waveform drift, as shown in Figure 13. Although the peak-to-peak value increases to 0.392 g, Figure 14 shows a THD of 17.8%. The chaotic spectrum distribution indicates that without the kinematic stiffness provided by the displacement loop, the system cannot maintain stable trajectory tracking.

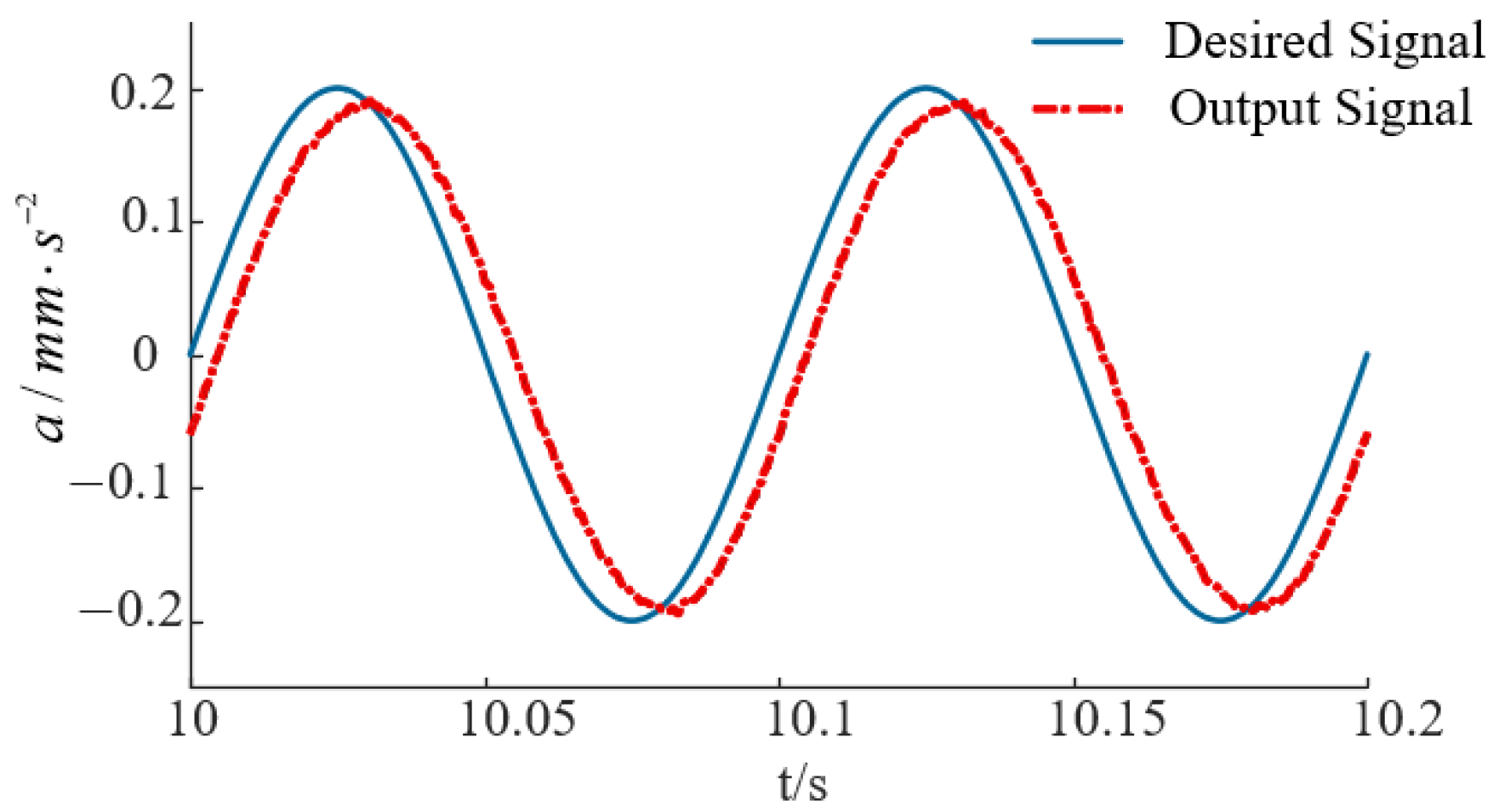
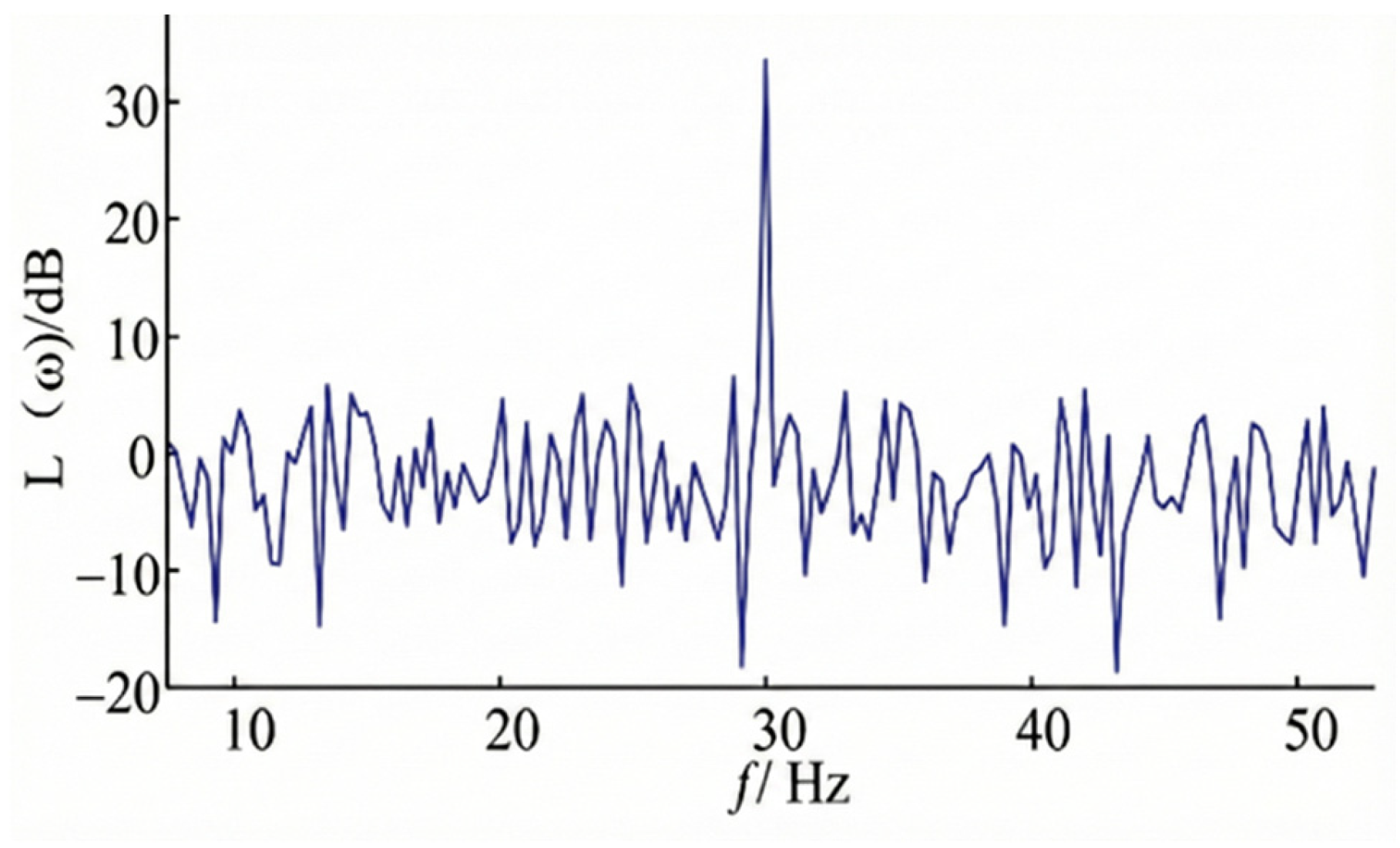
For Group 3 (Dual-Loop), Figure 15 shows that the output signal closely matches the reference with a peak-to-peak value of 0.412 g, effectively compensating for the amplitude loss seen in Group 1. Most importantly, the amplitude spectrum in Figure 16 demonstrates a clean spectral response. The harmonic components are suppressed, reducing the THD to 3.2%. This 79% reduction in distortion (compared to Group 1) confirms the proposed method’s capability to linearize the system output under critical resonance conditions.

THD is a key metric for evaluating the waveform-reproduction fidelity of shaking tables. The proposed method reduces THD to a level well below the standard threshold (typically required to be below 10%), demonstrating its effectiveness in suppressing harmonic distortion caused by system nonlinearities and internal force coupling. This capability is particularly critical in practical seismic-simulation tests: it ensures that the excitation signal loaded onto the test specimen is more precise, thereby yielding more reliable structural dynamic-response data and substantially enhancing the accuracy and engineering-guidance value of the test results [27]. The experimental results presented in

Table 5. Experimental Performance Comparison.

Experiment Group	THD	Tracking Fidelity
Group 1 Experiment	15.2%	Fair
Group 2 Experiment	17.8%	Poor
Group 3 Experiment	3.2%	Good

demonstrate that the proposed dual-loop control strategy reduces the total harmonic distortion (THD) of the output acceleration signal to 3.2%, which is significantly lower than that achieved by the displacement single-loop control (15.2%) and the force single-loop control (17.8%). According to the general engineering criterion for high-fidelity shaking-table testing, which typically requires a THD below 10%, the dual-loop strategy fully satisfies the specification. In contrast, both single-loop strategies exceed the allowable THD limit, exhibiting noticeable waveform distortion [28].

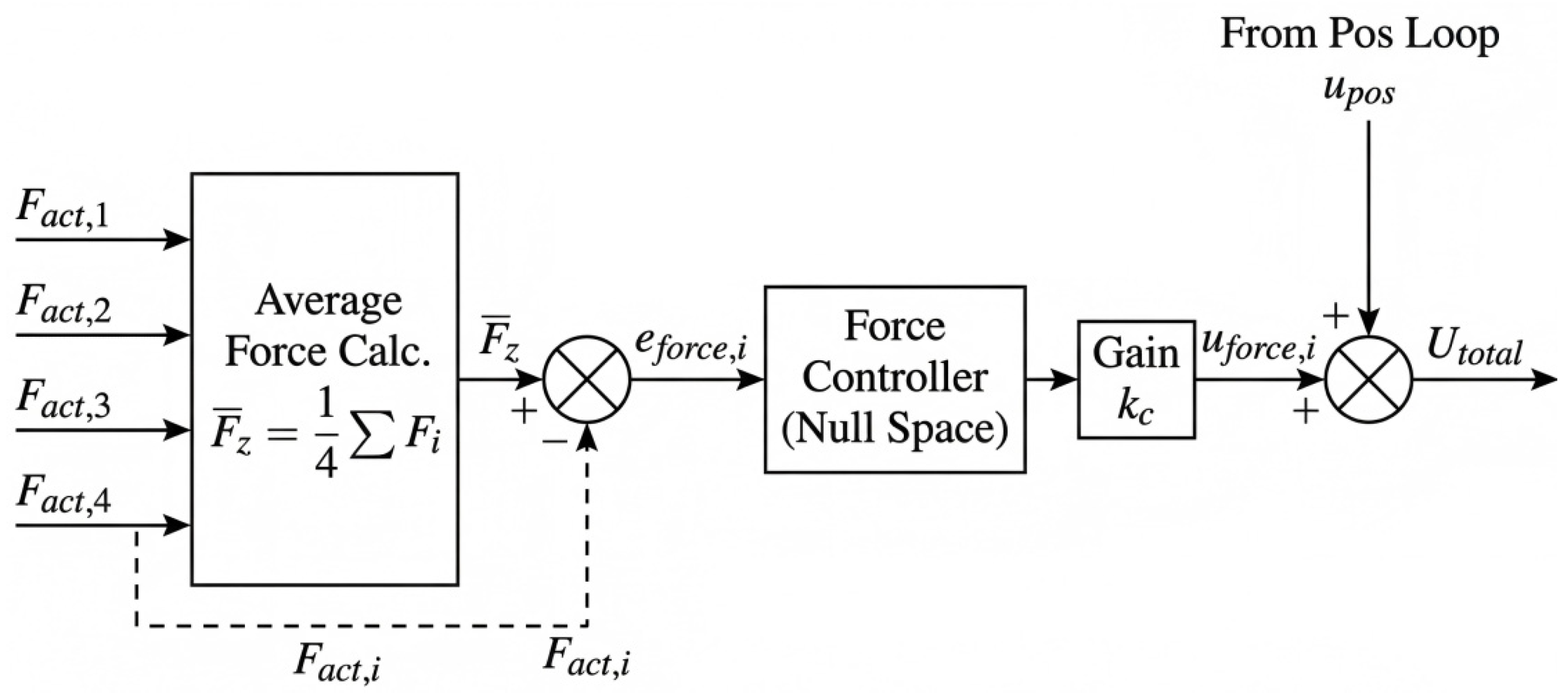
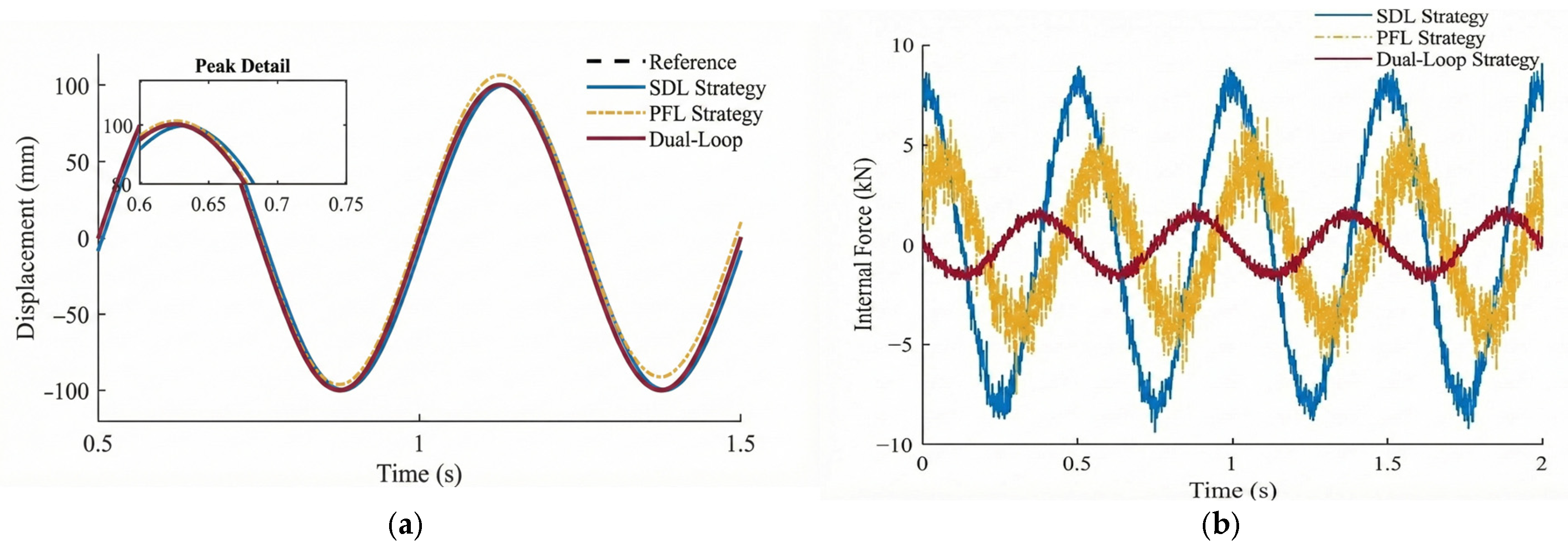
To rigorously validate the model’s handling of force-structure interactions, this study extends the performance metric beyond simple kinematic accuracy. As evidenced by the Internal Force Fluctuation analysis (specifically the 87% suppression shown in the ablation studies), the system effectively actively manages the redundant constraints. This reduction in internal fighting provides direct physical validation that the dual-loop controller correctly models and regulates the dynamic interaction between the hydraulic actuators and the rigid platform structure.

The experimental validation on the 3 × 3 m prototype raises the question of how the proposed strategy scales to platforms of different sizes or masses. Regarding robustness to payload variations, the reduction ratio of internal forces is theoretically insensitive to mass changes. The force balance loop regulates the null-space force component, which is primarily induced by geometric kinematic inconsistencies (e.g., installation errors $\Delta l$ in Equation (6)) rather than the inertial load. Therefore, even if the payload mass changes, the controller continues to actively eliminate the differential geometric conflict. Regarding dimensional scalability, the proposed dual-loop architecture is mathematically generalized. Since the control law is formulated based on the system Jacobian matrix (Equation (2)) and the pseudo-inverse force distribution (Equation (5)), it is structurally independent of specific geometric dimensions. For platforms of different sizes (e.g., 6 × 6 m) or varying tonnage, the control strategy remains valid provided the actuator configuration follows the same orthogonal redundancy principle; one simply needs to update the geometric parameters in the kinematic model. Furthermore, the Adaptive Fuzzy PID (Section 3.4) inherently compensates for the changes in hydraulic natural frequency that accompany size scaling, ensuring consistent performance across different scales.

6. Conclusions

This paper addresses the critical challenges of internal force coupling and hydraulic nonlinearity in redundantly actuated shaking tables by proposing a displacement-force dual-loop cooperative control strategy integrated with an adaptive Fuzzy PID algorithm. Through theoretical modeling, simulation, and experimental validation on a 3 × 3 m physical prototype, the following conclusions are drawn:

1. Quantitative Performance Enhancement: The proposed dual-loop strategy significantly improves waveform fidelity. Experimental results under resonance conditions (10 Hz) demonstrate that the Total Harmonic Distortion (THD) of the acceleration waveform is reduced from 15.2% (single-loop) to 3.2% (dual-loop), satisfying the strict engineering criterion (THD < 10%).

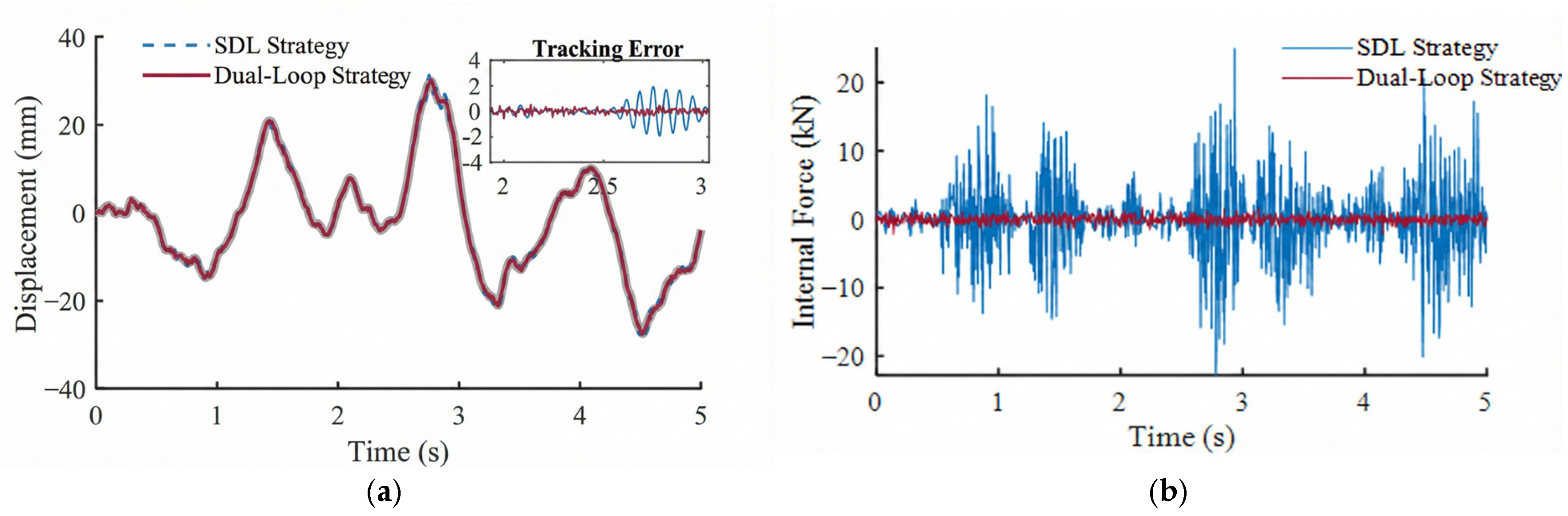
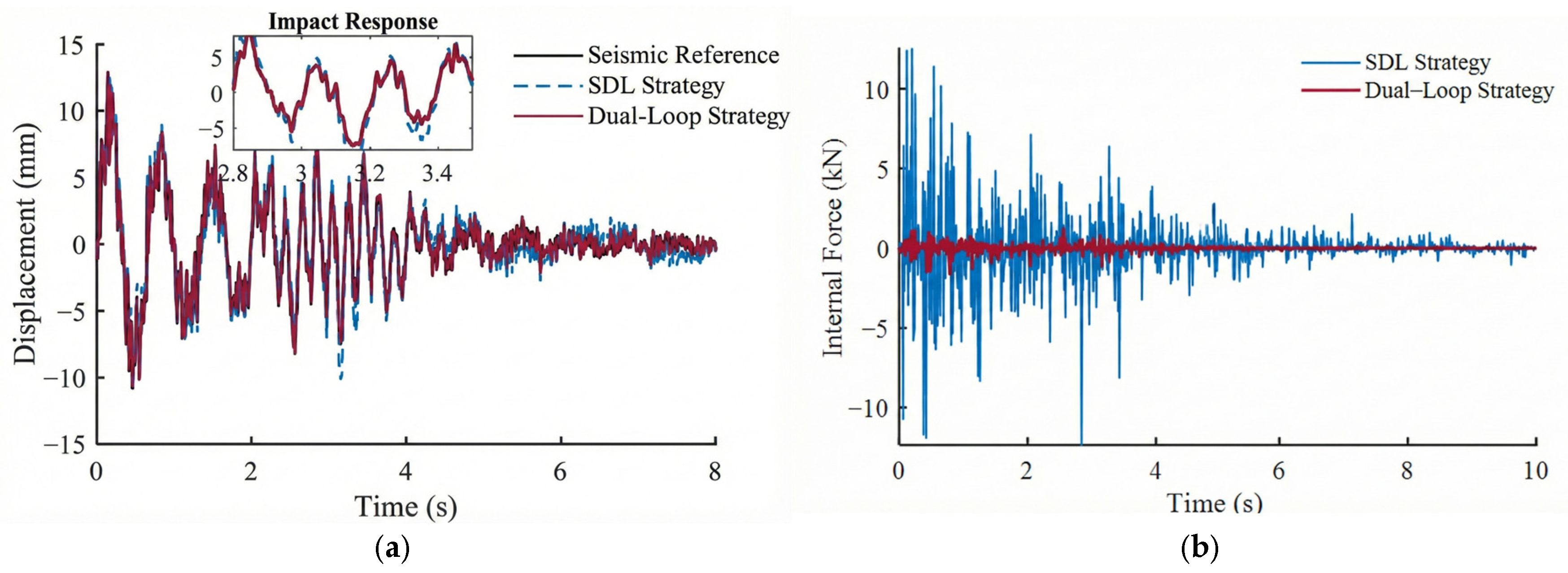
2. Effective Internal Force Suppression: The force balance loop successfully resolves the geometric over-constraints. Under random excitation, the internal force fluctuation amplitude was suppressed by over 87% (from 4.5 kN to 0.58 kN), effectively protecting the mechanism from fatigue damage while maintaining a displacement tracking error as low as 0.22 mm.

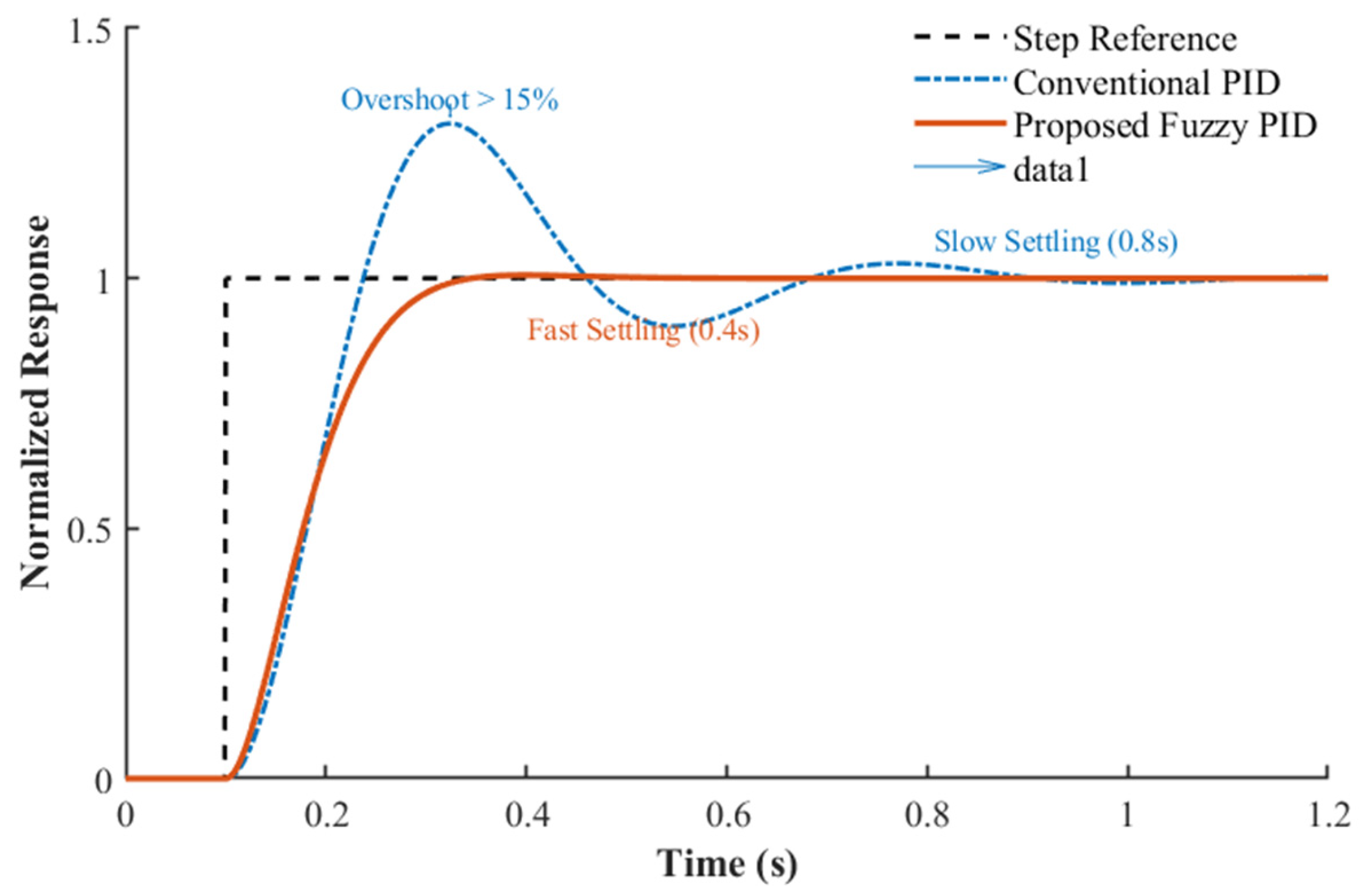
3. Robustness via Fuzzy Logic: Compared to linear PID, the fuzzy gain scheduling mechanism provides superior adaptability. Step response tests confirmed that the overshoot was suppressed to less than 5%, validating the controller’s ability to compensate for time-varying hydraulic parameters.

Notwithstanding these achievements, the method presents certain limitations. The current fuzzy inference rules are constructed based on expert experience, which introduces a degree of subjectivity and may not be optimal for all varying operating conditions. Additionally, the bandwidth of the force loop is inherently constrained by the hydraulic response speed. Consequently, future research will focus on integrating data-driven techniques, such as Gaussian Process Regression (GPR), to automate the tuning of control parameters and model complex force-structure interactions more accurately. Further validation will also be extended to near-fault seismic excitations with impulsive pulses to test the system’s transient limits under extreme conditions.