Finite Element Analysis of Tire–Pavement Interaction Effects on Noise Reduction in Porous Asphalt Pavements

Abstract

This study investigated the noise reduction performance of porous asphalt concrete (PAC) pavement under tire–pavement coupling conditions, addressing the limitations of field measurements and laboratory testing. First, tire excitation amplitude parameters were determined based on vibrational contact operational scenarios. Then, finite element simulations were conducted to systematically analyzing the tire–pavement coupling noise characteristics of PAC pavement. The results indicate that PAC pavement effectively reduces the air pumping noise due to its highly porous internal structure, leading to significant noise attenuation. Furthermore, the study examined the key factors influencing the tire–pavement coupling noise in PAC pavement. When maintaining constant vehicle parameters (300 kg load, 60 km/h speed), pavement thickness became the critical noise-control variable, achieving minimum vibration at 6 cm surface layer thickness. Additionally, tire tread depth (5–17 mm) and mold release angle (0–30°) had a more pronounced impact on the air pumping noise compared to groove width (20–60 mm). Increasing the mold release angle and reducing tread depth effectively mitigated the air pumping noise. However, the tire–pavement coupling noise in PAC pavement increased considerably with increasing vehicle speed and load. Particularly, as the speed increased from 30 km/h to 60 km/h, the growth of the air pumping noise was most pronounced, revealing an acoustic transition of tire–pavement coupling noise from vibration-dominated to air-pumping-dominated mechanisms.

1. Introduction

With the accelerated urbanization process and significant increase in road traffic volume, road traffic noise has become a critical environmental issue affecting urban residents’ quality of life and health [1,2,3,4,5,6]. According to World Health Organization statistics, prolonged exposure to high-noise environments adversely impacts human hearing, cardiovascular systems, and nervous systems [7]. Consequently, mitigating road traffic noise has become a pivotal task for governments in order to improve urban environmental quality.

Road traffic noise can be categorized into tire–pavement noise (TPN) and vehicle powertrain noise based on its sources [8]. Due to continuous advancements in vehicle manufacturing technology and engine powertrain systems, drivetrain noise has been significantly reduced [9]. Furthermore, the widespread adoption of electric vehicles in recent years has further controlled vehicle powertrain noise [10]. Therefore, TPN has become the dominant noise source on highways and urban expressways [11]. Numerous domestic and international scholars have conducted extensive experimental studies [12,13] to clarify the formation mechanisms of TPN and identify effective noise control strategies.

TPN has been identified as resulting from the combined action of tire structural vibrations and aerodynamic interactions [14], with primary classifications established as air pumping noise and vibration noise. Air pumping noise is generated by aerodynamic effects caused by the periodic compression and release of air within tire tread grooves during rolling. Furthermore, the sound intensity of air pumping noise is further amplified through Helmholtz resonance and groove cavity resonance mechanisms within the tire structure. Vibration noise is produced by structural vibrations occurring at the tire–pavement interface, including interactions with pavement surfaces and surrounding air [15,16]. These vibrational phenomena are categorized into three mechanisms: viscoelastic hysteresis effects, stick–slip friction mechanisms, and impact excitations induced by pavement texture irregularities [11,17,18]. The generation of TPN is recognized as a complex phenomenon, as its cause and mechanism involve multiple disciplines, including acoustics, tribology, vehicle dynamics, and materials science. However, from a vehicle dynamics perspective, TPN fundamentally stems from tire–pavement interactions [19]. Therefore, the investigation of TPN influence mechanisms through tire–pavement coupling friction analysis is considered to provide a systematic methodology for developing targeted noise mitigation strategies [9].

In prior research, primary emphasis was placed on structural and material enhancements of tires and pavements for TPN mitigation. The research focusing on tire design was concentrated on areas such as the optimization of tread patterns, the selection of tire materials, and structural improvements. Tread patterns have been widely recognized as a dominant determinant of TPN generation [20]. Researchers have conducted experiments by varying groove width, depth, and angle, as well as modifying the stiffness and shape of the pattern blocks, to evaluate the specific impacts of these parameters on the overall noise level [21,22]. However, the specific mechanisms by which these factors affect TPN remain unclear. Further acoustic analyses are required to quantify the contribution of tire structural components to TPN, which are guiding targeted noise reduction designs.

In pavement optimization, extensive studies [23,24,25] have revealed that variations in surface texture, resulting from differences in pavement structure types and gradation design, exert a particularly significant impact on TRN. On the one hand, in high-void pavement structures, air friction and viscous damping within voids convert acoustic energy into heat, thereby consuming the sound wave energy and reducing noise levels [26]. Additionally, the complex pore structure, such as microtubes and narrow slits, significantly increases the propagation path and the number of reflections of sound waves, which can effectively promote the attenuation of acoustic energy and thus improve the acoustic performance of the pavement [27]. On the other hand, the impact of surface texture on TPN cannot be overlooked [28]. In the analysis of the relationship between pavement surface texture and noise, researchers primarily focus on correlations between surface profile parameters and the TPN, such as the Mean Profile Depth (MPD) or Mean Texture Depth (MTD) [29,30,31]. However, it was indicated by Rasmussen et al. [32] that the utilization of a single surface profile parameter as a pavement texture characterization metric fails to accurately capture TRN generation mechanisms. Moreover, three-dimensional micro- and macro-scale interactions between tires and pavements are involved in TPN generation, which cannot be comprehensively described by two-dimensional indices such as MPD or MTD.

In the investigation of TPN generation mechanisms, traditional methodologies primarily relied on field measurements [33,34,35] and laboratory tests [36]. However, these approaches are generally limited to standard loads and low-speed conditions, failing to mimic real-world high-speed and heavy-load scenarios. For instance, the Coast-down Method and Trailer Method are constrained by the testing site and vehicle limitations, making them unsuitable for high-speed and heavy-load conditions [37]. The Laboratory Drum Method enables partially simulate tire rolling but cannot fully replicate high-speed aerodynamic effects [38]. Additionally, challenges such as high costs, prolonged testing cycles, and environmental noise interference hinder the acquisition of accurate data [16]. Consequently, studies on TPN under high-speed and heavy-load conditions remain scarce [39]. To address these limitations, researchers have turned to numerical simulation methods which have been increasingly employed, including Finite Element Analysis [40,41], Boundary Element Methods [42,43], and Computational Fluid Dynamics [34]. Although these methods facilitate high-speed and heavy-load simulations as well as systematic factor analysis, accurately modeling three-dimensional pavement textures remains challenging due to their complexity, measurement difficulties, and high computational costs [44]. Existing models often oversimplify pavements as rigid planes with full acoustic reflection or employ empirical excitation parameters, neglecting texture-induced excitation amplitudes and compromising TPN prediction accuracy.

Based on the above analysis, the multiple influencing factors of TPN were identified, including pavement surface texture and tire tread patterns. However, effective control of TPN remains an unresolved challenge. Current traffic noise control strategies have been predominantly implemented through physical barrier systems, where noise walls and acoustic screens are constructed along transportation corridors. These engineered structures have been shown to reduce ambient noise levels through combined mechanisms of sound wave reflection, diffraction, and absorption [45]. However, such approaches have been critically limited by their inability to address noise generation at the source, compounded by disadvantages including visual intrusion, elevated capital expenditures, spatial constraints in urban environments, and long-term maintenance requirements [46]. Consequently, researchers are shifting focus toward low-noise pavement technologies that minimize noise generation at the tire–pavement interface [47]. Among these, porous asphalt concrete (PAC) pavement shows a remarkable noise reduction effect in practical application and has received wide attention [48]. When compared to conventional noise barriers, this technology has been recognized for its superior cost-effectiveness ratios and lower environmental impacts [49]. Nevertheless, the high void content in PACs presents a trade-off—while effectively reducing air pumping noise, increased surface roughness may exacerbate vibration noise, resulting in complex overall acoustic behavior. This coupling effect necessitates comprehensive optimization of pavement design, material selection, and tread pattern engineering to achieve optimal noise reduction.

In summary, existing research has made substantial progress in understanding TPN generation mechanisms, influencing factors, and control strategies. However, the detailed mechanisms of noise formation under tire–pavement coupling, particularly under high-speed and heavy-load conditions, remain inadequately elucidated. Secondly, current simulation models overlook the influence of pavement texture on TPN, which compromises their accuracy and reliability. Additionally, the interaction mechanisms between PAC and multiple influencing factors require further investigation to optimize the noise reduction performance.

Based on the current research status, the novelty of this study lies in its detailed examination of tire–pavement coupling noise under high-speed and heavy-load conditions, with a particular focus on PAC pavement. Tire–pavement coupling noise was examined by employing finite element simulations to model dynamic tire–pavement interactions, with the noise characteristics of PAC pavements systematically analyzed under various operational conditions. Three-dimensional pavement textures were incorporated using laser texture scanning and finite element modeling to more accurately simulate tire–pavement contact and noise generation processes. Additionally, a novel simulation framework was introduced, integrating both vibration noise and air pumping noise into a unified model, providing a more comprehensive understanding of the complex noise generation mechanisms in tire–pavement interactions. The detailed research methodology and technical route of this study are illustrated in Figure 1.

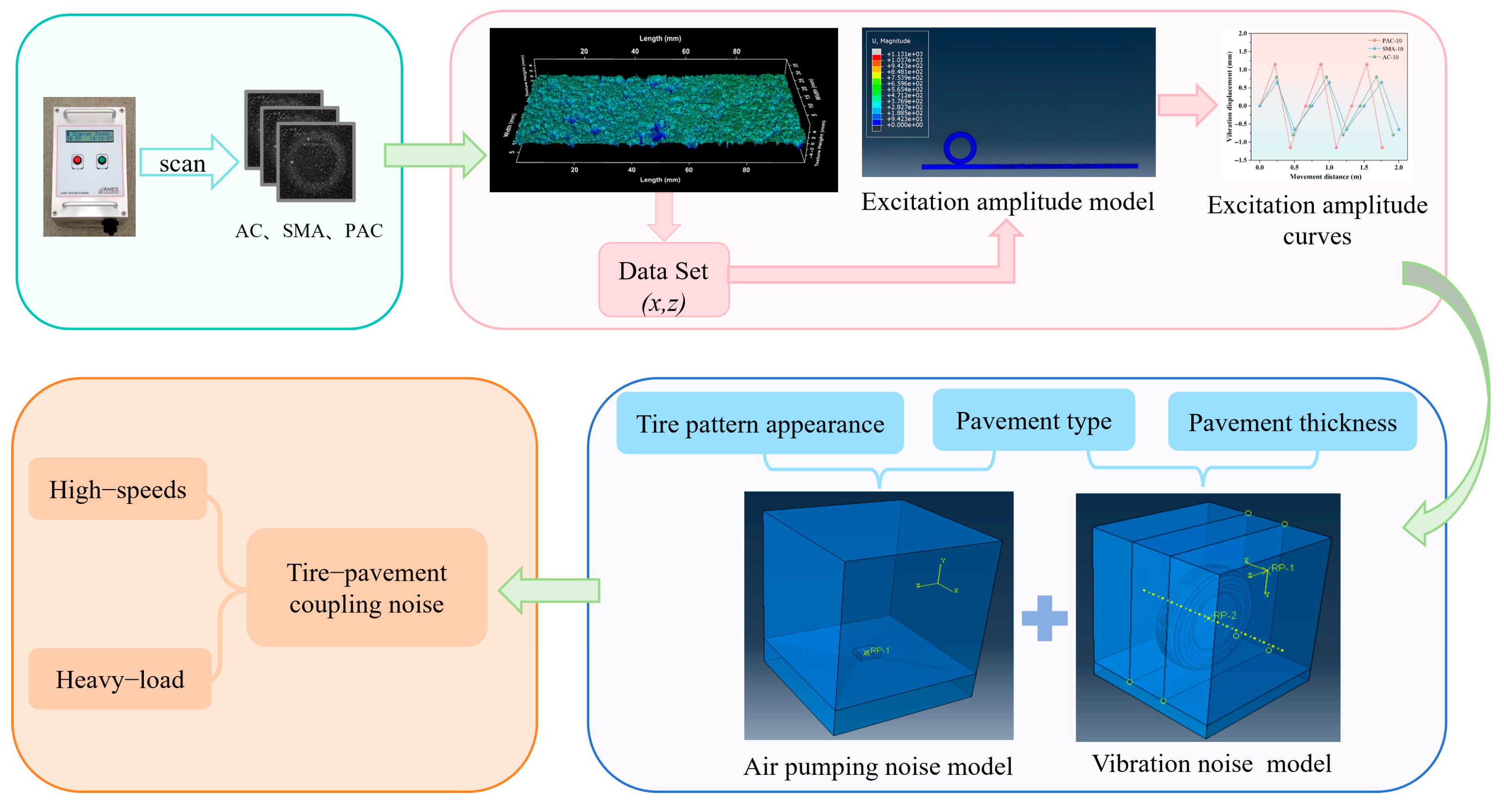
2. Materials and Methods

To explore the noise characteristics of asphalt pavements with different gradation types, three asphalt mixtures were selected: Porous Asphalt Concrete (PAC), Stone Mastic Asphalt (SMA), and Dense-Graded Asphalt Concrete (AC). All mixtures used SBS-modified asphalt, with basalt chosen as the coarse aggregate and limestone as the fine aggregate. According to the Specifications for Aggregate Testing in Highway Engineering (JTG E42-2005) [50], the physical properties of coarse and fine aggregates were tested, and the results are presented in

Table 1. Results of coarse aggregate technical standard tests.

Test Item		Unit	Test Result
Crushing Value		%	10.7
Los Angeles Abrasion Loss		%	6.0
Relative Apparent Density	9.5 mm~13.2 mm	g/cm3	2.802
	4.75 mm~9.5 mm		2.823
	2.36 mm~4.75 mm		2.690
Flakiness Content		%	9.6
Polished Stone Value		BPN	50.9
Asphalt Adhesion		Level	5

and

Table 2. Results of fine aggregate technical standard tests.

Test Item		Unit	Test Result
Relative Apparent Density	1.18 mm~2.36 mm	g/cm3	2.718
	0.6 mm~1.18 mm		2.716
	0.3 mm~0.6 mm		2.714
	0.15 mm~0.3 mm		2.714
	0.075 mm~0.15 mm		2.700
Content of Material Passing 0.075 mm		%	2
Sand Equivalent Value		%	79
Asphalt Blue Value		g/Kg	3
Angularity		s	38

. The fundamental properties of the binder (

Table 3. SBS modified asphalt basic performance test results.

Test Item	Unit	Technical Requirements	Test Result
Penetration (25 °C)	0.1 mm	40~60	57
Penetration Index (PI)	-	Min0	0.39
Ductility (5 °C)	cm	Min25	28
Softening Point (R&B)	°C	Min70	80
Kinematic Viscosity (135 °C)	Pa.s	Max3	2.1
Flash Point (Open Cup)	°C	Min230	308
Loss on Heating (48 h)	°C	Max2.5	1.5
Solubility	%	Min99	99.69
Resilience (25 °C)	%	Min85	94
Residual after TFOF (or RTFOT)
Quality Change	%	Max ± 1.0	−0.085
Residual Penetration Ratio	%	Min65	75
Residual Ductility (5 °C)	cm	Min15	16.1

), the mixture gradations, and the air void contents (

Table 4. Mineral aggregate gradation of asphalt pavement with different types.

Gradation Type	Percent of Aggregate Passing Through Each Sieve Size (%)										Asphalt-Aggregate Ratio	Air Voids (%)
	16 mm	13.2 mm	9.5 mm	4.75 mm	2.36 mm	1.18 mm	0.6 mm	0.3 mm	0.15 mm	0.075 mm
PAC-10	100	100	94.4	51.3	16.6	12.1	8.3	7.4	5.4	4.3	4.8	19.4
SMA-10	100	100	95.4	42.0	26.3	20.0	17.0	14.0	12.3	10.5	6.2	4.6
AC-10	100	100	98	64.5	46	27.5	21	14.0	10.0	8.5	4.5	4.3

) were determined in accordance with the Test Specifications for Highway Engineering Asphalt and Asphalt Mixtures (JTG E20-2011) [51]. Specifically, the air voids were calculated using the volumetric method, which involves measuring the bulk specific gravity and theoretical maximum specific gravity of the mixture, as displayed in Equation (1). Slab specimens for pavement surface texture measurement (PAC-10, SMA-10, and AC-10) were fabricated using a standard mold (30 cm × 30 cm × 5 cm):

$$Air Viods=\left(1-{\displaystyle \frac{{\rho }_B}{{\rho }_T}}\right)\times 100\%$$

(1)

where ${\rho }_B$ is the bulk relative density and ${\rho }_T$ is the theoretical maximum relative density.

A rectangular area measuring 40 mm × 100 mm was selected within the wheel path of the specimen (as depicted in Figure 2a). The surface texture of this area was measured using a Laser Texture Scanner (Ames Engineering LLC, Ames, IA, USA, Model LTS9400HD) based on laser ranging technology, generating a three-dimensional texture scatter dataset (x, y, z). The sampling intervals were set as follows: 0.1 mm along the X-axis, 0.00635 mm along the Y-axis, and a vertical resolution of 0.003 mm. The measurement path is illustrated in Figure 2b, with detailed equipment parameters provided in

Table 5. Equipment parameters of LTS.

Parameter Name	Numerical Value
Scan Area (mm)	104.00 × 72.00
Product Dimensions (mm) L × W × H	152.4 × 228.6 × 205
Weight (kg)	4.2
Vertical Resolution (mm)	0.003
Measurement Range (mm)	30
Maximum Length Resolution (mm)	0.00635
Maximum Width Resolution (mm)	0.0247
Triangulation Angle at center of range (°)	22
Dot size at center of range (μm)	25
Dot size at Max and Min range (μm)	60
Max laser sampling speed (Khz)	5

.

During pavement texture scanning, the high precision of the texture scanner combined with the inherent roughness of pavement surfaces and potential specimen misalignment may lead to data anomalies such as outliers and cross-sectional tilting in the measured elevation profiles. To address these issues, the following corrective procedures were implemented in MATLAB R2022a: First, outliers were replaced using the lower elevation value between adjacent data points, ensuring the outlier ratio in the dataset remained below 10%. Second, cross-sectional tilting was corrected through linear regression analysis to horizontally align the data, resulting in enhancing accuracy and reliability of the scanned data.

3. Tire–Pavement Coupling Noise Finite Element Modeling

Based on the formation mechanisms of TPN, this study employed the finite element software Abaqus/CAE 2021 to establish three analytical models: a tire–pavement vibrational excitation model, a tire–pavement vibration noise model, and an air pumping noise model, enabling comprehensive analysis of tire–pavement coupling noise.

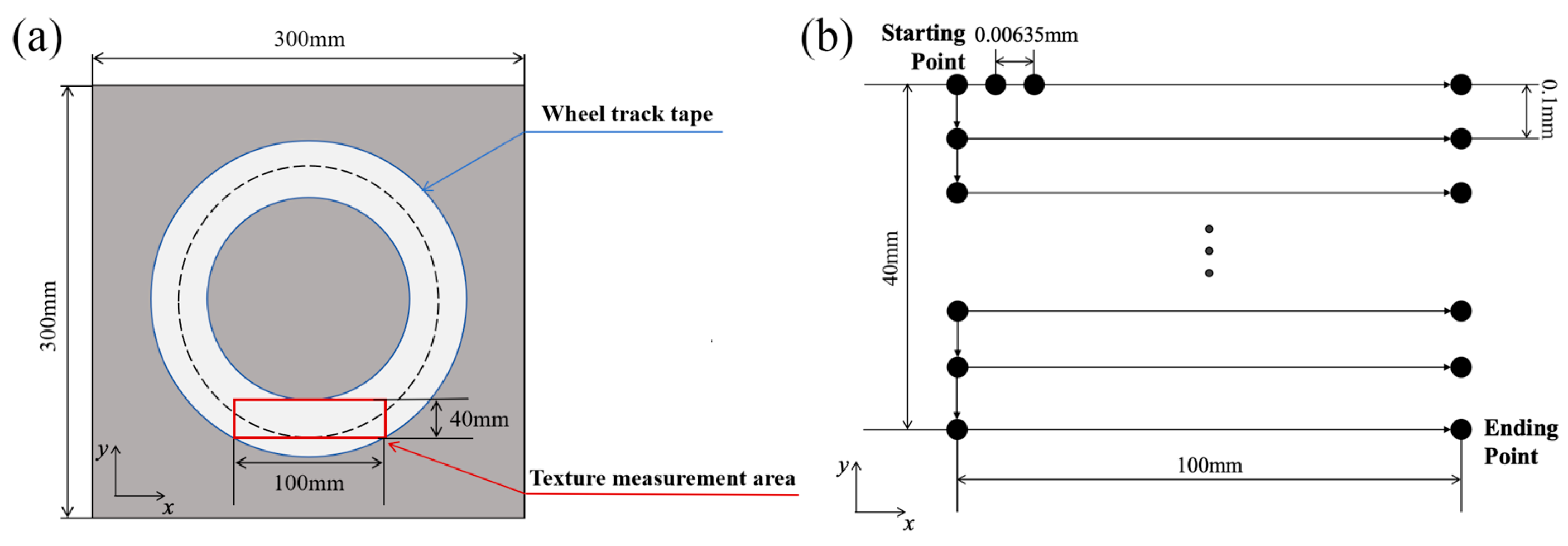
3.1. Finite Element Modeling of Tire–Pavement Vibrational Excitation Based on Surface Texture

3.1.1. Two-Dimensional Tire Model

Due to the nonlinear effects of factors such as tire geometry, material parameters, and contact interactions, the computational simulation of tires in the model faces serious convergence difficulties. To address these challenges, the tire geometry was simplified in this study, and its material was defined using hyper-elastic rubber parameters. The Yeoh constitutive model is a nonlinear elastic model widely used to simulate the mechanical response of rubber materials. When compared to other more complex rubber constitutive models, the Yeoh model is characterized by enhanced simplicity in handling small deformations, while still accurately capturing and fitting actual test data for rubber materials [52,53]. Therefore, this model was selected to establish the finite element model of the rolling tire.

For isotropic materials, the strain energy density can be expressed as the sum of the deviatoric strain energy and the volumetric strain energy, as shown in Equation (2):

$$U=f\left(\overline{I_1}-3,\overline{I_2}-3\right)+g\left(J-1\right)$$

(2)

Consider the function defined as $g={\displaystyle \sum }_{i=1}^N{\displaystyle \frac{1}{D_i}}{\left(J-1\right)}^{2i}$. Expanding this function through a Taylor series yields the following:

$$U={\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N{C}_{ij}{\left({\overline{I}}_1-3\right)}^i{\left({\overline{I}}_2-3\right)}^j+{\displaystyle \sum }_{i=1}^N{\displaystyle \frac{1}{D_i}}{\left(J-1\right)}^{2i}$$

(3)

In Equation (3), the parameter N represents the order of the polynomial, C denotes the shear modulus of the material, and D corresponds to the compressibility parameter.

In the phenomenological constitutive model, the initial shear modulus u₀ and initial bulk modulus k₀ are determined by the first-order polynomial coefficients (N = 1):

$$u_0=2\left(C_{10}+C_1\right)$$

(4)

$$k_0=2/D_1$$

(5)

For the polynomial model under the condition of N = 3, it can be reduced to the Yeoh form, as expressed in Equation (6):

$$U={\displaystyle \sum }_{i=1}^3{C}_{i0}{\left({\overline{I}}_1-3\right)}^i+{\displaystyle \sum }_{i=1}^3{{\displaystyle \frac{1}{D}}}_i{\left(J-1\right)}^{2i}$$

(6)

Based on the Yeoh constitutive model parameters displayed in

Table 6. Parameters of the Yeoh constitutive model.

Parameters	C10	C20	C30	D1	D2	D3	Density (kg/m3)
Numerical	0.7 × 106	−0.27 × 106	0.09 × 106	7.25 × 10−8	0	0	1100

, a two-dimensional finite element model of the 195/65R15 radial tire was developed, featuring an inner diameter of 381 mm and an outer diameter of 634 mm, as presented in Figure 3.

3.1.2. Two-Dimensional Pavement Model

A two-dimensional pavement model with a length of 2.0 m was developed in Abaqus/CAE 2021 by importing the (x, z) coordinates extracted from the three-dimensional dataset acquired by means of laser texture scanning to construct a surface texture profile. In addition, a 1.0 m straight pavement section was incorporated at the leading edge of the model to ensure tire acceleration to the preset velocity on the two-dimensional pavement model, as indicated in Figure 4.

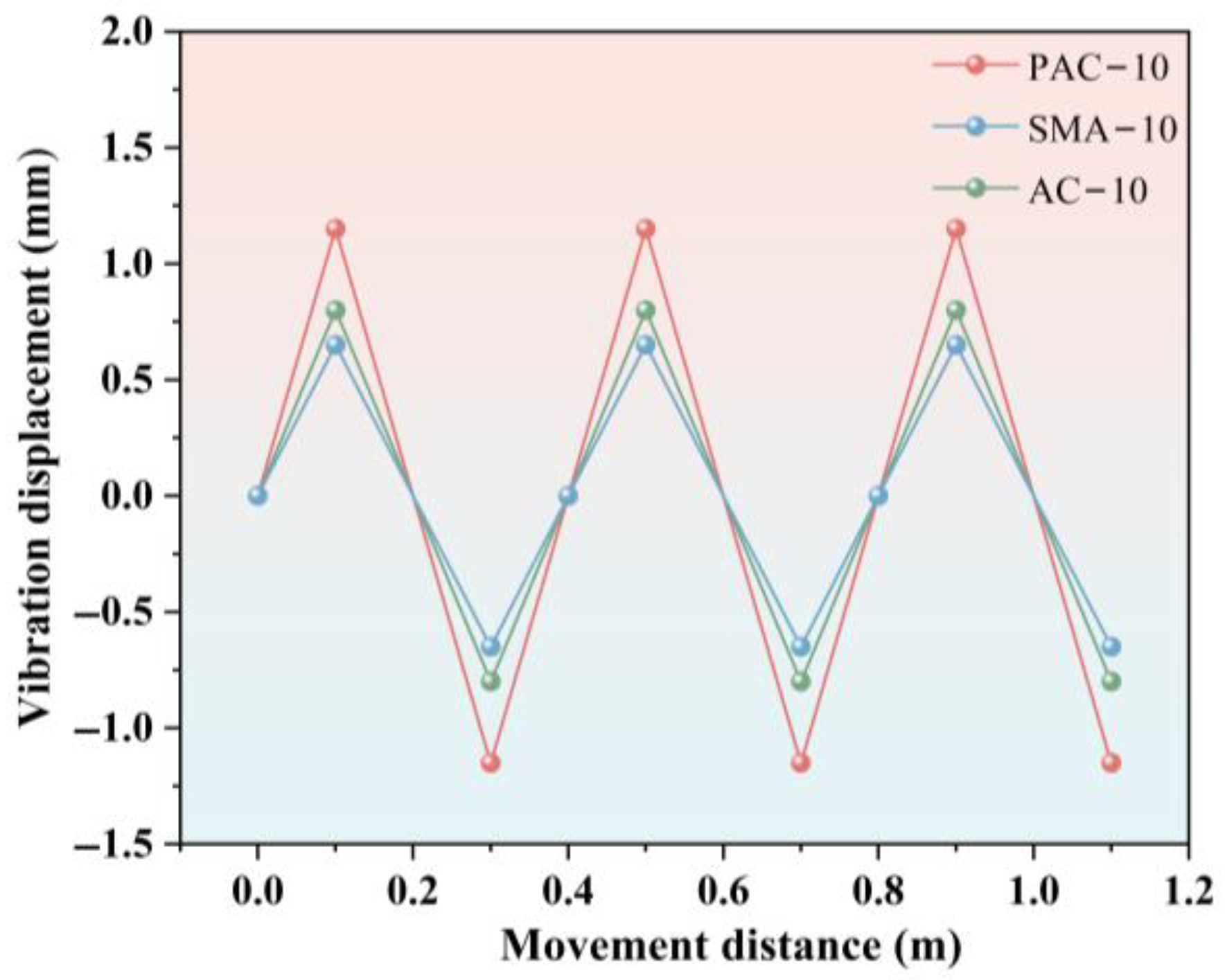
3.1.3. Extraction of Pavement Excitation Amplitude Curves

The vertical displacement of the tire centroid perpendicular to the pavement surface was adopted as the metric for the tire–pavement excitation effects. While employing a two-dimensional tire/pavement model to derive excitation involves a pragmatic simplification that cannot fully capture lateral pressure redistributions, transverse tread–block interactions, or anisotropic texture effects, this approach was justified for the current analysis. On the one hand, established research [8,54,55] indicates that for steady-state, straight-line rolling, the radial (vertical) vibration induced by road macro-texture is the primary driver of tire carcass excitation. The contribution of this vertical component to the overall sound pressure level (SPL) is significantly greater than that of lateral redistributions. On the other hand, the noise-reduction efficacy of Porous Asphalt Concrete (PAC) is predominantly governed by mitigation of the air pumping effect. As this mechanism is heavily localized in the longitudinal contact zone where tread grooves compress and release air, two-dimensional simplification effectively captures the essential acoustic characteristics.

Initially, the two-dimensional tire model was coupled with the two-dimensional pavement model, with constraints applied to the pavement’s base and lateral boundaries

Next, a tire–pavement friction coefficient of 0.6, rolling speed of 60 km/h, and vertical load of 300 kg were defined. Subsequently, the assembly was discretized into CPS4R elements to establish a complete two-dimensional tire–pavement rolling model, as shown in Figure 5. Finally, three pavement textures (PAC-10, SMA-10, and AC-10) were input into the model to compute the pavement excitation amplitude curves.

3.2. Finite-Element Modeling of Tire–Pavement Vibration Noise

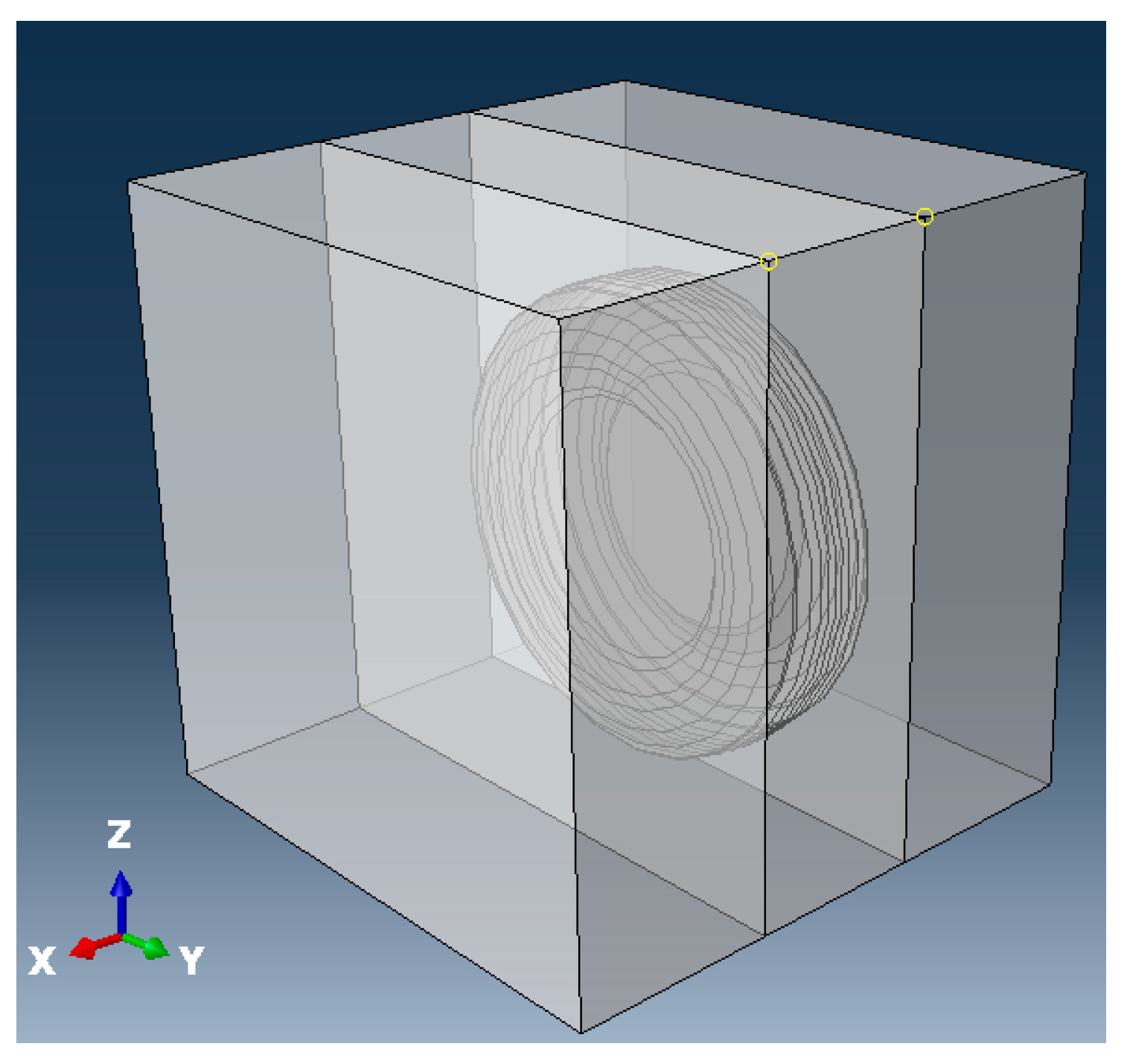
3.2.1. Three-Dimensional Tire Model

In this study, the model was treated as follows to reduce the model operation. (1) Fix The position of the tire in the model was fixed and only fixed-point rotation performed. (2) The Amplitude function module in finite element software was used to input relevant vibration amplitude parameters to represent the excitation effect of pavement on tire. (3) When modeling the tire structure, only the appearance of the rubber part was considered, as shown in Figure 6, with detailed structural parameters provided in

Table 7. Dimensional parameters of three-dimensional tire model.

	Outer Diameter (m)	Inner Diameter (m)	Width (m)	Thickness (m)
Tire tread	0.22	0.2	0.15	0.02
Sidewall	0.2	0.15	0.002	0.05

.

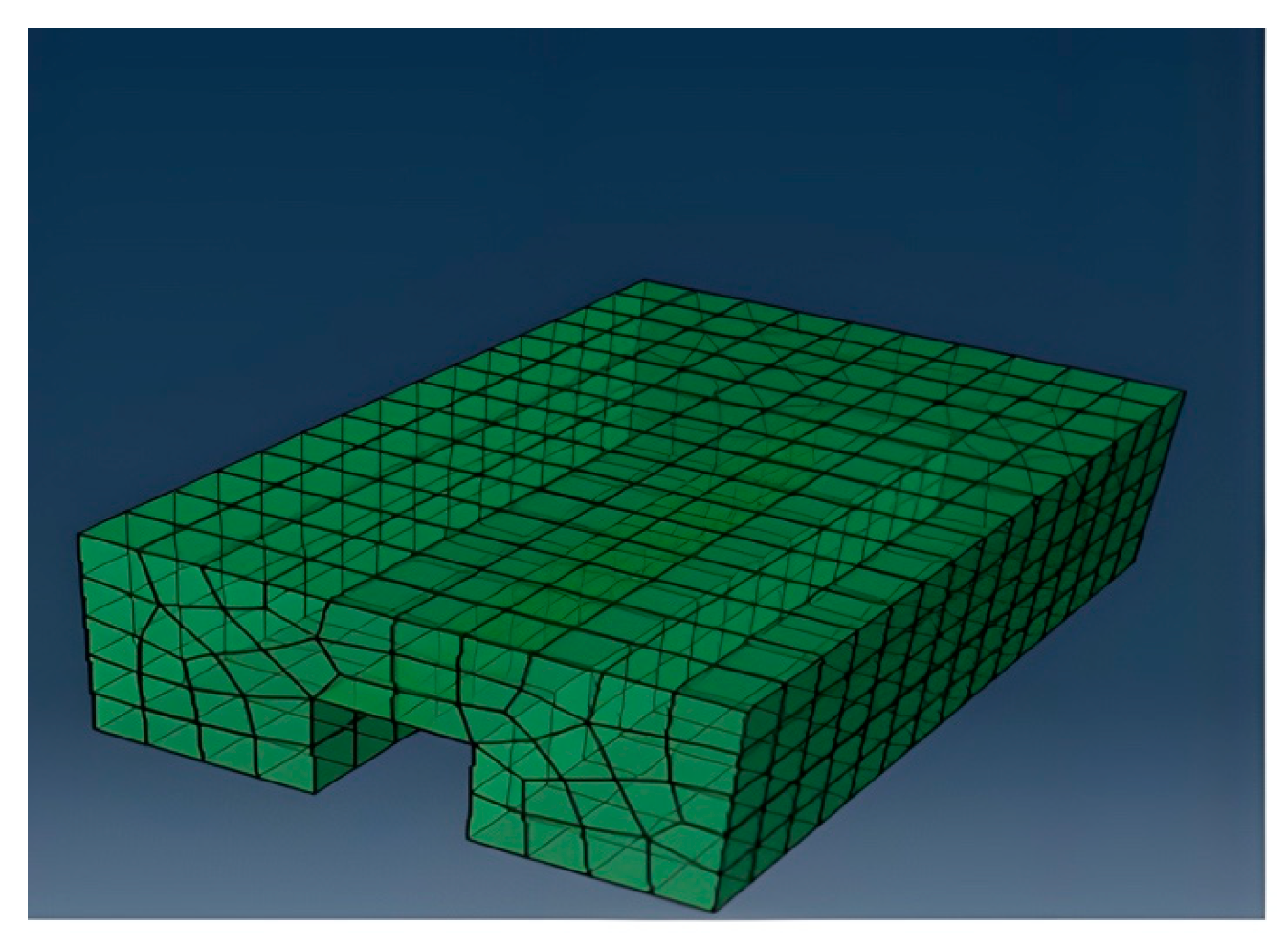
3.2.2. Three-Dimensional Pavement Model

With the aim of simulating the influence of pavement morphology on tire–pavement noise, the extracted excitation amplitude curves were input into both the vibration noise model and the air pumping noise model. The pavement slab in the three-dimensional model was defined as a linear elastic material, while material parameters for the other components are displayed in

Table 8. Material parameters of road surface in three-dimensional pavement model.

Structure Type	Density (kg/m3)	Elasticity Modulus (pa)	Poisson Ratio	Damping Ratio
Road surface	2400	1.6 × 109	0.32	0.06

. Specifically, the elasticity modulus (1.6 × 10⁹ Pa) and damping ratio (0.06) selected for the pavement represent the representative dynamic response of asphalt mixtures at 20 °C and a loading frequency of 10 Hz. This loading frequency corresponds to the tire contact patch duration at the vehicle speed of 60 km/h utilized in the simulations. Based on experimentally measured data (Table 4), specific void ratios were assigned to the different pavement types: PAC-10 (19.4%), SMA-10 (4.6%), and AC-10 (4.3%). For the PAC-10, the high internal void ratio is represented as a volumetric venting mechanism. This approach treats the interconnected pores as a path for high-pressure air to dissipate vertically into the pavement matrix during tread-pavement interaction, effectively mitigating the source-level air-pumping pressure gradients. Finally, the three-dimensional pavement model was constructed by discretizing the geometry with C3D8R elements.

3.2.3. Three-Dimensional Air Model

First, nonreflecting boundary conditions were applied to the air model with dimensions of 1000 mm × 1000 mm × 800 mm, and material parameters were defined as listed in

Table 9. Material parameters of three-dimensional air models.

Material	Elasticity Modulus (KPa)	Density (kg/m3)
Air	142	1.2

. Next, Boolean operations were performed by using the Assembly module to create a cavity conforming to the tire geometry within the air domain, ensuring accurate simulation of tire–air interactions and associated vibration/noise generation. Following these operations, the final 3D air model configuration is shown in Figure 7.

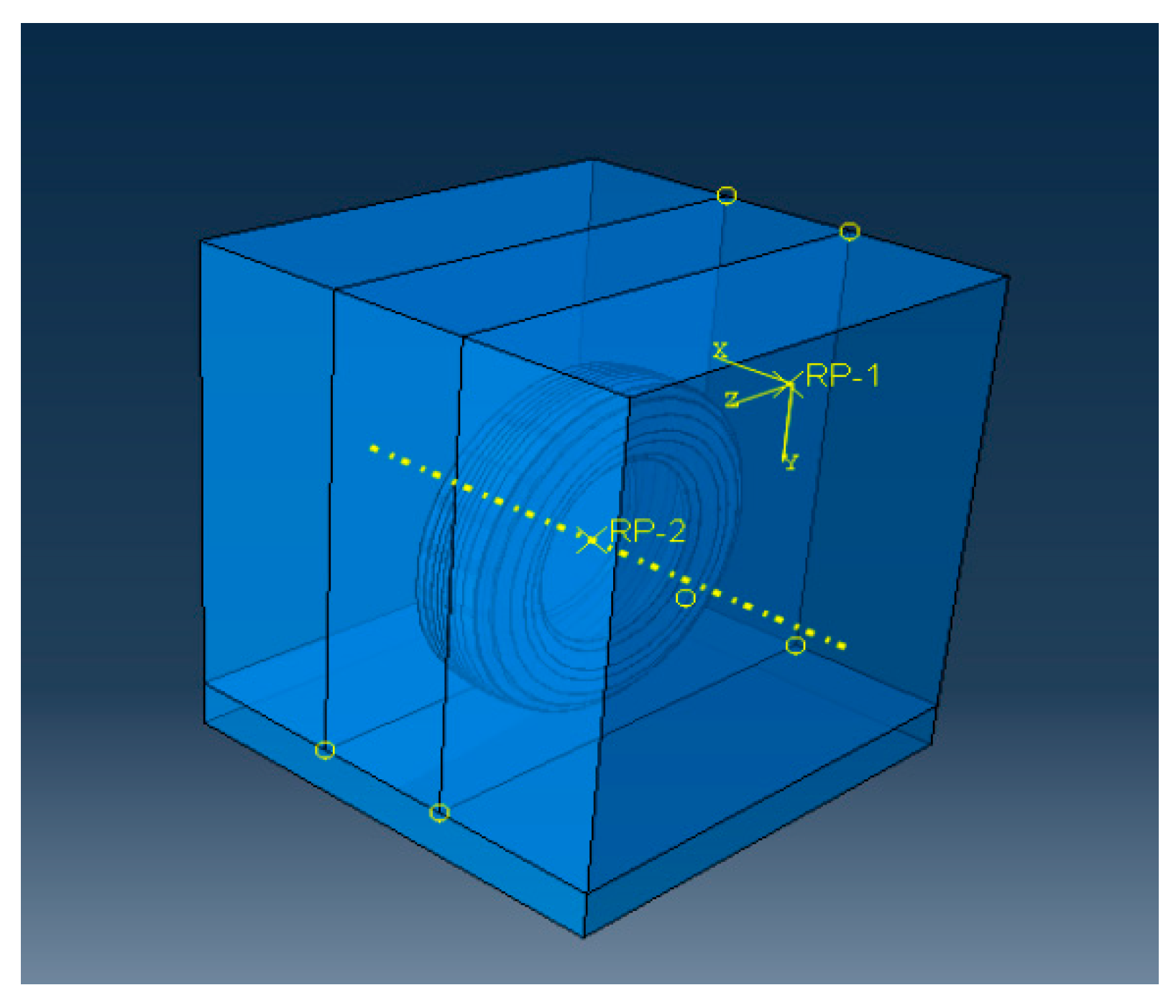
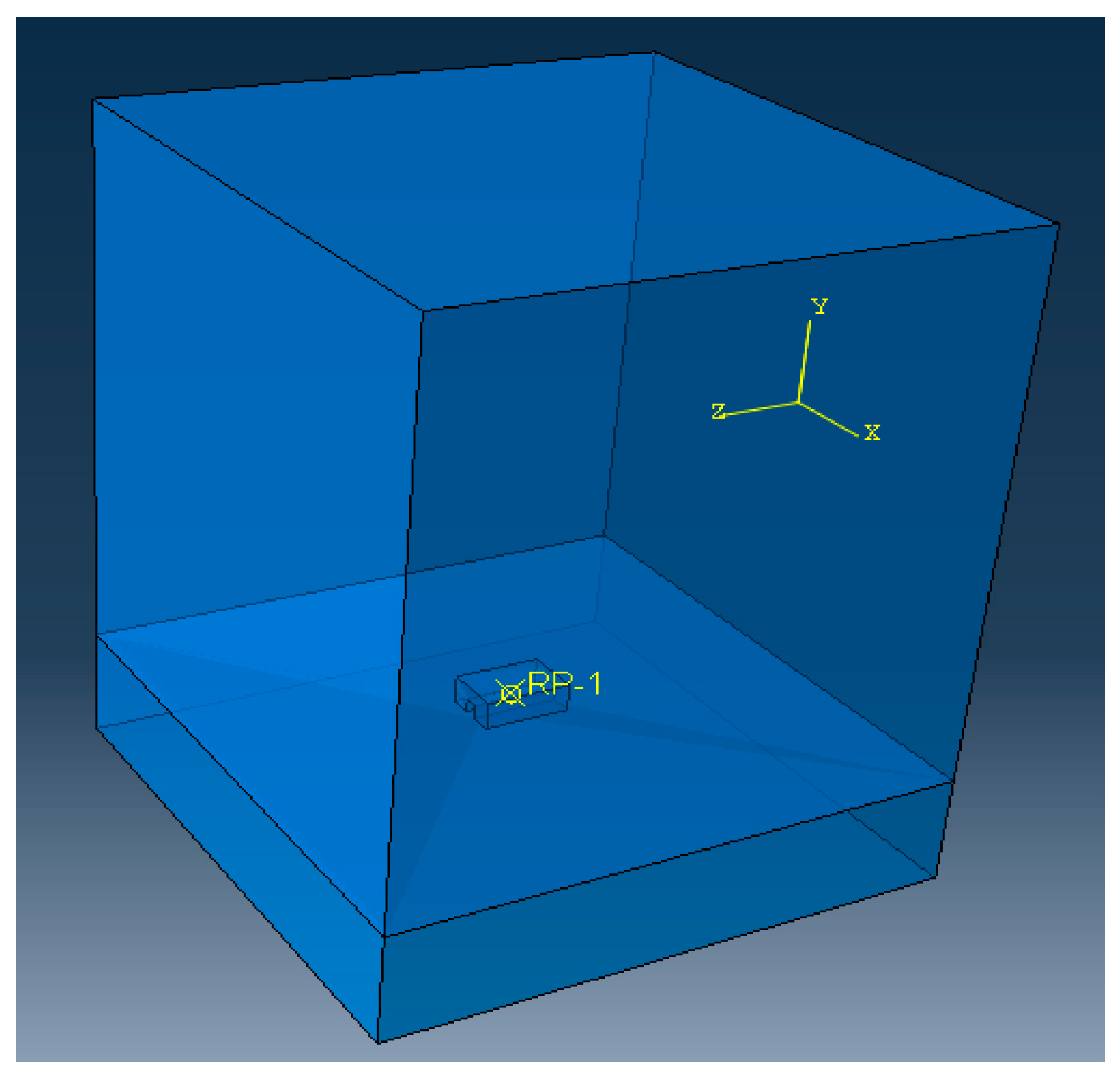
3.2.4. Assembly Model and Boundary Condition Configuration

The mutual interactions among the tire, pavement, and air models were defined in the Interaction module, with tie constraints applied to ensure kinematic compatibility. A frictional contact relationship was established between the tire and pavement models, accompanied by a concentrated force applied at the tire center to simulate vertical loading. The lateral and top surfaces of the air model were assigned non-reflective planar impedance to minimize acoustic wave reflections, while contact interfaces were configured as totally reflective to capture acoustic–structural interactions. Additionally, displacement and rotational constraints were imposed on the pavement slab to restrict rigid-body motion. The fully assembled vibration noise coupling model is illustrated in Figure 8.

3.3. Finite Element Modeling of Air Pumping Noise

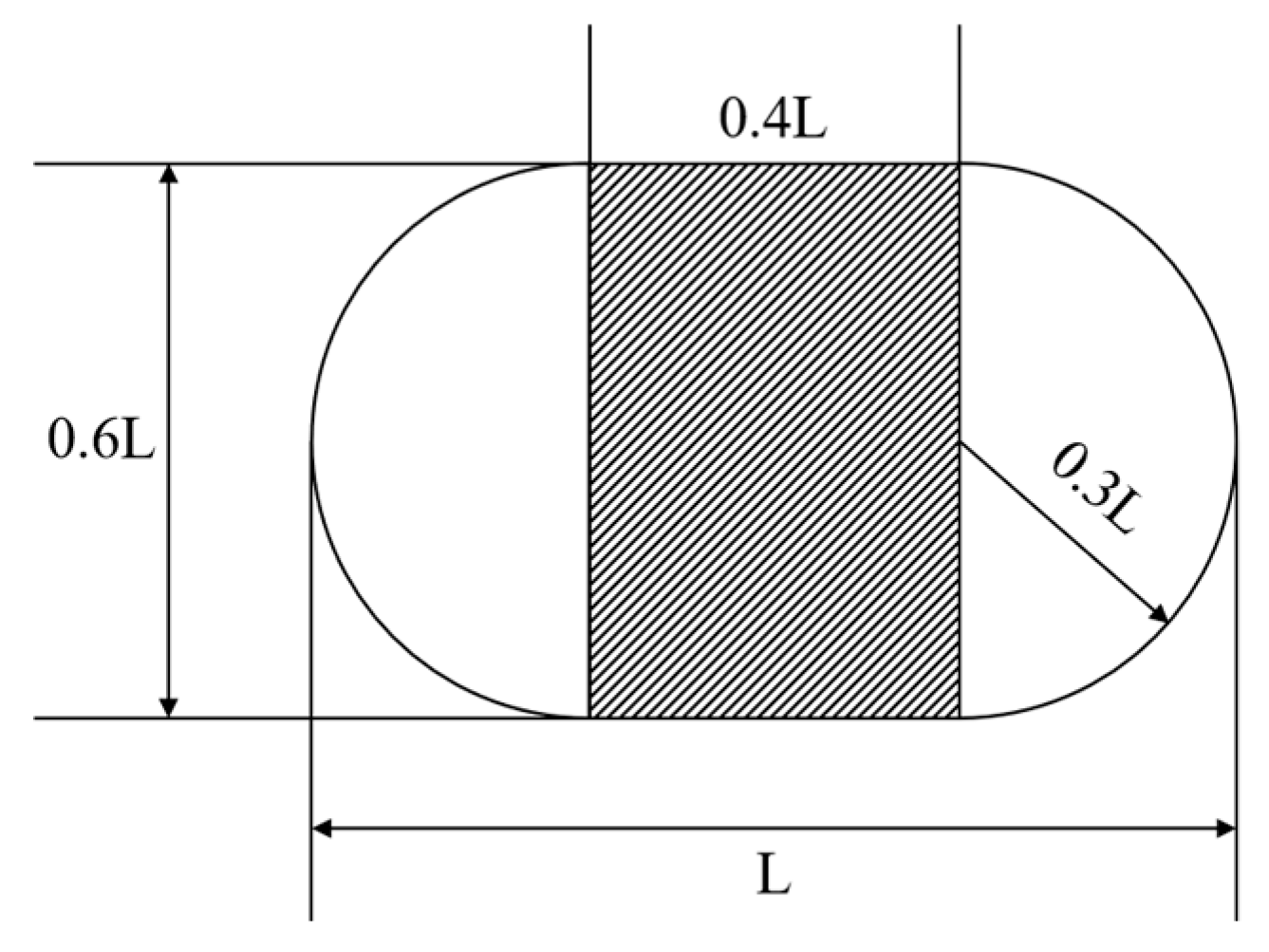
3.3.1. Tire Pattern Block Model

Air pumping noise predominantly originates from the tire–pavement contact zone and exhibits minimal correlation with other tire regions. Simulating the full tire structure introduces inaccuracies due to elastic rebound vibrations in non-contact regions when the tire disengages from the pavement. Given that tires are primarily composed of rubber, the air pumping noise generated during tire–pavement contact resembles that of an isolated rubber block. To address this, the contact region was simplified to a rubber block with longitudinal grooves replicating tread patterns [56], effectively reducing computational costs while preserving acoustic signature fidelity.

When subjected to loading, the tire deforms to create a contact patch that can be geometrically approximated as a composite surface comprising a 0.4 L × 0.6 L rectangular section with two semicircular ends of radius 0.3 L, as illustrated in Figure 9.

The ground contact area A_c is calculated as:

$$A_c=0.4L\times 0.6L+{\left(0.3\right)}^2\times \pi$$

(7)

The flattened length L, dependent on the axle load F and tire pressure p, is derived from the following:

$$L=\sqrt{{\displaystyle \frac{A_c}{0.5227}}}=\sqrt{{\displaystyle \frac{F}{0.5227p}}}$$

(8)

The full tire structure is replaced by a 250 mm × 150 mm × 25 mm rubber block modeled with C3D8H hybrid elements (Figure 10) for air pumping noise simulation, with computational efficiency being systematically preserved through this geometric simplification.

3.3.2. Model Assembly and Boundary Condition Configuration

The assembly of the air pumping noise model followed the same procedure as the vibration noise model. A cavity conforming to the rubber block geometry was first reserved within the pre-built air domain, after which contact interactions were defined at the rubber block-pavement, air-rubber block, and air-pavement interfaces. To realistically represent the physical system, the bottom of the pavement was constrained in the normal direction, lateral boundaries were assigned non-reflecting conditions to suppress spurious wave reflections, and the outer air boundaries were treated with impedance-type absorbing conditions to approximate free-field propagation. Tire–pavement interaction was modeled as surface-to-surface contact with a friction coefficient of 0.6. Finally, pressure was applied to the rubber block via the Load module, with excitation amplitudes consistent with those of the vibration noise model, to reproduce air pumping noise during tread–ground contact. The fully assembled model is illustrated in Figure 11.

3.4. Synthesis of Noise

The structural vibration responses of the tire–pavement system were solved in the solid domain, while acoustic wave propagation was calculated in the surrounding air domain. These two subsystems were coupled at the tire–pavement interface through pressure-displacement continuity conditions. The total sound pressure level (SPL) was obtained by superimposing the vibrational and air-pumping contributions in the frequency domain, following the principle of sound wave superposition. When n columns of sound waves coexist in the same medium with instantaneous sound pressures p_i, p₂, … p_n, the instantaneous sound pressure p of the synthesized acoustic field is expressed as follows:

$$p=p_1+p_2+p_3+\cdots +p_n=\sum p_i$$

(9)

where p_i denotes the instantaneous sound pressure of the i-th wave. Since noise comprises sound waves with distinct frequencies and phase differences, the average acoustic energy density of the synthesized field equals the summation of the individual wave energy densities:

$$p_{\epsilon }^2=p_{1\epsilon }^2+p_{2\epsilon }^2+p_{3\epsilon }^2\dots +p_{n\epsilon }^2$$

(10)

where p_ε represents the effective sound pressure of the synthesized field, and p_iε (i = 1,2,…, n) corresponds to the effective sound pressure of each wave component.

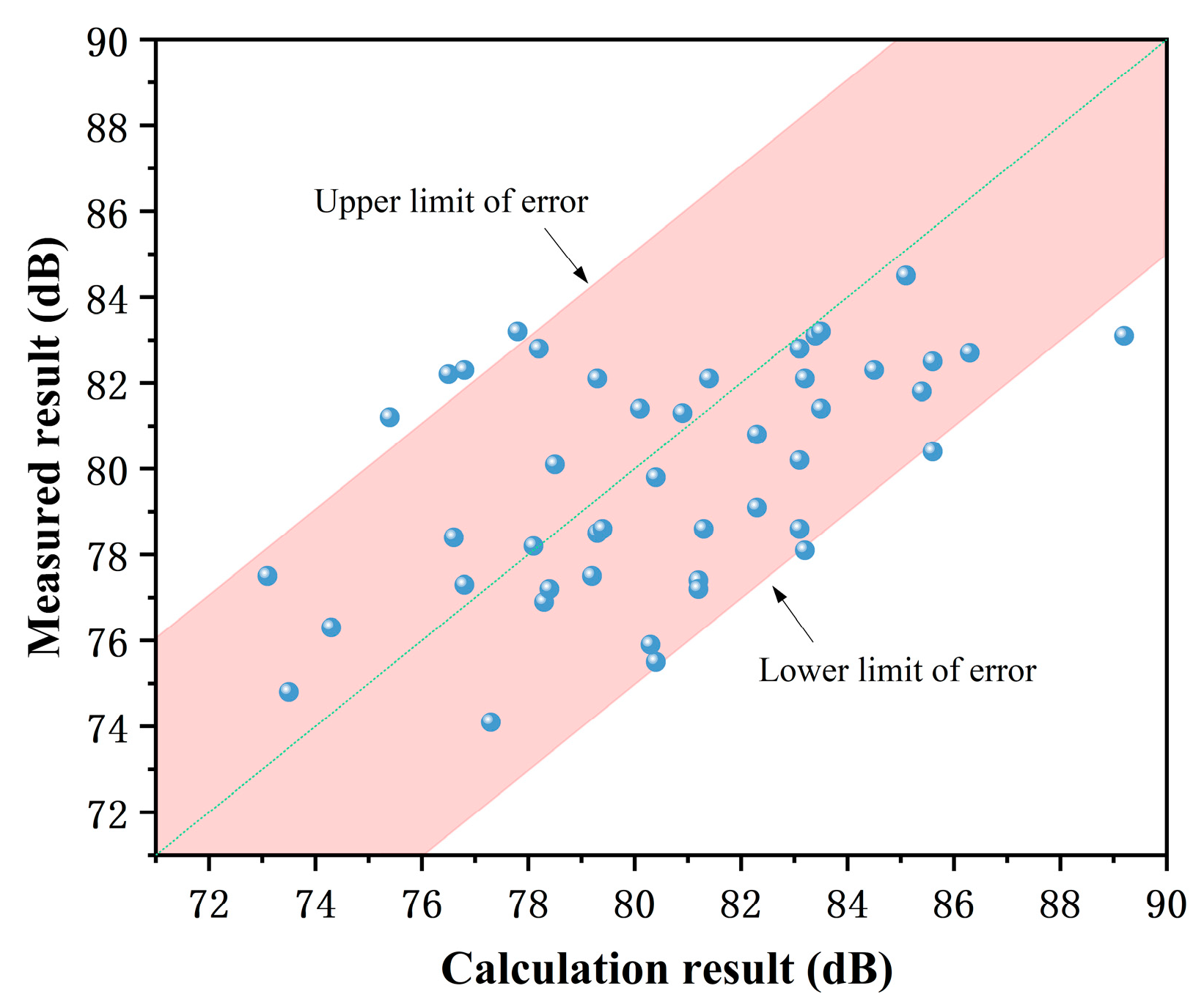
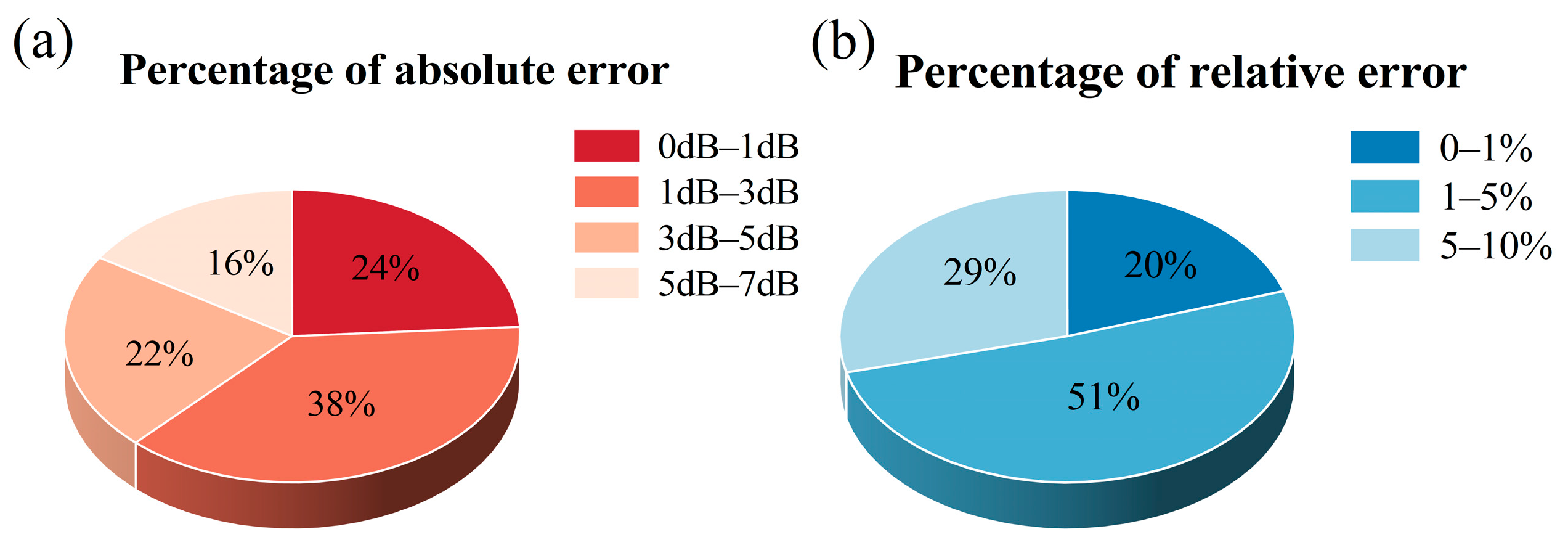
3.5. Model Validity Test

The experimental investigation was conducted using a Tire–pavement Dynamic Friction Analyzer (TDFA, Chongqing Jiaotong University, Chongqing, China) to mimic real-time tire–road interactions, with tire–pavement interaction noise levels under various operational conditions being directly measured through a Class A sound level meter (SMART SENSOR AR844). Forty-five datasets were systematically acquired in laboratory settings, where each dataset was collected over a 60 s measurement duration with 10 s interval sampling, followed by a time-averaged noise level calculation per dataset. Corresponding parameters, including pavement type, vehicle speed, axle load, and wheel characteristics, were input into simulation software to establish validation models for verifying the accuracy of the numerical results.

The TDFA system is composed of four integrated subsystems: hydraulic system, dynamic drive system, sensing system, and Frictional Instrument Center of Analysis and Control (FICAC, version 1.0.0.0) software, through which precise simulation of tire–pavement interactions under varying operational conditions is achieved [57]. Pressure is provided and controlled by the hydraulic system to ensure accuracy in tire load application. The rotation of pavement specimens is driven by a low-vibration silent motor in the power system to replicate actual wheel motion. Tire forces and speeds are monitored in real-time by pressure and velocity sensors within the sensing system, with collected data being transmitted to the FICAC system. Experimental parameters are set and adjusted in real-time through the FICAC software, which is designed to integrate multi-sensor data for centralized analysis. Figure 12 illustrates the TDFA’s physical configuration and the FICAC operation interface, while

Table 10. Equipment parameters of Class A sound level meter.

Item	Parameter
Calibration Source	94 dB @1 KHz
Measurement Range	30~130 dBA, 35~130 dBC
Accuracy	±1.5 dB (Reference Sound Pressure Standard, 94 dB @1 KHz)
Frequency Response	31.5 Hz~8.5 KHz
Resolution	0.1 dB
Measurement Range Gear	30~80, 50~100, 60~110, 30~130
Dynamic Range	50 dB/100 dB
Frequency Weighting	A and C
Digital Display	4 digits
Sampling Rate	20 times/second
AC Signal Output	4 Vrms/full scale, output impedance about 600 ohms
PWM Output	Duty Cycle = ${\displaystyle \frac{0.01 \times \mathrm{dB} value }{3.3}}\times 100\%$
Perpetual Calendar Accuracy	±30 s/day
Battery Capacity	4700 entries
Microphone	1/2 inch condenser microphone
Operating Voltage	6 V
Dimensions	67 × 30 × 183 mm
Battery Life	20 h (continuous use)

lists the technical specifications of the Class A sound level meter.

4. Results and Analysis

4.1. Model Validity Verification

As illustrated in Figure 13 and Figure 14, the model exhibits a mean absolute error of 2.6 dB, with errors distributed within the 1 dB to 3 dB range. The cumulative frequency of errors within 5 dB reaches 84%, of which 22% fall within the 0–1 dB range. For relative errors, 51% of data points cluster in the 1–5% range, while 20% demonstrate relative errors below 1%, and all relative errors remain under 10%. Furthermore, to statistically verify the model’s reliability, a paired-sample t-test was conducted on the 45 datasets. The Shapiro–Wilk test confirmed the normality of the differences (p = 0.070 > 0.05). The paired-sample t-test results (t = 1.47, p = 0.149 > 0.05) indicated no significant difference between the measured and simulated means, with a negligible mean bias of only 0.696 dB. These combined results demonstrate high consistency between the numerical simulations and experimental data, validating the model’s capability to accurately capture noise generation mechanisms in asphalt pavements under tire excitation.

4.2. Excitation Amplitude Curves

Figure 15 presents the excitation amplitude curves for three asphalt pavement types: AC-10, SMA-10, and PAC-10. These curves demonstrate pronounced similarities and disparities, all exhibiting periodic variations attributable to the repetitive profile segments stitched in the pavement model. The PAC-10 pavement exhibits the maximum excitation amplitude, while AC-10 shows the minimum amplitude, indicating that PAC generate stronger vibrational excitation due to their rougher surface morphology.

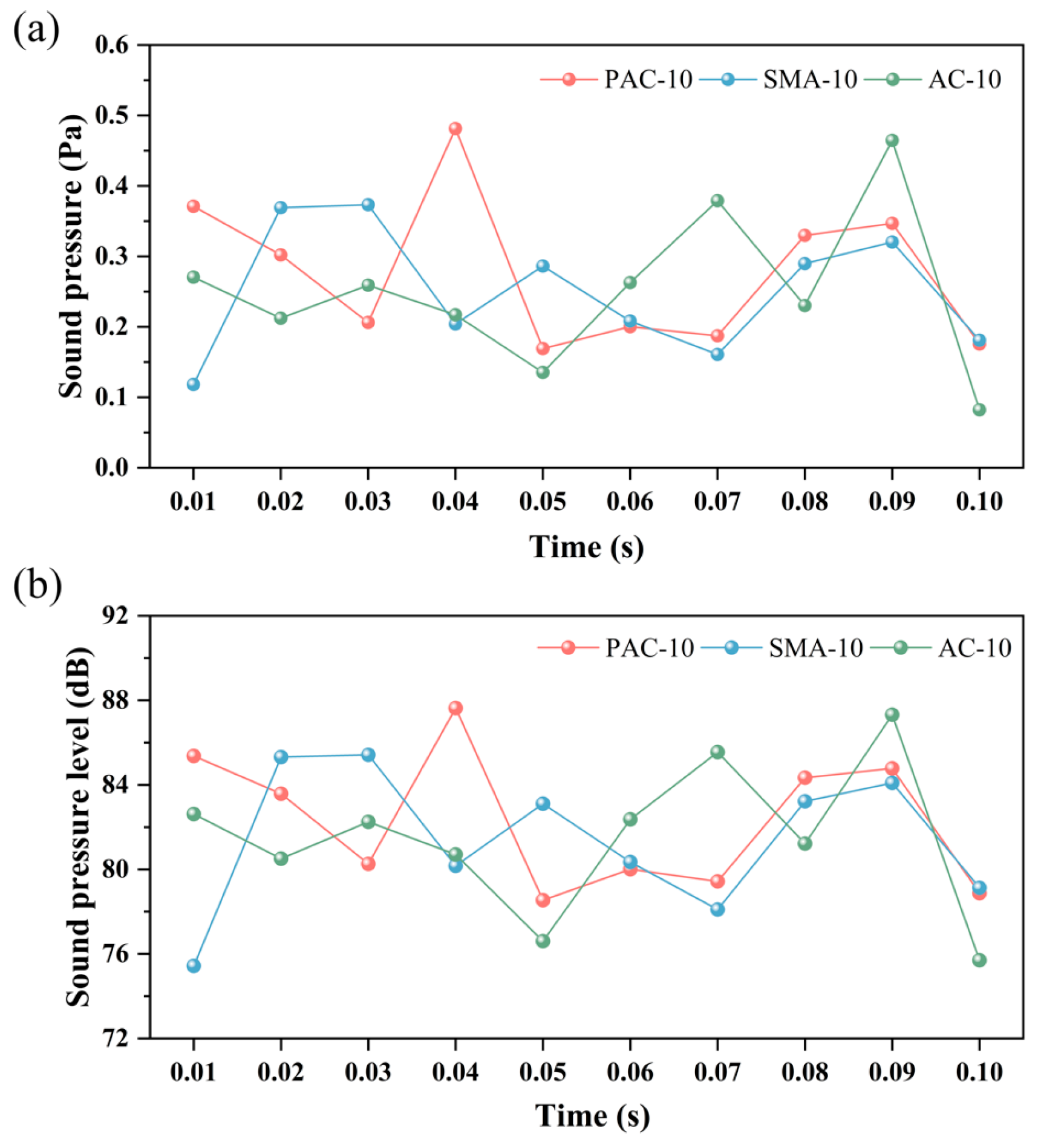
4.3. Vibration Noise Analysis

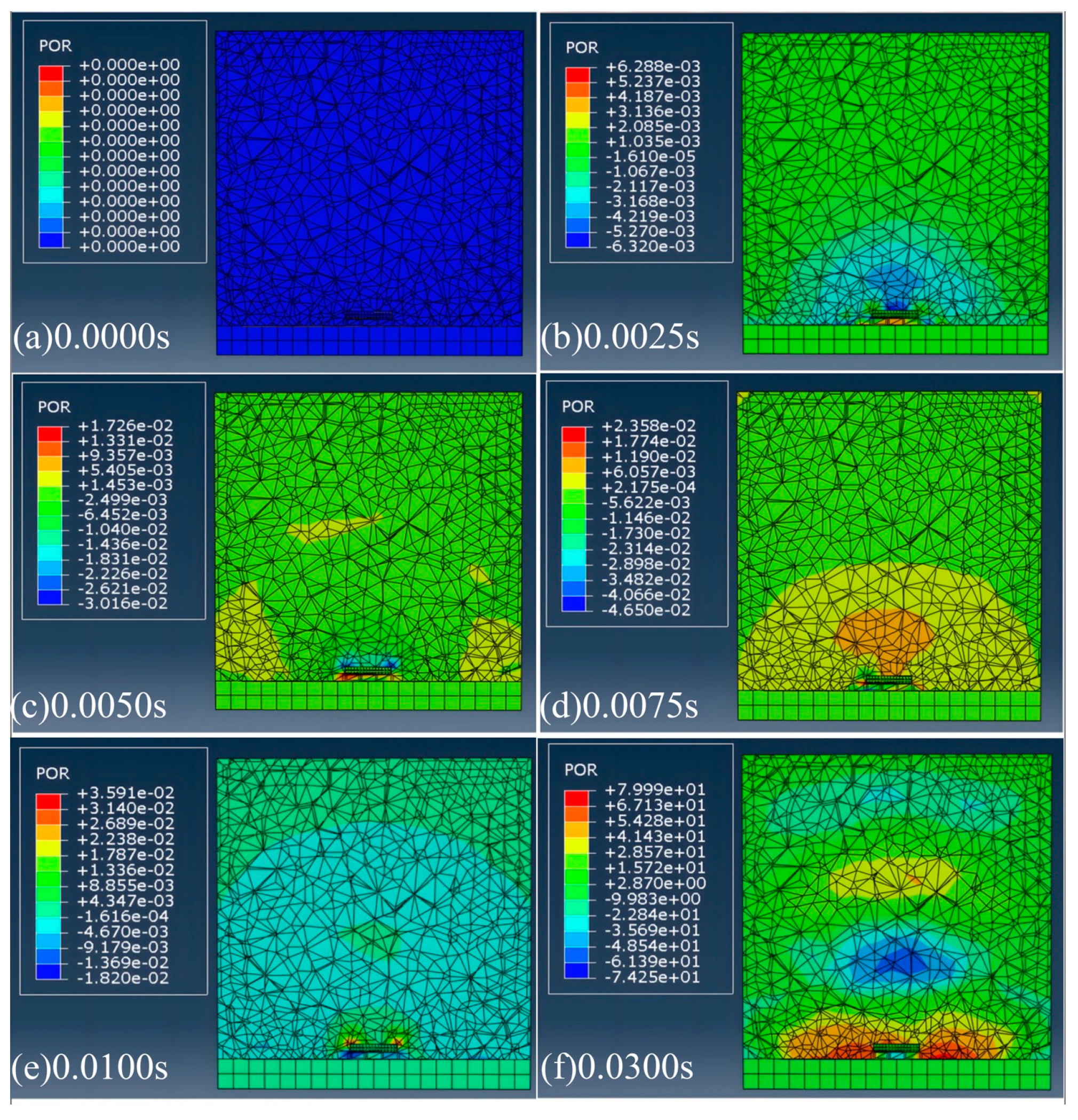
4.3.1. Vibration Noise Sound Pressure Contour Analysis

In the vibration noise model, the vehicle speed was set to 60 km/h, and the vibration excitation curve of PAC-10 was imported. Different vertical displacements were applied via the Amplitude module, and the analysis was performed using Abaqus/Explicit. The sound pressure contour maps of vibration noise on the PAC-10 pavement at different time steps were obtained, as shown in Figure 16.

Vibration noise sound pressure contour plots clearly visualize spatiotemporal sound pressure (POR) distributions, where color gradients mapped by virtue of a scale bar quantify pressure magnitudes. Analyzing plots from t = 0.00 s to t = 0.03 s reveals noise generation at the tire edge, semicircular propagation outward, and eventual evolution into spherical acoustic waves, demonstrating transient vibration noise dynamics.

4.3.2. Comparative Analysis of Vibration Noise of Different Pavement Types

Node 29 in the air domain 0.5 m from the tire–pavement contact point was selected as the reference location. Measurements at this node recorded time-resolved sound pressure and SPL of vibration noise for PAC-10, SMA-10, and AC-10 pavements at 60 km/h, with temporal evolution curves shown in Figure 17. The Figure reveals an obvious correspondence between sound pressure and SPL curves across all three pavement types, attributable to their shared noise source, that is tire–pavement vibrational interactions. As SPL represents the logarithmic transformation of sound pressure and both metrics share direct frequency-domain correlations, pressure fluctuations manifest analogous trends in SPL profiles.

Table 11. Average sound pressure and sound pressure level of different pavement.

Pavement	Sound Pressure (Pa)	Sound Pressure Level (dB)
PAC-10	0.277	82.3
SMA-10	0.251	81.4
AC-10	0.250	81.0

presents the average sound pressure and SPL of vibration noise for three pavement types. Data indicate that the ranking of vibration noise magnitudes (PAC-10 > SMA-10 > AC-10) aligns with their void ratio hierarchy. The PAC generates the highest noise due to its rougher surface texture, which amplifies tire excitation amplitudes [58] (Figure 15) and enhances acoustic wave scattering and reflection during propagation, hence elevating noise complexity and overall levels [59,60].

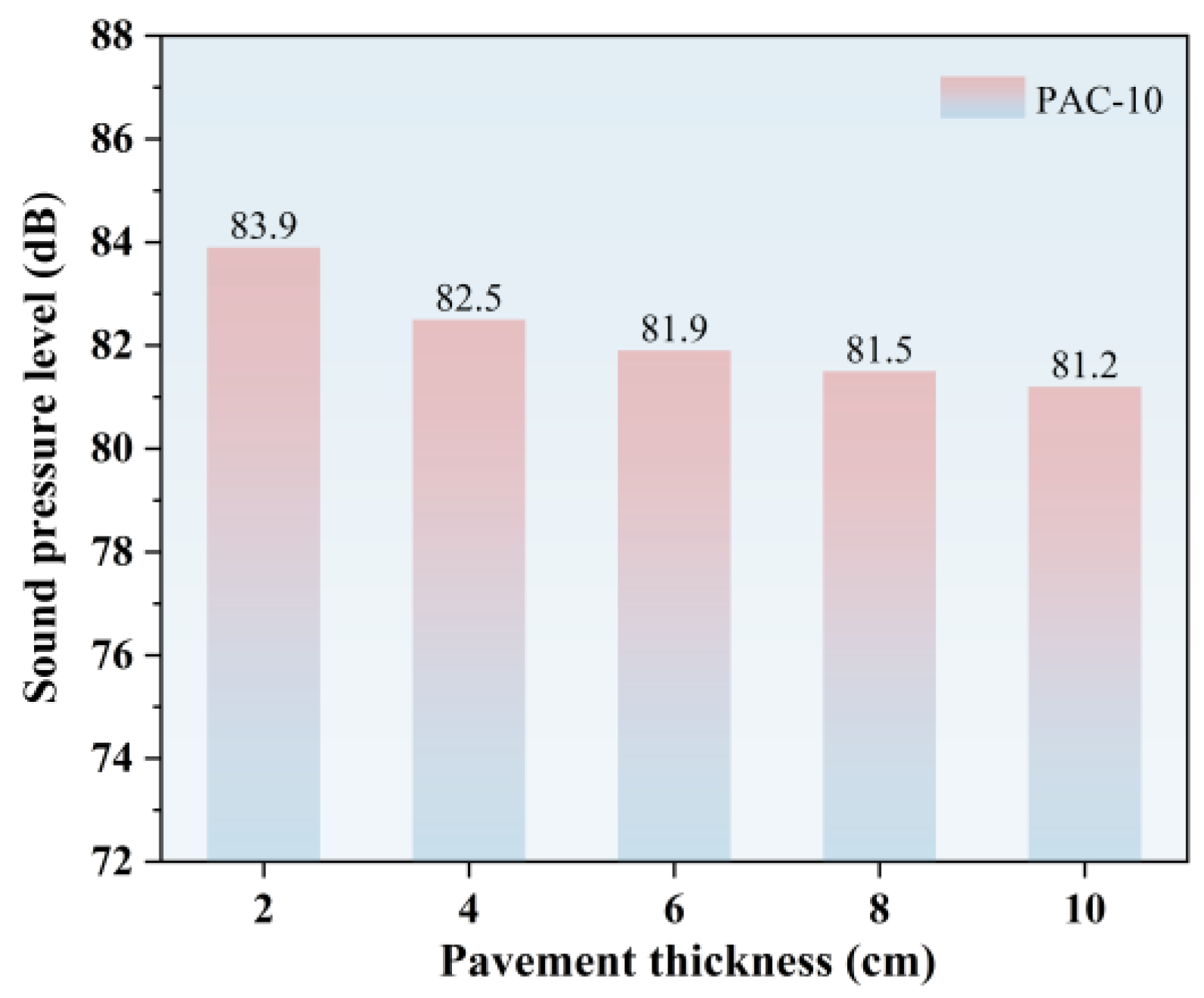
4.3.3. Influence of Pavement Thickness on Vibration Noise

Extensive research has confirmed pavement thickness critically governs noise attenuation mechanisms. In order to explore its effect, the simulations maintained identical parameters except for the PAC-10 surface layer thickness, which was varied at 2 cm, 4 cm, 6 cm, 8 cm, and 10 cm. Finite-element simulations with the vibration model generated SPL profiles for each thickness condition.

As depicted in Figure 18, the vibration noise SPL of the PAC-10 asphalt pavement exhibits a progressive reduction with increasing surface layer thickness. When the surface layer thickness increases from 2 cm to 6 cm, the reduction in vibration noise is significant; however, beyond 6 cm, the attenuation rate diminishes, indicating a saturation threshold for noise mitigation. This weakening effect arises from thicker pavements’ enhanced structural stiffness and damping characteristics, which more effectively disperse and absorb vibrational energy generated at the tire–pavement contact zone [61]. Concurrently, increased thickness amplifies the acoustic wave attenuation within the pavement matrix, further reducing noise radiation efficiency [62,63,64].

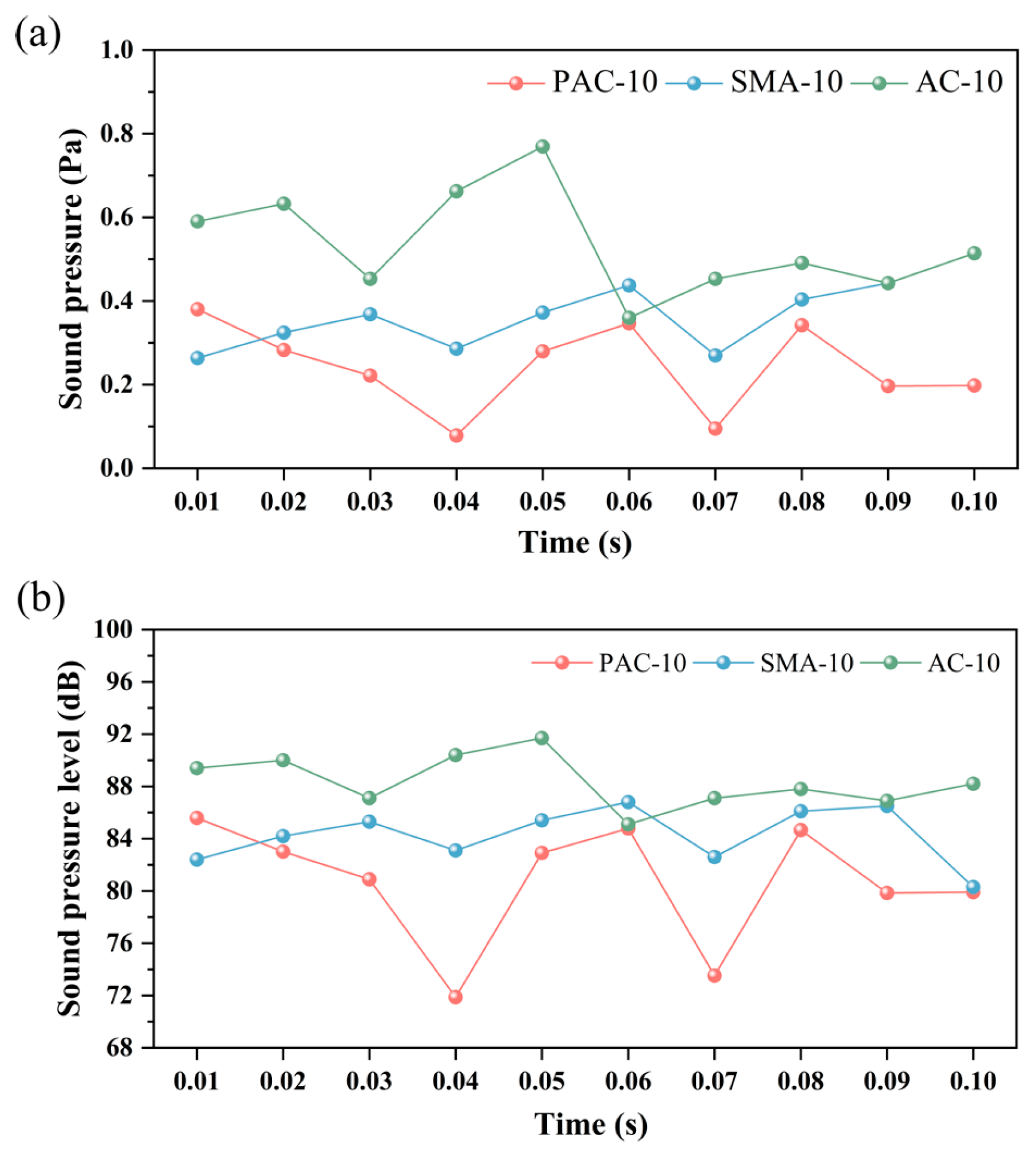
4.4. Air Pumping Noise Analysis

4.4.1. Air Pumping Noise Sound Pressure Contour Analysis

Figure 19 presents the sound pressure contours of the air pumping noise on PAC-10 pavement at different time instances. The air pumping noise originates at the edges of the rubber block and propagates outward. The rubber block can be approximated as an acoustic source, with sound waves radiating outward as spherical acoustic waves. Higher sound pressure values near the source region indicate more pronounced noise intensity close to the generation zone [65], aligning with real-world acoustic propagation characteristics [12].

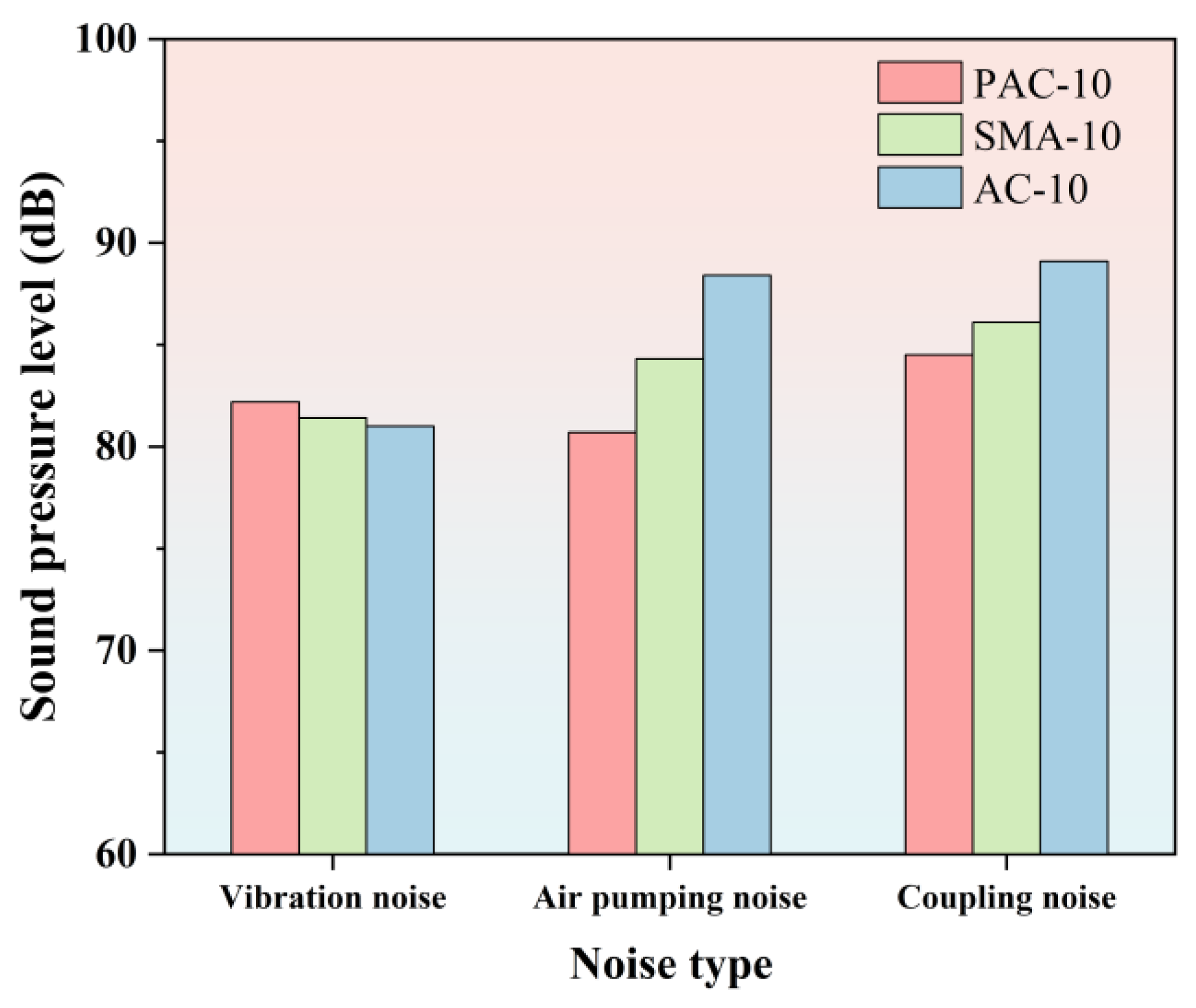
4.4.2. Comparative Analysis of Air Pumping Noise of Different Pavement Types

Figure 20 illustrates the temporal variations in sound pressure and SPL of the air pumping noise for three pavement types at 60 km/h. The PAC-10 pavement demonstrates lower values in both sound pressure and SPL compared to SMA-10 and AC-10 pavements. As shown in Figure 20a, the maximum sound pressure of PAC-10 measures approximately 0.38 Pa, while SMA-10 and AC-10 exhibit peak values of 0.51 Pa and 0.77 Pa, respectively. Figure 20b reveals that the SPL of PAC-10 fluctuates between 71 dB and 86 dB, compared to 80–87 dB for SMA-10 and 85–92 dB for AC-10, which displays the highest noise levels.

The superior noise reduction performance of PAC-10 can be attributed to its porous structure, which effectively absorbs and scatters sound waves through multiple internal reflections and dissipation mechanisms [66]. Conversely, the dense structure of AC-10 predominantly reflects sound waves at the surface interface rather than facilitating internal energy absorption [67], resulting in elevated SPLs and inferior noise mitigation performance. This hierarchical pattern in acoustic performance (PAC-10 < SMA-10 < AC-10) aligns with the structural characteristics and sound energy dissipation mechanisms inherent to each pavement type.

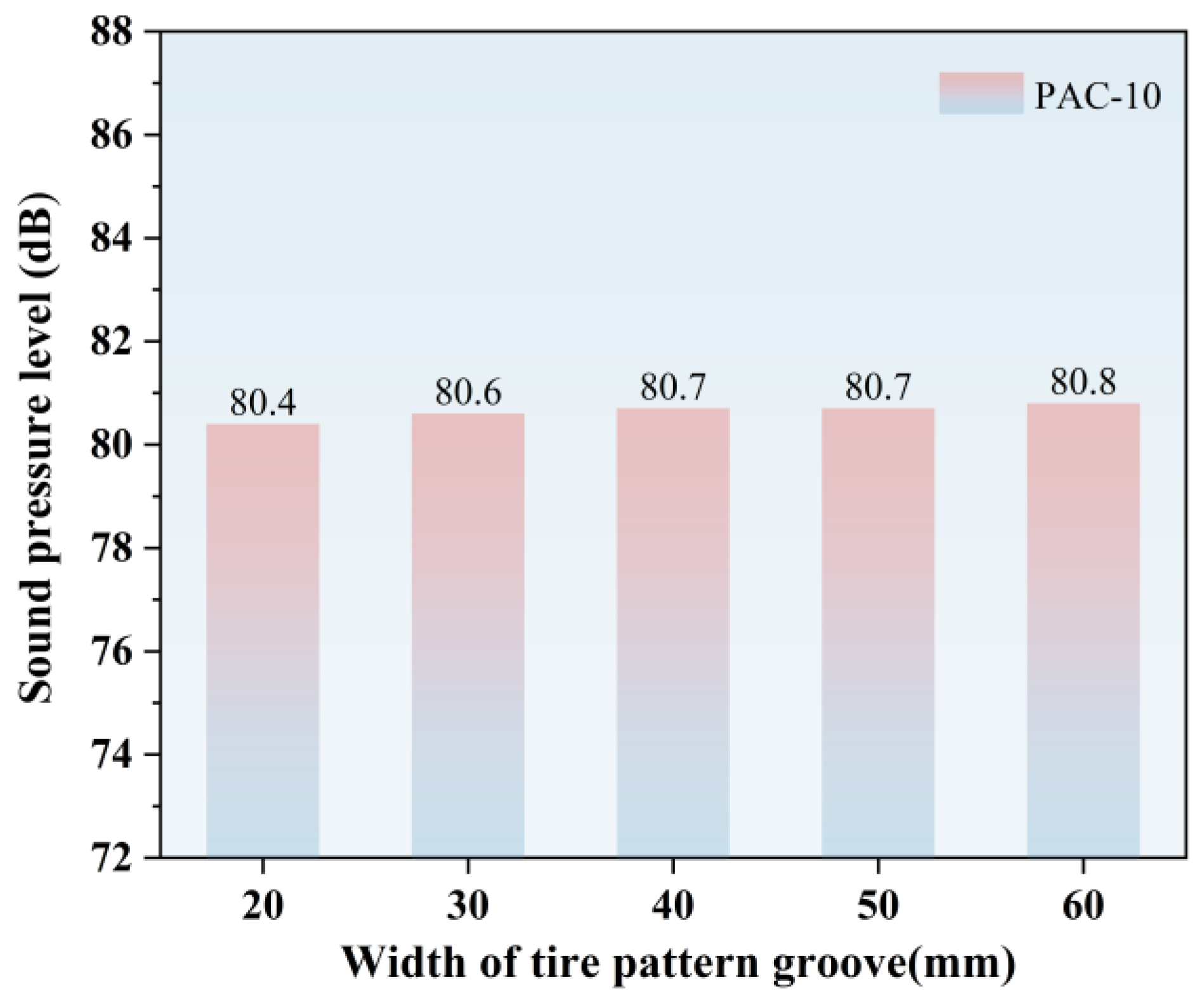
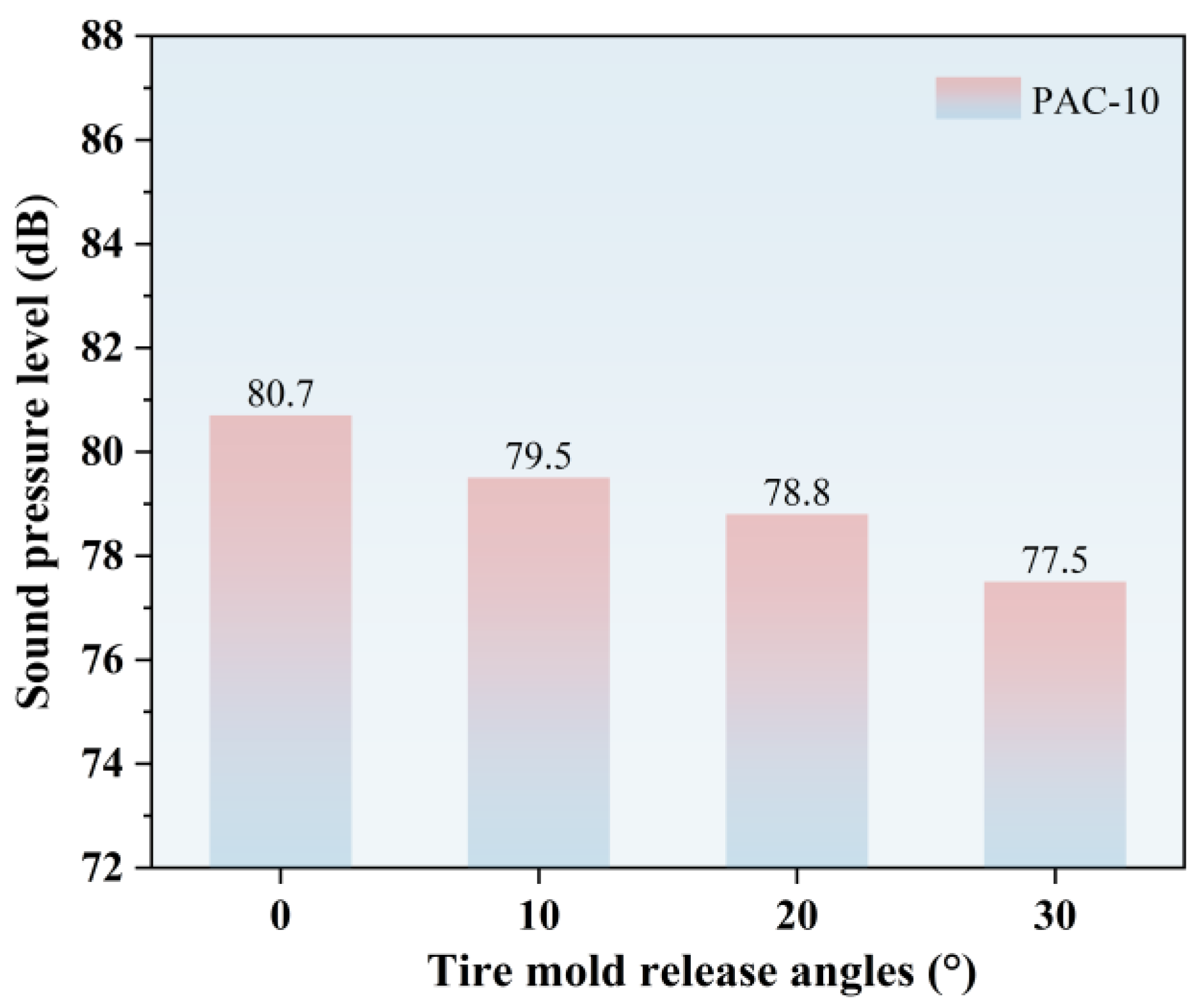
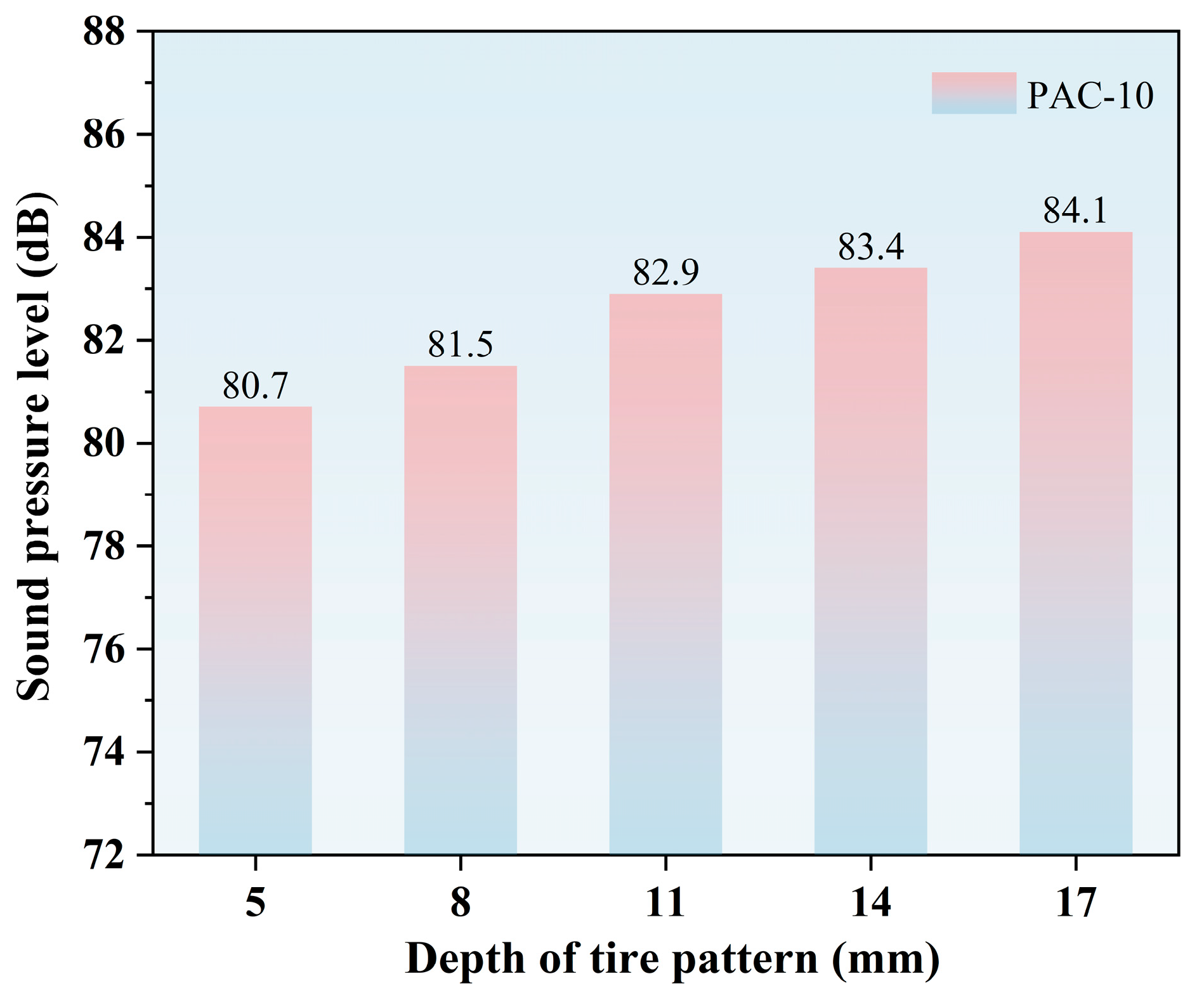
4.4.3. Influence of Tire Pattern Appearance on Air Pumping Noise

Significant influence of tire pattern appearance on tire–pavement pumping noise is observed, with its mechanisms primarily manifested through three aspects. First, during tire rotation, periodic compression and release are generated as tread blocks contacting the pavement surface, creating a “pumping effect” that induces air vibrations and noise generation [68]. Second, variations in tread design alter airflow patterns within the groove–road interface, where complex or irregular tread configurations are found to intensify air turbulence and vibrational energy, contributing to elevate noise levels [69]. Additionally, tread geometry and depth directly influence the contact area and pressure distribution between the tire and pavement, with uneven pressure distribution and increased contact area both contributing to amplified noise emissions [70]. In summary, tire pattern appearance plays a critical role in both the generation and propagation of the air pumping noise through these interconnected mechanisms. Therefore, this section systematically investigates the influencing mechanisms of tire patterns on air pumping noise from three dimensions: groove width, tread depth, and mold release angles.

(1) Tire Groove Width Variations

Tire groove widths were configured at 20 mm, 30 mm, 40 mm, 50 mm, and 60 mm while maintaining other parameters constant in the simulation model. As displayed in Figure 21, the corresponding SPLs of air pumping noise were measured as 80.4 dB, 80.6 dB, 80.7 dB, 80.7 dB, and 80.8 dB, respectively, with a mere variation amplitude of 0.4 dB (80.4–80.8 dB). This indicates that no significant alteration in air pumping noise levels was observed across the 20–60 mm groove width range. Hence, adjusting groove width alone within this interval is insufficient for effective noise mitigation, which necessitates integrated optimization of tread depth, material properties, and tire structural parameters.

Furthermore, tire tread groove width is critically linked not only to the generation of air pumping noise at the tire–pavement interface, but also to vehicular safety and ride comfort. To achieve optimal balance between air pumping noise suppression, safety performance (particularly water drainage and traction capabilities), wear resistance, ride comfort, and handling stability, a groove width of 40 mm was identified as the optimal design parameter through comprehensive multi-objective optimization analysis.

(2) Variations in Tire Mold Release Angles

With other parameters were maintained constant and the groove width fixed at 40 mm, mold release angles were sequentially set at 0°, 10°, 20°, and 30° in the air pumping noise simulation model. As evidenced in Figure 22, air pumping noise was progressively attenuated with increasing release angles, demonstrating a 3.2 dB reduction when the angle was elevated from 0° to 30°. This acoustic improvement stems from enlarged mold release angles reducing the effective air volume within tread grooves, resulting in weakening compression-release cycles during tire–pavement interaction [71]. Simultaneously, streamlined airflow patterns were achieved through tapered grooves due to increased release angles, where aerodynamic resistance and pressure pulsations were substantially mitigated. The synergistic effect of restricted cavity resonance and stabilized airflow dynamics effectively suppresses air pumping noise generation mechanisms at their origin [72].

(3) Tire Groove Depth Variations

Aiming to investigate the influence of tire groove depth on air pumping noise, groove depth was configured at 5 mm, 8 mm, 11 mm, 14 mm, and 17 mm while groove width (40 mm) and mold release angle (0°) were maintained. As presented in Figure 23, the air pumping noise intensity was found to increase significantly with greater groove depths, rising from 80.7 dB at 5 mm to 84.1 dB at 17 mm. This result indicates that deeper tire tread patterns intensify the compression and release of air within the grooves, thereby increasing the air pumping noise. Consequently, reducing groove depth during initial tire design phases is confirmed as an effective strategy for mitigating tire–pavement air pumping noise. However, excessive reduction of groove depth was observed to compromise skid resistance performance, particularly under wet pavement conditions, thereby elevating safety risks. To solve this design paradox, in the development of high-performance tires, in-depth investigations are required to enable tread depth reduction while traction performance is synergistically enhanced; ensuring an optimal balance between these competing parameters is achieved through material and geometric optimizations.

Through systematic analysis of tread parameter influences, groove depth and mold release angle were identified as dominant factors governing air pumping noise generation. Therefore, during the tire design process, under the precondition that safety performance is maintained, tread depth reduction or mold release angle enlargement can be implemented, resulting in effective suppression of tire–pavement air pumping noise [73,74].

4.5. Tire–Pavement Coupling Noise Analysis Based on Simulation Models

4.5.1. Comparative Analysis of Tire–Pavement Coupling Noise of Different Pavement Types

The tire–pavement coupling noise for three asphalt mixtures was calculated based on the principle of acoustic wave superposition, as demonstrated in Figure 24. When categorized by SPL, PAC-10 pavement showed superior noise reduction performance, followed by SMA-10, with AC-10 exhibiting the poorest noise mitigation capabilities. Notably, while PAC-10 pavement generated the highest vibration noise, its air pumping noise and tire–pavement coupling noise remained the lowest among the tested materials. This phenomenon indicates that air pumping noise exerts greater influence on the overall SPL of tire–pavement coupling noise, with its contribution weight significantly outweighing that of vibration noise components.

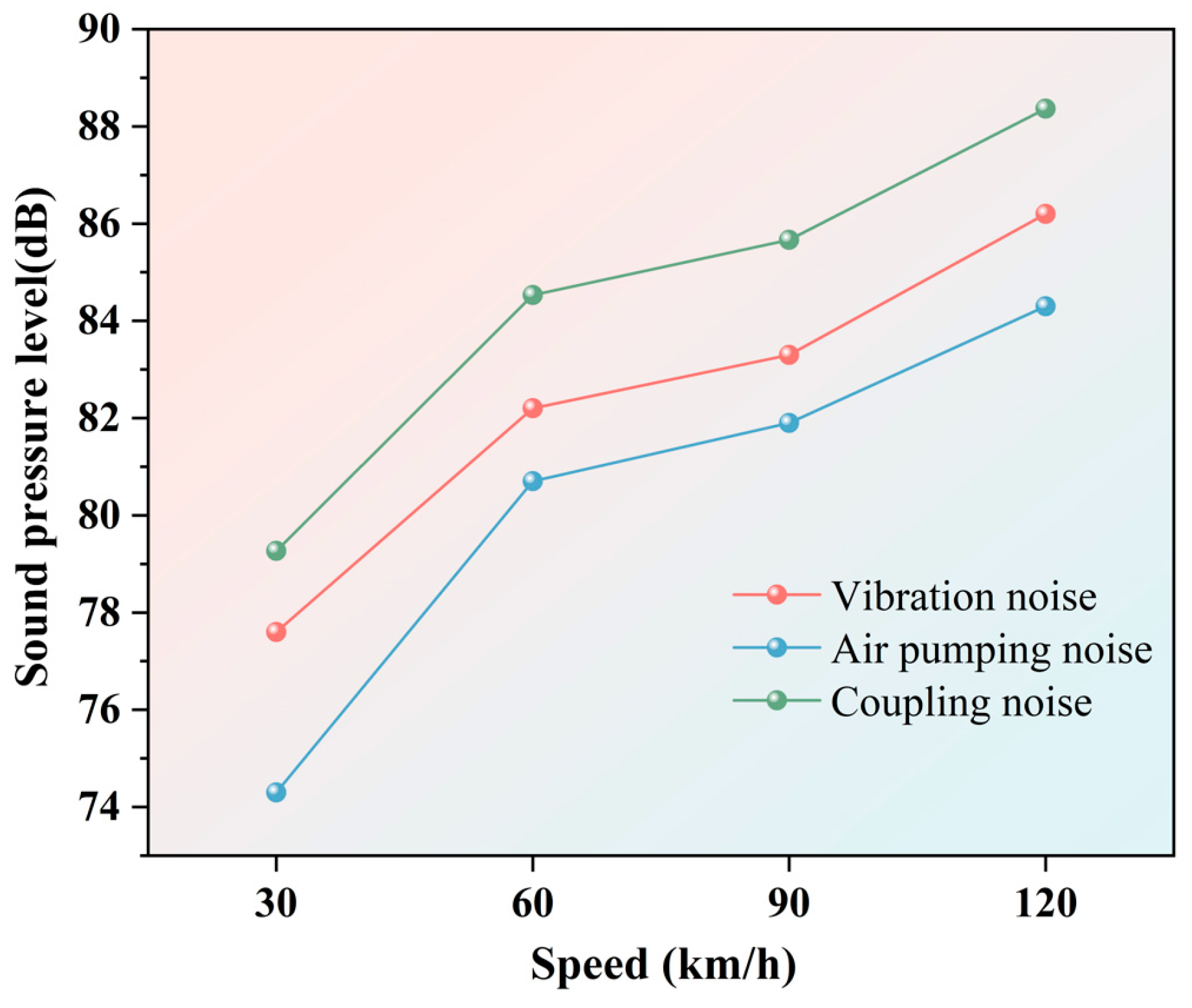
4.5.2. Influence of Vehicle Speed on Tire–Pavement Coupling Noise

PAC-10 pavement was selected as the test subject for analyzing tire–pavement coupling noise characteristics under varying speeds.

In the simulation model, a load of 300 kg was applied with vehicle speeds sequentially set at 30 km/h, 60 km/h, 90 km/h, and 120 km/h. As demonstrated in Figure 25, vibration noise, air pumping noise, and coupling noise were all found to increase with speed escalation. Specifically, when speed was elevated from 30 km/h to 120 km/h, vibration noise rose by 8.6 dB, air pumping noise increased by 10 dB, and coupling noise was amplified by 9.1 dB. For vibration noise, its enhancement was attributed to increased tire–pavement contact frequency and intensified impact forces; higher speeds were observed to exacerbate excitation effects through more frequent pavement texture excitation. Regarding air pumping noise, accelerated air compression-release cycles between tread grooves and pavement surfaces at elevated speeds were identified as the primary intensification mechanism; concurrent aerodynamic resonance within tread grooves at critical frequencies further amplified noise levels through air cavity resonance phenomena. Notably, the most pronounced air pumping noise growth (6.2 dB increment) occurred within the 30–60 km/h range. This transitional behavior was explained by a dominant vibration noise contribution at lower speeds, with air pumping noise mechanisms progressively governing the acoustic configuration as speed increased beyond 60 km/h.

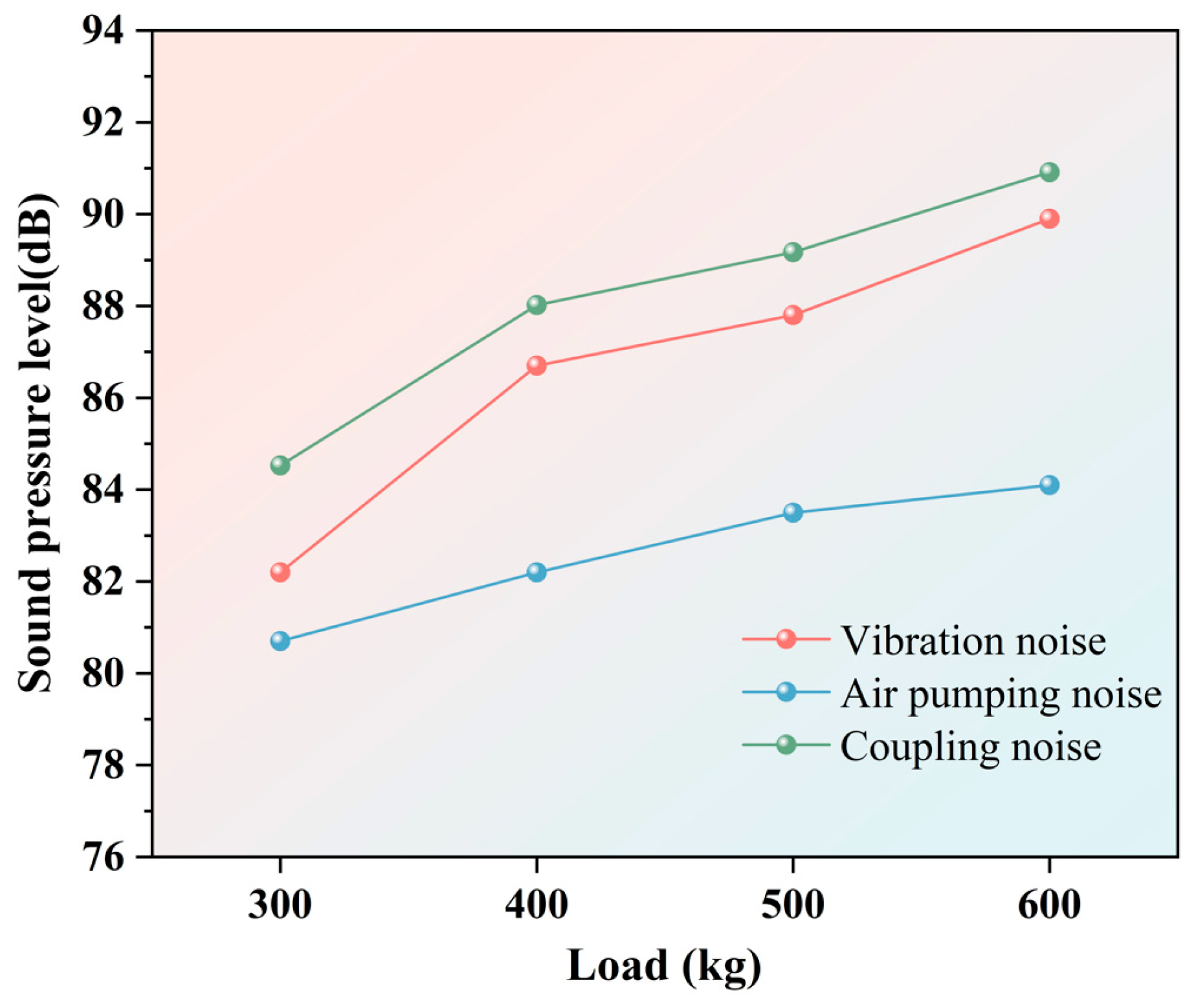
4.5.3. Influence of Vehicle Load on Tire–Pavement Coupling Noise

Given that modern passenger vehicles typically exhibit total weights of 1.2–2.0 metric tons with maximum payloads approximating 0.5 metric tons, single-wheel loads were investigated within the 0.3–0.6 metric ton range. Vehicle loads were configured at 300 kg, 400 kg, 500 kg, and 600 kg in the simulation model while maintaining other parameters constant. Through computational simulations and acoustic pressure conversion, SPLs under corresponding loading conditions were obtained, as presented in Figure 26.

All noise components exhibited load-dependent increases, though with distinct growth patterns and rates. Coupling noise demonstrated the highest SPLs across all loading conditions; vibration noise followed with the most pronounced load-induced increases, while air pumping noise maintained the lowest baseline levels and minimal incremental changes. The results indicate that under heavy-load conditions, comprehensive consideration of different noise types of impacts on overall tire–pavement noise are essential. Particular attention should be paid to vibration noise, as it exhibited the greatest magnitude of increase under high-load scenarios.

5. Conclusions

A tire–pavement coupling noise model of asphalt pavement was developed using the finite element simulation method in this study. Through this model, the noise characteristics of different asphalt pavement types were systematically analyzed, and the effects of pavement thickness, tire tread morphology, vehicle speed, and axle load on the noise reduction performance of PAC were investigated. The following conclusions were derived from experimental and numerical analyses:

• When compared to conventional dense-graded asphalt concrete (AC), PAC demonstrated enhanced noise reduction efficacy owing to its interconnected void structure, which effectively suppresses air pumping noise. High void ratios were observed to absorb and scatter sound waves, leading to attenuating noise propagation. However, increased vibration noise at the tire–pavement interface was attributed to the rough surface texture of PAC-10. Consequently, design optimization should prioritize balancing these competing mechanisms to maximize noise reduction benefits of PAC while mitigating vibration noise.
• Within the experimentally designed range of 2 cm to 10 cm, vibration noise was significantly reduced as the pavement surface layer thickness was increased, with the noise reduction effect tending to plateau when the thickness exceeded 6 cm. Considering both economic efficiency and noise reduction effects, the pavement thickness design is recommended to be no less than 6 cm.
• The sensitivity analysis of tire tread geometry indicates that the mold release angle (0~30°) and tread depth (5~17 mm) exert a pronounced influence on the air pumping noise and should be prioritized in optimization, whereas the groove width within the 20~60 mm range has only a minor effect. Nevertheless, tread design must balance noise reduction with traction performance. Accordingly, it is recommended to adjust the tread depth and mold release angle while maintaining sufficient friction to ensure both effective noise mitigation and driving safety.
• Tire–pavement coupling noise increases markedly with higher vehicle speeds and axle loads. In particular, within the 30~60 km/h range, tire–pavement coupling noise exhibits the most pronounced growth. This finding underscores the necessity of targeted optimization of tread aerodynamic characteristics and their interaction with porous asphalt pavements in this transitional speed range to achieve more effective noise mitigation.

In summary, this study not only validates the acoustic advantages of PAC pavements but also analyzes the critical factors influencing tire–pavement coupling noise, thereby providing a theoretical foundation for the design of PAC pavements and the optimization of tire patterns.

6. Discussion

A finite element workflow was developed in this study to quantify tire–pavement coupling noise through the integration of vibration and air pumping noise components. This integrated framework is considered to provide a more comprehensive perspective for elucidating the complex noise generation mechanisms in tire–pavement interactions.

High-precision capture of pavement surface geometries was enabled by the implementation of 3D laser texture scanning technology, which was subsequently integrated into the simulation models. Compared to the simplified pavement textures utilized in prior literature, the simulation fidelity of tire–pavement contacts and acoustic generation processes was significantly enhanced by this methodology.

Although the validity of the developed model was corroborated through experimental testing, specific simplifications were implemented to ensure numerical stability and convergence during the simulation process. The potential impacts of these approximations were evaluated as follows:

• The two-stage approach, which derives excitation from a 2D rolling model and applies the amplitude to a 3D vibration noise model, overlooks factors such as lateral pressure redistribution, lateral tread block interactions, and the anisotropy of pavement textures.
• The simplification of fixing the tire position while applying rotation and amplitude inputs introduces physical approximations. Specifically, this method may fail to account for the transient contact phenomena and the precise phase synchronization between aerodynamic air-pumping pulses and structural oscillations. The absence of real-time dynamic rolling contact may consequently affect the synchronization and spectral distribution of the predicted tire–pavement coupling noise.
• Different asphalt pavements were modeled as linear-elastic slabs, with distinctions confined to surface texture and void ratio. Mixture-specific parameters, such as loss factors and frequency-dependent acoustic absorption or impedance, were not explicitly accounted for. Moreover, the complex interior pore geometry (e.g., tortuosity and connectivity) were omitted from the air-pumping model, which may limit the precision of noise-reduction mechanism analysis for PAC mixtures.

Therefore, future research should prioritize the following directions:

4.

Future studies should transition from the current two-stage approach to a unified, fully dynamic 3D rolling contact framework. This will allow for the precise capture of lateral pressure redistributions and the complex phase synchronization between aerodynamic air-pumping pulses and structural vibrations.

5.

To move beyond macroscopic air void parameters, Scanning Electron Microscopy (SEM) and X-ray Computed Tomography (CT) should be utilized to characterize the internal microstructural geometry of PAC. Integrating parameters such as pore connectivity, tortuosity, and surface geometry into the model will significantly refine the analysis of noise-reduction mechanisms.

6.

Subsequent models should incorporate the frequency-dependent acoustic impedance and loss factors specific to various asphalt mixtures. Furthermore, investigating the chemical composition and aging characteristics of the binders may provide deeper insights into the long-term acoustic durability of porous pavements.