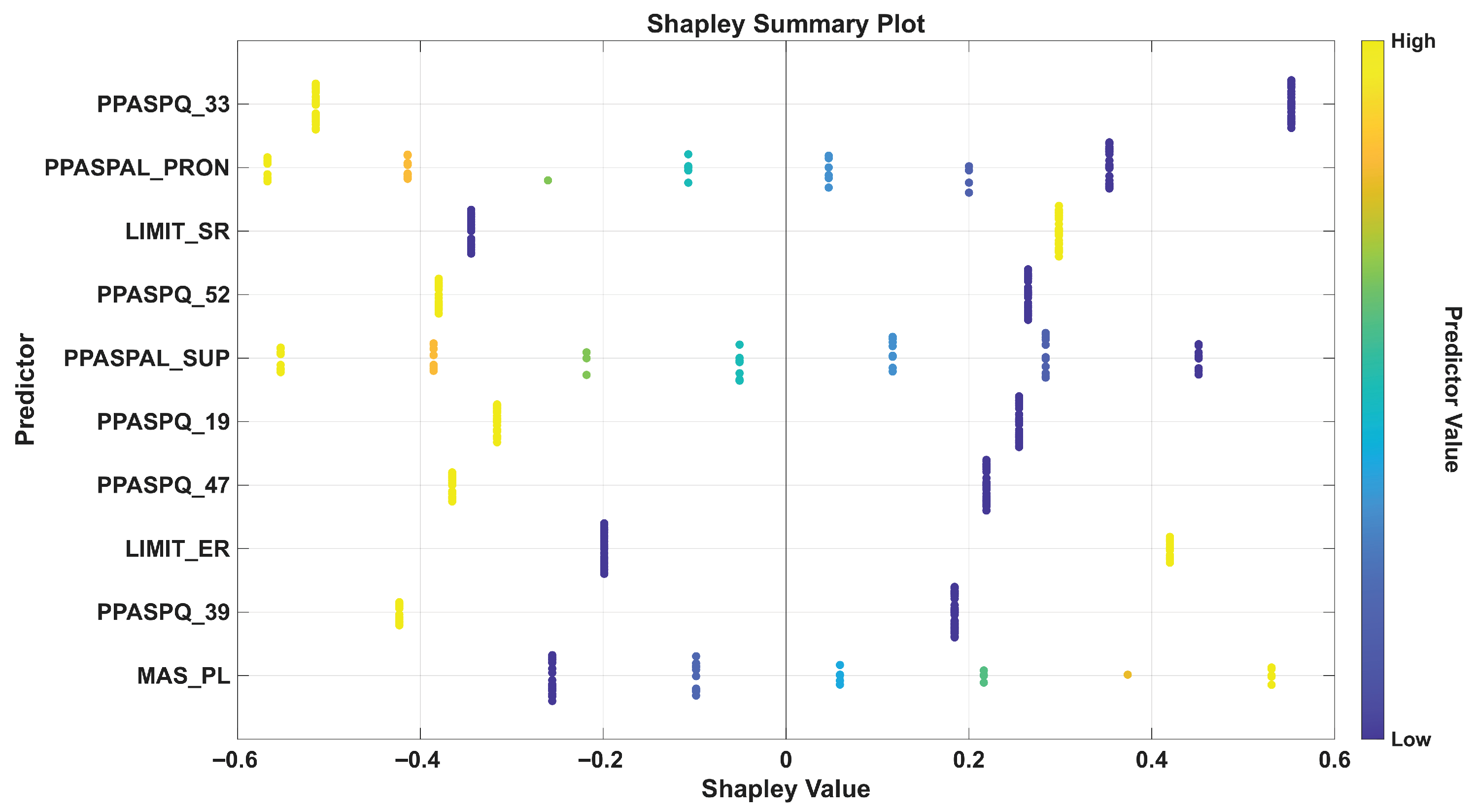
2.1. Description of the Dataset
As mentioned in the introduction, this study focuses on the functional assessment of adults suffering from CP. To do so, the study uses data collected by four physiotherapists of the Valencian Association of Cerebral Palsy (AVAPACE) centres in Valencia (Spain), with between 5 and 20 years of experience in the field of treating patients suffering from CP.
Concerning the sampled population, originally the data were collected from 58 adult users during functional and positional assessment tests. Nevertheless, it was impossible for the team to fully collect two of the registers. Thus, the data of those two users were discarded, and the dataset ended up having records of 56 users, who were aged between 19 and 74 (mean: 39.04 years; standard deviation: 14.11 years), 24 of them being female and the other 32 male. Before taking any test, all participants received an explanation of the research and gave their informed consent for using their data in this study, as approved by the Ethics Committee of Research in Humans of the Ethics Commission in Experimental Research of the University of Valencia (protocol code FIS-2837811).
To ensure consistent inter-rater assessments of the participants, before beginning with the study and aiming to reduce possible inter-rater biases, the researchers shared a manual with the physiotherapists in which the assessment protocol was explained. Moreover, physiotherapists were also given a seminar about how to apply the protocol. Finally, to further ensure inter-rater consistency, the assessments of the first data collection day were performed along with the four physiotherapists together, so that a consensus was reached for the evaluation criteria. In addition, concerning the consistency and coherence in the assessment of the GMFCS level, the scale itself has been reported to have a high degree of inter-rater agreement in the literature ([
20,
21]).
The dataset collected by the physiotherapists originally consisted of 94 independent variables from six domains: clinical record, postural quality, postural ability, the range of passive movement, the presence of certain bodily asymmetries and the muscle tone or degree of spasticity. Concerning the completeness of the dataset, no imputation method had to be applied, as it had been possible to fully collect the 94 variables for all the 56 participants. Apart from those independent variables, the dataset also contains each participant’s level in the GMFCS according to the empirical observations made by the physiotherapists, which is independent of all other variables in the dataset that do not directly measure gross motor function. This last variable corresponds to the class variable to identify with the ML analysis proposed in this work. The detailed explanation of the variables (both independent and class variables) will be given in the following paragraphs.
To begin with, the dataset’s first three variables correspond to the subject’s clinical record: the sex, the primary medical diagnosis (named DX_P in the dataset) and the subtype of CP (named CP_SUB in the dataset). The sex variable was considered binary, using 0 for female and 1 for male subjects. Then variable DX_P was ranged from 0 to 5, with the following meanings: 0 stands for cerebral palsy, 1 for infant CP, 2 for diparesis due to congenital encephalopathy, 3 for perinatal CP, 4 for intrauterine encephalopathy, and 5 for encephalopathy. The third and last variable, CP_SUB, included the subtype of CP that was diagnosed by the doctors (or, in the case of not having a subtype, it was assessed by the physiotherapists). This variable ranged from 0 to 6, values which, in increasing order, stand for spastic hemiplegia, spastic diplegia, spastic tetraplegia, dyskinetic or athetoid CP, ataxic CP, hypotonic athetoid CP and mixed CP.
The dataset’s second set of variables corresponds to postural quality, which was assessed using the Posture and Postural Ability Scale (PPAS) [
22]. This scale is a tool to measure both body alignment and the ability to maintain a stable position. In this study, the scale was applied to four functional positions (standing, sitting, supine and prone) assessed in both the frontal and sagittal planes. Depending on the functional position analysed, the postural assessment considered different bodily items: head, trunk, pelvis, hips, knees, legs, feet and arms. Another item assessed whether the person’s weight was evenly distributed for each functional position. For example, in the sitting position, this item would check whether both glutei and legs were evenly resting on the chair, supporting the weight equally on both sides. Finally, the last item assessed the overall quality of the posture for a position, understood as the sum of all the bodily items considered for that functional position (including the item for the weight distribution).
Nevertheless, not all items were evaluated in each position; the specific selection of items varied depending on the position adopted and the plane of observation. A total selection of six body and weight items, plus a seventh corresponding to the overall score for the selected position, was always maintained. Each item scored either 0 or 1, where 0 indicates the presence of asymmetry or deviation from the midline of the body, and 1 reflects symmetrical and adequate alignment. Concerning each position’s overall score, they could vary between 0 (complete asymmetry) and 6 (optimal postural alignment).
Thus, according to the previous explanation, the dataset contained a total of 56 postural quality-related PPAS features (named PPASPQ_
#, with the
# being an identifier numeral). The following table (
Table 1) gives a summarised explanation of the bodily items and functional positions represented by each of the PPASPQ_
# features.
In addition to the features associated with postural quality, the PPAS also incorporates the “Postural Ability Level” (PAL) component. This second component constitutes the third block of characteristics in the dataset and assesses the individual’s ability to maintain or modify their posture. This component is scored on a scale from 1 to 7, where 1 represents a total inability and 7 indicates complete independence. To be consistent with the naming methodology used for the PPASPQ features, the features related to the PAL have been named PPASPAL_position (see
Table 2).
The fourth group of variables identifies contractures and articulation limitations associated with postural asymmetries. To this end, the physiotherapists measured the subjects’ passive range of motion (ROM) using a universal goniometer according to the standards of the American Academy of Orthopaedic Surgeons [
23,
24]. The shoulder, elbow, hip, knee and ankle joints’ ROMs were evaluated bilaterally, recording the maximum extension achieved without causing pain. The ROM was considered limited when the hip’s, knee’s, or elbow’s extension was less than 0°, or when ankle dorsiflexion did not reach the neutral position. Thus, these variables were scored either 1 or 0 for the cases with or without any joint limitation, respectively.
In addition to those variables, and also linked to the ROM, the physiotherapists assessed pelvic tilt. This variable analyses the alignment of the anterior superior iliac spines in the frontal plane. It was considered that there was a pelvic asymmetry when one anterior superior iliac spine was visibly higher or lower than the contralateral one, which indicates a deviation from the midline and an alteration in pelvic position. This variable was included in the dataset under the name INPED and coded binary (1 = pelvic tilt, 0 = aligned pelvis).
In total, the dataset contained 11 features linked to ROM measurements. 10 of them correspond to joint limitations and were named according to the LIMIT_
xy system, where
x referred to the joint selected for the measurement and
y referred to the body side. For example, following the guide of
Table 3, the variable measuring the ROM limitation of the left elbow would be named as LIMIT_EL. The remaining variable, INPED, has a postural character and does not follow the aforementioned naming system because it assesses pelvic symmetry in the frontal plane rather than a specific joint limitation.
Following with the next set of variables, it relates to postural asymmetries of the different bodily segments (see
Table 4). These asymmetries were determined through direct clinical observation of the alignment of those segments in the three positions. Specifically, the physiotherapists analysed the presence of dorsal hyperkyphosis or lumbar hyperlordosis and the relative position of the pelvis, lower limbs, and upper limbs with respect to the body’s midline. The presence or absence of asymmetry was recorded as 1 or 0 for each segment, complementing the quantitative information obtained with the PPAS. In addition, scoliosis was recorded based on medical history, taking into account the Cobb angle [
25] and, when necessary, radiographic review of the medical history. Scoliosis was considered present (value 1) when lateral curvature of the spine with visible vertebral rotation was observed or when the patient had undergone spinal arthrodesis for this reason.
The last and sixth group of variables corresponds to muscle tone, which was assessed using the Modified Ashworth Scale (MAS) [
26]. The MAS is a tool that quantifies the increase in resistance to passive movement as an indicator of the degree of spasticity. Measurements were taken in a relaxed position and at a constant speed, covering different muscle groups: psoas, glutei, adductors, quadriceps, hamstrings, tibialis and calves. The scale assigns scores from 0 to 4, with an intermediate category (1+), where 1 represents a slight increase with minimal resistance at the end of the range of motion, 1+ indicates slight resistance at the beginning and during less than half of the range, 2 reflects a more marked increase in most of the range but with ease of movement, 3 corresponds to a considerable increase that hinders passive movement, and 4 indicates complete stiffness in flexion or extension. A score of 0 is interpreted as no spastic response. However, as the variable was to be used with ML, its values had to be discrete numbers. As 1+ is not a number, value 2 was used to represent the scale’s 1+ level and the scale scores from then on were represented with one more point with respect to their original scale value (i.e., value 2 in the scale is represented with 3 in the variable). Similarly to the ROM limit features, these features have been named according to the MAS_
xy system (see
Table 5), where
x refers to the muscle group and
y to the body side.
Finally, the class variable (named as GMFCS_LEV) corresponds to the level of gross motor function, which was classified using the expanded and revised version of the GMFCS, the GMFCS-E&R [
27]. Although this scale was originally designed for children up to 18 years of age, this study applied it to an adult population, exclusively focusing on users classified as levels IV and V. Of these, 27 were at level IV and 29 at level V. On the one hand, level IV was assessed when the person had the functional ability to stand actively, requiring little assistance. On the other hand, for level V, the standing posture is achieved passively with the help of two people who provide physical support, with minimal or residual active participation by the user. Although there are five scale levels, the authors decided to focus on these two classes because of their physical similarities and because they are the most limiting and because they have the greatest impact on the patients themselves, their relatives, the healthcare system and society in general.
2.2. Preprocessing the Dataset
After identifying all variables, the next step was to preprocess the dataset and prepare it for the classification stage, in which the GMFCS level of the users would be determined using ML techniques.
As explained, the original dataset contained 94 variables. Nevertheless, not all variables could be used as features with the ML algorithms. This work focuses on the problem of discriminating between GMFCS levels IV and V, which, respectively, represent users able or not to stand on their own or with very little help. This way, it would not make sense to consider the PPASPQ variables collected in the standing position, as they implicitly carry information about the user’s class. Therefore, the first 14 PPASPQ variables were filtered out from the database. Also, the PPASPAL_STAND variable was discarded for the same reason.
Then, the researchers standardised the remaining independent variables using z-score normalisation. With this, variables with bigger ranges are prevented from dominating the decisions of the ML, as all are transformed to have 0 and 1 mean and standard deviation values, respectively. The formula for applying the standardisation is presented in Equation (
1), where
is the standardised value for the variable sample,
is the variable sample,
is the mean value of the variable and
is the standard deviation of the variable.
In summary, after the aforementioned steps, the dataset consisted of 78 independent variables plus the class variable. This way, the dataset was ready for addressing the proposed classification problem using ML algorithms (this version of the dataset is available as
Supplementary Material attached to this article).