Laser Propulsion in Confinement Regime: The Role of Film Thickness in the Impulse Generation Process

Featured Application

This article provides an investigation of the mechanisms underlying the generation of a mechanical impulse by laser ablation, in the case in which the expansion of the ablation plume is confined by a thin layer. This technique shows potential applicability for the space propulsion of nanosatellites, allowing for thrust generation from a far distance not requiring propulsion systems on board or mechanical contact.

Abstract

A small amount of mass is generally ejected with high exhaust velocities from the surface of materials irradiated by intense laser pulses, so that a net impulse is generated on the target because of momentum conservation. This phenomenon proved to be a potential solution to generate thrust on far objects, with promising application in space debris removal and control of nanosatellites. Among the different tested strategies, the deposition on the surface of the target of a layer transparent to laser radiation results in a considerable increase in the generated impulse, due to the confinement of the expansion of the ablation plume. In this work impulse generation was measured, using aluminum as target, and PVC, SiO₂, TiO₂ and CNCs (cellulose nanocrystals) as confinement layers with thickness $0.3\sim 5 \mathsf{\mu }\mathrm{m}$. The results show that the generated impulses increase with the thickness of the ejected confinement layer. Additionally, the kinetic energy of the confinement layer, for a given material, does not depend on its thickness, but it is affected by the energy dissipation paths during the interaction with the laser pulse, where the strength of substrate–film adhesion and the Young’s modulus of the latter are shown to play an important role.

1. Introduction

With the recent advent of New Space Economy, laser ablation started to attract interest also as a possible innovative propulsion technique. This interest was raised mainly because of two emerging problems related to the vast exploitation of earth orbit: space debris mitigation [1] and nanosatellites orbit correction [2].

The former one is due to all the non-operating satellites, rocket stages, and other objects that are left orbiting around earth uncontrolled, in which motion may require years for them to re-enter into the atmosphere with their disintegration. All these objects represent a threat for future space missions, since they can lead to collisions with formation of a larger number of smaller debris. This phenomenon, predicted by Kessler [3], may lead to the onset of a collisional cascade; therefore, the only way to reduce the number of space debris is by their active removal from earth orbit.

The second problem comes from the recent exploitation of smaller and smaller satellites, deployed in a large number to form constellations, allowing for an improvement in earth observation and communications [4].

This led to a consistent reduction in the size and mass of satellites, that now have typical dimensions of tens of centimeters and masses of few kilograms, as it is typically seen in the case of CubeSats. Due to both their mass and small size, these satellites often cannot be equipped with their own on-board propulsion system and therefore it is not possible to control their orbit, reducing their operating times due to possible re-entry into the atmosphere because of residual drag.

A possible solution to both these problems requires a strategy to move objects in space, avoiding on-board propulsion.

During laser ablation, mass ejection occurs from the irradiated surface of a material. Due to the considerably high velocities of the ejected mass, because of momentum conservation, a mechanical impulse $J$ is generated on the irradiated material, that can be therefore expressed as follows [5,6]:

$$J=m_{\mathrm{e}}{v}_{\mathrm{e}}$$

(1)

where $m_e$ is the ejected mass and $v_{\mathrm{e}}$ is the ejection velocity. Laser ablation therefore allows for generating thrust on an object from a distant position and avoiding any mechanical contact. Additionally, no specific systems are needed on board of the object to exploit such propulsion technique, making it a really attractive solution for control of small satellites.

While in the case of space debris there is no possibility to choose the target material to generate impulse, in the case of nanosatellite propulsion the target material can be optimized in order to achieve better propulsion performance [7], which is usually expressed by the laser impulse coupling coefficient, $C_{\mathrm{m}}$, and specific impulse, $I_{\mathrm{s}\mathrm{p}}$, defined as follows:

$$C_{\mathrm{m}}={\displaystyle \frac{J}{E}}$$

(2)

$$I_{\mathrm{s}\mathrm{p}}={\displaystyle \frac{J}{g{m}_{\mathrm{e}}}}$$

(3)

where E is the laser pulse energy and g is the gravity acceleration on earth.

Several works report tests on different target materials aimed at increasing either $C_{\mathrm{m}}$ or $I_{\mathrm{s}\mathrm{p}}$. As a general observation, polymers show higher $C_{\mathrm{m}}$ values, compared to metals, that on the other side generate a higher $I_{\mathrm{s}\mathrm{p}}$. The strategies employed to increase $C_{\mathrm{m}}$, typically in polymers like PVC [7,8], GAP [9,10,11], POM [12,13,14], include the addition of an absorber in the material, in order to increase its interaction with the laser. These absorbers are usually dyes, while carbon nanoparticles proved to be more energetically efficient. The inclusion of nanoparticles as laser absorber was also used in other kinds of materials, like metal oxide frameworks [15], showing an improvement in the propulsion performances too.

Along with the optimization of the properties of the target material, impulse generation can also be enhanced through confined laser ablation. In this configuration, a layer transparent to laser radiation is positioned on the surface of the absorbing material, so that the laser pulse is absorbed at the interface, leading to the formation of a plasma layer in this region. The confined plasma in turn interacts with the laser radiation, leading to a strong pressure increase just under the confining layer, and resulting in some cases in the generation of shock waves both in the confining and absorbing materials, as described in [16]. This pressure increase opens the interface and brings to the rupture and the ejection of the confining layer, generating a mechanical impulse on the irradiated material. The addition of a confinement layer therefore allows to considerably increase the pressure on the surface of the absorbing material, thus possibly resulting in the full ejection of the transparent layer, so that a much higher mechanical impulse is generated.

Despite being an efficient technique to enhance impulse generation, confined laser ablation also presents some drawbacks. In particular, since the impulse is generated by the ejection of the confinement layer, after a single laser shot only the absorbing material is left on the irradiated region; therefore, a new region must be irradiated to generate a new impulse. Moreover, the ejection of the confinement layer causes a large mass loss; therefore, this mechanism suffers from the problem of mass consumption. In other words, $I_{\mathrm{s}\mathrm{p}}$ decreases. For this reason, the thin confinement layer becomes more attractive but the general aspects of impulse generation in this regime need to be better understood.

At present, experiments investigating impulse generation in confined ablation geometries have aluminum as the absorbing material, and consider confinement layers thicker than 100 μm [17], more often in the mm scale [18]. Additionally, the confinement layer is usually attached to the surface of the absorbing material by means of some adhesive [17], or just kept in contact with the absorbing surface by some support [16,18]. These kinds of systems therefore introduce some variability in the experimental conditions, especially considering the interface between the confining and absorption materials, making difficult a fine comparison among them.

Another common feature of these kind of experiments is that they are conducted using high fluences, often around 100 $\mathrm{J}/{\mathrm{c}\mathrm{m}}^2$ [16,17,18], which are not very convenient in laser ablation propulsion applications, due to the difficulty in reaching such high energy densities on far targets.

The recently reported self-confinement processes, in appropriately doped composite polymers [19], open the way to limit the problem of mass consumption by using limited values of laser energy fluence, but in the present work we want to see if the use of transparent thin films can still overcome the two problems.

This work considers indeed thinner confinement layers of PVC, SiO₂, TiO₂ and cellulose nanocrystals (CNCs) with thickness ranging from 0.3 μm to 5 μm, deposited on aluminum, irradiated in a low laser fluence regime. By using such samples, it is possible to highlight how the thickness and the material of the confinement layer affect impulse generation. Using a common substrate and no external agents to keep the confinement layer stuck on the absorbing surface, a coherent comparison of the results is possible.

It is proved that even with confinement layers of a few hundreds of nm, a considerable impulse increase can be generated. Furthermore, because of the adopted geometries, it was possible to propose a phenomenological description of the obtained results.

These results provide a better understanding of impulse generation in confined ablation regime, under conditions that are expected to be closer to those encountered in applications, while also enabling future development of multilayer structures.

2. Experimental

2.1. Materials

Aluminum (6082) was used as the absorbing material for all experiments. Aluminum square targets with size 26 × 26 × 1 mm were polished by using abrasive paste and cleaned with ethanol.

Poly(vinyl chloride) (PVC) (Sigma-Aldrich, Merck KGaA, Darmstadt, Germany; powder, average Mw ∼43,000, average Mn ∼22,000) was deposited by spin coating. In order to control the thickness of the confining layer, the viscosity of PVC solution was changed by dissolving the polymer in cyclohexanone with concentrations 5 wt%, 10 wt%, 20 wt% and a rotation velocity of 3000 RPM for 120 s was used for all the concentrations. An additional sample was prepared by using 1000 RPM for 120 s and the 20 wt% solution to obtain a thicker film. After deposition, the samples were dried at 160 °C for 3 h to ensure a complete evaporation of cyclohexanone, as previously observed in [7].

The SiO₂ films have been prepared from the precursor NN120-20 (DurXtreme GmbH, Ulm, Germany) (20 wt% solution of perhydropolysilazane (PHPS) in 80 wt% di-n-butylether (DBE)). The deposition of the films is carried out by spin coating (Model P6700, Specialty Coating Systems, Indianapolis, IN, USA), with different RPM: 500, 1000 and 8000 RPM. The time is set to 90 s for all the samples. After the deposition, the SiO₂ films were dried at room temperature overnight. The PHPS reacts with the moisture and oxygen present in the atmosphere releasing ammonia, thus crosslinking to obtain a structure closer to vitreous silica. Indeed, being the studied material a polymer-derived silica obtained at room temperature, the structure cannot be completely comparable with a fully polymerized silica glass obtained by melt quench. In the following, we will define this material as silica or SiO₂ for simplicity, but we stress that the layer still contains some organic moieties and can be rather considered a hybrid network.

TiO₂ deposition was performed by radio frequency (RF) sputtering of a TiO₂ target in an argon atmosphere. The argon pressure during deposition was kept at $8\times {10}^{-3}$ mbar, RF power was 150 W, and the distance of the substrate from the TiO₂ target was 5.5 cm while deposition times were 1 h, 2 h and 4 h.

CNCs were produced from cellulose pulp (SCA, Sundsvall, Sweden) by TEMPO mediated oxidation, according to the procedure of Saito [20] modified as reported by Bettotti et al. [21]. Briefly, water-swollen cellulose pulp is oxidized at alkaline pH by hypochlorite as primary oxidant and TEMPO and NaBr as catalysts, rinsed with deionized water and sonicated. This procedure removes the amorphous cellulose regions retaining the crystalline ones, and rod-shaped nanostructures with length and width approximately 150–250 nm and 3–5 nm, respectively, are obtained. Moreover, the oxidation introduces carboxylic groups at the C6 position of the cellobiose ring which bear a negative charge at neutral pH and confer colloidal stability. Sodium ions are present in the final CNC suspension as counter ions of the carboxylic groups. To obtain the films, the CNC suspensions were deposited uniformly at room temperature on solid square shaped Al substrates. Before deposition, Al substrates were washed using a mild detergent, rinsed several times, and soaked in deionized water for at least 48 h. The volume and concentration of the deposited CNC suspensions were properly adjusted to obtain variable thickness of the final films in the desired range.

2.2. UV-Vis

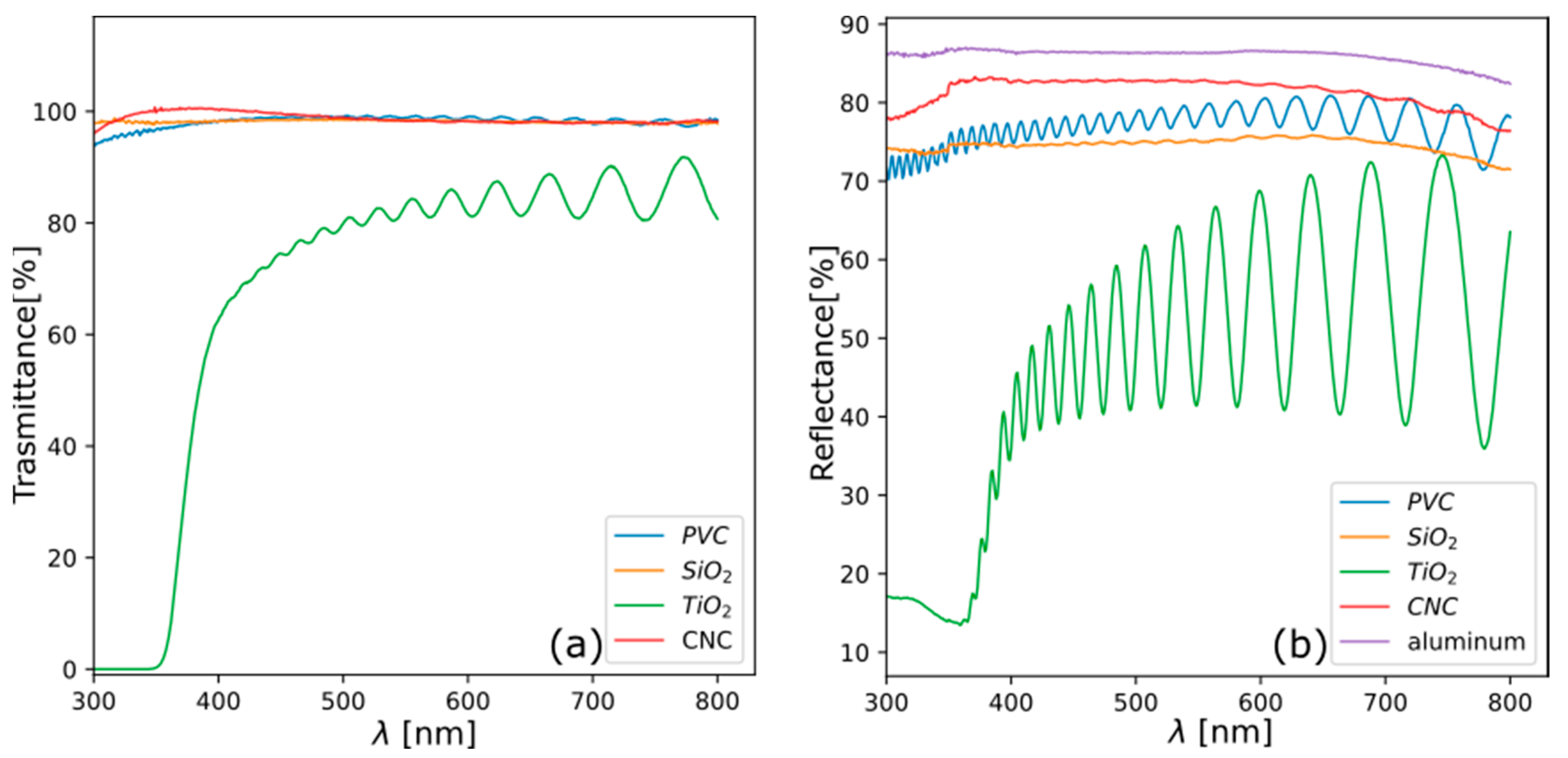
UV-visible spectroscopy (Varian Cary 5000, Santa Clara, CA, USA) was used to measure the transmittance and reflectance of the studied confinement layers. Transmittance measurements are made by depositing the confinement layers on a glass substrate, transparent to the employed laser wavelength, in order to confirm that they are not absorbing the incoming laser pulse.

The measurement of total reflected radiation on the other hand was exploited to assess the thickness of the deposited confinement layers. Because of the interference among multiple reflections at the surface of the film and at the interface between the confining layer and aluminum, oscillations in the reflectance spectrum of these samples can be observed. This allows to estimate the thickness t of the confinement layer by using the following relation [22]:

$$t={\displaystyle \frac{2}{4\left({\nu }_{i-1}\sqrt{n{\left({\nu }_{i-1}\right)}^2-sin\left(\varphi \right) }-{\nu }_i\sqrt{n{\left({\nu }_i\right)}^2-sin\left(\varphi \right) }\right)}}$$

(4)

where ${\nu }_i=1/{\lambda }_i$ is the wavenumber at which an extremum in the spectrum is observed and ${\lambda }_i$ is the wavelength, $n$ is the refractive index of the film and $\varphi$ is the incidence angle of light, which was 3° in the case of the used spectrophotometer, on which an integrating sphere was mounted.

2.3. Materials Characterization

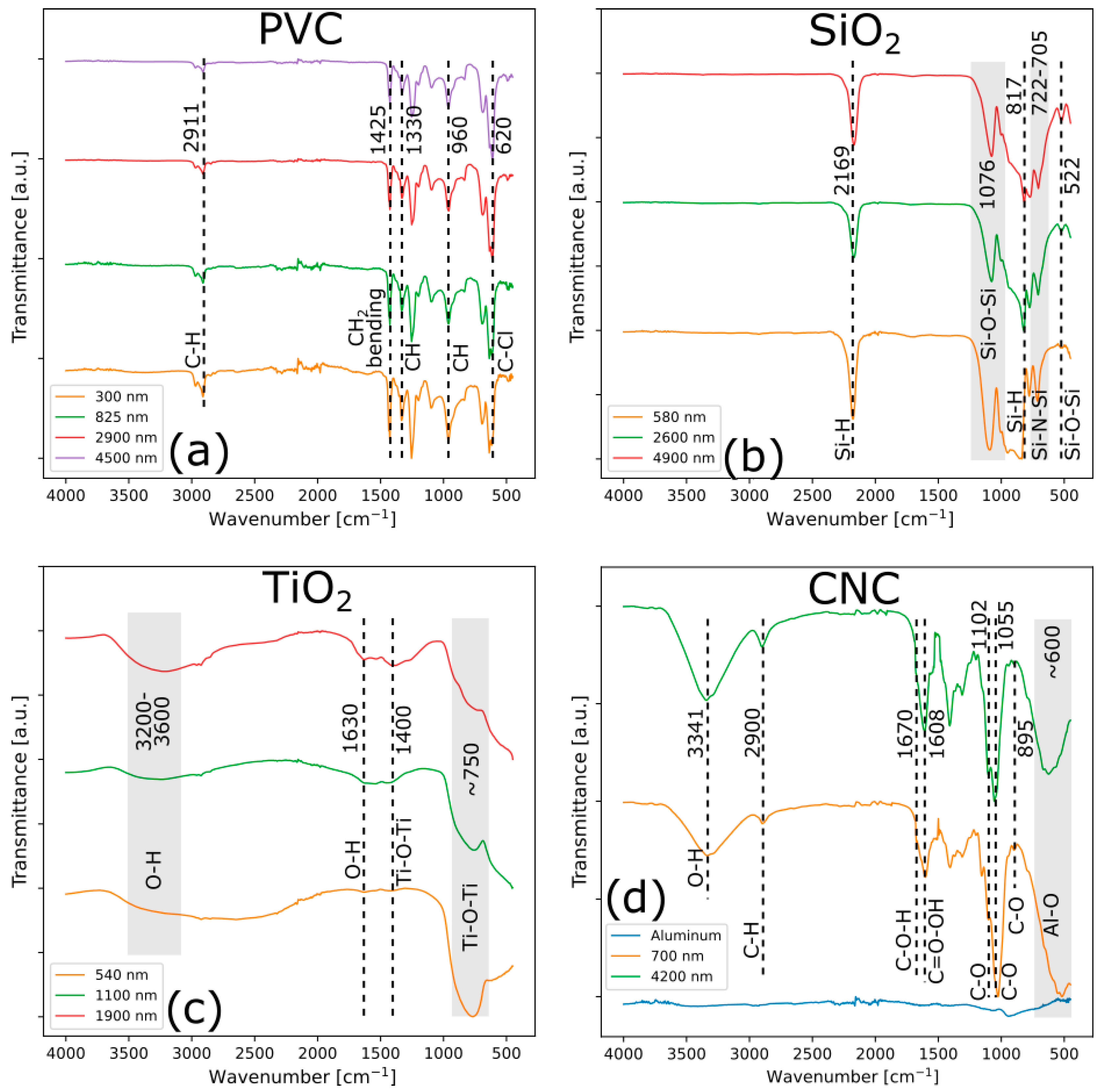
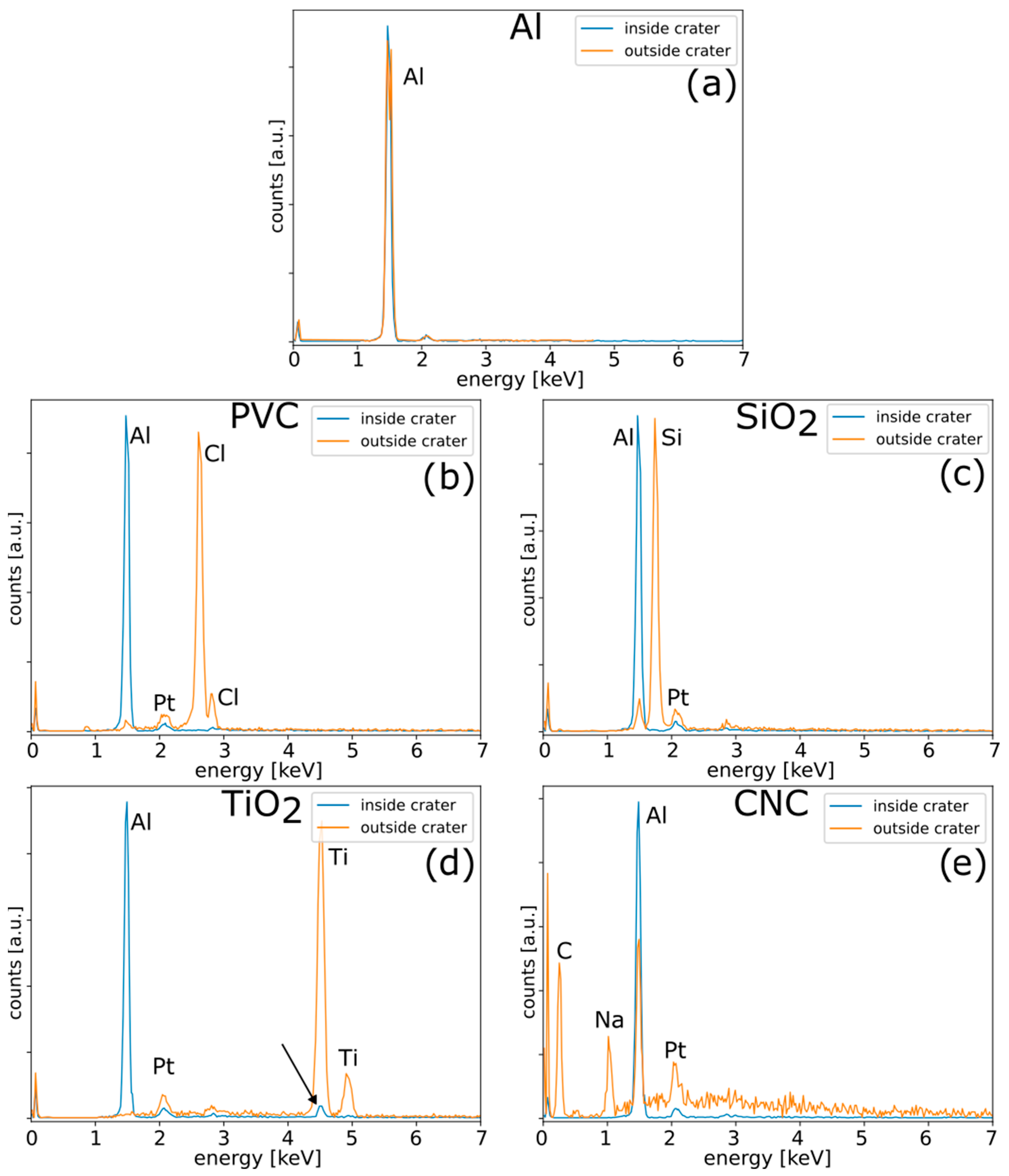
Samples are characterized before ablation by means of FTIR (PerkinElmer Spectrum Two, Shelton, CT 06484, USA) operating in ATR mode. The surface of the materials was also analyzed before and after ablation by SEM and EDS (JEOL JSM-5500, Tokyo, Japan) to clarify the role of the confinement layer in the ablation process and its effective removal. Since the deposited confinement layers are not conductive, samples were metallized with Pt/Pd before SEM characterization.

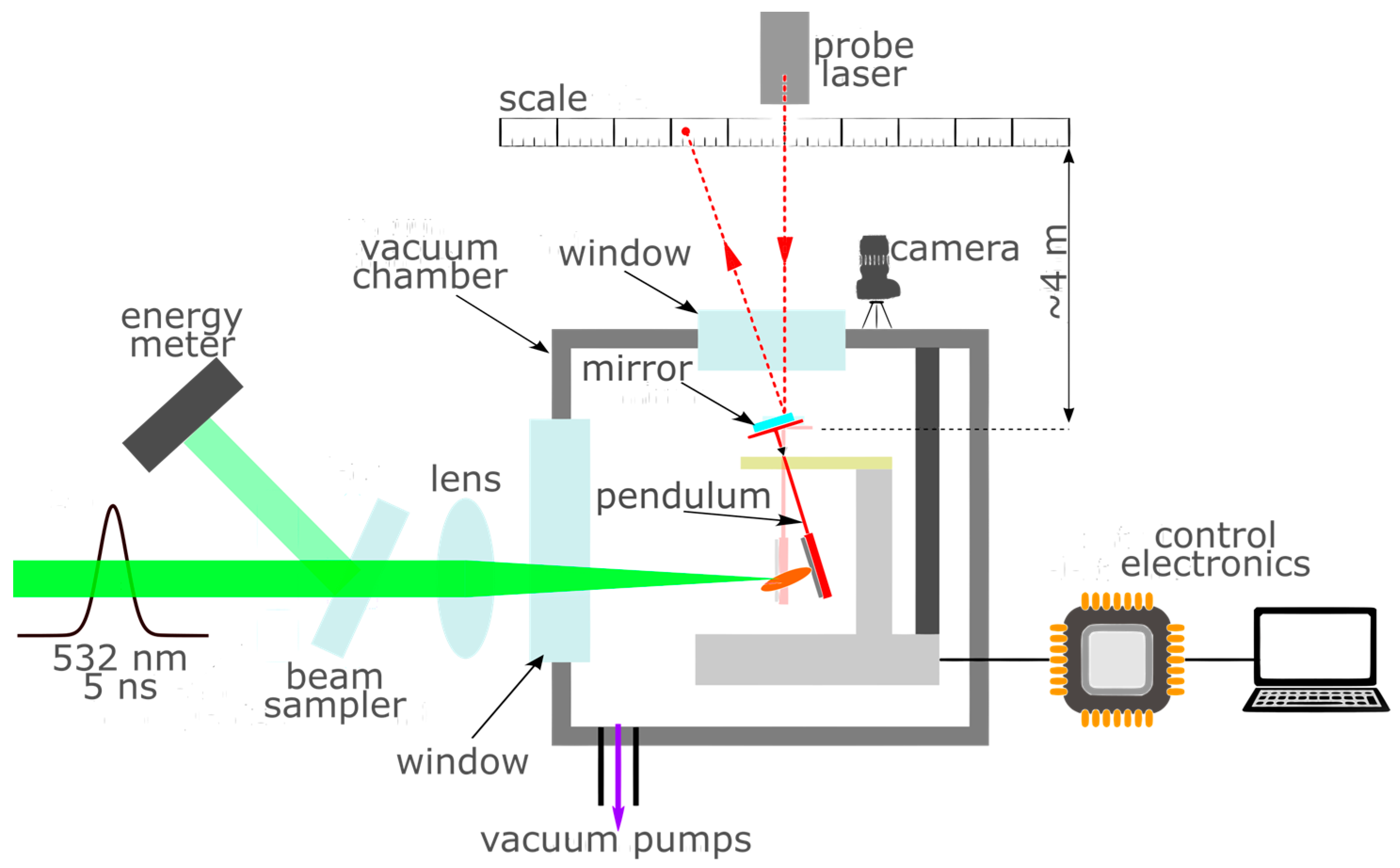
2.4. Impulse Measurements

Impulse measurements were performed by means of the experimental apparatus described in detail in [7,23] and represented in Figure 1.

The apparatus consists of a ballistic pendulum operating under vacuum conditions, at a pressure lower than ${10}^{-4}$ mbar. The impulse $J$ generated by laser ablation after a single laser pulse is obtained by measuring the generated variation in angular momentum of the pendulum, $\Delta L$, through the following relation:

$$J={\displaystyle \frac{\Delta L}{r}}={\displaystyle \frac{I\Delta \omega }{r}}$$

(5)

where $r$ is the distance of the irradiated spot from the rotation axis of the pendulum, I the moment of inertia of the pendulum and $\Delta \omega$ is the variation in its angular velocity caused by the impulse. $\Delta \omega$ is measured by reconstructing the motion of the pendulum, which is probed by means of a laser pointer reflected by a mirror fixed to the top of the pendulum. The oscillation of the pendulum, with amplitude usually smaller than 1°, is then acquired by recording the motion of the reflected probe laser on a graduated scale about 4 m away from the pendulum, in order to amplify it. The video is recorded at 1000 frames per second, and the pendulum motion is then reconstructed by an image analysis software developed in python (version 3.13.5).

Errors on $J$ are estimated by propagating the uncertainties on the parameters of Equation (5). This procedure, described more in detail in [23], yields errors comparable to the standard deviation of repeated measurements. The main source of uncertainty is $\Delta \omega$, since it is also dependent on the precision of the estimation of the time instant at which the impulse is generated, that is also measured during the reconstruction of the motion of the pendulum [23]. Consequently, when higher impulses are measured, the uncertainty on $\Delta \omega$ increases because, in general, larger oscillation amplitudes are observed.

In the case of the samples investigated in this work, a single laser pulse is expected to completely remove the confinement layer. A different location of the target must then be irradiated for each impulse measurement. In the present experiments, the irradiated area is $5.8 \mathrm{m}{\mathrm{m}}^2$ and the centers of nearby craters are always at a distance of 3 $\mathrm{m}\mathrm{m}$.

Since the used samples are flat, the impulse generated in different regions always has the same direction. By changing the irradiated location for every laser pulse, the distance $r$ of the irradiated spot from the rotation axis of the pendulum must be taken into consideration, since it affects the estimation of the generated impulse as expressed by Equation (5). The value of $r$ is measured for each spot by image analysis.

Following Equation (5), $r$ is measured for each crater in order to estimate the generated impulse.

Due to the complex shape of the pendulum, also $I$ must be measured. This is carried out by measuring the distance d of the center of mass of the pendulum from its rotation axis through the following relation:

$$I={\displaystyle \frac{T^{2}mgd}{{\left(2\pi \right)}^2}}$$

(6)

where T is the period of the pendulum, m is its mass, and g is gravity acceleration. Additionally, $d$ is measured by means of image analysis, by acquiring two images of the pendulum in equilibrium on two different points and tracing the vertical directions passing through them, so that their intersection indicates the position of the center of mass [7].

For the impulse and ablated mass experiments, the second harmonic of an Nd:YAG laser, with a wavelength of 532 nm and a pulse duration of 5 ns was used. Measurements were made in the fluence range between 0 and 7 $\mathrm{J}/\mathrm{c}{\mathrm{m}}^2$.

2.5. Ablated Mass Measurements

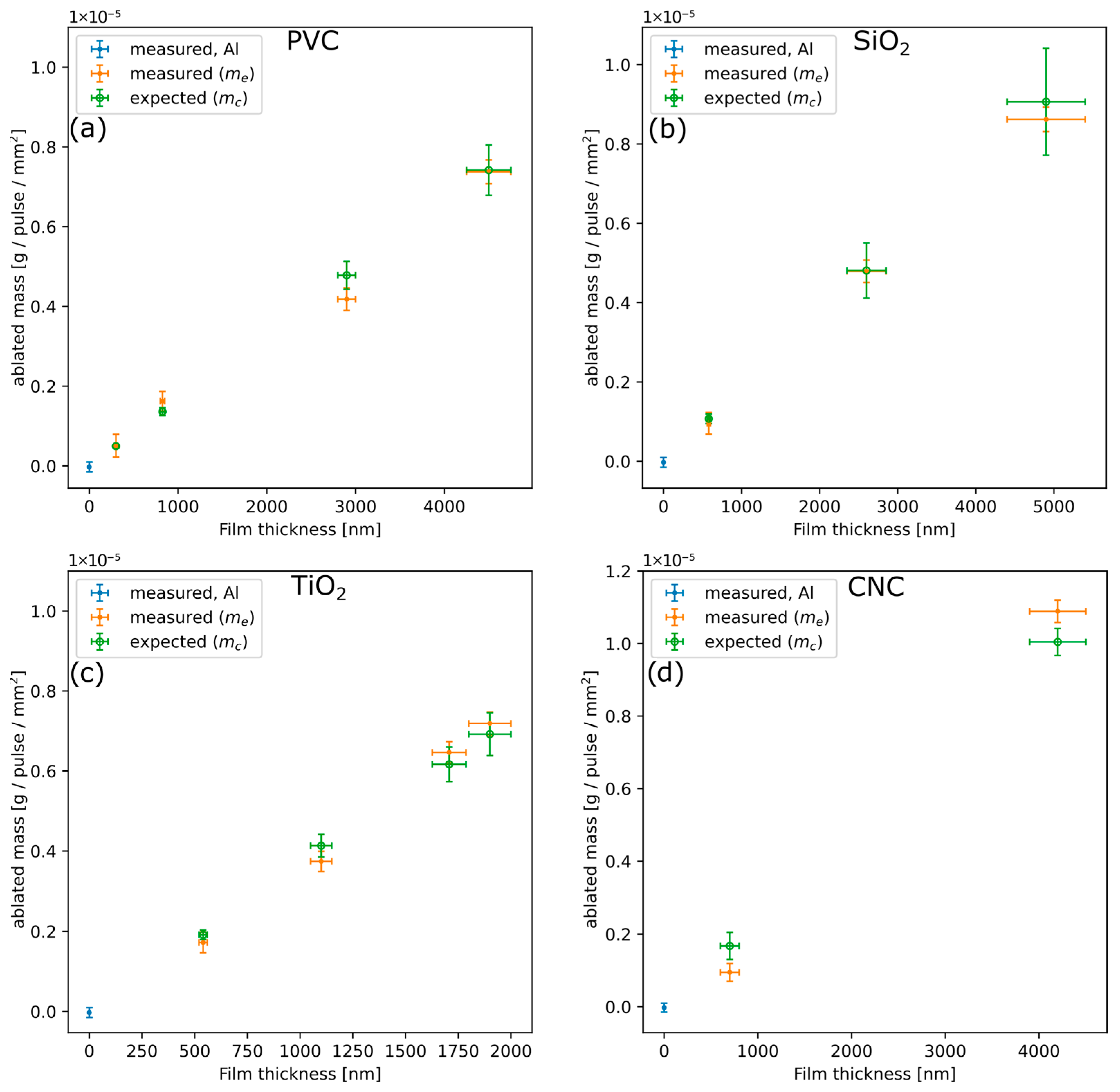
The measurement of the ablated mass was used to confirm the effective removal of the confinement layer, by comparing the measured removed mass by a single laser pulse, $m_e$, with the estimated mass of the confinement layer inside the irradiated region, $m_{\mathrm{c}}$. In fact, if all the confinement layer is ejected from the irradiated region, with no other significant ablation products, it is expected that $m_{\mathrm{e}}=m_{\mathrm{c}}$.

The average ablated mass per pulse was obtained by measuring the total mass difference $\Delta m$ by using a scale with ${10}^{-5}$ g resolution after a known number of pulses at a variable fluence between ∼1 $\mathrm{J}/\mathrm{c}{\mathrm{m}}^2$ and ∼7 $\mathrm{J}/\mathrm{c}{\mathrm{m}}^2$.

To measure $m_{\mathrm{e}}$, the sample was irradiated with $N=20$ laser pulses, moving the target after each pulse to always ablate a clean area. The distance between nearby pulses was chosen to be sufficiently large to avoid any modification of the surface due to previous irradiation in the surrounding regions. For this purpose, roughly 1 mm was always kept between the external borders of nearby craters. This distance proved to be sufficient also by the reproducibility of impulse measurements obtained by irradiation, with the same laser fluence, of different regions of the target surrounded by other craters.

The average ablated mass per pulse can then be estimated as follows:

$$m_{\mathrm{e}}=\Delta m/N$$

(7)

Since the confinement layer is expected to be completely ejected after a single laser pulse independently of laser fluence, as long as it is above the removal threshold, a different fluence was used for each pulse during the measurement. In this way, if a good agreement is observed between and $m_e$ and $m_c,$ it can also be confirmed that ablated mass does not depend on laser fluence. This holds for fluence high enough to remove the confinement layer; therefore, fluences in the range $1\sim 7 \mathrm{J}/\mathrm{c}{\mathrm{m}}^2$ were used for this measurement. This range was chosen by looking at the minimum fluence at which an impulse could be measured, indicating the ejection of the confinement layer.

On the other hand, $m_c$ was estimated through the following relation:

$$m_{\mathrm{c}}=m_{\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}}{\displaystyle \frac{A}{A_{\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}}}}$$

(8)

where $m_{\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}}$ is the total mass of the confinement layer before irradiation, which is deposited over an aluminum substrate of known area $A_{\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}}= 2$6 mm × 26 mm, while $A$ is the irradiated area, kept constant for all the experiments at 5.8 ± 0.1 $\mathrm{m}{\mathrm{m}}^2$.

3. Results and Discussion

3.1. Film Thickness and Interface

Figure 2a shows the transmittance of the used confinement materials, in the case of layers with similar thickness in the range $2\sim 4 \mathsf{\mu }\mathrm{m}$. PVC, SiO₂ and CNC films show a transmittance higher than 95% at laser wavelength, while in the case of TiO₂ a lower transmittance of about 80% is obtained. Only thick layers on glass have been considered for transmittance measurement, in order to mitigate possible effects on the morphology of the film of difference in rugosity between glass and polished aluminum.

In Figure 2a,b, both oscillations in transmittance or reflectance due to thin film interference are clearly visible, and can be exploited to measure the thickness of the film, as described by Equation (4). In the case of spin coating and drop casting deposition, the thickness of the film may be influenced by the substrate. Therefore, to know the thickness of the confinement layers, the measurement must be performed on samples deposited on aluminum. For this reason, oscillations in reflectance spectra (Figure S1) were used to compute confinement layer thickness. The measurement was carried out by considering each couple of successive maxima in the wavelength region in which the film is transparent and its refractive index slowly varying. To take into account also variations in the refractive index with wavelength, literature values have been used (PVC [24], SiO₂ [25], TiO₂ [26], CNC [27]). The thickness of the films was then obtained as the average of the values measured for each couple of maxima, and uncertainty was estimated as their standard deviation.

Table 1. Measured confinement layer thickness.

Layer Material	Layer Thickness [nm]	Procedure
PVC	$300\pm 20$	Spin coating, 5% solution, 3000 RPM
PVC	$825\pm 25$	Spin coating, 10% solution, 3000 RPM
PVC	$2900\pm 100$	Spin coating, 20% solution, 3000 RPM
PVC	$4500\pm 300$	Spin coating, 20% solution, 1000 RPM
SiO2	$580\pm 20$	Spin coating, 8000 RPM
SiO2	$2600\pm 250$	Spin coating, 1000 RPM
SiO2	$4900\pm 500$	Spin coating, 500 RPM
TiO2	$540\pm 20$	RF sputtering, 1 h deposition
TiO2	$1100\pm 50$	RF sputtering, 2 h deposition
TiO2	$1700\pm 70$	RF sputtering, 4 h deposition
TiO2	$1900\pm 100$	RF sputtering, 4 h deposition
CNC	$700\pm$100	Drop casting, low concentration
CNC	$4200\pm$300	Drop casting, high concentration

lists the obtained results for each sample.

3.2. Material Structure

The FTIR spectra of the different films SiO₂, PVC, TiO₂ and CNC are presented in Figure 3a–d, respectively.

Figure 3a shows the characteristic bands of PVC. The band around 2911 $\mathrm{c}{\mathrm{m}}^{-1}$ is associated to symmetric and asymmetric stretching of –CH₂– groups in the polymer backbone; the bending vibration typical for –CH₂– groups in polymers is around 1245 $\mathrm{c}{\mathrm{m}}^{-1}$; and a deformation vibration of –CH₂– groups occurs around 1330 $\mathrm{c}{\mathrm{m}}^{-1}$. From 960 to 1250 $\mathrm{c}{\mathrm{m}}^{-1}$, overlaps with C–C and C–Cl skeletal vibrations and from 600 to 1100 $\mathrm{c}{\mathrm{m}}^{-1}$ several overlapping modes in this region are seen, due to the polymer backbone.

Figure 3b shows the characteristic bands of PHPS-derived SiO₂ collected on samples with different layer thicknesses. The FTIR spectrum of the films deposited from a 20 vol% PHPS solution in DBE at room temperature (Figure 3b) demonstrates a partial conversion of the precursor into silica, as suggested by the absence of absorption peaks at 3380 $\mathrm{c}{\mathrm{m}}^{-1}$ and 1176 $\mathrm{c}{\mathrm{m}}^{-1}$ related to N–H stretching and bending, respectively. A clear absorption at 2169 $\mathrm{c}{\mathrm{m}}^{-1}$, corresponding to the Si–H stretching vibration at 817 $\mathrm{c}{\mathrm{m}}^{-1}$, associated with Si–H bending [28], and the Si–N band at 722–705 $\mathrm{c}{\mathrm{m}}^{-1}$ indicate that unreacted organic moieties remain and a complete conversion into silica cannot be achieved at room temperature. Indeed, we can observe the formation of a band between 1000 and 1100 $\mathrm{c}{\mathrm{m}}^{-1}$, which is the fingerprint of the formation of silica-like tetrahedra (asymmetric stretching) [29]. As the PHPS conversion into silica proceeds by a reaction with gas species from the atmosphere, the layer thickness is influenced by the occurring reaction involving the diffusion length across which the gases need to diffuse. As such, the Si–O–Si band strength substantially increases as the thickness of the layer decreases. Furthermore, we can observe a shift in vibrational features of the asymmetric Si–O–Si stretching with the layer thickness. Specifically, the peak moves to a higher wavenumber for thin layers. This can be easily attributed to a formation of a more polymerized silica structure where the tetrahedral unities contain a larger number of bridging oxygens [30].

Figure 3c shows the FTIR spectra of TiO₂. The band at 3200–3600 $\mathrm{c}{\mathrm{m}}^{-1}$ and at 1630 $\mathrm{c}{\mathrm{m}}^{-1}$ is attributed to O–H, while the peak at 1400 $\mathrm{c}{\mathrm{m}}^{-1}$ and the band around 750 $\mathrm{c}{\mathrm{m}}^{-1}$ are attributed to Ti–O–Ti stretching vibrations [31].

The FTIR spectrum of the drop-cast CNC films on aluminum exhibits characteristic bands of CNC as shown in Figure 3d. A broad absorption at ~3340 $\mathrm{c}{\mathrm{m}}^{-1}$ corresponds to O–H stretching vibrations, indicative of extensive intra- and intermolecular hydrogen bonding. The stretching vibrations of the methyl and methylene groups appear at ~2900 $\mathrm{c}{\mathrm{m}}^{-1}$. The band at 1608 $\mathrm{c}{\mathrm{m}}^{-1}$ (belonging to carboxylic groups) with the shoulder at 1670 $\mathrm{c}{\mathrm{m}}^{-1}$ (belonging to aldehydes) indicate that the oxidation step of the synthesis procedure was successful. The sharp peak at 1102 $\mathrm{c}{\mathrm{m}}^{-1}$ is ascribed to the crystalline C–O stretching vibration of β-glycosidic linkages. The intensity of this peak together with the lower signal at 895 $\mathrm{c}{\mathrm{m}}^{-1}$ assignable to the C–O of amorphous β-glycosidic linkages confirm the high crystallinity of the nanomaterial. The C–O stretching of secondary hydroxyl groups appears at 1055 $\mathrm{c}{\mathrm{m}}^{-1}$. Finally, a band at ∼600 $\mathrm{c}{\mathrm{m}}^{-1}$ could be attributed to the interfacial Al oxides introduced by the long soaking of the substrate in water, that weakly interacts with the polar groups of cellobiose rings. Overall, the spectrum of the film shows the characteristic CNC features whereas it highlights subtle interactions with the aluminum surface.

3.3. Impulse Measurements

Figure 4 shows the impulse generated by the different confinement materials as a function of laser fluence, compared with the impulse generated by direct ablation of polished aluminum. In all cases, the impulse is considerably enhanced compared to the direct ablation of polished aluminum, and increases with the confinement layer thickness. For all confinement materials, it is possible to observe that the impulse grows abruptly starting from a certain specific fluence. This fluence can be considered the threshold for impulse generation and is about 0.5 $\mathrm{J}/{\mathrm{c}\mathrm{m}}^2$ for PVC, SiO₂ and TiO₂ confinements, being instead about 1 $\mathrm{J}/{\mathrm{c}\mathrm{m}}^2$ for the thickest CNC confinement.

In the case of PVC, SiO₂ and CNC confinement, the impulse generated by the second laser pulse on an already irradiated region is the same as the one generated by polished aluminum, suggesting that no confinement layer is left after the irradiation by the first pulse. On the other hand, for TiO₂ confinement, the impulse generated by the second pulse is slightly higher than that generated by aluminum, probably due to the fact that some layer residuals are left in the crater. This is also suggested by the brownish color of the craters, not present in the case of the other confinement materials, and by EDS measurements in Section 3.5.

In the case of PVC confinement, the impulse generated by the two thicker layers shows a different behavior than the thinner ones. For fluences lower than about 2 $\mathrm{J}/{\mathrm{c}\mathrm{m}}^2$, the impulse generated by thicker layers appears to be lower than that generated by thinner layers. We suggest that this behavior is related to the Young’s modulus of PVC, which is more than an order of magnitude lower than that of the other three studied materials. Furthermore, it should be considered that the difference occurs near the laser fluence threshold for layer removal, and therefore PVC is capable of easily deforming under the application of a force that is indeed better absorbed and dissipated in thicker layers. At higher laser fluence, and the corresponding increase in pressure, the elastic properties become less significant. Additionally, it can be observed that, in the case of SiO₂ confinement, some saturation in the impulse curve can be observed at high fluence for thicker layers. This is usually linked to the shielding of the incoming laser pulse by the ejected confinement which depends not only on the energy of the laser pulse, but also on the nature of the atoms/ions that are part of the plume.

For all the materials, it can also be noticed that impulse measurements are more scattered in the case of thicker layers. This can be attributed to the ablation process, which is probably less reproducible when the fracture of a thicker film is involved, as can be better noticed in $C_{\mathrm{m}}$ curves, Figure S2 (Supplementary Material).

Table 2. Comparison of our experimental results and literature data. Due to the large number of variables present in each experiment, only the more relevant parameters have been considered. In the case of [16] a 3 ns, 1064 nm laser is used; in the case of [17] a 15 ns, 1064 nm laser is used; in the case of [18] a 15 nm, 1053 nm laser is used. Numbers marked by * are rough estimations based on other data presented in the cited work.

Substrate	Confinement Material	Thickness	Fluence [$\mathbf{J}/\mathbf{c}{\mathbf{m}}^2$]	${\mathit{C}}_{\mathbf{m},\mathbf{m}\mathbf{a}\mathbf{x}}$ [$\mathsf{\mu }\mathbf{N}/\mathbf{W}$]	${\mathit{I}}_{\mathbf{s}\mathbf{p},\mathbf{m}\mathbf{a}\mathbf{x}}\left[\mathbf{s}\right]$	Ref.
Cu	BK7 glass	7 mm	$0.1\sim {10}^3$	${10}^4$	$\sim 1 *$	[16]
Al	Fused silica	3 mm	$5\sim 75$	$\sim 500 *$	$\sim 2 *$	[17]
Al	PMMA	3 mm	$5\sim 75$	$\sim 230 *$	$\sim 2 *$	[17]
Al	Teflon	$125\mathsf{\mu }\mathrm{m}$	$5\sim 75$	$\sim 300 *$	$\sim 20 *$	[17]
Al	PE tape	$125 \mathsf{\mu }\mathrm{m}$	$5\sim 75$	$\sim 100 *$	$\sim 20 *$	[17]
Al	Parylene	$30 \mathsf{\mu }\mathrm{m}$	$5\sim 75$	$\sim 250 *$	$\sim 60 *$	[17]
Al	Acrylate tape	1 mm	$10\sim 25$	${10}^3$	$\sim 30 *$	[18]
Al	PVC	$0.3 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$46\pm 1$	$500\pm 300$	This work
Al	PVC	$0.825 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$88\pm 1$	$290\pm 40$	This work
Al	PVC	$2.9 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$155\pm 5$	$240\pm 20$	This work
Al	PVC	$4.5 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$191\pm 4$	$125\pm 5$	This work
Al	SiO2	$0.58 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$71\pm 1$	$1400\pm 400$	This work
Al	SiO2	$2.6 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$166\pm 3$	$490\pm 30$	This work
Al	SiO2	$4.9 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$242\pm 5$	$420\pm 20$	This work
Al	TiO2	$0.54 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$48\pm 1$	$170\pm 30$	This work
Al	TiO2	$1.1 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$98\pm 2$	$120\pm 10$	This work
Al	TiO2	$1.7 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$140\pm 3$	$97\pm 4$	This work
Al	TiO2	$1.9 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$135\pm 3$	$79\pm 3$	This work
Al	CNC	$0.7 \mathsf{\mu }\mathrm{m}$	$0.5\sim 7$	$68\pm 1$	$400\pm 100$	This work
Al	CNC	$4.2 \mathsf{\mu }\mathrm{m}$	$1\sim 7$	$215\pm 5$	$106\pm 4$	This work

compares our present results with literature data by highlighting the very low values of both thickness and laser fluence used in our investigation. In particular, the maximum measured value of coupling coefficient, $C_{\mathrm{m},\mathrm{m}\mathrm{a}\mathrm{x}}$, and the maximum value of specific impulse $I_{\mathrm{s}\mathrm{p},\mathrm{m}\mathrm{a}\mathrm{x}}$ are chosen as relevant parameters to compare the experimental results. $I_{\mathrm{s}\mathrm{p},\mathrm{m}\mathrm{a}\mathrm{x}}$ has been estimated from literature works by assuming all the confinement layer as ejected mass (see our analysis in Section 3.4).

It can be noted that a considerably high value of $C_{\mathrm{m},\mathrm{m}\mathrm{a}\mathrm{x}}$ is obtained in the case of [16], suggesting that also the substrate material may play an important role in the impulse generation process. In addition, the vacuum grease used to keep in close contact the absorbing material and the confinement may affect the result. Moreover, the thickness of the confinement layer is non-investigated in relation to $C_{\mathrm{m},\mathrm{m}\mathrm{a}\mathrm{x}}$ and therefore we cannot proceed with further comparisons. On the other hand, thanks to the well-controlled experimental conditions employed in this work, the increasing trend of $C_{\mathrm{m},\mathrm{m}\mathrm{a}\mathrm{x}}$ can be observed for all the confined materials.

A clear increase in $I_{\mathrm{s}\mathrm{p},\mathrm{m}\mathrm{a}\mathrm{x}}$ is instead observable for all the experiments when the thickness of the confinement layer is reduced. This allows to highlight one of the main advantages of considering confined laser ablation, that is considerably higher $I_{\mathrm{s}\mathrm{p},\mathrm{m}\mathrm{a}\mathrm{x}}$ values can be obtained by lowering the thickness. (See also our $I_{\mathrm{s}\mathrm{p}}$ curves as a function of laser fluence in Figure S4 of supplementary information).

3.4. Ablated Mass

Measurement of the mass expelled during ablation allows to clarify how ablation proceeds and the role of confinement in impulse generation. Given the geometry of the samples, the ejected mass is expected to be composed mainly of the confinement layer present inside the irradiated region. This comes from the fact that laser is absorbed by the surface of the aluminum substrate at the interface with the confinement layer, and penetrates only a few nm in the metal. Additionally, the plasma formed at the interface during irradiation shields the incoming laser, so that the interaction with the metal is further reduced. As a consequence of this mechanism, the ejected mass is also expected to depend only on the confinement layer and its thickness, and not on laser fluence, provided that it is sufficiently high to remove the layer.

This is confirmed by the obtained results, presented in Figure 5a–d, that show the comparison between $m_{\mathrm{e}}$ and $m_{\mathrm{c}}$, as in Equations (7) and (8).

The observed good agreement between $m_{\mathrm{e}}$ and $m_{\mathrm{c}}$ and their linear behavior with film thickness for all the confinement materials, strongly suggest that no changes in refractive index or density occur in the investigated thickness range. In addition, note that both in the case of polymers [32] and oxides like TiO₂ and SiO₂ [33], the mechanical and thermal properties approach the bulk values at thicknesses of few hundreds of nm.

3.5. Ablation Craters

Figure 6 presents SEM images of the central region of the ablation craters at a fluence of 5 $\mathrm{J}/{\mathrm{c}\mathrm{m}}^2$, obtained in the case of aluminum alone and after the ejection of all the used confinements. For each confinement material, the thickest layer has been considered. The presence of a confinement layer strongly modifies the morphology of the surface inside the ablation crater, with the formation of large structures of typical size in the order of tens of μm in the case of PVC, SiO₂ and CNC confinement, while smaller structures are observed for TiO₂.

The structures observed in Figure 6b–e are compatible with the solidification of molten material after the ablation process, as indicated by the presence of droplet-like structures. This suggests that the presence of a confinement layer avoids, before its ejection, the vaporization of Al material, so that heat accumulation favors melting below Al surface. Additionally, molten material is subject to the strong pressure applied by the confined plasma, generating the observed structures when the confinement layer is ejected and the molten material solidifies. The large size of the structures formed inside the ablation crater also affects the measurement of crater profiles, that appear less deep as expected and with a very rough structure, as shown in Figure S3 (Supplementary Material).

The smaller structures visible in Figure 6d left after the ejection of the TiO₂ layer, can be explained by considering that, as shown by impulse measurements, a lower pressure is applied to the surface.

Figure 7a–e shows EDS spectra comparing the composition in the region inside and outside the ablation crater, in the case of aluminum and all the investigated confinement materials. EDS spectra presented here correspond to the craters in Figure 6.

As visible in Figure 7a–c,e, only aluminum is left inside the ablation crater after irradiation, confirming the complete removal of the confinement layer, that, on the other hand, can be clearly identified in the non-irradiated region outside the crater. When confinement is obtained by means of TiO₂; however, Ti residuals are left inside the crater, as highlighted in Figure 7c. This also explains why the impulse measured by irradiating the region inside the ablation crater is different from the impulse generated by aluminum alone (Figure 4c), as expected for a complete removal of the confinement layer and observed for all other samples. The presence of Ti residuals in the ablation crater suggests a strong adhesion on Al substrate and that, during irradiation, the TiO₂ region closer to the interface must be subjected to thermodynamic conditions that lead to its vaporization confined to the region near the interface. Since TiO₂ does not interact strongly with the 532 nm laser radiation, as clear from Figure 2a, its temperature increase must then come from heat conduction at the interface from aluminum. Due to the short timescales involved in the irradiation process, TiO₂ can reach sufficiently high temperatures only in a region close to the interface, while the remaining part of the film is most probably ejected in the form of solid fragments, as happens for all the other confining materials and confirmed by ablated mass measurements in Figure 5.

4. Discussion

The experimental investigation resulted in the acquisition of both the generated impulse $J$ and the ejected mass $m_{\mathrm{e}}$ that was proven, for all used laser fluences, to be equal to the mass $m_{\mathrm{c}}$ of the confinement layer inside the irradiated area.

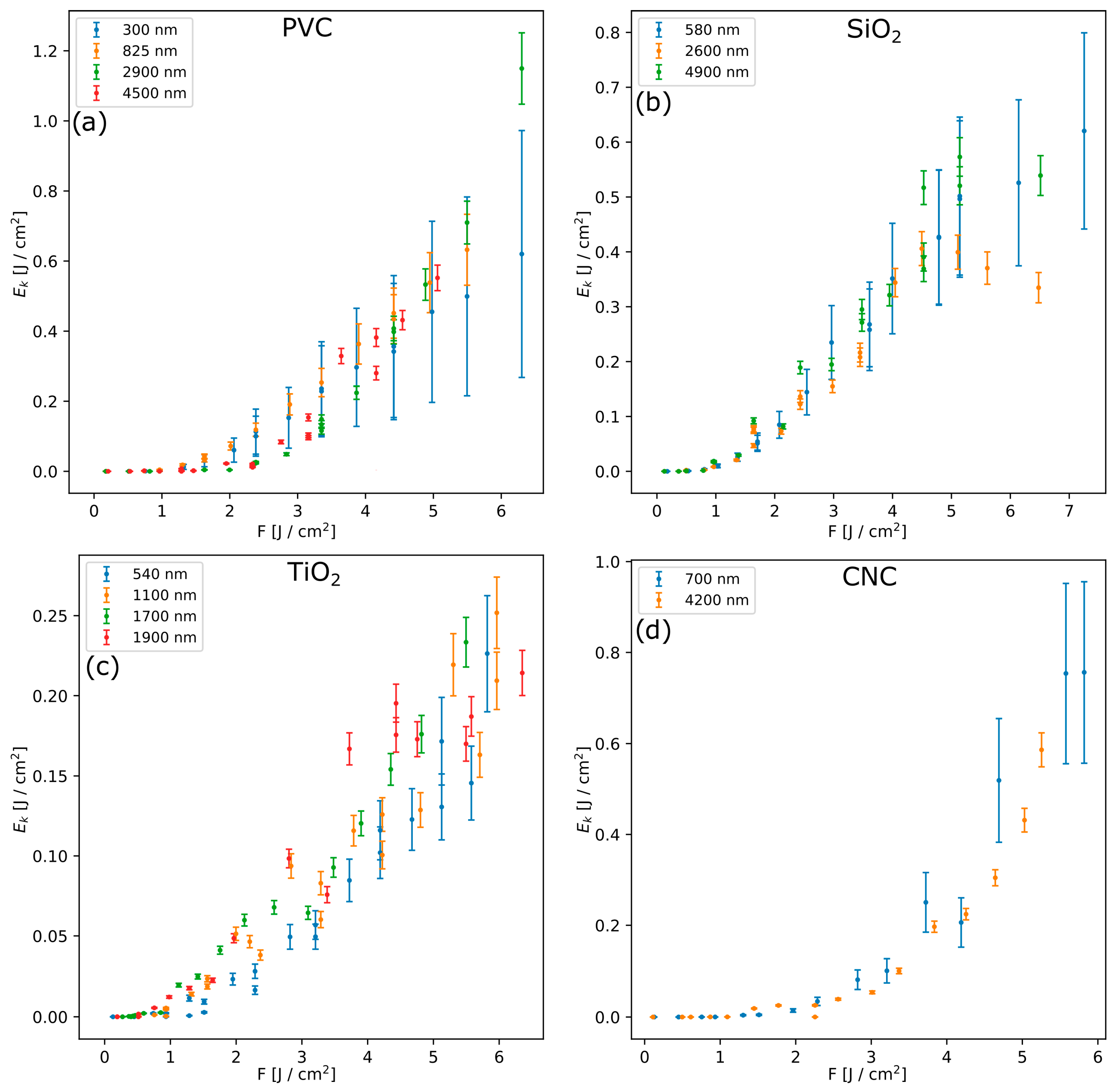
By knowing $J$ and $m_{\mathrm{e}}$, the final kinetic energy of the ejected confinement layer can be calculated as follows:

$$E_{\mathrm{K}}={\displaystyle \frac{J^2}{2m_{\mathrm{e}}}}$$

(9)

Figure 8 presents $E_{\mathrm{K}}$ per unit area of the ejected confinement layer as a function of laser fluence. Large errors are obtained in the case of the thinner PVC, SiO₂, and CNC films, due to the larger relative error affecting smaller $m_{\mathrm{e}}$ values, that propagates on the estimation of $E_{\mathrm{K}}$. A similar observation can be carried out on the ejection velocity of the confinement layer (Figure S4 supplementary information). However, the error on $E_{\mathrm{K}}$ decreases quickly with the thickness of the confinement layer, so that a meaningful comparison of the obtained curves is possible. As a first observation it is possible to say that similar values of $E_{\mathrm{K}}$, for fixed fluence, are obtained in the case of PVC, SiO₂ and CNC confinement, while lower values are observed in the case of TiO₂.

In order to understand these results, it is possible to consider a system composed by two slabs (Al target and confinement layer) that are accelerated in opposite directions, by a force applied at their interface that we attribute to the increasing pressure of plasma generated by the laser pulses on the Al surface layers. In such a system, momentum is conserved and the work carried out by the interface pressure is converted into the final kinetic energy of the two slabs as discussed by Fabbro et al. [16].

In the experiments presented in this work, the two slabs forming the interface have very different masses: on one side there is the aluminum substrate, which is fixed to the ballistic pendulum, so that its total mass is of a few g, while on the other side there is the ejected confinement layer, with a total mass always smaller than ${10}^{-5}$ g. The generated impulse is obtained by measuring the variation in momentum of the ballistic pendulum that, because of the conservation’s law, equals the momentum of the ejected confinement layer. Therefore, because of this large mass difference between the two sides of the interface, the ejected confinement moves with a velocity which is about ${10}^5$ times the velocity of the pendulum, and of the order of few km/s as represented in Figure S4 (Supplementary Material).

In the case of the samples considered in this work, the substrate, which was responsible for the interaction with the laser, was always kept identical. For a given confinement material, it is then reasonable to assume that the mechanical force separating the interface does not change, for the fixed laser fluence; therefore, the same work is carried out to accelerate the confinement layer and converted into its kinetic energy, independently of its thickness. This point is obviously valid in the case where the adhesion between Al and confining material is small as it happens for PVC, SiO₂ and CNC given the deposition method, but not in the case of TiO₂ deposited with RF sputtering which promotes greater adhesion given the initial energy of deposited atoms/ions.

By looking at $E_{\mathrm{K}}$ values in Figure 8, it can be noticed that the mechanical work carried out by plasma expansion to separate the interface only counts for a fraction of the incoming laser energy. During the whole ablation process, laser energy is in fact dissipated in different ways. In particular, most of laser energy is absorbed by aluminum surface and used to increase its temperature, leading to vaporization and plasma formation. Additionally, once a plasma layer is formed at the interface, it will strongly interact with the laser too, thus exploiting the absorbed energy to both eject the confinement layer, and to increase its internal energy [16].

Under this description, the lower $E_{\mathrm{K}}$ observed in the case of TiO₂ confinement, suggests that a large amount of energy is spent to overcome the adhesion force and only a part contributes to the vaporization that generates the thrust. This is consistent with EDS results in Figure 7.

5. Conclusions

PVC, SiO₂, TiO₂ and CNC layers, with thickness between 300 nm and 5 μm, have been deposited on polished aluminum, used as a common substrate, to investigate the confinement of laser ablation plasma plume by thin layers as an effective way to enhance thrust generation.

The optical properties of the deposited layers have been assessed by UV-vis spectroscopy. Transmittance measurements showed that all the considered confinement materials weakly absorb the laser radiation at the used wavelength, as required to achieve effective confinement, while optical interference observed in reflectance spectra was exploited to compute film thickness.

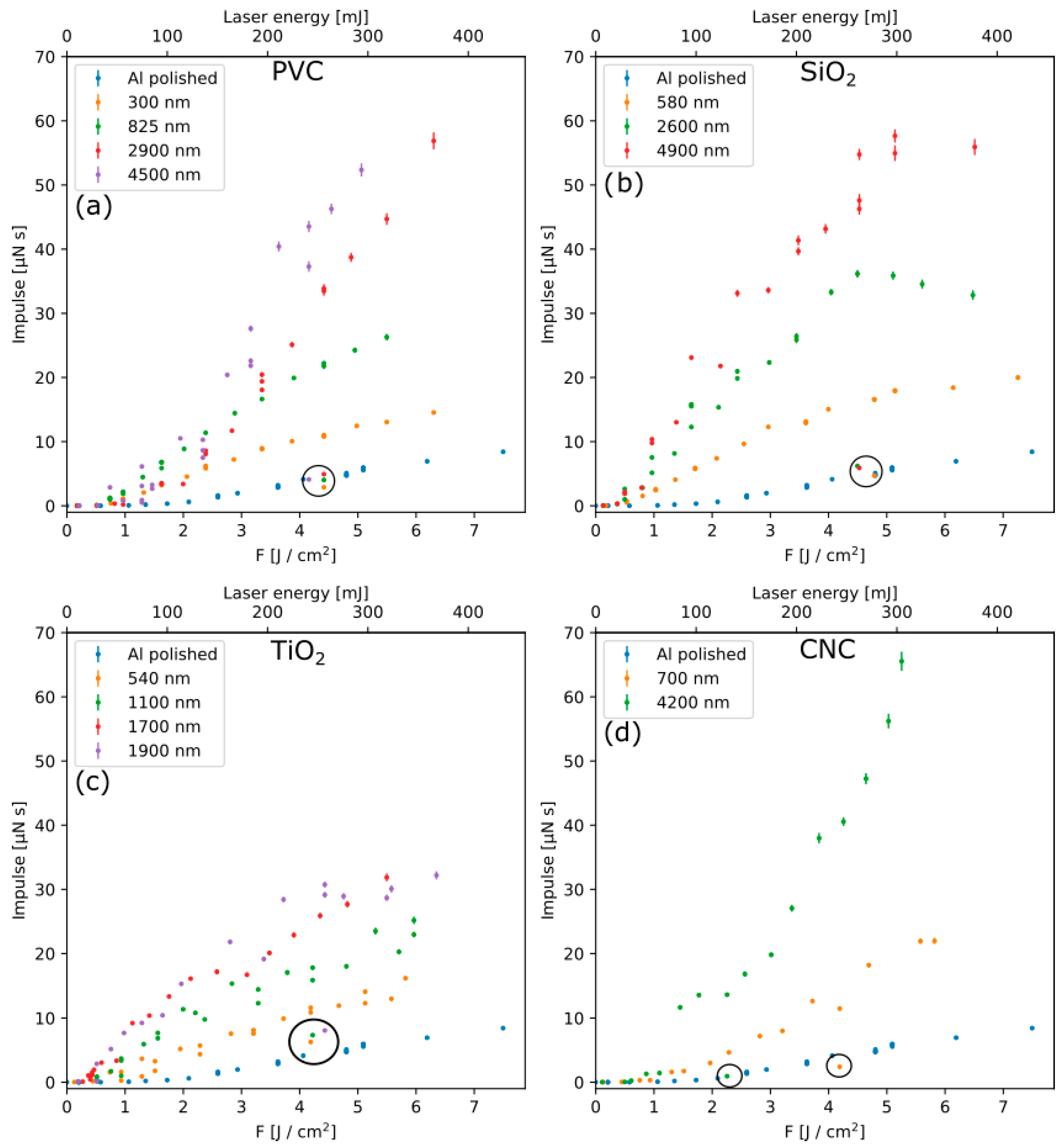
Impulse measurements demonstrated that thin films can effectively enhance impulse generation by confining the expansion of the laser generated plasma plume. Additionally, higher impulse is observed for thicker confinement.

To confirm that laser ablation effectively occurs with the ejection of the confinement layer, ablated mass measurements were conducted. Results showed that the average ablated mass per pulse corresponds to the mass of the confinement layer inside the irradiated region. In addition, it is observed that ablated the mass per pulse does not depend on laser fluence, provided that it is sufficiently high to remove the layer, and that ejected aluminum mass is negligible compared to the mass of ejected confinement layer.

In order to discuss the effect of the confinement layer on the ablation process, SEM and EDS analysis were conducted. The morphology of the ablation craters shows that the confinement layer promotes the melting of aluminum surface, while the elemental composition of the generated craters confirmed the complete ejection of the confinement layer, except for the case of TiO₂ confinement.

The generated impulse and ejected mass allowed to calculate the kinetic energy $E_K$ of the ejected layer, showing that, setting the laser fluence in the range $1\sim 6$ $\mathrm{J}/{\mathrm{c}\mathrm{m}}^2$, it does not depend on its thickness.

$E_{\mathrm{K}}$ obtained for the different confinement materials were compared, observing that smaller values are obtained in the case of TiO₂. This result was discussed in terms of energy balance by referring to the model of Fabbro et al. [16], showing that, because of the different deposition method, TiO₂ has a better adhesion on aluminum and that a large amount of energy is spent to overcome the adhesion force.

This work offers an experimental insight into impulse generation by laser ablation in a confined regime, in the case of thin confinement layers, indicating that the process is driven by the amount of laser energy that can be converted into mechanical work and that this conversion can be strongly affected by the interface properties.

The obtained results take advantage of the well-known geometrical properties of the investigated samples to point out more general properties of impulse generation in confined ablation regime. This knowledge can help in the development of materials that exploit this mechanism, allowing to optimize the thickness and mass of the confinement layer for a specific mission and overcome the present limitations of this technique.