Dynamic Characteristics and Vibration Behavior of SKL-15 Rail Fastening Clip in High-Speed Railway Systems

Abstract

Current research on the vibration characteristics of fastener clips primarily employs modal experiments combined with finite element simulations; however, limited attention has been given to the dynamic vibration behavior of clips during actual train operations. This study investigates both the quasi-static and dynamic vibration characteristics using an integrated approach of finite element simulation and dynamic testing. Based on the Vossloh W300-1 fastener system, a three-dimensional model is established. Modal and frequency response analyses, together with field test validation, reveal two significant vibration modes within 0–1000 Hz: a first-order mode at 500 Hz and a second-order mode at 560 Hz. These modes are characterized by vertical overturning of the clip arm. Dynamic testing demonstrates that the dominant frequency of the arm acceleration is strongly correlated with the second-order natural frequency, confirming that wheel–rail excitation readily triggers second-order mode resonance. The study further shows that, at train speeds of 200–350 km/h, rail corrugation with wavelengths of 99.2–173.6 mm induces high-frequency excitation at 560 Hz, resulting in resonance fatigue of the clip. As a mitigation measure, regular rail grinding is recommended to eliminate corrugation at critical wavelengths. Additionally, optimizing the clip structure to avoid resonance frequency bands is proposed. These findings elucidate the coupling mechanism between the vibration characteristics of the clip and dynamic loads, providing theoretical support for the safety evaluation of high-speed rail fastener systems and the vibration-resistant design of clips.

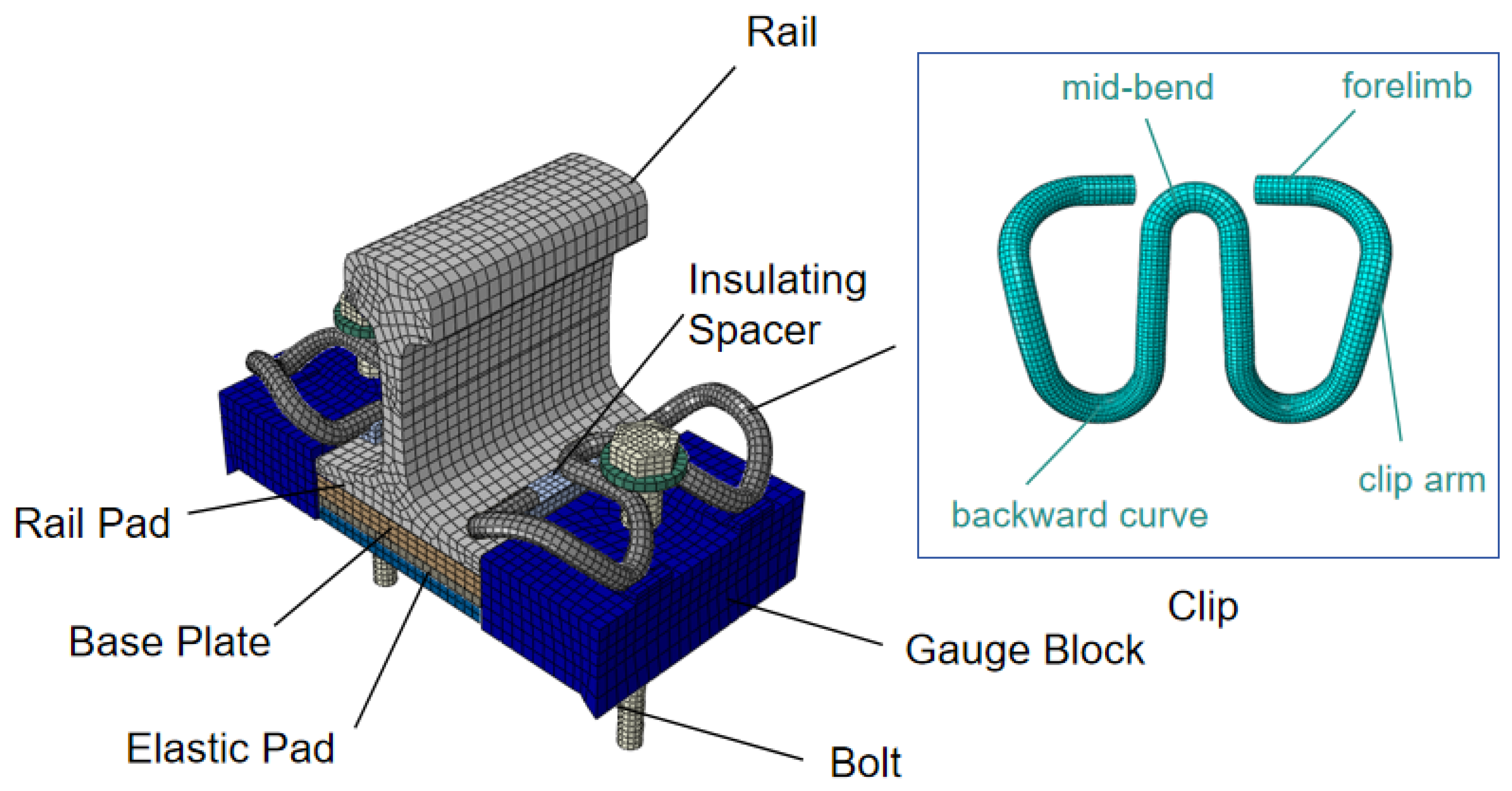
1. Introduction

As a fundamental component of high-speed railway track structures, the fastener system is essential for maintaining rail geometry, adjusting gauge and alignment, and mitigating vibration. Within this system, the clip serves as a critical load-bearing element, continuously subjected to multi-axial alternating stresses resulting from wheel–rail interactions [1] under prolonged cyclic loading. The service performance of the clip is directly associated with the structural stability of the rail and the operational safety of trains [2]. Research and field investigations have revealed instances of clip fractures on several high-speed railway lines in China, including the Wuhan–Guangzhou and Beijing–Shanghai high-speed railways. Although extensive studies have examined the fracture mechanisms of clips, the problem remains unresolved. Therefore, investigating the vibration characteristics of high-speed rail clips is of significant engineering importance, as it elucidates the mechanisms underlying fatigue failure and enhances service performance.

In theoretical studies of clips, Xiao et al. [3], in 1995, verified that the deformation energy theory (also known as the fourth strength theory) is more appropriate for strength calibration of clips. Their research demonstrated that an optimal level of residual deformation can enhance the fatigue life of clips. Using WJ-7 and WJ-8 fasteners as examples, Chen et al. [4] investigated the dynamic stiffness variations in these fastener systems at different temperatures and analyzed the effect of clip deformation on overall dynamic stiffness through finite element simulation. Wang [5] and Gao et al. [6] examined the influence of varying material parameters and clip structural configurations on the fatigue performance of rail clips. With increasing emphasis on the operation and maintenance of high-speed railways, researchers have found that the service performance of high-speed rail field fasteners is affected by their buckling pressure. Yu et al. [7] studied the force characteristics of X2-type fasteners under different buckling pressures, identified the most critical positions in the fastener system, and examined the effects of buckling pressure, lateral force, and loading frequency on fatigue life. Yan et al. [8] explored the impact of different installation conditions of the WJ-8 fastener system on the natural frequency of W1-type clips using hammering experiments. The results indicated that the natural frequency of the W1-type clip is highest under proper installation, while either excessive or insufficient tightening torque reduces it. Diego et al. [9], through quasi-static fatigue testing and finite element analysis, measured the maximum equivalent stress amplitude of the SKL1-type clip to be 134 MPa, which is significantly below the material fatigue limit of 301 MPa. The study confirmed the reliability of the heat treatment process and installation accuracy, indicating a very low probability of fatigue failure under standard service conditions. Moreover, modal analysis has become an essential method for understanding the structural characteristics of clips. Cui et al. [10] obtained the modal characteristics of WJ-8 fasteners in the range of 0–1000 Hz through hammering experiments and analyzed the changes in natural frequency under different installation conditions. Jiang et al. [11] applied a digital image correlation (DIC)-based technique to investigate the free and operating modes of ω-type fastener clips.

In response to the issue of fatigue fractures in clips observed during high-speed railway operations, Lakušić S et al. [12] found that the SKL-1 clip developed cracks after 353,000 loading cycles under dynamic conditions at a frequency of 5 Hz and an amplitude of 1.4 mm. Finite element analysis revealed that the equivalent stress at the critical location of the SKL-1 clip was 10% higher than that of the SKL-12, confirming the superior fatigue performance of the latter due to its lower stress level. Wei et al. [13] investigated the quasi-static effects of passenger cars and wagons on clip fatigue damage, analyzing the influence of fastener stiffness and rubber boot stiffness on clip fatigue. Wang and El-SAYED et al. [14,15] developed a high-fidelity fastening system model to assess the service performance of rail clips by applying mechanical loads or displacements. Xiao et al. [16] analyzed the force characteristics of the 60Si₂MnA clip under fatigue testing, finding pronounced stress concentration at the backward-bending pivot point, where surface defects significantly increased the risk of fatigue fractures. Numerous studies have demonstrated that high-frequency wheel–rail excitation [17,18,19] induces clip resonance, resulting in fatigue failures. Gao et al. [20] examined the frequency range of wheel–rail excitations under-rail corrugation and, by comparing these with the natural frequencies of clips at various torque levels, concluded that frequency overlap leads to resonance-induced fatigue damage. Based on these findings, they optimized the structural parameters of the SKL-15 clip. In a related study, Gao et al. [21] proposed a high-frequency dynamic failure mechanism for the W300-1 fastener system, utilizing modal testing combined with simulation. They also developed a specialized fatigue testing system for high-speed rail fasteners to verify this failure mechanism. Wang et al. [22]., through field testing, confirmed that the primary frequency caused by rail corrugation overlaps with the natural frequency of the fastener clip. This resonance between the primary excitation and the clip’s natural frequency was identified as a key contributor to fatigue-induced fractures. Additionally, researchers adopted an integrated approach combining a vehicle–track coupled dynamics model [23,24] and a fastening system model. The vehicle–track coupled dynamics model was first used to calculate the wheel–rail dynamic response, and the resulting wheel–rail forces or rail displacements were applied as excitation inputs to the fastening system model to independently calculate its dynamic response [25,26,27]. It can be summarized that the existing studies have primarily relied on indoor tests and finite element simulations, with results obtained under quasi-static loading conditions that do not fully reflect the actual vibration characteristics of the clip.

Under operational conditions, as a train passes over a fastener, the combined effects of train load, rail corrugation, and track irregularities inevitably induce clip deformation, thereby altering its vibration characteristics. To address this, this study selects the Vossloh W300-1 fastener system(The Vossloh W300-1 fastener system is produced by the German Vossloh Group, with its core production base located in: Neuss, Germany.), which is widely used in high-speed railways, as the research subject. A detailed finite element simulation model of the fastener is established to investigate the quasi-static and dynamic vibration characteristics of the SKL-15 clip under operational conditions, utilizing a combination of on-site dynamic testing, modal analysis, and frequency response analysis. Furthermore, the influence of rail corrugation on the clip’s vibration characteristics is examined. The objective is to provide a theoretical foundation for the dynamic safety assessment of fastener systems and the vibration-resistant design of clips in high-speed railway applications.

2. Materials and Methods

To analyze the intrinsic vibration characteristics of the SKL-15 clip, a three-dimensional solid finite element model was established based on ABAQUS, as shown in Figure 1. The model of the Vossloh W300-1 fastening system mainly consists of a clip, gauge stops, insulating shims, under-rail matting, iron matting, elastic matting, and related components. Each part of the fastener system is modeled based on actual dimensions, with appropriate simplifications made to certain components to improve computational efficiency. The specific material properties are shown in

Table 1. Material properties of the Vossloh W300-1 FE model.

Component	Material	Elastic Modulus (GPa)	Poisson’s Ratio	Density (kg/m3)
Rail	U75VG Steel	210	0.3	7850
SKL-15 Clip	38Si7 Steel	207	0.3	7850
Bolt	No. 35 Steel	206	0.3	7850
Bolt Washer	No. 35 Steel	206	0.3	7850
Rail Pad	EVA	2.45 × 10−2	0.3	950
Base Plate	Hot-rolled Wide Strip Steel	173	0.3	7800
Elastic Pad	EPDM Rubber	7.84 × 10−3	0.47	870
Gauge Block	PA66	8.5	0.4	1450
Insulating Spacer	PA66	8.5	0.4	1450

. All parts are meshed with a hexahedral mesh to ensure the simulation accuracy. To ensure computational accuracy in the finite element simulation, all components were discretized using hexahedral elements. The mesh consisted of three-dimensional solid elements, specifically eight-node hexahedral reduced integration elements (C3D8R), totaling 39,164 nodes and 34,176 elements.

It should be noted that when analyzing the modal frequencies and mode shapes of the clip within the small deformation range, a linear elastic constitutive model is adopted for the metal components, while polymeric parts such as the under-rail matting are assumed to possess equivalent linear stiffness. This simplification aims to effectively capture the intrinsic mode shapes of the clip while keeping the computational scale manageable. However, these simplifications also introduce corresponding limitations: the linear elastic model does not account for the nonlinear material behavior under large deformations or fatigue loading; the simplification of complex characteristics, such as the nonlinearity of rail pads, may lead to deviations in predicting system damping and high-frequency dynamic stiffness. These limitations imply that the current model is more suitable for qualitative analysis of the intrinsic characteristics of the clip. For accurate predictions of nonlinear transient responses or broadband vibration transmission, more sophisticated material constitutive relationships need to be introduced.

To simulate the actual installation state of the fastener system, appropriate contact interactions and constraints were defined for each component. The clip, being the primary focus of the present study, was modeled with friction contact. The tangential contact adopts the Coulomb friction model in ABAQUS with a friction coefficient of 0.3, and the normal contact is set as “hard contact”. To improve the computational efficiency of the model, the contact relationships among other components were simplified and modeled as binding constraints. The specific contact relationships are shown in

Table 2. Contact relationships in the Vossloh W300-1 fastening system finite element model.

Contact Pair	Contact Behavior	Contact Type	Contact Body	Target Body	Friction Coefficient [28]
Clip vs. Bolt Washer	Surface–Surface	Frictional	SKL-15 Clip	Bolt Washer	0.3
Clip vs. Gauge Block	Surface–Surface	Frictional	SKL-15 Clip	Gauge Block	0.3
Clip vs. Insulating Spacer	Surface–Surface	Frictional	SKL-15 Clip	Insulating Spacer	0.3
Bolt vs. Bolt Washer	Surface–Surface	Bonded	Bolt	Bolt Washer	N/A
Rail vs. Insulating Spacer	Surface–Surface	Bonded	Insulating Spacer	Rail	N/A
Rail vs. Rail Pad	Surface–Surface	Bonded	Rail	Rail Pad	N/A
Rail Pad vs. Base Plate	Surface–Surface	Bonded	Rail Pad	Base Plate	N/A
Base Plate vs. Elastic Pad	Surface–Surface	Bonded	Base Plate	Elastic Pad	N/A

. Vossloh W300-1 type fastener system is a shoulder-type fastener system where the relative displacement between gauge block and sleeper is approximately zero. As the present study focuses solely on the vibration characteristics of the clip, the gauge block was fully constrained to simulate the restraining effect of the sleeper on the fastener system.

To analyze the vibration characteristics of the fasteners, it is necessary to simulate their normal installation state. The Vossloh W300-1 fastener system is secured by bolts that fasten the clip. It is considered to be in the normal installation position when the middle curved portion of the clip comes in contact with the protruding part of the gauge baffle plate. Based on this condition, clamping forces ranging from 10 to 40 kN were applied to the fastener system model. The specific simulation results are shown in Figure 2.

As shown in

Table 3. Relationship between clamping force and displacement in FE simulation.

Mechanical Indicator	Value
Bolt pre-tensioning force (kN)	10	20	30	33	35	40
Mid-bend displacement of clip (mm)	5.2	10.6	16.0	18.1	18.2	18.2
Clip clamping force (kN)	3.9	7.8	12.5	13.8	14	14.2
Ref. [29]: Mid-bend displacement of clip (mm)	6.0	12.2	18.5	20.3	—	20.5
Ref. [29]: Clip clamping force (kN)	4.1	8.2	12.6	13.8	—	14

, when the bolt preload is applied at 33 kN, the middle curved portion of the clip comes in contact with the protruding part of the gauge baffle plate. Further increase in the preload does not cause significant additional displacement of the clip’s curved section, which remains approximately at 18 mm. Therefore, this state can be considered as a representation of the normal installation condition of the clip. When the bolt preload is applied at 33 kN, the displacement of the clip’s middle elbow is 18.1 mm, which closely matches the displacement value of 20.3 mm, as reported in the Ref. [28]. This result verifies that the finite element model of the Vossloh W300-1 fastener system accurately reflects the normal installation condition.

3. Results and Discussion

3.1. Modal and Frequency Response Analysis

During train operation, track irregularities, rail corrugation, and wheel out-of-roundness generate high-frequency excitation between the wheel and rail. When the excitation frequency falls within a specific frequency band, it will induce resonance of the clip. Therefore, modal and frequency response analysis of the SKL-15 clip was conducted to explore the intrinsic vibration modes and the sensitivity to the frequency.

3.1.1. Simulation Modal Analysis

Using the Lanczos method, the intrinsic frequency and eigenvectors of the model were obtained, and a free modal analysis of the SKL-15 clip was carried out without applying external forces or constraints. Since the excitation frequency of the wheel and rail of the high-speed railroad generally falls within the range of 0~1000 Hz [30], the present study focuses on the clip’s modal behavior within the frequency band. The computed modal frequencies and corresponding vibration modes within the range of 0~1000 Hz are shown in Figure 3, where the transparent shape represents the underperformed position of the clip, and the solid shape represents the deformed position. Specific descriptions of the modal shapes of each order are shown in

Table 4. Natural frequencies and mode shape characteristics of SKL-15 clip.

Mode Order	Natural Frequency (Hz)	Mode Shape Description
1st	262.96	Forelimb of clip bends toward mid-bend area
2nd	303.17	Coupled overturning motion: forelimb and clip arm in opposite-phase vertical oscillation
3rd	379.41	Vertical displacement at clip’s mid-bend section
4th	392.21	Backward curve section bends toward central axis
5th	415.29	Anti-phase vertical oscillation of forelimbs
6th	664.68	In-phase vertical oscillation: forelimb and clip arm synchronous motion
7th	719.44	Counter-phase vertical oscillation: forelimb and clip arm opposing motion

.

Using finite element simulation, the working modes of the SKL-15-type clip under the installed state of the Vossloh W300-1 type fastener system were computed, as shown in Figure 4. Within the frequency range of 0~1000 Hz, the clip exhibits two working modes: the first-order modal frequency at 503 Hz and the second-order modal frequency at 567 Hz. As shown in Figure 4, the vibration patterns corresponding to these working modes are primarily characterized by the movement of the clip arm. In particular, the first-order mode of the SKL-15-type clip occurs at 503 Hz, where the modal vibration pattern is characterized by the left and right clip arms performing up-and-down overturning motions in opposite directions. The second working mode appears at 567 Hz, where the left and right clip arms exhibit synchronized up-and-down overturning motions resembling the flapping of a butterfly’s wings. In both first- or second-order modal vibration patterns, the clip arm is pivoted at the backbend buckling points, leading to overturning vibrations. During this motion, the stress concentration at the backbend buckling points is higher than in other parts of the clip, making it more susceptible to damage.

3.1.2. Comparative Analysis of Modal Test and Simulation Results

To verify the accuracy of the finite element simulation results and to further analyze the vibration characteristics of the clip, a modal test was conducted on the SKL-15 clip installed on a high-speed railroad. A medium-sized elastic force hammer was used for excitation and multi-point hammering. A multi-point vibration pickup method was adopted. The field-testing setup and the measurement location are shown in Figure 5b. Acceleration sensors were installed at the bend and at the highest points of the clip arms on both sides of the clip. Using the force hammer, the clip was struck sequentially at 16 excitation points, and the hammer force signals, along with the clip vertical acceleration signals at each sensor location, were collected through a data acquisition system (DAQ). The impact points and sensor locations are as shown in Figure 6a.

The accelerometer used was an IEPE (Integrated Electronics Piezo-Electric) sensor with a measurement range of 1000 g, a sensitivity of 500 mV/g, a frequency response of 0.35–10,000 Hz, and a weight of 14 g. Acceleration data were collected by a networked intelligent data acquisition system. The base of the accelerometer was bonded to the clip using high-strength adhesive. Since the tensile–shear strength of the high-strength adhesive can reach 25–50 MPa or higher, the accelerometer and the clip can be considered as an integrated whole.

The frequency response function of the vibration acceleration at the clip arm and the mid-bend position is shown in Figure 6. The graphs indicate two predominant peaks in the frequency range of 0~1000 Hz, at 497 Hz and 571 Hz, corresponding to the first-order and second-order modes of the clip, respectively. Figure 7b shows that the peaks of the acceleration frequency response function at the mid-bend of the clip occur above 1500 Hz, and the maximum peak is observed at 2293 Hz. These results indicate that when the wheel–rail excitation is transmitted from the rail to the fastener, the modes related to the clip arm are more likely to cause resonance. In contrast, although the frequency response function at the mid-bend shows higher peaks, the related modes typically occur at higher frequencies, making resonance less likely under typical wheel–rail excitation conditions.

Based on the frequency response function of the clip, the impulse response function of the clip was computed. Using the system identification algorithm, the first two orders of the modal vibration patterns of the clip were obtained. The modal frequency and vibration pattern of the SKL-15 clip within the 0~1000 Hz range are shown in Figure 7. The green line in the figure is the spatial position of the clip before deformation, while the red and blue lines are the spatial position of the clip after deformation. As can be seen from Figure 8, the modal frequency of the clip obtained from the modal test closely matches the simulation results, with a deviation of less than 5%. Furthermore, the first two orders of the modal vibration pattern are consistent with the simulation results, effectively verifying the accuracy of the finite element simulation model of the Vossloh W300-1 fastener system.

3.1.3. Frequency Response Analysis

The vibration characteristics of the system can be represented by the displacement conductance curve within the excitation frequency range, where the displacement conductance reflects the ability of the system to conduct displacement under dynamic excitation. As a multi-degree-of-freedom system, the equation of motion of the fastener system is as follows:

$$\left[M\right]\left\{\ddot{x}\right\}+\left[C\right]\left\{\dot{x}\right\}+\left[K\right]\left\{x\right\}=\left\{F\right\}$$

(1)

where $\left[M\right]$ is the fastener system mass matrix; $\left[C\right]$ is the fastener system damping matrix; and $\left[K\right]$ is the fastener system stiffness matrix. $\left\{\ddot{x}\right\}$, $\left\{\dot{x}\right\}$, and $\left\{x\right\}$ are the acceleration, velocity, and displacement vectors of the system, respectively.

Transforming into the frequency domain via the Fourier transform yields the following:

$$(-{\omega }^2\left[M\right]+j\omega \left[C\right]+\left[K\right])\left\{X\left(\omega \right)\right\}=\left\{F\left(\omega \right)\right\}$$

(2)

The displacement admittance matrix $\left[Y_{ij}\left(\omega \right)\right]$ is the inverse of the impedance matrix $\left[Z\left(\omega \right)\right]=(-{\omega }^2\left[M\right]+j\omega \left[C\right]+\left[K\right])$:

$$\left[Y_{ij}\left(\omega \right)\right]={\left[Z\left(\omega \right)\right]}^{-1}$$

(3)

Each element $Y_{ij}\left(\omega \right)$ in the matrix represents the displacement response at point i due to a force applied at point j.

To further analyze the vibration characteristics of the SKL-15 clip, a steady-state dynamic analysis was conducted using the modal superposition method, and it was used to solve the frequency response when unit sinusoidal loads were applied at different locations. Based on the intrinsic frequencies obtained from the modal analysis, the excitation frequency range was set from 0 to 1000 Hz. When a train passes over the fasteners, compression of the fastener plate and the tipping of the rails cause deformation in the front of the clip that is buckled onto the rail 31. Therefore, a vertical unit sinusoidal load was applied at the pivot point on the front surface of the clip to simulate operational conditions. The displacement conductance and acceleration of the clips are obtained for the various parts of the clips under the installation state. Then, the displacement and acceleration responses of various parts of the clip under the installed condition were obtained, as shown in Figure 8. The results indicate that each part of the clip exhibits a single distinct resonance peak in both the displacement and acceleration conductance curves, occurring at a frequency of 566.7 Hz. Along with the results of modal analysis, this resonance peak corresponds to a frequency close to the second-order modal intrinsic frequency of the clip. It can thus be concluded that when the excitation frequency of the clip is near 570 Hz, the clip enters into resonance, primarily vibrating in its second-order working mode. This resonance is a critical factor contributing to fatigue damage in the clip during service.

Figure 8. Receptance response results at multiple sections of the SKL-15 clip.

Figure 8. Receptance response results at multiple sections of the SKL-15 clip.

3.1.4. Analysis of Bolt Preload Influence

The operational mode shapes and frequencies of a fastener clip are determined by its spatial geometry and boundary conditions. As a prefabricated component of the fastener system, the clip has a defined spatial geometry. However, during installation on high-speed railway sites, certain manual variations inevitably occur due to the practices of construction personnel, which subsequently influence the clip’s operational mode shapes and frequencies. Differences in the torque applied by construction personnel to the threaded spike during installation can result in the fastener clip being in an under-tightened state, a properly installed state, or an over-tightened state, as illustrated in the Figure 9. In the under-tightened state, insufficient torque means that the central bend of the clip does not contact the protruding part of the gauge block. Conversely, in the over-tightened state, excessive torque presses the central bend of the clip firmly against the protruding part of the gauge block, causing some deformation.

By applying different magnitudes of fastening force to the clip model, the on-site scenario where construction personnel apply varying torques to the threaded spikes was simulated. This resulted in the clip being in the under-tightened state, properly installed state, and over-tightened state. The Lanczos method was employed to solve for the natural frequencies and eigenvectors of the clip model under these three installation conditions. The results are presented in the

Table 5. Operational modal frequencies of the fastener clip under different installation states.

	1st Order Modal Frequency (Hz)	2nd Order Modal Frequency (Hz)
Under-tightened State	493	542
Properly Installed State	503	557
Over-tightened State	492	545

below. As can be seen from the Table 5, when the clip is in the properly installed state, i.e., when the central bend of the clip just makes contact with the protruding part of the gauge block, its first-order and second-order operational modal frequencies are the highest. Both under-tightening and over-tightening lead to a decrease in these frequencies. Therefore, during on-site installation, construction personnel should apply the specified appropriate torque according to regulations to ensure the service performance of the fastener system, particularly that of the clip.

3.2. Vibration Characteristics of the Clip Under Train Loading

When the train passes over the fastener system, the clip inevitably undergoes a certain degree of deformation due to the train load, which alters its vibration characteristics. In order to go beyond the traditional quasi-static analysis framework and further investigate the dynamic vibration characteristics of the SKL-15-type clip under high-speed traveling conditions, on-site dynamic tests were carried out on a straight section of a domestic high-speed railroad roadbed. These tests were aimed at obtaining the acceleration response of the clip at different locations. Since the measurement site was a newly constructed line, the influence of rail wave abrasion on the clip could be excluded. From the modal analysis, it is evident that the first two orders of the clip are mainly associated with the clip arms. Therefore, the acceleration response analysis was focused on these areas. Accelerometers were installed at the highest points of both the left and right clip arms. Additionally, three accelerometers were placed at the mid-bend region of the clip. The layout of field measurement points is shown in Figure 10. The accelerometer used has a measurement range of 1000 g, a sensitivity of 500 mV/g, a frequency range of 0.35–10,000 Hz, and a weight of 14 g. Acceleration data was collected by a networked intelligent acquisition system.

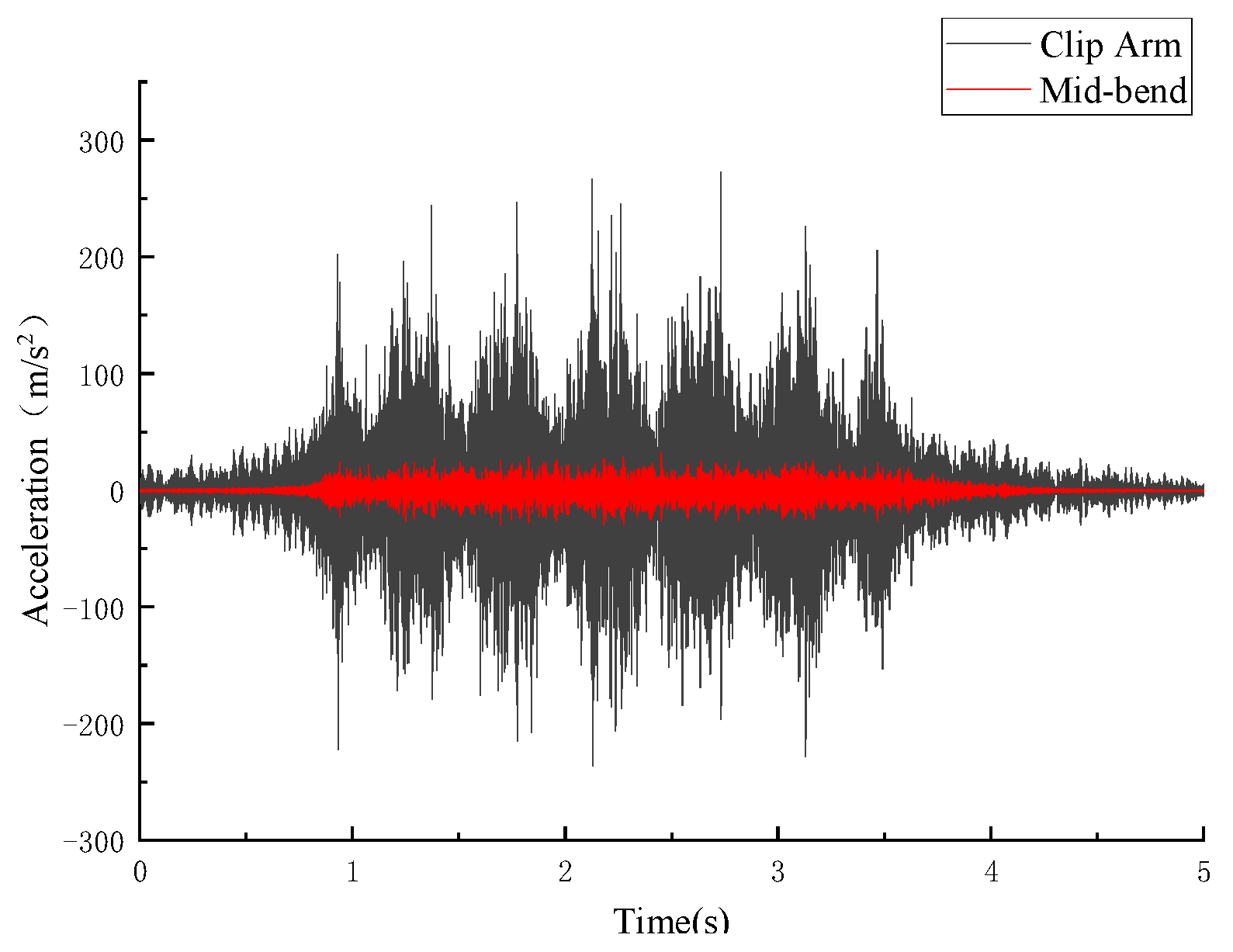
Typical acceleration curves of the clip at each position are shown in Figure 11. When the clip vibrates due to excitation from the train wheels and rails, the most significant vibration response occurs at the clip arm. In contrast, the mid-bend position shows minimal vibration response due to being preloaded and clamped onto the protruding part of the front end of the track gauge plate. From Figure 12, it can be observed that as the speed increases, the effective acceleration values of both the clip arm and the mid-bend in the clip increase, exhibiting an approximately linear trend.

The Fourier transform and subsequent data processing of the acquired acceleration time-domain signals were performed to obtain the power spectral density (PSD) of the acceleration at clip positions, as shown in Figure 13. It can be seen from Figure 13 that, under the train load, the clip arm exhibits a single prominent frequency, with the main acceleration frequency occurring near 560 Hz. According to modal analysis, the first two working modes of the clip within the range of 0~1000 Hz are 500 Hz and 560 Hz, respectively. The 560 Hz frequency corresponds to the second-order modal frequency, indicating that under the train load, the SKL-15 clip is more likely to excite the second working mode. Figure 13b shows that the main frequency at the middle bend of the clip is around 1800 Hz. Modal analysis shows that modes involving the mid-bend as the main deformation zone lie above 1000 Hz. Furthermore, under the train load, the SKL-15 clip does not resonate in relation to the first two working modes. Therefore, the attention should be focused on the clip arm, specifically on how the dominant acceleration frequency at this location varies with the train’s operating speed.

The main frequency of the acceleration at the clip arm position was determined for different train running speeds, as shown in Figure 14. At a speed of 180 km/h, the main acceleration frequency is 560 Hz. This increases to 578 Hz when the train speed reaches 290 km/h. This indicates that the excitation frequency of the clip arm under train load is near the frequency of the second-order intrinsic modal frequency of the clip throughout the speed range of 180–290 km/h. However, the results also show that the main acceleration frequency at the clip arm position increases gradually with rising train speed.

In order to investigate the reason for the increase in the main acceleration frequency at the clip arm position, a time–frequency analysis was carried out for different train speeds, as shown in Figure 15. The energy ratio represents the proportion of energy within a specific frequency band relative to the total energy, characterizing the share of vibration energy in a single band within the overall energy. Calculate the energy ratio within the 450–600 Hz frequency range. At a train speed of 180 km/h, the energy ratio is 54.5%. When train speed increases to 290 km/h, the energy ratio decreases to 25.9%. This indicates that as train speed increases, the vibration energy of the clip shifts from lower to higher frequencies, thereby increasing the dominant frequency of the clip acceleration. In summary, as train speed rises, the proportion of mid-to-high frequency components in the clip acceleration increases, and the dominant frequency of the clip also increases.

3.3. Analysis of the Impact of Rail Corrugation

As described in the Ref. [31], when the train passes through a track section affected by rail wave abrasion, the resulting high-frequency wheel–rail excitation coincides with the intrinsic modal frequency of the clip, leading to its resonance. This resonance can cause prolonged vibrations in the clip, ultimately leading to its fatigue failure. The relationship between rail wave abrasion, excitation frequency, and train speed is given by the following:

$$f={\displaystyle \frac{v}{0.0036\lambda }}$$

(4)

In Equation (4), $f$ is the excitation frequency, Hz; $v$ is the traveling speed, km/h; $\lambda$ is the wave mill wavelength, mm.

Vibration test results, in combination with the modal analysis, show that the second-order intrinsic modal frequency of the SKL-15 clip can be easily excited during train operation, i.e., 560 Hz is the sensitive frequency of the SKL-15 clip. Substituting this frequency value into Equation (1), it can be seen that when the train speed is in the range of 200~350 km/h, the wave abrasion of the rail with a wavelength between 99.2 and 173.6 mm will cause the resonance in the clip and will further lead to failure due to fatigue rupture.

Based on the comprehensive analysis in previous sections, during train operation, the vibration response of the clip arm position is most pronounced. The main acceleration frequency of the clip arm under train load is close to the second-order intrinsic modal frequency of the clip. When rail wave abrasion with wavelengths in a certain range exists in a track, it will cause clip resonance damage. Research indicates that the dominant frequency of the clip’s operational mode is close to the dominant frequency of wheel–rail noise, and suppressing the high-frequency vibration of the clip can contribute to a certain reduction in the overall level of wheel–rail noise.

4. Conclusions

This study investigates the vibration characteristics of the SKL-15 clip using finite element modeling and steady-state dynamics theory, supported by modal analysis, frequency response analysis, and vibration test results. The relationship between vibration characteristics and rail corrugation under train loading is also examined. The main conclusions are as follows:

(1) Based on finite element simulation and hammer modal testing, it is determined that within a 1000 Hz range, the SKL-15 clip exhibits two orders of working mode frequencies. The first order of the modal frequency is around 500 Hz, and the second-order modal frequency is near 560 Hz. Both modes primarily involve the up-and-down overturning motion of the clip arms.

(2) The vibration response of the SKL-15 clip under the train load is most pronounced at the clip arm position. The dominant acceleration frequency of the clip arm closely aligns with the second-order modal frequency. Combined with the results of the finite-element frequency response analysis, this confirms that the resonant behavior under the high-frequency excitation is primarily governed by its second-order intrinsic mode. Furthermore, as the train speed increases, the vibration energy shifts from the low-frequency band to the high-frequency band, resulting in a higher dominant acceleration frequency at the clip arm.

(3) When the train speed is in the range of 200~350 km/h, and the rail wave abrasion exhibits a wavelength between 99.2 and 173.6 mm, the resulting excitation frequency will coincide with the clip’s second-order modal frequency, leading to its resonance. Prolonged resonance will lead to fatigue damage of the clip.