A Heuristic Packing Strategy for Eccentric-Shaped Parts

Abstract

Efficient packing of irregular mechanical parts in limited container space is essential for reducing transportation and storage costs in automated manufacturing. This study focuses on eccentric-shaped parts characterized by geometric asymmetry, multiple orientations, and local irregularities, and proposes a two-stage three-dimensional packing strategy. In the first stage, an optimal single-layer layout is generated using a heuristic algorithm that combines grid scanning with a gravity-drop principle and tabu search to optimize part positions and orientations. In the second stage, the optimized layer template is vertically replicated with buffer layers to enhance stacking stability, ensuring feasible and non-overlapping arrangements. Comparative experiments with Best Fit, BLF, LHL, and Random methods show that the proposed approach increases average space utilization by 8.3%, 8.8%, 8.1%, and 15.5%, respectively, while maintaining high stability and reasonable computation time. The results demonstrate that this method achieves dense and stable packing, offering an effective solution for intelligent packing and automated production of irregular parts.

1. Introduction

The application of automation technology in manufacturing has increasingly emphasized the importance of automated packing systems for improving production efficiency and reducing labor costs [1]. In the engineering machinery industry, eccentric shafts are widely used as motion conversion and power transmission components in engine valve trains, fuel injection systems, hydraulic pumps, compressors, and various automated actuators. In industrial practice, thousands of such components are produced daily, with hundreds of identical parts often required to be packed into a single container. However, due to their complex geometry, these components are predominantly packed manually or semi-automatically into containers without any standardized arrangement, resulting in low space utilization and limited consistency.

The eccentric structure of these shafts is essential for converting rotational motion to reciprocating motion and vice versa. However, geometric features such as eccentric outer surfaces, stepped shaft segments, keyways, and eccentric holes introduce strong asymmetry and local irregularities [2,3]. These characteristics make conventional packing strategies designed for regular objects difficult to apply, often resulting in inefficient space usage or unstable stacking. Therefore, developing packing methods that explicitly consider the structural characteristics and placement constraints of eccentric shafts is of high practical significance.

The bin packing problem is a classical NP-hard optimization problem, where a set of objects must be placed into a container without overlap while maximizing space utilization [4]. Depending on the dimensionality, the problem can be classified as one-dimensional, two-dimensional, or three-dimensional. In industrial applications, the challenge is further increased by multi-pose constraints, geometric irregularity, and the need for physically stable arrangements. These challenges motivate the development of specialized three-dimensional packing strategies that are both computationally efficient and suitable for practical engineering use.

To address these challenges, this study investigates the three-dimensional packing problem of eccentric shafts and develops a heuristic packing strategy tailored to their structural and placement characteristics. The main contributions of this work are:

–

Formulation of a 3D packing model that explicitly considers geometric irregularity and pose constraints of eccentric shafts.

–

Development of a two-stage heuristic algorithm combining grid-scan, gravity-drop, tabu search, and layer-template replication to generate dense and physically plausible layouts under practical engineering constraints.

–

Validation of the proposed method through numerical experiments and physics-based stability evaluation using PyBullet, demonstrating effectiveness for eccentric-shaped mechanical components.

The novelty of this work lies in targeting a specific class of industrially important eccentric-shaped parts and integrating physical placement considerations into the packing strategy, including a template layer replay with inter-layer foam buffer to enhance stacking stability, thereby improving both space utilization and engineering-level stability in automated packing systems, while facilitating automated grasping and path planning for robotic loading.

2. Related Works

The bin packing problem is a typical NP-hard problem, and its computational complexity makes it difficult to obtain exact solutions within limited time. According to problem dimensionality, it is commonly classified into one-dimensional, two-dimensional, and three-dimensional models [4]. A wide range of studies have emerged for different application scenarios, covering online packing [5], loading optimization with multiple container types [6], and packing systems designed under practical constraints [7].

To improve computational efficiency, existing methods can be broadly categorized into two classes. The first class comprises metaheuristic algorithms, such as simulated annealing (SA) [8], genetic algorithms (GA) [9], ant colony optimization (AC) [10], tabu search (TS) [11,12], and large neighborhood search [13]. In recent years, deep reinforcement learning has also been applied to 2D and 3D loading problems [14,15], enabling approximate policy learning and end-to-end optimization [16]. The second class includes constructive heuristics, such as block-based loading [17], layer-based strategies, and depth-first search in 3D cases, as well as the bottom-left method [18], lowest horizontal line [19], and improved skyline-based approaches [20] in 2D problems.

Although these studies provide a solid theoretical and methodological foundation for complex packing problems, each method relies on specific assumptions. Their applicability is still limited when dealing with highly irregular parts, multi-pose constraints, true geometric nesting, and engineering-level stability requirements.

3. Analysis of the Packing Problem

The structural characteristics of eccentric shafts are primarily determined by their functional role within transmission systems, resulting in pronounced irregularity and asymmetry. These geometric features pose significant challenges for maintaining stable orientations during spatial packing and impose additional constraints on packing strategies and algorithms. As illustrated in Figure 1, eccentric shafts are generally fabricated from high-strength steel and, following heat treatment, exhibit locally reduced toughness, contributing to a substantial overall mass. During handling and packing operations, these shafts are highly susceptible to collisions and slippage, which can lead to localized structural damage or deformation. Such incidents not only compromise the safety and reliability of the transmission system but also negatively impact packing efficiency and the effectiveness of automated packing processes.

4. Mathematical Model

4.1. Problem Description

Let the total number of eccentric parts be $n$. The dimensions of the $i$-th part are denoted by $l_i,w_i,h_i$ ($i=1,2,\dots ,n$). There are $m$ types of available boxes, with the $j$-th box having a base of $L_j\times W_j$ and height $H_j$ ($j=1,2,\dots ,m$). A Cartesian coordinate system is used to represent the packing space, where the position of each part is defined by the coordinates of its left-rear-bottom corner $\left(x_i,y_i,z_i\right)$.

Due to the asymmetric geometry and the presence of eccentric features, each eccentric part exhibits a limited number of mechanically stable resting configurations when placed inside a container. In practical packing operations, arbitrary in-plane rotations generally do not improve packing efficiency significantly and may lead to unstable contact conditions. Therefore, in this study, only four representative and mechanically stable orientations, corresponding to 90° rotational variations around the vertical axis, are considered. These four orientations are illustrated in Figure 2. Preliminary investigations indicate that including additional in-plane rotations beyond these four provides negligible improvement in space utilization while substantially increasing computational complexity. Moreover, these four orientations are technologically feasible, avoiding placement on sensitive areas of the part and enabling reliable manipulation with the robotic gripper. These four orientations are sufficient to capture the dominant packing behaviors while maintaining computational tractability.

The objective of the packing problem is to determine the placement positions, layer assignments, and stable orientations of all eccentric parts within a selected container, so as to maximize space utilization under geometric feasibility and stability constraints, and to generate a detailed and orderly packing layout suitable for automated implementation.

4.2. Objective Function

Let the container be a rectangular box with a fixed base size L × W. The objective of the packing problem is to place a given set of eccentric parts into the container without overlap, such that the occupied container volume is maximized under geometric and stability constraints.

Denote the total number of parts by N, and let V_i be the volume of part $i$. The total packed volume is defined as

$$V_p=\sum _{i=1}^N{V}_i$$

Since the container base dimensions L and W are fixed, the optimization objective can be equivalently formulated as maximizing the three-dimensional space utilization ${\eta }_{3D}$, defined as

$${\eta }_{3D}={\displaystyle \frac{V_p}{L\times W\times H_c}}$$

where $H_c$ denotes the overall stacking height of the container after all parts have been placed.

The 3D packing problem can be formulated as the following optimization problem:

$$\max V_p or equivalently \min H_c$$

subject to the constraints that all parts are placed entirely within the container, no interpenetration occurs, and all placements satisfy the mechanical stability and orientation feasibility requirements.

To reduce computational complexity, the 3D packing problem is decomposed into a sequence of 2D layer packing subproblems. Let $A_c=L\times W$ be the container base area, and let $S_t$ be the total area of the planar projections of all parts within a layer. The planar packing efficiency for each layer is defined as

$${\eta }_{2D}={\displaystyle \frac{S_t}{A_c}}$$

By improving the planar packing efficiency ${\eta }_{2D}$ within each layer, more parts can be accommodated per layer, which increases the total packed volume $V_p$ under a given container height or layer limit. As a result, maximizing ${\eta }_{2D}$ contributes directly to the improvement of the overall 3D space utilization ${\eta }_{3D}$.

4.3. Constraints

Let the set of parts be $P=p_1,p_2,\dots ,p_n$. The 2D projection polygon of part $i$, denoted as $p_i$, is obtained by orthogonally projecting the 3D model onto the horizontal plane according to its selected orientation. The resulting polygon, exported as a CSV file, preserves the actual boundary of the part, including horizontal concave and eccentric features. To ensure that these simplifications do not cause undetected collisions during 3D stacking, the 3D occupied volume V_i of each part is retained and used for vertical placement and collision checks.

The container dimensions are $L\times W\times H$, and the allowable layer indices are $K=1,2,\dots ,m$, where $m=H/h_s$ and $h_s$ is the layer height. The placement variables of part $\mathrm{i}$ are $\left(x_i,y_i,k_i,{\mathsf{\theta }}_i\right)$, where $\left(x_i,y_i\right)$ are the bottom-left-rear coordinates, $k_i$ is the layer index, and ${\mathsf{\theta }}_i\in 0^{\circ },{90}^{\circ },{180}^{\circ },{270}^{\circ }$ is the orientation. Let $l_i\left(\mathsf{\theta }\right)$ and $w_i\left(\mathsf{\theta }\right)$ denote the bounding rectangle width and length in the X-Y plane under orientation $\mathsf{\theta }$.

The constraints are formulated as follows:

$$h_i\le h_s$$

(1)

$$0\le x_i\le L-l_i\left({\mathsf{\theta }}_i\right)$$

(2)

$$0\le y_i\le W-w_i\left({\mathsf{\theta }}_i\right)$$

(3)

$$\left(k_i-1\right)h_s\le z_i\le k_i{h}_s-h_i\left({\mathsf{\theta }}_i\right)$$

(4)

$$P_i\left(x_i,y_i,{\mathsf{\theta }}_i\right)\cap P_j\left(x_j,y_j,{\mathsf{\theta }}_j\right)=\mathrm{\varnothing },\forall i\ne j$$

(5)

$$V_i\cap V_j=\mathrm{\varnothing },\forall i\ne j$$

(6)

$$\left(x_i,y_i\right)\in C$$

(7)

where $C$ is the set of candidate placement points generated from initial positions, boundaries of placed parts, and the base grid. Constraint (1) ensures the part height does not exceed the layer height. Constraints (2) and (3) guarantee that the part projection is within the container base. Constraint (4) restricts the part’s vertical position within its assigned layer. Constraint (5) prevents 2D overlap within a layer. Constraint (6) prevents 3D interpenetration of parts. Constraint (7) limits placement to candidate points, reducing the search space and improving computational efficiency.

5. Heuristic Algorithm Design

Although heuristic algorithms do not guarantee the attainment of a global optimum, they are capable of delivering feasible and near-optimal solutions within a limited computational time for complex or large-scale packing problems, rendering them highly practical for real-world applications. In comparison with exact optimization methods, heuristic approaches offer significant advantages in terms of computational efficiency and scalability, making them particularly well-suited for industrial scenarios that involve irregularly shaped components, intricate geometric constraints, and stringent packing requirements.

5.1. Solution Strategy

Greedy Strategy

Directly pursuing a global optimum for complex irregular packing problems is computationally intensive and often infeasible within practical time constraints. To overcome this challenge, a greedy strategy is employed to decompose the original three-dimensional packing problem into two interconnected stages, allowing for a progressive approximation of an overall optimal solution.

In the first stage, under the assumption of an infinitely tall container, the two-dimensional packing problem for identical components is addressed, generating layer-wise layouts that maximize planar space utilization. Given that individual layer layouts may differ in packing density and spatial efficiency, the second stage focuses on identifying the optimal layer template, selecting a suitable container, and sequentially replicating this template along the vertical axis to achieve the highest possible overall packing efficiency. By integrating these two stages, the proposed approach effectively balances computational tractability with solution quality, ultimately producing a near-optimal three-dimensional packing configuration for irregular parts.

5.2. Model Solution

To optimize the packing arrangement of eccentric shafts, a two-stage heuristic framework is proposed. This model effectively balances computational efficiency, space utilization, and practical feasibility in industrial applications. In the first stage, rapid two-dimensional layer-level optimization is performed to generate compact and feasible layouts. The second stage constructs a three-dimensional stacked configuration by replicating the optimized layer template, thereby achieving a near-optimal overall packing solution.

5.2.1. Stage One: 2D Layer Optimization

The three-dimensional packing problem is initially reduced to a single-layer, two-dimensional placement problem for irregular parts. Considering the intricate boundaries and multiple possible rotational orientations of each component, a Grid-Scan Heuristic is employed to generate the initial layout. In this approach, the container base is discretized into a set of grid nodes, and each node is sequentially tested with all feasible orientations. If a part can be placed at a given node without geometric conflict or collision with previously placed parts, its position is immediately fixed according to a First-Fit Placement strategy.

While this discretization significantly reduces the computational complexity of the placement search, the finite set of candidate points may not capture every possible high-quality placement, particularly for components with intricate or highly irregular geometries. To mitigate this limitation, candidate placement points are generated not only from the initial grid but also from the boundaries of already placed parts. This boundary-informed sampling strategy enables the algorithm to accommodate tight-fitting arrangements and maintain a high planar packing efficiency, while preserving computational tractability.

As illustrated in Figure 3, to further improve packing compactness and enhance boundary conformity, a Gravity-like Drop strategy is incorporated. Once a feasible placement position is identified, the part is gradually shifted along the negative Y-axis until it contacts either the container base or neighboring parts, thereby ensuring both stability and geometric feasibility. The Gravity-like Drop mechanism is implemented strictly in the XY plane along a fixed direction. Each part is placed in one of four discrete orientations (upright, inverted, left-side, right-side), and continuous multi-directional rotation or arbitrary settling is not included in the model. To evaluate the robustness of this approach, post-placement perturbation tests were performed in which parts were subjected to small planar translations (±2 mm) and rotations (±3°). No collisions or displacements were observed, indicating that the layout remains stable and compact even for parts with uneven or curved surfaces.

Following this initial placement, Tabu Search is applied to iteratively optimize the layout. The algorithm explores the continuous neighborhood around each candidate point, generating feasible alternative positions and orientations. A tabu list is employed to prevent cycling and premature convergence to local optima, enabling progressive improvement in planar packing efficiency. The overall workflow of the algorithm is depicted in Figure 4, illustrating the stepwise integration of heuristic placement, micro-adjustment, and metaheuristic optimization for efficient 2D layer arrangement.

5.2.2. Stage Two: 3D Stacking Optimization

In the second stage, the optimal two-dimensional layer template is replicated to construct the three-dimensional packing layout. Given the uniformity of the identical irregular components, this template replication approach not only substantially reduces the computational complexity associated with 3D packing but also ensures a consistent and orderly spatial distribution throughout the container.

To further enhance the structural stability of the stacked layers, a foam buffer layer is introduced between adjacent levels. The thickness of the foam interlayer can be adjusted according to the component height and specific packaging requirements. This buffer layer provides compressibility and friction, effectively dissipating stresses and absorbing shocks during transportation or vibration, while simultaneously increasing interlayer friction to prevent sliding or tipping of the components. Such a design ensures the mechanical stability of the packing configuration and offers a reliable safety margin for the practical deployment of automated packing systems in industrial applications.

5.2.3. Tabu Search Parameter Settings

Tabu Search is employed as a refinement and robustness enhancement mechanism for the initial two-dimensional layout generated by the grid-scan and gravity-like heuristic. Rather than serving as a primary driver for packing density improvement, its role is to locally adjust part positions and orientations, mitigate discretization bias introduced by grid sampling, and prevent unfavorable local configurations caused by greedy placement.

A sensitivity study was conducted by varying key Tabu Search parameters, including the maximum number of iterations (NG), neighborhood sample size (NS), and tabu tenure (TA). The results indicate that, across a wide range of parameter settings, the final planar space utilization converges to the same value, while computational time varies moderately.

This behavior can be attributed to the highly structured nature of the problem: all parts are geometrically identical, and the initial heuristic already produces a near-optimal and tightly packed configuration. In such cases, the solution space exhibits strong symmetry, and multiple parameter configurations converge to the same packing pattern. The observed insensitivity of packing efficiency to Tabu Search parameters therefore demonstrates the robustness and stability of the proposed two-stage heuristic framework, rather than diminishing the role of the metaheuristic.

Based on these observations shown in

Table 1. Tabu Search algorithm parameters.

Parameter	Symbol	Value
Maximum iterations	NG	100
Neighborhood samples	NS	30
Tabu tenure	TA	10

, NG = 100, NS = 30, and TA = 10 were selected as balanced default values to ensure adequate local exploration while maintaining practical computational efficiency.

6. Algorithm Case Study

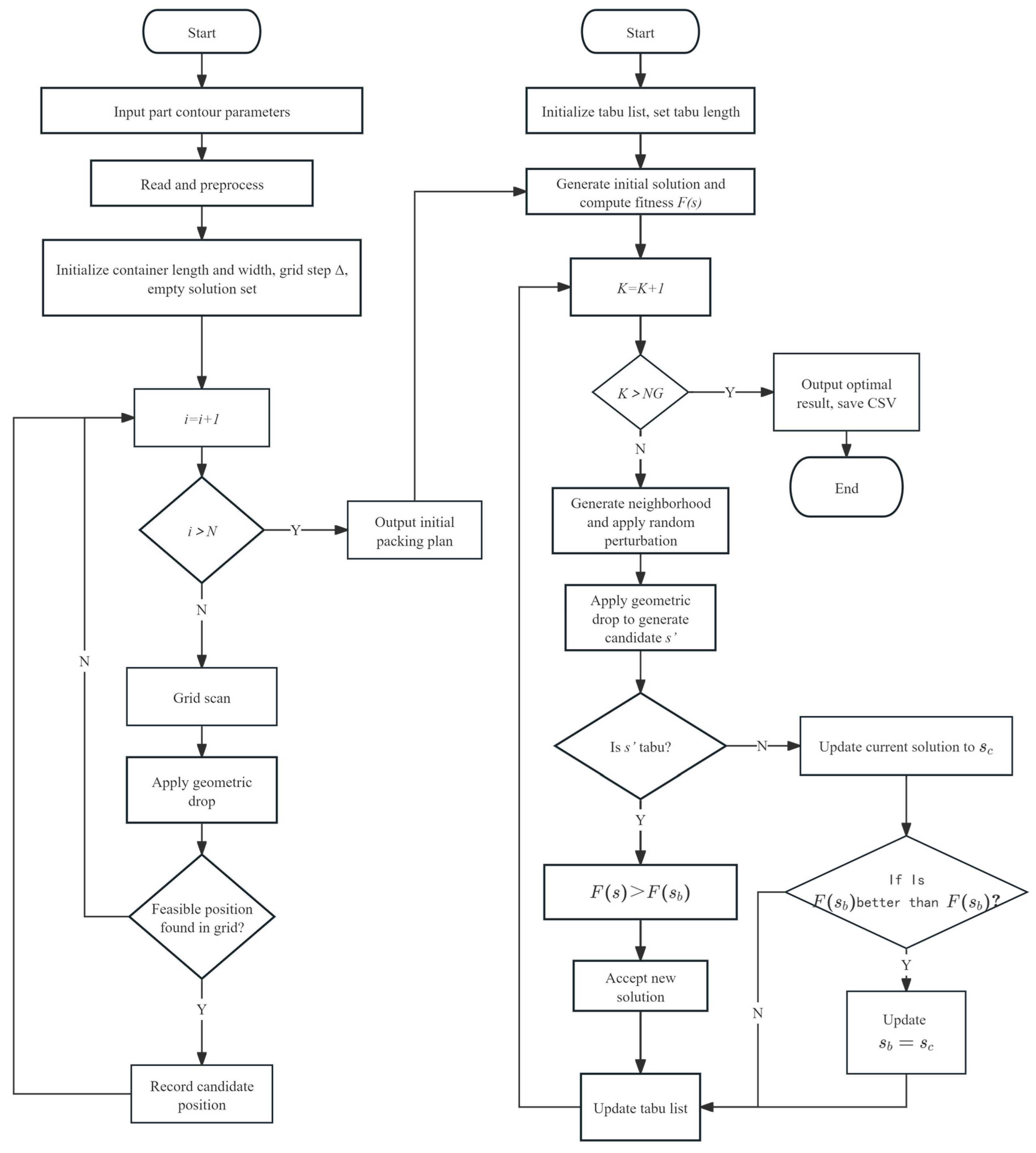
To verify the effectiveness of the proposed two-stage heuristic packing algorithm, this section presents experimental demonstrations and performance evaluations based on a representative case. The experiment first performs 2D layout optimization of irregular parts, then constructs the 3D packing model based on the optimal layer template, and finally compares the results with other algorithms to evaluate the advantages of the proposed method in terms of packing efficiency and computational performance.

6.1. Experimental Environment and Data Settings

The experiments were conducted on a personal computer equipped with an Intel Core i7-9750H processor, 8 GB of RAM, and running the Windows 11 operating system. The computational environment utilized Python 3.10 along with commonly used scientific computing libraries, including NumPy for numerical operations, Trimesh for 3D geometry processing, and Matplotlib 3.10.3 for visualization.

The experimental study focused on eccentric shafts, which exhibit irregular and non-symmetrical geometric features. The dataset comprised a total of 1000 identical components, and the packing container was a rectangular box. As a representative example, Box Type 1 had dimensions of 400 mm × 300 mm × 250 mm. This setup allowed for a comprehensive evaluation of the proposed packing algorithm’s performance under practical conditions involving large quantities of mechanically complex parts.

6.2. Results of the First-Stage 2D Layout

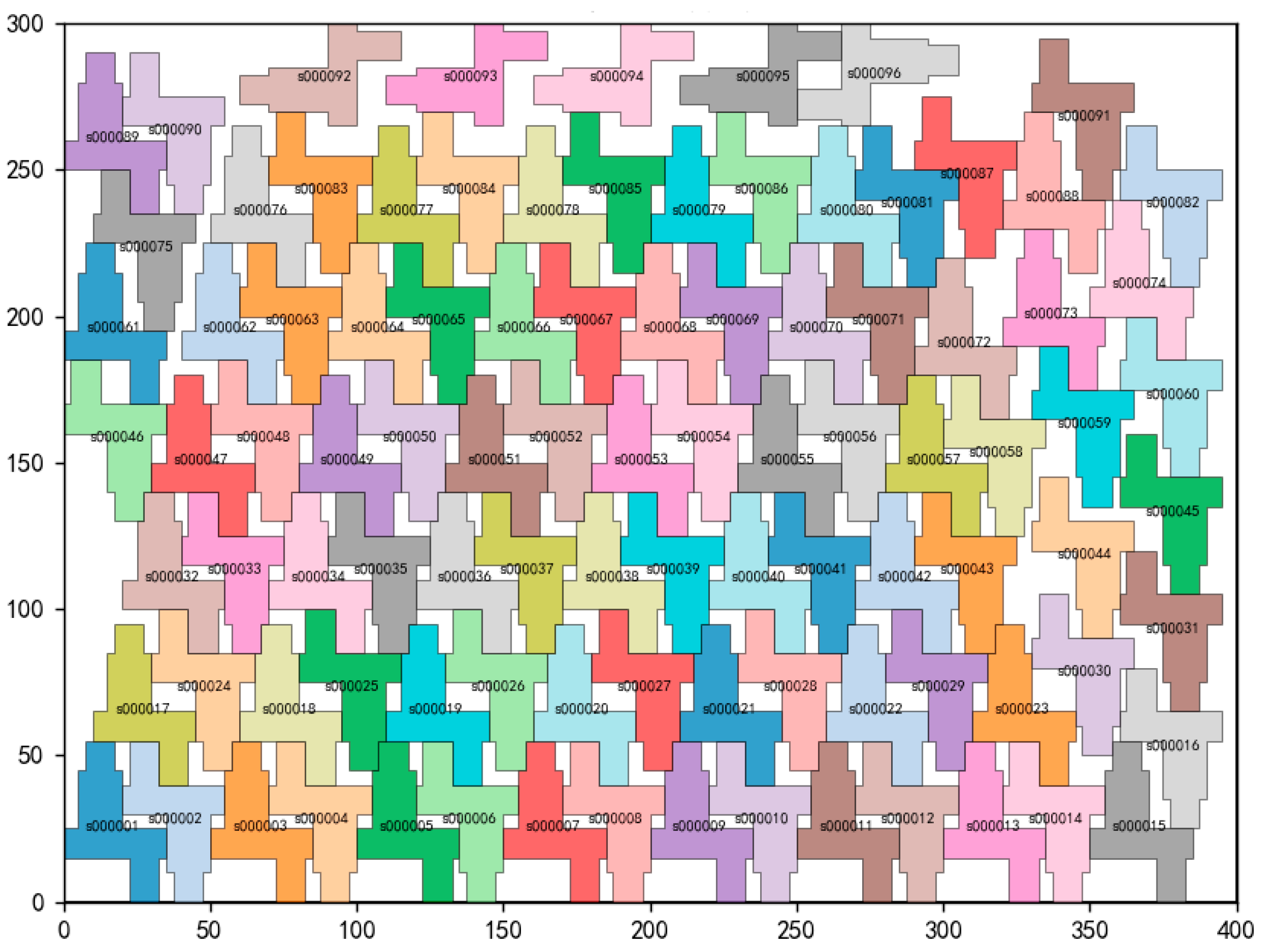
In the first stage of computation, the program generates a color-coded two-dimensional layout for each individual layer, providing a clear and intuitive representation of the initial packing arrangement. As illustrated in Figure 5, each eccentric shaft is represented by a polygon corresponding to its projection onto the plane, with different colors used to distinguish individual parts. To facilitate identification and subsequent post-processing, the index of each part is labeled directly within the corresponding polygon, typically at or near its center. This placement ensures that the part can be easily distinguished without ambiguity, supporting tasks such as data extraction, verification, collision detection, and integration with automated packing systems. The visual representation allows for immediate assessment of layer compactness, orientation distribution, and unused spaces, and provides essential information for guiding the subsequent three-dimensional stacking process, enhancing the overall packing efficiency and reliability.

In addition to the visual layout, the program automatically generates a CSV file that records each part’s ID, placement coordinates, and rotation angle, facilitating automated reading or manual verification in practical applications.

Experimental results indicate that the combination of grid scanning and tabu search heuristic optimization achieves a high space utilization rate within each layer. The eccentric shafts are compactly arranged with minimal gaps, and the orientation distribution is well distinguished, which benefits subsequent packing and manipulation tasks. The overall packing scheme can be generated rapidly with a high degree of standardization.

The exported CSV data and visual layout provide a reliable reference for downstream automated sorting, packing, and verification operations, demonstrating the feasibility and practicality of the proposed heuristic algorithm in eccentric-shaft packing. The 2D area utilization rate of the optimized layer reaches 72%, indicating an efficient use of the available planar space.

To further assess the robustness of the proposed first-stage layout strategy with respect to initialization randomness, a multi-start experiment was conducted. The complete two-dimensional layout generation process, including grid-based initial placement and Tabu Search optimization, was independently executed five times using different randomized initial configurations.

All experimental runs consistently converged to the same final 2D area utilization rate of 72%, yielding a standard deviation of 0 across trials. This result indicates that the proposed neighborhood perturbation and gravity-like projection mechanisms exhibit strong robustness and are not sensitive to the initial placement configuration. The consistent convergence behavior suggests that the search process is not trapped in poor local minima, and that the effective solution space is dominated by a stable high-quality packing structure under the given geometric constraints.

6.3. Template-Layer Replication Results

In the second stage of the proposed method, a three-dimensional packing model is constructed based on the optimal two-dimensional layout obtained during the first stage, employing a template-layer replication strategy. Given that all eccentric shafts are identical in type, their geometric features remain consistent across layers, which allows for a uniform and regular stacking pattern. The algorithm selects the most efficient 2D layer layout from the first stage as the template and replicates it proportionally along the vertical direction, spanning the full height of the container. While true three-dimensional nesting could theoretically enhance inter-layer interlocking for certain irregular objects, the geometric characteristics of the eccentric shafts in this study limit the feasibility of vertical interlocking. Therefore, the template-layer replication strategy is expected to provide a near-optimal 3D packing solution for these components, and additional three-dimensional nesting does not offer significant improvement.

To further enhance the mechanical stability of the stacked components, a thin foam interlayer may be optionally introduced between adjacent layers, which serves to increase friction, absorb shocks, and prevent relative displacement during handling or transportation. Although the introduction of buffer layers slightly increases the overall height and reduces the volume available for packing, the effect on the total packing-utilization rate is minor, and the trade-off favors improved stability without significantly compromising efficiency.

During the replication process, the algorithm performs automatic verification for boundary violations and inter-component collisions in each layer, ensuring that the three-dimensional arrangement is both geometrically feasible and mechanically stable. This approach guarantees that each layer aligns precisely with the template, maintaining consistent positioning and orientation of the components throughout the box.

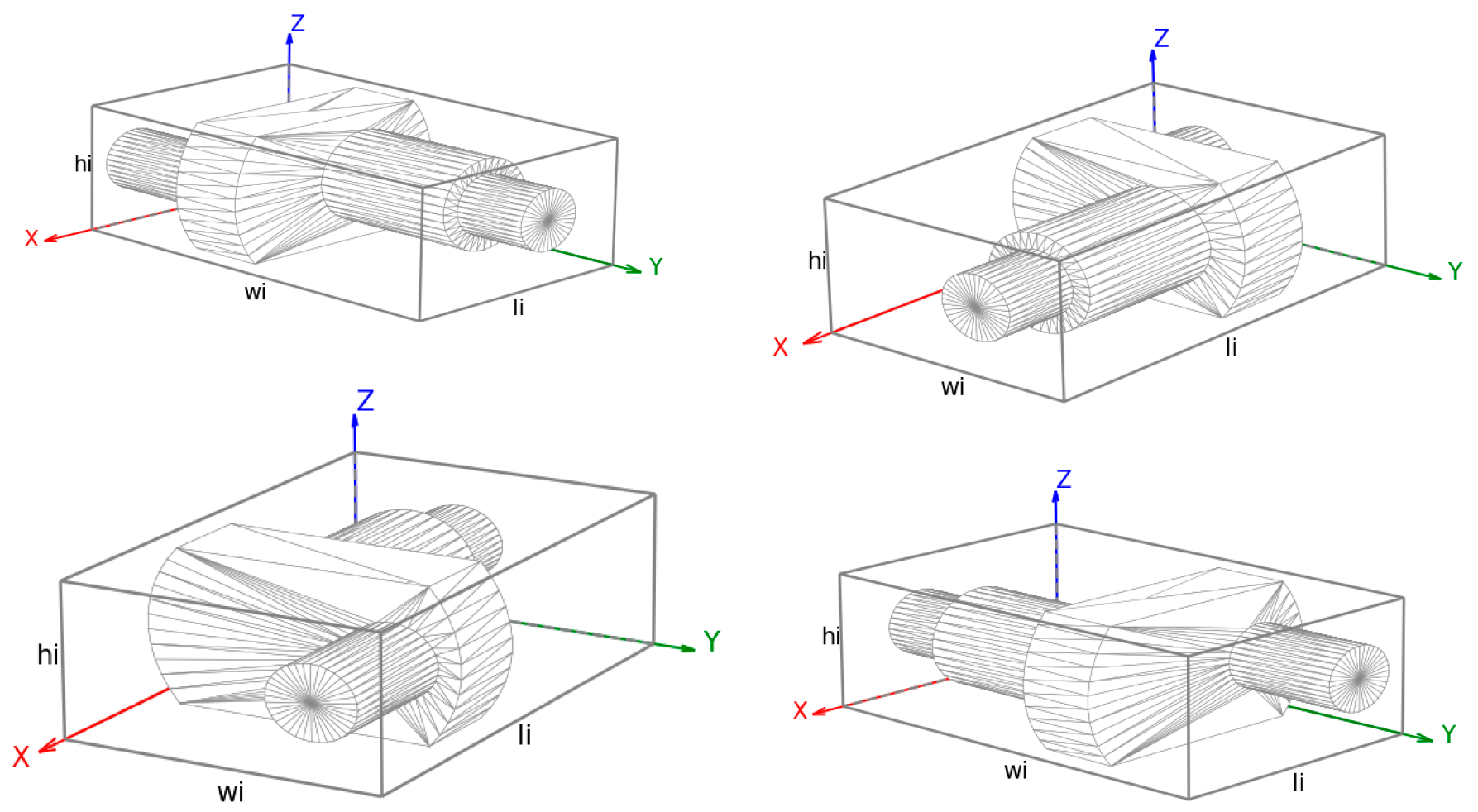
Figure 6 presents the final 3D packing configuration generated by the proposed algorithm. The experimental evaluation shows that, within a container measuring 400 mm × 300 mm × 250 mm, the algorithm successfully packs 920 individual eccentric shafts, achieving a total space utilization rate of 45.82%. These results underscore the algorithm’s capability to densely and efficiently arrange irregular, asymmetrical components while maintaining uniformity and stability across the stacked layers. The high packing density demonstrates the practical effectiveness of the template-layer replication approach, providing a robust and reliable solution for automated packing systems, particularly in industrial applications involving large quantities of mechanically complex parts. Moreover, the method’s systematic verification and stability measures ensure that the packed structure can withstand handling and transportation stresses without compromising the integrity of the components.

6.4. Dynamic Simulation Experiment

To further verify the stability of the three-dimensional packing structure under actual transportation and handling conditions, a three-dimensional dynamic simulation system was constructed based on PyBullet, using the previously generated 3D stacking structure from the 2D template replication. The dynamic stability of the eccentric shaft packing structure was analyzed under slight vibrations. Previous studies have demonstrated that physics-engine-based multi-body dynamic simulations can effectively evaluate the relative displacement of irregular parts under gravity and external disturbances [21], and that frequency-domain collision optimization methods can significantly improve collision detection efficiency in large-scale packing scenarios [22].

Following these methodological foundations, the present study adopts physics-based modeling for contact, collision, friction, and gravity response. Unlike approaches primarily focused on dynamic behavior analysis or collision-handling efficiency, the physics engine here is employed as a post-packing verification tool to assess the mechanical stability of the packing structure generated by the proposed algorithm. The PyBullet engine operates on principles similar to Box2D [23] and NVIDIA PhysX SDK [24] in collision detection, contact solving, and gravity response, enabling realistic simulation of collisions, friction, and stacking stability among multiple objects. This makes it particularly suitable for virtual verification of packing structure stability.

6.4.1. Initial Packing Verification and Simulation Setup

The experimental objects consisted of the three-dimensional packing solutions generated by the proposed packing algorithm, comprising a total of 920 eccentric shafts. The simulation container dimensions were set to 400 mm × 300 mm × 250 mm. Each part was assigned a mass of 1 kg, and the gravitational acceleration was set to 9.8 m/s².

To simulate slight vibrations during logistics transport or handling, a periodic disturbance with an amplitude of 0.05 rad and a frequency of 1 Hz was applied to the container for a total simulation duration of 5 s. These vibration parameters represent mild and repetitive disturbances, such as vehicle body swaying or slight tilting of a heavy truck during steady driving, gentle turns, or lane changes.

The initial positions and orientations of all parts were imported from the CSV file generated by the packing algorithm. Due to the highly irregular and sharp geometry of the eccentric shafts, direct mesh-based collision detection may introduce numerical instability or excessive computational cost. Therefore, convex hull approximations of the parts were adopted for collision detection, while the original STL meshes were retained for visualization. To improve contact resolution and reduce numerical penetration, the number of solver iterations was set to 1500, and the simulation time step was set to 1/480 s.

It should be noted that the primary objective of the dynamic simulation is post-packing stability verification, rather than high-precision contact mechanics validation. Although small numerical penetrations may occur when using convex hull–based collision models, the simulation parameters were selected to ensure stable and conservative evaluation of relative displacements under external disturbances. Detailed validation of solver convergence and mesh-level collision accuracy is beyond the scope of the present study and will be addressed in future work.

The vibration model employed in this study is intentionally simplified. A single-frequency harmonic excitation was applied as a baseline disturbance model, which has been widely adopted in packing and stacking stability studies due to its controllability and repeatability. While real transportation environments may involve broadband vibrations, stochastic disturbances, and occasional impacts, such complex excitations are expected to amplify displacement responses rather than fundamentally alter the observed stability trends. Accordingly, the current model provides a conservative and interpretable assessment of structural stability. Extension to multi-frequency and stochastic disturbance models is considered an important direction for future research.

6.4.2. Simulation Results and Stability Analysis

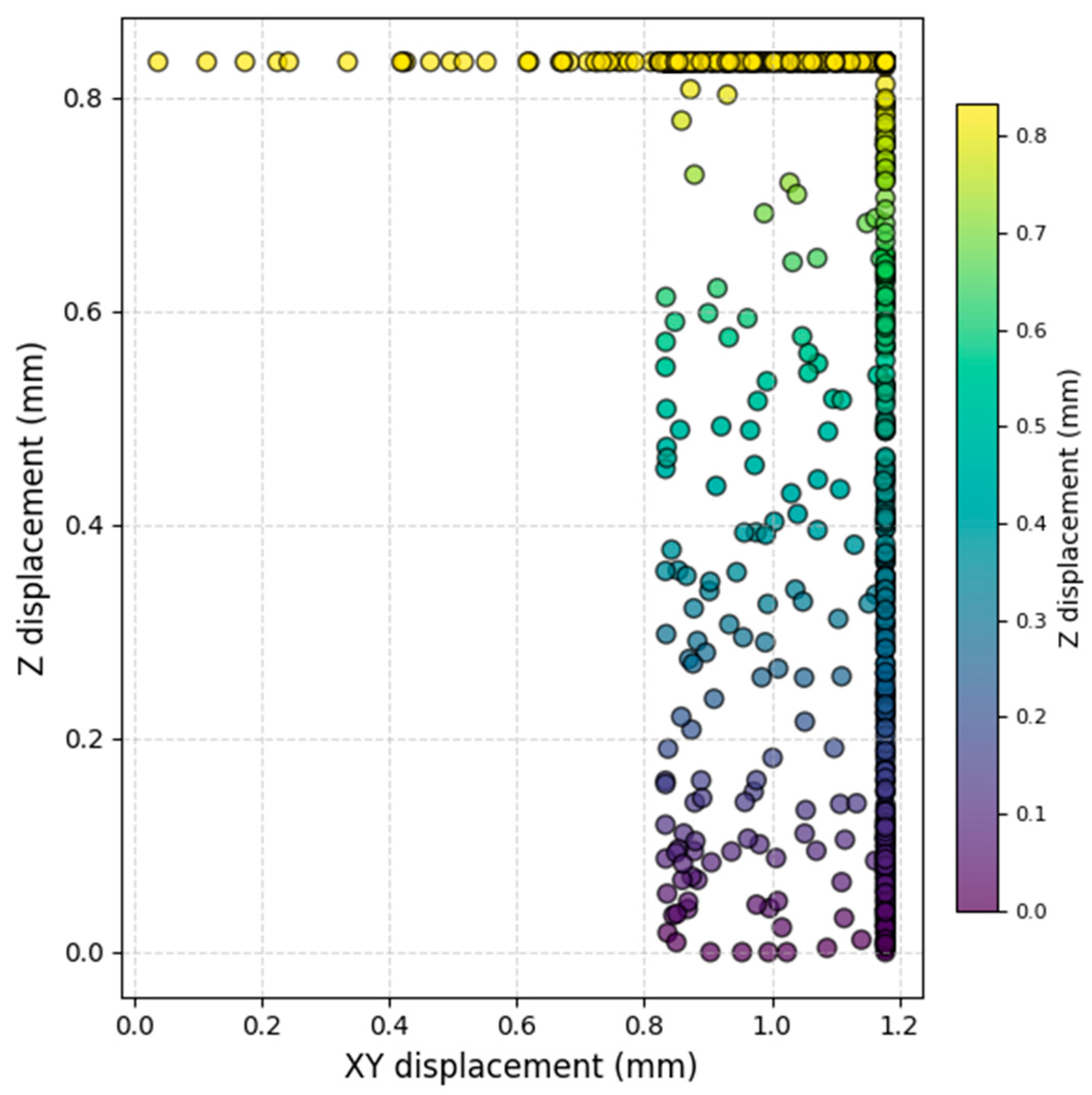
To quantify the stability of the packing structure, the spatial displacement of each part before and after the simulation was recorded, as shown in Figure 7. The XY-plane displacement was used as an indicator of horizontal stability, while the Z-axis displacement was used to assess inter-layer risk. Specifically, a part was considered “loose” if its XY displacement exceeded 2.0 mm, and “cross-layer” if its Z displacement exceeded 50% of a single layer height. These metrics allow direct quantification of structural stability and effectively reflect potential risks such as micro-movements, sliding, tipping, or collapse.

The results show that 920 eccentric shafts were successfully packed into the 400 mm × 300 mm × 250 mm container, achieving an overall packing efficiency of 45.82%. During the simulation, most parts exhibited only minor displacements, with a maximum XY displacement not exceeding 2.0 mm. Only a few parts were classified as loose, and no cross-layer movements were observed. The entire packing structure remained stable under slight vibrations, without local collapse or significant sliding, demonstrating that the proposed packing algorithm produces 3D structures with good spatial nesting and mechanical stability, suitable for practical engineering applications in transport and handling scenarios.

For more intuitive visualization of the simulation scene and stability performance, Figure 8 shows snapshots of the simulated model from different viewpoints. The figures clearly demonstrate that the parts remain tightly nested under disturbance, with only minor displacements.

Importantly, these dynamic simulation results also address potential concerns regarding the use of a 2D layer template for constructing the 3D packing configuration. Although the 3D arrangement is generated from a planar 2D layout, the template-layer replication strategy ensures consistent alignment across all layers. Automatic checks for boundary violations and inter-component collisions are performed during replication, preventing vertical misalignment, unsupported placements, or inter-layer instability.

The PyBullet-based simulation confirms that, under gravitational and vibration disturbances, the packed components maintain their relative positions with minimal horizontal displacement (≤2 mm) and no cross-layer movement. These observations indicate that any cumulative projection modifications from the 2D-to-3D conversion do not compromise geometric feasibility or mechanical stability. Consequently, the results validate the robustness of the proposed packing method and its suitability for practical industrial application

6.4.3. Robustness to Manufacturing-Induced Geometric Variations

In practical manufacturing scenarios, small geometric deviations inevitably arise due to machining tolerances, surface roughness, and material deformation. Unlike exact geometric nesting methods that rely on tight boundary fitting, the proposed packing strategy is driven by feasibility-based placement rather than exact contour matching. The grid-scan heuristic, discrete orientation set, and first-fit placement mechanism inherently introduce geometric clearance, which reduces sensitivity to small local shape perturbations.

Moreover, the gravity-like drop strategy further enhances robustness by allowing components to settle into mechanically supported positions based on contact interactions, rather than relying on predefined geometric constraints. As a result, minor deviations in local geometry are compensated through contact redistribution during placement.

The dynamic simulation experiments conducted using PyBullet provide indirect yet effective validation of this robustness. In these simulations, collision detection is performed using convex hull approximations instead of exact mesh geometries, which introduces additional geometric abstraction comparable to manufacturing-induced uncertainties. Despite these approximations and the application of external vibrational disturbances, the packing structure exhibited minimal displacement and no cross-layer instability. This observation indicates that the proposed method is not highly sensitive to small geometric perturbations and can maintain stable packing configurations under realistic non-ideal conditions.

Although explicit geometric noise injection experiments are not included in the present study, the combined effects of feasibility-based placement, gravity-driven stabilization, and physics-based post-verification collectively demonstrate the algorithm’s resilience to moderate manufacturing-induced geometric variations. A more detailed stochastic geometry perturbation analysis is identified as an important direction for future work.

6.5. Comparative Experiments

To comprehensively evaluate the performance of the proposed method under different box conditions, four representative packing algorithms were selected as benchmark methods for comparison:

–

BLF (Bottom-Left Fill): sequentially places parts in feasible gaps following the bottom-left priority rule, a widely used constructive heuristic in packing studies.

–

LHL (Lowest Horizontal Line): places parts along the lowest horizontal line to minimize voids, commonly applied in layer-based packing.

–

Best Fit: sorts and places parts according to the minimum residual space after placement, representing a residual-space optimization approach.

–

Random: randomly selects feasible positions and orientations, serving as a baseline reference to highlight the advantages of structured heuristics.

The proposed algorithm is compared with these benchmark methods from three perspectives: space utilization rate, computation time, and number of packed parts. This selection ensures a well-rounded comparison across different packing strategies and provides a substantiated basis to assess the effectiveness of the newly developed method.

6.5.1. Experimental Design and Box Configurations

To verify the adaptability of the proposed algorithm to different box types, eccentric shafts were used as test objects in multiple simulated packing experiments based on actual industrial packaging scenarios. The box configurations are listed in

Table 2. Dimensions of the available packing boxes.

Box No.	Dimensions (mm)
Box 1	400 × 300 × 250
Box 2	530 × 290 × 290
Box 3	430 × 210 × 270
Box 4	350 × 190 × 230

.

In the experiments, all boxes were loaded with the same type of irregular eccentric shafts to ensure consistency and comparability. The proposed heuristic packing algorithm was applied alongside four benchmark algorithms to systematically evaluate its performance. This comparative study aimed to assess the adaptability and effectiveness of the proposed method across various box dimensions and configurations. By analyzing the resulting packing layouts, space utilization, and placement efficiency, the experiments provide comprehensive insights into how the algorithm performs under different container conditions, thereby demonstrating its robustness, general applicability, and potential advantages over traditional packing strategies in practical industrial scenarios.

6.5.2. Results and Discussion

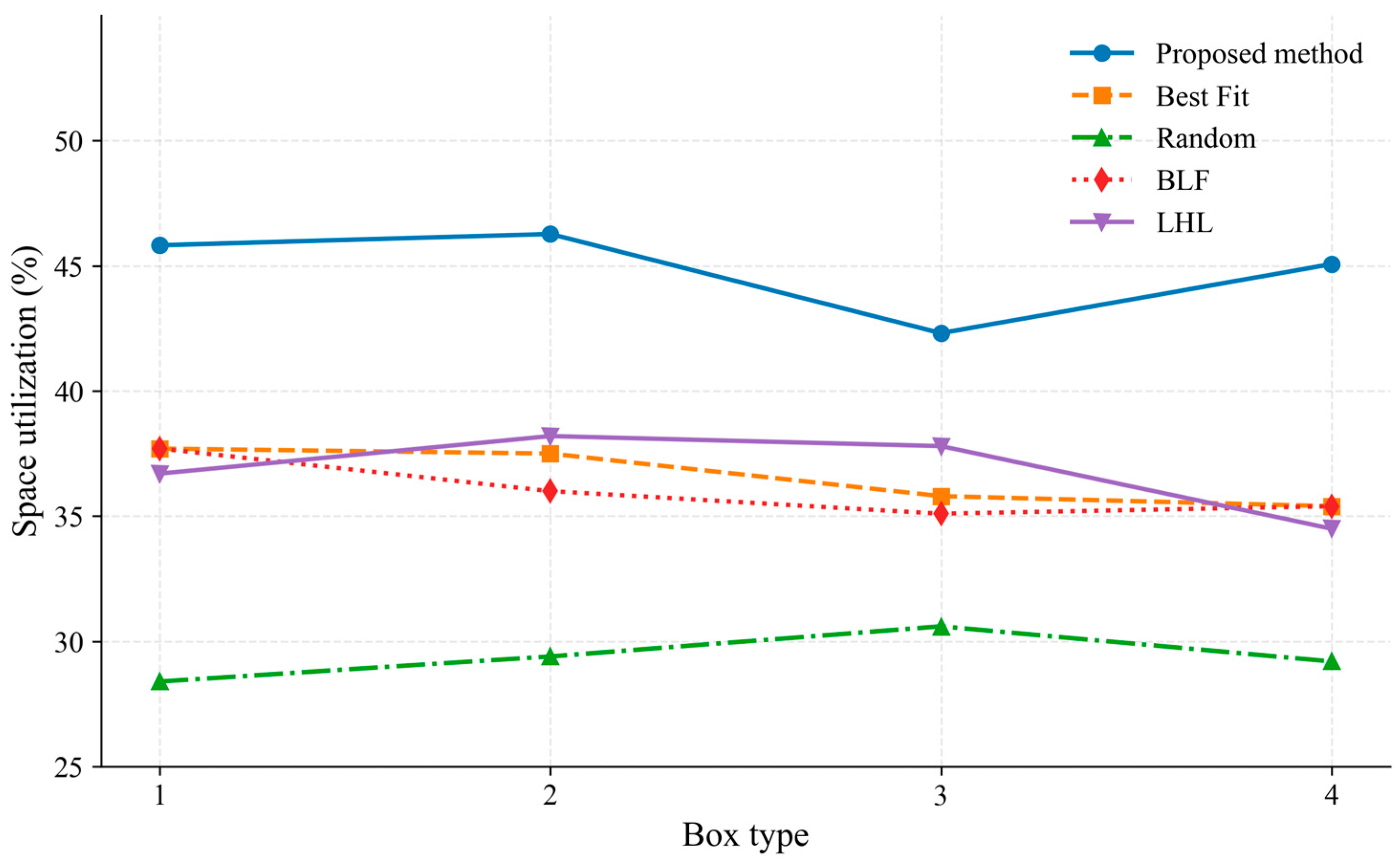
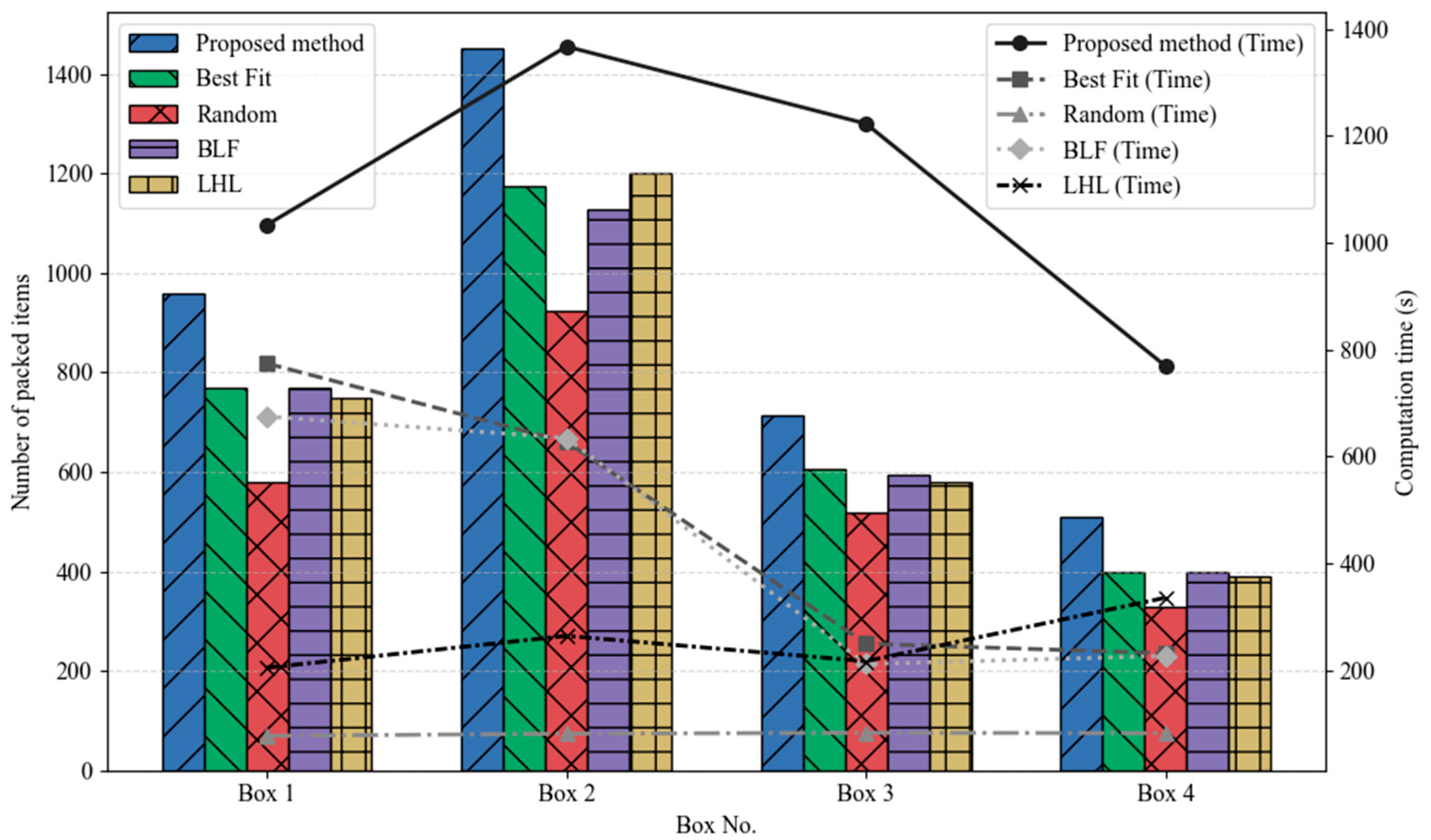
Figure 9 and Figure 10 present the comparative results in terms of space utilization and computation time across different box types.

As shown in the figures, the experimental results indicate that the proposed two-stage heuristic packing algorithm achieves higher space utilization and more compact layouts across all tested box types compared with conventional methods, including Bottom-Left Fill (BLF), Lowest Horizontal Line (LHL), Best Fit, and Random placement. Quantitative analysis shows that the average space utilization across the four box types reaches 44.9%, corresponding to improvements of approximately 8.8%, 8.3%, 8.1%, and 15.5% over the BLF, Best Fit, LHL, and Random algorithms, respectively. These results demonstrate the method’s capability to enhance packing efficiency, particularly for irregular eccentric parts, where even moderate improvements can lead to substantial volume savings in industrial scenarios.

Although the computational complexity of the proposed algorithm is higher and the runtime slightly exceeds that of traditional methods, the two-stage optimization process—incorporating gravity-like descent and tabu search—enables exploration of a larger solution space and the attainment of near-optimal packing configurations. The maximum observed runtime in the experiments was approximately 1366.8 s, which remains acceptable for practical industrial applications.

The algorithm ensures consistent layer geometry during three-dimensional stacking, resulting in more compact and orderly arrangements with reduced inter-layer gaps. Such structural consistency enhances the mechanical stability of packed items and provides clear geometric references for automated packing equipment, facilitating path planning and picking operations in automated feeding systems. Overall, the proposed algorithm demonstrates strong potential for deployment in real-world industrial packaging, offering both efficiency and reliability in handling irregular eccentric shafts or similar mechanical components.

6.5.3. Discussion on Benchmark Selection and Advanced Packing Methods

The comparative evaluation in this study focuses on representative constructive heuristic packing methods, including BLF, LHL, Best Fit, and Random placement. These algorithms are widely adopted in industrial packing systems due to their simplicity, determinism, and low computational overhead, making them practical baselines for large-scale automated packaging applications.

More advanced packing techniques, such as no-fit polygon (NFP)-based shape packing, continuous optimization methods, and hybrid metaheuristic frameworks, have been reported to achieve high packing densities for certain classes of irregular objects. However, these methods typically require complex geometric preprocessing, exact polygon decomposition, or intensive collision computations, which substantially increase implementation complexity and computational cost, especially for three-dimensional industrial-scale problems involving hundreds or thousands of parts.

In contrast, the proposed method is designed to balance packing quality, computational efficiency, and robustness under industrial constraints. By integrating grid-based candidate generation, gravity-like descent, and tabu search refinement, the algorithm achieves near-optimal packing performance while maintaining a predictable runtime and straightforward geometric handling. This design choice aligns with the practical requirements of automated packing systems, where robustness and scalability are often prioritized over marginal improvements in theoretical packing density.

Nevertheless, incorporating advanced shape-based or continuous optimization methods as additional benchmarks represents an important direction for future work. Such comparisons would provide deeper insights into the trade-offs between packing optimality, computational expense, and engineering feasibility for irregular mechanical components.

7. Conclusions

This study addresses the bin-packing problem of irregular eccentric shafts by proposing a two-stage heuristic packing algorithm that integrates grid-scanning and gravity-like descent for initial placement, followed by a tabu search refinement to iteratively optimize the layout. The proposed approach effectively generates compact and stable packing arrangements, maximizing space utilization while ensuring geometric feasibility and physical plausibility of the final configuration.

To evaluate the robustness and real-world stability of the packing structures, a PyBullet-based dynamic simulation framework was employed, incorporating gravity, vibration disturbances, and multi-body interactions with real STL collision geometries. The simulation results demonstrated minimal horizontal and vertical displacements of the packed eccentric shafts, with no cross-layer movement or structural collapse, confirming the strong mechanical stability of the algorithm′s output.

The proposed method shows significant potential for industrial applications, offering an efficient and practical solution for automated packing of irregular mechanical components. The use of repeated-layer templates for layers composed of identical parts simplifies three-dimensional stacking, enhances packing consistency, and improves mechanical stability in batch packaging scenarios. Extending the method to heterogeneous or mixed-part packing introduces additional geometric challenges and would require adaptive layer construction strategies, which will be investigated in future work.

Future research will also focus on improving computational efficiency and scalability for large-scale packing scenarios, including parallel computation, adaptive grid resolution, and the integration of more advanced metaheuristic strategies, to enable the application of the proposed algorithm to industrial-grade datasets containing tens of thousands of components.