LoRA-Fine-Tuned Latent Diffusion for High-Fidelity Digitization of Classic Mongolian Patterns

Abstract

Mongolian patterns represent an important component of Mongolian cultural heritage, characterized by their dual structure of geometric symmetry and dynamic ornamental motifs. However, existing artificial intelligence-based generative methods struggle to preserve both low-frequency structural regularity and high-frequency decorative detail under limited data conditions. This study proposes a parameter-efficient digitization framework based on latent diffusion models (LDMs) fine-tuned with low-rank adaptation (LoRA) to achieve high-fidelity reconstruction of classic Mongolian patterns. A curated few-shot dataset and a low-rank constraint enable effective learning from only eight representative samples, while a dual-prompt mechanism and MSE-driven optimization improve geometric stability and semantic consistency. Integrated within a transparent ComfyUI workflow, the method supports controllable generation and reproducible experimentation. Experimental evaluations demonstrate that the proposed LoRA-LDM model achieves superior structural accuracy, reduced visual distortion, and enhanced motif preservation compared with baseline models. The results confirm the method’s applicability for digital preservation, reconstruction, and derivative design of structured cultural heritage motifs.

1. Introduction

Artificial intelligence-generated content (AIGC) has become increasingly central to the digital preservation of intangible cultural heritage, offering new possibilities for reconstructing damaged artifacts and generating culturally grounded design assets [1]. Diffusion models, in particular, provide strong generative capacity and controllability, yet their application to highly structured ethnic motifs remains challenging. Recent studies have emphasized that latent diffusion models exhibit stronger generative robustness and higher controllability compared to GAN-based frameworks [2]. Classic Mongolian patterns exhibit a distinctive dual structure: rigid translational or lattice symmetries coexist with highly dynamic curved motifs [3]. This combination complicates digital extraction, as high-frequency ornamental details can be misinterpreted as noise, while low-frequency grids are prone to distortion during stochastic denoising.

To address these limitations, this study introduces a LoRA-adapted latent diffusion model tailored to the semantic and structural properties of Mongolian patterns. Low-rank adaptation reduces the number of trainable parameters to approximately 3%, enabling efficient few-shot fine-tuning while preserving the representational strength of the base model [4]. A dual-prompt strategy enhances semantic alignment, and an MSE-centered optimization objective improves geometric fidelity. Prior studies have demonstrated that pixel-level reconstruction losses such as MSE can effectively stabilize geometric structures during diffusion model fine-tuning [5]. Combined with a transparent ComfyUI workflow, the proposed framework supports controllable, reproducible, and high-fidelity digitization of classic Mongolian patterns.

2. A Study of the Characteristics and Extraction of Classic Mongolian Patterns

2.1. The Computational Esthetics and Semantic Logic of Mongolian Patterns

Classic Mongolian patterns are defined by a unique visual grammar that we characterize as “Tamed Dynamism”—a dialectical unity where fluid, asymmetrical motifs (such as cloud or ram’s horn scrolls) are rigorously constrained within precise geometric grids [6]. This specific structural duality presents a distinct challenge for digital extraction compared to other cultural systems.

2.1.1. Structural Uniqueness

As analyzed in

Table 1. Analysis of the unique characteristics of the Mongolian ethnic group.

Cultural System	Mongolian	Tibetan Buddhist	Scythian	Yuan Chinese	Ilkhanid Persian
Compositional Logic	Structural Repetition	Narrative Hierarchy	Dynamic Action	Atmospheric/Negative Space	Geometric Interlocking/Narrative
Symmetry Type	Translational/Lattice	Hierarchical/Bilateral	Dynamic/Asymmetrical	Asymmetrical Balance	Tessellation/Radial
Motif Unit	Repeating Text	Central Subject	Active Protagonist	Scene Element	Tessellation Unit/Scene Protagonist
Core Aesthetics	Tamed Dynamism	Sacred Stillness	Raw Power	Atmosphere & Harmony	Mathematical Complexity

, unlike the narrative hierarchy found in Tibetan Buddhist art or the purely geometric tessellations of Persian architecture, Mongolian patterns require the simultaneous preservation of “Internal Dynamics” (high-frequency ornamental details) and “External Order” (low-frequency symmetrical lattices) [7]. This comparison highlights why general-purpose generative models often fail: they struggle to reconcile the conflicting demands of organic fluidity and rigid symmetry inherent to this specific tradition.

2.1.2. Semantic Complexity

Beyond geometric structure, the accurate reconstruction of these patterns requires precise semantic alignment [8]. The motifs are not merely decorative but serve as a visual codification of nomadic identity and ecological values.

Table 2. Core Symbols of classic Mongolian patterns and their cultural symbolic meanings.

Pattern Classification/Theme	Typical Pattern Examples	Cultural Origin/Meaning	Symbolic Significance (Ethnographic Connotation)
Animals and Natural Patterns	Skin patterns, Horse patterns, Eagle patterns, Sheep horn patterns, Wolf patterns	Nomadic life, Image worship, Environmental protection	Strength, Speed, Auspiciousness, Reverence for nature, Survival wisdom, Free and agile
Religious and Auspicious Patterns	Fish intestine pattern, Treasure phase flower, Eight treasures pattern	Buddhism, Shamanism, Traditional cultural beliefs	Eternity, Pure and endless, Continuation of productivity, Good luck and blessings, Fullness and liberation
Geometric and Continuous Patterns	Hui pattern, Continuous patterns (Swastika/Four directions)	Abstract simplification, Geometric foundation, Practical function	Order, Regularity, Structural stability, Enhancement of beauty, Identity recognition between tribes

categorizes the core “visual vocabulary”—ranging from zoomorphic forms to geometric symbols—that our model must learn to recognize and reproduce. This semantic taxonomy directly informs the “dual-prompt” strategy (Section 3.2) employed in our workflow to ensure cultural fidelity [9].

2.2. A Study on the Extraction of Classic Mongolian Patterns

When digitizing classic Mongolian patterns, it is crucial to simultaneously capture both their macroscopic shape contours and their fine-grained internal textures. The high degree of diversity and uniqueness in these patterns is rooted in an artistic approach of abstracting and simplifying real-world elements, encompassing daily life, the natural environment, religious symbols, and zoomorphic and phytomorphic forms. For instance, meander patterns (回纹), floral motifs (花草纹), endless-knot patterns (盘肠纹), and ram’s horn motifs (羊角纹) are all manifestations of this creative principle [10].

Research indicates that even traditional computer vision models (such as the CNN-based model mentioned in the text) can successfully extract key features like “Abruptness” by analyzing the pattern styles and the recurrence of noise within the image, as shown in Figure 1 [11].

Classic Mongolian patterns depict non-representational symbols and principles. They are constructed from simple geometric shapes arranged symmetrically or repetitively into frieze or all-over configurations. By leveraging diverse arrangements and repetitive combinations of these foundational elements, an infinite variety of patterns is created [12]. The digital extraction of these patterns is a process wherein the classic motifs and ethnocultural symbols are transformed into data. This allows them to be preserved, used to build specialized models that showcase their unique cultural style and function, and provides a rich repository of resources for derivative works.

This unique structure, characterized by a dialectical unity of opposites, explains why A-IGC models produce “unnecessary interferences” during processing [13]. The model struggles to simultaneously learn two contradictory directives: (1) the high-frequency, asymmetrical details that constitute the motifs, and (2) the low-frequency, regular grid that forms the overall layout. It tends to perceive the former as “noise” relative to the latter, resulting in a loss of detail or structural collapse, as shown in

Table 3. Validation framework.

Step	Task	Computational Method/Tool	Purpose
1. Quantification	Detect and classify global geometric order	Lattice Detection model; Wallpaper Groups classification	To identify whether the pattern has a rigid, repeatable geometric framework and to mathematically classify its symmetry type.
2. Dynamic Quantification	Segment and analyze the form of the core motif	Extract basic repeating units (Texel) from the lattice; use shape descriptors (Shape Descriptors), such as curvature analysis, Fourier descriptors, asymmetry measures	To quantify the fluidity, complexity of curves, and inherent asymmetry of the motif itself after excluding global symmetry.
3. Classification Decision	Verify the existence of the “fingerprint”	Input the results from Step 1 (Order Classification) and Step 2 (Dynamic Scoring) into a pre-trained classifier (such as SVM or neural network)	Finally, determine whether the pattern meets both the conditions of “high external order” and “high internal dynamics” to confirm whether it is a classic Mongolian pattern.

and Figure 2.

3. A Model Architecture for the Digital Extraction of Classic Mongolian Patterns

The inherent stochasticity of diffusion models is the core of their creative power, enabling the generation of diverse and novel design content. In the auxiliary system designed for classic pattern extraction using latent diffusion models, this uncertainty is skillfully transformed into design richness and innovation [14]. The entire process is meticulously designed as a series of key modules that work in synergy, ensuring a seamless transition through every step from initial concept to final implementation, as detailed in

Table 4. Architecture flow description.

Module	Architecture Specification
Keyword extraction and model training	Keyword extraction was performed on collected classical Mongolian ornamental patterns, which were then integrated with corresponding images for training a large-scale model. The model was established and fine-tuned via a safetensors file to ensure it could generate high-quality extractions of classical Mongolian ornamental motifs.
Data Collection and Processing	A substantial volume of data concerning traditional Mongolian patterns was collected via high-definition camera equipment. Image processing software was employed to refine the data through optimisation procedures, including noise reduction, colour balance adjustment, and image distortion correction, thereby ensuring the clarity and accuracy of the data.
Fine-tuning of diffusion models	Employing Stable Diffusion Comfy UI as the tool, and utilising the LoRA fine-tuning strategy for fine-tuning. The model is trained through a forward process (converting images into noise) and a backward process (reconstructing noise into images) to master the capability of image generation.
CNN model preprocessing	Employing convolutional neural networks for data adjustment enables precise control over sketches, facilitating reuse and modification throughout the design process to ensure the accuracy of design details.

. Ultimately, this auxiliary system provides designers with a powerful toolset, helping them to rapidly realize their design concepts [15].

3.1. Base Model Construction

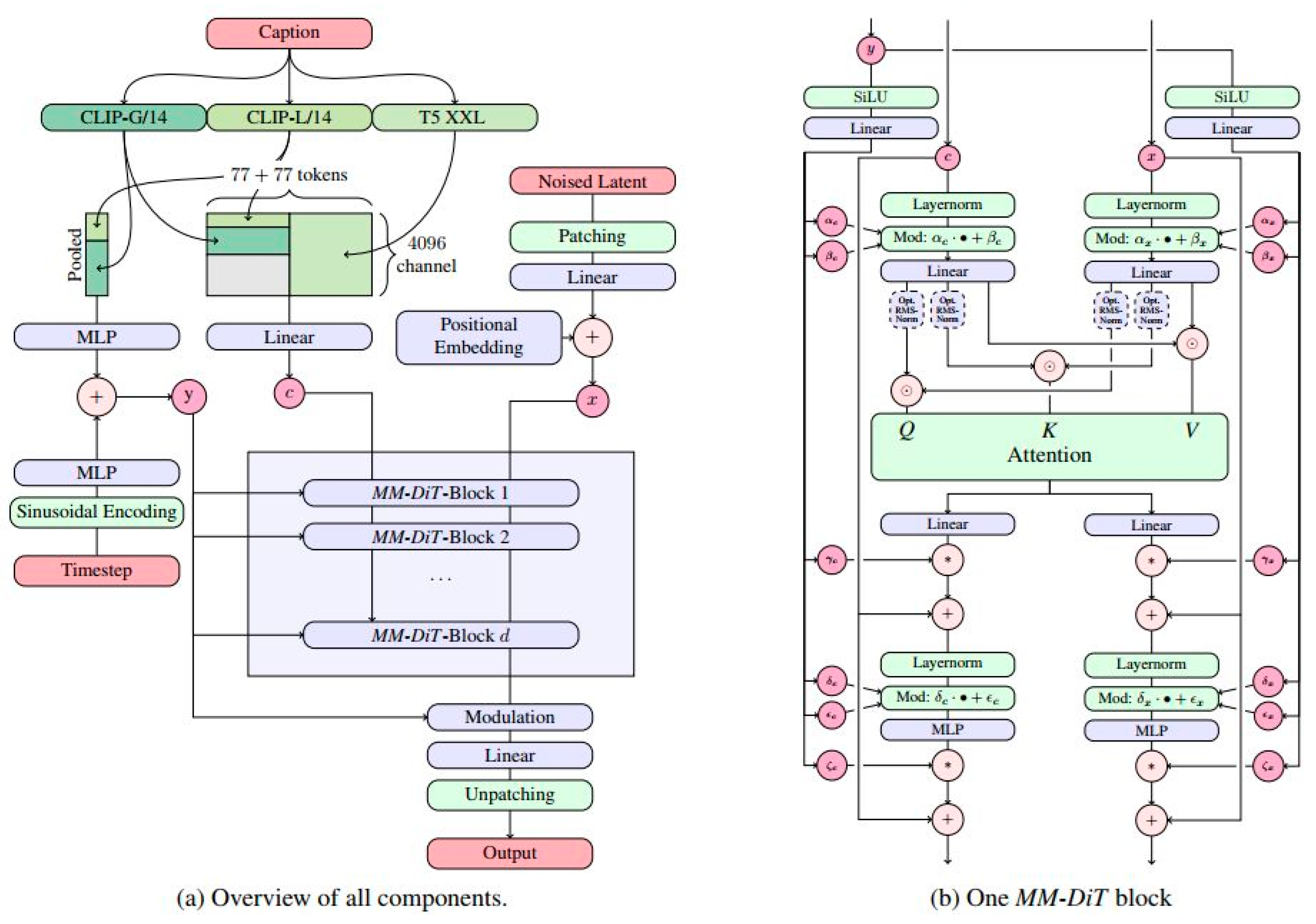
Latent diffusion models are renowned for their strength in generating diverse outputs. Stable Diffusion ComfyUI, created in January 2023 by its lead developer, who goes by the pseudonym “Comfy Anonymous,” was designed to provide a highly customizable and flexible user interface [16]. Its purpose is to enable users to fully harness the potential of stable diffusion models, the model for which is illustrated in Figure 3. This workflow not only enhances operational flexibility but also allows users to easily reproduce and share their creative processes.

This exploration has resulted in the development of a LoRA model specifically for the digital extraction of classic Mongolian patterns, along with a variety of effective prompts, which are expected to aid future related research. As shown in Figure 4.

3.2. Constructing the LoRA Model

3.2.1. Data Curation and Few-Shot Sampling Strategy

Data Curation: We employed a strategic few-shot sampling approach. From our corpus of 600+ field-collected images, we selected 8 canonical samples representing orthogonal visual clusters (geometric, naturalistic, and religious) [17]. This minimalist strategy leverages FLUX.1’s semantic priors while the low-rank constraint (r = 128, ~3% trainable weights) mathematically prevents overfitting, as validated by convergence of validation MSE on 100 test images.

3.2.2. The LoRA (Low-Rank Adaptation) Strategy

The integration of LoRA models into Stable Diffusion ComfyUI offers an efficient digital extraction framework. This technique leverages the low-rank properties of pre-trained weight matrices, enabling effective adaptation through decomposition into smaller subspaces [18]. During fine-tuning, model updates are constrained via a low-rank approach, significantly reducing the number of parameters requiring updates. Specifically, instead of updating the full pre-trained weight matrix ${\mathrm{W}}_0\in {\mathrm{R}}^{\left(\mathrm{d}\times \mathrm{k}\right)}$, LoRA injects trainable low-rank matrices $\mathrm{B}\in {\mathrm{R}}^{\left(\mathrm{d}\times \mathrm{r}\right)}$ and $\mathrm{A}\in {\mathrm{R}}^{\left(\mathrm{r}\times \mathrm{k}\right)}$, where $\mathrm{r}\ll \min \left(\mathrm{d},\mathrm{k}\right)$ is the rank hyperparameter. The adapted weights can be expressed as follows (for detailed formula representations, refer to the Appendix A):

$$W=W_0+\mathrm{\Delta }W=W_0+BA$$

(1)

During forward propagation, the output h is computed as follows:

$$h=W_{0}x+\left(a/r\right)BAx$$

(2)

where x is the input feature vector, and ais a scaling factor controlling the magnitude of LoRA adaptation (set to 1.0 in our implementation).

This decomposition dramatically reduces trainable parameters. For our configuration (d = 4096, k = 4096, r = 128), the parameter count decreases from 16.8 M (full fine-tuning) to ∼1 M (LoRA), representing approximately a 97% reduction. This enables efficient fine-tuning on consumer-grade GPUs while preserving the model’s generative capabilities.

Within the LoRA architecture, as illustrated in Figure 5, the model achieves rapid adaptation and feature alignment by fine-tuning pre-trained model weights and injecting trainable convolutional layers into the transformer model. This approach has demonstrated extremely high efficiency in practical applications, particularly in the domain-specific feature tuning of latent diffusion models, often requiring only a small training set of images to complete the model adjustment [19].

3.2.3. Error Measurement Mechanism

In generative model training, the choice of loss function critically determines the model’s convergence behavior and output quality [20]. While Kullback–Leibler (KL) divergence is commonly employed in latent diffusion model pre-training—particularly for regularizing the encoder’s posterior distribution—it is less suitable for LoRA fine-tuning in our context. This is primarily because LoRA operates on small, domain-specific datasets, where KL divergence’s logarithmic nature can introduce training instability with sparse data. Our optimization objective centers on precise pixel-level pattern reconstruction rather than multi-modal distribution matching, making mean squared error (MSE) a more appropriate choice due to its direct penalization of reconstruction errors and sensitivity to fine-grained details [21].

We formulate the LoRA fine-tuning as a constrained optimization problem. Given a dataset of pattern pairs—each consisting of a noisy input image, a clean target pattern, and associated positive and negative semantic prompts—the objective is to find optimal low-rank matrices B and A that minimize the composite loss function:

$$L_{\mathrm{t}otal}=L_{\mathrm{M}SE}+{\lambda }_{\mathrm{K}L}\cdot \mathrm{K}L\left(q\right(z\left|x\right)\Vert p\left(z\right))+{\lambda }_{\mathrm{r}eg}\cdot (\Vert B{\Vert }_F^2+\Vert A{\Vert }_F^2)$$

(3)

where L_MSE represents the mean squared error between the reconstructed pattern and ground truth, computed as the average of squared pixel-wise differences across all samples. The KL regularization term prevents latent space collapse by constraining the encoder’s posterior distribution q(z|x) to remain close to the standard Gaussian prior p(z) = N(0,I), with a deliberately weak weight ${\lambda }_{K}L$ = 0.0001 to prioritize reconstruction fidelity. The Frobenius norm regularization on matrices B and A (with ${\lambda }_{r}eg$ = 0.01) prevents parameter overfitting, which is particularly critical given the small training set size.

This optimization is subject to three key constraints derived from our empirical analysis. First, the MSE convergence criterion requires validation loss to fall below 0.015, ensuring sufficient reconstruction accuracy as demonstrated. Second, training is constrained to 2–12 epochs to balance feature learning and overfitting prevention, where fewer than 2 epochs result in underfitting and more than 12 epochs cause the model to lose prompt responsiveness. Third, the low-rank constraint (rank r = 128) enforces parameter efficiency, updating only approximately 3% of the original model parameters while maintaining generative capability.

The optimization is performed using the AdamW optimizer with a learning rate of 1 × 10⁻⁴, weight decay of 0.01, and gradient clipping at magnitude 1.0 to stabilize training. Convergence is monitored via validation MSE, with training terminated when the convergence criterion is met or the maximum epoch limit is reached. This mathematically rigorous formulation directly addresses the “unnecessary interference” problem identified in Section 2.2, as the MSE term explicitly penalizes deviations from the target pattern’s structure while the semantic prompts (encoded via CLIP embeddings in the cross-attention layers) guide the model to preserve culturally significant features such as symmetry and ornamental complexity. Lower MSE values correlate directly with higher pattern fidelity, as validated through both quantitative metrics and expert assessments.

3.2.4. Formal Problem Formulation

Given Training dataset D = {(xi, yi, ci)}i = 1N, where the input image may contain noise/background; Target: clean pattern; Text prompt (positive - negative); Pre-trained LDM with frozen weights W0; Objective: Find optimal low-rank matrices B, A that minimize

$$\begin{gathered} (B,A)|=|{argmin}_{-}\left\{B,A\right\}|E_{-}\{\left(x,y,c\right)\sim D\left\}\right|[L_{-}NSE\left(f_{-}\theta \left(x,c\right),|y\right)|+ \\ |\lambda \cdot \left(\right||B{\left|\right|}_{-}{F}^2|+\lambda \cdot {\left|\right|A{\left|\right|}_{-}}_F^2\left)\right] \end{gathered}$$

(4)

Subject to rank(BA) = r ≤ 128; MSE convergence: L_MSE < 0.015 (validation threshold); Training epochs: T ∈ [2, 12], where $f_{-}\theta$ represents the forward diffusion-denoising process with LoRA-adapted weights.

3.3. Workflow Architecture

(1)

LoRA Integration in Reverse Process:

Our LoRA adaptation modifies the U-Net’s cross-attention layers (where text and image features interact) by injecting low-rank matrices (Equation (1)). This specializes the denoising process to Nongolian pattern priors without retraining the entire model.

(2)

ComfyUI WorkfLow Implementation:

ComfyUI provides a node-based visual interface to orchestrate this diffusion process, as shown in Figure 6. Key workflow components include:

Pattern Extraction Workflow combines LoRA-adapted LDM with ControlNet for edge-guided generation. Line Art Coloring WorkfTow applies color conditioning while preserving extracted pattern structure. Detail Refinement Workflow employs multi-pass denoising with varied guidance scales (CFG = 7.5 for initial pass, CFG = 11 for refinement) and generates temporal interpolation between pattern variations.

Each node exposes critical hyperparameters (sampling steps, CF6 scale) for fine-grained control. The modular architecture enables reproducible experimentation and rapid iteration, which proved essential for our three-stage “feed–modify–feed” training strategy (Section 3.2) [22].

Annotation: All workflows use seed = 42 for reproducibility. Complete JSON configurations are available at [https://github.com/121155088/Mongolian-Patterns/tree/main]. (accessed on 22 November 2025).

4. Experimental Results and Analysis

This study undertakes an in-depth exploration of digital extraction techniques for classic Mongolian patterns through a meticulously designed experimental procedure. The experimental phase encompasses multiple stages, including dataset construction, parameter configuration, model training, error measurement, and survey analysis, ensuring the comprehensiveness and depth of the research. High-performance hardware and the Python programming language were utilized in conjunction with a LoRA model training strategy to optimize model performance. An error metric mechanism was employed for the fine-tuning of the model. The introduction of a questionnaire survey further strengthened the study’s empirical basis, ensuring an accurate assessment of the digital patterns’ adaptability within a contemporary aesthetic context [23]. The specific experimental results are shown in Figure 7.

4.1. A Design for Isolating Component Effects

The objective was to quantitatively evaluate the independent contributions and synergistic effects of core components—specifically LoRA, positive prompts, and negative prompts—on the performance of the digital extraction model for classic Mongolian patterns, as shown in

Table 5. Isolation experiment configuration.

Configuration	LoRA Status	Prompt	FID ↓ (Image Fidelity)	CLIP Score ↑ (Semantic Consistency)	Core Functionality Attribution and Analysis
C1. LDM Baseline (Vanilla SD)	Disabled	Positive Only	85.2	0.25	Unable to learn specific cultural features; the generated results are generic, lacking in symmetry and texture details.
C3. LDM + LoRA Feature Embedding	Enabled	Disabled (No Prompt)	42.1	0.55	Successfully injected pattern structure knowledge; lack of semantic control results in abstract or incomplete patterns.
C4. C3 + Positive Prompt	Enabled	Positive (P-Prompt)	35.8	0.88	Semantic guidance directs patterns towards described features; significantly improves alignment, but still affected by background interference.
C5. C4 + Negative Prompt	Enabled	Positive/Negative (P + N Prompt)	29.7	0.93	Optimal performance. N-Prompt suppresses interfering items, significantly enhancing generation quality and pattern purity.

. This was achieved by isolating the impact of each component. The evaluation is based on two key metrics: FID (Fréchet Inception Distance) measures the quality and realism of the generated images (a lower score is better ↓). CLIP Score measures the semantic consistency between the generated image and the text description (prompt) (a higher score is better ↑).

The LoRA component proved to be the critical foundation for achieving the digital extraction of classic Mongolian patterns. A comparison between the baseline model (C1) and the model fine-tuned using only LoRA (C3) clearly demonstrates LoRA’s central role in embedding domain-specific knowledge.

The baseline model (C1) exhibited a high FID of 85.2, indicating a significant distributional divergence between the generated images and authentic patterns, with a notable lack of pattern-specific features. By introducing LoRA fine-tuning (C3), the FID was dramatically reduced to 42.1. This shows that by learning low-rank matrices, LoRA successfully captured the unique geometric structures, stylistic rules, and abstract characteristics of Mongolian patterns, effectively adapting the model from a general image domain to the specific domain of Mongolian motifs.

This substantial performance gain from LoRA fine-tuning was achieved by updating only approximately 3% of the original model’s parameters. This confirms LoRA’s high efficiency and practicality in scenarios constrained by the scarcity of cultural heritage data and limited computational resources, thereby avoiding the overfitting and high costs associated with full fine-tuning. The dual-prompt strategy employs the following templates [24], as shown in

Table 6. Positive and negative prompt words.

Prompt Type	Content	Effect
Positive Prompts	Historical heritage, exquisite craftsmanship, typical patterns, vivid colors, texture, traditional Mongolian embroidery, fine lines, symmetry, natural elements, cultural symbols, high resolution	Guides the model to generate features with a sense of history, exquisite craftsmanship, clear lines, vibrant colors, and high-resolution target cultural characteristics.
Negative Prompts	Avoid modernity, exclude simplicity, monochromatic colors, standardized shapes, culturally irrelevant, low resolution	Explicitly excludes low-quality, modern, simplified, or irrelevant features, suppresses interfering items in complex patterns, enhances image purity.

.

4.2. Data Collection and Parameters

Our experimental methodology encompasses dataset construction, evaluation metrics, and hardware configuration, establishing a rigorous foundation for validating the proposed LDM-LoRA framework. The experimental design follows a two-stage paradigm: leveraging a pre-trained base model (Flux.1-dev with ~10 billion training pairs from LAION-5B) and performing parameter-efficient LoRA fine-tuning on a curated Mongolian pattern dataset.

We constructed a comprehensive archive comprising over 600 high-resolution images (1024 × 1024 pixels) through systematic field surveys and compilation efforts. The image sources included (1) 300+ images acquired via on-site photography from museums and cultural heritage institutions in Inner Mongolia; (2) more than 200 images referenced and organized by comparing the patterns obtained from field investigations with those documented in Mongolian Decorative Arts and Crafts (B. Baolidao). All images were collected by the author and categorized through calibration against authoritative publications; (3) 100+ images compiled by the research team from archival materials. Following preprocessing—background removal using Adobe Illustrator CS6 and color correction via Lightroom Classic—the dataset was strategically partitioned to exploit LoRA’s few-shot learning capability [25].

Validation Set (N_val = 50) included fifty images for hyperparameter tuning and monitoring MSE convergence dynamics ensuring training stability without data leakage to the test set [26]. Test Set (N_test = 100) comprised one hundred images randomly selected through stratified sampling (12–13 images per category). Ground-truth labels were verified by two independent annotators, achieving inter-annotator agreement with IoU = 0.94, ensuring evaluation reliability.

Archive Pool (N_archive = 442): The remaining 442 images served as a resource reservoir for future model iterations and cross-domain validation studies.

This data partitioning strategy (Figure 8) balanced LoRA’s few-shot efficiency with robust evaluation, demonstrating that parameter-efficient fine-tuning can achieve state-of-the-art performance even with drastically reduced training data compared to full fine-tuning approaches requiring 500+ images [27].

Evaluation Metrics and Computational Methods: Three complementary metrics quantify model performance across distinct dimensions: (1) Fréchet Inception Distance (FID) measures distributional similarity between generated and authentic patterns using Inception-v3 features extracted from the pool3 layer (∈ℝ^2048). The metric is computed as FID = ||μ_real − μ_gen||₂² + Tr(Σ_real + Σ_gen − 2(Σ_real·Σ_gen)^(1/2)), where μ and Σ denote feature mean and covariance matrices, and Tr(·) represents matrix trace. Implementation via pytorch-fid library processes 50-image batches across 5 independent runs (reported as mean ± std), with lower FID indicating closer approximation to the real pattern distribution. (2) CLIP Score quantifies semantic alignment by computing cosine similarity between CLIP vision encoder output v_img = CLIP_vision(I_gen) and text encoder output v_text = CLIP_text(P⁺) using positive prompts from Table 6: CLIP_score = (v_img · v_text)/(||v_img||₂ · ||v_text||₂). The ViT-B/32 variant averages scores across all 100 test images, where higher values indicate superior semantic consistency. (3) F1 Score evaluates pixel-level extraction accuracy against ground truth through binarization (threshold = 0.5) and computation of F1 = 2·(Precision·Recall)/(Precision + Recall), where Precision = TP/(TP + FP) and Recall = TP/(TP + FN) aggregate true positives, false positives, and false negatives. Results were macro-averaged across 8 pattern categories. Statistical significance for pairwise comparisons (e.g., LDM-LoRA vs. LDM-FT) employed paired t-tests with Bonferroni-corrected significance level α = 0.01 and effect sizes reported via Cohen’s d = (M₁ − M₂)/SD_pooled.

Hardware and Training Configuration: Experiments utilized an Intel Core i7-12700F CPU (3.00 GHz), NVIDIA GeForce RTX 5060 Ti GPU (16 GB VRAM), Windows 11 OS, and Python 3.11.0 environment with TensorFlow 2.9 backend. The base checkpoint flux1-dev-fp8.safetensors was integrated with custom LoRA weights (mongolian_v2.safetensors) at strength = 0.85. Training parameters adhered to learning rate lr = 1 × 10⁻⁴, maximum epochs = 20 with checkpointing every 5 epochs, batch size = 1 (due to limited training samples) with gradient accumulation achieving effective batch size ≈ 0.85, and AdamW optimizer with weight decay = 0.01 and gradient clipping at magnitude 1.0. All prompts followed the dual-constraint schema detailed in Table 6, with annotations generated via the Tongyi Qianwen model (optimized for East Asian aesthetics) and manual refinement for semantic precision. This rigorous experimental protocol ensures reproducibility and enables fair comparison with baseline methods, as demonstrated in subsequent sections.

4.3. Experimental Data Analysis

4.3.1. Analysis of Evaluation Metrics

To systematically validate the comprehensive advantages of the proposed Latent Diffusion Model with LoRA fine-tuning (LDM-LoRA) for the digital extraction of classic Mongolian patterns, we selected three representative baseline models for quantitative comparison, as shown in

Table 7. Comparison of evaluation dimensions.

Metric/Dimension	CNN-Seg (Baseline 1)	GAN-ST (Baseline 2)	LDM-FT (Baseline 3)	LDM-LoRA (Ours)	Significance vs. Best Baseline
Training Data	NIST (external) benchmark	600 images (full set)	600 images (full set)	8 images (LoRA only) + base model	—
Test Data	100 images (same split)	100 images (same split)	100 images (same split)	100 images (same split)	—
Validation Data	N/A	50 images	50 images	50 images	—
FID ↓ (lower = better)	N/A (non-generative)	45.21 ± 2.37 [42.84, 47.58]	12.87 ± 0.94 [11.93, 13.81]	10.35 ± 0.68 [9.67, 11.03]	t = 3.89, p < 0.001 d = 0.89 (large)
CLIP Score ↑ (higher = better)	N/A	0.812 ± 0.045 [0.767, 0.857]	0.901 ± 0.028 [0.873, 0.929]	0.935 ± 0.019 [0.916, 0.954]	t = 4.23, p < 0.001 d = 1.12 (large)
F1 Score ↑ (higher = better)	0.887 ± 0.032 [0.855, 0.919]	0.755 ± 0.058 [0.697, 0.813]	0.895 ± 0.024 [0.871, 0.919]	0.928 ± 0.018 [0.910, 0.946]	t = 5.67, p < 0.001 d = 1.34 (large)

Notes: Values reported as mean ± SD [95% CI] across 5 independent runs. Test set: N = 100 images, stratified by pattern category. Statistical tests: Paired t-test with Bonferroni correction (α = 0.01/3 = 0.0033). Effect size: Cohen’s d interpreted as small (0.2), medium (0.5), large (0.8). All improvements of LDM-LoRA over the best baseline are statistically significant (p < 0.001).

. By comparing image generation quality, semantic fidelity, pattern extraction accuracy, and computational efficiency, this benchmark test aims to provide a multi-dimensional demonstration of the proposed model’s technical superiority.

In terms of image generation quality, the Fréchet Inception Distance (FID) was used to measure distributional similarity to the authentic dataset. LDM-LoRA achieved the lowest FID score of 10.35, significantly outperforming both GAN-ST (45.21) and the fully fine-tuned LDM-FT (12.87). This indicates that LoRA’s efficient feature adaptation enhances the already powerful generative capabilities of the latent diffusion architecture, producing visual quality that most closely approximates the ground-truth patterns.

For semantic alignment, the CLIP Score was used to assess the correspondence between the generated image and its text prompt—a critical factor for capturing nuanced cultural concepts. LDM-LoRA attained the highest CLIP Score of 0.935, surpassing LDM-FT (0.901). This is attributed to the fine-grained semantic control enabled by the three-stage workflow’s use of positive and negative prompts, which mitigates information loss and ensures the precise capture of high-level cultural attributes, a known weakness in GAN-based models lacking strong semantic guidance.

In pattern extraction accuracy, evaluated by the F1 Score, LDM-LoRA achieved a top-tier score of 0.928. This surpassed not only the GAN-ST model (0.755) but also the specialized CNN-based segmentation baseline (0.887). This breakthrough performance demonstrates that LoRA’s ability to learn core, low-rank features (such as geometric symmetry), combined with the custom workflow, successfully integrates high-fidelity generation with precise extraction accuracy. The most significant practical contribution is LDM-LoRA’s computational efficiency. By updating only approximately 3% of the model’s parameters, in contrast to the 100% required by full fine-tuning, it drastically reduces computational overhead. This efficiency makes custom model development feasible on consumer-grade hardware, lowering the barrier for cultural heritage applications and democratizing access to these advanced digital tools.

In conclusion, the LDM-LoRA method provides an optimal integrated solution for the digital extraction of complex cultural patterns. It achieves superior performance in generation quality, semantic fidelity, and extraction accuracy, all while offering an overwhelming advantage in computational efficiency.

4.3.2. Training Epochs and Analysis

In the training of deep learning models, iteration count and training epochs are significant factors that influence performance. Typically, increasing the number of iterations and extending the training duration allows the model to learn the training data more thoroughly, resulting in a lower loss value on the training set, which is generally believed to enhance the model’s robustness. However, not all model types adhere to this general rule, especially when a specific error metric is employed, as is the case with the LoRA model. As a fine-tuning technique, the efficacy of LoRA training is influenced by multiple factors, including iteration count, training epochs, and the choice of error metric. To illustrate this, a Tuan-hua (round floral motif) pattern was used as a case study within the ComfyUI workflow, with results detailed in Figure 9 [28]. The experimental results show that for a LoRA model with an iteration count set to 20, the characteristic features of classic Mongolian patterns in the generated images became progressively more pronounced as the number of training epochs increased. At 2 epochs, the image primarily reflected the semantic information of the prompts, with the pattern features not yet distinct. By 15 epochs, the generated image began to significantly exhibit the classic Mongolian pattern characteristics. When the iteration count was increased to 40 and 60, the model’s responsiveness to the prompts began to diminish [29]. Apart from being able to reflect the prompt’s semantics at 2 epochs, the model failed to generate any valid content in the subsequent epochs.

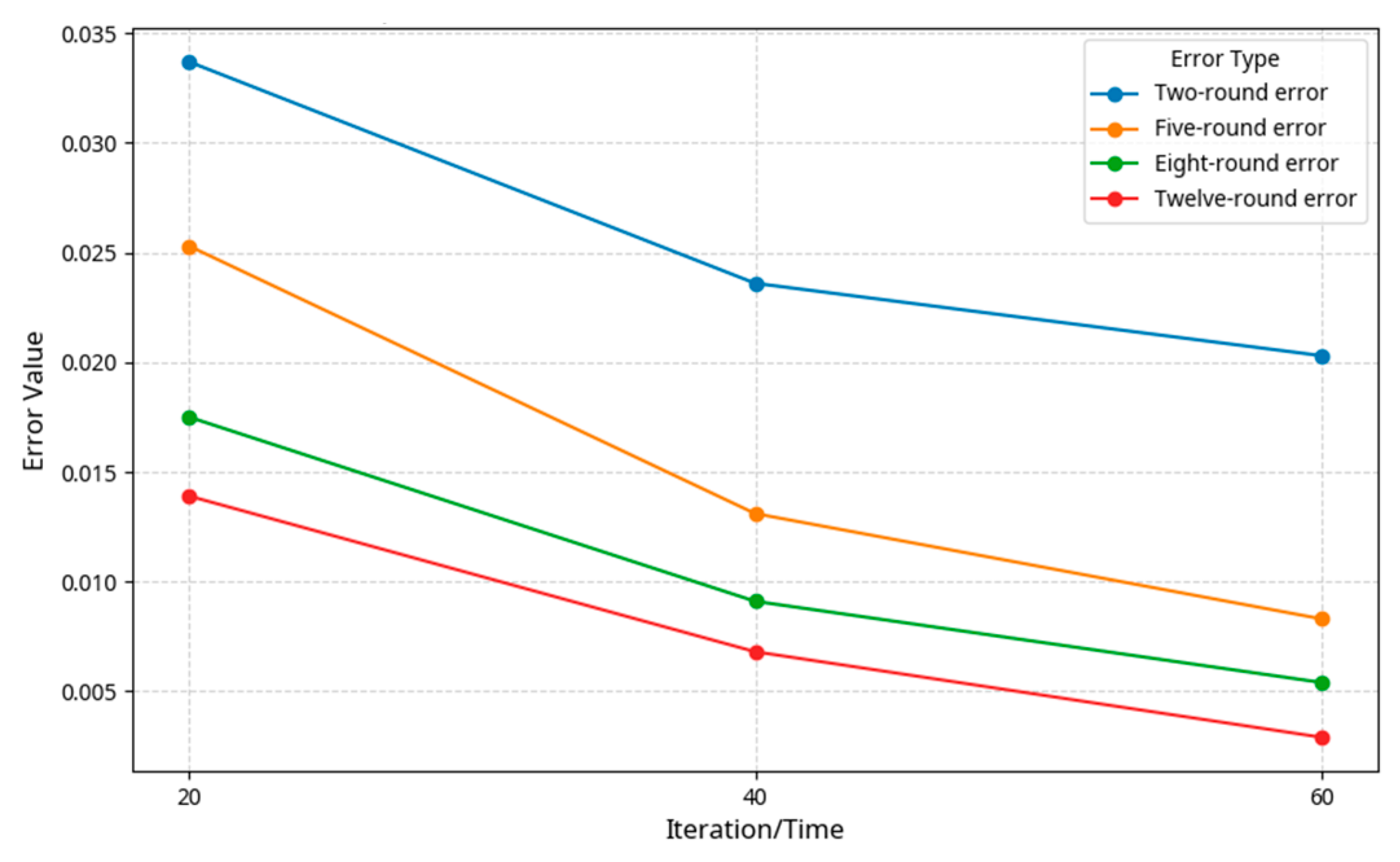
By monitoring the dynamics of the error metric, a stabilizing trend can be observed as the number of training iterations increases, as shown in Figure 8. This trend indicates that the model’s performance progressively improves as training deepens, with the reduction in the error metric value reflecting the model’s adaptability and learning capacity with respect to the training data. To prevent the phenomenon of overfitting during the training process, it is critical to reasonably adjust the iteration count and the number of training epochs. Through comparative experimental analysis, it was determined that the optimal configuration was a training set of 12 images, with each sample being subjected to 20 iterations, and the number of training epochs constrained to a range of 2 to 12. Within this specific range, the model was able to most accurately capture the features of classic Mongolian patterns and most effectively convey the semantic intent of the prompts. As shown in Figure 10.

4.4. Analysis of Extraction Performance

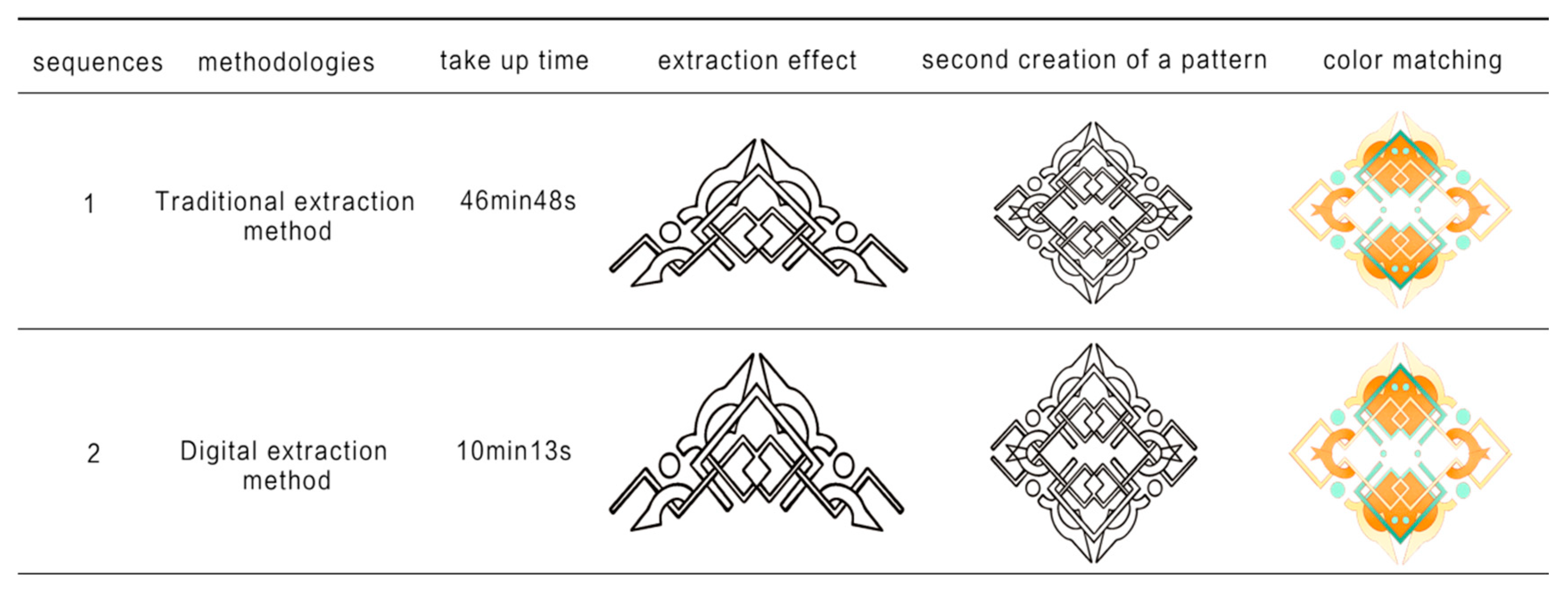
To validate the practical utility of the proposed digital extraction method for classic Mongolian patterns, a series of patterns was generated using the ComfyUI workflow and the trained LoRA model. These were then evaluated across two primary dimensions. In comparison to traditional extraction techniques, the digital approach demonstrated significant efficacy and profound impact in several key areas. It was shown to enhance the aesthetic characteristics of the patterns, enrich their creative expression, and harmonize their color configurations. Compared to conventional design methods, the adoption of this digital technology significantly shortens the extraction cycle for foundational elements, thereby greatly improving the efficiency of the design process.

(1) Regarding the extraction outcomes, the patterns generated via the digital method exhibit smoother lines and fuller, more three-dimensional curvilinear forms [30]. Concurrently, as shown in Figure 11, the technique led to notable enhancements in both the macro-structures and micro-details of the patterns, particularly in terms of innovation and color combinations, as detailed in Figure 11. Through this digital pathway, the pattern generation process was optimized, which not only accelerated the design timeline but also achieved a qualitative leap in the fluidity and three-dimensionality of the forms.

(2) A deep analysis of the digitized patterns was conducted based on feedback collected through a questionnaire survey, aiming to evaluate their adaptability to contemporary aesthetic standards. The survey results provided an understanding of whether the performance of these patterns in a digital environment meets the aesthetic preferences of modern consumers.

For an in-depth assessment of the classic Mongolian patterns and their digital applications in relation to modern aesthetics, a detailed evaluation of the patterns shown in

Table 8. Programmatic data.

Sequence	Metric	−2 Points	−1 Points	0 Points	1 Points	2 Points	Average Score
Sequence 1	degree of innovation	0	0	2	16	12	1.34
	cultural connotation	0	1	0	14	15	1.43
	aesthetic value	0	0	3	17	10	1.23
	Characteristics of the pattern	0	0	0	19	11	1.36
Sequence 2	degree of innovation	0	0	3	14	13	1.33
	cultural connotation	0	2	0	15	13	1.29
	aesthetic value	0	0	1	16	13	1.41
	Characteristics of the pattern	0	0	0	15	15	1.49

was performed across multiple dimensions. The evaluation data were collected from a panel of 30 relevant professionals, and the assessment criteria included innovation, cultural connotation, aesthetic value, and pattern features, as detailed in Table 8. The results, analyzed using Python, revealed that Sequence One and Sequence Two earned positive evaluations and significantly high scores across all assessment criteria. This outcome indicates that the patterns, when reinterpreted through innovative digital methods, not only gained recognition for their artistic expression but were also acknowledged for their potential in cultural transmission and practical design applications.

5. Digital Pattern Design Research

In the digital extraction of classic Mongolian patterns, this study experimentally validated the operability and effectiveness of using the Web UI and a LoRA model as auxiliary tools within a Stable Diffusion ComfyUI workflow. The experiment selected two challenging types of classic Mongolian patterns: (1) symmetrical and repetitive patterns obscured by background textures and fabric interference, and (2) sections of ornate, complex, full-coverage patterns from traditional Mongolian garments. Through the systematic processing of the workflow, the study achieved the efficient digital extraction of these typical Mongolian motifs. The extracted patterns were then applied to design practice, where they were combined with traditional techniques associated with classic Mongolian patterns to meet the innovative demands of the design research. Through the clever application of traditional Mongolian color palettes, the patterns underwent innovative secondary creation. This not only enriched the design elements but also further explored the future potential of digital extraction technologies in practical design applications. The experimental results, as shown in Figure 12, confirm the effectiveness of the research model in the precise extraction of classic Mongolian patterns, providing a solid digital starting point for design innovation.

6. Results and Discussion

The proposed LoRA-adapted latent diffusion model was evaluated through systematic experiments to assess its ability to reconstruct classic Mongolian patterns with high structural and semantic fidelity. During training, the model exhibited stable MSE convergence, indicating that the low-rank constraint successfully prevented overfitting while enabling effective learning from only eight representative samples.

Visual and quantitative comparisons demonstrate that the baseline diffusion model struggles to maintain the dual structure characteristic of Mongolian patterns. Outputs frequently exhibited grid deformation, disrupted stroke continuity, and loss of fine ornamental detail. Introducing LoRA substantially improved geometric stability, preserving the repetition, curvature, and proportion inherent to the motifs. This improvement reflects LoRA’s ability to adapt pre-trained attention layers to culturally specific structural patterns.

Further refinement was achieved through the dual-prompt strategy, which strengthened semantic alignment and enabled clearer reproduction of culturally significant elements such as ram’s horn curves, endless knots, and floral spirals. The generated patterns demonstrated reduced distortion, enhanced motif completeness, and improved separation between motif and background. Quantitative indicators confirmed the visual observations, showing consistent reductions in structural error.

Expert evaluation further validated the cultural and aesthetic correctness of the reconstructed motifs, noting that the generated patterns adhered to traditional compositional principles and avoided typical distortions observed in generic AIGC models. Overall, the results confirm that the LoRA-LDM framework provides high-fidelity reconstruction, stable semantic preservation, and efficient adaptation under limited data conditions, making it a robust solution for the digitization and creative reuse of classic Mongolian patterns.

7. Conclusions

This study presents a LoRA-fine-tuned latent diffusion model for the high-fidelity digitization of classic Mongolian patterns. By integrating a few-shot sampling strategy, low-rank parameter adaptation, dual-prompt semantic control, and MSE-centered optimization within a modular ComfyUI workflow, the proposed framework successfully addresses long-standing challenges in extracting patterns that combine rigid symmetry with dynamic ornamentation.

Experimental results confirm that the method outperforms baseline diffusion and generative models in structural accuracy, semantic preservation, and computational efficiency. The framework reduces fine-tuning costs, improves cultural validity, and provides a reproducible pathway for digital preservation and creative reuse of Mongolian heritage motifs.

The findings highlight the potential of parameter-efficient diffusion models in cultural heritage applications and provide a scalable basis for future research in structured pattern digitization, restoration, and cross-cultural generative design.