Lightweight Transformer with Adaptive Rotational Convolutions for Aerial Object Detection

Abstract

Oriented object detection in aerial imagery presents unique challenges due to the arbitrary orientations, diverse scales, and limited availability of labeled data. In response to these issues, we propose RASST—a lightweight Rotationally Aware Semi-Supervised Transformer framework designed to achieve high-precision detection under fully and semi-supervised conditions. RASST integrates a hybrid Vision Transformer architecture augmented with rotationally aware patch embeddings, adaptive rotational convolutions, and a multi-scale feature fusion (MSFF) module that employs cross-scale attention to enhance detection across object sizes. To address the scarcity of labeled data, we introduce a novel Pseudo-Label Guided Learning (PGL) framework, which refines pseudo-labels through Rotation-Aware Adaptive Weighting (RAW) and Global Consistency (GC) losses, thereby improving generalization and robustness against noisy supervision. Despite its lightweight design, RASST achieves superior performance on the DOTA-v1.5 benchmark, outperforming existing state-of-the-art methods in supervised and semi-supervised settings. The proposed framework demonstrates high scalability, precise orientation sensitivity, and effective utilization of unlabeled data, establishing a new benchmark for efficient oriented object detection in remote sensing imagery.

1. Introduction

Oriented object detection in aerial imagery is a cornerstone of remote sensing, with applications spanning urban planning [1], disaster response [2], environmental monitoring [3], and security surveillance [4]. Unlike conventional object detection tasks, where objects are assumed to align with image axes, aerial imagery presents a unique challenge: objects often appear at arbitrary orientations. This variability in orientation increases the complexity of both data annotation and algorithmic detection, necessitating specialized approaches capable of effectively handling rotational invariance [5,6,7].

Recent advancements in Vision Transformers (ViTs) have revolutionized computer vision, delivering superior performance across a wide range of tasks, including image classification and object detection [8,9]. Concurrently, semi-supervised learning has emerged as a promising paradigm to address the scarcity of labeled data, a common challenge in real-world applications [10,11]. However, despite their individual strengths, existing methods often fail to effectively integrate these advancements for oriented object detection. Specifically, they lack robust mechanisms to ensure rotational invariance [12] and are unable to fully leverage unlabeled data to improve generalization [13].

In this paper, we present the RASST, a novel framework designed to address these challenges in oriented object detection. RASST leverages a hybrid Vision Transformer architecture that incorporates rotationally aware patch embeddings and adaptive rotational convolutions. To enhance the learning process in data-scarce environments, RASST employs a pseudo-label-guided learning framework that refines pseudo-labels through rotation-aware adaptive weighting (RAW) and global consistency (GC) losses. These innovations collectively enable the model to detect objects at arbitrary orientations with high precision, even under limited supervision.

The key contributions of this work are as follows:

• We propose a ViT-based backbone that integrates rotationally invariant patch embeddings and positional encodings, enhancing the model’s ability to handle objects at varying orientations.
• A new convolutional module dynamically aligns convolutional kernels with object orientations, enabling the extraction of more robust features.
• By employing RAW and GC losses, our semi-supervised framework effectively utilizes unlabeled data, improving model generalization and pseudo-label reliability.
• The effectiveness of RASST is validated on the DOTA-v1.5 benchmark, where it achieves superior performance compared to existing methods in both fully supervised and semi-supervised settings.

Through these contributions, RASST addresses critical gaps in the literature, providing a comprehensive solution to the challenges of oriented object detection in aerial imagery. By combining advancements in ViTs with innovative mechanisms for rotational invariance and semi-supervised learning, RASST sets a new benchmark for accuracy and robustness in this domain.

The rest of the paper is organized as follows: Section 2 provides an overview of related work. Section 3 details the proposed methodology, including the architectural components and learning framework. Section 4 describes the experimental setup and compares RASST performance with SOTA methods. Section 5 discusses the implications and limitations of the results, and Section 6 provides concluding remarks and outlines future research directions.

2. Background Research

Oriented object detection in aerial imagery has garnered significant research attention due to its critical applications in urban planning, environmental monitoring, and disaster response. Existing approaches to this problem can be broadly categorized into three main areas: rotational invariance methods, semi-supervised learning techniques, and Vision Transformer-based architectures. This section reviews these areas, emphasizing their contributions and limitations within the context of oriented object detection.

2.1. Rotational Invariance in Object Detection

Rotational invariance poses a fundamental challenge in oriented object detection [14]. Conventional convolutional neural networks (CNNs), though highly effective in general object detection, exhibit limitations when addressing objects at arbitrary angles in aerial images [15,16]. To mitigate this, approaches such as RoI Transformer [17] and Oriented R-CNN [18] have been developed, introducing rotation-specific enhancements, including rotated bounding boxes, to improve detection accuracy. However, these methods often rely on fixed rotational anchors or rigid transformations, which constrain their performance when dealing with diverse object orientations.

Dynamic rotational mechanisms, such as ARC, have been proposed to better align features for rotated objects. While these methods offer improved feature extraction, they are typically associated with significant computational costs and limited scalability for large-scale datasets. RASST builds upon these advancements by incorporating rotationally aware patch embeddings and adaptive rotational convolutions within a transformer framework. This integration achieves robust rotational invariance while maintaining computational efficiency.

2.2. Semi-Supervised Learning for Object Detection

The limited availability of labeled data in aerial imagery has driven research into semi-supervised learning approaches, which aim to utilize both labeled and unlabeled data effectively. Frameworks such as SOOD [19] and PSCD [20] have employed pseudo-labeling and consistency-based training strategies to improve model performance in low-label settings. These methods have demonstrated potential, particularly in enhancing generalization across diverse datasets.

Despite their advantages, existing semi-supervised approaches often struggle with noisy pseudo-labels, a challenge that is especially pronounced in oriented object detection where precise rotational annotations are critical. RASST addresses this issue through its Pseudo-Label Guided Learning (PGL) framework, which employs RAW and GC losses to refine pseudo-labels. By reducing noise and enhancing the reliability of pseudo-labels, RASST ensures a more robust learning process, even in scenarios with limited labeled data.

2.3. Vision Transformers for Object Detection

ViTs have emerged as a powerful tool for capturing global context and long-range dependencies in visual data. Early implementations in object detection, such as Pyramid Vision Transformer (PVT) and E-PVT [21], demonstrated their potential to outperform traditional CNN-based methods. However, standard ViTs lack inherent mechanisms to address rotational invariance, a critical requirement for oriented object detection.

To bridge this gap, hybrid architectures combining ViTs with convolutional layers have been explored. For example, POE [22] integrates convolutional inductive biases to enhance local feature extraction while preserving the global representation capabilities of ViTs. RASST advances this concept by introducing rotationally aware positional encodings and patch embeddings, enabling it to effectively handle objects at arbitrary orientations. Additionally, the inclusion of adaptive rotational convolutions allows RASST to capture both global and local patterns with high precision, making it particularly well-suited for oriented object detection tasks.

2.4. Multi-Scale Feature Fusion

Aerial imagery often contains objects of varying sizes, posing an additional challenge for detection models. Multi-scale feature fusion techniques, such as those employed in Feature Pyramid Networks (FPNs) [23], have been shown to improve detection accuracy across diverse object scales. Existing methods like Oriented R-CNN and RoI Transformer incorporate multi-scale features to enhance robustness. However, they often fail to appropriately weigh the importance of features from different scales, leading to suboptimal performance, particularly for small or densely packed objects.

RASST addresses this limitation by incorporating a Multi-Scale Feature Fusion (MSFF) module that employs cross-scale attention to adaptively weigh features from different scales. This ensures that the most informative features are prioritized, enabling the model to achieve high accuracy in detecting objects of varying sizes.

Despite the progress made, significant limitations remain in the field. Many existing methods for oriented object detection rely on fixed rotation anchors or face computational inefficiencies when employing dynamic rotational mechanisms. Semi-supervised frameworks frequently struggle with noisy pseudo-labels, limiting their effectiveness in scenarios with limited labeled data. Additionally, multi-scale feature fusion methods often overlook the importance of adaptive weighting, which is crucial for detecting small or densely packed objects effectively.

By integrating rotationally aware mechanisms, refining pseudo-labels through novel loss functions, and leveraging multi-scale feature fusion with lightweight attention mechanisms, RASST provides a comprehensive solution to these challenges. This innovative architecture not only achieves SOTA performance but also establishes a new benchmark for robustness and scalability in oriented object detection. Through its contributions, RASST significantly advances the capabilities of object detection in aerial imagery.

3. Proposed Methodology

This section outlines the architecture and learning framework of the RASST, as illustrated in Figure 1. It integrates rotationally aware patch embeddings, ARC, and MSFF to tackle the challenges of oriented object detection. Additionally, the PGL framework is introduced, employing RAW and GC losses to enhance the utilization of unlabeled data. The proposed methodology highlights robustness to object orientations, scalability across varying object scales, and efficiency in semi-supervised learning.

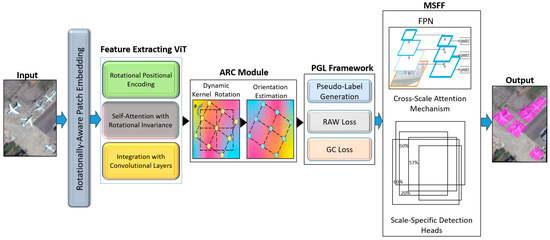
Figure 1 illustrates how the RASST framework incorporates a rotationally aware patch embedding mechanism integrated with a ViT to encode orientation information. The ARC module dynamically aligns convolutional kernels with local object orientations, while the PGL framework refines pseudo-labels using RAW and GC losses. MSFF enhances the model ability to detect objects at varying scales, delivering robust performance across diverse aerial imagery scenarios.

3.1. Hybrid Vision Transformer Architecture

The backbone of RASST is a hybrid ViT that integrates convolutional inductive biases for rotational invariance. Unlike traditional ViTs, which use fixed patch embeddings, RASST employs rotationally aware patch embeddings that maintain orientation consistency. Additionally, rotational positional encoding is introduced to enhance the model’s ability to differentiate between objects at different angles.

3.1.1. Rotationally Aware Patch Embedding

In a standard ViT, an input image $\mathrm{I}\in {\mathbb{R}}^{H\times W\times C}$, where $H,W,\mathrm{a}\mathrm{n}\mathrm{d}C$ represent the height, width, and number of channels, respectively, is divided into a sequence of flattened image patches $x_p\in {\mathbb{R}}^{N\times (P^2·C)}$, where $P^2$ is the patch size, and $N={\displaystyle \frac{H\times W}{P^2}}$ is the number of patches. To incorporate rotational invariance, we modify the patch extraction process to be rotationally aware. Each patch is not only extracted based on its spatial location but also adjusted according to the dominant orientation ${\theta }_p$ of the local features within that patch. The rotationally aware patch embedding is defined as:

$$z_p={E\left(R\right(x}_p{\theta }_p))+E_{pos}\left(p\right),$$

(1)

where ${R(x}_p{\theta }_p)$ is the rotated version of the patch $x_p$ by angle ${\theta }_p$, $E(\cdot )$ is the linear embedding function, $E_{pos}\left(p\right)$ is the positional encoding of the patch’s original position $p$. The rotational adjustment ${R(x}_p{\theta }_p)$ ensures that each patch is aligned with the dominant orientation, making the model more robust to rotational variations in the data.

3.1.2. Rotational Positional Encoding

Positional encoding is crucial in ViTs as it provides the model with information about the spatial relationships between patches. In the RASST model, we extend the standard positional encoding to include rotational information, allowing the model to account for the orientation of each patch.

The positional encoding for a patch at position $p=(p_x,p_y$) with rotation ${\theta }_p$ is defined as:

$$E_{pos}\left(p,{\theta }_p\right)=\mathrm{P}\mathrm{E}\left(p\right)+\mathrm{R}\mathrm{E}\left({\theta }_p\right),$$

(2)

where $\mathrm{P}\mathrm{E}\left(p\right)$ is the standard 2D sine-cosine positional encoding defined as:

$$\mathrm{P}\mathrm{E}\left(p\right)\left[2i\right]=\sin \left({\displaystyle \frac{p_x}{{10000}^{\frac{2i}{d}}}}\right),\mathrm{P}\mathrm{E}\left(p\right)\left[2i+1\right]=\cos \left({\displaystyle \frac{p_y}{{10000}^{\frac{2i}{d}}}}\right),$$

(3)

where $i$ indexes the dimensions and $d$ is the embedding dimension. $\mathrm{R}\mathrm{E}\left({\theta }_p\right)$ is the rotational encoding, which is similarly defined using sine and cosine functions to represent the rotation:

$$\mathrm{R}\mathrm{E}\left({\theta }_p\right)\left[2j\right]=\sin \left({\theta }_p\right),\mathrm{R}\mathrm{E}\left({\theta }_p\right)\left[2j+1\right]=\cos \left({\theta }_p\right),$$

(4)

where $j$ indexes the dimensions specific to the rotational encoding.

By integrating $E_{pos}\left(p,{\theta }_p\right),$ the ViT is better equipped to differentiate between patches not only based on their spatial position but also based on their orientation, thus improving its capability to handle rotated objects.

3.1.3. Self-Attention with Rotational Invariance

The core of the ViTs architecture is the self-attention mechanism, which computes the relationships between different patches. In the RASST model, the self-attention mechanism is modified to account for rotational invariance.

The standard self-attention is computed as:

$$Attention(Q,K,V)=softmax\left({\displaystyle \frac{Q{K}^{⊺}}{\sqrt{d_k}}}\right)V$$

(5)

where Q = $W_{Q^{z_p}}$, K = $W_{K^{z_p}}$, V = $W_{V^{z_p}}$ are the query, key, and value matrices, $d_k$ is the dimension of the key vectors.

In our modified version, we introduce rotational alignment between patches by incorporating rotational encoding directly into the self-attention computation:

$$\mathrm{R}-Attention(Q,K,V,R)=softmax\left({\displaystyle \frac{{Q(K+R)}^{⊺}}{\sqrt{d_k}}}\right)V$$

(6)

where $\mathrm{R}$ is the rotational adjustment matrix derived from the rotational encoding $\mathrm{R}\mathrm{E}\left({\theta }_p\right)$. The rotational adjustment ensures that patches with similar orientations have stronger attention weights. This modification enhances the model ability to focus on relevant patches that are similarly oriented, thereby improving the detection of objects that appear at arbitrary angles.

3.1.4. Integration with Convolutional Layers

While the self-attention mechanism captures global relationships, it lacks the ability to model fine-grained local patterns. To address this, we integrate convolutional layers early in the architecture, which serve as an inductive bias for detecting local features such as edges and textures. The feature maps produced by these convolutional layers are then passed to the ViT, providing a rich representation that includes both local and global information. The hybrid feature representation $f$is computed as:

$$f=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\left(\mathrm{I}\right)+\mathrm{V}\mathrm{i}\mathrm{T}(z_p,E_{pos}\left(p,{\theta }_p)\right),$$

(7)

where Conv(I) represents the convolutional features extracted from the input image I, $\mathrm{V}\mathrm{i}\mathrm{T}(z_p,E_{pos}\left(p,{\theta }_p)\right)$ represents the output of the Vision Transformer with rotationally aware patch embeddings and positional encoding. This combination of convolutional and transformer features provides a robust representation that is both rotation-invariant and capable of capturing complex patterns across the entire image.

3.2. Adaptive Rotational Convolution Module

The ARC module dynamically adjusts convolutional kernels based on the local orientation of detected features. This ensures that the extracted features are robust to rotations, improving the accuracy of the model in detecting objects with arbitrary orientations. The degree of rotation for each kernel is determined by the orientation prediction from a preceding layer, allowing the model to adapt on the fly.

3.2.1. Motivation and Overview

In the context of oriented object detection, objects in aerial imagery often appear at arbitrary angles, making it essential for the convolutional layers to be sensitive to these orientations. The ARC module introduces rotation-invariant convolutional kernels that adapt to the dominant orientation within each receptive field, enabling the model to extract more discriminative features regardless of the object orientation.

The core idea behind the ARC module is to dynamically rotate the convolutional kernels based on the orientation of the local features detected in the input. This rotation is performed in real-time during the forward pass, ensuring that the feature extraction process is always aligned with the orientation of the objects.

3.2.2. Dynamic Kernel Rotation

The $\mathrm{F}\in {\mathbb{R}}^{H\times W\times C}$ input feature map to a convolutional layer, where $H,W$, and $C$ represent the height, width, and number of channels, respectively. A standard convolution operation with a kernel $\mathrm{K}\in {\mathbb{R}}^{k\times k\times C}$ where $k$ is the kernel size, is defined as:

$${\mathrm{F}}_{out}(i,j)={\sum }_{m=1}^k{\sum }_{n=1}^k\mathrm{K}(m,n)·\mathrm{F}(i+m,j+n),$$

(8)

where ${\mathrm{F}}_{out}\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times C^{\prime }}$ is the output feature map after the convolution.

In the ARC module, instead of using a fixed kernel $\mathrm{K}$, we introduce a dynamic rotation of the kernel based on the local orientation $\theta (i,j)$ detected within the receptive field centered at $(i,j).$ The rotated kernel ${\mathrm{K}}_{\theta }$ is given by:

$${\mathrm{K}}_{\theta }\left(m,n\right)={\mathrm{R}}_{\theta }\mathrm{K}\left(m,n\right),$$

(9)

where ${\mathrm{R}}_{\theta }$ is a rotation matrix that rotates the kernel by the angle $\theta$. The rotation matrix ${\mathrm{R}}_{\theta }$ is defined as:

$${\mathrm{R}}_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right],$$

(10)

Applying this rotated kernel in the convolution operation results in the following output:

$${\mathrm{F}}_{out}(i,j,\theta )={\sum }_{m=1}^k{\sum }_{n=1}^k{\mathrm{K}}_{\theta }(m,n)·\mathrm{F}(i+m,j+n),$$

(11)

This dynamic adjustment allows the convolutional filter to align with the dominant orientation of features in each local region, improving the model ability to detect and represent objects that are rotated in the image.

3.2.3. Orientation Estimation

To determine the appropriate rotation angle $\theta (i,j)$ for each receptive field, we introduce an orientation estimation step before the convolution. This step involves calculating the dominant gradient direction within the receptive field, which serves as a proxy for the orientation of the object. The gradient of the feature map $\mathrm{F}$ at position $(i,j)$ is given by:

$$\mathrm{G}\left(i,j\right)=\left({\displaystyle \frac{\partial \mathrm{F}}{\partial x}},{\displaystyle \frac{\partial \mathrm{F}}{\partial y}}\right),$$

(12)

where ${\displaystyle \frac{\partial \mathrm{F}}{\partial x}}\mathrm{a}\mathrm{n}\mathrm{d}{\displaystyle \frac{\partial \mathrm{F}}{\partial y}}$ are the gradients along the $x$-axis and $y$-axis, respectively. The dominant orientation $\theta (i,j)$ is then computed as the angle of the gradient vector:

$$\theta \left(i,j\right)={\tan }^{-1}\left({\displaystyle \frac{\frac{\partial \mathrm{F}}{\partial y}(i,j)}{\frac{\partial \mathrm{F}}{\partial x}(i,j)}}\right),$$

(13)

This angle $\theta (i,j)$ is used to rotate the convolutional kernel $K$ before applying it to the receptive field centered at $(i,j)$.

The ARC module is integrated into the standard convolutional layers of the RASST model. For each convolutional layer, the orientation $\theta (i,j)$ is estimated across the entire feature map, and the convolutional kernels are dynamically rotated to match these orientations. This process can be mathematically represented as:

$${\mathrm{F}}_{ARC}\left(i,j\right)={\mathrm{F}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\left(i,j,\theta (i,j)\right),$$

(14)

where ${\mathrm{F}}_{ARC}$ represents the feature map after the application of the ARC module. By applying the ARC module, the RASST model achieves rotation-invariant feature extraction, enabling it to more effectively detect objects with arbitrary orientations in aerial imagery. While the dynamic rotation of kernels introduces additional computational complexity, this is mitigated by the significant performance gains in oriented object detection. The rotation operation is efficiently implemented using interpolation methods that allow for fast computation, ensuring that the ARC module can be integrated into deep neural networks without incurring a prohibitive computational cost.

3.3. Pseudo-Label Guided Learning

The PGL framework is a critical component of the RASST model that enables effective semi-supervised learning for oriented object detection. The PGL framework leverages both labeled and unlabeled data to improve the model performance, particularly in scenarios where labeled data is scarce. By utilizing a teacher-student architecture, PGL refines pseudo-labels generated from unlabeled data, guiding the student model learning process. The PGL framework employs a teacher-student architecture, where the teacher model generates pseudo-labels for the unlabeled data, and the student model learns from both the labeled data and these pseudo-labels. The teacher model, denoted as $T$, is updated as an Exponential Moving Average (EMA) of the student model, denoted as $\mathrm{S}$. ${\mathcal{D}}_L$ represent the labeled dataset, and ${\mathcal{D}}_u$ represent the unlabeled dataset. The objective is to train the student model $\mathrm{s}$ using the labeled data ${\mathcal{D}}_L$ and the pseudo-labeled data ${\mathcal{D}}_P$generated by the teacher model from ${\mathrm{D}}_{\mathrm{u}}$. The overall loss function used to train the student model is a combination of the supervised loss ${\mathcal{L}}_s$ on the labeled data and the unsupervised loss ${\mathcal{L}}_u$ on the pseudo-labeled data:

$$\mathcal{L}={\mathcal{L}}_s\left({\mathcal{D}}_L\right)+{\lambda }_u{\mathcal{L}}_u\left({\mathcal{D}}_P\right),$$

(15)

where ${\lambda }_u$ is a weighting factor that balances the contributions of the supervised and unsupervised losses.

3.3.1. Pseudo-Label Generation

For each unlabeled sample $x_i\in D_{\mathrm{u}}$, the teacher model generates a pseudo-label ${\widehat{\mathrm{y}}}_i=T\left({\mathrm{x}}_i\right)$, which consists of the predicted oriented bounding box ${\widehat{\mathrm{b}}}_i$ and the predicted class label ${\widehat{\mathrm{c}}}_i$. These pseudo-labels are then used to train the student model. The confidence score associated with each pseudo-label, denoted as ${\widehat{\mathrm{s}}}_i$, is used to filter out low-confidence pseudo-labels. Only pseudo-labels with confidence scores above a certain threshold $\tau$ are retained:

$${\mathcal{D}}_P=\left\{\right({\mathrm{x}}_i,{\widehat{\mathrm{y}}}_i\left)\right\}|{\widehat{\mathrm{s}}}_i>\tau ,$$

(16)

3.3.2. Rotation-Aware Adaptive Weighting (RAW) Loss

Given that the pseudo-labels may contain noise, particularly in terms of the orientation of the predicted bounding boxes, we introduce the RAW Loss. The RAW Loss dynamically adjusts the impact of each pseudo-label based on the orientation difference between the teacher and student models. This ensures that pseudo-labels with more accurate orientations contribute more to the learning process$.{\theta }_T$ and ${\theta }_S$ are the orientations of the bounding box predicted by the teacher and student models, respectively. The orientation difference $∆\theta$ is defined as:

$$∆\theta =|{\theta }_T-{\theta }_S|,$$

(17)

The RAW Loss introduces a modulating factor ${\omega }_{rot}$ based on this orientation difference:

$${\omega }_{rot}\left(∆\theta \right)=(1+\alpha ·{\displaystyle \frac{∆\theta }{\pi }}),$$

(18)

where $\alpha$ is a hyperparameter that controls the sensitivity to orientation differences. The unsupervised loss ${\mathcal{L}}_u$ is then weighted by ${\omega }_{rot}:$

$${\mathcal{L}}_u={\sum }_{i=1}^{N_p}{\omega }_{rot}(∆{\theta }_i)·{\mathcal{L}}_u({\mathrm{x}}_i,{\widehat{\mathrm{y}}}_i),$$

(19)

where $N_p$ is the number of pseudo-labeled samples. This dynamic weighting mechanism allows the student model to focus more on pseudo-labels with accurate orientations, improving the robustness of the learning process.

3.3.3. Global Consistency Loss

In addition to the RAW loss, we introduce the GC loss, which enforces consistency between the global layout of pseudo-labels and the predictions made by the student model. This loss is inspired by optimal transport theory and is designed to ensure that the spatial relationships between detected objects are preserved. ${\mathrm{P}}_T$ and ${\mathrm{P}}_S$ are the sets of positions of the bounding boxes predicted by the teacher and student models, respectively. The GC Loss aims to minimize the optimal transport cost between these two distributions:

$${\mathcal{L}}_{GC}=\underset{\mathrm{P}}{\min }{\sum }_{i,j}\mathrm{C}({\mathrm{P}}_{Ti},{\mathrm{P}}_{Sj})P_{i,j},$$

(20)

where $\mathrm{C}({\mathrm{P}}_{Ti},{\mathrm{P}}_{Sj})$ is the cost of transporting mass from position ${\mathrm{P}}_{Ti}$ in the teacher’s prediction to position ${\mathrm{P}}_{Sj}$ in the student’s prediction, and P is the transport plan that defines how mass is moved between these positions. The transport cost is typically defined as a combination of the spatial distance and the difference in confidence scores:

$$\mathrm{C}({\mathrm{p}}_{T_i},{\mathrm{p}}_{S_j})={\mathsf{\lambda }}_d·||{\mathrm{p}}_{T_i}-{\mathrm{p}}_{S_j}{||}_2^2+{\mathsf{\lambda }}_s·|{\widehat{\mathrm{s}}}_{T_i}-{\widehat{\mathrm{s}}}_{S_j}|,$$

(21)

where ${\mathsf{\lambda }}_d$ and ${\mathsf{\lambda }}_s$ are weighting factors for the spatial and confidence score differences, respectively. The GC Loss is computed using the optimal transport theory, ensuring that the student model learns to replicate the global spatial relationships present in the teacher’s predictions, even when pseudo-labels are noisy.

The overall unsupervised loss ${\mathcal{L}}_u$ in the PGL framework is the sum of the RAW loss and the GC loss:

$${\mathcal{L}}_u={\mathcal{L}}_{RAW}+{\mathcal{L}}_{GC},$$

(22)

By combining these losses, the PGL framework ensures that the student model is trained not only to mimic the teacher’s predictions but also to respect the global structure and orientation accuracy of the objects in the scene. The training process in the PGL framework involves iterating between updating the student model using the combined loss function and updating the teacher model using the EMA of the student model’s weights. This iterative process continues until the model converges, resulting in a robust oriented object detection model that leverages both labeled and unlabeled data effectively.

3.4. Multi-Scale Feature Fusion Model

To effectively detect objects of varying sizes, RASST incorporates a MSFF strategy. This approach combines features from different scales using cross-scale attention, allowing the model to handle small, dense objects as well as larger, sparse ones. In oriented object detection, objects may appear in various sizes and scales within an image. Traditional single-scale approaches may miss small objects or fail to capture the details of large objects. To overcome this, the MSFF module leverages a FPN structure that extracts features at multiple scales and fuses them to create a unified feature representation that is rich in detail across all scales. The MSFF module combines features from different layers of the network, each corresponding to a different scale of the input image. These features are then fused using an attention mechanism that selectively highlights the most informative features from each scale, ensuring that the final detection output is robust to variations in object size.

3.4.1. Feature Pyramid Network

The FPN is the backbone of the MSFF module. It is designed to build a multi-scale feature pyramid from a single input image, enabling the model to detect objects at different scales. $C_{2,} C_{3,} C_{4,} C_5$ represent the feature maps extracted from different stages of a convolutional backbone, where each subsequent feature map is down sampled by a factor of 2. The FPN generates a set of multi-scale feature maps $P_2{,P}_3,P_4{,P}_5$ as follows:

$$\begin{gathered} {\mathrm{P}}_5={\mathrm{C}}_5 \\ {\mathrm{P}}_4={\mathrm{C}}_4+UpSample\left({\mathrm{P}}_5\right) \\ {\mathrm{P}}_3={\mathrm{C}}_3+UpSample\left({\mathrm{P}}_4\right) \\ {\mathrm{P}}_2={\mathrm{C}}_2+UpSample\left({\mathrm{P}}_3\right) \end{gathered}$$

(23)

where $\mathrm{U}\mathrm{p}\mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}(\cdot )$ denotes an upsampling operation that scales up the feature map by a factor of 2. Each $P_i$ represents a feature map at a different scale, with $P_2$ capturing high-resolution details and $P_5$ capturing more global context.

3.4.2. Cross-Scale Attention Mechanism

While the FPN provides a hierarchical representation of the input image, not all scales are equally important for detecting objects of varying sizes. The MSFF module introduces a cross-scale attention mechanism that adaptively weighs the contributions of different scales based on their relevance to the detection task. $F_l$ represent the feature map at level $l$ in the pyramid. The cross-scale attention mechanism computes attention weights ${\alpha }_l$ for each scale:

$${\alpha }_l=softmax\left(w_a^{⊺}GAP\right(F_l\left)\right)+b_a,$$

(24)

where $\mathrm{G}\mathrm{A}\mathrm{P}(\cdot )$ is the global average pooling operation that reduces the feature map $F_l$ to a vector, $w_a^{⊺}$ is a learnable weight vector, $b_a$ is a learnable bias term. The attention weights ${\alpha }_l$ determine the importance of each scale, and the final fused feature map $F_{fused}$ is computed as a weighted sum of the multi-scale feature maps:

$$F_{fused}={\sum }_{l=2}^5{\alpha }_l{F}_l,$$

(25)

This fusion process ensures that the most relevant features from each scale are combined, enhancing the model’s ability to detect objects of varying sizes.

After the feature maps are fused, scale-specific detection heads are applied to the fused feature map to generate the final predictions. Each detection head is responsible for predicting the oriented bounding boxes and class scores for objects at a particular scale. $H_l$ represent the detection head applied to the feature map at level l. The detection head consists of a series of convolutional layers followed by output layers for bounding box regression and classification:

$$\begin{gathered} {\mathrm{B}}_l={Conv}_b\left({\mathrm{F}}_{fused}\right) \\ {\mathrm{C}}_l={Conv}_c\left({\mathrm{F}}_{fused}\right) \end{gathered}$$

(26)

where ${Conv}_b$ and ${Conv}_c$ are convolutional layers for bounding box regression and classification, respectively. ${\mathrm{B}}_l$is the predicted bounding box for scale level $l$, ${\mathrm{C}}_l$ is the predicted class score for scale level $l.$ The final detection output is obtained by aggregating the predictions from all scale levels:

$$\mathrm{B}={\sum }_{l=2}^5{B}_l,\hspace{1em}\mathrm{C}={\sum }_{l=2}^5{C}_l$$

(27)

This aggregation ensures that the model can accurately detect objects at different scales, leveraging the information from all relevant feature maps. The MSFF module is implemented in a way that allows it to be seamlessly integrated into the RASST model. The attention mechanism is lightweight and adds minimal computational overhead, making it suitable for real-time applications. The use of scale-specific detection heads ensures that the model maintains high accuracy across all scales, particularly in challenging aerial imagery scenarios.

4. Experimental Setup and Result

To evaluate the performance of the RASST in oriented object detection, a comprehensive set of experiments was conducted. These experiments were designed to assess the effectiveness of RASST across fully supervised and semi-supervised settings, with comparisons made to SOTA methods. The following subsections detail the datasets, evaluation metrics, implementation details, and comparative analysis.

4.1. Datasets and Evaluation Metrics

The experiments were conducted on the DOTA-v1.5 dataset [24], a benchmark specifically designed for oriented object detection in aerial imagery. DOTA-v1.5 consists of high-resolution aerial images containing objects with diverse orientations, scales, and densities. It includes 15 object categories, such as airplanes, ships, and vehicles, with annotations in the form of oriented bounding boxes. This dataset is well-suited for evaluating both rotational invariance and multi-scale feature fusion capabilities.

The primary evaluation metric used in these experiments is the mAP, calculated for Intersection over Union (IoU) [25] thresholds ranging from 0.5 to 0.95. This metric provides a comprehensive measure of detection accuracy across all object classes and is particularly useful for assessing performance in scenarios with challenging orientations and scales.

4.2. Implementation Details

The RASST model was implemented in PyTorch 2.2 and trained on an NVIDIA RTX 3090 GPU with 24 GB of memory. The training procedure used the stochastic gradient descent (SGD) optimizer [26] with a momentum of 0.9 and a weight decay of 10⁻⁴. The learning rate was initialized at 0.0025 and reduced at predefined intervals during training. Strong and weak data augmentations were employed to increase robustness, with strong augmentations applied to the student model and weak augmentations to the teacher model.

The training process involved 180,000 iterations, with learning rate adjustments at 120,000 and 160,000 iterations. For the semi-supervised setting, labeled data subsets of 10%, 20%, and 30% were created, while the remaining data were treated as unlabeled. Pseudo-labels were generated by the teacher model and refined using the RAW and GC losses. The confidence threshold for pseudo-labeling was set to 0.7, ensuring that only high-confidence predictions were utilized for training, described in

Table 1. Experimental Environment and Parameter Settings.

Component	Details
Hardware Platform	NVIDIA RTX 3090
GPU	CUDA-enabled GPU
Memory	24 GB
Framework	PyTorch
Optimizer	SGD with Momentum (0.9)
Learning Rate	0.0025 (initial)
Batch Size	16
Training Iterations	180,000
Learning Rate Schedule	Decay at 120 k and 160 k iterations
Augmentations	Strong (Student Model), Weak (Teacher Model)

.

4.3. Comparison with Other SOTA Methods

All methods were evaluated on the DOTA-v1.5 datasets, a benchmark commonly used for oriented object detection in aerial imagery Figure 2. The dataset includes objects with varying scales and orientations, making it ideal for testing the robustness of different models. The evaluation metric used was the mAP, which measures the accuracy of object detection across different classes. Both fully supervised and semi-supervised scenarios were considered in the comparisons. The results of the comparison are summarized in

Table 2. Comparison of RASST framework with other SOTA methods on the DOTA-v1.5 dataset.

Method	Fully Supervised mAP	Semi-Supervised mAP (20% Labeled Data)	Semi-Supervised mAP (30% Labeled Data)
POE [22]	65.12	56.78	59.34
E-PVT [21]	66.40	55.58	59.23
OrientedR-CNN [18]	67.10	57.20	60.15
SOOD [19]	66.50	56.90	59.80
PSCD [20]	66.38	53.93	57.86
RoI-Trans.-ACM [17]	67.02	57.85	59.99
RASST (Ours)	67.70	59.23	62.10

, where RASST is compared against the aforementioned methods under both fully supervised and semi-supervised settings.

In Table 2 as presented RASST achieves the highest mAP of 67.70 in the fully supervised setting, outperforming all other methods. The integration of rotationally aware mechanisms and multi-scale feature fusion contributes significantly to this superior performance, as these components allow RASST to handle a wider variety of object orientations and sizes. In semi-supervised settings, where only 20% and 30% of the labeled data are used, RASST again outperforms the other methods, achieving mAPs of 59.23 and 62.10, respectively. This demonstrates RASST ability to effectively leverage unlabeled data through the PGL framework, which includes innovative loss functions such as the RAW Loss and GC Loss. While SOOD also uses a semi-supervised framework, RASST provides better results due to its advanced handling of rotational invariance and multi-scale features. Specifically, the ARC module and the MSFF module in RASST contribute to its enhanced performance. Although the Adaptive Rotated Convolution method shows strong performance due to its focus on rotational adjustments, RASST surpasses it by effectively combining these adjustments with a robust transformer-based architecture and semi-supervised learning strategies. RASST maintains its superior performance across different proportions of labeled data, indicating its scalability and robustness. The ability to maintain high accuracy even when the amount of labeled data is reduced is particularly beneficial for applications where labeled data is limited or expensive to obtain. In addition to quantitative comparisons, qualitative results were examined. RASST demonstrated superior ability in detecting small and densely packed objects that were challenging for other methods. The rotationally aware components of RASST provided better alignment with the ground truth orientations, reducing the number of false positives and improving overall detection quality. While RASST introduces additional computational complexity due to its dynamic convolutional operations and attention mechanisms, the performance gains justify the added complexity. Furthermore, the architecture is optimized to ensure that the increase in computational demand does not hinder its applicability to real-time or large-scale tasks. The comparisons clearly indicate that RASST sets a new SOTA in oriented object detection, particularly in semi-supervised settings. The integration of advanced components such as POE [22], E-PVT [21], OrientedR-CNN [18], SOOD [19], PSCD [20], RoI-Trans.-ACM [17] framework allows RASST to excel in scenarios with challenging orientations and scales, making it a versatile and powerful tool for oriented object detection.

To further corroborate the effectiveness of each component in the RASST framework, additional ablation studies were performed using the DOTA-v1.5 dataset. In these experiments, critical parts of the RASST framework were ablated in turn or selectively disabled to determine whether and how much each contributed to overall performance metrics. Specifically, an analysis was performed regarding Rotationally Aware Patch Embedding (RPE), the Adaptive Rotational Convolution (ARC) module, the Pseudo-Label Guided Learning (PGL) framework, and the Multi-Scale Feature Fusion (MSFF) module. The Mean Average Precision (mAP) values from each ablation configuration are summarized in

Table 3. Ablation study of the RASST framework on the DOTA-v1.5 dataset.

Model Variant	Fully Supervised mAP (%)	Semi-Supervised mAP (20% Labeled) (%)
Full RASST Model	67.70	59.23
w/o Rotationally Aware Patch Embedding	65.85	57.10
w/o Adaptive Rotational Convolution	66.02	57.45
w/o Pseudo-Label Guided Learning	65.40	53.82
w/o Multi-Scale Feature Fusion	66.10	56.92

. We see that by using 20% of labeled data, the complete RASST model has a fully supervised mAP of 67.70% and a semi-supervised mAP of 59.23%. Removing the RPE module decreases the fully supervised mAP to 65.85%, while also lowering the semi-supervised mAP to 57.10%, reflecting the importance of rotational robustness provided by the RPE module. Removing the ARC module has a similar negative effect, where the fully supervised mAP reduces to 66.02%. In comparison, the semi-supervised mAP lowers to 57.45%, thus reinforcing the necessity of dynamic orientation adaptation during feature extraction. Disabling the PGL framework yields a higher penalty, resulting in a 65.40% fully supervised mean Average Precision (mAP) score and a 53.82% semi-supervised mAP score. It reflects how critical pseudo-label refinement mechanisms, e.g., Rotation-Aware Adaptive Weighting (RAW) and Global Consistency (GC) losses, are to effective adaptation when using unlabeled data. Additionally, removing the MSFF module lowers the model ability to handle scale variations, further resulting in mAP scores of 66.10% in a fully supervised setting and 56.92% in a semi-supervised setting.

The results in Table 3 suggest that each component of the RASST approach contributes significantly to how effective it is, and the synergistic relation among these factors results in better recognition of focused objects regardless of changing scales and observation levels.

5. Discussion

The experimental results demonstrate the effectiveness of the RASST in improving oriented object detection in aerial imagery. Its SOTA performance in fully supervised and semi-supervised settings underscores its robustness and scalability. By incorporating rotationally aware patch embeddings and adaptive rotational convolutions, RASST addresses the critical challenge of detecting objects at arbitrary orientations, making it especially valuable for applications such as disaster response and urban planning, where precise orientation is essential.

RASST success in semi-supervised settings highlights the impact of its PGL framework. Through the refinement of pseudo-labels using RAW and GC losses, the model effectively utilizes unlabeled data, extending its applicability to scenarios where labeled data is scarce or costly to obtain. The MSFF module enhances RASST versatility by improving detection of objects at varying scales. The adaptive cross-scale attention mechanism ensures accurate detection of both small, densely packed objects and larger, more sparse ones, making the model adaptable to diverse datasets and use cases. Despite its strengths, RASST has limitations. The rotational and semi-supervised mechanisms introduce computational overhead, which may hinder performance in resource-constrained environments or on ultra-large datasets. Additionally, reliance on a fixed confidence threshold for pseudo-labeling could exclude useful low-confidence data. Optimizing these aspects could further enhance the model’s scalability and efficiency. The DOTA-v1.5 dataset used for evaluation, while comprehensive, does not cover extreme conditions such as severe occlusions, adverse weather, or highly dynamic scenes. Testing on additional datasets with such conditions could validate the model robustness further. Similarly, extending evaluations to domain-specific datasets, like those for maritime environments or autonomous navigation, could broaden RASST applicability. The promising results achieved by RASST open avenues for future research. Exploring more efficient architectures or optimization techniques could reduce computational costs, enhancing its deployment on edge devices. Incorporating uncertainty modeling into the pseudo-labeling framework could improve the handling of noisy or low-confidence labels, further strengthening its performance in semi-supervised scenarios. Integrating RASST with active learning or few-shot learning approaches could enable effective operation with even smaller labeled datasets, addressing annotation challenges more sustainably. In future work, we plan to explore model optimization techniques such as structured pruning and post-training quantization to mitigate the computational overhead of the dynamic elements of RASST. Model pruning allows for the removal of redundant parameters and layers, while quantization reduces numerical precision during computation, thus leading to substantial savings in both memory footprint and computational requirements. By incorporating these efficient optimization techniques, our goal is to maintain RASST’s high detection accuracy while also enhancing its run-time efficiency, making it a competitive candidate for deployment in edge computing and resource-limited settings. Such advances would make the framework more suitable for real-world applications in environments where data acquisition is limited or computational resources are inadequate.

RASST advances oriented object detection by integrating robust rotationally aware mechanisms, effective semi-supervised learning strategies, and scalable multi-scale feature fusion. While there is room for improvement, this framework provides a strong foundation for future exploration, offering a pathway to more efficient, accurate, and generalizable solutions for aerial imagery tasks. These contributions hold significant potential to inspire the next generation of object detection models in both research and practical applications.

6. Conclusions

This paper presented the RASST, a novel framework for oriented object detection in aerial imagery. By incorporating rotationally aware patch embeddings, adaptive rotational convolutions, and a MSFF module, RASST effectively detects objects at arbitrary orientations and varying scales. Its PGL framework, leveraging RAW and GC losses, enhances the utilization of unlabeled data, achieving superior performance in semi-supervised settings. Evaluations on the DOTA-v1.5 benchmark demonstrated that RASST outperforms SOTA methods in both fully supervised and semi-supervised scenarios, achieving higher mAP scores and showing robustness in complex and densely packed scenes. Despite its strengths, RASST faces challenges related to computational overhead and reliance on fixed confidence thresholds for pseudo-labeling. Testing on more diverse datasets, including those with extreme conditions, would further validate its generalizability. Future research could refine RASST efficiency, incorporate uncertainty modeling for pseudo-labeling, and explore applications in other domains such as maritime surveillance or medical imaging.

In conclusion, RASST offers significant advancements in oriented object detection, combining robust rotational invariance, effective semi-supervised learning, and adaptable multi-scale feature fusion. It provides a strong foundation for future research and practical applications, inspiring the development of more efficient and scalable solutions in aerial imagery and beyond.