Experimental Investigation of Motion Control of a Closed-Kinematic Chain Robot Manipulator Using Synchronization Sliding Mode Method with Time Delay Estimation
Abstract
1. Introduction
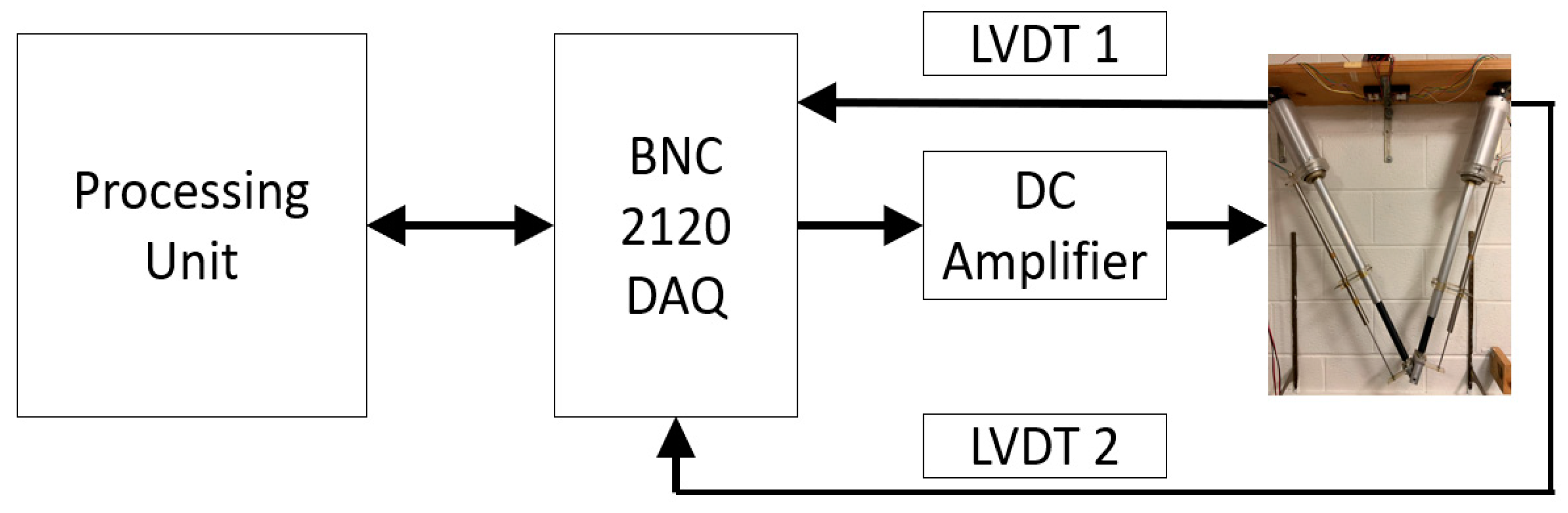
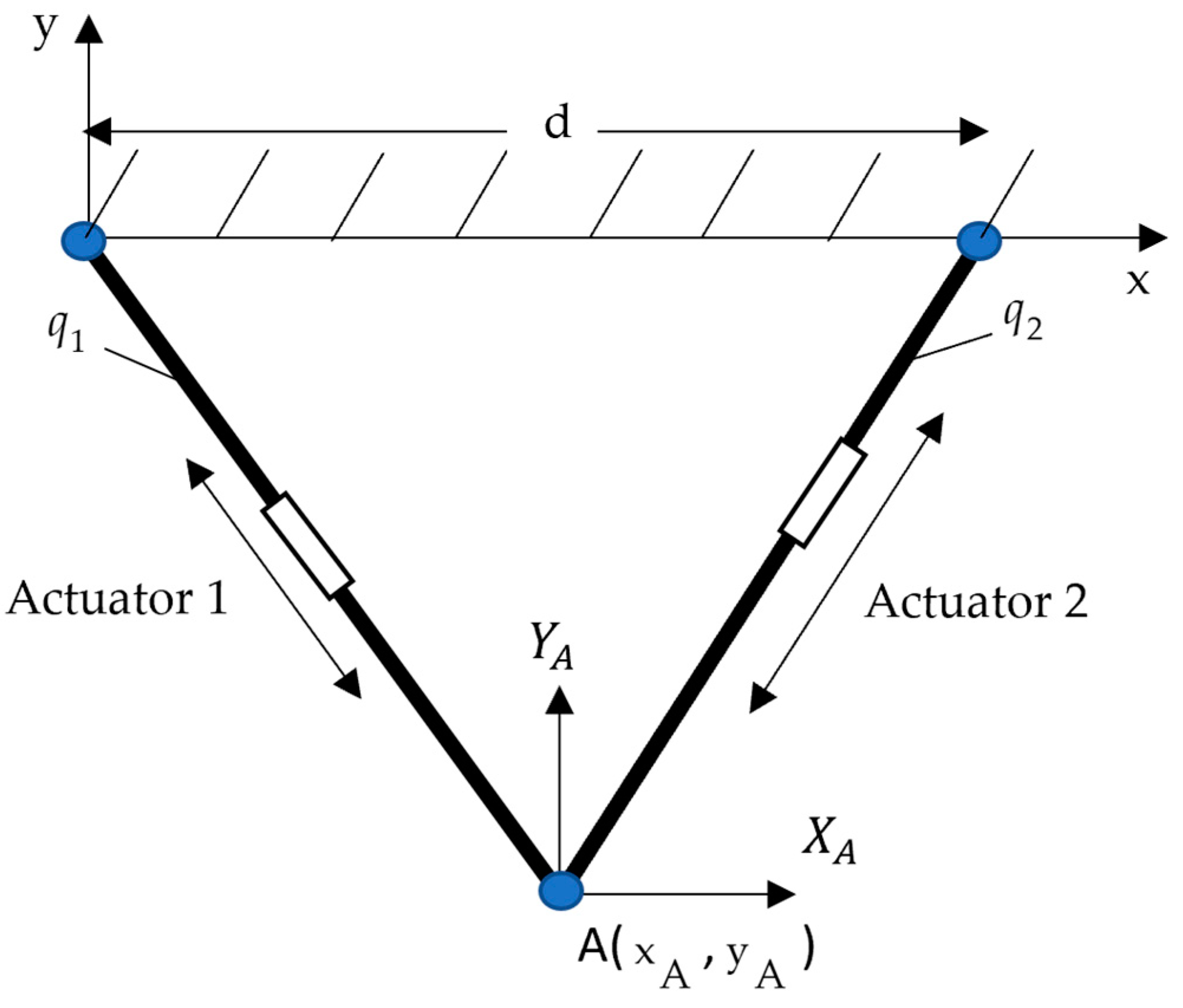
2. The Real 2-DOF CKCM
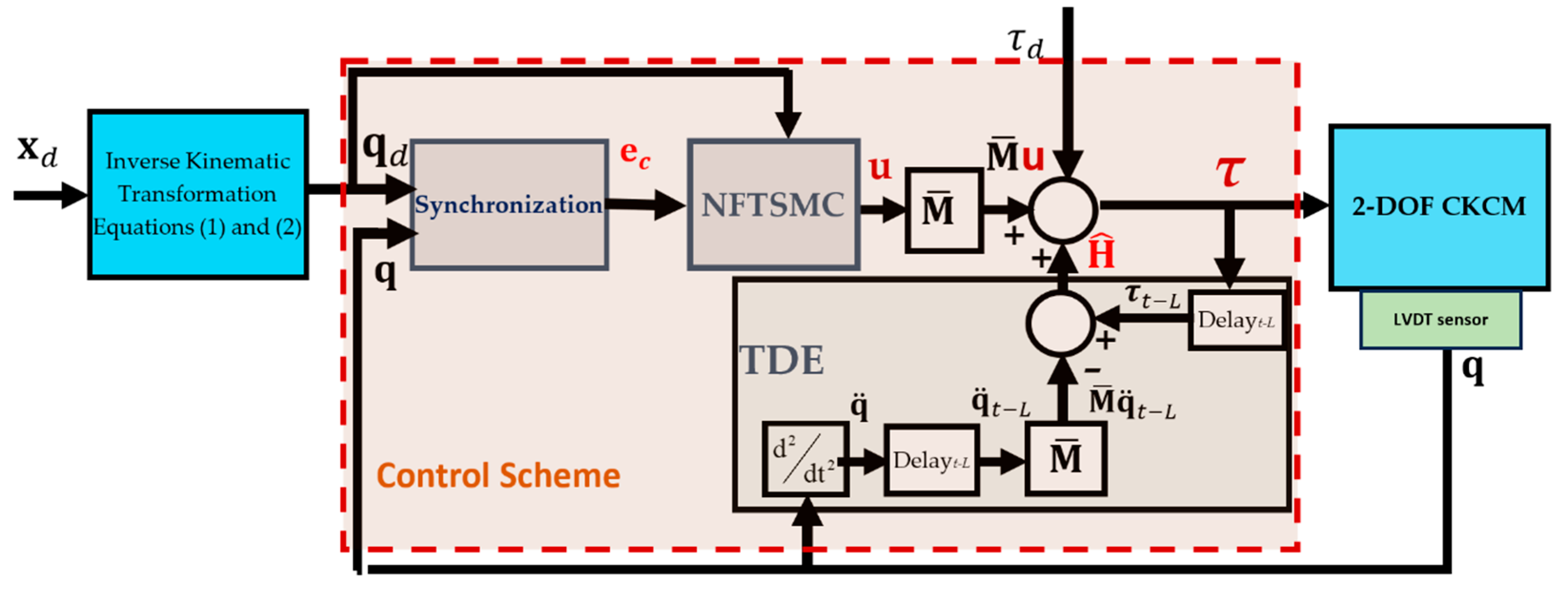
3. The Control Scheme
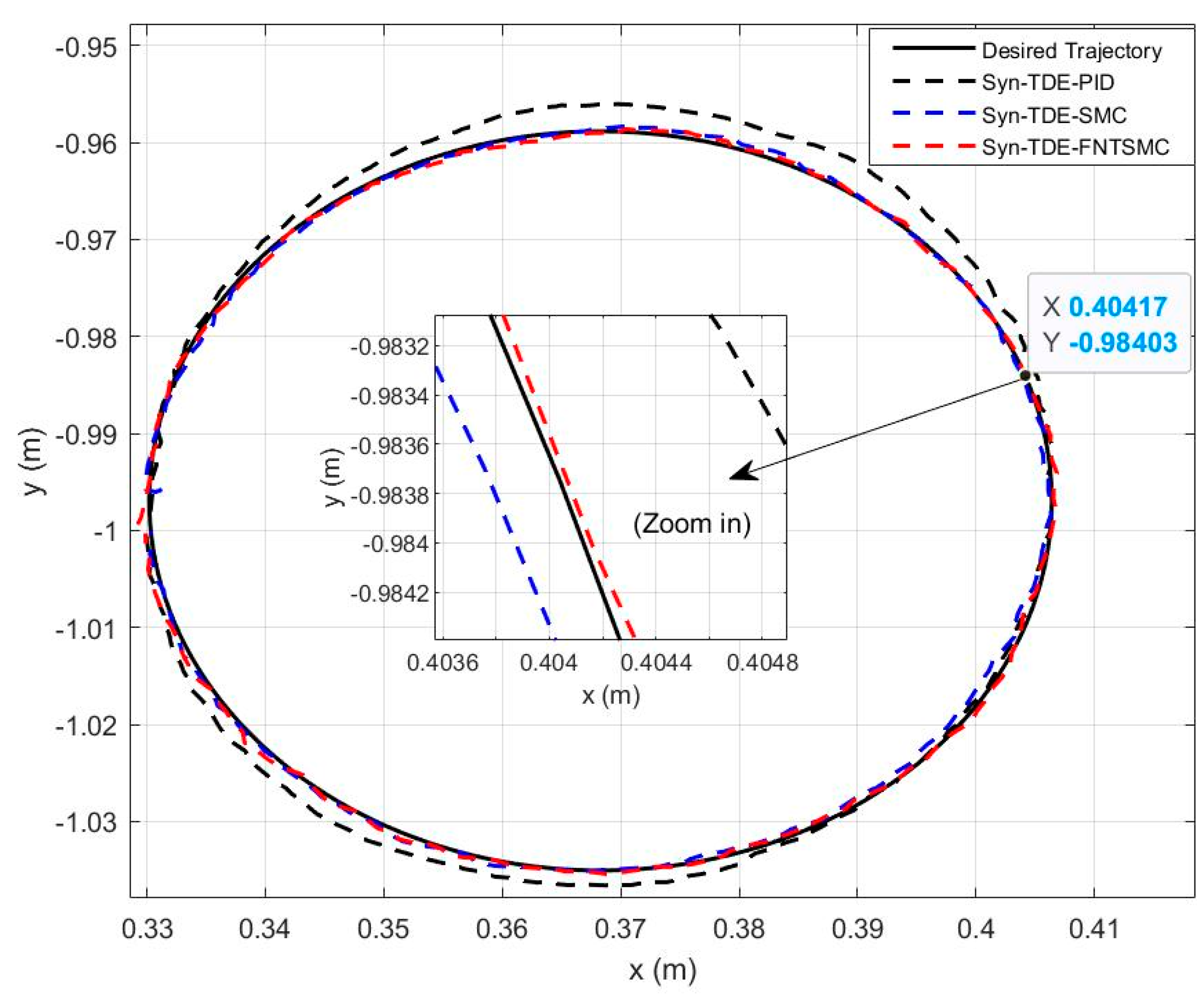
4. Experimental Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Existing Control Schemes Used in Experimental Study
- TDE-based PID with synchronization errors (Syn-TDE-PID)
- , , and are PID gain diagonal design matrices.
- TDE-based SMC with synchronization errors (Syn-TDE-SMC) [13]
- The nonsingular terminal sliding surface is defined as follows:
- , , and are diagonal design matrices.
References
- Patel, Y.D.; George, P.M. Parallel Manipulators Applications—A Survey. Mod. Mech. Eng. 2012, 02, 57–64. [Google Scholar] [CrossRef]
- Nguyen, C.; Pooran, F. Kinematic Analysis and Workspace Determination of a 6 dof CKCM Robot End-Effector. J. Mech. Work. Technol. 1989, 20, 283. [Google Scholar] [CrossRef]
- Nguyen, C.C.; Pooran, F.J. Dynamic analysis of a 6 DOF CKCM robot end-effector for dual-arm telerobot systems. Robot. Auton. Syst. 1989, 5, 377. [Google Scholar] [CrossRef]
- Nguyen, C.C.; Antrazi, S.S.; Zhou, Z.; Campbell, C.E. Adaptive control of a stewart platform-based manipulator. J. Robot. Syst. 1993, 10, 657. [Google Scholar] [CrossRef]
- Rodriguez-Angeles, A.; Nijmeijer, H. Mutual Synchronization of Robots via Estimated State Feedback: A Cooperative Approach. IEEE Trans. Control Syst. Technol. A Publ. IEEE Control Syst. Soc. 2004, 12, 542–554. [Google Scholar] [CrossRef]
- Sun, D.; Mills, J.K. Adaptive synchronized control for coordination of multirobot assembly tasks. IEEE Trans. Robot. Autom. A Publ. IEEE Robot. Autom. Soc. 2002, 18, 498–509. [Google Scholar]
- Doan, Q.V.; Le, T.D.; Vo, A.T. Synchronization Full-Order Terminal Sliding Mode Control for an Uncertain 3-DOF Planar Parallel Robotic Manipulator. Appl. Sci. 2019, 9, 1756. [Google Scholar] [CrossRef]
- Koren, Y. Cross-coupled biaxial computer control for manufacturing systems. J. Dyn. Syst. Meas. Control 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Su, Y.; Sun, D.; Ren, L.; Mills, J. Integration of saturated PI synchronous control and PD feedback for control of parallel manipulators. IEEE Trans. Robot. A Publ. IEEE Robot. Autom. Soc. 2006, 22, 202. [Google Scholar]
- Zhao, D.; Li, S.; Gao, F. Fully adaptive feedforward feedback synchronized tracking control for Stewart Platform systems. Int. J. Control Autom. Syst. 2008, 6, 689–701. [Google Scholar]
- Su, Y.X.; Sun, D.; Ren, L.; Wang, X.; Mills, J.K. Nonlinear PD Synchronized Control for Parallel Manipulators. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Duong, T.T.C.; Nguyen, C.C.; Thien, T.D. An Advanced PD Controller for Robot Manipulators with Time-Delay Estimation. In Proceedings of the 2022 World Automation Congress (WAC), San Antonio, TX, USA, 11–15 October 2022. [Google Scholar]
- Duong, T.T.C.; Thien, T.D.; Tri, N.T.; Nghi, D.V. Synchronization Sliding Mode Control with Time-Delay Estimation for a 2-DOF Closed-Kinematic Chain Robot Manipulator. In Proceedings of the 2021 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 26–28 August 2021. [Google Scholar]
- Tran, D.T.; Dao, H.V.; Ahn, K.K. Adaptive synchronization sliding mode control for an uncertain dual-arm robot with unknown control direction. Appl. Sci. 2023, 13, 7423. [Google Scholar] [CrossRef]
- Duong, T.T.C.; Nguyen, C.C.; Tran, T.D. Synchronization Sliding Mode Control of Closed-Kinematic Chain Robot Manipulators with Time-Delay Estimation. Appl. Sci. 2022, 12, 5527. [Google Scholar] [CrossRef]
- Dinh, T.X.; Thien, T.D.; Anh, T.H.V.; Ahn, K.K. Disturbance Observer Based Finite Time Trajectory Tracking Control for a 3 DOF Hydraulic Manipulator Including Actuator Dynamics. IEEE Access 2018, 6, 36798–36809. [Google Scholar] [CrossRef]
- Nuño, E.; Basañez, L.; Ortega, R. Adaptive control for the synchronization of multiple robot manipulators with coupling time-delays. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Zhao, D.; Li, S.; Gao, F. A new terminal sliding mode control for robotic manipulators. Int. J. Control 2009, 82, 1804. [Google Scholar] [CrossRef]
- Zhihong, M.; Paplinski, A.; Wu, H. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control 1994, 39, 2464. [Google Scholar] [CrossRef]
- Tang, Y. Terminal sliding mode control for rigid robots. Automatica 1998, 34, 51. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, J.; Lu, K.; Zhou, N. Finite Time and Cooperative Control of Flight Vehicles, 1st ed.; Advances in Industrial Control; Springer: Singapore, 2019; p. 400. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhäuser: Basel, Switzerland, 2014. [Google Scholar]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 2011, 21, 1865. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite Time Fault Tolerant Control for Robot Manipulators Using Time Delay Estimation and Continuous Nonsingular Fast Terminal Sliding Mode Control. IEEE Trans. Cybern. 2017, 47, 1681. [Google Scholar] [CrossRef]
- Zhao, D.; Li, S.; Gao, F. Finite time position synchronised control for parallel manipulators using fast terminal sliding mode. Int. J. Syst. Sci. 2009, 40, 829. [Google Scholar] [CrossRef]
- Hsia, T.; Lasky, T.; Guo, Z. Robust independent joint controller design for industrial robot manipulators. IEEE Trans. Ind. Electron. A Publ. IEEE Ind. Electron. Soc. 1991, 38, 21. [Google Scholar] [CrossRef]
- Baek, J.; Cho, S.; Han, S. Practical Time-Delay Control with Adaptive Gains for Trajectory Tracking of Robot Manipulators. IEEE Trans. Ind. Electron. A Publ. IEEE Ind. Electron. Soc. 2018, 65, 5682. [Google Scholar] [CrossRef]
- Bae, H.-J.; Jin, M.; Suh, J.; Lee, J.Y.; Chang, P.-H.; Ahn, D.-S. Control of Robot Manipulators Using Time-Delay Estimation and Fuzzy Logic Systems. J. Electr. Eng. Technol. 2017, 12, 1271. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Chang, P.H.; Choi, C. Practical Nonsingular Terminal Sliding-Mode Control of Robot Manipulators for High-Accuracy Tracking Control. IEEE Trans. Ind. Electron. A Publ. IEEE Ind. Electron. Soc. 2009, 56, 3593. [Google Scholar]
- Martinez, D.R.; Bond, R.A.; Vai, M.M. High Performance Embedded Computing Handbook: A Systems Perspective; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jabbari, P.F. Dynamics and Control of Robot Manipulators with Closed-Kinematic Chain Mechanism. Ph.D. Thesis, Catholic University of America, Washington, DC, USA, 1990. [Google Scholar]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159. [Google Scholar] [CrossRef]

| Manipulator Parameters | Description | Value | Unit |
|---|---|---|---|
| Link’s total mass | 4.91 | kg | |
| Link’s moving part mass | 0.59 | kg | |
| Ground’s horizontal distance | 0.74 | m | |
| Link’s fixed length | 0.26 | m | |
| g | Gravitational acceleration constant | 9.81 | m/s2 |
| Link’s minimum length | 0.84 | m | |
| Link’s maximum length | 1.22 | m | |
| Actuator Specifications | Description | Value | Unit |
| Motor | Permanent magnet | ||
| Voltage | 24 VDC | VDC | |
| Speed | 3000 RPM | RPM | |
| Diameter | 0.076 | m | |
| Stroke | 0.406 | m | |
| Gear reduction | 10:1 | ||
| Max velocity | 1.78 | cm/second |
| LVDT | Description | Value | Unit |
|---|---|---|---|
| Linear range | ±7.5 | inch | |
| Linearity | Best fit straight line | ||
| Resolution | Infinite (theoretically) | ||
| Input | ±14.5 to ±28 VDC, ±100 mA | ||
| Output | ±5 | VDC | |
| Operating temperature range | −67 to 257 | F |
| Parameter | Description | Formula |
|---|---|---|
| Joint force vector | ||
| Past joint force vector | ||
| , | diagonal design matrices | |
| Positive odd integers | ||
| Control law vector | ||
| Nonsingular terminal sliding surface vector | ||
| Sign function of sliding surface vector | ||
| Past acceleration vector | ||
| Desired acceleration joint vector | ||
| Positive odd integers | ||
| Diagonal positive definite matrix | ||
| Identity matrix | ||
| Synchronization transformation matrix | ||
| Tracking error vector | ||
| Synchronization error vector | ||
| Cross-coupling error vector |
| Control Schemes | Control Parameters |
|---|---|
| Syn-TDE-PID | s, = diag(0.5, 0.5) |
| Syn-TDE-SMC | s, = diag(0.5, 0.5) |
| Syn-TDE-NFTSMC | = diag(0.5, 0.5) |
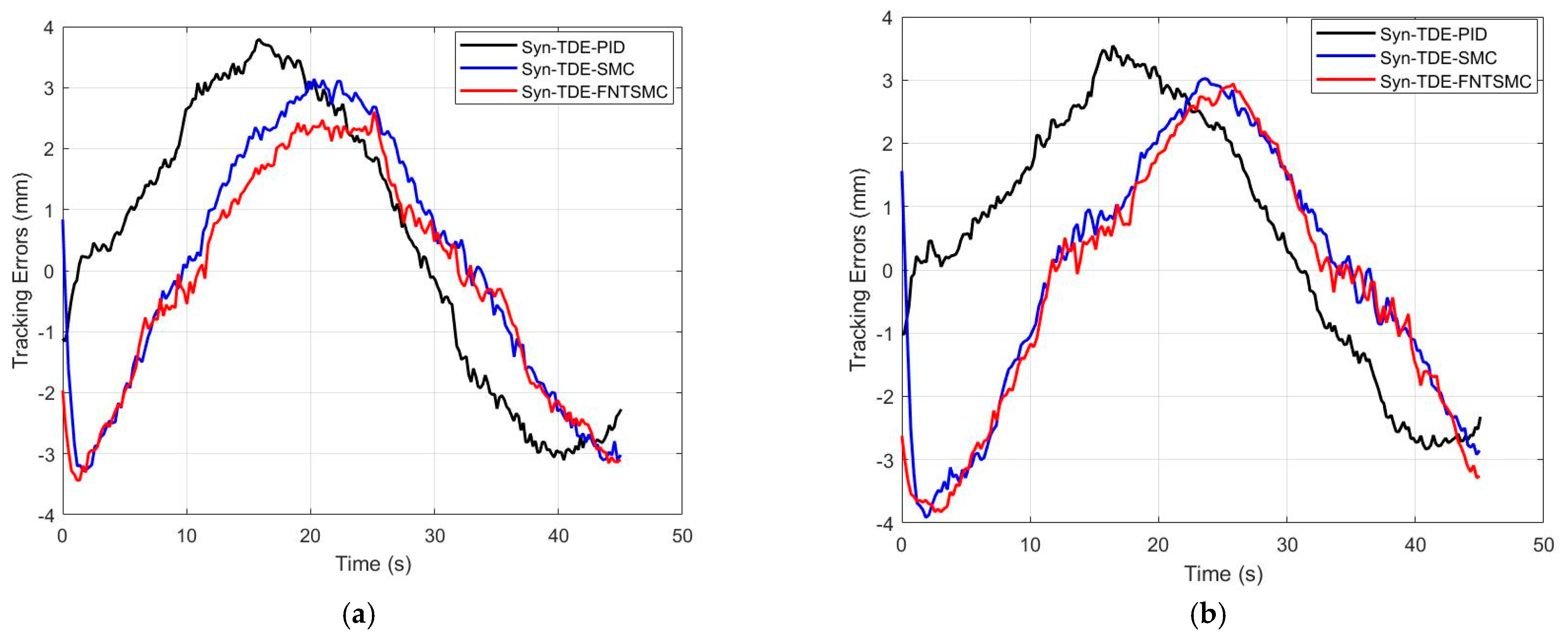
| Tracking Errors | Syn-TDE-PID | Syn-TDE-SMC | Syn-TDE-NFTSMC |
|---|---|---|---|
| (mm) | 0.7 | 0.2 | 0.127 |
| (mm) | 0.8 | 0.18 | 0.13 |
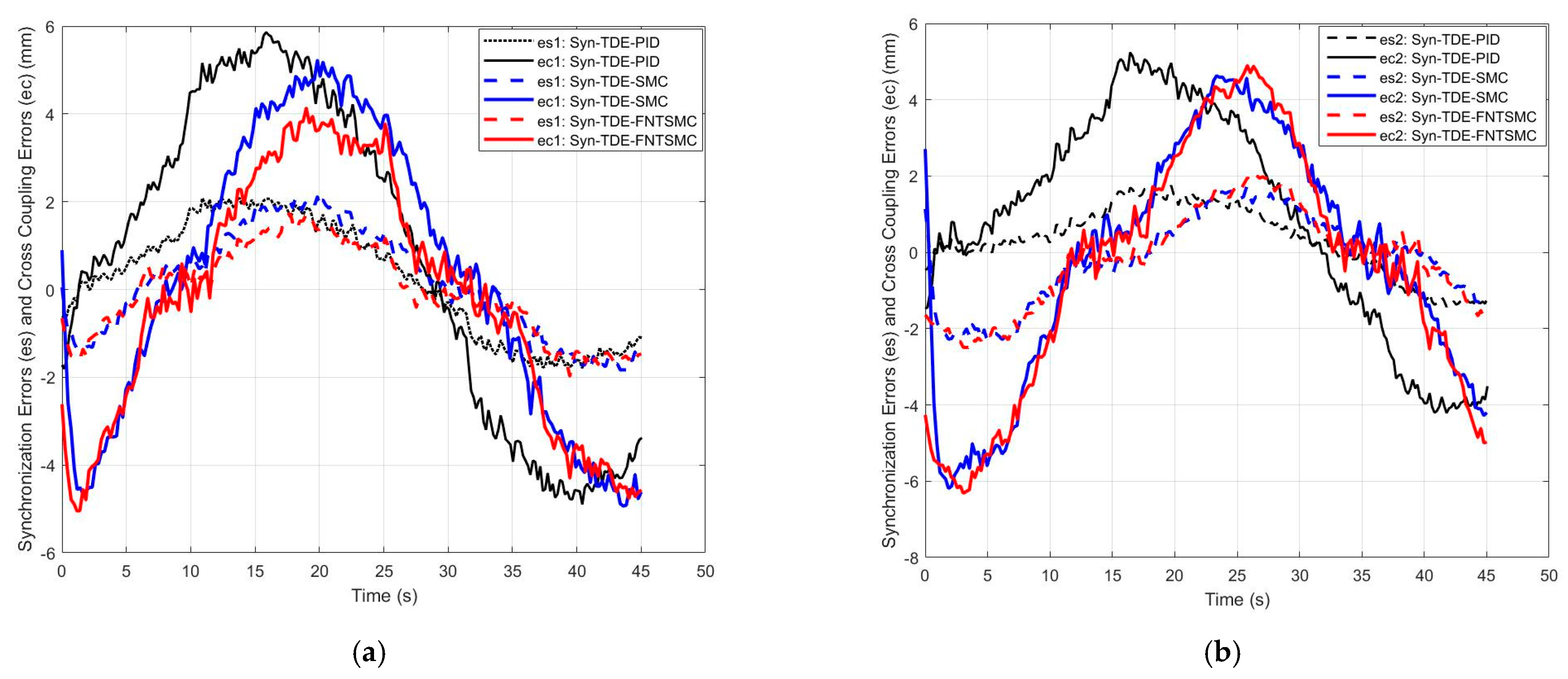
| Errors | Syn-TDE-PID | Syn-TDE-SMC | Syn-TDE-NFTSMC |
|---|---|---|---|
| (mm) | 0.24 | 0.134 | 0.06 |
| (mm) | 0.32 | 0.19 | 0.15 |
| (mm) | 0.77 | 0.21 | 0.2 |
| (mm) | 0.91 | 0.49 | 0.27 |
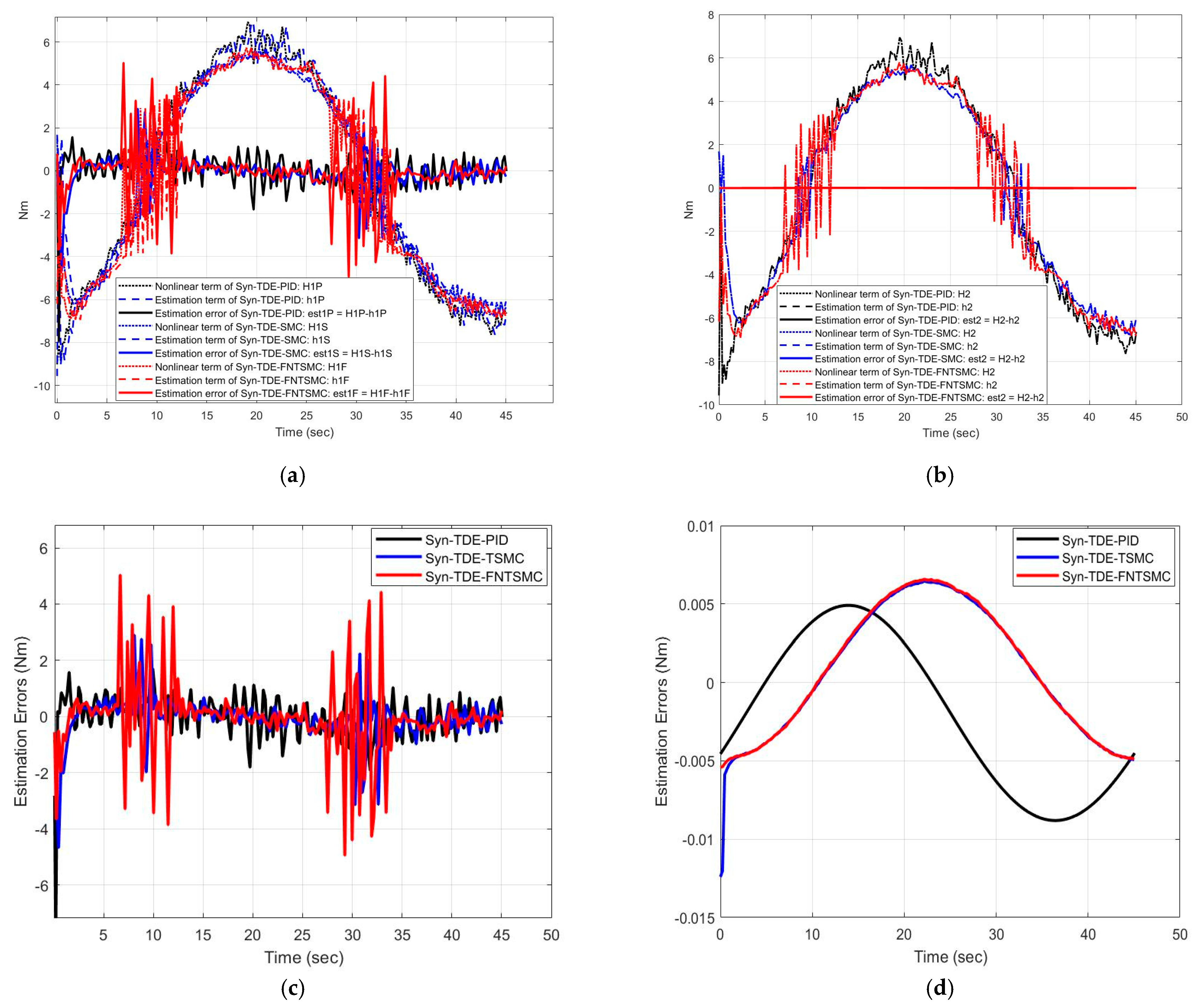
| AAEE | Syn-TDE-PID | Syn-TDE-SMC | Syn-TDE-NFTSMC |
|---|---|---|---|
| (Nm) | 0.03 | 0.01 | 0.017 |
| (Nm) | 0.002 | 0.0006 | 0.0006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duong, T.T.C.; Nguyen, C.C.; Tran, T.D. Experimental Investigation of Motion Control of a Closed-Kinematic Chain Robot Manipulator Using Synchronization Sliding Mode Method with Time Delay Estimation. Appl. Sci. 2025, 15, 5206. https://doi.org/10.3390/app15095206
Duong TTC, Nguyen CC, Tran TD. Experimental Investigation of Motion Control of a Closed-Kinematic Chain Robot Manipulator Using Synchronization Sliding Mode Method with Time Delay Estimation. Applied Sciences. 2025; 15(9):5206. https://doi.org/10.3390/app15095206
Chicago/Turabian StyleDuong, Tu T. C., Charles C. Nguyen, and Thien Duc Tran. 2025. "Experimental Investigation of Motion Control of a Closed-Kinematic Chain Robot Manipulator Using Synchronization Sliding Mode Method with Time Delay Estimation" Applied Sciences 15, no. 9: 5206. https://doi.org/10.3390/app15095206
APA StyleDuong, T. T. C., Nguyen, C. C., & Tran, T. D. (2025). Experimental Investigation of Motion Control of a Closed-Kinematic Chain Robot Manipulator Using Synchronization Sliding Mode Method with Time Delay Estimation. Applied Sciences, 15(9), 5206. https://doi.org/10.3390/app15095206








