An Improved Multi-Objective Grey Wolf Optimizer for Aerodynamic Optimization of Axial Cooling Fans
Abstract
1. Introduction
2. Improved Multi-Objective Grey Wolf Optimizer
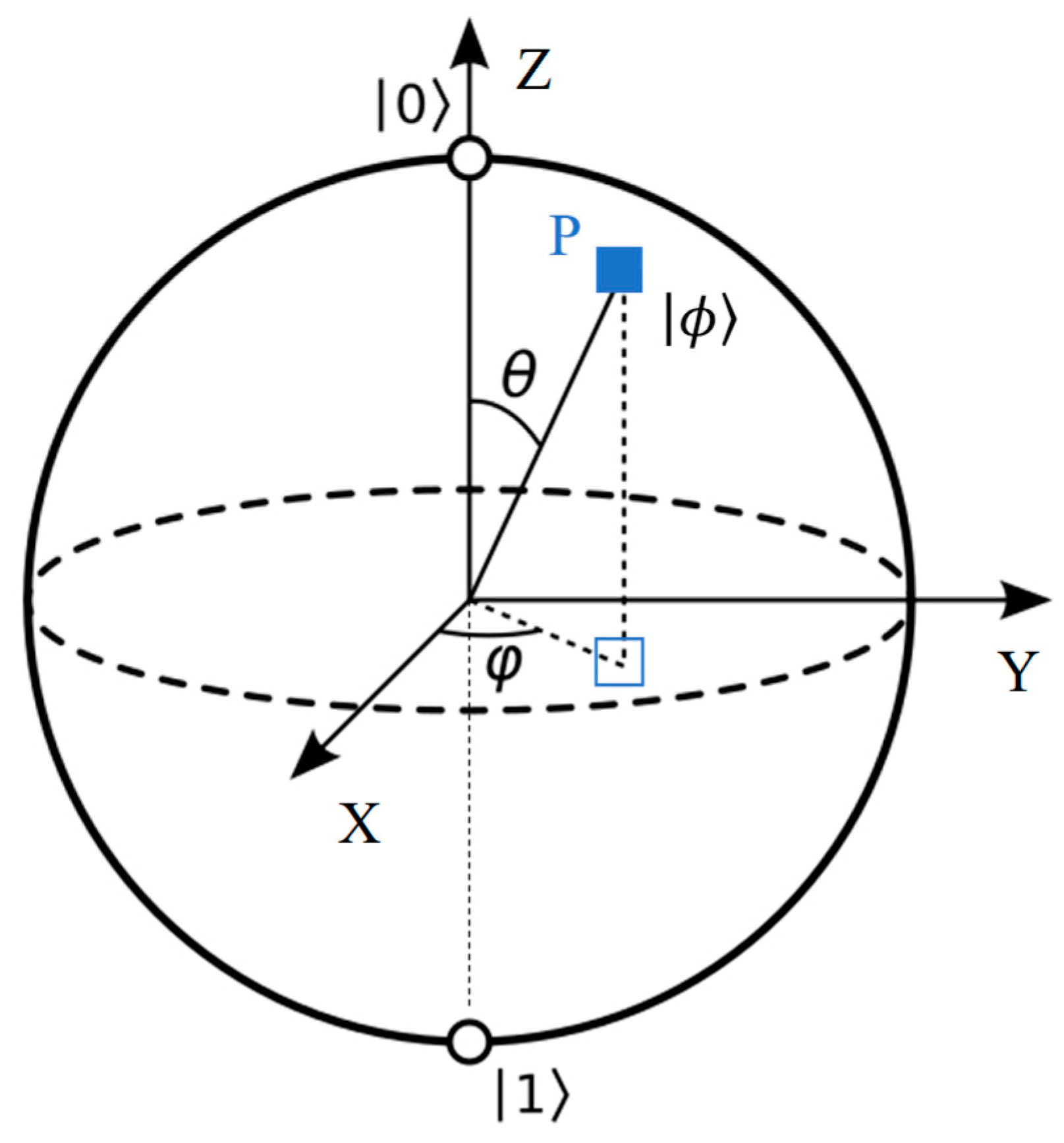
2.1. Population Initialization Based on Bloch Coordinates of Qubits
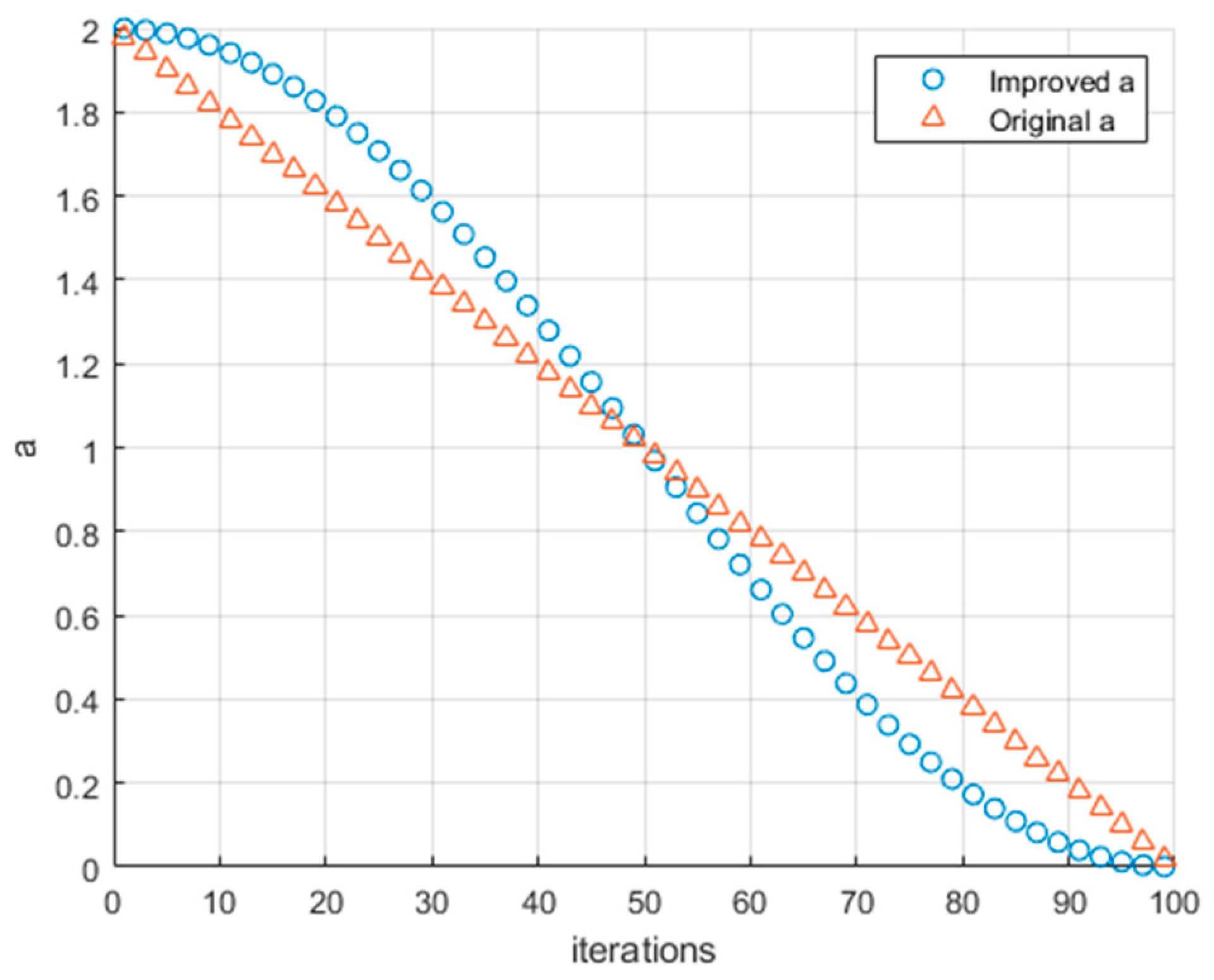
2.2. Nonlinear Convergence Factor
2.3. Grey Wolf Hunting with Manta Ray Foraging
2.4. Associative Learning for Archive Update
3. Results and Discussion
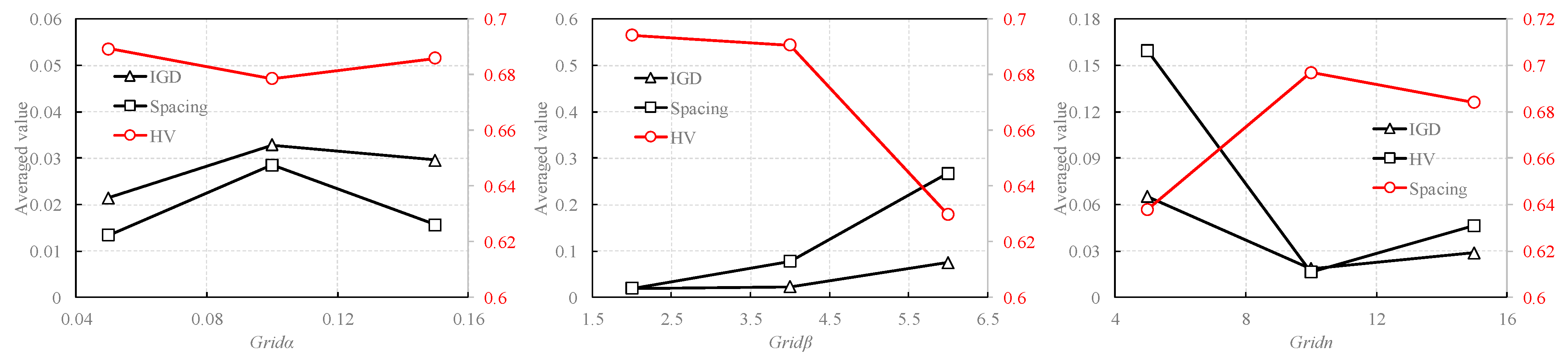
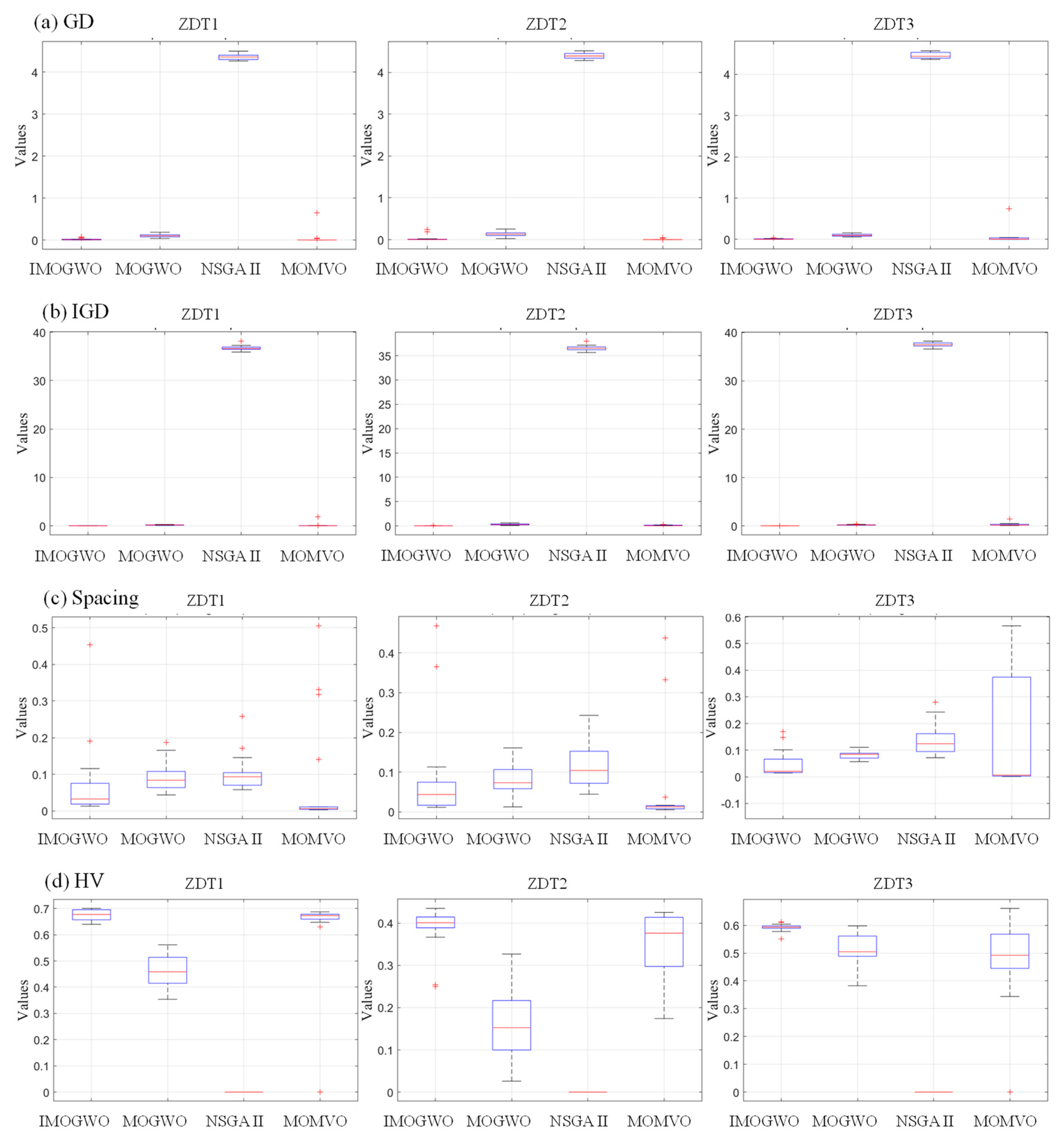
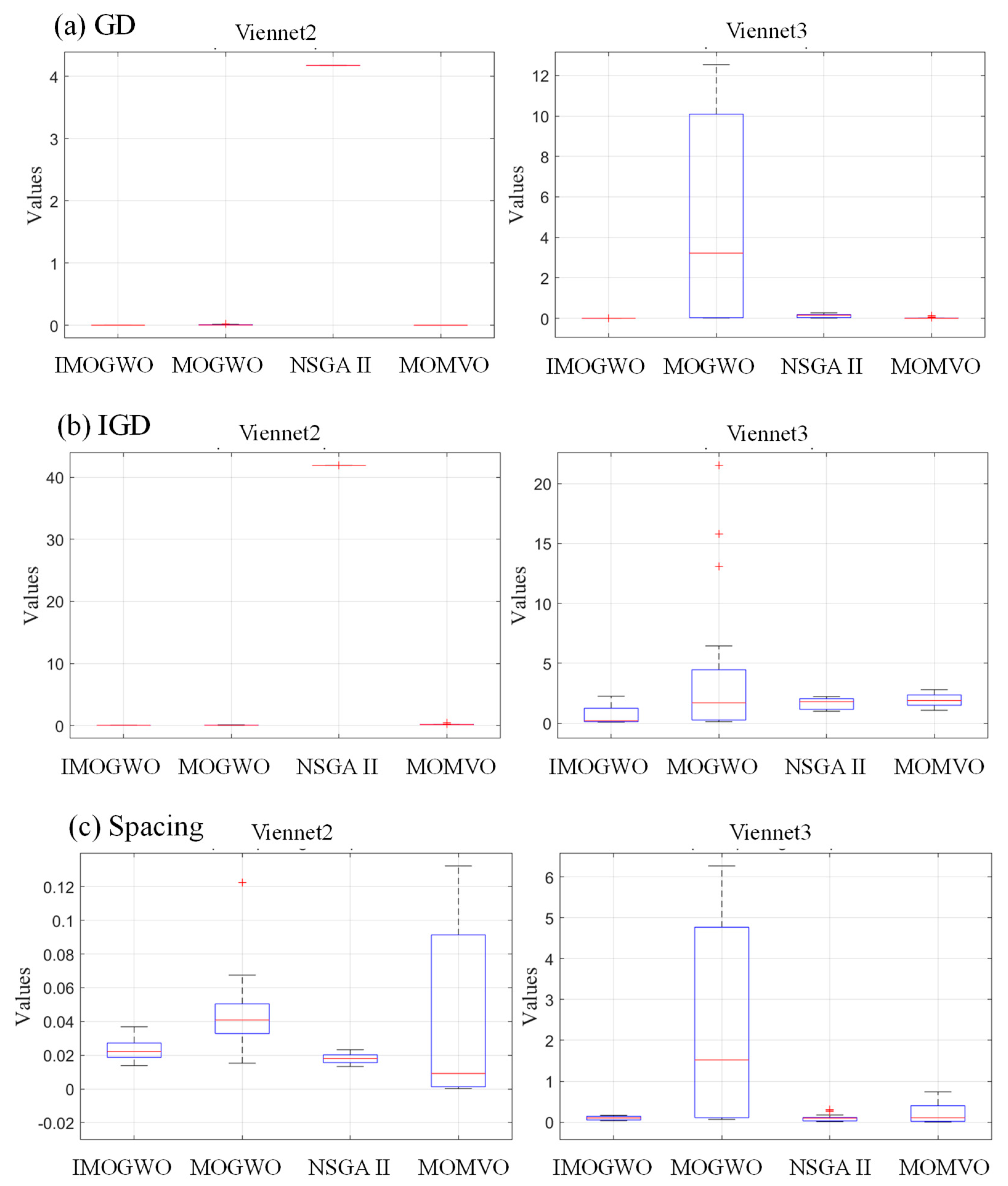
3.1. Evaluation of Benchmark Functions
3.1.1. Experimental Setup
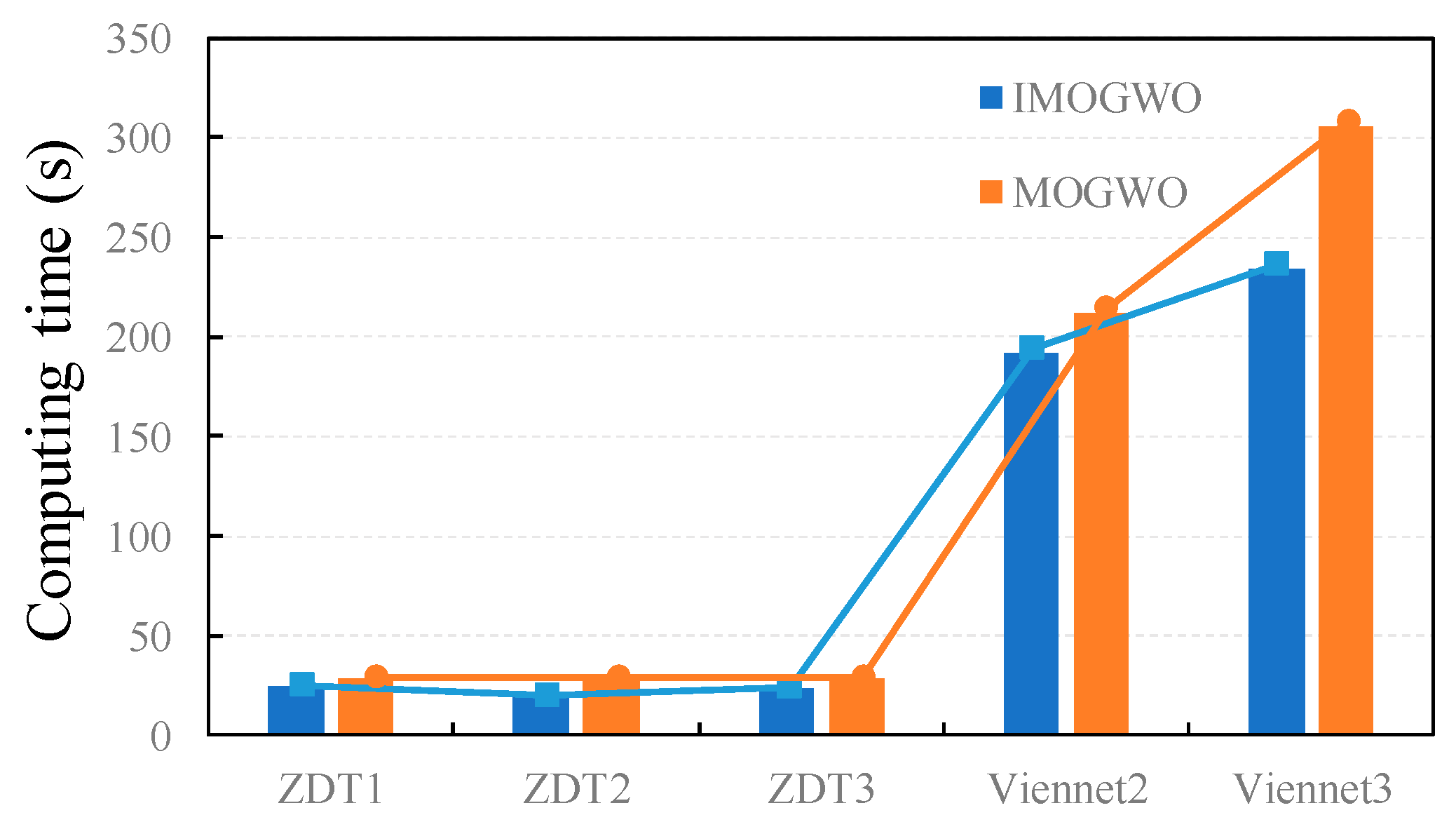
3.1.2. Discussion of the Results
3.2. Aerodynamic Optimization with IMOGWO
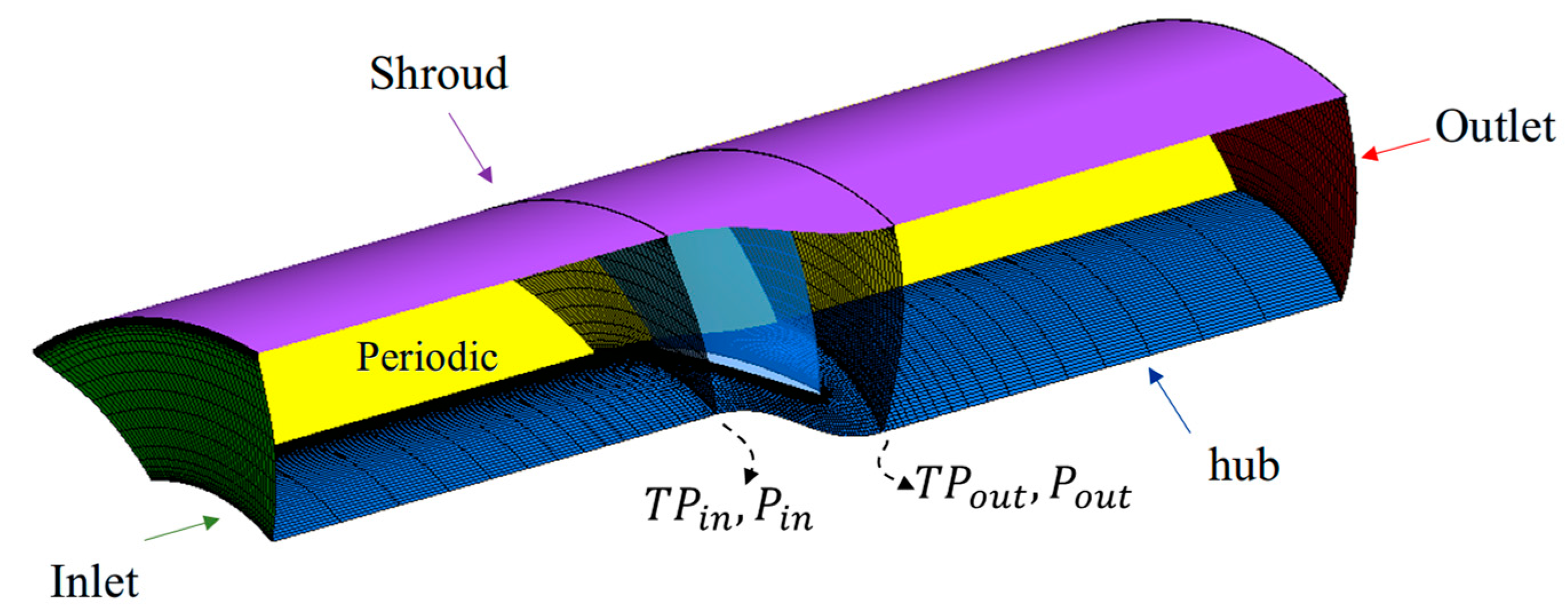
3.2.1. Definition of Optimization Problem
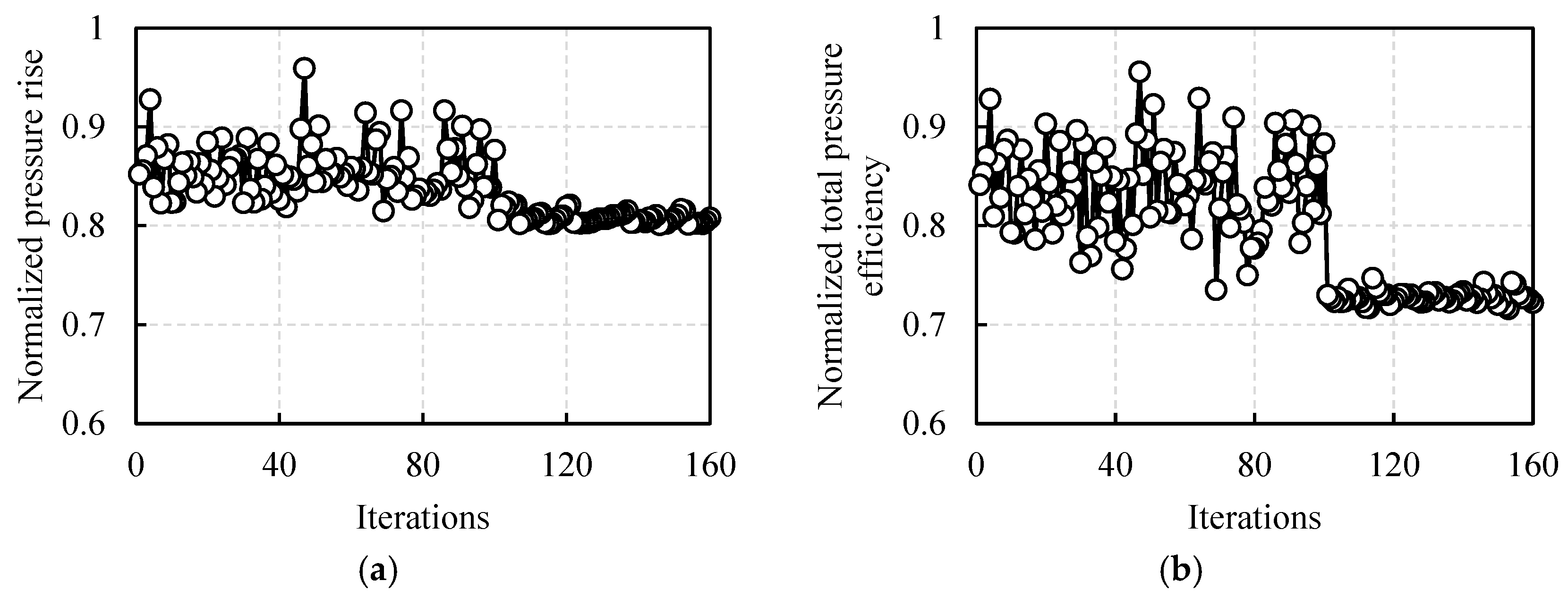
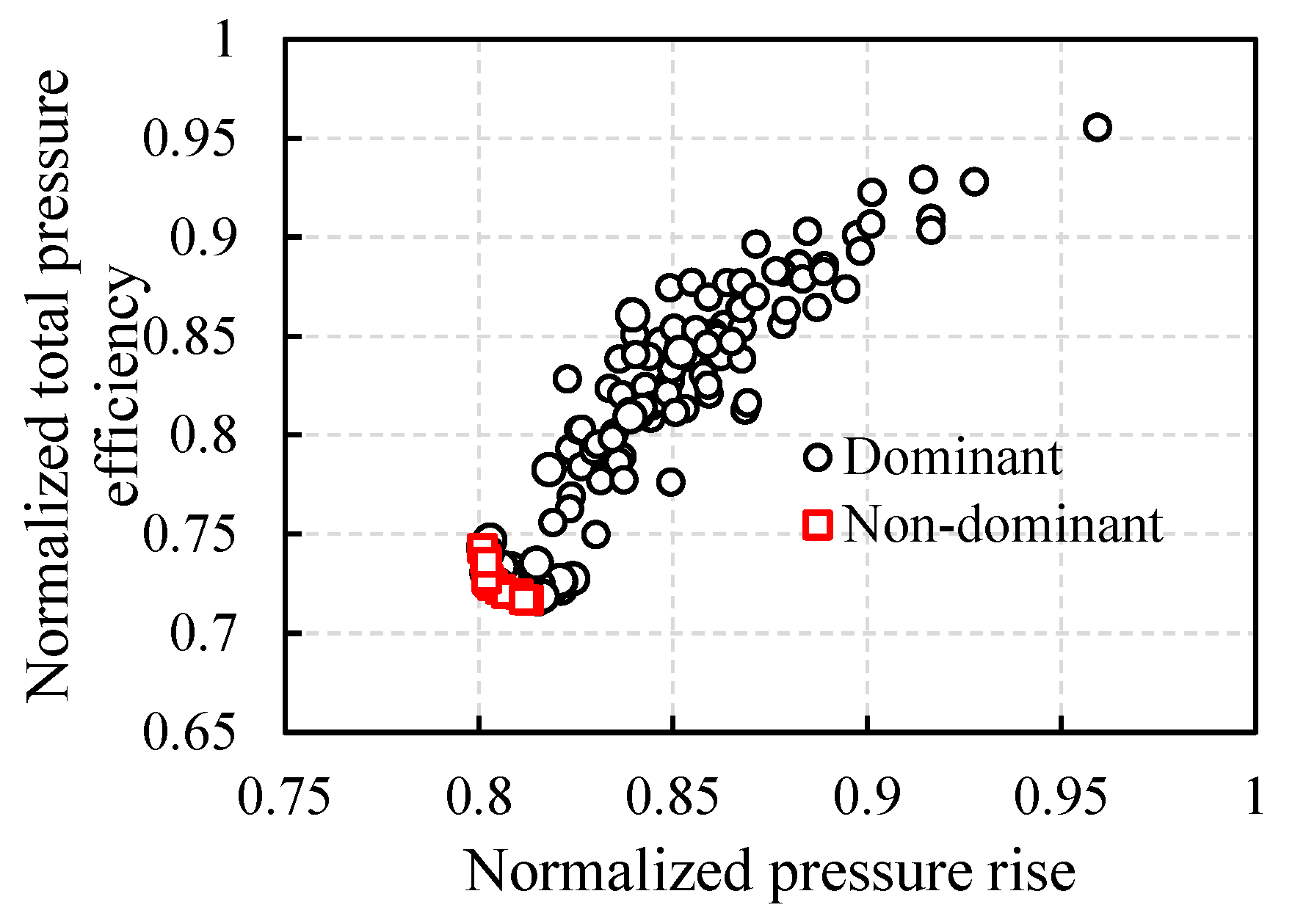
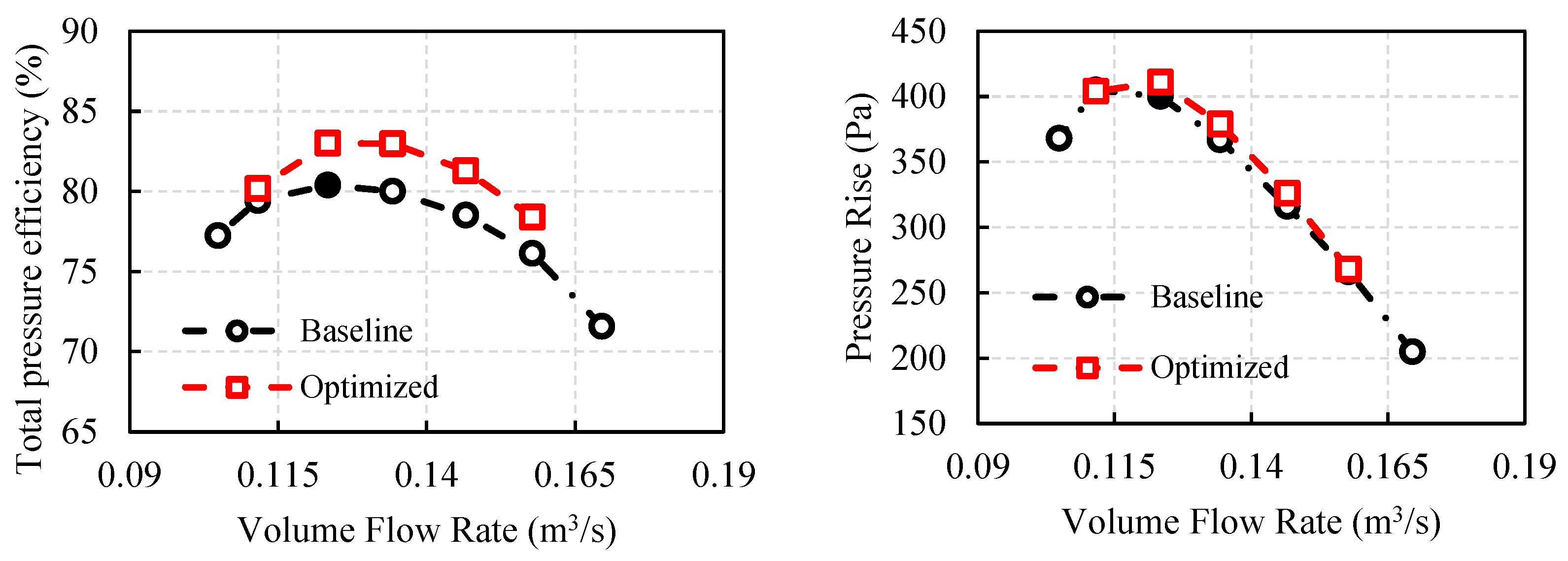
3.2.2. Optimization Results
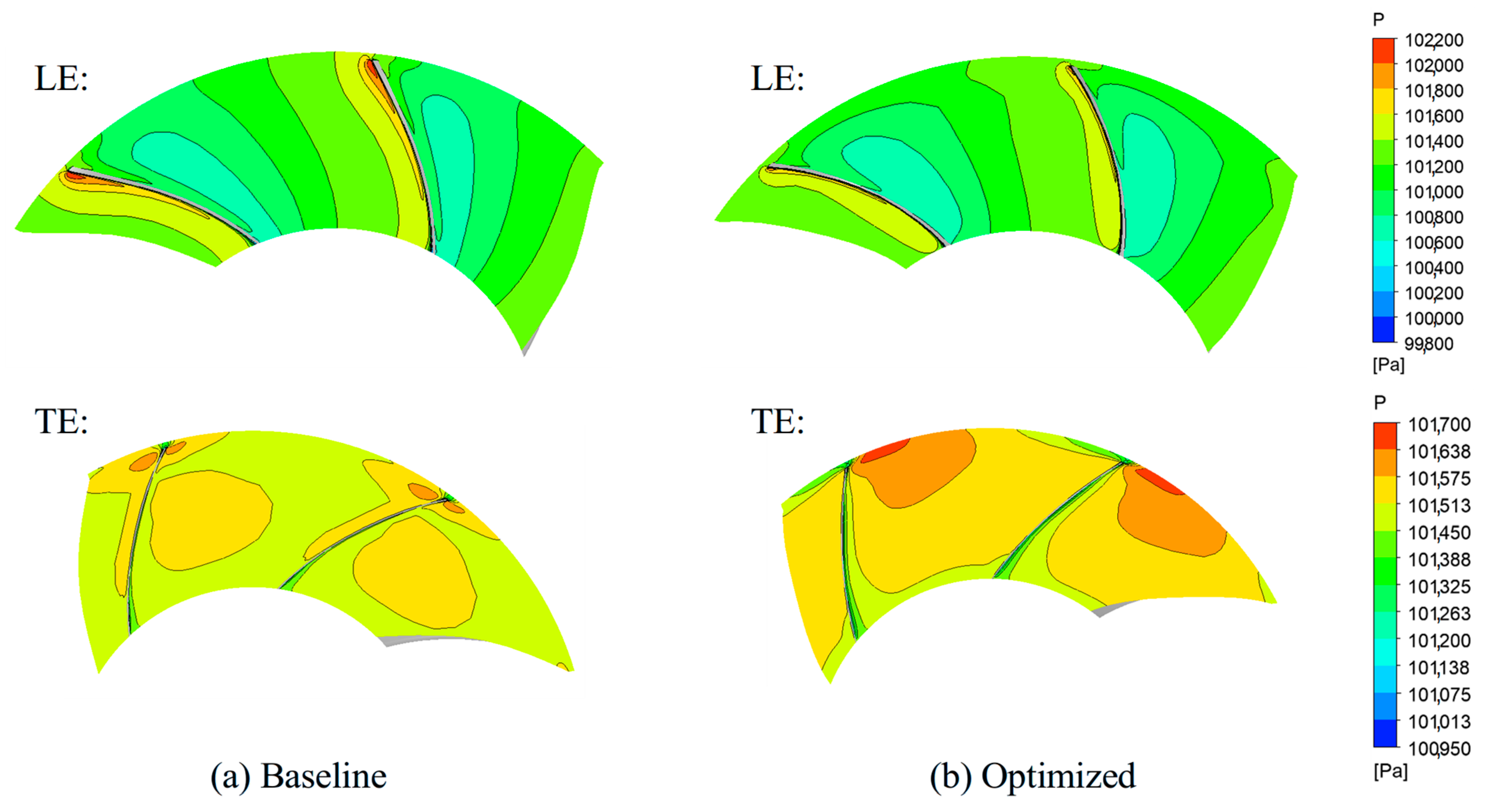
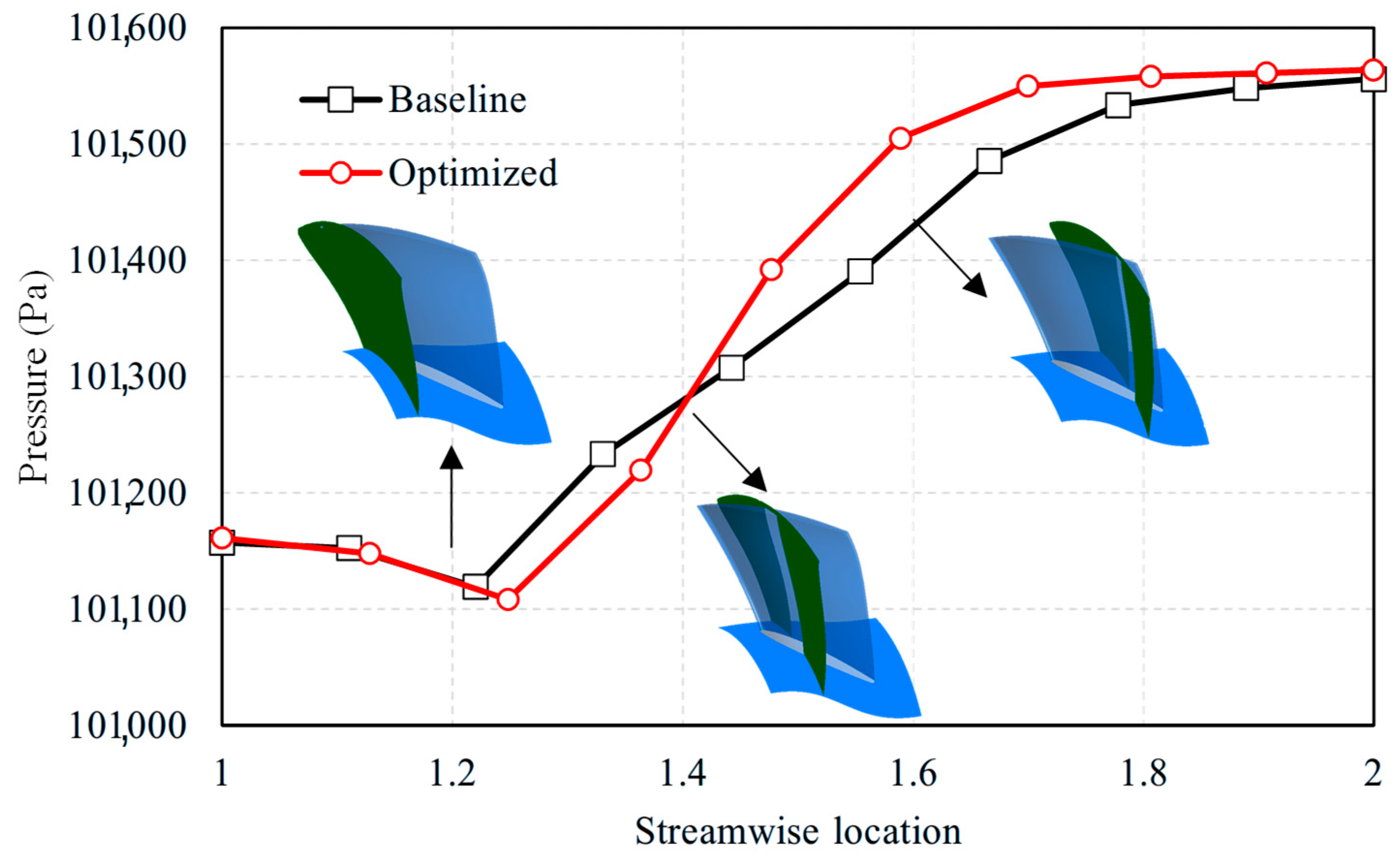
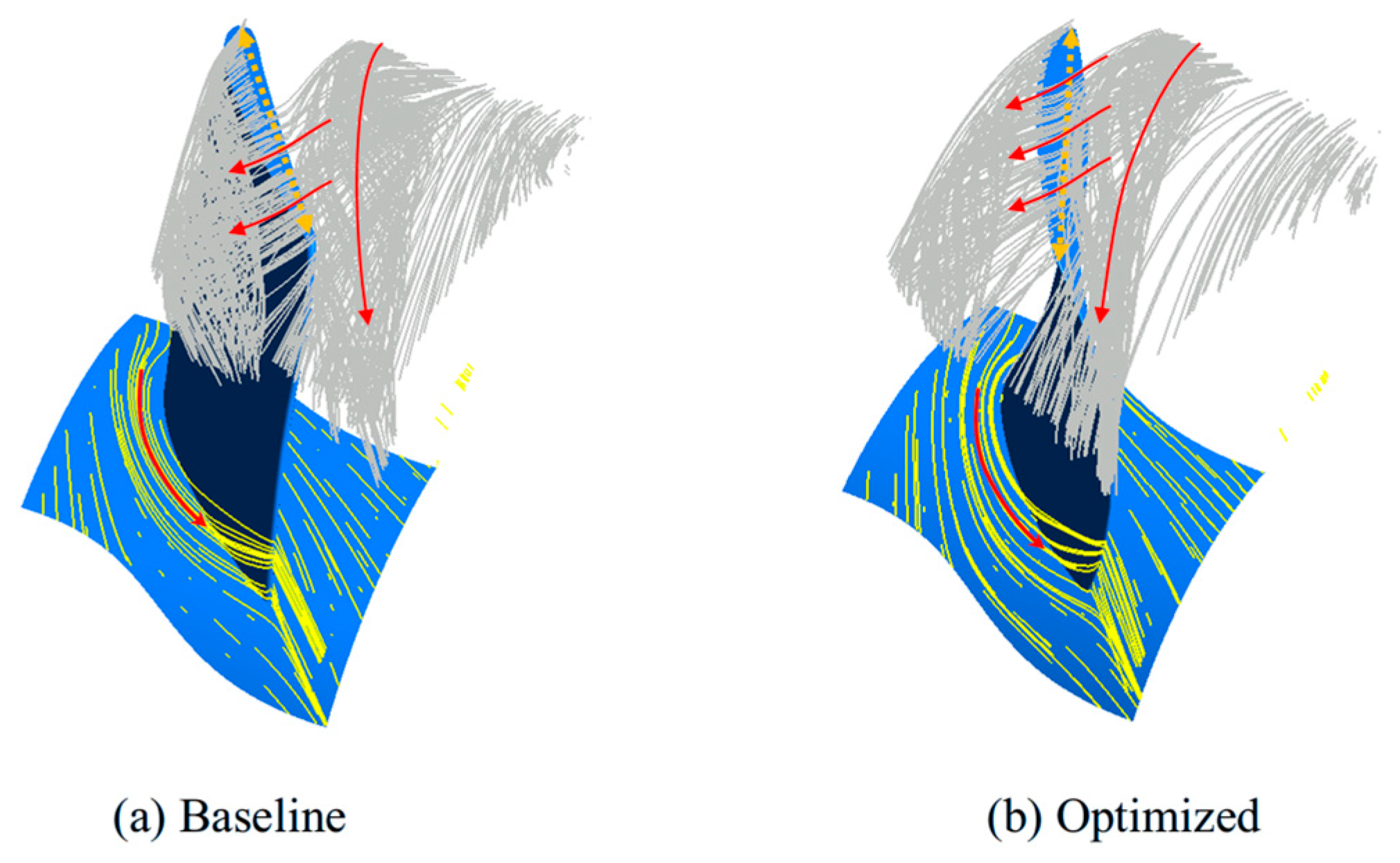
3.2.3. Flow Field Analysis
4. Conclusions
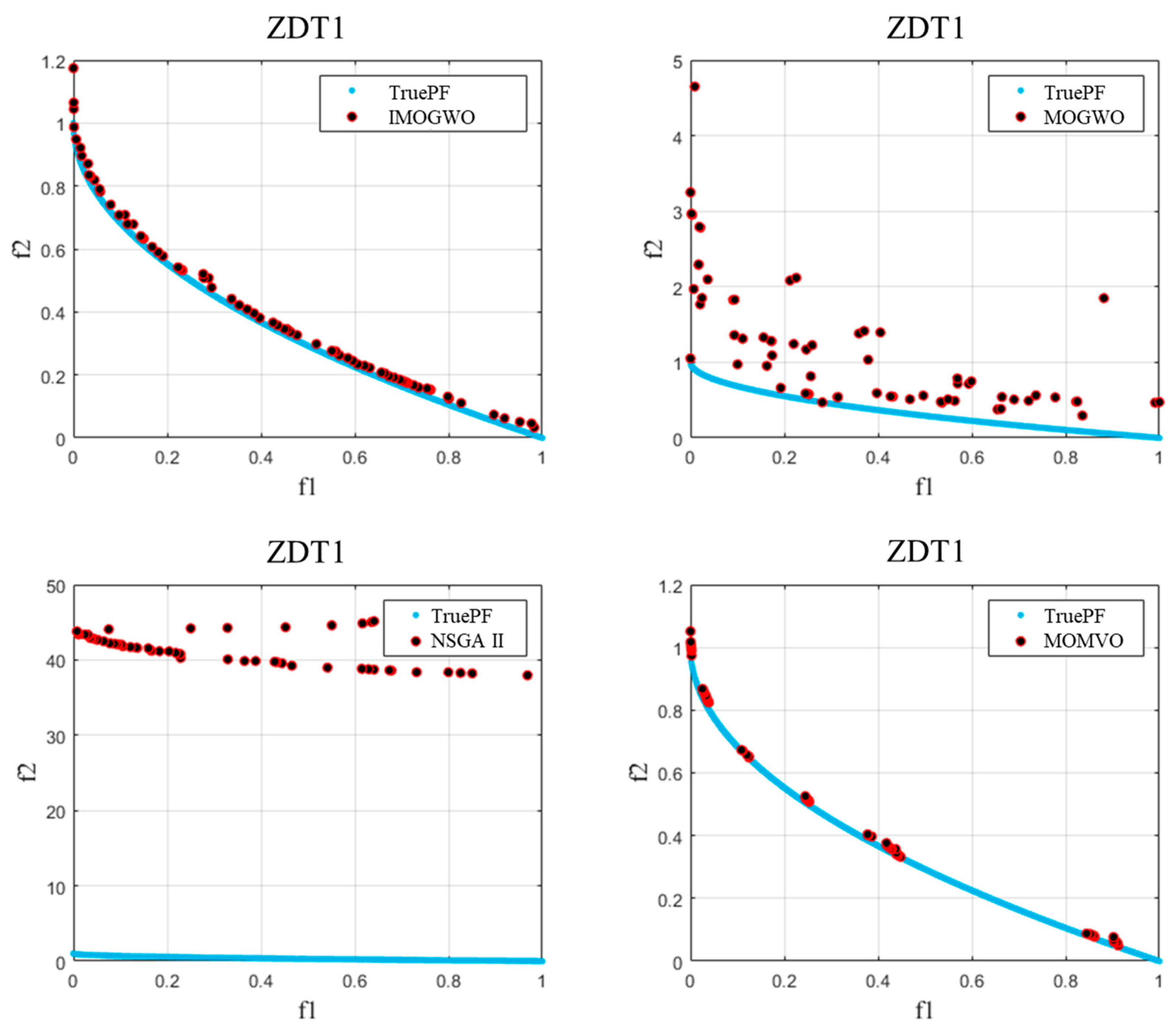
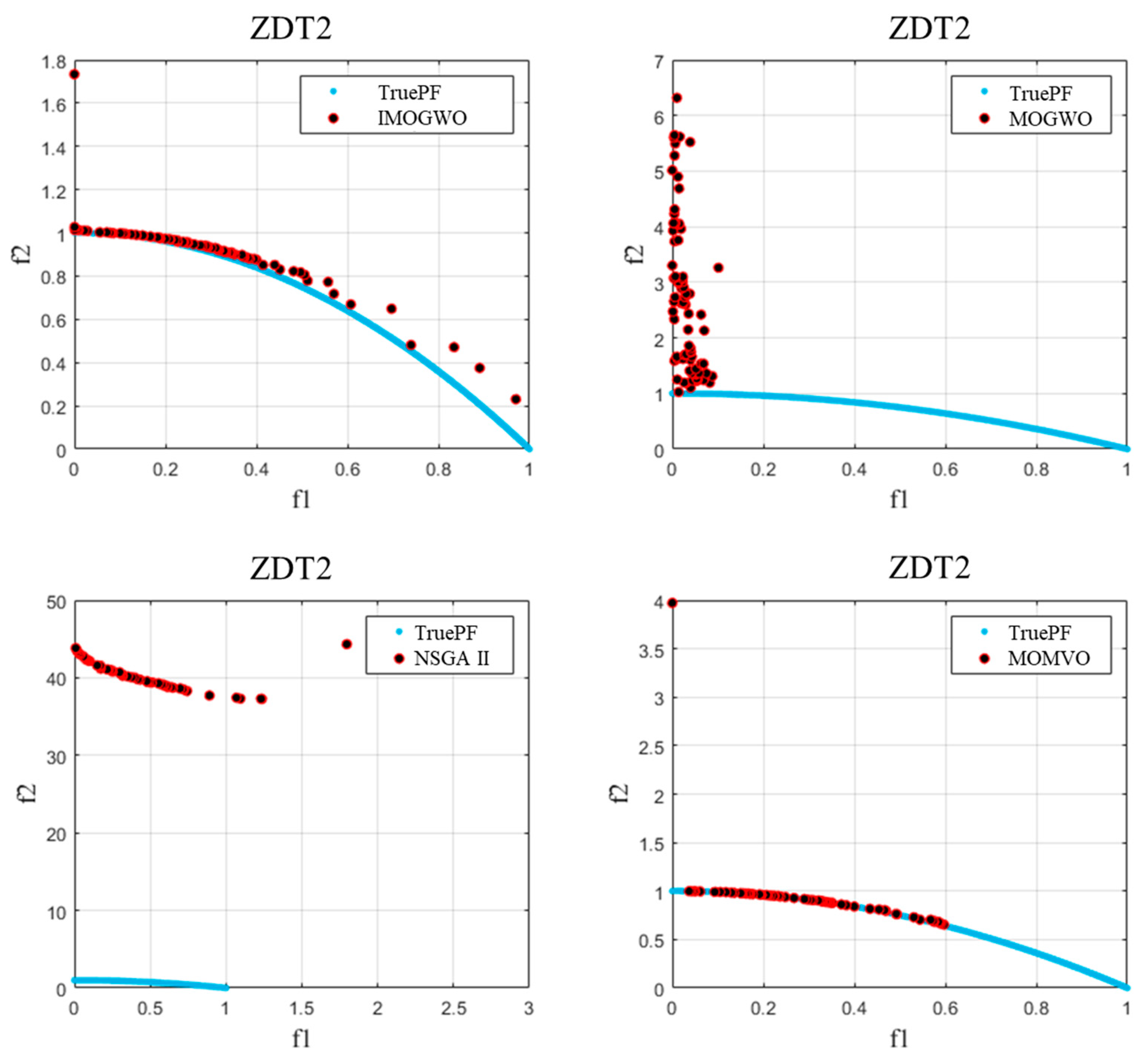
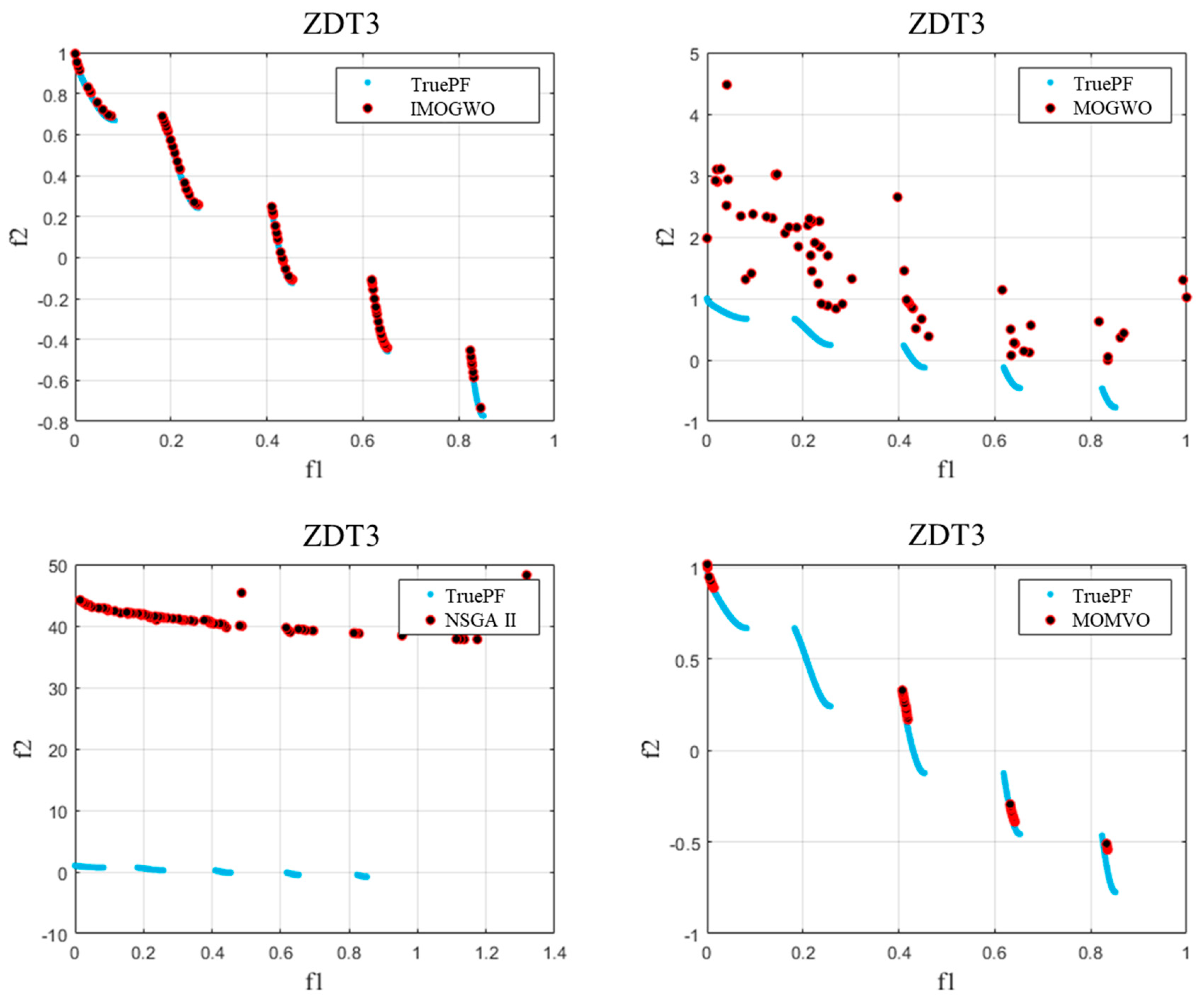
- For two-objective benchmark functions (ZDT1–3), the four performance indicators (GD, IGD, Spacing, and HV) demonstrated that the IMOGWO exhibited enhanced performance in the approximation of the true Pareto-optimal compared with MOGWO, NSGA II, and MOMVO for convex, concave, and discontinuous optimization problems. The analysis results showed that the superiority of the IMOGWO originated from improved exploration and exploitation capabilities.
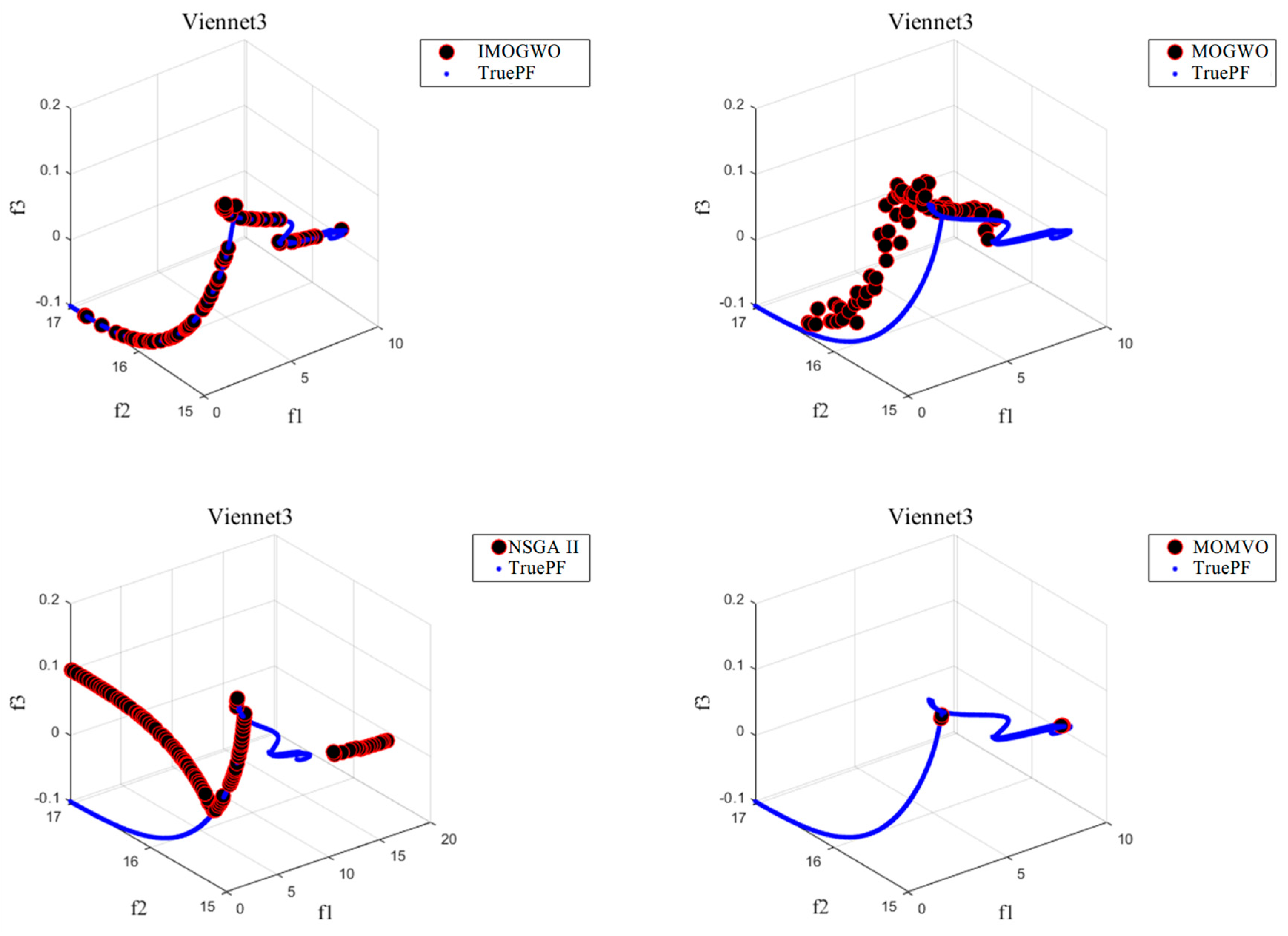
- For three-objective benchmark functions (Vinnet2 and Vinnet3), the three performance indicators (GD, IGD, and Spacing) generally also proved the IMOGWO outperforms MOGWO, NSGA II, and MOMVO. The IMOGWO has an improvement in convergency accuracy and coverage. It can deal with both continuous and discontinuous optimization problems efficiently.
- The multi-objective optimization method integrated with CFD and the IMOGWO increased the total pressure efficiency and pressure rise by 3.2% and 2.75%, respectively, at the design point. It implied that the proposed IMOGWO was able to solve real engineering problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Kalyanmoy, D.; Amrit, P.; Sameer, A.M.T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Shen, J.; Tang, S.; Ariffin, M.K.A.M.; As’Arry, A.; Wang, X. NSGA-III algorithm for optimizing robot collaborative task allocation in the internet of things environment. J. Comput. Sci. 2024, 81, 102373. [Google Scholar] [CrossRef]
- Fan, M.; Chen, J.; Xie, Z.; Ouyang, H.; Li, S.; Gao, L. Improved multi-objective differential evolution algorithm based on a decomposition strategy for multi-objective optimization problems. Sci. Rep. 2022, 12, 21176. [Google Scholar] [CrossRef]
- Hassanzadeh, H.R.; Rouhani, M. A Multi-Objective Gravitational Search Algorithm. In Proceedings of the 2010 2nd International Conference on Computational Intelligence, Communication Systems and Networks, Liverpool, UK, 28–30 July 2010; pp. 7–12. [Google Scholar]
- Junsittiwate, R.; Srinophakun, T.R.; Sukpancharoen, S. Multi-objective atom search optimization of biodiesel production from palm empty fruit bunch pyrolysis. Heliyon 2022, 8, e09280. [Google Scholar] [CrossRef]
- Beirami, A.; Vahidinasab, V.; Shafie-Khah, M.; Catalão, J.P. Multiobjective ray optimization algorithm as a solution strategy for solving non-convex problems: A power generation scheduling case study. Int. J. Electr. Power Energy Syst. 2020, 119, 105967. [Google Scholar] [CrossRef]
- Jangir, P.; Mirjalili, S.Z.; Saremi, S.; Trivedi, I.N. Optimization of problems with multiple objectives using the multi-verse optimization algorithm. Knowl.-Based Syst. 2017, 134, 50–71. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Toscano-Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Pradhan, P.M.; Panda, G. Solving multiobjective problems using cat swarm optimization. Expert Syst. Appl. 2012, 39, 2956–2964. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.d.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Gaidhane, P.J.; Nigam, M.J. A hybrid grey wolf optimizer and artificial bee colony algorithm for enhancing the performance of complex systems. J. Comput. Sci. 2018, 27, 284–302. [Google Scholar] [CrossRef]
- Vijay, R.K.; Nanda, S.J. A Quantum Grey Wolf Optimizer based declustering model for analysis of earthquake catalogs in an ergodic framework. J. Comput. Sci. 2019, 36, 101019. [Google Scholar] [CrossRef]
- Panwar, K.; Deep, K. Transformation operators based grey wolf optimizer for travelling salesman problem. J. Comput. Sci. 2021, 55, 101454. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Zamani, H.; Bahreininejad, A. GGWO: Gaze cues learning-based grey wolf optimizer and its applications for solving engineering problems. J. Comput. Sci. 2022, 61, 101636. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Abdulkadir, S.J.; Rais, H.M.; Mirjalili, S.; Alhussian, H.; Ragab, M.G.; Alqushaibi, A. Binary Multi-Objective Grey Wolf Optimizer for Feature Selection in Classification. IEEE Access 2020, 8, 106247–106263. [Google Scholar] [CrossRef]
- Lu, C.; Xiao, S.; Li, X.; Gao, L. An effective multi-objective discrete grey wolf optimizer for a real-world scheduling problem in welding production. Adv. Eng. Softw. 2016, 99, 161–176. [Google Scholar] [CrossRef]
- Sreenu, K.; Malempati, S. Aggressive Packet Combining Scheme with Packet Reversed and Packet Shifted Copies for Improved Performance. IETE J. Res. 2018, 65, 141–147. [Google Scholar]
- Sreenu, K.; Malempati, S. FGMTS: Fractional grey wolf optimizer for multi-objective task scheduling strategy in cloud computing. J. Intell. Fuzzy Syst. 2018, 35, 831–844. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, B.; Wang, S.; Jin, T.; Li, S. An enhanced multi-objective grey wolf optimizer for service composition in cloud manufacturing. Appl. Soft Comput. 2020, 87, 106003. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Z.; Li, D. A multiple search strategies based grey wolf optimizer for solving multi-objective optimization problems. Expert Syst. Appl. 2020, 145, 113134. [Google Scholar] [CrossRef]
- Javidsharifi, M.; Niknam, T.; Aghaei, J.; Mokryani, G.; Papadopoulos, P. Multi-objective day-ahead scheduling of microgrids using modified grey wolf optimizer algorithm. J. Intell. Fuzzy Syst. 2019, 36, 2857–2870. [Google Scholar] [CrossRef]
- Eappen, G.; Shankar, T. Multi-Objective Modified Grey Wolf Optimization Algorithm for Efficient Spectrum Sensing in the Cognitive Radio Network. Arab. J. Sci. Eng. 2020, 46, 3115–3145. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, T.; Zou, K.; Tan, S.; Sun, Z. Multi-Objective Grey Wolf Optimizer Based on Improved Head Wolf Selection Strategy. In Proceedings of the 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 1922–1927. [Google Scholar]
- Liu, J.; Liu, Z.; Wu, Y.; Li, K. MBB-MOGWO: Modified Boltzmann-Based Multi-Objective Grey Wolf Optimizer. Sensors 2024, 24, 1502. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, X. Quantum Particle Swarm Optimization Based on Bloch Coordinates of Qubits. In Proceedings of the 2013 Ninth International Conference on Natural Computation (ICNC), Shenyang, China, 23–25 July 2013. [Google Scholar]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Heidari, A.A.; Aljarah, I.; Faris, H.; Chen, H.; Luo, J.; Mirjalili, S. An enhanced associative learning-based exploratory whale optimizer for global optimization. Neural Comput. Appl. 2019, 32, 5185–5211. [Google Scholar] [CrossRef]
- Chase, N.; Rademacher, M.; Goodman, E. A benchmark study of multi-objective optimization methods. BMK-3021 Rev 2009, 6, 1–24. [Google Scholar]
- Li, J.; Guo, X.; Yang, Y.; Zhang, Q. A Hybrid Algorithm for Multi-Objective Optimization—Combining a Biogeography-Based Optimization and Symbiotic Organisms Search. Symmetry 2023, 15, 1481. [Google Scholar] [CrossRef]
- Liao, Q.; Sheng, Z.; Shi, H.; Zhang, L.; Zhou, L.; Ge, W.; Long, Z. A Comparative Study on Evolutionary Multi-objective Optimization Algorithms Estimating Surface Duct. Sensors 2018, 18, 4428. [Google Scholar] [CrossRef]
- Adjei, R.A.; Fan, C. Multi-objective design optimization of a transonic axial fan stage using sparse active subspaces. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2325488. [Google Scholar] [CrossRef]

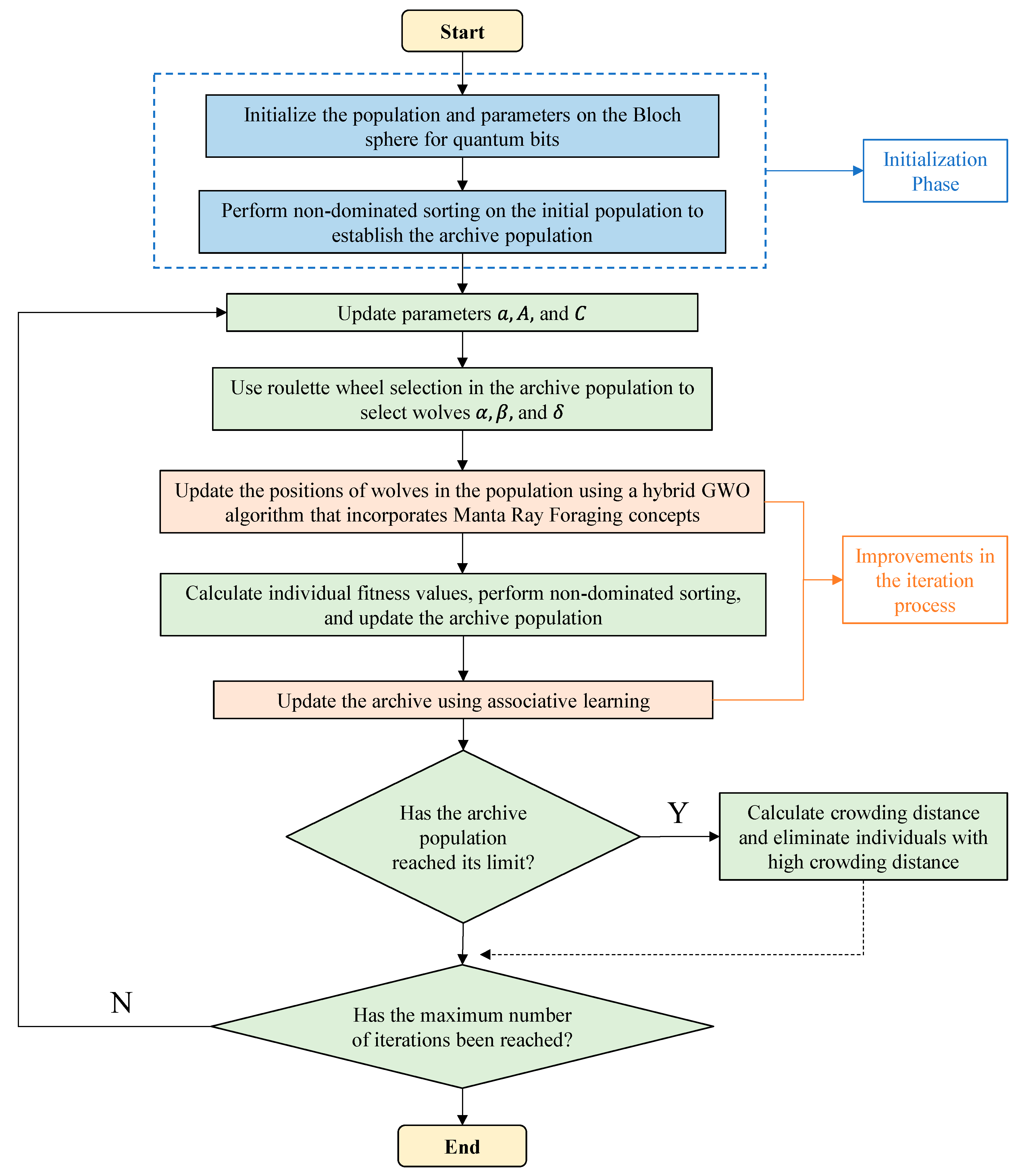


| For each individual in the population size (Popsize): |
| Set Grey Wolves[].Velocity to 0 Initialize Grey Wolves[].Position as a zero vector of length Var % The three coordinates of qubits For each variable in Var: Generate random angle in the range [0, 2] Generate random angle in the range [0, 2] Calculate chrom1[] as cos() sin() Calculate chrom2[] as sin() sin() Calculate chrom3[] as cos() End For % Transform to the solution space of this problem Calculate quantum[1].Position using the transformation formula with chrom1 Calculate quantum[2].Position using the transformation formula with chrom2 Calculate quantum[3].Position using the transformation formula with chrom3 % Evaluate the cost of each quantum position Set quantum[1].Cost to the result of the objective function fobj evaluated at quantum[1].Position Set quantum[2].Cost to the result of the objective function fobj evaluated at quantum[2].Position Set quantum[3].Cost to the result of the objective function fobj evaluated at quantum[3].Position % Determine domination status among quantum solutions Determine domination status for quantum solutions Create a list domi containing the domination status of quantum[1], quantum[2], and quantum[3] Find indices of non-dominated solutions and store in num If num is empty: Set Grey Wolves[].Position to quantum[1].Position Set Grey Wolves[].Cost to quantum[1].Cost Else: Set Grey Wolves[].Position to the position of the first non-dominated solution in quantum[num[1]] Set Grey Wolves[].Cost to the cost of the first non-dominated solution in quantum[num[1]] End If Set Grey Wolves[].Best.Position to Grey Wolves[].Position Set Grey Wolves[].Best.Cost to Grey Wolves[].Cost End For Clear variables quantum, domi, num |
| % Calculate weight factor w and factor b (Equations (15) and (16)) %w = (wmax − wmin) * current_iteration/max_iterations + wmin %b = (max_iterations − current_iteration + 1)/max_iterations r3 = random_vector(1, num_variables) % = 2exp(r3 b) sin(2r3) % Select a random individual random_selection = random_individual (population_size) % Update grey wolf position with Manta Ray Foraging (Equations (11)) % Boundary checking ].Position, lower_bound, upper_bound) % Calculate the cost of the new position ].Position) |
| % Dominance relationships, archiving, grid updates Determine domination among Grey Wolves Extract non-dominated wolves from Grey Wolves and store in non_dominated_wolves % Add non-dominated wolves to the archive Archive = Archive + non_dominated_wolves % Randomly updating archive using associative learning Archive_num = size_of(Archive) Archive = Associative_Rep(fobj, Archive, gamma, lb, ub, current_iteration, max_iterations, num_variables, Archive_num, Alpha) Determine domination among Archive Extract non-dominated solutions from Archive % Update grid index for each solution in the archive For each solution in Archive: Calculate GridIndex and GridSubIndex for the solution End For % Ensure archive size does not exceed maximum If size_of(Archive) > Archive_size: EXTRA = size_of(Archive) − Archive_size Delete EXTRA solutions from Archive using parameter gamma /% Recalculate costs and update grid Archive_costs = calculate_costs(Archive) G = create_hypercubes(Archive_costs, nGrid, alpha) End If |
| Problem | Pareto-Optimal Front | Number of Objectives | Constraint Condition |
|---|---|---|---|
| ZDT1 | convex | 2 | |
| ZDT2 | concave | 2 | |
| ZDT3 | discontinuous | 2 | |
| Viennet2 | discontinuous | 3 | |
| Viennet3 | continuous | 3 |
| . | IMOGWO | MOGWO | NSGA II | MOMVO | IMOGWO | MOGWO | NSGA II | MOMVO | |||
| ZDT1 | max | 1.144 | 1.119 | 0.986 | 1.023 | Viennet2 | max | 1.144 | 1.438 | 0.994 | 1.294 |
| min | 0.638 | 0.788 | 0.968 | 0.738 | min | 0.989 | 0.860 | 0.992 | 0.997 | ||
| mean | 0.876 | 0.971 | 0.975 | 0.872 | mean | 1.072 | 1.089 | 0.993 | 1.123 | ||
| std | 0.158 | 0.111 | 0.006 | 0.089 | std | 0.057 | 0.171 | 0.001 | 0.124 | ||
| ZDT2 | max | 1.439 | 1.216 | 0.987 | 1.067 | ||||||
| min | 0.773 | 0.734 | 0.968 | 0.830 | |||||||
| mean | 1.103 | 0.996 | 0.976 | 0.933 | |||||||
| std | 0.253 | 0.120 | 0.007 | 0.076 | |||||||
| ZDT3 | max | 1.044 | 1.218 | 1.000 | 1.948 | Viennet3 | max | 1.360 | 0.987 | 1.190 | 1.724 |
| min | 0.749 | 0.911 | 0.975 | 0.819 | min | 0.940 | 0.556 | 0.850 | 1.002 | ||
| mean | 0.906 | 1.072 | 0.985 | 1.503 | mean | 1.203 | 0.834 | 0.980 | 1.323 | ||
| std | 0.105 | 0.089 | 0.007 | 0.431 | std | 0.139 | 0.136 | 0.116 | 0.274 |
| No. | Design Variable | Description | Range |
|---|---|---|---|
| 1 | S_mid | Sweep at mid span | −15%~+15% |
| 2 | S_tip | Sweep at blade tip | −15%~+15% |
| 3 | T_mid | Twist at mid span | −5%~+5% |
| 4 | T_tip | Twist at blade tip | −5%~+5% |
| 5 | L_mid | Lean at mid span | −30%~+30% |
| 6 | L_tip | Lean at blade tip | −30%~+30% |
| 7 | Th_mid | Thickness at mid span | −10%~+10% |
| 8 | Th_tip | Thickness at blade tip | −10%~+10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Adjei, R.A.; Tao, G.; Zeng, Y.; Fan, C. An Improved Multi-Objective Grey Wolf Optimizer for Aerodynamic Optimization of Axial Cooling Fans. Appl. Sci. 2025, 15, 5197. https://doi.org/10.3390/app15095197
Gong Y, Adjei RA, Tao G, Zeng Y, Fan C. An Improved Multi-Objective Grey Wolf Optimizer for Aerodynamic Optimization of Axial Cooling Fans. Applied Sciences. 2025; 15(9):5197. https://doi.org/10.3390/app15095197
Chicago/Turabian StyleGong, Yanzhao, Richard Amankwa Adjei, Guocheng Tao, Yitao Zeng, and Chengwei Fan. 2025. "An Improved Multi-Objective Grey Wolf Optimizer for Aerodynamic Optimization of Axial Cooling Fans" Applied Sciences 15, no. 9: 5197. https://doi.org/10.3390/app15095197
APA StyleGong, Y., Adjei, R. A., Tao, G., Zeng, Y., & Fan, C. (2025). An Improved Multi-Objective Grey Wolf Optimizer for Aerodynamic Optimization of Axial Cooling Fans. Applied Sciences, 15(9), 5197. https://doi.org/10.3390/app15095197






