Abstract
Foundation models have achieved remarkable success across various domains, but still face critical challenges such as limited data availability, high computational requirements, and rapid knowledge obsolescence. To address these issues, we propose a novel framework that integrates model merging with federated learning to enable continual foundation model updates without centralizing sensitive data. In this framework, each client fine-tunes a local model, and the server merges these models using multiple merging strategies. We experimentally evaluate the effectiveness of these methods using the CLIP model for image classification tasks across diverse datasets. The results demonstrate that advanced merging methods can surpass simple averaging in terms of accuracy, although they introduce challenges such as catastrophic forgetting and sensitivity to hyperparameters. This study defines a realistic and practical problem setting for decentralized foundation model updates, and provides a comparative analysis of merging techniques, offering valuable insights for scalable and privacy-preserving model evolution in dynamic environments.
1. Introduction
Supervised learning is a frequently used paradigm in deep learning. In this paradigm, models learn the mapping between input and output using labeled training data. Increasing the training data improves model performance by enabling models to learn from a broader range of samples. However, the cost of annotating data significantly limits data expansion, which is a major bottleneck to improving model performance. To address this limitation, self-supervised learning [1] enables models to learn the relationships and structures inherent in data using unlabeled data. By eliminating the requirement for manual annotation, self-supervised learning dramatically increases the amount of data available for training models, thereby facilitating pretraining methods that produce general representations.
Building on recent advances, foundation models (FMs) [2] have emerged as large-scale architectures pretrained on extensive and diverse data using self-supervised learning. These models acquire broadly useful representations and can be fine-tuned on relatively small datasets for specific downstream tasks. This approach reduces reliance on specialized solutions and allows a single model to handle multiple tasks. Recent progress also includes the development of multimodal FMs that can process various input types, such as images, text, audio, video, sensor data, and structured data. Examples include GPT-4V [3], LLaVA [4], Gemini [5], BLIP [6], and CLIP [7]. The inclusion of diverse modalities expands the range of applications and improves performance on challenging tasks that are difficult for conventional methods [8].
Although FMs offer significant benefits, their training process is centralized, which leads to several challenges [9,10]:
- Limitations in Scaling Training Data: High-quality data are essential for improving model performance; however, their availability is expected to become increasingly limited. If the current trend of large-scale model development continues, estimates suggest that all publicly available human text data will be entirely exhausted by 2028 [11]. In addition, privacy and security concerns further restrict open data access, making it increasingly difficult to construct large and diverse datasets.
- Computational Resource Constraints: FMs, which contain many parameters [12], require enormous computational resources to train on large datasets. This poses challenges for individuals and organizations lacking the necessary infrastructure to train FMs. In addition, computational resources are increasingly concentrated among financially powerful entities, creating an imbalance that limits broader innovation.
These challenges hinder sustainable and equitable FM development. Furthermore, these challenges lead to issues such as the inability to incorporate data from local deployment environments and the rapid obsolescence of model knowledge [13]. Therefore, there is a growing need for methods that enable diverse individuals and organizations to train FMs while collaboratively ensuring data privacy and security.
This study focuses on model merging [14,15] to address these training challenges. Model merging fuses multiple fine-tuned models for different tasks into a single high-performance model without the need for additional training. This process typically involves carefully adjusting model parameters and merging learned representations, typically via techniques such as weighted averaging or parameter alignment, to preserve and integrate the specialized knowledge of each constituent model. By repeatedly merging FMs that have been fine-tuned on local datasets owned by various entities, the abilities of these models can be continuously enhanced [16]. During this process, data are distributed rather than centralized, ensuring data privacy. Each entity contributes local model updates derived from sensitive data, which are merged without exposing the raw data. This approach leverages sensitive data that cannot be used directly in conventional centralized training and enables models to acquire fine-grained and diverse knowledge from various sources. In addition, by fine-tuning each model using the computational resources available to individual entities, the overall computational load is distributed relative to centralized training, thereby encouraging broader participation in FM development.
Although model merging and federated learning (FL) aim to improve decentralized models, model merging fuses fine-tuned models into a unified model only once. This approach contrasts with the traditional FL cycle in which a global model is continuously updated by aggregating local updates. Nevertheless, continuous updates via model merging share motivations with FL [17], in which data holders, known as clients, collaboratively build a unified model without directly exchanging their private data. FL is a promising approach that can potentially increase the applicability of sensing data. It is also being actively researched in communication. In FL, a server distributes the global model, which is then fine-tuned locally and aggregated in each round. In previous studies on model merging, the merged model was evaluated in a single round, similar to a single round of FL. However, few studies have investigated models that are continuously updated through repeated cycles of aggregation and fine-tuning [16]. This continuous update mechanism ensures that the model’s knowledge remains current but introduces challenges, including potential inconsistencies among merged models over successive rounds. Addressing these challenges requires a realistic and promising problem setting and can democratize access to high-performance FMs while ensuring data privacy and efficient use of distributed computational resources.
In this study, we propose a research setting centered on continuously updating FMs and experimentally analyze the impact of incorporating model merging techniques during FL aggregation on model accuracy. To the best of our knowledge, there is no comprehensive research on model merging methods for this type of problem. Specifically, to evaluate the effectiveness of model merging in FL, we employ the open-vocabulary CLIP model to assess accuracy across multiple image classification tasks. Here, open-vocabulary models classify images based on arbitrary text corresponding to class names rather than predefined labels. Each client fine-tunes the model on different datasets, and the resulting models are then merged. This process aims to retain the knowledge acquired during pretraining while incorporating new information. The experimental results indicate that the model merging techniques investigated in this study exhibit superior accuracy compared to conventional parameter averaging commonly used in FL. However, we found that higher accuracy on a new task increases the likelihood of forgetting the knowledge obtained from pretraining. In addition, our experimental results reveal that model merging methods are sensitive to hyperparameters and require dynamic control mechanisms to achieve unbiased model updates.
Finally, we summarize the contributions of this study.
- We construct a novel problem setting for continually updating FMs with distributed data using an FL framework.
- We analyze the effectiveness of existing model merging methods and consider the issues and the directions to address them.
2. Related Work
In this section, we review the literature on several key areas that form the basis of our research: continual updating of FMs, FL, FL with FMs, and model merging.
2.1. Continual Updating of Foundation Models
FMs are pretrained on diverse datasets and capture extensive knowledge up to pretraining. However, real-world environments are dynamic and continuously evolving, leading to new tasks and subdomains that may render pretrained knowledge obsolete. Retraining or fully updating these models each time new data emerges is impractical because of the enormous computational cost.
Recent research on continual and lifelong learning aims to incorporate newly acquired knowledge incrementally, addressing issues such as catastrophic forgetting [18], a phenomenon in which models lose previously learned information when integrating new information. Conventional continual learning approaches generally fall into two categories. The first category includes regularization-based methods. These methods add a penalty to the loss function based on the parameters’ importance and suppress the variation in each parameter based on how important that parameter was in the execution of previous tasks. In elastic weight consolidation (EWC), a typical method, the importance is calculated using the Fisher information matrix [19]. The second category includes replay-based approaches, which store subsets of prior data or synthetic examples and use them alongside new data during training [20].
Although conventional approaches are practical in some scenarios, they tend to be computationally expensive and less efficient when applied to large-scale models [21]. Thus, the concept of continual pretraining has gained traction. This approach begins with a pretrained FM and incrementally updates it with new data in a manner that scales to larger models and more complex tasks [22]. Despite its promise, continual pretraining remains underexplored, particularly regarding the integration of model merging techniques. Most previous work in this area has focused on adjusting training strategies through refined regularization objectives [23] or tailored learning rate schedules [24] without addressing how to effectively combine multiple fine-tuned models over successive update cycles.
In addition, no existing work has investigated the application of FL frameworks for continual pretraining. This study explores how model merging can be embedded in a federated setting while maintaining a fixed training strategy and continuously updating the model. This research direction is crucial for reducing the overhead of full retraining and ensuring that the FM remains current in dynamic environments.
2.2. Federated Learning
FL is a decentralized training framework that allows multiple participants to collaboratively train models without exchanging their private raw data [25]. Most FL methods are based on the federated averaging (FedAvg) algorithm [17], which aggregates local model updates to form a global model. FedAvg is extensively used because it minimizes communication costs and effectively aggregates model updates. This property is critical in FL environments with numerous participants and limited communication bandwidth.
For FL to become practical in real-world applications, several key challenges must be addressed. A primary challenge is the presence of nonindependent and identically distributed (non-IID) data. Variations in data distribution across clients can result in biased models that favor certain participants [26,27]. In addition, system heterogeneity and scalability pose significant challenges. Differences in the computational and communication capabilities of clients can result in uneven contributions to model training. As the number of participants increases, efficient aggregation algorithms and scalable infrastructure are essential for effectively managing global model updates.
FL’s future development will be driven by theoretical advancements and practical applications across various industries. In particular, FL is expected to play a crucial role in artificial intelligence solutions that prioritize user privacy and data sovereignty.
2.3. Federated Learning with Foundation Model
FL is a promising solution to the data aggregation challenges inherent in training large-scale FMs [9,10]. Early efforts, such as FedBERT [28], demonstrated the feasibility of pretraining large language models, such as BERT, in a federated environment, to achieve competitive performance without centralizing sensitive data. More recent advancements have extended FL to the fine-tuning stage, in which parameter-efficient methods have proven beneficial.
Techniques such as LoRA [29] reduce the number of trainable parameters by applying low-rank approximations to transformer weight matrices, significantly lowering communication overhead and computational demands, which are critical factors in federated settings, particularly for resource-constrained devices [30]. In addition, prompt tuning approaches, in which the core model remains fixed while the prompt parameters are learned, have been explored to optimize resource efficiency during federated fine-tuning [31,32].
However, although prior studies have primarily focused on FL for either pretraining or fine-tuning in isolation, this study distinguishes itself by addressing the continuous pretraining of FMs. We systematically evaluate how FL frameworks can support ongoing model updates in dynamic, large-scale environments, bridging the gap between static FL setups and the demands of continual model evolution.
2.4. Model Merging
Model merging is an emerging technique designed to integrate the parameters of multiple models, each fine-tuned for distinct tasks or data distributions, into a single high-performance model without requiring a complete retraining cycle [14,15]. Unlike conventional ensemble methods [33], which combine the outputs of multiple models during inference, leading to increased computational costs and memory usage, model merging consolidates the learned representations into one model. This consolidation offers significant advantages in terms of efficiency, inference speed, and storage.
One straightforward and commonly used model merging approach is parameter averaging [34,35]. However, more advanced techniques, such as weighted averaging, assign different weights to models based on their relative contribution or performance regarding the target task [36,37]. The success of these techniques typically stems from observations indicating that fine-tuned models originating from the same pretrained initialization tend to occupy similar regions within the loss landscape, thereby facilitating effective linear interpolation [38].
A critical concept in this domain is the task vector [39], defined as the difference between the parameters of a fine-tuned model and those of the original pretrained model. Task vectors are considered to encapsulate the specific knowledge acquired during fine-tuning. By performing arithmetic operations on these vectors (e.g., addition or subtraction), the specialized skills of different models can be effectively manipulated or combined. Despite its promise, task vector manipulation is susceptible to interference when merging multiple vectors, and recent studies have proposed strategies to mitigate these effects [40,41].
Beyond simple parameter averaging, some studies have investigated layer-wise merging techniques that aim to independently align and integrate model parameters at each layer [42,43]. These methods offer more granular control over the merging process, potentially better preserving the specialized knowledge of individual models. However, most existing research on model merging evaluates the integrated model in a single merging round rather than a continuous update framework.
Our study addresses this gap by adopting a continual pretraining strategy in which the base model undergoes cycles of fine-tuning and merging [16]. This iterative approach provides insights into the robustness and stability of model merging over time and highlights the challenges of maintaining consistent performance across multiple update cycles. In particular, we examine the sensitivity of merging outcomes to hyperparameter settings and propose dynamic control mechanisms to mitigate the risk of performance degradation over successive rounds.
3. Analysis of Model Merging in Distributed Data Settings
This section presents the analytical methods and experimental setup used in this study. In Section 3.1, we introduce an important model merging challenge for updating an FM under an FL framework. In Section 3.2, we describe the CLIP model used in this study. In Section 3.3, we explain the fine-tuning procedure for CLIP. Finally, in Section 3.4, we detail the model merging strategies used in our experiments.
3.1. Problem Definition
We propose a new problem setup that builds on conventional model merging research by integrating an FL framework and explicitly considering changes in model parameters over time. In this setup, the server distributes the current global model to multiple clients, each of which fine-tunes it in parallel using their local data. The server then aggregates the updated parameters using a selected merging method to form a new global model. This process is repeated over multiple rounds, allowing the model to adapt to evolving data distributions across clients while preserving decentralized training. A summary of this procedure is shown in Figure 1, and the performance of the final global model is evaluated based on its accuracy.
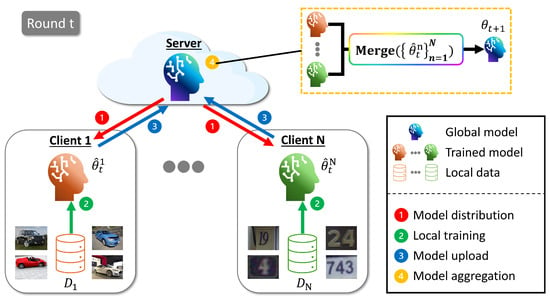
Figure 1.
Overview of proposed model merging framework.
At the beginning of each round , the server distributes the current global model to N participating clients. Each client possesses a local dataset and performs local fine-tuning on for a predetermined number of local epochs. This local adaptation yields an updated model , incorporating client-specific knowledge learned from . After local training, each client uploads its updated parameters to the server, which merges these updates via a model merging function to obtain the new global model as follows:
The initial model represents a pretrained model that serves as the starting point of the iterative learning process.
In this problem setting, the model aims to be optimized for all local datasets. In addition, a reference dataset is constructed separately from the local datasets and is used only for accuracy verification during testing. Because the reference dataset is not explicitly trained, it is used as a baseline to demonstrate whether the model can retain the knowledge it acquires through pretraining.
A key contribution of this work is the development of a novel framework for continuously updating foundation models in decentralized environments through iterative model merging. This framework is designed for realistic FL scenarios involving distributed, heterogeneous data, and allows for comprehensive analysis of model behavior over time. By formulating this new problem setting and systematically evaluating existing merging techniques within it, we identify practical challenges and limitations, thereby offering new insights into the deployment of model merging in real-world continual updating systems.
3.2. CLIP Model
This section briefly describes an overview of the CLIP model [7], a foundational model used in this study. CLIP is an open-vocabulary model that enables the multimodal processing of images and text. Unlike typical image classification models, the open-vocabulary CLIP model is not restricted to a fixed classification space defined during training. In contrast, it can generalize to unseen categories by leveraging textual descriptions of class names.
The model comprises the following components:
- A vision encoder that calculates image embeddings from images.
- A text encoder that calculates text embeddings from texts.
For a given image–text pair, these two encoders are jointly trained to maximize the cosine similarity of correct pair embeddings while reducing the cosine similarity of incorrectly matched pairs. This allows the CLIP model to acquire a multimodal embedding space for images and text.
For classification tasks, a set of captions , where M represents the number of classes, is generated using the text descriptions of the target classes and a predefined template. Given an image x, the CLIP model calculates the similarity scores between the image features and the text-encoded class descriptions as follows:
where represents the cosine similarity. Then, the model classifies the image by assigning it to the class with the caption that maximizes the similarity between the image and the features, as follows:
3.3. Local Training
In this section, we introduce a fine-tuning approach for clients that preserves the open-vocabulary property of the model. In this study, the text encoder is frozen, and only the visual encoder is learnable following the fine-tuning of the CLIP model in conventional image classification tasks [44].
We use cross-entropy loss to fine-tune the image encoder to improve classification performance. Rather than relying solely on similarity-based inference, we introduce a supervised learning objective that explicitly optimizes accurate class assignments. In particular, the similarity scores are normalized using the softmax operation to obtain a probability distribution across the candidate classes.
where denotes the one-hot encoding, which represents the correct class label. The model is optimized using the following standard cross-entropy loss:
This approach ensures that the image encoder learns to map images to their corresponding textual descriptions, which improves classification accuracy.
When performing classification tasks with an open-vocabulary model such as CLIP, a common approach is to introduce a task-specific classification head that is jointly trained with the image encoder, as described above. However, our method requires model aggregation after each client fine-tunes the model on its local training data; thus, maintaining a unified model architecture across clients is essential.
Following the approach in [36] to address this issue, we construct a matrix that functions as a fixed classification layer. Specifically, we calculate the text embeddings of all class captions for each dataset and concatenate them. By calculating the dot product between the image features and text embeddings in the matrix, similarity scores for individual classes can be generated. This design eliminates the need for an additional, learnable classification head, thereby ensuring structural consistency across all clients, which is essential for effective model aggregation. Note that only the visual encoder is merged when the model is aggregated. In addition, as demonstrated in [36], using this fixed classification layer has a minimal impact on accuracy compared to using an entirely learnable classifier. During the testing phase, the same matrix is employed as the classification layer, which is consistent with the training procedure.
3.4. Merge Method
In this section, we detail the model merging techniques used as the merge function in our experiments. We investigate six model merging methods in Table 1. Model merging methods may have hyperparameters, which are generally determined based on the accuracy of a separately prepared evaluation dataset. In contrast, the training data are only held by the client in the FL setting; thus, hyperparameter tuning using the evaluation dataset is not possible. Therefore, we used values that would result in the highest final accuracy in our experiments.

Table 1.
Model merging methods used or analyzed in this study.
3.4.1. Averaging [17,34]
A basic approach to merging fine-tuned models is to compute the parameter-wise averages among the models. This method, known as FedAvg, is expressed as follows:
3.4.2. PAINT [36]
PAINT (Patching with Interpolation) combines open-vocabulary models (e.g., CLIP [7]) by interpolating between the models before fine-tuning parameters and those obtained through task-specific fine-tuning. Using the mixing coefficients , the merged model is given by
In this study, we adopted a fixed value for all parameters after fine-tuning rather than optimizing the mixing coefficients to reduce computational overhead.
3.4.3. Task Arithmetic [39]
Task arithmetic interprets the updates introduced by fine-tuning as task vectors. The client-specific fine-tuning update at round t is defined as follows:
The aggregated update is then computed by adding a scaled sum of all task vectors to the original model as follows:
where represents the scaling factor.
3.4.4. TIES Merging [40]
TIES Merging enhances task arithmetic by minimizing interference through three key steps. First, for each client n at round t, the task vector is sparsified by retaining only the top-k% of the parameters based on their absolute values, and the remaining parameters are set to zero:
Next, for each parameter index , the dominant sign is determined as follows:
where represents the value of the parameter of specified by index p. Finally, we average only the values in that have a sign that matches the dominant sign for each parameter index p as follows:
The final model is updated using , similar to task arithmetic.
3.4.5. DARE [41]
DARE (Drop And REscale) is a method to reduce the redundancy of the task vector in task arithmetic. Unlike TIES Merging, rather than pruning based solely on magnitude, DARE applies a random binary mask generated from the Bernoulli distribution parameterized by the drop rate q to each task vector . The remaining parameters are rescaled by amplifying them with . Consequently, each task vector is integrated as follows:
where ⨀ represents the Hadamard product, which is the element-wise product of the matrix. The final model is updated by adding to as with task arithmetic.
3.4.6. Breadcrumbs [45]
Breadcrumbs modifies the task vector by masking parameters that are extremely large or small in the absolute value distribution of each layer. In particular, the parameter values are sorted by their absolute values for each layer L of the task vector. Here, let u be an index that indicates the sorted order of the parameters. Then, the proportions of the top and bottom are masked for each layer as follows:
Here, we obtain by adding all sparsified task vectors applied to the generated masks. The final model is updated by adding to , consistent with task arithmetic.
3.4.7. MagMax [46]
MagMax adopts a strategy that selects the update with the largest absolute value among all task vectors for each parameter. Given the set of candidate updates , the merged update for each parameter p is defined as follows:
The final global model is then obtained by adding these updates to .
4. Experiments
To verify the effectiveness of these model merging methods in the problem setting of this study, we experimented on an image classification task using multiple datasets and the CLIP model. In the experiment, we quantitatively evaluated the accuracy of the global model in the final round. This section explains the details of the experimental settings and results.
4.1. Datasets
We used the following nine datasets as the client dataset and ImageNet [47] as the reference dataset. Table 2 provides an overview of the dataset statistics, detailing the number of samples used for training, validation, and testing, along with the number of classes associated with each dataset.

Table 2.
Statistics for client and reference datasets.
- Cars [48]: The Stanford cars dataset is designed for fine-grained vehicle classification. It comprises a diverse collection of car images that capture subtle differences between car makes and models.
- DTD [49]: The describing textures in the wild (DTD) dataset focuses on texture recognition. It contains images representing a wide variety of textures found in natural and artificial environments.
- EuroSAT [50]: EuroSAT is a remote sensing dataset derived from Sentinel-2 satellite imagery. It provides geo-referenced images covering a broad range of land use and cover types.
- GTSRB [51]: The German Traffic Sign Recognition Benchmark (GTSRB) dataset contains images of traffic signs collected from real-world driving environments.
- KITTI [52]: The KITTI dataset is extensively used in autonomous driving research. It includes diverse driving scenes captured in urban and suburban settings and provides data from multiple sensors such as cameras and light detection and ranging. The dataset supports multiple objectives such as object detection, object tracking, and stereo vision tasks.
- MNIST [53]: The MNIST dataset is a well-known benchmark for handwritten digit recognition consisting of grayscale images of handwritten numbers (0–9).
- RESISC45 [54]: RESISC45 is a remote sensing imagery dataset designed for scene recognition tasks. It encompasses many geographic scenes, providing a solid foundation for developing and assessing algorithms focused on scene understanding and classification in remote sensing imagery.
- SUN397 [55]: The SUN397 dataset contains an extensive set of scene imagery covering a wide range of indoor and outdoor settings. It is commonly applied to scene recognition, providing diverse scene categories to benchmark the effectiveness of models in scene interpretation tasks.
- SVHN [56]: The street view house numbers (SVHN) dataset contains digit samples collected from real-world street view images. It is primarily used for digit recognition tasks in natural contexts with challenges such as varying backgrounds, illumination, and perspectives.
- ImageNet [47]: ImageNet is a widely used visual recognition dataset, providing millions of labeled images spanning numerous object classes.
Each dataset offers unique challenges and is suited to different applications, such as computer vision, remote sensing, and autonomous driving.
4.2. Settings
In this study, we used a pretrained CLIP vision transformer (ViT-B/32) as the core backbone of our model. We adapted the backbone to our task by fine-tuning it over 10 local epochs with a batch size of 128. The learning rate was initialized at and decays according to the cosine annealing schedule to promote stable convergence. To further improve generalizability and mitigate overfitting, we leveraged the AdamW optimizer with a weight decay coefficient of 0.1. Hyperparameter tuning was conducted via grid search based solely on the training data, without utilizing any test data, thereby eliminating concerns about data leakage or overfitting. We adopted top-1 accuracy as the primary evaluation metric. All experiments were implemented in PyTorch 1.7.1 and executed on an NVIDIA RTX 4090 GPU, ensuring efficient training and inference. Our implementation builds on the publicly available code from [36], providing reproducibility and transparency.
4.3. Results
Table 3 presents the experimental results obtained under our evaluation settings. The table reports the accuracy of each method across different datasets, with the results organized by row. The topmost row provides the accuracy of the pretrained model, which serves as a baseline and is labeled as zero-shot. Our findings indicate that, despite its simplicity and ease of implementation, the averaging method achieves accuracy comparable to or exceeding that of other model merging techniques. These results are consistent with the effectiveness of FedAvg in conventional FL. A key advantage of the averaging method is its ability to achieve relatively consistent accuracy across different datasets, exhibiting less variance in performance compared to other model merging strategies. Although it did not exhibit a particular advantage on any single dataset, its overall average accuracy exceeded that of PAINT and MagMax. This suggests that the averaging method provides a more balanced approach, effectively generalizing across diverse datasets without being overly influenced by specific dataset characteristics. In contrast, PAINT exhibited the highest accuracy on ImageNet, which was used as the reference dataset. This can be attributed to the weighted averaging strategy of PAINT, which incorporates model parameters before and after fine-tuning. This allows the parameters of the updated model to be retained because they are not significantly different from the parameters of the pretrained model. Consequently, PAINT probably mitigates the catastrophic forgetting of knowledge obtained through pretraining. These results highlight the importance of explicitly incorporating mechanisms that preserve pretraining knowledge when continuously updating FMs via model merging. Conventional model merging methods often fail to sufficiently retain the knowledge acquired during pretraining, leading to degraded performance or forgetting of foundational capabilities. In addition, the sparsity-based model merging methods, such as DARE and Breadcrumbs, also exhibit high accuracy. This suggests that task vectors derived from fine-tuning contain many redundant parameters, which may introduce interference during aggregation in our settings.

Table 3.
Classification accuracy obtained on each test dataset after 10 rounds in our experimental setting. The bold numbers in the table indicate the best results, and the underlined numbers represent the second-best results.
Figure 2 shows the accuracy trends over multiple rounds as the scaling factor in task arithmetic is varied. When the scaling factor is set to 0.1 or lower, accuracy increases monotonically with each round. Conversely, when the scaling factor is 0.2, the accuracy curve exhibits a convex shape. In addition, when the scaling factor exceeds 0.3, the accuracy peaks before round 10 and subsequently decreases. However, with a scaling factor of 0.5, accuracy increases after round 5. In this experiment, the number of clients is set to 9, and averaging the task vectors corresponds to scaling by . The strong performance observed at a scaling factor of approximately 0.1 further reinforces the effectiveness of the averaging process, which is also shown to yield high accuracy in Table 3.
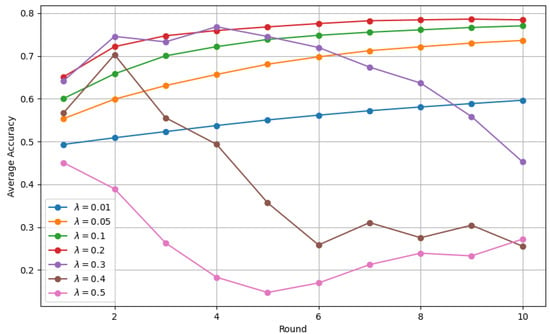
Figure 2.
Change in average accuracy in each round when the scaling factor is changed in task arithmetic. The colors of the plotted graphs represent the accuracy of each scaling factor.
Figure 3 depicts the cosine similarity of the task vectors between the initial and final rounds of task arithmetic. A similarity value of 0 indicates that the task vectors are orthogonal, which implies minimal interference between them. As shown in Figure 3, the task vector similarity is generally low; however, in the initial round, the similarity between MNIST and SVHN is relatively high (0.17). This may be because both datasets contain digit images, leading to higher task similarity. In contrast, in the final round, the similarity of all task vectors decreases to below 0.05. As training progresses, learning converges, and the task vectors become increasingly independent. Consequently, task vectors naturally exhibit orthogonality in later rounds even without explicit sparsification techniques. This indicates that additional sparsification processes are unnecessary and lead to adverse effects.
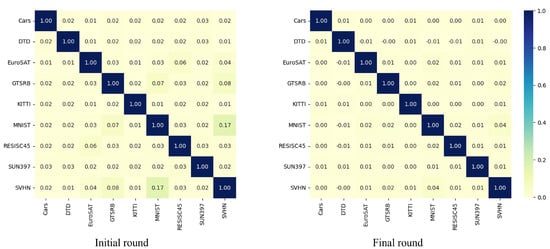
Figure 3.
Cosine similarity of task vectors in first and last rounds when models are merged using task arithmetic. The darker the color, the higher the similarity between the task vectors; the lighter the color, the more orthogonal the task vectors are.
5. Discussion
The experimental results confirm the effectiveness of the model merging techniques. In particular, the model merging methods exhibited superior accuracy improvements compared to simple averaging within the FL context. Specifically, we observed that model merging resulted in a significant increase in accuracy for new tasks, highlighting its advantage in adapting to unseen data distributions. However, there was a trade-off between improving accuracy on new tasks and retaining previously acquired knowledge. Our experiments identified several key considerations for the practical application of continuous model merging methods. These insights are summarized as follows:
- Challenges in Selecting Effective Methods: In this study, we applied a single model merging method iteratively to update the model. However, as illustrated in Figure 3, the similarity between the task vectors varies significantly between the initial and final rounds of continuous model updating. This suggests that the interference between task vectors, which has conventionally been a concern in model merging, is not significant in later rounds. Consequently, techniques such as sparsification, which are typically employed to mitigate such interference, may become unnecessary in the later stages of training.Deeper analysis of the task vectors reveals that the model increasingly adapts to different datasets as learning progresses, which results in the task vectors becoming more orthogonal. The extent of interference between the task vectors decreases over time, potentially reducing the need for explicit sparsification mechanisms in later rounds. More broadly, this finding highlights a gap in existing research regarding the selection of appropriate model merging strategies for different training phases. Depending on the similarity between tasks and the stage of learning progression, different merging algorithms may be more effective. Therefore, exploring a variety of merging techniques is essential for enhancing the generality and adaptability of the proposed framework.
- Challenges in Hyperparameter Optimization: In this study, the hyperparameters of each model merging method were determined empirically. However, as demonstrated in Figure 2, model accuracy is highly sensitive to the choice of hyperparameters. In task arithmetic, variations in the scaling factor resulted in accuracy differences of approximately 50%, highlighting the critical impact of hyperparameter selection.Typically, hyperparameters are fine-tuned to maximize performance on a predefined evaluation dataset. However, defining a single evaluation dataset is inherently challenging in distributed data environments, such as the setting of the present study. This confuses the process of hyperparameter selection and tuning. To address this issue, it is important to develop hyperparameter optimization methods that do not rely on explicitly defined evaluation datasets. Based on these observations, we plan to develop hyperparameter selection and control mechanisms as an important direction for future work, aiming to enable more robust and scalable training in decentralized learning environments.Furthermore, the results presented in Table 3 indicate that conventional model merging methods struggle to retain previously acquired knowledge, instead primarily specializing in new tasks. To mitigate this issue, it is essential to establish a framework that facilitates the acquisition of new knowledge and actively prevents catastrophic forgetting. Developing mechanisms that balance knowledge retention and adaptation to new tasks remains critical for future research.
In summary, continuous model merging can significantly improve accuracy for new tasks; however, it poses a risk of forgetting previously learned knowledge. Over time, interference among task vectors decreases, suggesting that techniques such as sparsification may be less critical in later rounds. In addition, hyperparameter tuning remains challenging without a unified evaluation dataset, underscoring the need for adaptive strategies that balance knowledge retention and adaptation to new tasks.
In future work, we will investigate the effectiveness of existing continual learning approaches in mitigating knowledge forgetting, particularly those that do not rely on storing data buffers. In this context, integrating parameter preservation mechanisms such as EWC [19] can help stabilize model updates while retaining previously learned knowledge. In addition, we plan to explore task similarity-aware dynamic model updating strategies that can adjust model aggregation weights based on the relationships between tasks. Furthermore, we will conduct a comprehensive analysis of the computational cost, memory usage, and communication overhead associated with different model merging methods. In particular, we aim to quantify the costs of operations such as communication and per-layer processing during merging, as these factors are critical for evaluating the scalability of the proposed framework to large-scale foundation models. A thorough evaluation of these aspects is essential for validating the practicality and deployability of our framework in real-world federated learning systems.
6. Conclusions and Outlooks
We established a novel problem setting for continually updating FMs using model merging methods and analyzed the effectiveness of various merging approaches. Our findings demonstrate that although model merging achieves higher accuracy than simple averaging, explicit mechanisms to mitigate knowledge forgetting are essential for preserving previously learned information. Furthermore, we identified hyperparameter dependence as a critical bottleneck that limits the scalability of model merging methods.
In our experiments, each client fully fine-tuned the image encoder of the CLIP model to enable a fundamental analysis of the proposed framework. However, given the numerous parameters in large-scale models, full fine-tuning on resource-constrained clients is impractical. As an alternative, parameter-efficient fine-tuning (PEFT) methods [57], such as LoRA, are typically employed to reduce computational costs. In future work, we plan to incorporate PEFT into our framework and investigate model merging strategies that remain effective under resource-constrained settings while maintaining computational efficiency.
In addition, we plan to extend our experimental environment to more realistic scenarios in order to further investigate the limitations of conventional model merging methods. A key future direction is the development of new merging techniques that can dynamically assign aggregation weights to fine-tuned models without relying on explicitly defined evaluation data, thereby enhancing adaptability and robustness in distributed learning environments. We also aim to evaluate these techniques under heterogeneous client conditions, such as varying data distributions and resource constraints, to better validate their practical effectiveness.
Author Contributions
Conceptualization, K.K., R.T., K.M. and T.O.; methodology, K.K., R.T., K.M. and T.O.; software, K.K.; validation, K.K.; data curation, K.K.; writing—original draft preparation, K.K.; writing—review and editing, K.K., R.T., K.M. and T.O.; visualization, K.K.; funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by JSPS KAKENHI Grant Numbers JP24K02942, JP23K21676, JP23K11211, and JP23K11141.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
A publicly available datasets were used in this work. The datasets can be found here; Cars: https://www.kaggle.com/datasets/cyizhuo/stanford-cars-by-classes-folder, DTD: https://www.robots.ox.ac.uk/~vgg/data/dtd, EuroSAT: https://github.com/phelber/eurosat, GTSRB: https://benchmark.ini.rub.de, KITTI: https://www.cvlibs.net/datasets/kitti/eval_object.php?obj_benchmark, MNIST: http://yann.lecun.com/exdb/mnist/, RESISC45: https://1drv.ms/u/s!AmgKYzARBl5ca3HNaHIlzp_IXjs, SUN397: https://vision.princeton.edu/projects/2010/SUN, SVHN: http://ufldl.stanford.edu/housenumbers/ (accessed on 25 April 2025).
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish results.
References
- Jaiswal, A.; Babu, A.R.; Zadeh, M.Z.; Banerjee, D.; Makedon, F. A survey on contrastive self-supervised learning. Technologies 2020, 9, 2. [Google Scholar] [CrossRef]
- Bommasani, R.; Hudson, D.A.; Adeli, E.; Altman, R.; Arora, S.; von Arx, S.; Bernstein, M.S.; Bohg, J.; Bosselut, A.; Brunskill, E.; et al. On the opportunities and risks of foundation models. arXiv 2021, arXiv:2108.07258. [Google Scholar]
- Achiam, J.; Adler, S.; Agarwal, S.; Ahmad, L.; Akkaya, I.; Aleman, F.L.; Almeida, D.; Altenschmidt, J.; Altman, S.; Anadkat, S.; et al. Gpt-4 technical report. arXiv 2023, arXiv:2303.08774. [Google Scholar]
- Liu, H.; Li, C.; Wu, Q.; Lee, Y.J. Visual instruction tuning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 9–15 December 2024; Volume 36. [Google Scholar]
- Team, G.; Anil, R.; Borgeaud, S.; Alayrac, J.B.; Yu, J.; Soricut, R.; Schalkwyk, J.; Dai, A.M.; Hauth, A.; Millican, K.; et al. Gemini: A family of highly capable multimodal models. arXiv 2023, arXiv:2312.11805. [Google Scholar]
- Li, J.; Li, D.; Xiong, C.; Hoi, S. Blip: Bootstrapping language-image pre-training for unified vision-language understanding and generation. In Proceedings of the International Conference on Machine Learning (ICML), Baltimore, MD, USA, 17–23 July 2022; pp. 12888–12900. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning (ICML), Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Jin, Y.; Li, J.; Liu, Y.; Gu, T.; Wu, K.; Jiang, Z.; He, M.; Zhao, B.; Tan, X.; Gan, Z.; et al. Efficient multimodal large language models: A survey. arXiv 2024, arXiv:2405.10739. [Google Scholar]
- Ren, C.; Yu, H.; Peng, H.; Tang, X.; Zhao, B.; Yi, L.; Tan, A.Z.; Gao, Y.; Li, A.; Li, X.; et al. Advances and Open Challenges in Federated Foundation Models. arXiv 2024, arXiv:2404.15381. [Google Scholar] [CrossRef]
- Zhuang, W.; Chen, C.; Lyu, L. When foundation model meets federated learning: Motivations, challenges, and future directions. arXiv 2023, arXiv:2306.15546. [Google Scholar]
- Villalobos, P.; Sevilla, J.; Heim, L.; Besiroglu, T.; Hobbhahn, M.; Ho, A. Will we run out of data? An analysis of the limits of scaling datasets in machine learning. arXiv 2022, arXiv:2211.04325. [Google Scholar]
- Shoeybi, M.; Patwary, M.; Puri, R.; LeGresley, P.; Casper, J.; Catanzaro, B. Megatron-lm: Training multi-billion parameter language models using model parallelism. arXiv 2019, arXiv:1909.08053. [Google Scholar]
- Hartvigsen, T.; Sankaranarayanan, S.; Palangi, H.; Kim, Y.; Ghassemi, M. Aging with grace: Lifelong model editing with discrete key-value adaptors. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 9–15 December 2024; Volume 36. [Google Scholar]
- Yang, E.; Shen, L.; Guo, G.; Wang, X.; Cao, X.; Zhang, J.; Tao, D. Model merging in llms, mllms, and beyond: Methods, theories, applications and opportunities. arXiv 2024, arXiv:2408.07666. [Google Scholar]
- Li, W.; Peng, Y.; Zhang, M.; Ding, L.; Hu, H.; Shen, L. Deep model fusion: A survey. arXiv 2023, arXiv:2309.15698. [Google Scholar]
- Dziadzio, S.; Udandarao, V.; Roth, K.; Prabhu, A.; Akata, Z.; Albanie, S.; Bethge, M. How to Merge Your Multimodal Models Over Time? arXiv 2024, arXiv:2412.06712. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Yang, Y.; Zhou, J.; Ding, X.; Huai, T.; Liu, S.; Chen, Q.; Xie, Y.; He, L. Recent advances of foundation language models-based continual learning: A survey. ACM Comput. Surv. 2024, 57, 1–38. [Google Scholar] [CrossRef]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
- Rolnick, D.; Ahuja, A.; Schwarz, J.; Lillicrap, T.; Wayne, G. Experience replay for continual learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Gui, Z.; Sun, S.; Li, R.; Yuan, J.; An, Z.; Roth, K.; Prabhu, A.; Torr, P. kNN-CLIP: Retrieval Enables Training-Free Segmentation on Continually Expanding Large Vocabularies. arXiv 2024, arXiv:2404.09447. [Google Scholar]
- Roth, K.; Udandarao, V.; Dziadzio, S.; Prabhu, A.; Cherti, M.; Vinyals, O.; Hénaff, O.; Albanie, S.; Bethge, M.; Akata, Z. A Practitioner’s Guide to Continual Multimodal Pretraining. arXiv 2024, arXiv:2408.14471. [Google Scholar]
- Steiner, A.; Kolesnikov, A.; Zhai, X.; Wightman, R.; Uszkoreit, J.; Beyer, L. How to train your vit? data, augmentation, and regularization in vision transformers. arXiv 2021, arXiv:2106.10270. [Google Scholar]
- Zhang, G.; Wang, L.; Kang, G.; Chen, L.; Wei, Y. Slca: Slow learner with classifier alignment for continual learning on a pre-trained model. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 19148–19158. [Google Scholar]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. In Proceedings of the Machine Learning and Systems, Austin, TX, USA, 2–4 March 2020; Volume 2, pp. 429–450. [Google Scholar]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated learning with non-iid data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- Tian, Y.; Wan, Y.; Lyu, L.; Yao, D.; Jin, H.; Sun, L. FedBERT: When federated learning meets pre-training. ACM Trans. Intell. Syst. Technol. (TIST) 2022, 13, 1–26. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. Lora: Low-rank adaptation of large language models. arXiv 2021, arXiv:2106.09685. [Google Scholar]
- Babakniya, S.; Elkordy, A.R.; Ezzeldin, Y.H.; Liu, Q.; Song, K.B.; El-Khamy, M.; Avestimehr, S. SLoRA: Federated parameter efficient fine-tuning of language models. arXiv 2023, arXiv:2308.06522. [Google Scholar]
- Zhao, H.; Du, W.; Li, F.; Li, P.; Liu, G. Fedprompt: Communication-efficient and privacy-preserving prompt tuning in federated learning. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Zhu, H.; Togo, R.; Ogawa, T.; Haseyama, M. Prompt-based personalized federated learning for medical visual question answering. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 1821–1825. [Google Scholar]
- Dietterich, T.G. Ensemble learning. Handb. Brain Theory Neural Netw. 2002, 2, 110–125. [Google Scholar]
- Wortsman, M.; Ilharco, G.; Gadre, S.Y.; Roelofs, R.; Gontijo-Lopes, R.; Morcos, A.S.; Namkoong, H.; Farhadi, A.; Carmon, Y.; Kornblith, S.; et al. Model soups: Averaging weights of multiple fine-tuned models improves accuracy without increasing inference time. In Proceedings of the International Conference on Machine Learning (ICML), Baltimore, MD, USA, 17–23 July 2022; pp. 23965–23998. [Google Scholar]
- Ramé, A.; Ahuja, K.; Zhang, J.; Cord, M.; Bottou, L.; Lopez-Paz, D. Model ratatouille: Recycling diverse models for out-of-distribution generalization. In Proceedings of the International Conference on Machine Learning (ICML), Honolulu, HI, USA, 23–29 July 2023; pp. 28656–28679. [Google Scholar]
- Ilharco, G.; Wortsman, M.; Gadre, S.Y.; Song, S.; Hajishirzi, H.; Kornblith, S.; Farhadi, A.; Schmidt, L. Patching open-vocabulary models by interpolating weights. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 29262–29277. [Google Scholar]
- Matena, M.S.; Raffel, C.A. Merging models with fisher-weighted averaging. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 17703–17716. [Google Scholar]
- Frankle, J.; Dziugaite, G.K.; Roy, D.; Carbin, M. Linear mode connectivity and the lottery ticket hypothesis. In Proceedings of the International Conference on Machine Learning (ICML), Virtual, 13–18 July 2020; pp. 3259–3269. [Google Scholar]
- Ilharco, G.; Ribeiro, M.T.; Wortsman, M.; Gururangan, S.; Schmidt, L.; Hajishirzi, H.; Farhadi, A. Editing models with task arithmetic. arXiv 2022, arXiv:2212.04089. [Google Scholar]
- Yadav, P.; Tam, D.; Choshen, L.; Raffel, C.A.; Bansal, M. Ties-merging: Resolving interference when merging models. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 9–15 December 2024; Volume 36. [Google Scholar]
- Yu, L.; Yu, B.; Yu, H.; Huang, F.; Li, Y. Language models are super mario: Absorbing abilities from homologous models as a free lunch. In Proceedings of the International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Yang, E.; Wang, Z.; Shen, L.; Liu, S.; Guo, G.; Wang, X.; Tao, D. Adamerging: Adaptive model merging for multi-task learning. arXiv 2023, arXiv:2310.02575. [Google Scholar]
- Akiba, T.; Shing, M.; Tang, Y.; Sun, Q.; Ha, D. Evolutionary optimization of model merging recipes. Nat. Mach. Intell. 2025, 7, 195–204. [Google Scholar] [CrossRef]
- Wortsman, M.; Ilharco, G.; Kim, J.W.; Li, M.; Kornblith, S.; Roelofs, R.; Lopes, R.G.; Hajishirzi, H.; Farhadi, A.; Namkoong, H.; et al. Robust fine-tuning of zero-shot models. In Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 2022; pp. 7959–7971. [Google Scholar]
- Davari, M.; Belilovsky, E. Model breadcrumbs: Scaling multi-task model merging with sparse masks. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September–4 October 2024; pp. 270–287. [Google Scholar]
- Marczak, D.; Twardowski, B.; Trzciński, T.; Cygert, S. Magmax: Leveraging model merging for seamless continual learning. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September–4 October 2024; pp. 379–395. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25. [Google Scholar]
- Krause, J.; Stark, M.; Deng, J.; Fei-Fei, L. 3d object representations for fine-grained categorization. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops, Sydney, Australia, 1–8 December 2013; pp. 554–561. [Google Scholar]
- Cimpoi, M.; Maji, S.; Kokkinos, I.; Mohamed, S.; Vedaldi, A. Describing textures in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 3606–3613. [Google Scholar]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Eurosat: A novel dataset and deep learning benchmark for land use and land cover classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef]
- Stallkamp, J.; Schlipsing, M.; Salmen, J.; Igel, C. The German traffic sign recognition benchmark: A multi-class classification competition. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011; pp. 1453–1460. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Xiao, J.; Ehinger, K.A.; Hays, J.; Torralba, A.; Oliva, A. Sun database: Exploring a large collection of scene categories. Int. J. Comput. Vis. 2016, 119, 3–22. [Google Scholar] [CrossRef]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS) Workshop, Granada, Spain, 12–14 December 2011; Volume 2011, p. 4. [Google Scholar]
- Han, Z.; Gao, C.; Liu, J.; Zhang, J.; Zhang, S.Q. Parameter-efficient fine-tuning for large models: A comprehensive survey. arXiv 2024, arXiv:2403.14608. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).