Abstract
As a major emission pollutant from diesel engines, NOx is extremely harmful to the environment and human health. In order to reduce NOx emissions, countries around the world have been implementing increasingly stringent emissions regulations. The urea injection strategies of the Selective Catalytic Reduction (SCR) system are the main factors affecting NOx emissions and NH3 slips of diesel engines. In this study, test data were obtained from an engine test stand and a Support Vector Machine (SVM) was developed using the test data to predict NOx conversion efficiency and NH3 slip. The SVM model was optimized using the Crested Porcupine Optimizer (CPO) to improve its prediction accuracy and was made to replace the mathematical model to save computational time. Finally, the Nondominated Sorting Genetic Algorithm II (NSGA-II) was used to optimize the urea injection volume for all conditions. The optimized urea injection volume maximizes the NOx conversion efficiency of the SCR system while controlling the NH3 slip within 10 ppm. In addition, based on this method, the urea injection pulse spectrum under full operating conditions was obtained, and the optimized urea injection amount can effectively reduce the NOx accumulation of the WHTC cycle by about 7.5%, as shown through bench testing.
1. Introduction
Exhaust emissions from diesel vehicles have long been a major contributor to nitrogen oxides (NOx) in the air, and NOx has been shown to be a serious hazard to both the natural environment and humans [1,2,3]. With the introduction of the Euro VII emission regulations [4], more stringent emission standards are about to be implemented, which means that the emission limits for NOx will be further reduced compared to the Euro VI emission regulations. Although exhaust gas recirculation (EGR) can effectively reduce NOx emissions [5], selective catalytic reduction (SCR) is still the most efficient technology to reduce NOx emissions [6,7,8].
The SCR system requires the injection of aqueous urea solution during operation, which undergoes hydrolysis to produce ammonia (NH3), and which undergoes a reduction reaction with NOx to produce N2 and H2O, catalyzed by a catalyst within the SCR [9]. Although increasing urea injection can improve the NOx conversion efficiency of the SCR system and reduce NOx emissions, excessive urea injection will create more NH3 slip, and NH3 jeopardizes the natural environment and human health [10,11].
In recent years, many have been conducted to improve NOx conversion efficiency, studies such as optimizing the catalyst formulation in SCR and high-pressure SCR spray systems [8,12]. However, the study of catalysts and SCR structure is usually complicated because it involves the interaction of several aspects, and optimizing only one of these factors not only has a limited effect on the improvement of NOx conversion efficiency, but also requires a large number of bench tests for validation, which consumes time and financial resources. Secondly, prior studies have neglected the effect of NH3 slip. Currently, in order to improve NOx conversion efficiency as much as possible within the NH3 emission limits required by the emission regulations, finding an optimization strategy using a mathematical model-based approach is an effective method [13,14]. Hu et al. studied and developed a time-discretized and space-integrated (TDSI) SCR model with dual temperature-dependent parameters [15]. Their spatial integration model was improved by introducing NH recovery, which improved the accuracy of the model estimation. Bozbağ et al. modeled the transient kinetics of seven different catalysts and developed a model-based catalyst screening strategy to control NOx emissions [16]. Gao et al. developed a comprehensive selective catalytic reduction (SCR) model detailing the global kinetic reactions in the catalyst involving both high and low temperature NH3 adsorption/desorption sites, as well as low-temperature H2O storage for the design and optimization of SCR catalysts [17]. Yan et al. applied a physicochemical model-based Nondominated Sorting Genetic Algorithm II to obtain the desired urea dosage feed ratio and to achieve an optimal trade-off between NOx reduction and NH3 slip to realize benefits such as improved fuel and urea efficiency [18]. Capetillo et al. measured the effects of three urea injection parameters—injection velocity, injection angle and droplet size—on NH3 distribution and wall film formation in a SCR system and optimized the performance of the SCR system using a linear regression model with the help of 23 full factorial DoE for multiphase CFD simulations [19]. Although the use of mathematical model-based methods can achieve the prediction of NOx and NH3 emissions or optimize the control strategy to control NOx emissions, the running time of the model is still a concern due to the large number of factors considered by the mathematical model. The computational volume and complexity of the complex model will increase during the running process, which affects the computational speed of the model [20]. Although the simplified mathematical model can improve the computational speed, the simplified assumptions make it difficult for the model to meet the accuracy requirements or cause it to fail to take into account the NOx conversion efficiency and NH3 slip at the same time [13,21,22]. Therefore, it is a worthwhile study to find a high-precision model to optimize the urea injection amount of SCR system to control NOx emission and NH3 slip under the premise of reducing the calculation time.
In order to solve the above problems, this paper proposes a new optimization method for urea injection in diesel engines based on the CPO-SVM-NSGA-II model. The method uses the CPO optimization algorithm to optimize the SVM model and, under the premise of ensuring the prediction accuracy of the SVM model for NOx conversion efficiency and NH3 slip, the SVM model is used as the objective function to optimize the SCR urea injection using the NSGA-II to improve the NOx conversion efficiency of the SCR as much as possible within the NH3 emission limits required by the emission regulations. Also, the optimization time of the model proposed in this study will be reduced considerably compared to the mathematical model.
2. Test Equipment and Data Acquisition
A 3-L, four-cylinder inline diesel engine with supercharged intercooling was selected for the test, and the aftertreatment system was a combination of Diesel Oxidation Catalyst (DOC) + Diesel Particulate Filter (DPF) + SCR + Ammonia Slip Catalyst (ASC). The parameters of each component of the aftertreatment system are shown in Table 1. The bench test utilized a Dynas3 electric dynamometer to control the speed and torque of the diesel engine. The engine raw NOx and post-SCR NOx were collected and measured by a HORIBA MEXA-ONE gas analyzer (±2.0 per cent of the reading), and the NH3 slip was collected and measured by a HORIBA FTX-ONE-CS/RS (±2.0 per cent of the reading). Other data, such as exhaust temperature and exhaust flow, were displayed and saved in real time by the STARS system. The engine parameters are shown in Table 2. The type of urea used in the test was an aqueous urea solution of 32.5. Specific information about the test equipment, such as temperature and pressure, is shown in Table 3.

Table 1.
Test bench aftertreatment system parameter.

Table 2.
Engine specifications.

Table 3.
Test Equipment.
In this study, the diesel engine bench test procedure was to regulate the speed of the diesel engine from 1000 rpm to 2800 rpm at intervals of 100 rpm, with test data collection at 50 Nm intervals. The collected data include the following: diesel engine speed, torque, exhaust temperature, SCR inlet temperature, exhaust flow rate, NOx emission before SCR, NOx emission after SCR, NH3 slip and other parameters. The original engine emission parameters are shown in Figure 1.
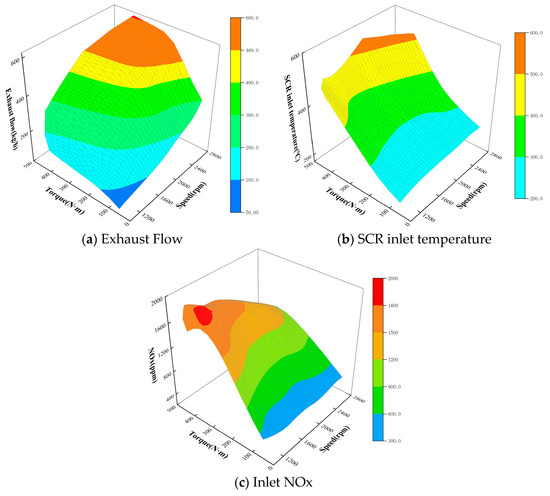
Figure 1.
Original engine emission parameters.
The test data for engine performance and emission parameters under some operating conditions are shown in Table 4. As shown in the table, each SCR inlet NOx concentration corresponds to a unique set of SCR inlet temperatures as well as exhaust flow rates. Therefore, the urea injection volume can be used as a unique parameter to control the SCR outlet NOx concentration. Considering the constant SCR inlet temperature, NOx concentration and exhaust flow rate for each operating condition, different SCR outlet NOx concentrations and NH3 slip are obtained for each urea injection amount. Therefore, for all operating conditions, varying the urea injection amount, 25 sets of corresponding SCR outlet NOx concentrations and NH3 slip amounts were obtained.

Table 4.
Engine performance and emission parameters.
3. Optimization Models
3.1. Crested Porcupine Optimizer (CPO) Optimization
The Support Vector Machine (SVM) was proposed by Cortes and Vapnik in 1995 and shows many unique advantages in solving small samples and in nonlinear and high-dimensional pattern recognition, and it can be generalized to other machine learning problems such as function fitting [23]. In this study, for each working condition point there are 25 sets of experimental data. Therefore, in the case of fewer data samples, it is obvious that SVM is more advantageous compared to other machine learning methods such as neural networks.
Most machine learning algorithms have a number of parameters that can be tuned, called hyperparameters. Hyperparameters are very important in building effective and accurate models. They help us find a balance between bias and variance, thus preventing the model from overfitting or underfitting. In order to improve the predictive accuracy of SVM models, it is necessary to find the optimal hyperparameter penalty coefficient C, as well as the kernel function coefficient gamma.
The Crested Porcupine Optimizer (CPO) algorithm was proposed by Mohamed Abdel-Basset and, along with the Particle Swarm Optimization (PSO) algorithm, is a population-based algorithm. Population-based algorithms have advantages over single-based algorithms due to their strong search space and global optimum. In addition, the core advantage of CPO and PSO optimization of SVM is its global search capability, efficiency and ease of use, and it is especially suitable for complex kernel function parameter optimization and small sample scenarios. Its robustness can be further enhanced when combined with hybrid strategies or adaptive improvement. Therefore, it will be combined with genetic algorithm in the subsequent optimization process to avoid overfitting. However, the CPO algorithm is more effective than its counterparts in terms of average fitness, standard deviation, convergence curve and computational cost [24]. Therefore, in this paper, the CPO algorithm is used to optimize the hyperparameters of the SVM model and the optimization results are compared with those of the PSO algorithm.
The CPO optimization algorithm combines exploration and exploitation mechanisms by visualizing the search space. The first two of these defense strategies (vision and sound) correspond to exploratory behaviors, and the last two (odor and physical attack) correspond to exploitative behaviors. The algorithm is similar to other population metaheuristics in that the search is initiated from an initial set of candidate solutions and the quality of individuals is evaluated by an objective function.
The optimization problem consists of multiple dimensions, all of which need to be applied to minimize or maximize. The CPO algorithm begins by randomly initializing the dimensions within the search space of each problem, as shown in Equation (1).
where denotes the number of individuals (population size), is the ith candidate solution in the search space, and are the lower and upper boundaries of the search range, respectively, and is a vector randomly initialized between 0 and 1. The initial population can be represented by Equation (2).
where X is the population matrix, is the ith member of the population. denotes the jth position of the ith solution, is the number of candidate solutions and d denotes the size of the dimension of the given problem.
The CPO optimization algorithm introduces a cyclic population reduction technique designed to accelerate convergence and maintain population diversity. The technique simulates a mechanism whereby only threatened population members initiate a defense response. During the optimization process, some of the population members are temporarily withdrawn to accelerate convergence and subsequently reintroduced to enhance diversity and avoid local optima. This cyclic process is controlled by the variable T, which determines the number of executions. The mathematical expression for population size reduction is given in Equation (3).
where T is the variable that determines the number of cycles, t is the current number of function evaluations, is the maximum number of function evaluations, % stands for the remainder or modulus operator and is the minimum number of individuals in the newly generated population, i.e., the size of the population must not be smaller than .
In the exploration phase of the CPO optimization algorithm, population members adopt two defense strategies based on predator distance: a visual strategy and an acoustic strategy. In the first strategy, population members create the illusion of larger size by lifting and flapping their feathers, forcing the predator to choose between approaching or moving away. If the predator moves closer, the distance between the two decreases, promoting local area exploration to accelerate convergence; if the predator moves away, the distance is maximized, promoting the search of unexplored areas for potential solutions. This behavior is simulated by generating random values through a normal distribution, the mathematical expression of which is shown in Equation (4).
where is the optimal solution of the function evaluating t, is a vector generated between the current population member and a randomly selected population member from the population, representing the position of the predator at iteration t, is a random number based on a normal distribution and is a random value in the interval [0, 1]. can be expressed by Equation (5):
where r is a random number between [1, N]. This equation provides the CPO optimization algorithm with a strong potential to cover the entire search space as much as possible, thus avoiding falling into local minima.
The second defense strategy is as follows: in this strategy, members of the population use acoustic methods to create noise and threaten predators. When a predator approaches, the porcupine’s voice becomes louder. To model this behavior mathematically, it is represented using Equation (6):
where and are two random integers between [1, N] and is a random value generated between 0 and 1.
In the development phase of the CPO optimization algorithm, when a predator approaches, the population members employ odor and physical attack strategies that focus on local search to exploit potential areas.
The CPO algorithm uses these strategies to approximate the optimal solution in the search space. In the third strategy, population members secrete foul odors to discourage predators from approaching, the mathematical simulation of which is shown in Equation (7):
where is a random number between [1, N], is a parameter controlling the search direction, defined by Equation (8), is the position of the ith individual at iteration t, is a defense factor defined by Equation (9), is the odor diffusion factor, defined by Equation (10).
where denotes the value of the objective function of the ith individual at iteration t, is a small value to avoid division by zero, is a vector containing random numbers between 0 and 1, is a random number between 0 and 1, N is the population size, t is the current number of iterations, and is the maximum number of iterations. The vector simulates three scenarios: (1) when = 0, the predator stops moving and the population members stop spreading odors at the same distance, (2) when = 1, the population members release noticeable odors and (3) when is a combination of 0 and 1, the predator maintains a safe distance from the population members without the need to release large amounts of odors.
The fourth defense strategy is physical attack. When a predator approaches, members of the population attack with short, thick feathers, simulating a one-dimensional inelastic collision. Its mathematical expression is shown in Equation (11).
where is the optimal solution, denoting the population member, is the position of the ith individual at iteration t, denoting the predator at that position, is the convergence rate factor, is a random value in the interval [0, 1] and is the average force affecting the ith predator’s population member, as provided by the non-elastic collision law given by Equation (12):
where is the mass of the ith individual (predator) at iteration t, denotes the objective function, is the final velocity of the ith individual at the next iteration t + 1, assigned according to a random solution chosen from the current population, is the initial velocity of the ith individual at iteration t, is the current number of iterations and is a vector including random values between 0 and 1.
In the SCR system, the parameters affecting the NOx conversion efficiency are mainly the SCR inlet temperature, exhaust flow rate, SCR inlet NOx concentration and urea injection volume. Therefore, these four data points are selected as input parameters of the SVM model for each condition, and the output parameters are NOx conversion efficiency and NH3 slip. The output parameter NH3 slip is the NH3 slip before ASC, and the NH3 slip after ASC is not selected because it is more difficult to observe the NH3 slip when the urea injection volume is low. in order not to affect the prediction accuracy of the SVM model for the NH3 slip, the NH3 slip before ASC is selected as the output parameter of the model. The NOx conversion efficiency is calculated by Equation (13).
where is the NOx conversion efficiency, %, and are SCR inlet and outlet NOx concentrations, respectively, ppm.
Of the 25 sets of data for each operating condition, a randomized division was used to divide the dataset in order to eliminate the subjective errors of manual division. A total of 70% of the data (18 sets) were selected to train the SVM model, and the remaining 30% (7 sets) were used to test it. Before training the model, the four input parameters have different magnitudes; in order not to affect the model training results and eliminate the effect of magnitude, the input parameters are normalized using Equation (14). Taking 1800 rpm-300 Nm as an example, 25 sets of test data are shown in Table 5.
where is the sample data, is the maximum value of the sample data and is the minimum value of the sample data.

Table 5.
Test data under the 1800 rpm-300 Nm operating condition.
In support vector machines (SVMs), the penalty coefficient C and the kernel function coefficient gamma are the two most critical tuning parameters, both of which directly affect the classification performance and generalization ability of the model. The penalty coefficient C is defined to control the penalty strength of classification error and balance the model complexity and training error. The kernel coefficient gamma is defined to control the “width” of the Gaussian kernel function, which determines the influence of a single sample. Both parameters can be set when building the SVM model. In this paper, in order to find the optimal penalty coefficient C and kernel coefficient gamma, these two parameters are used as the parameters to be optimized; the empirical range of values for these two parameters is [10−2, 103]. Both parameters have an upper bound of 1000 and a lower bound of 0.01, and their values are real numbers. The population size for both optimizations was 20 and the number of iterations was 50. Finally, the model was evaluated using the coefficient of determination R2 and Root Mean Square Error (RMSE).
In order to compare the optimization of the two algorithms, three working conditions, 1200 rpm-75 Nm, 1800 rpm-300 Nm, 2400 rpm-450 Nm, were selected to show the results of the optimization among all the working conditions. Table 6 lists the optimal parameter penalty coefficients C and the kernel function coefficients gamma.

Table 6.
Optimal parameters.
Figure 2 and Figure 3 show the test results with NOx conversion efficiency and NH3 slip as SVM model outputs, respectively. For model accuracy, the coefficient of determination R2 and RMSE were used to assess the model accuracy, as shown in Table 7 and Table 8. For the prediction of NOx conversion efficiency, it can be seen that the CPO optimization algorithm as well as the PSO optimization algorithm are able to make accurate predictions of NOx conversion efficiency under the three operating conditions. The coefficient of determination R2 of the SVM model optimized by the CPO optimization algorithm is above 0.98 and RMSE for the three conditions is 0.76, while the coefficient of determination R2 of the SVM model optimized by the PSO optimization algorithm is about 0.96 and the RMSE for the three conditions is 2.05. It can be seen that the SVM model optimized by the CPO optimization algorithm can predict the NOx conversion efficiency accurately as compared with that of the PSO optimization algorithm; the SVM model has higher prediction accuracy for NOx conversion efficiency.
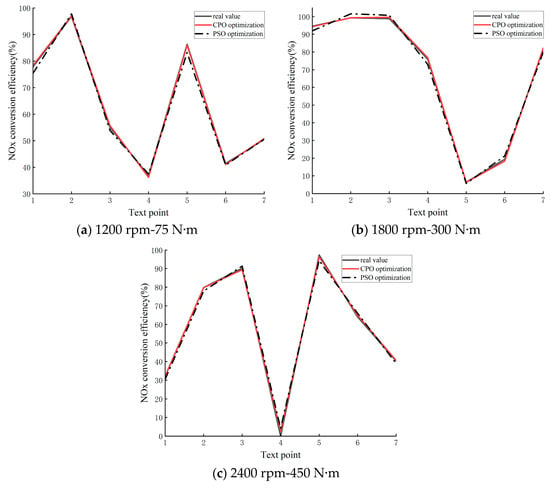
Figure 2.
NOx conversion efficiency prediction results.
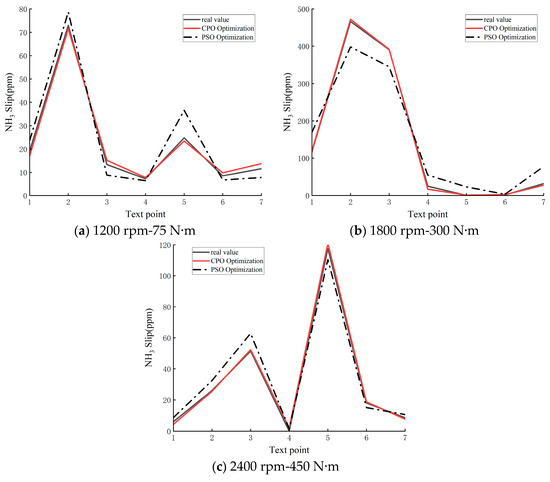
Figure 3.
NH3 slip prediction results.

Table 7.
Evaluation of the accuracy of NOx conversion efficiency prediction.

Table 8.
Evaluation of the accuracy of NH3 slip prediction.
For the prediction of NH3 slip, the CPO optimization algorithm is still able to accurately predict the NH3 slip under the three operating conditions. On the other hand, the PSO optimization algorithm was able to predict the NH3 slip more accurately only at 2400 rpm-450 Nm, and the prediction of NH3 slip for the other two conditions, especially at 1200 rpm-75 Nm, had a large deviation. This phenomenon may be due to the fact that the established SVM model has two output parameters, and the PSO optimization algorithm is unable to find the optimal parameters that can take into account the two output parameters, so the prediction accuracy of the NOx conversion efficiency is first considered when optimizing the model using the PSO algorithm. Compared with the PSO optimization algorithm, the CPO optimization algorithm has the ability to extensively explore the search space (which enables it to avoid falling into local minima) and to protect population diversity based on the novel cyclic population reduction mechanism, which enables it to find the optimal parameter that can take into account the two output parameters within the specified parameter range, allowing it to accurately predict both output parameters. Therefore, the SVM model optimized by the CPO optimization algorithm can be used for the prediction of NOx conversion efficiency and NH3 slip.
3.2. Nondominated Sorting Genetic Algorithm II (NSGA-II) Optimization
In SCR systems, there is a trade-off between NOx emissions and NH3 slip. Increasing the urea injection rate will reduce NOx emissions but increase NH3 slip, which is not allowed by emission regulations. In this study, the objective of the optimization is to find the optimum urea injection rate to maximize the NOx conversion efficiency of the SCR while meeting the regulatory NH3 slip limits.
NSGA-II, which was proposed by Deb et al. [25], can significantly improve the performance and efficiency of the algorithm by introducing an elite strategy and an improved non-dominated sorting method. It uses a multi-objective genetic algorithm to solve the multi-objective optimization problem of NOx conversion efficiency and NH3 slip of SCR system, from which the Pareto chart is obtained, and then finds the optimal solution, providing a better approach.
In NSGA-II, it is usual to maximize or minimize all the objective values. Since the objective NOx conversion efficiency to be optimized in this paper is to be maximized, all the NOx conversion efficiencies are treated by taking negative values.
In this paper, the multi-objective optimization process is carried out in MATLAB R2023a using the optimized SVM as the objective function and the returned scalar vectors are NOx conversion efficiency and NH3 slip. Urea injection is used as the only variable of the system. The constraints on the system variables are defined in the form of upper and lower bounds. The parameters of the genetic optimization algorithm and their values are shown in Table 9.

Table 9.
Parameters and their values.
4. Results and Discussion
In this study, all the optimization processes were carried out on the same device with the following specifications: CPU-Intel Core 7 12700H, GPU-NVIDIA GeForce RTX 3070 and RAM-32 GB. The time required to complete an overall optimization process could be kept within 15 s for each working condition. In order to demonstrate the genetic algorithm optimization process, three operating conditions–1200 rpm-75 Nm, 1800 rpm-300 Nm and 2400 rpm-450 Nm—were also selected. Figure 4 shows the Pareto plots of the targets for the three operating conditions.
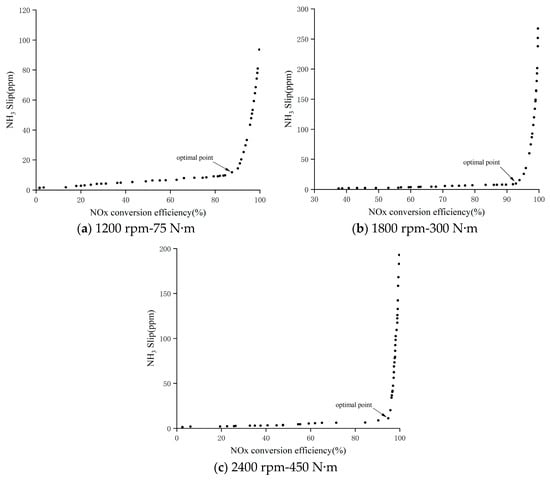
Figure 4.
Optimization result of urea injection (Pareto front).
In this study, a combination of SCR + ASC is used for the aftertreatment system. According to the regulatory requirement that NH3 slip should not be higher than 10 ppm, the actual NH3 slip after ASC is considered when finding the optimum point in the Pareto plot. At SCR inlet temperatures above 275 °C, the NH3 conversion efficiencies after ASC were verified on the test rig to be above 90%. At SCR inlet temperatures below 275 °C, the NH3 conversion efficiency after ASC is also above 80%. The optimum point is selected to maximize the NOx conversion efficiency as much as possible while ensuring that the NH3 slip is less than 10 ppm. The SCR inlet temperature is 264 °C at 1200 rpm-75 Nm. The optimal result is shown in Figure 4a and the coordinate of the optimal point is (87.5, 9.7). The urea injection corresponding to this point is 42.7 mg/s. That is, the urea injection rate to optimize the performance of the SCR (NOx conversion efficiency of 87.5% and NH3 slip of 9.7 ppm) was 42.7 mg/s under this operating condition.
At operating condition 1800 rpm-300 Nm, the SCR inlet temperature is 315 °C. As shown in Figure 4b, the optimum point coordinate is (93.6, 9.4). The urea injection corresponding to this point is 394.1 mg/s. That is, the urea injection rate to optimize the performance of the SCR (NOx conversion efficiency of 93.6% and NH3 slip of 9.4 ppm) was 394.1 mg/s under this operating condition.
At operating condition 2400 rpm-450 Nm, the SCR inlet temperature was 521 °C. As shown in Figure 4c, the optimum point coordinate is (96.1, 9.5). This point corresponds to a urea injection of 542.8 mg/s. That is, the urea injection rate to optimize the performance of the SCR (NOx conversion efficiency of 96.1% and NH3 slip of 9.5 ppm) was 542.8 mg/s under this operating condition.
In order to observe the urea optimization results for all working conditions, the NSGA-II is used to optimize the urea injection amount for all working conditions, all the optimal urea injection amounts are obtained and the optimal solution NOx conversion efficiency and NH3 slip are calculated according to the model. A comparison of the results before and after optimization of the SCR system is shown in Figure 5.
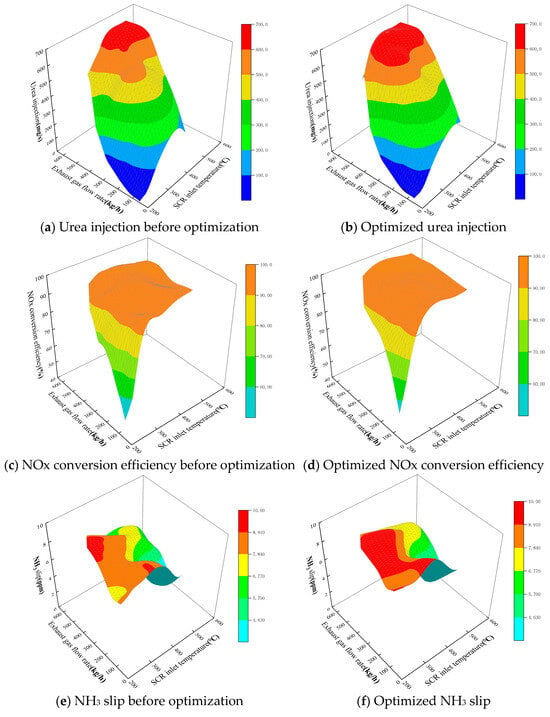
Figure 5.
Comparison of results before and after optimization of the SCR system.
In Figure 5d, it can be seen that after optimization, when the SCR inlet temperature is in the range of 200 °C to 300 °C, the NOx conversion efficiency rises more obviously with the increase in urea injection. When the SCR inlet temperature exceeds 450 °C, the NOx conversion efficiency shows a decreasing trend. This is mainly due to the fact that when the SCR inlet temperature exceeds a certain value (about 450 °C), an oxidation reaction of NH3 occurs through Equation (15). The product of this reaction is NO. Therefore, the increase in temperature leads to a decrease in the NOx conversion efficiency, but the overall remains in a high conversion efficiency range (above 95%).
On the other hand, the SCR inlet temperature is the main factor affecting the NOx conversion efficiency at low engine exhaust flow rates. The increase in exhaust temperature increases the chemical reaction rate inside the SCR. Therefore, at low exhaust flow rates, the NOx conversion efficiency shows a rapid increase with increasing temperature. When the exhaust flow rate is higher, the effect of SCR inlet temperature on NOx conversion efficiency becomes smaller and smaller with the increase of exhaust flow rate, but the increase of exhaust flow rate makes NH3 slip more likely to occur, so the overall NH3 slip shows a rising trend. Finally, the NH3 slip always stays below 10 ppm throughout the SCR operating interval, as shown in Figure 5f.
The optimized urea injection amount was written into the ECU, and the diesel engine was tested for the WHTC cycle. The cumulative NOx emissions are shown in Table 10. After optimization, the NOx accumulation of World Harmonized Transient Cycle (WHTC) is 1.62 g, and the test results show that the optimized urea injection rate can effectively reduce the NOx accumulation of the WHTC cycle, and the reduction is about 7.5%.

Table 10.
WHTC transient cyclic NOx accumulation.
5. Conclusions
In this study, engine test data were obtained from an engine test stand under 176 operating conditions. The urea injection volume was varied under each operating condition to obtain 25 sets of data corresponding to the NOx concentration at the SCR outlet and NH3 slip. An SVM model was built to predict the NOx conversion efficiency and NH3 slip from the experimental data and was optimized using the CPO algorithm to improve its prediction accuracy; the optimized SVM model was used instead of the mathematical model to save computational time. Then, it was used as an objective function to optimize the urea injection volume for all operating conditions using the NSGA-II algorithm. As the urea injection volume increases, although it leads to an increase in NOx conversion efficiency, it also leads to an increase in NH3 slip, which is not permitted by emission regulations. Therefore, the optimization aims to find the optimal urea injection rate for each condition to maximize the NOx conversion efficiency, keeping at the same time the NH3 slip within 10 ppm. Finally, the optimized urea injection rate can effectively reduce the NOx accumulation of the WHTC cycle by about 7.5% via the bench test.
The results show that the calibration of the urea injection rate of the SCR system can be accomplished by using the method based on the CPO-SVM-NSGA-II model. The optimal urea injection map established using this method can help the engine bench test to complete the calibration of some urea injection quantities, which can greatly shorten the calibration period and provide a reference or benchmark for the control system and calibration work.
The contributions of this paper are mainly as follows:
- Urea injection optimization is transferred to a computer, which can be done in only 15 s for each working condition. The calibration cycle is shortened substantially.
- Based on the CPO and genetic algorithms, the optimization of urea injection amount is completed while ensuring the model has high prediction accuracy.
- The study provide a reference or benchmark for diesel engine control systems and urea injection calibration.
Author Contributions
X.C.: Investigation, experiment, Data curation, Writing—original draft. C.M.: Formal analysis, Validation. Q.D.: Data analysis, Software. K.S.: Conceptualization, Methodology. S.B.: Project administration, Writing—review & editing, Funding acquisition. Z.L.: Visualization, Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Shandong Province Key R&D Program, China (2021CXGC010207), and the open funds of the National Engineering Laboratory of Mobile Source Pollution Control Technology of China (Grant No. NELMS2019A01).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors would like to thank the reviews whose constructive and detailed critique contributed to the quality of this paper.
Conflicts of Interest
Authors Changhai Ma and Quanli Dou were employed by the company Weichai Power Co. Ltd. Author Zhenguo Li was employed by the company China Automotive Technology & Research Center Co. Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EGR | exhaust gas recirculation |
| SCR | selective catalytic reduction |
| TDSI | time-discretized and space-integrated |
| NSGA-II | Nondominated Sorting Genetic Algorithm II |
| SVM | Support Vector Machine |
| DOC | Diesel Oxidation Catalyst |
| DPF | Diesel Particulate Filter |
| ASC | Ammonia Slip Catalyst |
| CPO | Crested Porcupine Optimizer |
| PSO | Particle Swarm Optimization |
| RMSE | Root Mean Square Error |
| WHTC | World Harmonized Transient Cycle |
| ECU | Engine Control Unit |
References
- Mulholland, E.; Miller, J.; Minjares, R.; Harmsen, R.; German, J.; Chambliss, S.; Akbar, U.; Hernández, G.; Javid, U.; Zachariadis, T.; et al. The role of NOx emission reductions in Euro 7/VII vehicle emission standards to reduce adverse health impacts in the EU27 through 2050. Transp. Eng. 2022, 9, 100133. [Google Scholar] [CrossRef]
- Anenberg, S.C.; Miller, J.; Minjares, R.; Du, L.; Henze, D.K.; Lacey, F.; Lefevre, E.; Gilbert, F.; Tackett, J.; Farkas, C.; et al. The global burden of transportation tailpipe emissions on air pollution-related mortality in 2010 and 2015. Environ. Res. Lett. 2019, 14, 094012. [Google Scholar] [CrossRef]
- Liu, J.; Xu, M.; Guo, W.; Zhang, X.; Li, Y.; Huang, R.; Wei, P.; Zhou, Q.; Wang, F.; Chen, L. Flow and heat transfer mechanism of a regenerative cooling channel mounted with pin-fins using supercritical CO2 as coolant. Int. J. Therm. Sci. 2025, 208, 109425. [Google Scholar] [CrossRef]
- European Commission, Regulation (EU) 2024/1257 of the European Parliament and of the Council of 24 April 2024 on Type-Approval of Motor Vehicles and Engines and of Systems, Components and Separate Technical Units Intended for Such Vehicles, with Respect to Their Emissions and Battery Durability (Euro 7), Amending Regulation (EU) 2018/858 of the European Parliament and of the Council and repealing Regulations (EC) No 715/2007 and (EC) No 595/2009 of the European Parliament and of the Council, Commission Regulation (EU) No 582/2011, Commission Regulation (EU) 2017/1151, Commission Regulation (EU) 2017/2400 and Commission Implementing Regulation (EU) 2022/1362Text with EEA Relevance. Available online: http://data.europa.eu/eli/reg/2024/1257/oj (accessed on 20 March 2025).
- Elkelawy, M.; El Shenawy, E.A.; Habib, K.; Ali, M.; Taha, M.; Abdel-Hamid, T.M.; Hassan, H.; Rashwan, M.; Said, M.; Hefny, M. Impacts of EGR on RCCI engines management: A comprehensive review. Energy Convers. Manag. X 2022, 14, 100216. [Google Scholar] [CrossRef]
- Skalska, K.; Miller, J.S.; Ledakowicz, S. Trends in NOx abatement: A review. Sci. Total Environ. 2010, 408, 3976–3989. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.T.; Tan, W. Mathematical modeling, optimal design and control of an SCR reactor for NOx removal. J. Taiwan Inst. Chem. Eng. 2012, 43, 409–419. [Google Scholar] [CrossRef]
- Guan, B.; Zhan, R.; Lin, H.; Huang, Z.; Li, Z.; Ma, Y.; Deng, Y.; Wu, X.; Zhou, D.; Fan, X. Review of state of the art technologies of selective catalytic reduction of NOx from diesel engine exhaust. Appl. Therm. Eng. 2014, 66, 395–414. [Google Scholar] [CrossRef]
- Elkaee, S.; Phule, A.D.; Yang, J.H.; Park, H.; Kim, Y.; Lee, J.; Li, X.; Ahmed, A.; Al-Salem, S.M.; Farooq, M.; et al. Advancements in (SCR) technologies for NOx reduction: A comprehensive review of reducing agents. Process Saf. Environ. Prot. 2024, 184, 854–880. [Google Scholar] [CrossRef]
- Tong, F.; Sun, Y.; Wang, B.; Zhao, Q.; Liu, Y.; Zhang, J.; Li, H.; Ma, X.; Chen, Z.; Zhou, K. Airpollution control policies and impacts: A review. Renew. Sustain. Energy Rev. 2024, 191, 114071. [Google Scholar]
- Wang, H.; Zhou, J.; Li, Y.; Chen, M.; Liu, K.; Zhang, W.; Deng, F.; Xu, H.; Tian, Y.; Zhu, Q. Review on recent progress in on-line monitoring technology for atmospheric pollution source emissions in China. J. Environ. Sci. 2023, 123, 367–386. [Google Scholar] [CrossRef]
- Kaario, O.T.; Vuorinen, V.; Larmi, M.; Keskinen, J.; Niemi, S.; Hämäläinen, J.; Karvonen, T.; Koskela, T.; Räsänen, M.; Silvonen, K. Mixing and evaporation analysis of a high-pressure SCR system using a hybrid LES-RANS approach. Energy 2017, 120, 827–841. [Google Scholar] [CrossRef]
- Zhao, J.; Chang, G.; Xu, Y.; Chen, J.; Sun, Y.; Wang, R.; Liu, X.; Tan, Y.; Luo, F.; Yang, C. Real-time nonlinear model predictive control for optimizing the ammonia coverage ratio of an SCR system based on TC-QPSO. Control Eng. Pract. 2023, 132, 105409. [Google Scholar] [CrossRef]
- Chen, P.; Wang, J. Nonlinear model predictive control of integrated diesel engine and selective catalytic reduction system for simultaneous fuel economy improvement and emissions reduction. J. Dyn. Systems. Meas. Control Trans. ASME 2015, 137, 081008. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, B.; Zhang, W.; Zhao, L.; Yang, S.; Xu, M.; Chen, H.; Liu, Y.; Feng, Q.; Liu, J. A temporal discretization and spatial integration SCR model with dual temperature-related parameters. Fuel 2024, 367, 131405. [Google Scholar] [CrossRef]
- Bozbağ, S.E.; Şanlı, D.; Yılmaz, A.; Koca, H.; Dalkılıç, A.S.; Özcan, H.; Turan, A.; Sönmez, Y.; Kaya, M.; Uzun, M. Development of a model based strategy for catalyst screening to control NOx and N2O emissions in NH3-SCR process towards Eu7 readiness. J. Environ. Chem. Eng. 2023, 11, 110232. [Google Scholar] [CrossRef]
- Gao, Z.; Pihl, J.; Curran, S.; Storey, J.; Sluder, C.; Parks, J.E.; Toops, T.; Fernandes, S.; Lance, M.; Edwards, K.; et al. Global kinetic modeling of NH3-SCR with two sites of NH3 storage on Cu-SSZ-13. Chem. Eng. J. 2021, 406, 127120. [Google Scholar] [CrossRef]
- Wang, J.; Shen, L.; Liu, Z.; Chen, R.; Wang, M.; He, J.; Zhou, Y.; Zhang, X.; Hu, C.; Zhang, P. Modeling and optimization of a light-duty diesel engine at high altitude with a support vector machine and a genetic algorithm. Fuel 2021, 285, 119137. [Google Scholar] [CrossRef]
- Capetillo, A.; Ibarra, F.; Santos, H.; Moreno, R.; Martinez, J.; Alvarez, M.; Gonzalez, F.; Reyes, J.; Dominguez, A.; Perez, R. Multiphase injector modelling for automotive SCR systems: A full factorial design of experiment and optimization. Comput. Math. Appl. 2017, 74, 188–200. [Google Scholar] [CrossRef]
- Faghihi, E.M.; Shamekhi, A.H. Development of a neural network model for selective catalytic reduction (SCR) catalytic converter and ammonia dosing optimization using multi objective genetic algorithm. Chem. Eng. J. 2010, 165, 508–516. [Google Scholar] [CrossRef]
- Li, W.; Yan, F.; Zhao, C.; Liu, L.; Wu, H.; Zhang, T.; Wang, X.; Yu, Y.; Chen, H.; Wang, J. NOx conversion efficiency optimization based on NSGA-II and state-feedback nonlinear model predictive control of selective catalytic reduction system in diesel engine. Appl. Energy 2017, 206, 959–971. [Google Scholar]
- Chen, P.; Wang, J. Estimation and adaptive nonlinear model predictive control of selective catalytic reduction systems in automotive applications. J. Process Control 2016, 40, 78–92. [Google Scholar] [CrossRef]
- Huang, H.; Wei, X.; Zhou, Y. An overview on twin support vector regression. Neurocomputing 2022, 490, 80–92. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl. Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).