Non-Homogeneous Poisson Process Software Reliability Model and Multi-Criteria Decision for Operating Environment Uncertainty and Dependent Faults

Abstract

The importance of software has increased significantly over time, and software failures have become a critical concern. As software systems have diversified in functionality, their structure has become more complex, and the types of failures that can occur in software have also diversified, stimulating the development of diverse software reliability models. In this study, we make certain assumptions regarding complex software, thereby proposing a new type of non-homogeneous Poisson process (NHPP) software reliability model that considers both dependent cases of software failure and cases that originate from the differences between the developed and actual operating environments. In addition, a new multi-criteria decision method ($MCDM$) that uses the maximum value for a comprehensive evaluation was proposed to demonstrate the effectiveness of the developed model. This improves the judgment of model excellence through multiple criteria and is suitable for multiple interpretations. To demonstrate the effectiveness of the proposed model, 15 NHPP software reliability models were compared using 13 evaluation criteria and three $MCDM$ methods across two datasets. The results showed that one dataset performed well for all the criteria, whereas the other dataset performed well for the newly proposed a multi-criteria decision method using maximum ($MCDMM$). The sensitivity analysis also showed a change in the mean value function with a change in the parameters. These results demonstrate that an extended structure for complex software can lead to improved software reliability.

1. Introduction

Software has become increasingly important over time. Previously, software was used to read data from memory using a programming language or to perform certain operations and present results. However, through software development that utilizes the strengths of various programming languages, software has been assigned roles ranging from simple tasks to entire systems. Furthermore, software is now used in various fields, including artificial intelligence (AI), to develop autonomous systems.

This increasing reliance on software underscores the severity of software failures. Regardless of whether an error or fault occurs in a small part of the software or involves the entire system, it can cause problems that differ considerably from previous software failures. Previously, software failures were caused by code errors or bugs, owing to the relatively simple architecture of earlier software. In contrast, modern software performs a wide variety of functions and has a complex structure. Therefore, many different failure scenarios have emerged. Software faults and failures caused by code errors, bugs, external shocks, compatibility issues, and technical errors can cause major social and economic problems. Two examples illustrate the damage caused by software failure.

Lime launched an electric-scooter service in October 2018 in Auckland, New Zealand. By February 2019, the company had received 155 reports on incidents involving scooter braking. By conducting independent investigations, the company found that the electric brakes suddenly engaged when travelling downhill at full speed, locking the scooter’s front wheel. This problem affected over 110 people and caused approximately $350,000 in damages. In another case, Vyaire Medical Ventilators with software version 6.0.1600.0, distributed in February 2021, experienced an error when the device stopped if the data communication port was set to a specific channel. Because this could result in severe injuries that could lead to death, the U.S. Food and Drug Administration (FDA) ordered a recall, and Vyaire Medical addressed the issue using a software patch. Software failures and faults occur in various forms, including operational problems when software is placed in an environment different from that used for development, and the resulting socioeconomic losses are significant. In particular, the characteristics of certain application fields can directly impact human life, thereby necessitating rigorous research into software reliability to prevent and mitigate software failures.

Software reliability evaluates the extent to which the software can be used without failure. Various methods have been studied to improve software reliability, such as error inflow, failure rate, and curve-fitting models [1,2,3,4]. Figure 1 shows an introduction to the different methodologies for software reliability modelling.

Among these, software reliability models that assume that software failures follow a nonhomogeneous Poisson process (NHPP) with a nonconstant mean at each point in time are being actively studied. In 1979, an NHPP software reliability model was developed based on the Goel (GO) model, assuming that the occurrence of failures increases exponentially over time [5]. Other NHPP software reliability models were developed according to the form of failure, including a software reliability model in which the cumulative failure of software follows an S-shape or occurs in a U-shape [6,7,8].

Recently, software reliability models based on the assumption of Weibull distribution or bathtub-shaped shapes have been proposed. In addition, various studies on software failure occurrences or incomplete debugging entail different efforts, focusing on the testing phase rather than the form of failure [9,10,11,12,13,14,15].

Because software is used in various fields and its structure has become very complex, software failure cases have become more diverse, such as when a software failure is caused by the dependent effects of other failures [16,17] or the difference between the actual and developed operating environments [18,19,20,21,22]. Therefore, research on software reliability models that consider various assumptions, such as dependent failures and operating environment uncertainties, has been continuously conducted. Recent studies have assumed that software test environments are not consistent or ideal and include uncertain factors such as test effort, test coverage, and differences in hardware and software configurations [23,24]. In addition, studies have been conducted to improve reliability through the relationship with the hardware to which it is applied, rather than by applying it in the isolation of software failures [25].

In this study, we extended the NHPP software reliability model to failures arising from complex software, thereby proposing an NHPP software reliability model that considers both operating environment uncertainty and dependent failure occurrence. Previously, proposed software reliability models were based on a single assumption. However, because software failures can be caused by various factors, we propose a software reliability model that includes the assumptions of dependent failure occurrence. This describes when failures affect each other, as well as the operating environment uncertainty caused by the difference between the development and operating environments. In addition, the software reliability was evaluated using various methods to determine the goodness of fit. However, because various criteria have different characteristics, evaluating excellence using only a few values is infeasible [26,27,28]. Therefore, we use a multi-criteria decision-making method ($MCDM$) for a comprehensive evaluation, demonstrating the effectiveness of the proposed model through the new $MCDM$, which reflects the size of the criteria for all models to be compared.

In summary, the contributions of this study are as follows:

• This study proposes an NHPP software reliability model that considers both the uncertainty of the operating environment and dependent faults.
• This study demonstrates the superiority of the proposed model through $MCDM$ using the maximum value to approach comprehensive assessment and multi-faceted interpretation.

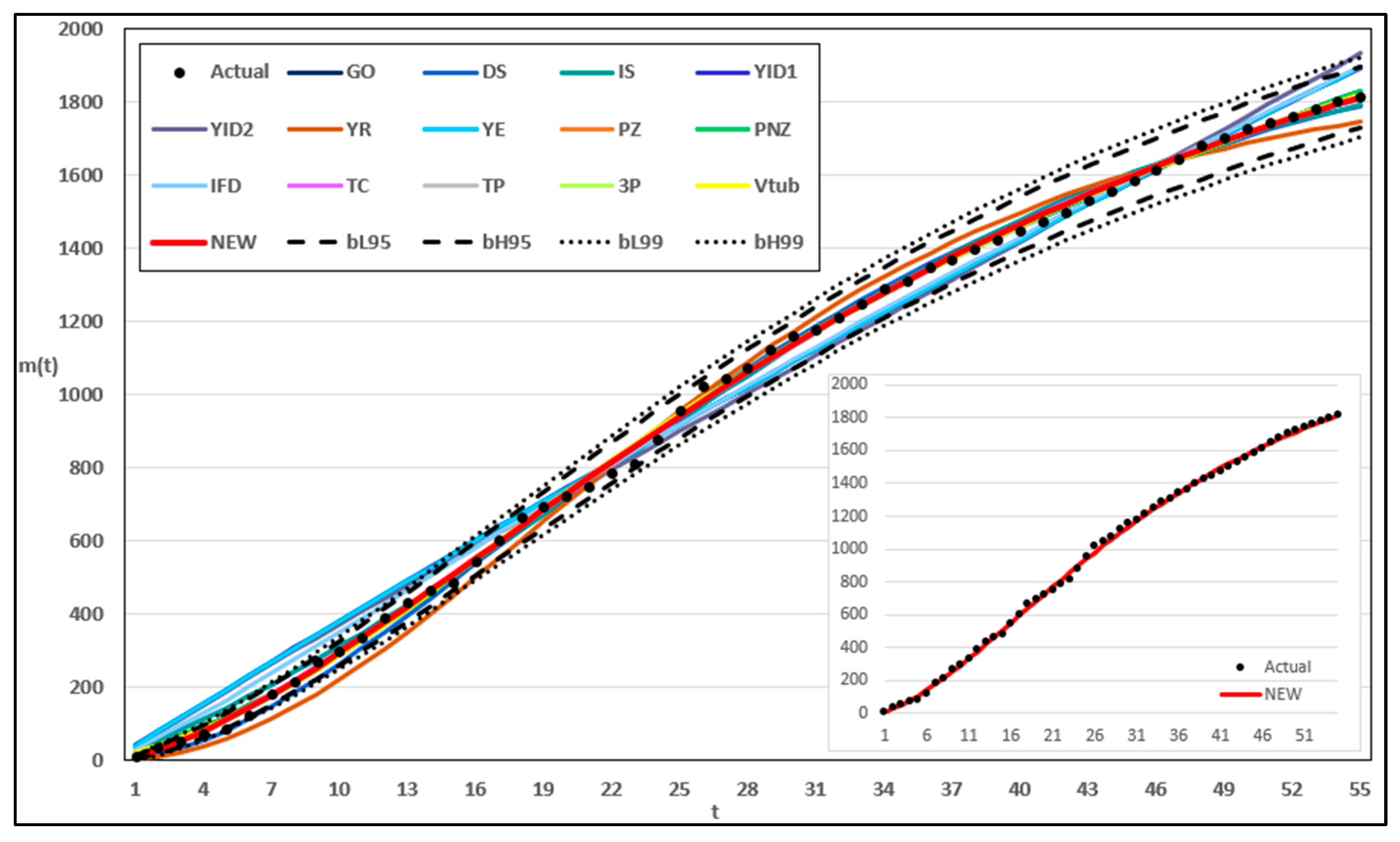
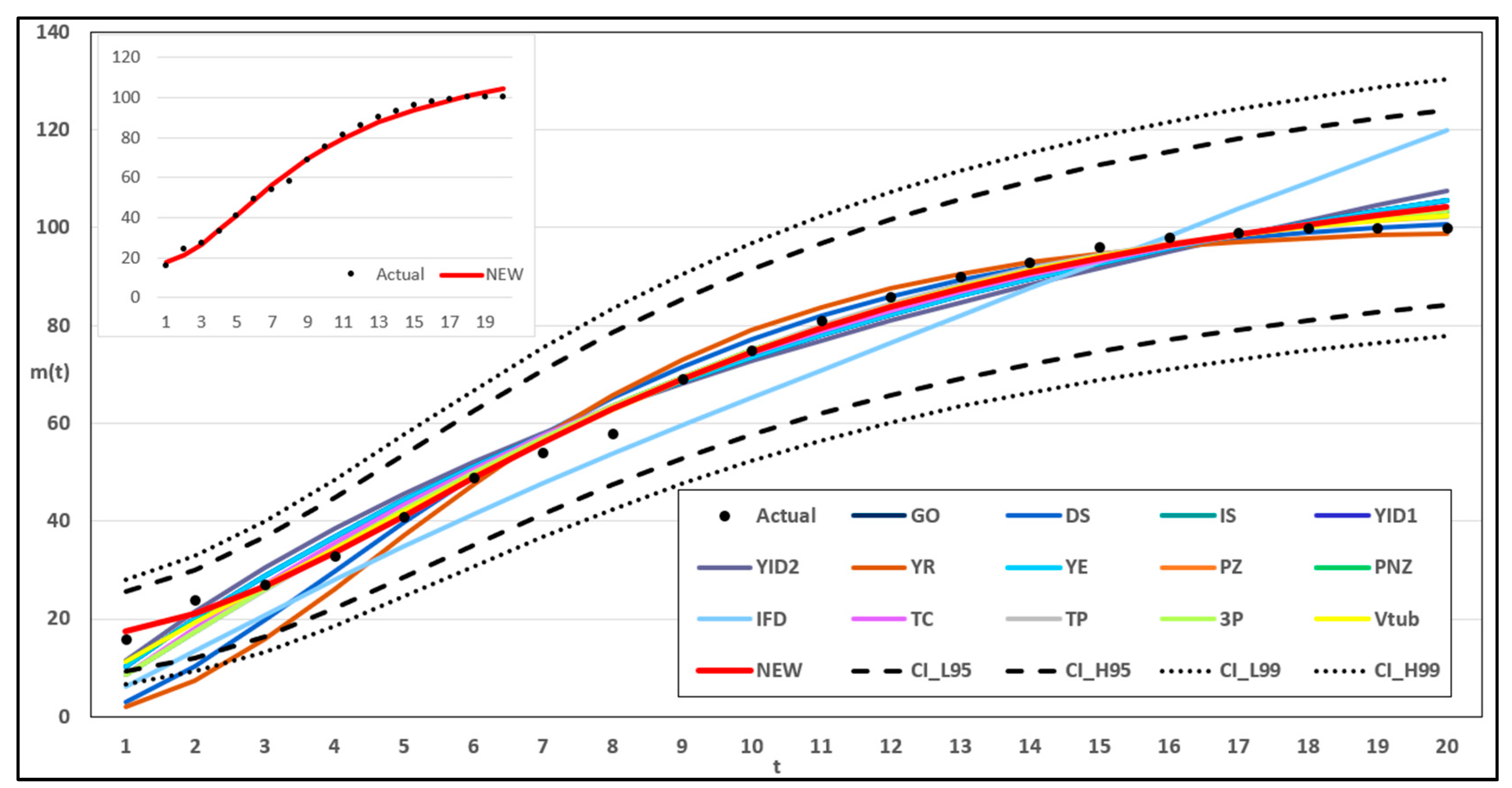
The remainder of this paper is organized as follows: Section 2 introduces the general NHPP software reliability model and the new NHPP software that considers dependent failures and operating environment uncertainties. Section 3 introduces the criteria and $MCDM$s used for model comparison and proposes a new $MCDM$. Section 4 presents the data and fit, along with numerical example results. Finally, Section 5 concludes the study.

2. New Software Reliability Model

2.1. Software Reliability Model

Software reliability assesses the ability of software to provide consistent results without faults. This is calculated using the reliability function $R\left(t\right)$, which is defined as the probability that it is still working after a certain point in time $t$. $R\left(t\right)$ is equal to the result of integrating the probability density function $f\left(t\right)$ with respect to the time of failure occurrence from t to infinity. The formula used is as follows:

$$R\left(t\right)=P(T>t)={\int }_t^{\mathrm{\infty }}f\left(u\right)du$$

To calculate the reliability function $R\left(t\right)$, we assumed a Poisson distribution with $\lambda$ as the mean number of failures per unit time. Here, $\lambda$ is a constant and follows a homogeneous poison process (HPP) with the number of failures per unit time constant over time. However, in real life, the number of software failures per unit time is time-dependent, which has led to the development of software reliability models that follow a nonhomogeneous Poisson process. NHPP is derived by using a mean value function $m\left(t\right)$, instead of the mean number of failures $\lambda$, based on the Poisson process [29,30].

$$P(N\left(t\right)=n)={\displaystyle \frac{\{{m\left(t\right)\}}^n}{n!}}{e}^{-m\left(t\right)},n=\mathrm{0,1},2,\cdots ,t\ge 0$$

where $N\left(t\right)$ is the number of failures up to time $t$, and mean value function $m\left(t\right)$ is the mean number of failures from time $0$ to $t$.

2.2. Proposed NHPP Software Reliability Model

Differential equations were used to derive the traditional NHPP software reliability model. The functions required to compute the NHPP software reliability model comprise those for the mean value function $m\left(t\right)$, number of failures $a\left(t\right)$, and failure detection rate function $b\left(t\right)$, which are derived using Equation (1), assuming that software failures occur independently [5].

$${\displaystyle \frac{dm\left(t\right)}{dt}}=b\left(t\right)[a\left(t\right)-m(t)]$$

(1)

However, as software is utilized in various ways and its structure has become more complex, software failures typically depend on other failures, leading to failures in otherwise functioning software. In addition, as software utilization diversifies, the differences between software development and operating environments can result in software failure. Therefore, we propose a software reliability model for predicting and integrating multiple failures in diverse software applications. Previously, many software reliability studies assumed that software was independent, which is insufficient for describing complex software. Thus, research has been conducted on models that incorporate various assumptions, such as operating environment uncertainty and dependent failures. In this paper, we propose an NHPP software reliability model that considers both the uncertainty of the operating environment and dependent failures by extending a previously developed NHPP software reliability model. The differential equation for assuming operating environment uncertainty is expressed in Equation (2) [19].

$${\displaystyle \frac{dm\left(t\right)}{dt}}=\mathsf{\eta }b\left(t\right)\left[a\left(t\right)-m\left(t\right)\right]$$

(2)

where $a\left(t\right)$ is the total expected number of failures $N$, and $\eta$ follows a probability density function $g$ generalized gamma distribution with shape parameter $\alpha$ and scale parameter $\beta$. When the initial value $m\left(0\right)=0$, the process derives the mean value function $m\left(t\right)$ using Equation (3).

$$m\left(t\right)={\int }_{\mathsf{\eta }}N\left(1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-\eta {\int }_0^{t}b\left(x\right)dx\right)\right)dg\left(\eta \right)$$

(3)

Furthermore, by defining $b\left(t\right)={\displaystyle \frac{{\gamma }^{2}t}{\gamma t+1}}$ and reorganizing Equation (3) using the Laplace transform, we obtain Equation (4) [31]:

$$m\left(t\right)={N\left(1-{\displaystyle \frac{\beta }{\gamma +{\int }_0^t\frac{{\gamma }^{2}s}{\gamma s+1}ds}}\right)}^{\alpha }$$

(4)

where $\gamma$ is the failure detection rate and is included in the denominator of Equation (4) and in the expression of $b\left(t\right)={\displaystyle \frac{{\gamma }^{2}t}{\gamma t+1}}$. The assumption of operating environment uncertainty is also included in the failure detection rate $\gamma$, which assumes that dependent failures occurring in the operating environment are also considered. Therefore, the newly proposed NHPP software reliability model assumes both the dependent failure occurrence and operating environment uncertainty, as expressed in Equation (5).

$$m\left(t\right)={N\left(1-{\displaystyle \frac{\beta }{\gamma +\gamma t-\mathrm{l}\mathrm{n}\left(\gamma t+1\right)}}\right)}^{\alpha }$$

(5)

Table 1. Software reliability models.

No.	Model	Mean Value Function	Note
1	Goel-Okumoto (GO) [5]	$\mathrm{m}\left(t\right)=\mathrm{a}\left(1-e^{-bt}\right)$	Concave
2	Yamada et al. (DS) [7]	$m\left(t\right)=\mathrm{a}\left(1-\left(1+\mathrm{b}\mathrm{t}\right)e^{-bt}\right)$	S-Shape
3	Ohba (IS) [8]	$m\left(t\right)={\displaystyle \frac{\mathrm{a}\left(t1-e^{-bt}\right)}{1+\beta e^{-bt}}}$	S-Shape
4	Yamada et al. (YID 1) [9]	$m\left(t\right)={\displaystyle \frac{\mathrm{a}b}{\alpha +b}}\left(e^{\alpha t}-e^{-bt}\right)$	Concave
5	Yamada et al. (YID 2) [9]	$m\left(t\right)=\mathrm{a}\left(1-e^{-bt}\right)\left(1-{\displaystyle \frac{\alpha }{b}}\right)+\alpha at$	Concave
6	Yamada et al. (YR) [10]	$m\left(t\right)=\mathrm{a}\left(1-e^{-\gamma \alpha \left(1-e^{-\beta t^2/2}\right)}\right)$	S-Shape
7	Yamada et al. (YE) [10]	$m\left(t\right)=\mathrm{a}\left(1-e^{-\gamma \alpha \left(1-e^{-\beta t}\right)}\right)$	Concave
8	Pham-Zhang (PZ) [12]	$m\left(t\right)={\displaystyle \frac{(\left(\mathrm{c}+\mathrm{a}\right)\left[1-e^{-bt}\right]-\left[\frac{ab}{b-\alpha }\right]\left(e^{-at}-e^{-bt}\right))}{1+\beta e^{-bt}}}$	Both
9	Pham et al. (PNZ) [13]	$m\left(t\right)={\displaystyle \frac{\mathrm{a}\left(1-e^{-bt}\right)\left(1-\frac{\alpha }{b}\right)+\alpha at}{1+\beta e^{-bt}}}$	Both
10	Pham (IFD) [26]	$m\left(t\right)=\mathrm{a}\left(1-e^{-bt}\right)\left(1+\left(\mathrm{b}+\mathrm{d}\right)t+bd{t}^2\right)$	Concave
11	Chang et al. (TC) [20]	$m\left(t\right)=\mathrm{N}\left[1-{\left({\displaystyle \frac{\beta }{\beta +{\left(at\right)}^b}}\right)}^{\alpha }\right]$	Both
12	Teng-Pham (TP) [18]	$m\left(t\right)={\displaystyle \frac{a}{p-q}}\left[1-{\left({\displaystyle \frac{\beta }{\beta +\left(\mathrm{p}-\mathrm{q}\right)\ln \left(\frac{c+e^{bt}}{c+1}\right)}}\right)}^{\alpha }\right]$	S-Shape
13	Song et al. (3P) [21]	$m\left(t\right)=\mathrm{N}\left[1-\left({\displaystyle \frac{\beta }{\beta -\frac{a}{b}\ln \left(\frac{\left(1+c\right)e^{-bt}}{1+c{e}^{-bt}}\right)}}\right)\right]$	S-Shape
14	Pham (Vtub) [19]	$m\left(t\right)=\mathrm{N}\left[1-{\left({\displaystyle \frac{\beta }{\beta +a^{bt}-1}}\right)}^{\alpha }\right]$	S-Shape
15	Proposed Model	$m\left(t\right)={N\left(1-{\displaystyle \frac{\beta }{\gamma +\gamma t-\mathrm{l}\mathrm{n}\left(\gamma t+1\right)}}\right)}^{\alpha }$	S-Shape

lists the 15 NHPP software reliability models used in the study. Models 1–14 are traditional software reliability models with different assumptions of software failure, such as independent occurrence, dependent occurrence, and operating environment uncertainty. Model 15 is a new type of NHPP software reliability model proposed in this study, which considers both dependent failures and operating environment uncertainty.

3. New Criteria for Model Comparison

3.1. Criteria

To demonstrate the superiority of the proposed NHPP software reliability model, which simultaneously assumes dependent failures and operating environment uncertainty, we compared the proposed model with 14 traditional software reliability models using 13 criteria. These 13 criteria judge the superiority of the model based on the difference between the actual value $y_i$ and the estimated value $\widehat{m}\left(t_i\right)$. $n$ and $m$ are the number of observations and parameters in each model, respectively.

The mean squared error (MSE), mean absolute error (MAE), predictive ratio risk (PRR), and predictive power (PP) were based on the difference between the actual and predicted values, where PRR was determined by the ratio of the estimated value and PP was determined by the ratio of the actual value [32,33,34].

$$MSE={\displaystyle \frac{{\sum }_{i=1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2}{n-m}},MAE={\displaystyle \frac{{\sum }_{i=1}^n\left|\widehat{m}\left(t_i\right)-y_i\right|}{n-m}}$$

$$PRR=\sum _{i=1}^n{\left({\displaystyle \frac{\widehat{m}\left(t_i\right)-y_i}{\widehat{m}\left(t_i\right)}}\right)}^2,PP=\sum _{i=1}^n{\left({\displaystyle \frac{\widehat{m}\left(t_i\right)-y_i}{y_i}}\right)}^2$$

$R^2$ and ${adj\_R}^2$ are the coefficients of determination and the modified coefficient of determination of the regression equation, respectively [35].

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y_i}\right)}^2}},{adj\_R}^2=1-{\displaystyle \frac{\left(1-R^2\right)\left(n-1\right)}{n-m-1}}$$

Akaike’s information criterion (AIC) and Bayesian information criterion (BIC) are used to compare the likelihood function maximization, as they aim to maximize the Kullback-Leibler level of agreement between the model and the probability distribution of the data, and BIC is a modified form of AIC [36]. The predicted relative variation (PRV) and root-mean-square prediction error (RMSPE) are the standard deviations of the prediction bias [37,38].

$$AIC=-2\log L+2m,BIC=-2\log L+m\log n$$

$$PRV=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{m}\left(t_i\right)-\sum _{i=1}^n\left[\frac{\widehat{m}\left(t_i\right)-y_i}{n}\right]\right)}^2}{n-1}}},$$

$$RMSPE=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{m}\left(t_i\right)-\sum _{i=1}^n\left[\frac{\widehat{m}\left(t_i\right)-y_i}{n}\right]\right)}^2}{n-1}}+{\sum _{i=1}^n\left[{\displaystyle \frac{\widehat{m}\left(t_i\right)-y_i}{n}}\right]}^2}$$

The tail statistic (TS) is the average percentage deviation from the mean at all the time points. Pham’s information criterion (PIC) and Pham’s criterion (PC) consider the tradeoff between the number of parameters in the model by increasing the penalty for each additional parameter in the model when the sample is small. In particular, the PC includes a penalty for PIC [39,40,41].

$$\mathrm{T}\mathrm{C}=100\times \sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{m}\left(t_i\right)\right)}^2}{{\sum }_{i=1}^n{y_i}^2}}},PIC=\sum _{i=1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2+m\left({\displaystyle \frac{n-1}{n-m}}\right),$$

$$PC={\displaystyle \frac{n-m}{2}}\times \mathit{log}\left({\displaystyle \frac{\sum _{i=1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2}{n}}\right)+\mathrm{m}\left({\displaystyle \frac{n-1}{n-m}}\right)$$

The proposed 13 criteria were used to judge the excellence of the model. The closer $R^2$ and ${adj\_R}^2$ are to 1, the better the model; the closer the remaining 11 criteria are to 0, the better the model. The parameters of each model were estimated using MATLAB R2024b and R with the LSE method, and the criteria were calculated [42].

3.2. Existing Multicriteria Decision Method

In the past, researchers have compared criteria to demonstrate the superiority of the developed NHPP software reliability model. The criteria for comparison were the distance between the actual and estimated values or the actual and predicted values, whereby the shorter the distance, the better the model. However, various criteria with different characteristics make it difficult to judge whether a software reliability model is superior simply because only one criterion is superior. Therefore, complex assessment and multifaceted interpretations are required to determine the superiority of the NHPP software reliability model [43,44,45].

A multi-criteria decision method facilitates a comprehensive interpretation. In this study, we use $MCDM$ to demonstrate the superiority of the proposed model by comparing multiple criteria. First, matrix $C$ was constructed to compare the software reliability models based on the criteria calculated by the models, which are represented as follows:

$$C=\left(\begin{array}{ccc}\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}& \cdots & \begin{array}{c}{C}_{1k}\\ C_{2k}\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{C}_{s1}& C_{s2}\end{array}& \cdots & C_{sk}\end{array}\right)$$

(6)

From matrix $C$, we create a new matrix $Y$ with components $y_{ij}$ for the objective criterion by normalizing each goodness of fit: $y_{ij}={\displaystyle \frac{C_{ij}}{{\sum }_{i=1}^s{C}_{ij}}}(i=\mathrm{1,2},\cdots ,m;j=\mathrm{1,2},\cdots ,n)$, thereby summing the components in each row, to define $MCDM$ with components ${SY}_1$ to ${SY}_s$. The defined $Y$ and $MCDM$ are represented by Equation (7).

$$Y=\left(\begin{array}{ccc}\begin{array}{cc}{y}_{11}& y_{12}\\ y_{21}& y_{22}\end{array}& \cdots & \begin{array}{c}{y}_{1k}\\ y_{2k}\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{y}_{s1}& y_{s2}\end{array}& \cdots & y_{sk}\end{array}\right), MCDM=\left(\begin{array}{c}{y}_{11}+y_{12}+\cdots +y_{1k}\\ \begin{array}{c}{y}_{21}+y_{22}+\cdots +y_{2k}\\ ⋮\end{array}\\ y_{s1}+y_{s2}+\cdots +y_{sk}\end{array}\right)=\left(\begin{array}{c}{SY}_1\\ \begin{array}{c}{SY}_2\\ ⋮\end{array}\\ {SY}_s\end{array}\right)$$

(7)

We compared the size of each component of the matrix $MCDM$ such that the smaller the value, the better the overall model.

3.3. Multiple Criteria Decision Making Using Maximum

In $MCDM$, the most important issue is determining the weights based on fitness. Various methods exist for determining the weights, such as the Monte Carlo simulation, entropy, and the technique for performance by similarity with an ideal solution (TOPSIS). In particular, $MCDM$ through ranking ($MCDMR$), which considers both quantitative and qualitative methods simultaneously, has been proposed [46]. However, because the weights were differentiated through ranking, even if the difference between the criteria of the two models was large, the difference in the reflected weights was the same. For instance, suppose that three random models have mean-squared error (MSE) values, as listed in

Table 2. Examples of $MCDM$.

Model	MSE	Rank	Weight-Rank	Weight-Max
Model 1	100	3	0.50	1.0
Model 2	20	2	0.33	0.2
Model 3	10	1	0.17	0.1

. If the first model had an MSE of 100, the second had an MSE of 20, and the third had an MSE of 10, the difference in rank between the first and second models was 1, and the difference in MSE values was 80. The difference in rank between the second and third models was also one, but the difference in the MSE values was 10. The problem with simply reflecting the rankings is that if multiple models are equally spaced and perform well, a considerably small difference can result in a large penalty.

In this study, the previous problem was addressed using a multi-criteria decision method using maximum ($MCDMM$), which reflects the size of the criteria, instead of simply applying a ranking by dividing the values corresponding to the column criteria into ranges while computing the $MCDM$. Matrix $M$ was constructed to utilize this size. The components of the matrix $M$ are calculated by Equation (8) through $w_{ij}={\displaystyle \frac{C_{ij}}{\mathrm{m}\mathrm{a}\mathrm{x}{C}_j}}(i=\mathrm{1,2},\cdots ,m,j=\mathrm{1,2},\cdots ,n)$, where the maximum value of each criterion according to each model is distributed, utilizing the size.

$$M=\left(\begin{array}{ccc}\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\end{array}& \cdots & \begin{array}{c}{w}_{1k}\\ w_{2k}\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{w}_{s1}& w_{s2}\end{array}& \cdots & w_{sk}\end{array}\right)$$

(8)

The matrix $Y\odot M$ is defined by the product of the respective components of matrix $M$ and matrix $Y$ after the transformation process explained in 3.2, and follows from Equation (9).

$$Y\odot M=\left(\begin{array}{ccc}\begin{array}{cc}{w_{11}y}_{11}& w_{12}{y}_{12}\\ {w_{21}y}_{21}& w_{22}{y}_{22}\end{array}& \cdots & \begin{array}{c}{w}_{1k}{y}_{1k}\\ w_{2k}{y}_{2k}\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{w_{s1}y}_{s1}& w_{s2}{y}_{s2}\end{array}& \cdots & w_{sk}{y}_{sk}\end{array}\right)$$

(9)

We define $MCDMM$ by Equation (10) using ${YM}_1$ to ${YM}_s$ as the components that are summed in each row of the combined matrix $Y\odot M$. The component sizes were compared to determine the overall excellence of the model based on smaller values.

$$MCDMM=\left(\begin{array}{c}{w}_{11}{y}_{11}+w_{12}{y}_{12}+\cdots +{w_{1k}y}_{1k}\\ \begin{array}{c}{w}_{21}{y}_{21}+{w_{22}y}_{22}+\cdots +{w_{2k}y}_{2k}\\ ⋮\end{array}\\ {w_{s1}y}_{s1}+{w_{s2}y}_{s2}+\cdots +w_{sk}{y}_{sk}\end{array}\right)=\left(\begin{array}{c}{YM}_1\\ \begin{array}{c}{YM}_2\\ ⋮\end{array}\\ {YM}_s\end{array}\right)$$

(10)

This study utilizes $MCDM$, which improves the existing method of judging the goodness of models, and proposes a new $MCDMM$ that reflects the continuous value of criteria. We propose and utilize a new $MCDMM$ to assess the goodness of fit of models with complex evaluations and multifaceted interpretations.

4. Numerical Example

4.1. Data Information

Two datasets are used to evaluate the effectiveness of the proposed model. The first dataset was the failure data from the PIG project, which is a platform for analyzing large datasets. The PIG project was used to display the parallelized data analysis programs. The PIG project has had five releases, with versions 0.2.0 through 0.5.0 defined as Release 1, versions 0.6.0 through 0.8.0 defined as Release 2, versions 0.8.1 through 0.9.2 defined as Release 3, version 0.10.0 defined as Release 4, and versions 0.10.1 through 0.12.0 defined as Release 5. A total of 1814 failures were observed monthly between April 2009 and October 2013 [47]. The second dataset comprises the failure data of a tandem computer with multiple central processing units inside a single computer. The system was tested for 10,000 h, and 100 failures occurred during testing. The data exhibited a concave shape with many failures at the beginning, followed by a gradual decrease [48].

4.2. Results of Dataset 1

Table 3. Parameter estimation of model from Dataset 1.

No.	Model	$\widehat{\mathit{a}}$	$\widehat{\mathit{b}}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	$\widehat{\mathit{N}}$	$\widehat{\mathit{\gamma }}$	$\widehat{\mathit{c}}$	$\widehat{\mathit{p}}$	$\widehat{\mathit{q}}$	$\widehat{\mathit{d}}$
1	GO	8874.738	0.004367
2	DS	2116.271	0.060638
3	IS	2006.643	0.070081		4.556844
4	YID1	8381.19	0.004642	7.73 × 10−5
5	YID2	437.5306	0.087785	0.078345
6	YR	2269.766		0.923509	0.001184		1.905442
7	YE	8911.425		0.619214	1.94 × 10−5		362.1234
8	PZ	162,359.5	0.118437	0.000134	4.351755			836.2331
9	PNZ	839.1432	0.118376	0.025688	4.364091
10	IFD	368.735	0.076678								4.22 × 10−7
11	TC	0.000221	1.475181	7509.944	6.142695	2155.745
12	TP	301.2389	0.182161	1.137592	0.847396			3.508369	0.087644	0.005934
13	3P	0.315812	0.18365		16.45598	3854.995		3.561905
14	Vtub	2.109497	0.617114	0.148282	23.85692	3197.256
15	NEW			0.734214	0.001093	2594.496	0.001092

lists the estimated parameter values for each model obtained from dataset 1. In this study, the proposed model has four parameters: $\alpha$, $\beta$, $\gamma ,$ and $N$, and the estimated values of dataset 1 are $\widehat{\alpha }=0.7342$, $\widehat{\beta }=0.001093$, $\widehat{\gamma }=0.001092,$ and $\widehat{N}=2594.496$. Figure 2 shows the cumulative number of failures and estimates for the 15 models at each time point from Dataset 1. The black dots represent the actual cumulative number of failures in Dataset 1, and the red line represents the estimated value of the software reliability model proposed in this study. Compared with the estimates of other existing software reliability models, the estimates of the proposed model are closest to the actual cumulative number of failures. In addition, the thick black dashed and thin black dotted lines represent the 95% and 99% confidence intervals of the proposed software reliability model, and all the actual values are within the confidence intervals.

Table 4. Comparison of criteria from Dataset 1.

Model	MSE	PRR	PP	MAE	R2	adj_R2	AIC	BIC	PRV	RMSPE	TS	PC	PIC
GO	3017.775	2.426	14.218	47.533	0.991	0.991	636.406	640.420	52.680	54.392	4.720	213.381	159,944.1
DS	539.960	6.214	1.137	20.579	0.998	0.998	532.665	536.679	22.463	23.011	1.996	167.781	28,619.9
IS	587.384	1.031	3.516	20.749	0.998	0.998	544.631	550.653	23.501	23.778	2.062	167.425	30,547.1
YID1	3078.198	2.443	14.389	48.499	0.991	0.991	637.655	643.677	52.606	54.412	4.721	210.492	160,069.4
YID2	3699.782	2.339	13.480	53.137	0.989	0.989	667.306	673.328	59.058	59.677	5.176	215.274	192,391.8
YR	2216.822	24.191	2.545	42.812	0.994	0.993	620.157	628.187	43.891	45.723	3.968	198.758	113,062.1
YE	3136.404	2.427	14.230	49.395	0.991	0.990	640.449	648.478	52.622	54.394	4.720	207.606	159,960.8
PZ	285.207	0.447	1.004	13.543	0.999	0.999	527.946	537.982	16.222	16.250	1.409	144.348	14,265.7
PNZ	279.679	0.448	1.006	13.277	0.999	0.999	525.986	534.015	16.223	16.252	1.409	145.968	14,267.9
IFD	1883.516	1.610	6.338	37.886	0.995	0.994	593.414	599.436	41.885	42.576	3.693	197.720	97,945.9
TC	302.382	0.135	0.189	14.502	0.999	0.999	518.597	528.634	16.720	16.733	1.451	145.810	15,124.5
TP	293.365	0.305	0.584	14.301	0.999	0.999	525.980	540.031	16.136	16.148	1.400	140.962	14,089.4
3P	281.614	0.297	0.563	13.698	0.999	0.999	521.957	531.994	16.137	16.148	1.400	144.031	14,086.1
Vtub	287.974	0.443	1.208	14.127	0.999	0.999	524.983	535.020	16.313	16.329	1.416	144.589	14,404.1
NEW	273.018	0.694	0.351	13.483	0.999	0.999	518.486	526.515	16.057	16.058	1.393	145.353	13,928.1

and

Table 5. Comparison of multi-criteria from dataset 1.

Multi-criteria	GO	DS	IS	YID1	YID2	YR	YE	PZ	PNZ	IFD	TC	TP	3P	Vtub	NEW
$MCDM$	1.5382	0.6458	0.5799	1.5489	1.7141	1.6166	1.5543	0.3956	0.3947	1.0714	0.3833	0.3870	0.3842	0.3998	0.3864
$MCDMR$	0.1642	0.0500	0.0440	0.1782	0.2166	0.1693	0.1788	0.0152	0.0154	0.0927	0.0153	0.0131	0.0084	0.0162	0.0062
$MCDMM$	1.3285	0.2775	0.2652	1.3464	1.6562	1.3058	1.3556	0.1780	0.1774	0.6815	0.1775	0.1763	0.1747	0.1785	0.1731

present the results for the calculated criteria and multi-criteria based on Table 3. $MSE$, $R^2$, $Adj\_R^2$, $AIC$, $BIC$, $PRV$, $RMSPE$, $TS$, and $PIC$ have the best results, with 273.018, 0.999, 0.999, 518.486, 526.515, 16.057, 16.058, 1.393, and 13,928.1, respectively, whereas $PP$ and $MAE$ have the second-best results, with 0.351 and 13.483, respectively. The proposed model has the third-best result in $MCDM$ with 0.3864 and the best results in $MCDMR$ and $MCDMM$ with 0.0062 and 0.1731, respectively. TC had the best result for $MCDM$ but the fifth-best result for $MCDMR$ and $MCDMM$. This demonstrates the importance of assigning weights for a comprehensive evaluation. Figure 3 is a graphical representation of the three-dimensional plots of the $MCDM$, $MCDMR$, and $MCDMM$ for the top five of the 15 models listed in Table 1 for Dataset 1.

4.3. Results of Dataset 2

Table 6. Parameter estimation of model from Dataset 2.

No	Model	$\widehat{\mathit{a}}$	$\widehat{\mathit{b}}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	$\widehat{\mathit{N}}$	$\widehat{\mathit{\gamma }}$	$\widehat{\mathit{c}}$	$\widehat{\mathit{p}}$	$\widehat{\mathit{q}}$	$\widehat{\mathit{d}}$
1	GO	130.2015	0.083166
2	DS	103.9842	0.265379
3	IS	110.8287	0.172063		1.204647
4	YID1	129.8017	0.08345	0.000146
5	YID2	72.35301	0.169462	0.036291
6	YR	115.816		1.565434	0.017194		1.268592
7	YE	130.4047		0.657408	0.000264		478.892
8	PZ	0.253469	0.172063	1846.288	1.204651			110.5752
9	PNZ	110.8099	0.172083	9.88 × 10−6	1.204507
10	IFD	12.22918	0.440572								8.20 × 10−7
11	TC	0.018183	1.109733	86,418.84	13,230.13	118.5624
12	TP	90.28151	0.088191	25.76277	1.159252			19.25739	0.95604	0.092387
13	3P	1.398567	0.172062		0.00897	110.8898		1997.82
14	Vtub	3.761085	0.420911	7.023092	169.2326	105.9848
15	NEW			1.956081	0.029012	127.2589	0.044502

lists the estimated parameters for the 15 models in Dataset 2. The estimated values are $\widehat{\alpha }=1.9561$, $\widehat{\beta }=0.02901$, $\widehat{\gamma }=0.04450,$ and $\widehat{N}=127.2589$. Figure 4 shows the cumulative number of failures and estimates for the 15 models at each time point in Dataset 2. The black dots represent the actual cumulative number of failures in Dataset 2, and the red line represents the estimates of the software reliability models from Dataset 2. The thick black dashed and thin black dotted lines represent the 95% and 99% confidence intervals of the proposed software reliability models, respectively. The estimated value of the proposed model was the closest to the true value compared to the results of the other models, and all were within the confidence interval of the true value.

Table 7. Comparison of criteria from Dataset 2.

Model	MSE	PRR	PP	MAE	R2	adj_R2	AIC	BIC	PRV	RMSPE	TS	PC	PIC
GO	12.908	0.378	0.203	3.405	0.986	0.984	91.959	93.951	3.496	3.497	4.540	24.183	234.453
DS	28.063	19.580	1.081	3.520	0.969	0.965	111.228	113.220	4.946	5.146	6.694	31.173	507.239
IS	10.564	0.868	0.305	2.659	0.989	0.987	90.266	93.253	3.042	3.073	3.991	22.010	182.937
YID1	13.688	0.378	0.203	3.609	0.986	0.983	93.984	96.971	3.498	3.500	4.544	24.212	236.054
YID2	20.264	0.250	0.188	4.483	0.979	0.975	99.356	102.343	4.257	4.258	5.528	27.547	347.844
YR	49.421	57.178	1.497	5.519	0.951	0.938	128.759	132.742	6.110	6.435	8.375	34.168	795.482
YE	14.539	0.378	0.203	3.834	0.986	0.982	95.976	99.959	3.498	3.499	4.543	24.379	237.366
PZ	11.972	0.868	0.305	3.014	0.989	0.985	94.266	99.245	3.042	3.073	3.991	22.795	185.918
PNZ	11.225	0.867	0.305	2.826	0.989	0.986	92.269	96.252	3.042	3.073	3.992	22.310	184.354
IFD	95.295	3.369	0.851	9.411	0.900	0.882	124.499	127.487	8.663	9.206	11.988	40.706	1623.369
TC	14.494	0.830	0.300	3.600	0.987	0.982	97.871	102.849	3.367	3.382	4.392	24.229	223.750
TP	11.944	0.863	0.301	2.955	0.990	0.985	95.356	102.326	2.819	2.857	3.711	23.552	165.504
3P	11.972	0.868	0.305	3.014	0.989	0.985	94.266	99.245	3.042	3.073	3.991	22.795	185.918
Vtub	6.869	0.239	0.137	2.346	0.994	0.991	87.500	92.479	2.291	2.327	3.023	18.628	109.369
NEW	5.650	0.040	0.038	2.075	0.994	0.993	88.732	92.715	2.181	2.181	2.832	16.818	95.153

and

Table 8. Comparison of multi-criteria from Dataset 2.

Multi-Criteria	GO	DS	IS	YID1	YID2	YR	YE	PZ	PNZ	IFD	TC	TP	3P	Vtub	NEW
$MCDM$	0.6335	1.3213	0.5780	0.6459	0.7963	2.1961	0.6593	0.6027	0.5896	2.2936	0.6670	0.5865	0.6027	0.4370	0.3906
$MCDMR$	0.0403	0.1479	0.0198	0.0494	0.0787	0.2721	0.0555	0.0305	0.0279	0.2889	0.0523	0.0294	0.0306	0.0064	0.0043
$MCDMM$	0.2450	0.6751	0.2084	0.2541	0.3522	1.7409	0.2643	0.2263	0.2167	2.1920	0.2644	0.2227	0.2263	0.1530	0.1410

present the results for the calculated criteria and multi-criteria based on Table 6. $MSE$, $MAE$, $PRR$, $PP$, $R^2$, $Adj\_R^2$, $PRV$, $RMSPE$, $TS$, $PC$ and $PIC$ have the best values of 5.650, 0.040, 0.038, 2.075, 0.994, 0.993, 2.181, 2.181, 2.832, 16.818, and 95.153, respectively, whereas $AIC$ and $BIC$ have the second highest values of 88.732 and 92.715, respectively. The best results for $MCDM$, $MCDMR$, and $MCDMM$ with the 13 criteria were 0.3906, 0.0043, and 0.1410, respectively. Figure 5 is a graphical representation of the three-dimensional plots of the $MCDM$, $MCDMR$, and $MCDMM$ for the top five of the 15 models listed in Table 1 for Dataset 2.

4.4. Sensitivity Analysis

Because the software reliability model is highly sensitive to changes in the mean value function $m\left(t\right)$ whenever the parameters change, this study compares the changes in the $m\left(t\right)$ owing to changes in the four parameters through a sensitivity analysis [49,50]. In this study, we use two datasets to compare the most affected parameters of the mean value function $m\left(t\right)$ when the parameters of the estimated model are varied by −20%, −10%, 10%, and 20%.

The changes in the four parameters of Dataset 1 are shown in Figure 6. For $N$ and $\gamma$, the estimated mean value function $m\left(t\right)$ became larger with increasing values, while for $\alpha$ and $\beta$, the $m\left(t\right)$ became smaller with increasing values. Furthermore, the magnitude of the change in mean value function $m\left(t\right)$ increased with increasing time point for $N$, $\gamma$ gradually decreased, and $\beta$ showed relatively small changes compared to the changes in other parameters.

The changes in the four parameters of Dataset 2 are shown in Figure 7. For N and γ, the estimated mean value function m(t) became larger with increasing values, while for α and β, m(t) became smaller with increasing values. For N, the variation in the mean value function m(t) increased as the time point increased, while α showed very small variation overall. γ and β showed very large variation initially but gradually became smaller.

5. Conclusions

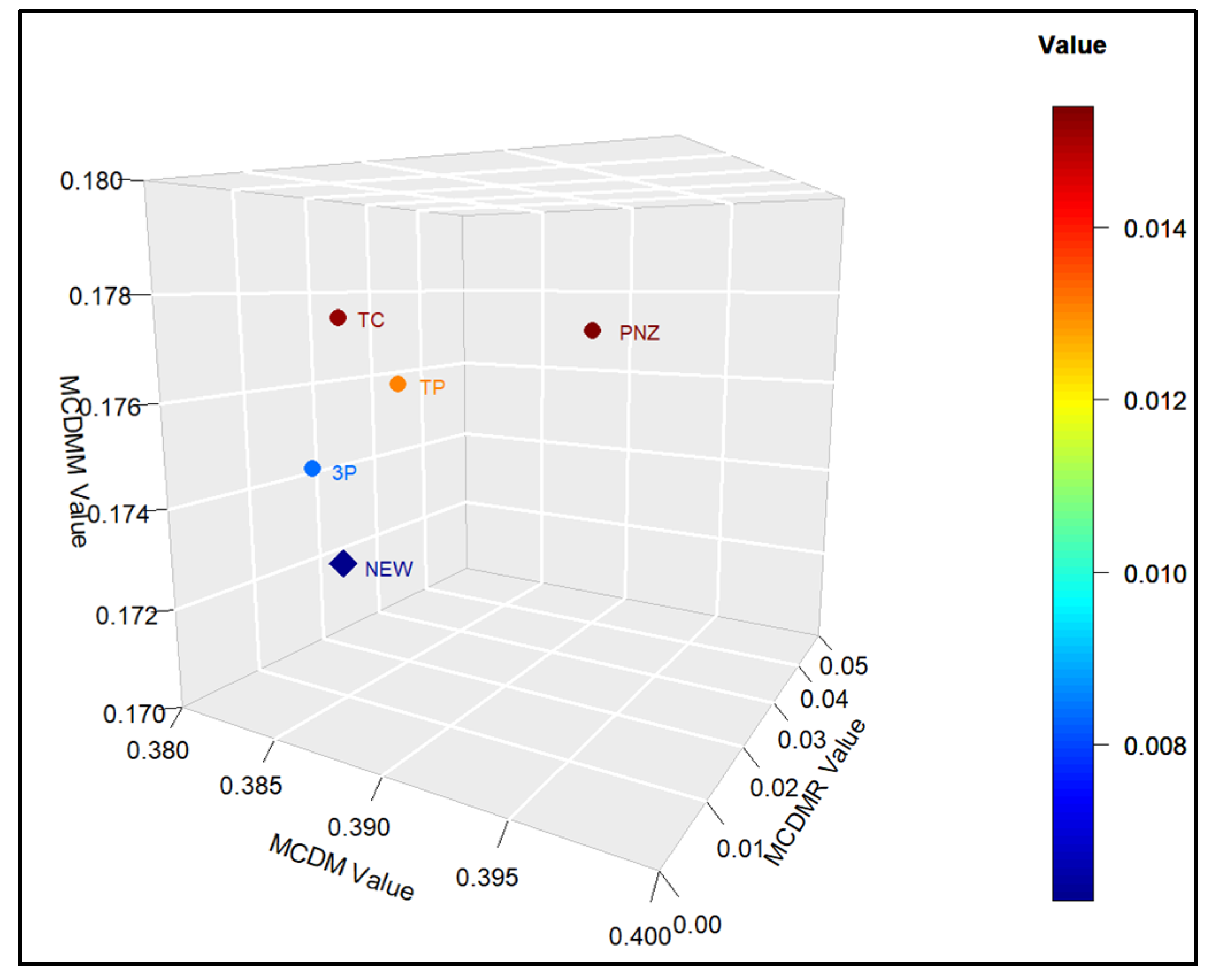
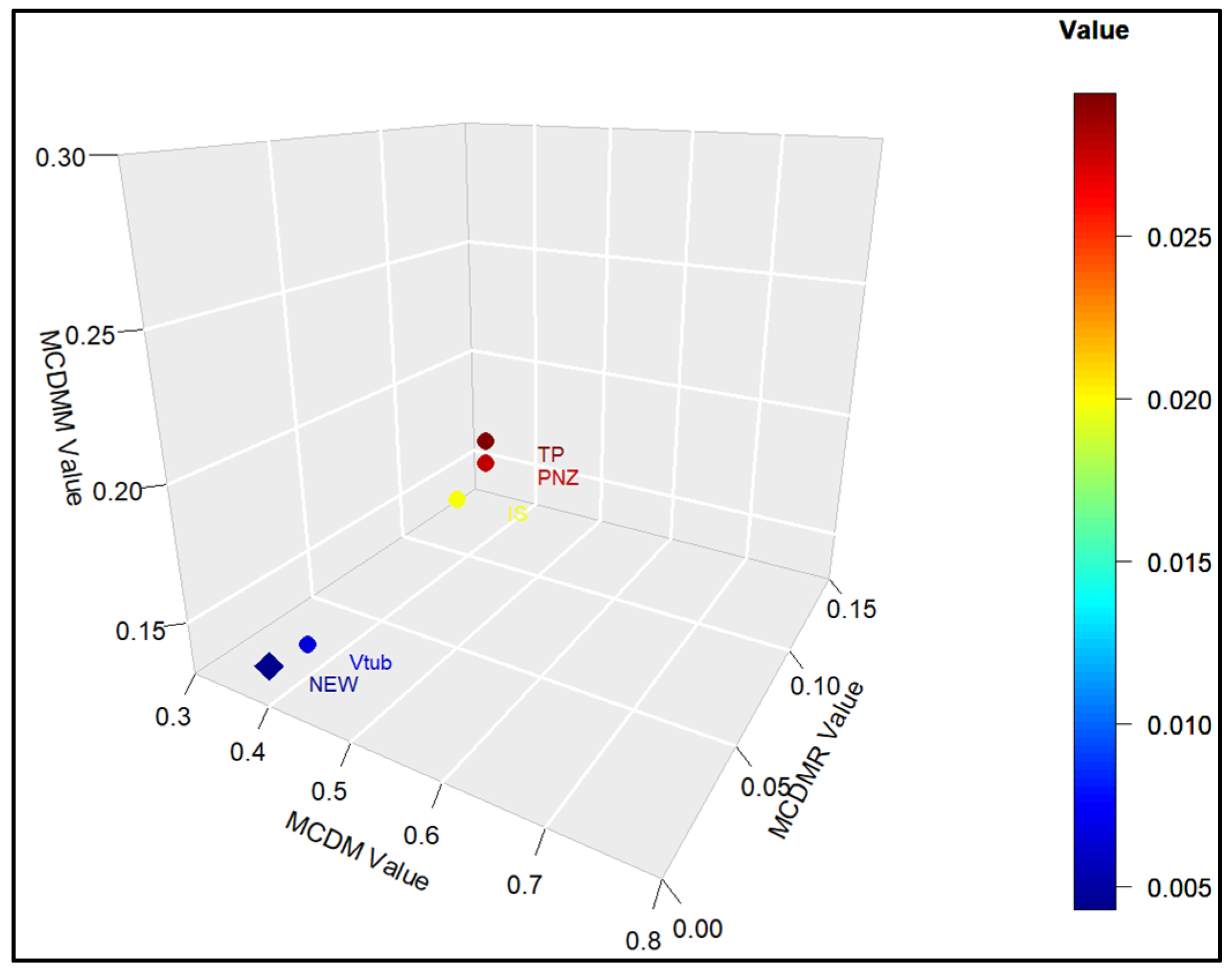
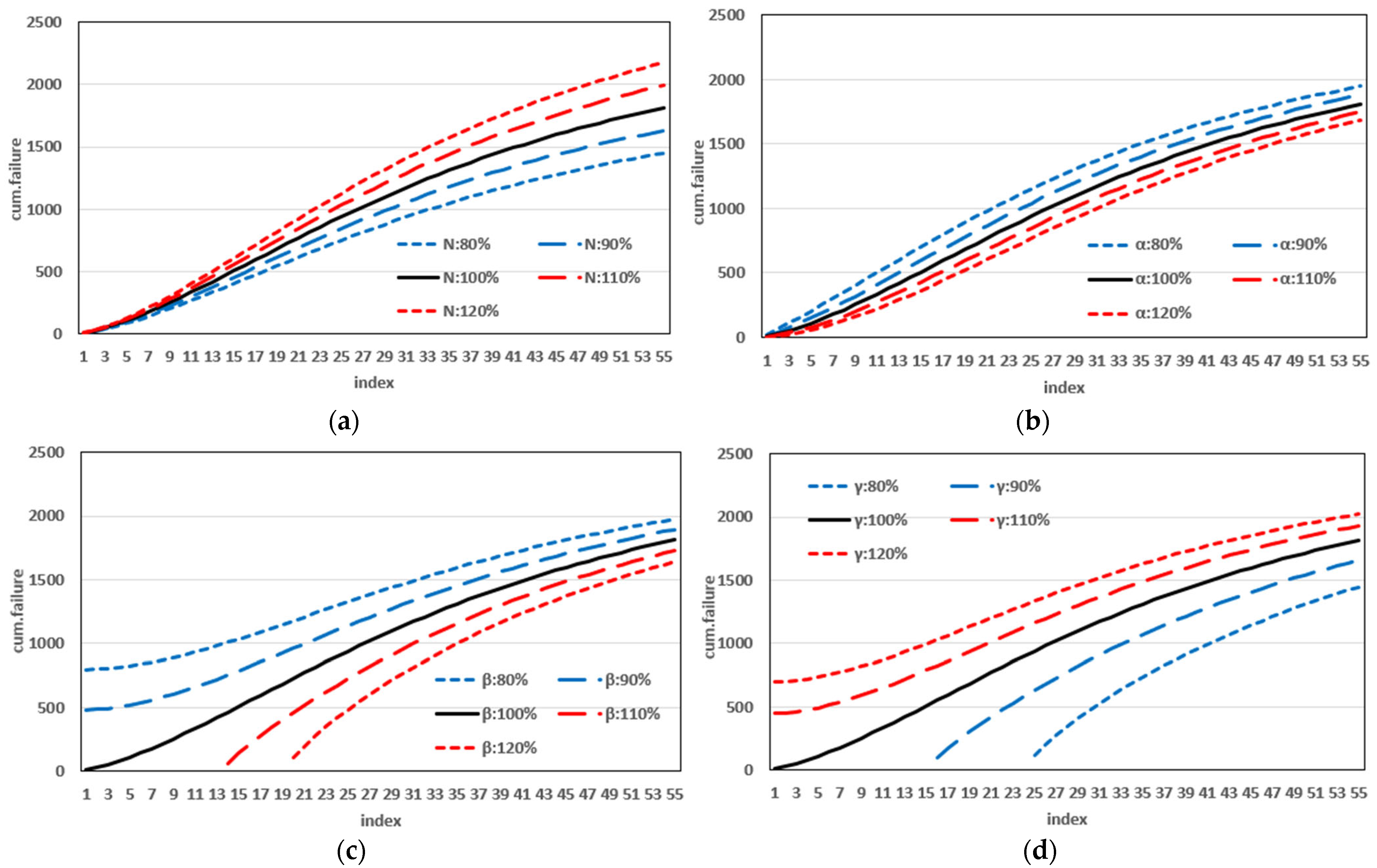
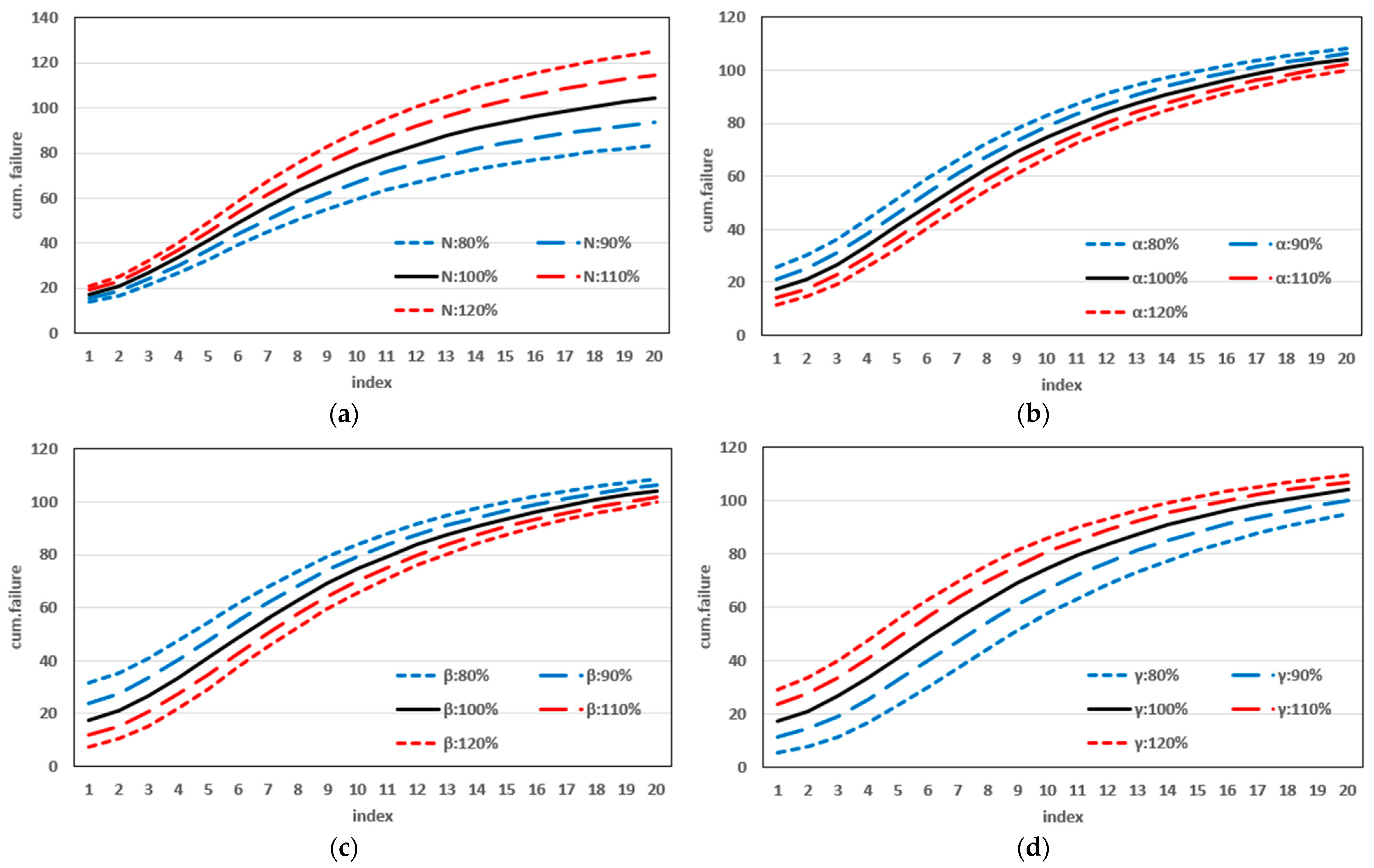
This study introduced a new type of NHPP software reliability model that simultaneously assumes uncertainty in the operating environment and dependent failure occurrence. Unlike previous studies, this study extends the range of failures that can occur in complex and diverse software by presenting a model that can predict the probability of occurrence in various environments. In addition, to demonstrate the effectiveness of the developed software reliability model, an $MCDM$ using the maximum value, which can be interpreted in various manners. This method evaluates the effectiveness of a model through a comprehensive interpretation because when assessing the effectiveness of a model based on each criterion, it is particularly useful when multiple models perform well across individual criteria. In an analysis with 15 models across two datasets, it was showed that in Dataset 1, the proposed model performed best on all criteria, and in Dataset 2, the existing $MCDM$ showed the third-best result, whereas the newly proposed $MCDMM$ showed the best result. Therefore, the $MCDMM$, which improves the existing $MCDM$ method, can increase the level of comparison by considering both quantitative and qualitative evaluations. The sensitivity analysis was conducted to compare the changes in the mean value function $m\left(t\right)$ due to changes in the parameters for the two datasets. The changes for $N$ showed a trend of increasing variation as the value increases, $\alpha$ showed a relatively small variation compared to other parameters, and $\beta$ showed a trend of decreasing variation as the value increases. The changes in the mean value function $m\left(t\right)$, that is, the impact on software failure prediction owing to changes in the parameters included in the model, varied per parameter and showed changes with common characteristics.

With the development of the software industry, the complexity and diversity of software have led to various software failures. Research on assumptions such as dependent failures and operating environment uncertainties is underway to predict these failures. Further research should be conducted based on additional assumptions to extend these studies. This study proposes a model with multiple assumptions, and there is a possibility of errors when these assumptions are changed. Therefore, additional research is required on generalizable software reliability models to predict software failure.