Bi-Directional Point Flow Estimation with Multi-Scale Attention for Deformable Lung CT Registration

Abstract

Deformable lung CT registration plays a crucial role in clinical applications such as respiratory motion tracking, disease progression analysis, and radiotherapy planning. While voxel-based registration has traditionally dominated this domain, it often suffers from high computational costs and sensitivity to intensity variations. In this work, we propose a novel point-based deformable registration framework tailored to the unique challenges of lung CT alignment. Our approach combines geometric keypoint attention at coarse resolutions to enhance the global correspondence with attention-based refinement modules at finer scales to accurately model subtle anatomical deformations. Furthermore, we adopt a bi-directional training strategy that enforces forward and backward consistency through cycle supervision, promoting anatomically coherent transformations. We evaluate our method on the large-scale Lung250M benchmark and achieve state-of-the-art results, significantly surpassing the existing voxel-based and point-based baselines in the target registration accuracy. These findings highlight the potential of sparse geometric modeling for complex respiratory motion and establish a strong foundation for future point-based deformable registration in thoracic imaging.

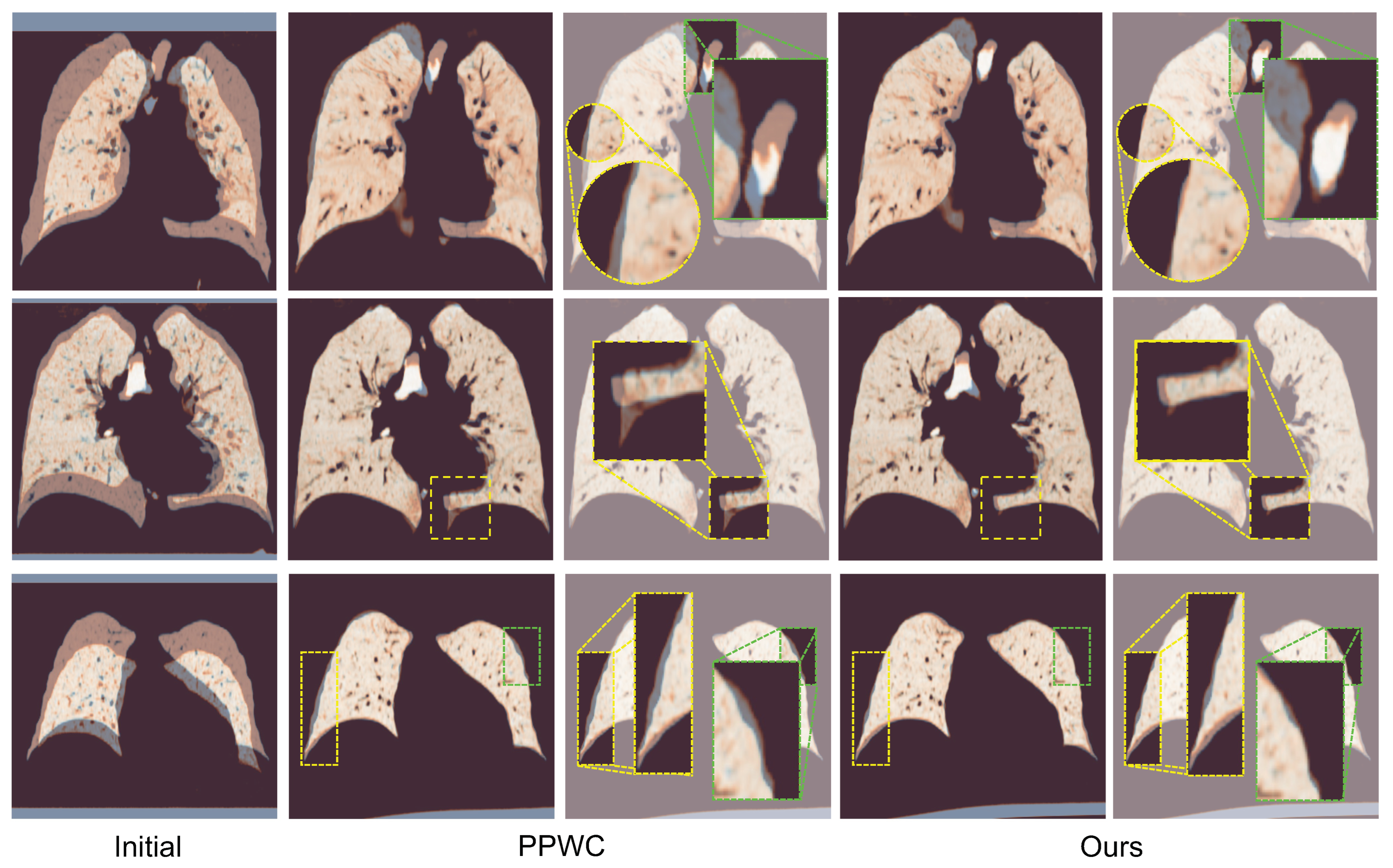
1. Introduction

Deformable registration of lung CT scans plays a pivotal role in real-world clinical workflows, including respiratory motion compensation [1,2], longitudinal disease monitoring [3,4,5], and radiation therapy planning [6,7]. Unlike rigid registration methods [8,9,10,11] that assume static global transformations, deformable lung CT registration accounts for the complex non-linear anatomical changes induced by respiration, enabling precise spatial alignment across different breathing phases.

Traditionally, voxel-based registration has been the dominant paradigm for lung CT registration. These methods optimize the spatial transformation fields using intensity-based similarity metrics, such as mutual information [12,13] or normalized cross-correlation [14]. While voxel-level registration provides dense deformation estimates, it suffers from critical limitations: (1) high computational and memory costs due to the dense volumetric nature of CT images [15] and (2) sensitivity to the inconsistencies in intensity caused by artifacts, noise, and contrast variability [7,16].

Recent advances in geometric deep learning and 3D point cloud representations have enabled a new class of point-based deformable registration, offering computational efficiency and robustness to variations in intensity [17,18,19]. These methods typically leverage sparse surface-based representations and geometric feature extraction to estimate dense deformation fields. However, they have not addressed the unique challenges of lung CT registration, where large, non-rigid respiratory deformations and fine-scale anatomical details must be jointly handled.

Against this backdrop, the recent release of the Lung250M dataset [16] has introduced high-resolution lung CT point clouds across different respiratory phases, enabling foundational studies of point-based registration in lung CT scans. Unlike general registration tasks [17,18,19], lung CT registration requires precise modeling of both the global anatomical structure (e.g., inter-lobar coherence) and local correspondence across complex structures such as bronchial trees and vascular bifurcations. In clinical terms, reliable registration of these structures is essential for tracking the disease progression in COPD and measuring the treatment response in pulmonary fibrosis or the accumulating radiation dose across respiratory cycles. These demands necessitate a multi-scale, context-aware framework that can simultaneously capture the long-range consistency and fine-level alignment.

In this work, we propose a novel point-based deformable lung CT registration framework designed to combine coarse-to-fine flow refinements with bi-directional geometric consistency. Specifically, our approach introduces three key innovations:

• Geometric keypoint attention at coarse resolutions to enhance global-structure-aware feature matching across widely separated regions;
• Context-aware flow refinement at finer levels via attention-based feature interactions, enabling precise modeling of subtle local deformations;
• A bi-directional registration strategy that jointly estimates the forward and backward flow fields, enforcing transformation consistency and improving the anatomical plausibility.

By incorporating these components into a unified architecture, the proposed method achieves accurate, stable, and anatomically consistent alignment of lung CT point clouds, significantly improving over the existing point-based baselines [17,20]. Moreover, our method’s use of vascular structures as the keypoints aligns with clinically interpretable anatomical landmarks, offering better transparency and usability than fully voxel-based models.

2. Related Work

2.1. Deformable Lung CT Registration

Deformable registration of lung CT scans is a fundamental task in medical imaging, supporting a wide range of clinical applications such as respiratory motion modeling for radiotherapy [6,21,22] and quantitative analyses of the disease progression in chronic obstructive pulmonary disease (COPD) [5,21]. By aligning inspiratory and expiratory scans, registration enables the computation of regional ventilation maps and volumetric changes over time [23]. These applications demand a high registration accuracy, especially in anatomically critical regions such as the lung lobes, bronchial trees, and vascular structures [24].

However, lung CT registration poses unique challenges compared to that in other organs. The lungs undergo large, non-linear deformations between breathing phases, and the sliding motion at the lung—pleura interface introduces discontinuities that are difficult to capture using smooth deformation models. Furthermore, the CT intensity values vary with air content, making the standard intensity-based metrics less reliable [25]. Techniques addressing these issues include biomechanically inspired models such as mass- or volume-preserving registration [26,27] which incorporate constraints on the local tissue conservation. In addition, the Demons algorithm [28], free-form B-spline deformation [29], and hybrid intensity–feature methods [30] optimize a similarity metric and a smooth deformation field. Although these methods have been widely evaluated on benchmarks (e.g., EMPIRE10 [3]), their reliance on iterative optimization and the voxel intensities limits both their scalability and robustness in complex respiratory motion scenarios.

2.2. Voxel-Based Deformable Registration

Voxel-based deformable registration has traditionally relied on intensity-driven optimization frameworks, often augmented with anatomical priors. For example, Schmidt-Richberg et al. [31] jointly optimize fissure segmentation and registration to improve the alignment near the inter-lobar boundaries, while Ding et al. [24] propose lobe-wise registration strategies to accommodate the sliding motion between lobes better. These methods incorporate domain knowledge to improve their physiological plausibility but often depend on manual annotations and are sensitive to segmentation errors.

To enhance the robustness in regions affected by noise, low contrast, or modality variations, several studies have introduced hand-crafted descriptors into the voxel-based pipeline. The Modality Independent Neighborhood Descriptor (MIND) [32], for instance, encodes local self-similarity patterns and has been widely adopted as a replacement for the raw intensity in similarity metrics, particularly for multi-modal or artifact-prone registrations. More recently, deep-learning-based methods such as VoxelMorph [33] and DLIR [34] have been proposed as data-driven alternatives to iterative registration. These models typically adopt U-Net-style encoder–decoder architectures [35] to directly regress dense voxel-wise displacement fields from input image pairs. Trained in an unsupervised manner using a combination of similarity and smoothness losses, these networks replace conventional optimization with a single forward pass, enabling efficient inference.

Despite their advantages, voxel-based models remain computationally demanding and are inherently sensitive to intensity inconsistencies, noise, and modality shifts. These limitations have motivated the exploration of alternative data representations—such as point-based methods—that aim to improve efficiency and robustness, especially in the presence of large deformations and variations in appearance.

2.3. Point-Based Registration

Recent approaches have explored representing anatomical structures—such as airway centerlines or vascular trees—as sparse 3D point clouds [36,37], enabling alternative formulations of deformable registration beyond traditional voxel grids. This shift has made it possible to leverage advances in 3D scene flow estimation. Models like FlowNet3D [18] and PointPWC-Net [17] have demonstrated effective ways to estimate dense motion fields between point sets through hierarchical features and cost volume aggregation. However, prior point-based approaches have primarily focused on generic scene flow or rigid alignment tasks, with limited investigation into deformable registration in lung CT.

The Lung250M-4B benchmark [16] addresses this gap by providing paired inspiratory–expiratory CT scans with vessel point clouds and high-quality anatomical correspondence, enabling systematic evaluation of point-based registration under realistic respiratory deformation. Both optimization- and learning-based methods [17,20] demonstrate a competitive performance with reduced inference costs; however, the inherent sparsity of point clouds poses challenges for deformation regularization, particularly in anatomically homogeneous or low-feature regions. Our work addresses these limitations through a hierarchical architecture with attention-guided refinements and bi-directional consistency tailored to lung CT registration.

3. The Proposed Approach

In this section, we first formalize our bi-directional objective for deformable lung CT registration (Section 3.1), describe the multi-scale point feature extraction backbone (Section 3.2), elaborate on geometric keypoint attention (Section 3.3), detail the progressive refinement of the flow predictions with flow attention (Section 3.4), and finally outline our comprehensive bi-directional training objective (Section 3.5).

3.1. The Problem Setup

Given a pair of lung CT scans, the task of deformable lung CT registration aims to estimate a dense, non-rigid transformation that accurately aligns the anatomical structures between a fixed scan (source) and a moving scan (target). Formally, let $\mathcal{P}={\left\{{\mathbf{p}}_i\right\}}_{i=1}^N$ and $\mathcal{Q}={\left\{{\mathbf{q}}_j\right\}}_{j=1}^N$ represent the 3D point clouds extracted from the source and target scans, respectively, where N denotes the number of sampled points. Our objective is to find a transformation $\mathcal{F}={\left\{f_i\right\}}_{i=1}^N$, mapping each source point ${\mathbf{p}}_i\in \mathcal{P}$ to its corresponding target location ${\mathbf{q}}_j\in \mathcal{Q}$.

We parameterize this transformation as a displacement field, where each point-specific transformation function $f_i:{\mathbb{R}}^3\mapsto {\mathbb{R}}^3$ is defined as

$$\begin{array}{c}\hfill f_i\left({\mathbf{p}}_i\right)={\mathbf{p}}_i+{\mathbf{v}}_i,\end{array}$$

(1)

with ${\mathbf{v}}_i\in {\mathbb{R}}^3$ being the displacement vector to predict. Given a set of ground-truth correspondences $\mathcal{C}$ between the source and target points (precomputed using external tools such as corrField [15]), the registration problem is formally expressed as minimizing

$$\begin{array}{c}\hfill {\mathcal{F}}^{*}=\underset{\mathcal{F}}{arg\; min}\sum _{(i,j)\in \mathcal{C}}{\parallel f_i\left({\mathbf{p}}_i\right)-{\mathbf{q}}_j\parallel }_2^2.\end{array}$$

(2)

This optimization encourages the transformed source points $f_i\left({\mathbf{p}}_i\right)$ to closely match their ground-truth correspondences ${\mathbf{q}}_j$, thereby achieving accurate anatomical alignment and maintaining spatial coherence.

In this work, we propose a learning-based approach to directly estimating the displacement field $\mathcal{F}$ from the input lung CT point clouds. Inspired by the point-based scene flow framework [17], our architecture incorporates two key innovations. First, we introduce specialized attention mechanisms—geometric keypoint attention at the coarse scale and progressive flow attention at the fine scale—to capture both global structural relationships and local deformation cues better. Second, we employ a bi-directional flow estimation strategy, simultaneously predicting the forward flow ($\mathcal{F}$, source-to-target) and the backward flow ($\mathcal{G}={\left\{g_j\right\}}_{j=1}^N$, target-to-source). Formally, the backward transformation is defined as

$$\begin{array}{c}\hfill g_j\left({\mathbf{q}}_j\right)={\mathbf{q}}_j+{\mathbf{u}}_j,\end{array}$$

(3)

where ${\mathbf{u}}_j\in {\mathbb{R}}^3$ denotes the displacement vector for the target points. The backward flow is optimized by minimizing

$$\begin{array}{c}\hfill {\mathcal{G}}^{*}=\underset{\mathcal{G}}{arg\; min}\sum _{(i,j)\in \mathcal{C}}{\parallel {\mathbf{p}}_i-g_j\left({\mathbf{q}}_j\right)\parallel }_2^2.\end{array}$$

(4)

This bi-directional formulation enables the network to leverage mutual consistency between the forward and backward transformations, resulting in more stable, accurate, and anatomically plausible registration outcomes. Figure 1 provides an overview of our network design, and we detail each module in the subsequent sections.

3.2. Multi-Scale Feature Extraction

3.2.1. The PointConv Backbone

We extract hierarchical point features using PointConv layers [38], which extend conventional convolutions to irregular 3D point sets. Formally, given an input point cloud $\mathcal{X}={\left\{{\mathbf{x}}_i\right\}}_{i=1}^{\left|\mathcal{X}\right|}$ with the associated per-point features ${\mathbf{F}}_{\mathcal{X}}\in {\mathbb{R}}^{\left|\mathcal{X}\right|\times D_{\mathrm{emb}}}$, each PointConv layer aggregates the local features as follows:

$$\begin{array}{c}\hfill \mathrm{PointConv}{({\mathbf{F}}_{\mathcal{X}};\mathcal{X})}_{(i,:)}=\sum _{{\mathbf{x}}_j\in \mathcal{N}\left({\mathbf{x}}_i\right)}S\left({\mathbf{x}}_j\right){\mathbf{W}}_{(:,i)}{\left({\mathbf{F}}_{\mathcal{X}}\right)}_j,\end{array}$$

(5)

where $\mathcal{N}\left({\mathbf{x}}_i\right)$ denotes the local neighborhood of point ${\mathbf{x}}_i$, $S\left({\mathbf{x}}_j\right)$ is an inverse density scale factor computed via kernel density estimation, and $\mathbf{W}$ represents the learnable convolutional weights conditioned on relative spatial coordinates. By stacking multiple PointConv blocks in a U-Net-style encoder–decoder [35], we generate a coarse-to-fine hierarchy of informative point feature embeddings.

3.2.2. The Coarse-to-Fine Pipeline

To efficiently handle large deformations while preserving anatomical completeness, we progressively downsample the input point clouds using farthest point sampling (FPS) [39], ensuring that the sampled points are broadly distributed across the lung’s geometry without over-concentrating on local regions. Since the original point clouds were extracted primarily from critical anatomical structures such as bronchial trees and vascular networks, FPS maintains essential structural coverage with high fidelity. This results in a hierarchical set of point clouds ${\left\{{\mathcal{X}}^{\left(l\right)}\right\}}_{l=1}^L$, from the finest resolution ($l=1$) to the coarsest resolution ($l=L$), where each sampled point at the coarsest level encodes a broader anatomical region of the lung, facilitating global alignment. This multi-scale representation is critical for our attention-driven alignment strategy, where global coarse-level correspondences are first established and subsequently refined at higher resolutions.

3.3. Geometric Keypoint Attention

The geometric keypoint attention module captures the global structural correspondences prior to finer-scale refinement. At this stage, capturing the long-range geometric structure is essential for reducing the ambiguity of the correspondence under large respiratory motion, which motivates our use of a geometry-aware attention formulation. Consider the coarse-level feature embeddings ${\mathbf{F}}_{\mathcal{P}}^{\left(L\right)}\in {\mathbb{R}}^{\left|\mathcal{P}\right|\times D_{L-\mathrm{emb}}}$. The output attention-enhanced feature ${\mathbf{H}}_{\mathcal{P}}^{\left(L\right)}$ is computed as an attention-weighted aggregation:

$$\begin{array}{c}\hfill {\mathbf{h}}_{{\mathcal{P}}_i}^{\left(L\right)}=\sum _{j=1}^{\left|\mathcal{P}\right|}{\alpha }_{i,j}\left({\mathbf{f}}_{{\mathcal{P}}_j}^{\left(L\right)}{\mathbf{W}}^V\right),\end{array}$$

(6)

where the attention weights ${\alpha }_{i,j}$ measure the pairwise geometric relations among points:

$$\begin{array}{c}\hfill {\alpha }_{i,j}=\mathrm{Softmax}\left({\displaystyle \frac{\left({\mathbf{f}}_{{\mathcal{P}}_i}^{\left(L\right)}{\mathbf{W}}^Q\right){({\mathbf{f}}_{{\mathcal{P}}_j}^{\left(L\right)}{\mathbf{W}}^K+{\mathbf{r}}_{i,j}{\mathbf{W}}^R)}^{\top }}{\sqrt{d_t}}}\right).\end{array}$$

(7)

Here, ${\mathbf{r}}_{i,j}$ represents the geometric embeddings, as proposed in GeoTransformer [40], while ${\mathbf{W}}^Q,{\mathbf{W}}^K,{\mathbf{W}}^V,{\mathbf{W}}^R\in {\mathbb{R}}^{D_{L-\mathrm{emb}}\times D_{L-\mathrm{emb}}}$ are learnable projection matrices for queries, keys, values, and geometric embeddings, respectively. Analogous computations are performed for the target cloud features ${\mathbf{F}}_{\mathcal{Q}}^{\left(L\right)}$.

A similar attention mechanism is adopted for cross-attention, which explicitly models inter-cloud interactions by exchanging information between the source and target point clouds. Compared to self-attention, the key difference is that the query $\left({\mathbf{f}}_{{\mathcal{P}}_i}^{\left(L\right)}{\mathbf{W}}^Q\right)$ is computed from one point cloud (e.g., $\mathcal{P}$), while the key and value $({\mathbf{f}}_{{\mathcal{Q}}_j}^{\left(L\right)}{\mathbf{W}}^K,{\mathbf{f}}_{{\mathcal{Q}}_j}^{\left(L\right)}{\mathbf{W}}^V)$ are taken from the other (e.g., $\mathcal{Q}$). This directional change allows the network to attend across point clouds and capture alignment-relevant correspondences at the coarsest level.

To robustly capture both the intra-cloud structure and inter-cloud correspondence cues, the self- and cross-attention modules are alternated for $N_c$ iterations, resulting in enhanced features ${\widehat{\mathbf{F}}}_{\mathcal{P}}^{\left(L\right)}\in {\mathbb{R}}^{|{\mathcal{P}}^{\left(L\right)}|\times D_{L-\mathrm{emb}}}$ and ${\widehat{\mathbf{F}}}_{\mathcal{Q}}^{\left(L\right)}\in {\mathbb{R}}^{|{\mathcal{Q}}^{\left(L\right)}|\times D_{L-\mathrm{emb}}}$. This interleaved design allows the network to iteratively refine the coarse-level representations by jointly reasoning about the global geometry and alignment consistency, which is particularly beneficial in reducing ambiguity in the correspondence under large deformations.

3.4. Progressive Flow Refinement

At each decoder level l, we progressively refine the flow estimation by leveraging coarser predictions from level $l+1$, as shown in Figure 2 (In the following sections, we focus on describing the forward flow $\mathcal{F}$ (source-to-target) for clarity and conciseness. The backward flow $\mathcal{G}$ (target-to-source) is computed in an analogous manner using the same architecture and refinement process.).

3.4.1. Warping and Cost Volume Construction

The estimated flow ${\mathbf{v}}^{(l+1)}$ at the coarser level $l+1$ is propagated to the finer level through inverse distance weighted interpolation, producing an initial flow estimate ${\tilde{\mathbf{v}}}^{\left(l\right)}$ at the resolution l. We use the upsampled flow ${\tilde{\mathbf{v}}}^{\left(l\right)}$ to warp the target points:

$${\widehat{\mathcal{Q}}}^{\left(l\right)}=\{{\mathbf{q}}_i^{\left(l\right)}+{\tilde{\mathbf{v}}}_i^{\left(l\right)}|{\mathbf{q}}_i^{\left(l\right)}\in {\mathcal{Q}}^{\left(l\right)}\},$$

bringing the target points into approximate alignment with the source. This reduces large residual displacements and stabilizes the subsequent refinement steps.

Next, we construct a cost volume encoding the local geometric and feature-level differences. For each source point ${\mathbf{p}}_i^{\left(l\right)}\in {\mathcal{P}}^{\left(l\right)}$, we first identify its k-nearest neighbors among the warped target points ${\widehat{\mathcal{Q}}}^{\left(l\right)}$. Then, leveraging the warped target features ${\mathbf{F}}_{\widehat{\mathcal{Q}}}^{\left(l\right)}$, we compute the residual feature embeddings between the source features ${\mathbf{F}}_{\mathcal{P}}^{\left(l\right)}$ and their corresponding neighboring warped target features. These residual embeddings are subsequently aggregated via PointConv layers [38], resulting in the cost volume features ${\mathbf{C}}^{\left(l\right)}$, which effectively encode the geometric proximity and the discrepancies in the local appearance to guide the flow refinement.

3.4.2. The Flow Estimator

The cost volume features ${\mathbf{C}}^{\left(l\right)}$ and source features ${\mathbf{F}}_{\mathcal{P}}^{\left(l\right)}$ are concatenated to form the refinement input:

$${\mathbf{Z}}_{\mathcal{P}}^{\left(l\right)}=[{\mathbf{C}}^{\left(l\right)},{\mathbf{F}}_{\mathcal{P}}^{\left(l\right)}]\in {\mathbb{R}}^{|{\mathcal{P}}^{\left(l\right)}|\times D_{l-\mathrm{ref}}}.$$

To enhance the flow estimation accuracy, we introduce a contextual attention module composed of alternating self-attention and cross-attention layers. At this stage, the goal is to refine the localized residual flow patterns based on the learned contextual properties. Specifically, we first employ standard multi-head self-attention (MHSA) within the source point cloud to capture the internal structural context:

$$\begin{array}{c}\hfill {\left({\mathbf{Z}}_{\mathcal{P}}^{\left(l\right)}\right)}^{\prime }=\mathrm{MHSA}\left({\mathbf{Z}}_{\mathcal{P}}^{\left(l\right)}\right),\end{array}$$

(8)

where MHSA is defined as

$$\begin{array}{cc}\hfill \mathrm{MHSA}\left(\mathbf{X}\right)& =\mathrm{Concat}[{\mathrm{head}}_1,\cdots ,{\mathrm{head}}_h]{\mathbf{W}}^O,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\mathrm{head}}_m& =\mathrm{Softmax}\left({\displaystyle \frac{\left(\mathbf{X}{\mathbf{W}}_m^Q\right){\left(\mathbf{X}{\mathbf{W}}_m^K\right)}^{\top }}{\sqrt{d_k}}}\right)\mathbf{X}{\mathbf{W}}_m^V,\hfill \end{array}$$

(10)

with ${\mathbf{W}}_m^Q,{\mathbf{W}}_m^K,{\mathbf{W}}_m^V,{\mathbf{W}}^O$ as the learnable linear projection matrices and h as the number of attention heads.

Subsequently, to explicitly incorporate the inter-cloud correspondence cues, we perform a cross-attention operation between these self-attended source features ${\left({\mathbf{Z}}_{\mathcal{P}}^{\left(l\right)}\right)}^{\prime }$ and the corresponding warped target features ${\mathbf{F}}_{\widehat{\mathcal{Q}}}^{\left(l\right)}\in {\mathbb{R}}^{|{\widehat{\mathcal{Q}}}^{\left(l\right)}|\times D_{L-\mathrm{emb}}}$. This step aggregates relevant information from the warped target points to refine the source features:

$$\begin{array}{cc}\hfill {\left({\widehat{\mathbf{Z}}}_{\mathcal{P}}^{\left(l\right)}\right)}_i& =\sum _{j=1}^{|{\widehat{\mathcal{Q}}}^{\left(l\right)}|}{\beta }_{i,j}\left({\left({\mathbf{Z}}_{\widehat{\mathcal{Q}}}^{\left(l\right)}\right)}_j{\mathbf{W}}^V\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\beta }_{i,j}& =\mathrm{Softmax}\left({\displaystyle \frac{\left({\left({\mathbf{Z}}_{\mathcal{P}}^{\left(l\right)}\right)}_i^{\prime }{\mathbf{W}}^Q\right){\left({\left({\mathbf{F}}_{\widehat{\mathcal{Q}}}^{\left(l\right)}\right)}_j{\mathbf{W}}^K\right)}^{\top }}{\sqrt{d_k}}}\right),\hfill \end{array}$$

(12)

where ${\mathbf{W}}^Q,{\mathbf{W}}^K,{\mathbf{W}}^V\in {\mathbb{R}}^{D_{l-\mathrm{ref}}\times D_{l-\mathrm{ref}}}$ are the query, key, and value projection matrices, respectively.

By iteratively alternating the self-attention (intra-cloud) and cross-attention (inter-cloud) layers for $N_f$ steps, we obtain refined embeddings ${\widehat{\mathbf{Z}}}_{\mathcal{P}}^{\left(l\right)}$ that jointly leverage the internal point cloud context and the external correspondence information.

Finally, these enriched embeddings ${\widehat{\mathbf{Z}}}_{\mathcal{P}}^{\left(l\right)}$ are input into a residual flow prediction network (MLP) to estimate the residual displacements $\Delta {\mathbf{v}}^{\left(l\right)}$:

$$\begin{array}{c}\hfill \Delta {\mathbf{v}}^{\left(l\right)}=\mathrm{MLP}\left(\left({\widehat{\mathbf{Z}}}_{\mathcal{P}}^{\left(l\right)}\right)\right).\end{array}$$

(13)

The refined flow at level l is then computed by adding the residual displacement to the initial estimate:

$$\begin{array}{c}\hfill {\mathbf{v}}^{\left(l\right)}={\tilde{\mathbf{v}}}^{\left(l\right)}+\Delta {\mathbf{v}}^{\left(l\right)},\end{array}$$

(14)

which is recursively applied at each decoder level until the finest resolution is reached, producing the final flow prediction ${\mathbf{v}}^{\left(1\right)}$.

Note that the same refinement procedure is applied in the reverse direction to obtain the backward flows ${\left\{{\mathbf{u}}^{\left(l\right)}\right\}}_{l=1}^L$.

3.4.3. Post-Processing for Dense Deformation Estimation

Although our model estimates the displacements only at sparse vessel-derived points, a dense deformation field across the entire lung volume is required. To achieve this, we employ Thin Plate Spline (TPS) interpolation, a classical method in landmark-based registration. Specifically, given the predicted displacements at a sparse set of source points, this interpolates the transformation to the entire 3D space, allowing the displacement vectors for all of the voxels in the volume to be computed. This design is motivated by the anatomical coupling between the vascular structures and lung parenchyma deformation, ensuring that clinically relevant motion patterns are faithfully captured across the lung.

3.5. The Training Objective

Our training objective combines supervised bi-directional flow losses with the unsupervised cycle consistency loss to promote accurate, coherent, and invertible transformations. By simultaneously supervising both the forward and backward displacement predictions at multiple resolutions and additionally enforcing consistency between these two directions, the network is guided towards robust and anatomically plausible lung registrations.

3.5.1. Bi-Directional Multi-Scale Flow Loss

At each resolution level l, we supervise the predicted displacement fields by comparing them against their corresponding ground-truth flows. Specifically, we define a bi-directional loss that penalizes deviations from the ground truth in both the forward (source-to-target) and backward (target-to-source) directions:

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{flow}}^{\left(l\right)}=\sum _{{\mathbf{p}}_i\in {\mathcal{P}}^{\left(l\right)}}\parallel {\widehat{f}}_i^{\left(l\right)}\left({\mathbf{p}}_i\right)-f_i^{\left(l\right)}\left({\mathbf{p}}_i\right){\parallel }_2+\sum _{{\mathbf{q}}_i\in {\mathcal{Q}}^{\left(l\right)}}{\parallel {\widehat{g}}_i^{\left(l\right)}\left({\mathbf{q}}_i\right)-g_i^{\left(l\right)}\left({\mathbf{q}}_i\right)\parallel }_2,\end{array}$$

(15)

where ${\widehat{f}}^{\left(l\right)}$ and ${\widehat{g}}^{\left(l\right)}$ denote the predicted forward and backward displacement functions, respectively, while $f^{\left(l\right)}$ and $g^{\left(l\right)}$ represent their ground-truth counterparts. This symmetric formulation provides balanced supervision, encouraging consistent flow estimation in both directions.

3.5.2. The Cycle Consistency Loss

To enhance the geometric plausibility and reversibility of the predicted transformations further, we introduce an unsupervised cycle consistency loss. Let ${\widehat{\mathcal{F}}}^{\left(l\right)}={\left\{{\widehat{f}}_i^{\left(l\right)}\right\}}_{i=1}^{|{\mathcal{P}}^{\left(l\right)}|}$ and ${\widehat{\mathcal{G}}}^{\left(l\right)}={\left\{{\widehat{g}}_i^{\left(l\right)}\right\}}_{i=1}^{|{\mathcal{Q}}^{\left(l\right)}|}$ be the sets of predicted forward and backward displacement functions, respectively. Additionally, let ${\mathbf{T}}_{\widehat{\mathcal{F}}}^{\left(l\right)}(·)$ and ${\mathbf{T}}_{\widehat{\mathcal{G}}}^{\left(l\right)}(·)$ denote the transformation functions that deform a point cloud by applying the corresponding per-point displacements; for instance, ${\mathbf{T}}_{\widehat{\mathcal{F}}}^{\left(l\right)}\left({\mathcal{P}}^{\left(l\right)}\right)={\sum }_i{\widehat{f}}_i\left({\mathbf{p}}_i^{\left(l\right)}\right)={\sum }_i\left({\mathbf{p}}_i^{\left(l\right)}+{\widehat{\mathbf{v}}}_i^{\left(l\right)}\right)$.

The cycle consistency loss penalizes deviations after performing forward and backward transformations sequentially, promoting reversible mappings between point clouds:

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{cycle}}^{\left(l\right)}=\mathrm{CD}\left({\mathbf{T}}_{\widehat{\mathcal{G}}}^{\left(l\right)}\circ {\mathbf{T}}_{\widehat{\mathcal{F}}}^{\left(l\right)}\left({\mathcal{P}}^{\left(l\right)}\right),{\mathcal{P}}^{\left(l\right)}\right)+\mathrm{CD}\left({\mathbf{T}}_{\widehat{\mathcal{F}}}^{\left(l\right)}\circ {\mathbf{T}}_{\widehat{\mathcal{G}}}^{\left(l\right)}\left({\mathcal{Q}}^{\left(l\right)}\right),{\mathcal{Q}}^{\left(l\right)}\right),\end{array}$$

(16)

where the Chamfer Distance (CD) between two point clouds $S_1$ and $S_2$ is defined as

$$\begin{array}{c}\hfill \mathrm{CD}(S_1,S_2)={\displaystyle \frac{1}{|S_1|}}\sum _{x\in S_1}\underset{y\in S_2}{min}{\parallel x-y\parallel }_2^2+{\displaystyle \frac{1}{|S_2|}}\sum _{y\in S_2}\underset{x\in S_1}{min}{\parallel x-y\parallel }_2^2.\end{array}$$

(17)

This unsupervised regularization term ensures geometric coherence and encourages mutually consistent bi-directional flows.

3.5.3. The Final Training Objective

Our complete multi-scale training objective integrates these two losses across all resolution levels:

$$\begin{array}{c}\hfill \mathcal{L}=\sum _{l=1}^L\left({\mathcal{L}}_{\mathrm{flow}}^{\left(l\right)}+\lambda ·{\mathcal{L}}_{\mathrm{cycle}}^{\left(l\right)}\right),\end{array}$$

(18)

where the hyperparameter $\lambda$ controls the influence of the cycle consistency regularization and is empirically set to 0.1.

4. Experiments

4.1. Dataset

The experiments utilize the Lung250M dataset, which consists of approximately 250 million points extracted from 248 lung CT scans (124 patients), excluding the full-resolution voxel data (4B) provided in Lung250M-4B [16]. Lung250M integrates scans from Empire10 [3], TCIA-NSCLC [4,41,42,43,44], TCIA-Ventilation [4,6], L2R-LungCT [7], TCIA-NLST [4,45], and DIR-LAB COPDgene [1]. Each dataset features distinct imaging protocols, scanner settings, and pathology distributions, enhancing the diversity and complexity of the lung deformations. The detailed composition of the dataset is summarized in

Table 1. Detailed composition of the training, validation, and testing split of the Lung250M-4B dataset.

Split	Sub-Dataset	Index	# Pair
Training	Empire10 [3]	0–1, 3–7, 9–11	97
	TCIA-NLST [4,45]	12–33
	TCIA-NSCLC [4,41,42,43,44]	34–53
	L2R-LungCT [7]	57–83
	TCIA-Ventilation [4,6]	84–93, 95–96, 98–103
Validation	Empire10 [3]	2, 8	17
	L2R-LungCT [7]	54–56
	TCIA-Ventilation [4,6]	94, 97
	TCIA-NLST [4,45]	114–123
Testing	DIR-LAB COPDgene [1]	104–113	10

.

4.2. Evaluation Metrics

To quantitatively assess the registration performance, we follow the evaluation protocol as in the Lung250M-4B benchmark [16], adopting the Target Registration Error (TRE) as our primary metric. In addition to the mean TRE, we report the $\{25, 50, 75\}$ percentile TRE values to provide a more comprehensive view of the registration accuracy across different anatomical regions and difficulty levels. Moreover, we evaluate the alignment quality using the Dice Similarity Coefficient (DSC) between the transformed source and the target mask. A higher DSC indicates a better anatomical overlap, while the TRE assesses the quality of landmark registration.

4.3. Implementation Details

4.3.1. Training Details

We implement our method using PyTorch [46] and conduct all experiments on a machine equipped with an Intel(R) Xeon(R) Gold 5218R CPU and a single NVIDIA Tesla V100 GPU with 32 GB of memory. The model is trained using the Adam optimizer [47] with an initial learning rate of 0.001, decayed at epochs 1200 and 1400 by a factor of 0.1 using a multi-step learning rate scheduler. We train for 1500 epochs with a batch size of 4. For data augmentation, we apply random rigid transformations and Gaussian noise to improve the generalization. Ground-truth correspondences are obtained using corrField [15].

4.3.2. Model Hyperparameters

The network is built as a five-level hierarchical encoder–decoder ($L=5$), where the number of points progressively decreases across levels as follows: $N\to {\displaystyle \frac{N}{4}}\to {\displaystyle \frac{N}{16}}\to {\displaystyle \frac{N}{32}}\to {\displaystyle \frac{N}{128}}(l=1\to 5)$. The corresponding feature dimensions at each level are set to $[64,128,256,512,256]$. All of the attention modules use 4-head multi-head attention and are applied iteratively with $N_c=N_f=3$ steps for both geometric keypoint attention and flow attention.

4.4. The Experimental Results

We evaluate our method on the COPD test set and compare it with several point-based baselines, including optimization-based [20] and learning-based approaches [17]. As shown in

Table 2. Quantitative results on the COPD test cases of point-based methods, reported as the mean TRE with 25/50/75% percentiles (in mm) and the DSC (in %). A lower TRE and a higher DSC indicate a better performance. The performance metrics for the other methods are sourced from the Lung250M-4B [16] paper.

Method	TRE ↓	25%	50%	75%	DSC ↑
initial	16.25	10.14	15.94	21.76	75.8
VoxelMorphw/o IO [33]	6.53	3.38	5.82	8.50	-
VoxelMorph++w/o IO [48]	4.47	2.41	3.74	5.69	-
CPD [20]	3.13	1.51	2.28	3.58	-
CPD w/ labels [20]	2.59	1.36	2.01	3.16	-
PPWCsup [17]	2.85	1.52	2.33	3.54	-
PPWCsyn [17]	2.73	1.52	2.28	3.45	-
Ours	2.24	1.16	1.79	2.77	91.4

, our method achieves the best performance across all evaluation metrics, including the mean TRE and its 25th, 50th, and 75th percentiles. Notably, compared to the state-of-the-art method, e.g., PPWC [17], our model reduces the mean TRE from 2.85 mm to 2.24 mm and achieves a lower median (50%) TRE of 1.79 mm versus 2.33 mm. Additionally, our method achieves a DSC (due to the lack of publicly reported evaluations for other baselines, we only report our DSC value) of 91.4%, indicating a high degree of anatomical overlap after registration.

In addition to the quantitative gains, the qualitative results (Figure 3) demonstrate that our method produces smoother and more anatomically consistent deformations compared to those with PPWC [17]. Notably, our model preserves the alignment in both the vascular and boundary regions better, capturing complex respiratory motion more effectively.

4.5. Ablation Studies

To assess the contribution of each model component, training objective, and key hyperparameter, we perform extensive ablation studies.

4.5.1. The Model Components

Table 3 shows the effect of each architectural component. Starting from a base model without any attention modules or bi-directional refinement (Table 3 (a)), we first add the geometric keypoint attention at the coarsest level (Table 3 (b)). This yields a minor improvement, suggesting that global alignment provides more stable initialization. In contrast, adding the flow attention module alone (Table 3 (c)) results in a more substantial performance gain, highlighting the importance of context-aware fine-level refinements. When both attention modules are employed jointly (Table 3 (d)), we observe further improvements across all metrics, indicating that the two modules complement each other by handling large and small deformations at different scales. Finally, incorporating both bi-directional refinement and attention modules yields the best performance, with a mean TRE of 2.24 mm and the lowest errors across all evaluated percentiles (25%, 50%, and 75%).

4.5.2. The Loss Function

In Table 4, we analyze the impact of the training objectives. Using only the multi-scale flow loss (Table 4 (a)) provides a strong supervised baseline. However, relying solely on the cycle consistency loss (Table 4 (b)) leads to unstable training and an inferior performance, underscoring the necessity of ground-truth supervision. When both losses are combined, as in our full model, the cycle consistency term serves as an effective regularizer, leading to more consistent and anatomically coherent transformations.

4.5.3. The Weight Factor for Cycle Consistency

To investigate the effect of the cycle consistency loss weight $\lambda$, we performed a grid search over $\lambda \in \{0.01,0.05,0.1,0.5\}$, balancing it against the supervised multi-scale flow loss. As summarized in Table 5, a very small value (e.g., Table 5 (a)) had a minimal regularizing impact, while overly large values (e.g., Table 5 (c)) over-smoothed the deformation field, reducing the DSC. The optimal value $\lambda =0.1$ provided the best trade-off—enforcing inverse consistency while maintaining local flexibility—and consistently yielded the best TRE and DSC.

4.5.4. The Number of Attention Heads

We conducted an ablation study on the number of attention heads $N_h$ used in both the geometric keypoint and flow attention modules. As shown in Table 6, increasing the number of heads improved the alignment up to a point, but diminishing returns were observed beyond $N_h=4$. We found this achieved the best balance between accuracy and stability, producing the lowest TRE and hthe ighest DSC, and thus we used $N_h=4$ in our final model.

Table 3. Ablation study on model components.

Ref.	Keypoint Attn.	Flow Attn.	Bi-Dir. Refine	TRE ↓	25%	50%	75%	DSC ↑
(a)				2.85	1.52	2.33	3.54	89.9
(b)	✓			2.83	1.54	2.28	3.32	89.9
(c)		✓		2.67	1.38	2.27	3.40	90.1
(d)	✓	✓		2.54	1.29	2.10	3.12	90.2
Ours	✓	✓	✓	2.24	1.16	1.79	2.77	91.4

Table 3. Ablation study on model components.

Ref.	Keypoint Attn.	Flow Attn.	Bi-Dir. Refine	TRE ↓	25%	50%	75%	DSC ↑
(a)				2.85	1.52	2.33	3.54	89.9
(b)	✓			2.83	1.54	2.28	3.32	89.9
(c)		✓		2.67	1.38	2.27	3.40	90.1
(d)	✓	✓		2.54	1.29	2.10	3.12	90.2
Ours	✓	✓	✓	2.24	1.16	1.79	2.77	91.4

Table 4. Ablation study on loss function.

Ref.	Multi-Scale Flow	Consistency	TRE ↓	25%	50%	75%	DSC ↑
(a)	✓		2.32	1.25	2.01	2.98	90.9
(b)		✓	Fail to converge
Ours	✓	✓	2.24	1.16	1.79	2.77	91.4

Table 4. Ablation study on loss function.

Ref.	Multi-Scale Flow	Consistency	TRE ↓	25%	50%	75%	DSC ↑
(a)	✓		2.32	1.25	2.01	2.98	90.9
(b)		✓	Fail to converge
Ours	✓	✓	2.24	1.16	1.79	2.77	91.4

Table 5. Analysis of the weight factor $\lambda$.

Ref.	$\mathit{\lambda }$	TRE ↓	DSC ↑
(a)	0.01	2.35	90.4
(b)	0.05	2.26	91.2
Ours	0.1	2.24	91.4
(c)	0.5	2.57	90.0

Table 5. Analysis of the weight factor $\lambda$.

Ref.	$\mathit{\lambda }$	TRE ↓	DSC ↑
(a)	0.01	2.35	90.4
(b)	0.05	2.26	91.2
Ours	0.1	2.24	91.4
(c)	0.5	2.57	90.0

Table 6. Analysis of the # of attention heads $N_h$.

Ref.	${\mathit{N}}_{\mathit{h}}$	TRE ↓	DSC ↑
(a)	1	2.34	91.1
(b)	2	2.31	90.8
Ours	4	2.24	91.4
(c)	8	2.25	91.0

Table 6. Analysis of the # of attention heads $N_h$.

Ref.	${\mathit{N}}_{\mathit{h}}$	TRE ↓	DSC ↑
(a)	1	2.34	91.1
(b)	2	2.31	90.8
Ours	4	2.24	91.4
(c)	8	2.25	91.0

Overall, these ablation studies demonstrate that each proposed component—ranging from the attention modules and bi-directional training objectives to the key hyperparameter configurations—contributes meaningfully to the improved accuracy, stability, and robustness of our method.

4.6. Analysis of Generalizability

To evaluate the generalization capability of our framework, we conducted cross-dataset experiments using external CT datasets that differed from those used during training. Specifically, the model was trained on the Empire10 [3] and TCIA-NLST [4,45] datasets and then directly tested—without any fine-tuning—on three unseen datasets, L2R-LungCT [7], TCIA-Ventilation [6], and DIR-LAB COPDgene [1], which represent diverse imaging protocols, scanner vendors, and population characteristics.

As shown in

Table 7. Generalizability experiment results on various datasets. The model was trained on the Empire10 [3] and TCIA-NLST [4,45] datasets and evaluated on L2R-LungCT [7], TCIA-Ventilation [4,6], and DIR-LAB COPDgene [1]. We refer the readers to Table 1 for further dataset details.

Dataset		TRE ↓	25%	50%	75%	DSC ↑
L2R-LungCT [7]	initial	26.04	21.59	25.90	31.05	65.2
	result	4.53	2.63	3.79	5.73	84.8
TCIA-Ventilation [4,6]	initial	15.82	11.17	16.03	20.69	71.4
	result	4.33	2.44	3.26	4.50	88.8
DIR-LAB COPDgene [1]	initial	16.25	10.14	15.94	21.76	75.8
	result	3.53	1.89	2.92	4.59	89.3

, our method achieves consistent improvements across all external datasets, with substantial reductions in the mean Target Registration Error (TRE) and corresponding increases in the Dice Similarity Coefficient (DSC). These results demonstrate that the model generalizes effectively to unseen anatomical variations and imaging domains, despite being trained on a limited number of source datasets. This robustness to domain shifts underscores the clinical applicability of our point-based framework, as it maintains a reliable performance without requiring retraining or tuning for each target dataset.

4.7. Analysis of Model Efficiency

In addition to evaluating the registration accuracy, we assessed the computational efficiency of our method in comparison with that of a representative voxel-based approach, VoxelMorph++ [48].

Table 8. Efficiency comparison between VoxelMorph++ [48] and ours. Lower is better.

Method	Representation	Train Mem.	Inference Mem.	FLOPS	Time
		(GB)	(GB)	(G)	(ms)
VoxelMorph++	Voxel	5.70	4.97	318.72	266.88
Ours	Point cloud	2.78	0.82	56.89	74.55

summarizes the training memory consumption, inference memory usage, floating point operations (FLOPS), and inference time per scan pair for both methods.

Our point-cloud-based model demonstrates substantial efficiency advantages. Specifically, the training memory usage is reduced from 5.70 GB to 2.78 GB, and the inference memory usage is decreased from 4.97 GB to 0.82 GB. In terms of the computational complexity, our method achieves a five-fold reduction in FLOPS (318.72 G vs. 56.89 G). Furthermore, the inference time per scan pair is significantly shortened from 266.88 ms to 74.55 ms, indicating a substantial gain in the processing speed.

These results highlight that by leveraging the sparsity and flexibility of point cloud representations, our method achieves a superior computational efficiency compared to that of voxel-based models while maintaining a competitive registration performance. This efficiency is particularly advantageous for potential clinical applications where fast and memory-efficient processing is critical.

5. Discussion

Our results demonstrate that the proposed point-based deformable registration framework achieves a state-of-the-art performance on the Lung250M benchmark [16]. By incorporating geometric keypoint attention at coarse resolutions, contextual flow refinement at finer scales, and bi-directional learning objectives, our method achieves a superior accuracy across all TRE metrics compared to that of the prior optimization-based and learning-based approaches. These findings validate our core hypothesis: that accurate lung CT registration requires joint modeling of the long-range structural consistency and localized deformation patterns, particularly given the large respiratory motion and anatomical variability inherent in this domain.

Compared to prior point-based methods primarily developed for rigid registration or generic scene flow tasks [17,18], our approach is the first to specifically target deformable lung CT alignment using sparse point clouds, building on the recent Lung250M dataset [16]. While voxel-based learning methods have achieved notable success in brain MRI and abdominal CT registration, their application to thoracic imaging remains limited by the computational costs and sensitivity to variations in intensity. Our method addresses these limitations by leveraging sparse geometric inputs and multi-scale feature interactions, offering a more efficient and robust alternative.

Moreover, the use of bi-directional training with cycle consistency constraints across all resolution levels contributes to the deformation stability by enforcing multi-scale coherence in the flow predictions. This regularization, in combination with a coarse-to-fine refinement architecture, enhances the robustness to noisy or imperfect training correspondences. The empirical consistency of our model’s performance across datasets further suggests resilience to residual noise in the pseudo-ground-truth labels without requiring additional denoising mechanisms.

From a clinical standpoint, the proposed framework offers practical benefits. Its efficiency enables rapid deployment across large-scale datasets, while its anatomical interpretability—grounded in vascular keypoints—aligns with radiologists’ mental models for thoracic anatomy. Such properties suggest its promising utility in workflows such as longitudinal disease monitoring and dose accumulation analyses in radiotherapy, where consistent, reliable registration is critical.

Despite these advantages, our framework also has limitations. As it operates on vessel-derived point clouds, the registration accuracy in regions without clear geometric landmarks—such as homogeneous parenchymal areas—is less directly evaluated. In addition, our training supervision relies on the pseudo-ground-truth correspondences generated by corrField [15]. Although these correspondences have demonstrated high reliability, with reported mean TREs of 1.45 mm (test) and 2.67 mm (validation) against manual landmark annotations [16], a certain level of noise is inevitable. Our model mitigates the potential supervision noise through bi-directional cycle consistency regularization, but an explicit analysis of the robustness to correspondence noise remains an area for future investigation.

Future work could explore hybrid architectures that fuse the voxel-level appearance with the point-based geometry, potentially enhancing the deformation estimations in texture-rich but landmark-sparse regions. Incorporating semantic priors such as airway labels or fissure segmentations may improve the regional interpretability and clinical usability further. Additionally, injecting controlled perturbations into the training correspondences would help quantify the model’s sensitivity and reinforce its reliability. Expanding this framework to handle full 4D CT sequences or to quantify the registration uncertainty also presents promising future directions.

In conclusion, we present a novel attention-based, bi-directional point cloud registration framework specifically designed for deformable lung CT alignment. Through architectural innovations and rigorous evaluations on a challenging large-scale dataset, we show that point-based learning, when tailored to the characteristics of respiratory deformation, can offer an accurate, efficient, and anatomically consistent registration performance. Beyond algorithmic improvements, our framework also provides interpretable and efficient deformation estimates that align with clinically meaningful structures, making it a strong candidate for deployment in medical image analysis workflows. We believe this work provides an important step toward more robust geometric modeling in medical image analysis.