Abstract
Phase space methods, particularly Wigner functions, provide intuitive tools for representing and analyzing quantum states. We focus on systems with SU(2) dynamical symmetry, which naturally describes spin and a wide range of two-mode quantum models. We present a unified phase space framework tailored to these systems, highlighting its broad applicability in quantum optics, metrology, and information. After reviewing the core SU(2) phase-space formalism, we apply it to states designed for optimal quantum sensing, where their nonclassical features are clearly revealed in the Wigner representation. We then extend the approach to systems with an indefinite number of excitations, introducing a generalized framework that captures correlations across multiple SU(2)-invariant subspaces. These results offer practical tools for understanding both theoretical and experimental developments in quantum science.
1. Introduction
Phase space methods offer a compelling alternative to the traditional Hilbert-space approach in quantum theory, providing useful tools for visualizing and analyzing quantum states. Within this framework, observables are represented as functions instead of operators, mirroring their classical counterparts while adhering to distinct algebraic rules. By interpreting quantum mechanics as a statistical theory on phase space, this perspective facilitates a more seamless and intuitive transition to the classical world [1,2,3,4].
The rudiments of the method were laid in the groundbreaking works of Weyl [5] and Wigner [6]. Later, Groenewold [7] and Moyal [8] built upon this foundation, which has since evolved into a comprehensive discipline with applications in numerous fields.
The cornerstone of this approach lies in a bona fide mapping that assigns operators to functions (commonly known as the associated symbols) defined on a smooth manifold with a well-established mathematical structure [9]. However, this mapping is not uniquely determined; rather, a whole family of symbols can consistently correspond to a given operator. In particular, quasiprobability distributions are the symbols of the density operator [10,11,12,13,14,15]. For continuous variables, such as Cartesian position and momentum—the paradigmatic example that originally spurred interest in this field—the most widely used mappings include the time-honored P (Glauber–Sudarshan) [16,17], W (Wigner) [6], and Q (Husimi) [18] functions.
The formalism has been generalized to systems exhibiting diverse symmetries. Beyond the harmonic oscillator, an important example is the SU(2) symmetry, where the Bloch sphere serves as the phase space [19,20,21]. Likewise, the Euclidean group E(2), associated with the cylinder as its phase space, has produced valuable results [22,23,24,25,26,27,28], and plays a key role in analyzing the orbital angular momentum of twisted photons [29]. More recently, systems with SU(1,1) symmetry have been described using a two-sheeted hyperboloid as the basic manifold [30,31], which plays a central role in modeling two-photon effects [32,33,34,35]. This topic has gained renewed interest with the advent of nonlinear interferometers, which promise remarkable enhancements in phase measurement sensitivity [36,37,38,39]. Furthermore, generalizations to broader classes of dynamical groups have also been investigated [40,41,42,43,44,45].
In the late 1980s, researchers began exploring how to represent qubits—and more generally, qudits—in phase space. In 1987, both Feynman [46] and Wootters [47] independently proposed versions of the Wigner function for discrete systems. Feynman’s work, based on earlier informal ideas about negative probabilities, focused specifically on spin-1/2 particles. Wootters, on the other hand, developed a more general approach using a discrete toroidal lattice, which works for systems whose dimensions are prime powers. Since then, there has been ongoing effort to extend this framework and make it more widely applicable [48,49,50,51,52,53,54,55,56].
As quantum technologies advanced into the twenty-first century, the direct measurement of phase space shifted from a theoretical goal to a practical and powerful technique. The Wigner function, with its distinctive visual and mathematical properties, has become essential in a wide range of research areas.
There are two primary experimental approaches to access the Wigner function: indirect and direct. The indirect method involves first reconstructing the full quantum state—typically by determining the density matrix—and then computing the Wigner function through a mathematical transformation. This approach supports both continuous and discrete variables. The review presented in [57] includes a complete and updated list of references to recent experiments.
The direct method, on the other hand, enables a point-by-point measurement of the Wigner function without reconstructing the entire quantum state. This is possible because the Wigner function can be expressed as the expectation value of a specific observable: the displaced parity operator [58]. Measuring this value samples the Wigner function directly [59,60], transforming an abstract concept into a measurable reality.
In this work, we revisit the foundations of Wigner functions for quantum systems governed by SU(2) dynamical symmetry—a framework of particular relevance to spin-like systems [61,62,63], where the full Hilbert space is effectively constrained to symmetric subspaces. More generally, SU(2) symmetry, as realized through the Jordan–Schwinger construction [64,65,66] (which expresses the algebra in terms of two harmonic oscillator modes), provides a powerful and unifying approach to a wide range of two-mode quantum systems. This includes strongly correlated systems [67], polarization of quantum fields [68,69,70,71,72], and partially coherent classical Gaussian Schell-model beams [73,74,75], among others, and has applications in quantum computing [76], and provides insights into the spin–statistics connection [77,78]. Within this context, we offer conceptual and methodological tools that may guide a broad range of experiments in modern quantum science and technology.
This paper is organized as follows. In Section 2, we briefly review the essential ingredients needed to understand the phase space of the Wigner function for SU(2) dynamical symmetry. In Section 3, we apply this formalism to a menagerie of quantum states that have been proposed for quantum optimal sensing. The exceptional properties of these states are rendered with striking clarity through their Wigner functions. This formalism is fully applicable in scenarios where the number of excitations in the system is fixed; in other words, when working within a single Fock layer [79]. The case of an indefinite number of excitations is addressed in Section 4, where we introduce a generalized SU(2)-based phase-space framework capable of faithfully capturing the quantum correlations inherent in superpositions across multiple SU(2)-invariant subspaces. Section 5 is devoted to illustrate this approach with simple examples that offer insight into the rich and sometimes counter-intuitive structure of these correlations. Finally, our conclusions are summarized in Section 6.
2. Wigner Function for a Spin S
Any quantum system with a Hilbert space of finite dimension can be formally regarded as a spin S. The dynamical symmetry group of such a system is SU(2), generated by three self-adjoint operators (the superscript ⊤ denoting the transpose), that satisfy the commutation relations (with throughout)
and cyclic permutations.
We consider here a pure spin-S state living in the Hilbert space , spanned by the angular momentum basis of the simultaneous eigenstates of and . This space serves as the carrier of the irreducible representation (irrep) of spin S of SU(2), which is isomorphic to . Since physical states are identified up to an overall phase factor (i.e., by rays in ), the manifold of physically distinct states is given by the projective space [80].
As heralded in the Introduction, the Jordan–Schwinger representation [64,65] provides a useful way to realize the operators in terms of two independent bosonic modes, specified by operators () and () with standard commutation relations , with . In this representation, the spin operators read
which are nothing but the Stokes operators for the two-mode problem [81] and the corresponding phase space is naturally identified with the unit sphere .
If we define the operator , one can verify that
where is the identity in . Therefore, the spin S corresponds to (half) the total number of excitations, whereas the eigenvalue m corresponds to , where is the number of excitations in mode . Furthermore, since , different irreps can be treated independently.
According to the axiomatic approach, we associate each operator acting on with its symbol, , a c-number function defined in the unit sphere . Such a (invertible) map depends on the ordering rules of functions of noncommutative operators. Here, we will deal exclusively with the symmetric operator ordering, also known as the Weyl ordering. This ordering is particularly advantageous as it ensures a better semi-classical limit, preserving the connection between quantum and classical descriptions. Additionally, it results in balanced quantum corrections in perturbative expansions and is well-suited for spin systems [82]. For a more thorough and detailed exploration, the reader is encouraged to consult the monograph [83].
The map is established as
where is a Stratonovich–Weyl quantizer [19]:
Here, are the spherical harmonics and are the irreducible tensor operators [84,85,86]
with denoting the Clebsch–Gordan coefficients that couple a spin and a spin to a total spin S. They are nonzero only when the standard angular momentum coupling rules hold: and .
According to the properties of the Clebsch–Gordan coefficients, K takes the values , and , giving rise to operators that constitute a basis for the space of linear operators acting on . This is guaranteed by the property
These operators are, in general, non-Hermitian. However, due to their symmetry properties, they satisfy the relation for every fixed S. Most importantly, they have the correct transformation properties under SU(2) transformations: for SU(2), we have
where stands for the Wigner D-function [86] and we have used the compact notation for the three Euler angles characterizing the rotation.
The kernel is normalized as
with as the invariant measure on the sphere . All this ensures that the symbol of any (trace class) operator is covariant under rotations and provides the important overlap relation
As required, the map is invertible, so the operator can be reconstructed from its symbol via
Given the properties of the irreducible tensors, any operator can be expanded as
with . In this way, its symbol takes the form
and satisfies the normalization condition
The symbol of the density operator is precisely the Wigner function, whereas the corresponding expansion coefficients are the so-called state multipoles [85]. They contain all the information about the state, but arranged in a manifestly SU(2)-invariant form. Apart from their theoretical relevance, they can be experimentally determined using simple measurements [87]. They are the Kth directional moments of the state and, therefore, the multipoles resolve progressively finer angular features.
Let us consider the simplest case of a single qubit. This corresponds to and can be implemented in different physical systems, such as a spin , the polarization of a photon, or a two-level atom. The Hilbert space is now isomorphic to ; accordingly, the density matrix can be expanded as (for simplicity, we omit the superscript 1/2, as there is no risk of confusion):
and one can check that
where is the identity matrix in and are the spherical components of the Pauli basis. We recall that a vector operator with Cartesian components has spherical components
Due to normalization, and the physical relevant information comes from the dipole . In fact,
are nothing but the spherical components of the Bloch vector [88]. In terms of this vector, , the Wigner function for the qubit reads
3. A Menagerie of Wigner Functions
The primary application of SU(2) in metrology is likely phase estimation. To this end, we will attempt to illustrate quantum states commonly employed in quantum interferometry for such tasks and assess their usefulness based on these visualizations. In this endeavor, the Wigner function introduced in this work proves highly valuable, as it enables us to visualize the symmetry of a quantum state with respect to a given axis.
We start with SU(2) (or spin) coherent states [89,90], as they are the most classical states allowed by quantum mechanics. Their robustness against decoherence and their natural emergence in systems with SU(2) symmetry make them a fundamental tool in both theoretical and experimental quantum information.
They are defined in direct analogy with the standard coherent states, as a displaced version on the sphere of a fiducial state that we take as the north pole:
where the displacement over the sphere is given in terms of the SU(2) ladder operators by . They can be expressed as
The corresponding multipoles can be readily computed [62]; the result reads
and, according to the general recipe in (13), the Wigner function turns out to be
If, for simplicity, we assume that the coherent state is centered along the x axis (that is , so that it is an eigenstate of ), we have
From here, we obtain
with
This expression is involved and can only be evaluated numerically. However, in the limit , this Wigner function simplifies to an approximate form, enabling more intuitive analytical insights [83]:
This Wigner function for the coherent state (24) is represented for various values of S in Figure 1. As we can appreciate, this function is sharply peaked around the classical phase space point and spreads over an area proportional to . As S increases, the state becomes increasingly localized and so more classical.
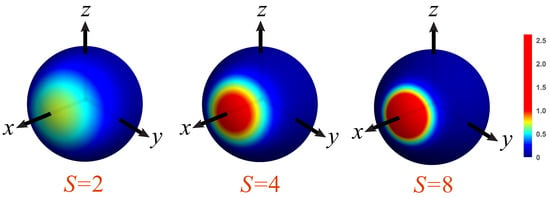
Figure 1.
Density plots on the unit Bloch sphere of the Wigner functions for spin coherent states located at the X axis, with the indicated values of S. The scale of the colormap is indicated at the right.
The ultimate constraint on measurement precision in interferometry is dictated by quantum effects. This limitation is most effectively analyzed using a Mach–Zehnder interferometer, where output measurements serve to estimate the relative phase between its two arms. It is well established that, when an N-photon number state is injected into one input port, the achievable phase sensitivity follows the standard quantum limit (SQL) [91], scaling as , where denotes the variance. Several theoretical proposals [92,93,94,95,96,97,98] have aimed to surpass this limit, reducing phase variance to the Heisenberg limit, . However, these methods rely on two key constraints: they require the phase difference to be either zero or very small to achieve optimal scaling, and they assume access to the asymptotic limit of a large number of measurement repetitions.
For limited resources, it is better to look for states that give optimal phase precision for single-shot estimation with no prior information. These states were identified by Berry and Wiseman in ref. [99]; they have the expression:
They are particularly effective when combined with adaptive measurement strategies, where phase shifts are dynamically adjusted based on prior outcomes, allowing for precise estimation over a broad range of phase values.
The Wigner function of Berry–Wiseman states must be computed numerically, with the results displayed in Figure 2. As observed, the central peak undergoes increased squeezing as the parameter S grows, accompanied by small side oscillations.
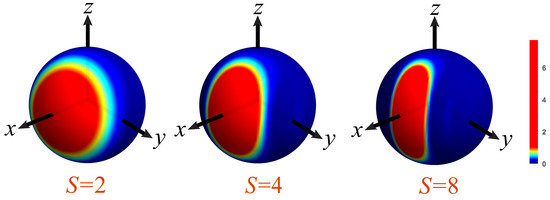
Figure 2.
Density plots on the unit Bloch sphere of the Wigner functions for the optimal Berry–Wiseman states (28) with the indicated values of S. The scale of the colormap is indicated at the right.
In the same vein, spin-squeezed states have been proposed to enhance the precision of phase estimation beyond the SQL [100]. However, their advantage is primarily realized in the asymptotic limit, where multiple measurement repetitions allow for statistical averaging. In contrast, for single-shot measurements or scenarios where the phase shift is not necessarily small or well-known, spin-squeezed states may not be the optimal choice.
Consider the case where S is integer. Then, a state which comes close to minimizing the squeezing parameter is the Yurke state [101]:
where denote eigenstates of . The minimum value of the squeezing parameter (which is of the order ) is achieved as [102]. In this limit, the state is invariant under a rotation of around the z axis. That is, in a single-shot measurement, it would be impossible to distinguish between a rotation of and one of .
Yurke states exhibit quantum correlations and interference properties that make them particularly well-suited for interferometric phase estimation. These states enable sensitivity beyond the standard quantum limit by leveraging entanglement and quantum superposition. Their Wigner functions, depicted in Figure 3, provide a visual representation of their phase space structure, revealing a high degree of symmetry. This symmetry is a key indicator of their potential for phase estimation, as it reflects the underlying coherence and phase resolution capabilities of the state.
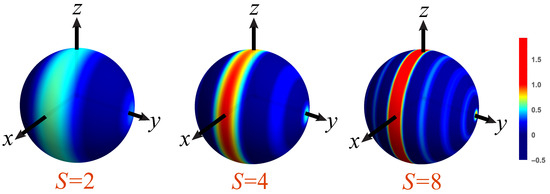
Figure 3.
Density plots on the unit Bloch sphere of the Wigner functions for Yurke states (29) with and the indicated values of S. The scale of the colormap is indicated at the right.
Finally, we consider the famous NOON states [103], which, when expressed in the basis, take the form
Like Yurke states, NOON states enable phase measurements with a sensitivity times better than that of a coherent state [100]. Their key advantage lies in their ability to achieve Heisenberg-limited phase estimation. However, they are invariant under a z-rotation of , which imposes a strict requirement on prior knowledge of the phase. Specifically, for NOON states to be useful in practical applications, the phase must already be known to an accuracy of at least . This constraint significantly limits their applicability in scenarios where the phase is initially unknown or needs to be estimated over a broad range, making them less versatile than other quantum-enhanced states such as spin-squeezed or Yurke states. In addition, NOON states are highly sensitive to photon loss or decoherence: even the loss of a single photon can drastically reduce their performance, making them impractical for many real-world applications.
The Wigner function for NOON states can be directly calculated; the final result is
where
Here, and represent the Wigner functions of two spin coherent states located at the north and south poles of the Bloch sphere, respectively. The third term introduces an interference pattern characterized by a band of fringes along the equator, with the number of negative regions equal to . As S increases, this interference pattern becomes more localized along the equator. Additionally, the term significantly suppresses the Wigner function between the equator and the poles. This effect is visually evident in Figure 4.
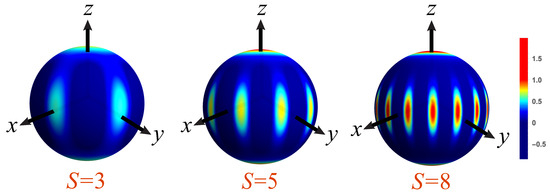
Figure 4.
Density plots on the unit Bloch sphere of the Wigner functions for NOON states, with the indicated values of S. The scale of the colormap is indicated at the right.
4. Generalized Wigner Function
In two-mode systems, fluctuations in the number of excitations are generally inevitable. As described in (3), the corresponding phase space becomes then foliated into a series of nested spheres, with radii proportional to the excitation number—commonly referred to as Fock layers in photonic systems [104]. To address this structure, we must extend earlier approaches to encompass systems whose state spaces form a direct sum of distinct SU(2) irreps. Our strategy follows the framework introduced in ref. [63], which employs a natural generalization of irreducible tensor operators [85]; namely,
The range of the indices is still and . The tensors (33) also form an orthonormal basis
and transform under rotations as in (8).
In consequence, we can expand any operator as
By redefining the summation indices as , and applying the resummation identity
where indicates that K takes values starting from 0 for integer J and from for half-integer J, we obtain the following result:
Now, we can define the corresponding Stratanovitch–Weyl quantizer as
This quantizer possesses all the desired properties [105] and can be used as an invertible mapping of arbitrary operator into c-number functions. The symbol of the operator can be consequently defined as
so that
One immediately finds the reconstruction to be
where . Note that if acts in a single irrep of SU(2), then in this equation and we recover the standard symbol as discussed in the previous section.
An important remark is in order. Since we do not fix the dimension of the group representation, the quantizer—and consequently the associated symbols—depends on three angles. In this setting, the mapping defined in (40) does not correspond to a representation of operators on a classical phase space, which must possess even dimensionality. The key distinction from the conventional Stratonovich–Weyl mapping lies in its capacity to fully reconstruct an operator, including the density matrix, rather than merely projecting onto irreducible subspaces. Nevertheless, the J-symbol of any operator confined to a single SU(2) irreducible representation is independent from the angle and adheres to the standard Stratonovich–Weyl form. It is also noteworthy that the index J assumes only integer values for symbols that do not depend on the angle .
5. Examples
Let us illustrate this new approach with a couple of simple examples. First of all, the J-symbols of the algebra have the crystal-clear form
Here, the -functions indicate the admissible values of the index J and are components of the unitary vector .
As a second example, we consider the two-mode Bell-like states
where indicates one photon in mode A and vacuum in mode B, and so on. These states have been used to explore the bizarre feature of vacuum–one photon entanglement [106,107,108,109,110], which has been demonstrated in the laboratory [111].
In the angular momentum basis, they are represented as
Interestingly, each state belongs to a single irrep with and the standard SU(2) Wigner map (5) can be used; the result reads
This Wigner function is plotted in Figure 5. Their complementary character under the swapping of the phase can be clearly observed.
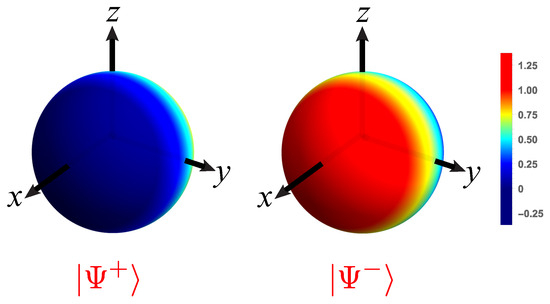
Figure 5.
Density plots on the unit Bloch sphere of the states . The scale of the colormap is indicated at the right.
In contradistinction, the states are the superpositions from two irreps with and , and the generalized Wigner function is required to capture their correlation properties. In particular, the density matrices of these states can be decomposed as
which includes nondiagonal tensors and , accounting for the interference between subspaces. A direct calculation gives now
The Wigner function resides in the subspaces corresponding to . The term , however, is associated with the action of the operator , which is nondiagonal in the SU(2) representation basis. This term captures a key characteristic of the Wigner function for Bell-like states; namely, the presence of coherence between different spin polarization states.
This nondiagonal structure implies that the Wigner function encodes quantum coherence across different irreps, which is reflected in the dependence on the angle . When this term is integrated over , it yields a mixed state , corresponding to and terms. It is interesting to observe that the term has a similar structure as the significant contribution in , after replacing in the latter; meanwhile, the phase typically reflects a relative phase between spin components in a fixed irrep, and the phase can thus be interpreted as encoding relative phase between different irreps. The pieces and are plotted in Figure 6, confirming the previous comments.
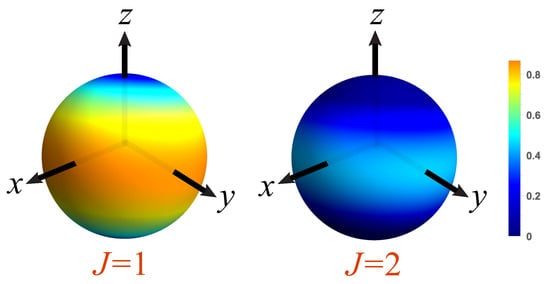
Figure 6.
Density plots on the unit Bloch sphere of the pieces and corresponding to the Wigner function (47). The scale of the colormap is indicated at the right.
6. Conclusions
Visualizing how discrete systems work helps us understand the complexity of quantum states, operations, and computations. We have introduced a comprehensive toolbox that enables the definition of Wigner functions for qubits and symmetric multi-qubit systems, offering an intuitive representation of quantum states on the Bloch sphere. Unlike density matrices, this approach provides a more accessible depiction of quantum coherence, superposition, and entanglement, while facilitating the analysis of quantum operations and gate effects. By seamlessly connecting theory with practice, the visualization of qubits enhances the accessibility and practicality of quantum information tasks.
Author Contributions
Conceptualization, L.L.S.-S. and A.B.K.; methodology, L.L.S.-S., A.B.K. and G.L.; formal analysis, A.B.K., A.M. and P.d.l.H.; writing—original draft preparation, L.L.S.-S. and A.B.K.; writing—review and editing, L.L.S.-S. and G.L.; visualization, A.M. and P.d.l.H.; supervision, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Agencia Estatal de Investigación (Grant PID2021-127781NB-I00), the Mexican CONAHCyT (Grant CBF2023-2024-50), and the Chilean Agencia Nacional de Investigación y Desarrollo (Postdoctoral Fellowship 74240083).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We are indebted to A. Goldberg and H. de Guise for discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Schroek, F.E. Quantum Mechanics on Phase Space; Kluwer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Schleich, W.P. Quantum Optics in Phase Space; Wiley-VCH: Berlin, Germany, 2001. [Google Scholar]
- Zachos, C.K.; Fairlie, D.B.; Curtright, T.L. (Eds.) Quantum Mechanics in Phase Space; World Scientific: Singapore, 2005. [Google Scholar]
- Albert, V.V.; Pascazio, S.; Devoret, M.H. General phase spaces: From discrete variables to rotor and continuum limits. J. Phys. A Math. Theor. 2017, 50, 504002. [Google Scholar] [CrossRef]
- Weyl, H. Quantenmechanik und Gruppentheorie. Z. Phys. 1927, 46, 1–46. [Google Scholar] [CrossRef]
- Wigner, E.P. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Groenewold, H.J. On the principles of elementary quantum mechanics. Physica 1946, 12, 405–460. [Google Scholar] [CrossRef]
- Moyal, J.E. Quantum mechanics as a statistical theory. Proc. Camb. Philos. Soc. 1949, 45, 99–124. [Google Scholar] [CrossRef]
- Kirillov, A.A. Lectures on the Orbit Method; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2004; Volume 64. [Google Scholar]
- Tatarskii, V.I. The Wigner representation in quantum mechanics. Sov. Phys. Usp. 1983, 26, 311–327. [Google Scholar] [CrossRef]
- Balazs, N.L.; Jennings, B.K. Wigner’s function and other distribution functions in mock phase spaces. Phys. Rep. 1984, 104, 347–391. [Google Scholar] [CrossRef]
- Hillery, M.; Connell, R.F.O.; Scully, M.O.; Wigner, E.P. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar] [CrossRef]
- Lee, H.W. Theory and application of the quantum phase-space distribution functions. Phys. Rep. 1995, 259, 147–211. [Google Scholar] [CrossRef]
- Weinbub, J.; Ferry, D.K. Recent advances in Wigner function approaches. Appl. Phys. Rev. 2018, 5, 041104. [Google Scholar] [CrossRef]
- Ferry, D.K.; Nedjalkov, M. The Wigner Function in Science and Technology; IOP Publishing: Bristol, UK, 2018. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264–314. [Google Scholar] [CrossRef]
- Stratonovich, R.L. On distributions in representation space. JETP 1956, 31, 1012–1020. [Google Scholar]
- Berezin, F.A. General concept of quantization. Commun. Math. Phys. 1975, 40, 153–174. [Google Scholar] [CrossRef]
- Varilly, J.C.; Gracia-Bondía, J.M. The Moyal representation for spin. Ann. Phys. 1989, 190, 107–148. [Google Scholar] [CrossRef]
- Mukunda, N. Wigner distribution for angle coordinates in quantum mechanics. Am. J. Phys. 1979, 47, 182–187. [Google Scholar] [CrossRef]
- Plebański, J.F.; Prazanowski, M.; Tosiek, J.; Turrubiates, F.K. Remarks on deformation quantization on the cylinder. Acta Phys. Pol. B 2000, 31, 561–587. [Google Scholar]
- Chumakov, S.M.; Klimov, A.B.; Wolf, K.B. Connection between two Wigner functions for spin systems. Phys. Rev. A 2000, 61, 034101. [Google Scholar] [CrossRef]
- Rigas, I.; Sánchez-Soto, L.L.; Klimov, A.B.; Řeháček, J.; Hradil, Z. Orbital angular momentum in phase space. Ann. Phys. 2011, 326, 426–439. [Google Scholar] [CrossRef]
- Kastrup, H.A. Wigner functions for the pair angle and orbital angular momentum. Phys. Rev. A 2016, 94, 062113. [Google Scholar] [CrossRef]
- Kastrup, H.A. Wigner functions for angle and orbital angular momentum: Operators and dynamics. Phys. Rev. A 2017, 95, 052111. [Google Scholar] [CrossRef]
- Fabre, N.; Klimov, A.B.; Murenzi, R.; Gazeau, J.P.; Sánchez-Soto, L.L. Majorana stellar representation of twisted photons. Phys. Rev. Res. 2023, 5, L032006. [Google Scholar] [CrossRef]
- Franke-Arnold, S.; Allen, L.; Padgett, M. Advances in optical angular momentum. Laser Photon. Rev. 2008, 2, 299–313. [Google Scholar] [CrossRef]
- Seyfarth, U.; Klimov, A.B.; Guise, H.d.; Leuchs, G.; Sanchez-Soto, L.L. Wigner function for SU(1,1). Quantum 2020, 4, 317. [Google Scholar] [CrossRef]
- Klimov, A.B.; Seyfarth, U.; de Guise, H.; Sánchez-Soto, L.L. SU(1, 1) covariant s-parametrized maps. J. Phys. A Math. Theor. 2021, 54, 065301. [Google Scholar] [CrossRef]
- Wodkiewicz, K.; Eberly, J.H. Coherent states, squeezed fluctuations, and the SU(2) and SU(1,1) groups in quantum-optics applications. J. Opt. Soc. Am. B 1985, 2, 458–466. [Google Scholar] [CrossRef]
- Gerry, C.C. Dynamics of SU(1,1) coherent states. Phys. Rev. A 1985, 31, 2721–2723. [Google Scholar] [CrossRef]
- Gerry, C.C. Correlated two-mode SU(1,1) coherent states: Nonclassical properties. J. Opt. Soc. Am. B 1991, 8, 685–690. [Google Scholar] [CrossRef]
- Gerry, C.C.; Grobe, R. Two-mode intelligent SU(1,1) states. Phys. Rev. A 1995, 51, 4123–4131. [Google Scholar] [CrossRef]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU(2) and SU(1,1) interferometers. Phys. Rev. A 1986, 33, 4033–4054. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Liu, C.; Zhou, Z.; Ou, Z.Y.; Zhang, W. Realization of a nonlinear interferometer with parametric amplifiers. Appl. Phys. Lett. 2011, 99, 011110. [Google Scholar] [CrossRef]
- Hudelist, F.; Kong, J.; Liu, C.; Jing, J.; Ou, Z.Y.; Zhang, W. Quantum metrology with parametric amplifier-based photon correlation interferometers. Nat. Commun. 2014, 5, 3049. [Google Scholar] [CrossRef] [PubMed]
- Chekhova, M.V.; Ou, Z.Y. Nonlinear interferometers in quantum optics. Adv. Opt. Photon. 2016, 8, 104–155. [Google Scholar] [CrossRef]
- Brif, C.; Mann, A. A general theory of phase-space quasiprobability distributions. J. Phys. A Math. Gen. 1998, 31, L9–L17. [Google Scholar] [CrossRef]
- Mukunda, N.; Marmo, G.; Zampini, A.; Chaturvedi, S.; Simon, R. Wigner–Weyl isomorphism for quantum mechanics on Lie groups. J. Math. Phys. 2005, 46, 012106. [Google Scholar] [CrossRef]
- Klimov, A.B.; de Guise, H. General approach to SU(n) quasi-distribution functions. J. Phys. A Math. Theor. 2010, 43, 402001. [Google Scholar] [CrossRef]
- Tilma, T.; Nemoto, K. SU(N)-symmetric quasi-probability distribution functions. J. Phys. A Math. Theor. 2012, 45, 015302. [Google Scholar] [CrossRef]
- Tilma, T.; Everitt, M.J.; Samson, J.H.; Munro, W.J.; Nemoto, K. Wigner Functions for Arbitrary Quantum Systems. Phys. Rev. Lett. 2016, 117, 180401. [Google Scholar] [CrossRef]
- Rundle, R.P.; Tilma, T.; Samson, J.H.; Dwyer, V.M.; Bishop, R.F.; Everitt, M.J. General approach to quantum mechanics as a statistical theory. Phys. Rev. A 2019, 99, 012115. [Google Scholar] [CrossRef]
- Feynman, R.P. Quantum Implications: Essays in Honour of David Bohm; Chapter Negative Probabilities; Routledge: New York, NY, USA, 1987; pp. 235–248. [Google Scholar]
- Wootters, W.K. A Wigner-function formulation of finite-state quantum mechanics. Ann. Phys. 1987, 176, 1–21. [Google Scholar] [CrossRef]
- Galetti, D.; de Toledo-Piza, A.F.R. An extended Weyl-Wigner transformation for special finite spaces. Phys. A 1988, 149, 267–282. [Google Scholar] [CrossRef]
- Galetti, D.; de Toledo-Piza, A.F.R. Discrete quantum phase spaces and the mod N invariance. Phys. A 1992, 186, 513–523. [Google Scholar] [CrossRef]
- Heiss, S.; Weigert, S. Discrete Moyal-type representations for a spin. Phys. Rev. A 2000, 63, 012105. [Google Scholar] [CrossRef]
- Gibbons, K.S.; Hoffman, M.J.; Wootters, W.K. Discrete phase space based on finite fields. Phys. Rev. A 2004, 70, 062101. [Google Scholar] [CrossRef]
- Vourdas, A. Quantum systems with finite Hilbert space. Rep. Prog. Phys. 2004, 67, 267–320. [Google Scholar] [CrossRef]
- Klimov, A.B.; Mu noz, C.; Romero, J.L. Geometrical approach to the discrete Wigner function in prime power dimensions. J. Phys. A 2006, 39, 14471–14497. [Google Scholar] [CrossRef]
- Vourdas, A. Quantum systems with finite Hilbert space: Galois fields in quantum mechanics. J. Phys. A Math. Theor. 2007, 40, R285–R331. [Google Scholar] [CrossRef]
- Björk, G.; Klimov, A.B.; Sánchez-Soto, L.L. The discrete Wigner function. Prog. Opt. 2008, 51, 469–516. [Google Scholar] [CrossRef]
- Klimov, A.B.; Romero, J.L.; Björk, G.; Sánchez-Soto, L.L. Discrete phase-space structure of n-qubit mutually unbiased bases. Ann. Phys. 2009, 324, 53–72. [Google Scholar] [CrossRef]
- Rundle, R.P.; Everitt, M.J. Overview of the Phase Space Formulation of Quantum Mechanics with Application to Quantum Technologies. Adv. Quantum Technol. 2021, 4, 2100016. [Google Scholar] [CrossRef]
- Royer, A. Wigner function as the expectation value of a parity operator. Phys. Rev. A 1977, 15, 449–450. [Google Scholar] [CrossRef]
- Deléglise, S.; Dotsenko, I.; Sayrin, C.; Bernu, J.; Brune, M.; Raimond, J.M.; Haroche, S. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 2008, 455, 510–514. [Google Scholar] [CrossRef] [PubMed]
- Harder, G.; Silberhorn, C.; Rehacek, J.; Hradil, Z.; Motka, L.; Stoklasa, B.; Sánchez-Soto, L.L. Local Sampling of the Wigner Function at Telecom Wavelength with Loss-Tolerant Detection of Photon Statistics. Phys. Rev. Lett. 2016, 116, 133601. [Google Scholar] [CrossRef]
- Agarwal, G.S. Relation between atomic coherent-state representation, state multipoles, and generalized phase-space distributions. Phys. Rev. A 1981, 24, 2889–2896. [Google Scholar] [CrossRef]
- Dowling, J.P.; Agarwal, G.S.; Schleich, W.P. Wigner distribution of a general angular momentum state: Application to a collection of two-level atoms. Phys. Rev. A 1994, 49, 4101–4109. [Google Scholar] [CrossRef]
- Klimov, A.B.; Romero, J.L.; de Guise, H. Generalized SU(2) covariant Wigner functions and some of their applications. J. Phys. A Math. Theor. 2017, 50, 323001. [Google Scholar] [CrossRef]
- Jordan, P. Der Zusammenhang der symmetrischen und linearen Gruppen und das Mehrkörperproblem. Z. Phys. 1935, 94, 531–535. [Google Scholar] [CrossRef]
- Schwinger, J. On angular momentum. In Quantum Theory of Angular Momentum; Biedenharn, L.C., Dam, H., Eds.; Academic: New York, NY, USA, 1965. [Google Scholar]
- Chaturvedi, S.; Marmo, G.; Mukunda, N.; Simon, R.; Zampini, A. The Schwinger representation of a group: Concept and Applications. Rev. Math. Phys. 2006, 18, 887–912. [Google Scholar] [CrossRef]
- Dalton, B.J.; Ghanbari, S. Two mode theory of Bose–Einstein condensates: Interferometry and the Josephson model. J. Mod. Opt. 2012, 59, 287–353. [Google Scholar] [CrossRef]
- Sehat, A.; Söderholm, J.; Björk, G.; Espinoza, P.; Klimov, A.B.; Sánchez-Soto, L.L. Quantum polarization properties of two-mode energy eigenstates. Phys. Rev. A 2005, 71, 033818. [Google Scholar] [CrossRef]
- Marquardt, C.; Heersink, J.; Dong, R.; Chekhova, M.V.; Klimov, A.B.; Sánchez-Soto, L.L.; Andersen, U.L.; Leuchs, G. Quantum Reconstruction of an Intense Polarization Squeezed Optical State. Phys. Rev. Lett. 2007, 99, 220401. [Google Scholar] [CrossRef] [PubMed]
- Klimov, A.B.; Björk, G.; Söderholm, J.; Madsen, L.S.; Lassen, M.; Andersen, U.L.; Heersink, J.; Dong, R.; Marquardt, C.; Leuchs, G.; et al. Assessing the Polarization of a Quantum Field from Stokes Fluctuations. Phys. Rev. Lett. 2010, 105, 153602. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.R.; Stoklasa, B.; Peuntinger, C.; Gabriel, C.; Řeháček, J.; Hradil, Z.; Klimov, A.B.; Leuchs, G.; Marquardt, C.; Sánchez-Soto, L.L. Quantum polarization tomography of bright squeezed light. New J. Phys. 2012, 14, 085002. [Google Scholar] [CrossRef]
- de la Hoz, P.; Klimov, A.B.; Björk, G.; Kim, Y.H.; Müller, C.; Marquardt, C.; Leuchs, G.; Sánchez-Soto, L.L. Multipolar hierarchy of efficient quantum polarization measures. Phys. Rev. A 2013, 88, 063803. [Google Scholar] [CrossRef]
- Sundar, K.; Mukunda, N.; Simon, R. Coherent-mode decomposition of general anisotropic Gaussian Schell-model beams. J. Opt. Soc. Am. A 1995, 12, 560–569. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N. Shape-invariant anisotropic Gaussian Schell-model beams: A complete characterization. J. Opt. Soc. Am. A 1998, 15, 1361–1370. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N. Optical phase space, Wigner representation, and invariant quality parameters. J. Opt. Soc. Am. A 2000, 17, 2440–2463. [Google Scholar] [CrossRef]
- Aniello, P.; Cagli, R.C. An algebraic approach to linear-optical schemes for deterministic quantum computing. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S711. [Google Scholar] [CrossRef][Green Version]
- Sunko, D.K.; Svrtan, D. Generating function for angular momentum multiplicities. Phys. Rev. C 1985, 31, 1929–1933. [Google Scholar] [CrossRef]
- Berry, M.V.; Robbins, J.M. Indistinguishability for Quantum Particles: Spin, Statistics and the Geometric Phase. Proc. R. Soc. Lond. 1997, A453, 1771–1790. [Google Scholar] [CrossRef]
- Müller, C.R.; Madsen, L.S.; Klimov, A.B.; Sánchez-Soto, L.L.; Leuchs, G.; Marquardt, C.; Andersen, U.L. Parsing polarization squeezing into Fock layers. Phys. Rev. A 2016, 93, 033816. [Google Scholar] [CrossRef]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Goldberg, A.Z.; de la Hoz, P.; Björk, G.; Klimov, A.B.; Grassl, M.; Leuchs, G.; Sánchez-Soto, L.L. Quantum concepts in optical polarization. Adv. Opt. Photon. 2021, 13, 1–73. [Google Scholar] [CrossRef]
- Klimov, A.B. Exact evolution equations for SU(2) quasidistribution functions. J. Math. Phys. 2002, 43, 2202–2213. [Google Scholar] [CrossRef]
- Klimov, A.B.; Chumakov, S.M. A Group-Theoretical Approach to Quantum Optics; Wiley: Meinheim, Germany, 2009. [Google Scholar]
- Fano, U.; Racah, G. Irreducible Tensorial Sets; Academic: New York, NY, USA, 1959. [Google Scholar]
- Blum, K. Density Matrix Theory and Applications; Plenum: New York, NY, USA, 1981. [Google Scholar]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore, 1988. [Google Scholar]
- Goldberg, A.Z.; Klimov, A.B.; de Guise, H.; Leuchs, G.; Agarwal, G.S.; Sánchez-Soto, L.L. From polarization multipoles to higher-order coherences. Opt. Lett. 2022, 47, 477–480. [Google Scholar] [CrossRef]
- Feynman, R.P.; Vernon, F.L., Jr.; Hellwarth, R.W. Geometrical Representation of the Schrödinger Equation for Solving Maser Problems. J. Appl. Phys. 1957, 28, 49–52. [Google Scholar] [CrossRef]
- Perelomov, A. Generalized Coherent States and Their Applications; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Gazeau, J.P. Coherent States in Quantum Physics; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Braginsky, V.B. Classical and Quantum Restrictions on the Detection of Weak Disturbances of a Macroscopic Oscillator. JETP 1967, 53, 1434–1441. Available online: http://jetp.ras.ru/cgi-bin/dn/e_026_04_0831.pdf (accessed on 2 May 2025).
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693–1708. [Google Scholar] [CrossRef]
- Yuen, H.P. Contractive states and the standard quantum limit for monitoring free-mass position. Phys. Rev. Lett. 1983, 51, 719–722. [Google Scholar] [CrossRef]
- Jaekel, M.T.; Reynaud, S. Quantum limits in interferometric measurements. Europhys. Lett. 1990, 13, 301–305. [Google Scholar] [CrossRef]
- Luis, A.; Sánchez-Soto, L.L. Multimode quantum analysis of an interferometer with moving mirrors. Phys. Rev. A 1992, 13, 8228–8234. [Google Scholar] [CrossRef] [PubMed]
- Holland, M.J.; Burnett, K. Interferometric detection of optical phase shifts at the Heisenberg limit. Phys. Rev. Lett. 1993, 71, 1355–1358. [Google Scholar] [CrossRef] [PubMed]
- Sanders, B.C.; Milburn, G.J. Optimal Quantum Measurements for Phase Estimation. Phys. Rev. Lett. 1995, 75, 2944–2947. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef]
- Berry, D.W.; Wiseman, H.M. Optimal States and Almost Optimal Adaptive Measurements for Quantum Interferometry. Phys. Rev. Lett. 2000, 85, 5098–5101. [Google Scholar] [CrossRef]
- Bollinger, J.J.; Itano, W.M.; Wineland, D.J.; Heinzen, D.J. Optimal frequency measurements with maximally correlated states. Phys. Rev. A 1996, 54, R4649–R4652. [Google Scholar] [CrossRef]
- Yurke, B. Input States for Enhancement of Fermion Interferometer Sensitivity. Phys. Rev. Lett. 1986, 56, 1515–1517. [Google Scholar] [CrossRef]
- Combes, J.; Wiseman, H.M. States for phase estimation in quantum interferometry. J. Opt. B Quantum Semiclass. Opt. 2005, 7, 14–21. [Google Scholar] [CrossRef][Green Version]
- Dowling, J.P. Quantum optical metrology—The lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Donati, G.; Bartley, T.J.; Jin, X.M.; Vidrighin, M.D.; Datta, A.; Barbieri, M.; Walmsley, I.A. Observing optical coherence across Fock layers with weak-field homodyne detectors. Nat. Commun. 2014, 5, 5584. [Google Scholar] [CrossRef]
- Klimov, A.B.; Romero, J.L. A generalized Wigner function for quantum systems with the SU(2) dynamical symmetry group. J. Phys. A Math. Theor. 2008, 41, 055303. [Google Scholar] [CrossRef]
- Tan, S.M.; Walls, D.F.; Collett, M.J. Nonlocality of a single photon. Phys. Rev. Lett. 1991, 66, 252–255. [Google Scholar] [CrossRef] [PubMed]
- Björk, G.; Jonsson, P.; Sánchez-Soto, L.L. Single-particle nonlocality and entanglement with the vacuum. Phys. Rev. A 2001, 64, 042106. [Google Scholar] [CrossRef]
- van Enk, S.J. Single-particle entanglement. Phys. Rev. A 2005, 72, 064306. [Google Scholar] [CrossRef]
- Guerreiro, T.; Monteiro, F.; Martin, A.; Brask, J.B.; Vértesi, T.; Korzh, B.; Caloz, M.; Bussières, F.; Verma, V.B.; Lita, A.E.; et al. Demonstration of Einstein–Podolsky-Rosen Steering Using Single-Photon Path Entanglement and Displacement-Based Detection. Phys. Rev. Lett. 2016, 117, 070404. [Google Scholar] [CrossRef]
- Qiao, L.F.; Jiao, Z.Q.; Xu, X.Y.; Gao, J.; Zhang, Z.Y.; Ren, R.J.; Zhou, W.H.; Wang, X.W.; Jin, X.M. Multistage quantum swapping of vacuum-one-photon entanglement. Phys. Rev. A 2021, 104, 022415. [Google Scholar] [CrossRef]
- Hessmo, B.; Usachev, P.; Heydari, H.; Björk, G. Experimental Demonstration of Single Photon Nonlocality. Phys. Rev. Lett. 2004, 92, 180401. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).