Research on the Resilience of a Railway Network Based on a Complex Structure Analysis of Physical and Service Networks

Abstract

This study examines railway network resilience through a complex network analysis of both the physical infrastructure and service operations. The objectives were to quantify the resilience characteristics of China’s railway network, assess its performance under different disturbance types, and evaluate recovery strategy effectiveness. Network resilience was measured through accessibility, invulnerability, and restorability dimensions. The simulation results demonstrate that targeted disruptions cause significantly more damage than random disturbances, particularly when high-betweenness nodes are affected. Statistical analysis confirmed that betweenness-based recovery strategies outperform degree-based and random approaches. These findings provide a quantitative foundation for infrastructural planning, emergency response protocols, and resource allocation in railway systems.

1. Introduction

As of the end of 2022, the total operating mileage of railways in China had reached 155,000 km, including 42,000 km of high-speed railways. In that year, 4100 km of new railway lines were commissioned, including 2082 km of high-speed rail. The proportion of double-track railways reached 59.6%, while 73.8% of the network was electrified. Nationwide, the railway network density stood at 161.1 km per 10,000 square kilometers.

With the vigorous development of the Chinese economy, the construction of China’s railway network has undergone a remarkable evolution, exhibiting a clear trend toward greater scale and sophistication. The continuous extension of railway lines has enhanced the efficiency and accessibility of passenger and freight transportation across the country. Nevertheless, this process has also introduced new challenges. The proliferation of newly constructed stations and the increasing structural complexity of the network have transformed China’s railway system from a relatively simple configuration into a highly intricate one. This transformation is not merely an increase in scale but is more reflected in the diversity and complexity of the network.

Railway accidents, though relatively infrequent, continue to occur due to system malfunctions or force majeure events. Disruptions at specific segments of the railway network or at individual stations can compromise the stable operation of the broader system. When issues arise at critical nodes or key lines, the entire network system will be subjected to significant fluctuations.

Railway network resilience refers to the system’s capacity to sustain essential operational functions and rapidly restore to the normal state when confronted with natural disasters, technical glitches, or other unforeseen disruptions. This concept aims to ensure that the railway system exhibits sufficient adaptability and robustness when subjected to external shocks.

Simultaneously, in order to deeply comprehend and enhance the resilience of railway networks, the theory of complex networks provides a powerful analytical framework. Railway networks can be modeled as typical complex systems, where nodes can be stations, hubs, or intervals, and the connections between nodes represent railway lines. By applying this theoretical approach, it is possible to analyze the topological structure, node importance, path diversity, and other key characteristics of the railway network, thereby assessing the resilience of the system and identifying its vulnerable points.

Currently, the research on railway network resilience still confronts multiple challenges: First, the inherent complexity and dynamic nature of railway systems pose considerable difficulties in accurately assessing their resilience. Second, maintaining the efficient operation of the railway network while rationally planning and adjusting the network structure to enhance its resilience and anti-interference ability remains an unresolved issue. Moreover, efforts to enhance resilience must account for economic constraints and practical feasibility in order to identify optimal and implementable solutions.

In view of the aforementioned challenges, this investigation endeavors to present an evaluation, analysis, and optimization of railway network resilience. Through the construction of a robust mathematical model and the identification of critical nodes and edges within China’s railway infrastructure, this study aims to enhance the understanding of resilience characteristics under various disturbance scenarios.

A systematic review of the extant literature indicates that previous investigations have frequently addressed either the physical infrastructure or operational performance in isolation, without sufficient integration of these for complementary perspectives. Furthermore, there remains a significant absence of empirical evidence regarding the differential effects of various disturbance typologies on railway networks and the comparative efficacy of recovery strategies across diverse scenarios.

Based on the identified research gaps, this study seeks to quantify resilience characteristics through rigorous analytical methods, assess network performance under heterogeneous disturbance conditions, and evaluate the relative effectiveness of alternative recovery strategies in restoring network functionality.

Predicated upon these research objectives and the synthesis of the extant literature, this investigation addresses critical knowledge gaps in railway network resilience studies by formulating three specific hypotheses:

(1)

Different types of disturbance events (external attacks, natural disasters, technical failures, and passenger/freight flow fluctuations) will impact railway network resilience in distinct patterns;

(2)

The resilience of railway networks can be comprehensively evaluated through the integration of three complementary measures: accessibility, invulnerability, and restorability;

(3)

Strategic recovery approaches based on topological importance (betweenness centrality and node degree) will significantly outperform random recovery strategies in restoring network functionality.

The primary aim of this study is to develop and validate a comprehensive resilience evaluation framework that bridges physical and service network perspectives, thereby providing railway administrators with practical tools to identify critical vulnerabilities and optimize recovery strategies when facing various disturbance events. Through simulation analysis of China’s railway network, this research offers empirical evidence to support infrastructural planning and emergency management decisions that enhance overall network resilience.

To establish a clear analytical framework for this study, we define three key resilience dimensions that will be used throughout this paper:

(1)

Accessibility: A measure of the railway network’s ability to maintain connections between stations when subjected to disturbances. Accessibility quantifies how effectively the network preserves paths between station pairs, maintains clustering coefficients, and sustains overall network efficiency during disruption events.

(2)

Invulnerability: A measure of the railway network’s resistance to cascade failures when critical components are compromised. Invulnerability examines how well the network withstands progressive degradation when initial failures trigger subsequent component failures through load redistribution mechanisms.

(3)

Restorability: A measure of the railway network’s capacity to regain functionality following disruptions. Restorability evaluates the efficiency of different recovery strategies in reinstating network performance, particularly the relative effectiveness of targeted versus random approaches to component restoration.

These three dimensions collectively provide a comprehensive characterization of railway network resilience, addressing both the network’s capacity to withstand disturbances and its ability to recover from them. By analyzing these dimensions across different types of disturbance events, this study aims to identify critical vulnerabilities and optimal recovery strategies for China’s railway transportation system.

The full text is divided into five sections, and the content of each section is arranged as follows: Section 1 introduces the research background and significance of railway network resilience in China, and outlines the key challenges currently faced in this field. Section 2 collates and makes a summary analysis of the domestic and international research status on the resilience research into transportation networks and the complex structure analysis of transportation networks. Section 3, based on the operational characteristics of China’s railway network and existing resilience studies, develops a comprehensive resilience evaluation model. This includes the construction of an index system encompassing accessibility, invulnerability, and restorability. Furthermore, it simulates the network’s performance under four categories of disruptions—external attacks, natural disasters, technical failures, and fluctuations in passenger and freight flows—to investigate dynamic changes in resilience. Section 5, as the conclusion and prospect section, primarily summarizes the entire text, encompassing the main contents, innovations, and conclusions of the research, and presents an outlook on the future research directions.

2. Related Work

2.1. Transportation Network Resilience

Resilience refers to a system’s capacity to sustain its core functions in the face of adverse events. This concept was initially proposed by Canadian systems ecologist C.S. Holling [1] and introduced into the field of system ecology. The theory holds that ecosystems are constantly in a state between dynamic equilibrium and disequilibrium, emphasizing how the system can maintain its functions, adapt to changes, and recover from disturbances in some cases when faced with interference. Since its inception in ecology, the concept of resilience has been extended and adapted across various disciplines, including engineering, psychology, and sociology. In these fields, resilience has evolved into a foundational framework for understanding how systems respond to stress, shocks, and environmental changes.

The concept of resilience in the transportation system was first clearly defined by Murray-Tuite et al. [2], who proposed that ten dimensions, such as redundancy, diversity, efficiency, autonomous components, strength, collaborative ability, adaptability, mobility, safety, and the ability of rapid recovery, collectively constitute the resilience of the transportation system. This multidimensional framework provides a foundation for the development of standardized resilience assessment metrics. Pan et al. [3] systematically reviewed research methods addressing transportation system resilience and vulnerability. They categorized resilience into two primary dimensions: static resilience and dynamic resilience. Static resilience mainly considers the ability of the system to maintain its core functions when subjected to pressure or interference. Dynamic resilience, on the other hand, focuses on the speed and efficiency of the system in returning to normal operation after experiencing significant disturbances. Mattsson et al. [4] defined and discussed the concepts of vulnerability and resilience in the transportation system and proposed two distinct research methods: one based on graph theory, which evaluates network vulnerability from a topological perspective, and another that incorporates supply–demand dynamics to assess the broader societal and user-level consequences of disruptions. Gonçalves et al. [5] defined urban transportation resilience as the system’s ability to resist, mitigate, and absorb various disturbances, which is called static resilience. Additionally, they emphasized the system’s ability to return to normal operation within a reasonable time and cost, which is referred to as dynamic resilience. In addition, Y Gu et al. [6] explored the interrelated concepts of reliability, vulnerability, and resilience within transportation networks. They established quantitative indicators for each concept, examined their similarities and distinctions, and used numerical simulations to analyze their behavior under different disturbance scenarios.

In the resilience assessment of transportation networks, many scholars choose to proceed from the perspective of complex networks: Testa et al. [7] used the New York City metropolitan area as a case study and simulated the impacts of extreme climate events by removing nodes and edges in coastal areas, thereby analyzing changes in topological attributes of the transportation network. Xing Y. et al. [8] adopted the passenger flow volume and the distance between stations as resilience indicators and developed a resilience measurement model to evaluate the resilience response changes in the network under attacks. Using the Shanghai metro system as an example, they analyzed the network’s vulnerability to both random failures and deliberate disruptions. Hou Y. et al. [9] investigated the impact of heterogeneous load redistribution mechanisms within network allocation models on system stability. Their findings suggest that weak heterogeneity in load redistribution can mitigate cascading failures, whereas strong heterogeneity may exacerbate the extent of final system collapse. David K. et al. [10] quantified the resilience of the public transportation network in Toronto, Canada, using the efficiency of the entire network to measure the impact of node failure on network performance. Their research method has strong universality.

In addition, a large number of scholars have examined the impact of disturbances on passenger travel indicators. Nanxi Wang et al. [11] developed a passenger behavior model based on passenger transfer rules, integrating three transportation modes—bus, subway, and taxi—into a unified framework. By incorporating both passenger demand and system supply into the evaluation criteria, they proposed a resilience assessment method for urban multimodal transportation systems. Adjetey-Bahun et al. [12] considered the interdependence among various subsystems—transportation, power, telecommunications, and organizational components—that collectively constitute the railway transportation system. They proposed a simulation model that quantifies system resilience using passenger delays and flow volumes as performance indicators.

2.2. Complex Structure Analysis of Transportation Networks

The research on complex network theory can be traced back to the 18th century, when the mathematician Euler introduced the foundational concepts of graph theory through the well-known “Seven Bridges of Königsberg” problem. This work marked the inception of network-related research. Nevertheless, early mathematical investigations primarily focused on simple graph theory, which addressed basic node–edge connections without capturing the structural complexity of real-world systems. In the mid-20th century, random graph theory emerged as the starting point of complex network research. Erdős and Rényi introduced the seminal ER random graph model to describe systems in which nodes are connected at random. However, this model failed to capture some distinctive features of real-world networks. In 1998, Watts and Strogatz [13] proposed the small-world network model, revealing some extraordinary characteristics existing in real-world networks. Subsequently, in 1999, Barabási and Albert [14] introduced the scale-free network model, highlighting that certain nodes possess significantly higher degrees than others, forming a power-law degree distribution. This discovery catalyzed a surge in research on network topology and structure. These two landmark studies served as significant turning points in complex network research and are generally regarded by the academic community as the beginning of complex network research. Complex networks are ubiquitous, encompassing both physical networks in Euclidean space, such as power networks, the Internet, and transportation networks; and abstract networks, including social and organizational structures.

Therefore, in integrating the complex network theory with transportation science, the concept of a railway complex network abstracts the railway transportation system into a network model. By analyzing the structural and dynamic properties of this network, researchers can investigate key characteristics and develop optimization strategies for railway systems. In this model, railway stations—including stations and transfer stations—are represented as nodes (or vertices) of the network, while the railway connection lines between stations are modeled as edges (or links) connecting these nodes. This abstraction transforms the originally intricate railway system into a graph structure, allowing for systematic analysis within a mathematical and computational framework. The complex network science combines the methods of graph theory and statistics, providing powerful tools for studying the development laws, statistical characteristics, and overall behaviors of the railway network. This approach not only facilitates the identification of critical structural features but also offers a theoretical foundation for advancing research on the resilience of railway transportation systems.

Cao W et al. [15] investigated the structural and spatial characteristics of the Chinese High-Speed Railway Network (CHSRN) at both the node and network levels. They calculated and analyzed indicators such as the degree and betweenness centrality of cities in the CHSRN, and examined the scale-free properties, spatial heterogeneity, and hierarchical nature of the CHSRN based on train flow intensity. Ghosh S et al. [16] modeled the Indian Railway Network (IRN) as a weighted complex network for research. Their study encompassed small-world properties, node degree distributions, and the exponential distribution of edge weights, and further analyzed the relationship between traffic volume and network topology. Ouyang M et al. [17] used the Chinese railway system as a case study to evaluate accessibility and flow-based vulnerability. They applied three representative complex network models and compared the results with those obtained from the Real Train Flow Model (RTFM). Zhou J et al. [18] proposed an enhanced railway fault propagation model, which modified the SIR model to be applicable for analyzing the dynamic process of fault propagation. This model provides valuable insights into simulating and quantifying the impact of faults in railway systems. Zhang J et al. [19] assessed the structural vulnerability of the high-speed railway networks in China and Japan, respectively, using the complex network theory, focusing on the performance of the two networks when facing different types of malicious attacks. Their findings revealed that the Japanese network outperforms the Chinese network in terms of global connectivity, whereas the Chinese network demonstrates superior local connectivity and transport capacity. Yin L et al. [20] constructed the physical network of the Chinese railway through methods based on complex networks, linear references, and dynamic segmentation methods. They evaluated the vulnerability of the geographical railway network in high-seismic-risk areas, with the objective of improving disaster prevention and resilience capabilities against earthquake hazards.

2.3. Research Gaps and Potential Contributions

A critical analysis of the existing literature reveals several significant research gaps in railway network resilience studies. Despite advances in resilience theory and complex network analysis, their integration for railway systems remains inadequate in several aspects.

Most studies examine railway networks through either physical infrastructure or service performance perspectives, rarely integrating both dimensions. The methodological approaches often lack comprehensiveness, focusing on singular aspects like connectivity, vulnerability, or fault propagation rather than the full spectrum of resilience characteristics. Additionally, simulation approaches typically address limited disruption scenarios, with insufficient research on recovery strategies and their comparative effectiveness. A comparison with existing studies is shown in

Table 1. Comparison between this research and existing studies.

Research Aspect	Existing Studies	Our Research
Network Scale	Primarily urban transit or regional networks [8,11]	National railway network at station level
Network Layers	Single-layer analysis focusing on either physical or service aspects [16,19]	Dual-layer analysis integrating physical infrastructure and service performance
Resilience Metrics	Limited metrics focusing on single aspects like connectivity or efficiency [7,18]	Comprehensive metrics covering accessibility, invulnerability, and restorability
Disruption Types	Usually limited to one or two disruption scenarios [9,20]	Four distinct disruption types: external attacks, natural disasters, technical failures, and flow fluctuations
Recovery Strategy	Rarely addressed or simplified recovery models [17]	Multiple recovery strategies evaluated: random, degree-based, and betweenness-based
Simulation Approach	Static or simplified dynamic models [4,15]	Advanced cascade failure model with load redistribution mechanisms
Application Focus	Theoretical analysis with limited practical guidance [5,6]	Clear implications for railway planning and emergency management

.

This research seeks to address these gaps by developing an integrated framework for railway network resilience that combines physical and service network perspectives, employs multiple complementary resilience metrics, evaluates performance under diverse disruption scenarios, and assesses the effectiveness of different recovery strategies. By adopting this comprehensive approach, the study aims to advance both theoretical understanding and practical applications in railway network resilience, ultimately contributing to more robust and adaptable railway systems.

3. Resilience Measurement of Railway Physical Network and Service Network Based on Complex Structure Analysis

3.1. The Construction of Railway Complex Network Model and the Fundamental Theory of Resilience

(1) Complex Network Models of Railways

A topological graph of a railway transportation network can consist of a collection of stations $G$and a collection of line segments between stations, which can be expressed as $G=\left(V,E\right)$, where $V=\left(v_1,v_2,v_3,\dots ,v_n\right)$ represents the set of all nodes (stations) in the railway transportation network and $E=\left(e_1,e_2,e_3,\dots ,e_n\right)$ represents the set of all edges (lines) in the railway transportation network. Therefore, it can be represented by an N-order square matrix as follows:

$$\mathrm{A}=\left[\begin{array}{ccccc}0& {\mathrm{a}}_{1,2}& \dots & {\mathrm{a}}_{1,\mathrm{n}-1}& {\mathrm{a}}_{1,\mathrm{n}}\\ {\mathrm{a}}_{2,1}& 0& \dots & {\mathrm{a}}_{2,\mathrm{n}-1}& {\mathrm{a}}_{2,\mathrm{n}}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ {\mathrm{a}}_{\mathrm{n}-1,1}& {\mathrm{a}}_{\mathrm{n}-1,2}& \dots & 0& {\mathrm{a}}_{\mathrm{n}-1,\mathrm{n}}\\ {\mathrm{a}}_{\mathrm{n},1}& {\mathrm{a}}_{\mathrm{n},2}& \dots & {\mathrm{a}}_{\mathrm{n},\mathrm{n}-1}& 0\end{array}\right]$$

(1)

where A represents the adjacency matrix of the railway network, with elements $a_{ij}$ (i,j = 1, 2, 3, …, n − 1, n) indicating the presence (non-zero value) or absence (zero value) of a direct connection between stations i and j. The diagonal elements are zero as self-loops do not exist in railway networks.

If the elements in the square matrix$a_{ij} \left(i,j=1,2,3,\dots ,n-1,n\right)$ are non-zero constants, it indicates that there is a direct line connection between stations; otherwise, there is no connection. Moreover, since there is no case in the real world where a certain station is self-connected to form a loop, all the diagonal elements are zero. Simultaneously, when there are different research purposes, different modeling methods are often required to construct the railway topological network.

The commonly used model construction methods for building railway topological networks include Space B, Space C, Space L, and Space P.

The characteristics of each modeling approach are presented in

Table 2. Common methods of model building for transportation topology networks.

Construction Methods	Model Characteristics
Space B	Both the stations and routes in the transportation network are regarded as nodes of the topological model. The adjacent station nodes to a route node represent all the stations covered by that route; the adjacent route nodes to a station node represent all the routes served by that station.
Space C	The routes in the transportation network are regarded as the nodes of the topological model. Moreover, if a direct transfer is possible between two routes, then in the network graph, there will be a connection between the nodes corresponding to these two routes.
Space L	The stations in the transportation network are taken as nodes in the topological model, and the sections between adjacent stations on the same route are abstracted as edges (or arcs).
Space P	The stations in the transportation network are regarded as the nodes of the topological model, and the sections between adjacent stations on the same route, that is, all the pairwise connections among stations on the same route.

.

Among these, the Space L method and the Space P method are the most commonly used in the modeling of the topological model of rail transit networks.

(2) Railway Network Resilience Measurement

The resilience of railway networks refers to the adaptability and recovery capability of the railway system when encountering unexpected events. Research on railway network resilience aims to provide a theoretical basis for the management and mitigation of disturbance events. Railway operations generally adhere to a predefined train schedule, requiring seamless coordination across various subsystems. However, when disruptions occur—impacting certain functional components—the railway management authorities must implement repair and rescheduling strategies to restore normal operations. This includes the rehabilitation of stations and lines to reinstate their service capabilities and return the system to its pre-disturbance state. This process demonstrates the adaptability and recovery capability of the railway network in the face of disturbance events, which is the core content of the research on the resilience of railway networks.

In the field of railway transportation, the resilience theory has not yet been widely accepted by many scholars with a unified definition. It is generally agreed that the core components of transportation system resilience are resistance, absorption, and recovery. Figure 1 presents the “resilience triangle”, which has been recognized by the majority of scholars in current resilience research. The curve in the figure shows the variation in system performance over time. When the system encounters a major disturbance, its performance experiences a sharp decline. Following the implementation of emergency response measures, performance gradually recovers, reflecting the system’s capacity to resist and rebound from disruptions. The dark blue shaded area under the performance curve serves as a quantitative representation of the system’s resilience level—that is, its ability to recover from external shocks.

As illustrated in the figure, the type of disturbance to which the system is subjected is directly related to the resilience level. The system demonstrates varying degrees of resilience in response to different types of disturbances. Therefore, it is essential to conduct research on network resilience based on different scenarios of disturbance types. Due to variations in the research object and the definition of resilience between studies, the shaded area representing the “resilience triangle” may differ in shape. Figure 1 presents a simplified, basic form of the resilience triangle, though the underlying concept it conveys remains consistent across different graphical representations.

The resilience of a railway network refers to its ability to maintain structural integrity and transportation functionality under external disturbances, ensuring the continuous movement of passengers or goods toward their destinations, as well as a prompt restoration to normal operations following disruptions. Concurrently, this study defines the resilience of the railway network in response to different disturbances as the resilience value of the network against that disturbance, which is employed to evaluate the network performance of the railway infrastructural network (physical network) and the railway service network (service network) subsequent to the occurrence of the disturbance.

To precisely assess the resilience of the railway network, it is essential to introduce a set of quantifiable indicators, referred to in this study as resilience measurement indicators. Simultaneously, railway network resilience is reflected in multiple dimensions, including the ability to maintain structural integrity under external disturbances, preserve network connectivity, and recover functionality after disruptions. Therefore, in order to comprehensively evaluate the network’s resistance to interference, it is necessary to propose diverse measurement approaches from different perspectives. Each metric captures a distinct aspect of resilience, where the selection of appropriate indicators is critically important for the validity of the assessment. The resilience measurement of the railway network should encompass the entire process from the normal operational state, through the experience of failure states, to the ultimate restoration to the normal state, thereby fully reflecting its adaptability and restorability. Adaptability describes the ability of the system to adopt measures to isolate the affected parts and reallocate resources in order to maintain the unaffected critical transportation services after experiencing a disturbance event. Restorability, on the contrary, focuses on the ability to repair the damaged infrastructure and restore it to its original service level after the fault is resolved or the disturbance event concludes. The higher the resilience of the system, the shorter the time required for both adaptation and recovery; conversely, prolonged response and restoration times indicate lower resilience. To provide a theoretical foundation for our resilience measurement system, we integrate insights from established transportation resilience research. Our three-dimensional framework (accessibility, invulnerability, and restorability) is grounded in complementary theoretical perspectives from the literature. The accessibility dimension builds upon Murray-Tuite et al.’s identification of accessibility as a fundamental component of transportation resilience, while Reggiani [21] emphasized the critical role of topological connectivity in network resilience analysis. The invulnerability dimension draws from Mattsson and Jenelius’s [4] conceptualization of vulnerability as a network’s sensitivity to disruptions that significantly reduce service capacity, with Zhou et al. [22] providing the theoretical basis for our cascade failure model by defining vulnerability as the performance level maintained during disturbances. The restorability dimension incorporates Li et al.’s [23] distinction between static and dynamic resilience, with the latter focusing on a system’s ability to efficiently return to normal operations after major disturbances. Li et al.’s resilience metrics, which simultaneously measure recovery speed and cumulative network performance loss, align with our methodological approach. Together, these three dimensions provide a comprehensive assessment of railway network resilience throughout the entire disruption-to-recovery cycle, consistent with Gonçalves et al.’s definition of urban transportation resilience as both a system’s ability to resist, mitigate, and absorb various disturbances and its capacity to restore normal operations within reasonable time and cost constraints. As illustrated in Figure 2, a resilience measurement system covering the various stages of operation, defense, buffering, damage, and recovery is constructed by taking the three evaluation dimensions as the vertices:

Next, detailed explanations will be provided for the definitions of these three measurement indices and the network performance they describe:

(1)

The accessibility measure of railway network resilience reflects the capacity of the railway network to maintain the interconnection among all parts of the network and ensure the normal operation of transportation functions when confronted with various disturbances. It primarily concerns the extent to which effective connections between stations can still be established through available paths when the network is subjected to specific disruptions. The accessibility measure is directly related to the ability of the railway network to continuously provide basic transportation services when encountering disturbances and is a crucial indicator for assessing the resilience of the railway physical network.

(2)

The invulnerability measure of railway network resilience gauges the extent to which the network structure of the railway network can be sustained and the degree of impairment of network functions after withstanding disturbances of a specific intensity. It reflects the network’s capacity to sustain connectivity under external shocks, as well as its ability to redistribute and reconfigure traffic flows. The invulnerability measure embodies the stability of the railway physical network when confronted with severe disturbances and is a crucial parameter for determining the network’s capacity to resist external attacks.

(3)

The restorability measure of railway network resilience focuses on the speed and efficiency with which a railway network resumes its normal operational status after encountering a disturbance. Specifically, it indicates the ability of the railway network to reorganize the service patterns within a certain period after the occurrence of a disturbance and restore to a level close to or reaching the original service level. This metric highlights the adaptability and dynamic recovery capabilities of the railway system in response to disruptions and serves as a key indicator for evaluating its ability to manage emergencies and promptly resume regular service.

Meanwhile, for the purpose of intuitively grasping how the resilience of the railway network in China varies under different disturbance events, the resilience measure must be quantifiable. Accordingly, a quantifiable algorithm design for the resilience measure of the railway network will be presented in the subsequent text.

To sum up, these three measures jointly constitute a framework for the comprehensive assessment of the resilience of the railway network. This framework encompasses not only the physical structure and service capacity of the network but also its response and recovery capabilities in the face of disturbances. As such, it provides a robust theoretical foundation and practical guidance for enhancing the resilience of railway systems.

3.2. Design of the Algorithm for Measuring Railway Network Resilience

In this study, we distinguish between two complementary network representations of the railway system.

Physical Network: This represents the actual infrastructure of the railway system, where nodes are physical stations and edges are the physical rail connections between adjacent stations. This network captures the spatial topology and geographical constraints of the railway infrastructure, focusing on the physical connectivity between locations. The physical network is modeled using the Space L method, where stations are represented as nodes and direct rail connections between adjacent stations are represented as edges.

Service Network: This represents the operational and functional aspects of the railway system, where nodes are still stations but edges represent direct service connections (trains running between stations without intermediate stops). Unlike the physical network, the service network captures how trains actually operate and serve passengers, reflecting scheduled services rather than mere physical connections. This network is modeled using the Space P method, accounting for service frequency, capacity, and operational patterns. The difference between the two networks in resilience analysis is shown in Figure 3.

(1)

The Algorithm for Measuring the Accessibility of Physical Network Resilience

The accessibility measure of the resilience of the physical network reflects the ability of the railway network to maintain interconnectivity among its components and ensure the continued operation of transportation functions under various disturbance scenarios. This measure encompasses factors such as the number of alternative paths that allow effective connections between stations despite disruptions. The accessibility measure is directly related to the ability of the railway network to consistently deliver essential transportation services during disturbances and serves as a critical indicator for assessing the resilience of the physical railway infrastructure. The corresponding characteristic operator is defined as follows:

(1) Reachable Node Pairs

Taking the reachable node pairs in the initial railway network model as a reference baseline, the status of the remaining node pairs after simulating disturbance events is observed and analyzed to evaluate changes in network accessibility.

$$\mathrm{K}={\displaystyle \frac{{\mathrm{k}}^{\prime }}{\mathrm{k}}}$$

(2)

where $K$ denotes the accessibility metric based on reachable node pairs, k’ represents the number of reachable node pairs after disturbance, and k represents the total number of reachable node pairs in the initial undisturbed network.

(2) Clustering Coefficient

When the nodes (stations) and edges (routes) in the railway network model are subjected to disturbances, previously connected nodes may become isolated, leading to a reduction in local node aggregation and consequently affecting the overall clustering coefficient of the network.

$$G={\displaystyle \frac{1}{N}}{\displaystyle \sum }_{i=1}^N{G}_i={\displaystyle \frac{1}{N}}{\displaystyle \sum }_{i=1}^N{\displaystyle \frac{2E_i}{k_i\left(k_i-1\right)}}$$

(3)

where G represents the average clustering coefficient of the network, N is the total number of nodes, G_i is the clustering coefficient of node i, k_i denotes the degree of node i, and E_i indicates the actual number of edges among the nodes adjacent to node i.

(3) Network Efficacy

Network efficiency is a crucial metric for evaluating network connectivity and overall operational efficacy. It is defined by comparing the alterations in the sum of the reciprocals of the actual shortest path lengths between all node pairs before and after a disturbance. By analyzing the variation in network efficiency after the removal of a specific node, one can evaluate the impact of that node on network connectivity and operational performance. This metric enables the identification of critical nodes whose removal would significantly impair network functionality and efficiency. The calculation formula for network efficiency is given as follows:

$$E={\displaystyle \frac{1}{N\left(N+1\right)}}\sum i,j\in N{\eta }_{ij}$$

(4)

where E represents the network efficiency, N is the total number of nodes in the network, and ${\eta }_{ij}=1/d_{ij}$ is the reciprocal of the shortest path length $d_{ij}$ between nodes $i$ and $j$. The shorter the path between two nodes, the higher their contribution to overall network efficiency.

Upon completion of the aforementioned indicator calculations, the resulting data are normalized to the range [0, 1] using the maximum value normalization method. Let $x$ represent a value in the original dataset, and $x_{max}$ denote the maximum value within that dataset. The normalized value $x_{norm}$ is then computed using the following formula:

$$x_{norm}={\displaystyle \frac{x}{x_{max}}}$$

(5)

Table 3. Reachability measurement feature operators.

Measuring of Accessibility Characteristic Operator	Quantitative Implication	Characterizing Network Performance
Reachable node pairs	Referring to the proportion of reachable node pairs of the initial network	Node accessibility
Clustering coefficient	The coefficient characterizing the extent of clustering among the vertices in the graph	Degree of network clustering
Network efficiency	The velocity and stability of data transmission and communication within network systems	The overall efficiency of the network

elaborates the quantitative implications of these three feature operators and the corresponding real-world network performance.

After normalizing the aforementioned indicators, the measure of resilience and accessibility can be represented as

$$T=aK+bG+cL$$

(6)

where a, b, and c are conversion coefficients, all being taken as 1/3.

The specific design procedures of the metric algorithm for the resilience and accessibility of the physical network are as follows:

Step 1. Export the adjacency matrix A of the geographical model of the railway transportation network in China using Gephi (v0.9.2) software and import it into MATLAB (R2022b).

Step 2. Calculate and sort the betweenness centrality and degree of each node in the network.

Step 3. Calculate the indicators, such as the number of reachable node pairs, network efficiency, and clustering coefficient, for the initial network using the specified formulas.

Step 4. Simulate the railway network perturbation events on the network.

Step 5. Calculate indicators such as the number of reachable node pairs, network efficiency, and clustering coefficient in the newly generated network according to the formulas. Traverse whether all nodes and edges in the network have undergone the simulation of railway network perturbation events. If not, return to Step 4. If yes, proceed to Step 6.

Step 6. Normalize the simulation results and calculate the accessibility metric of the network according to the formulas and output the results.

(2)

The algorithm for measuring the invulnerability (or resilience) of the physical network

The invulnerability of a network describes the ability of a system to remain functional with little or no impact when confronted with perturbation events. Drawing upon relevant studies, this paper adopts a cascading failure model to analyze the changes in invulnerability of railway transportation networks under disturbance scenarios. As a measurement index, the ratio of the number of nodes in the maximum connected subgraph to the number of nodes in the initial state of the network is selected in this paper. This indicator effectively reflects the extent to which the connectivity and functionality of the network are preserved after experiencing perturbations, providing a practical tool for evaluating and enhancing the resilience of railway networks.

$$L={\displaystyle \frac{B^{\prime }}{B}}$$

(7)

The cascading failure of a network is a common phenomenon in complex network systems, characterized by the propagation of faults following an initial disturbance. When one or more nodes (such as power stations in an electrical grid or stations in a railway network) or connections (i.e., links between nodes, such as power lines or railway tracks) experience perturbation events, the resulting failure can trigger a sequence of subsequent faults. This adverse impact can trigger a series of further faults, thereby influencing other parts of the network and ultimately possibly leading to the large-scale paralysis of the entire network. The occurrence of cascading failure begins with the failure of a node or connection in the network, which can be induced by external attacks, natural disasters, technical issues, or inadequate maintenance. Once a node or connection fails, the load it was bearing (for example, electricity, traffic, or information) is redistributed to other parts of the network. This redistribution might cause certain nodes or connections to bear a load exceeding their designed capacity. Due to the redistribution of the load, some nodes or connections that were originally operating normally might fail because of overload. These new failures further exacerbate the burden on the remaining components of the network, triggering a cycle of failure, load redistribution, and subsequent failure. This process can continue iteratively, resulting in a chain reaction that escalates network failures. In the worst-case scenario, this chain reaction may lead to the failure of the majority or all of the network, seriously affecting the normal functions and services of the network.

The cascading failure process of the railway transportation network can be subdivided into two scenarios: node failure and edge failure. At a superficial level, this process represents a series of chain reactions initiated by the failure of a single or a few components. However, it reflects a deeper aspect of the complexity and interdependence inherent in the entire railway network system. This phenomenon is not confined to physical-level faults, such as damage to tracks and bridges, but also extends to technical-level issues, such as signal system malfunctions and power supply disruptions, and even includes operational management decisions and response strategies. Any component in the railway network does not exist in isolation. When an operational failure occurs at a station, or a certain section of the railway is temporarily closed due to maintenance, natural disasters, and other reasons, the direct impact might be the cancellation or delay of train services at that station or section. Although this primary impact is localized, due to the close connection of the railway network, its indirect impact quickly spreads. As the primary fault spreads, the railway management department is required to adjust the operational plan. These adjustments not only have an impact on the directly affected sections but might also affect the operational efficiency and carrying capacity of other parts of the network. For instance, the closure of a major line might force trains to take longer detours, which not only increases operational costs but might also cause overcrowding on the detour routes, thereby triggering new operational problems. The risk of cascading failure is particularly pronounced during peak operational periods when the railway network operates under high resource utilization and capacity constraints. During such times, the network’s ability to buffer disruptions is limited, amplifying the likelihood and severity of cascading failures. Failures occurring during peak hours are not only more difficult to resolve promptly but also have more significant socio-economic consequences, given the high volume of passengers and goods in transit.

Drawing on the research methodologies and conceptual frameworks from the relevant literature, this paper employs the load–capacity model as the basis for developing the cascading failure model of the railway transportation network in China. In this model, the initial time period is denoted as t, and the initial load Vi(t) of each node i in the network at time t is defined based on the node betweenness B(i):

$$Vi\left(t\right)=B\left(i\right)$$

(8)

This approach uses the betweenness centrality of a node—defined as the frequency with which the node appears in all shortest paths—as a measure of its load, thereby assessing the importance and carrying capacity of each node in the network. The initial load represents the initial flow of the nodes in the network, and its capacity $Ci$ has a direct proportional relationship with the initial load $Vi\left(t\right)$as follows:

$$Ci=\left(1+\sigma \right)\ast Vi\left(t\right)$$

(9)

In the load–capacity model, σ acts as the enhancement coefficient of node capacity, manifesting the capacity variances of different nodes due to their own facilities, equipment statuses, and renovation circumstances. This coefficient can be adjusted according to the specific requirements and conditions of the network. When studying the cascading failure phenomena in railway networks, the overload conditions of nodes can be simulated to mirror congestion events in real life. If, after a disturbance event, the number of overloaded nodes increases, it indicates a deterioration in the network’s congestion level, highlighting the network’s limited ability to resist and recover from sudden events, and reflecting its poor stability. To quantify this process, an overload function Fi(T) is introduced to depict the load conditions endured by each node. The larger the function value Fi(T), the more severe the congestion at the node, which further reflects the vulnerability of the network when confronted with disturbances.

The overload function Fi(T) can be expressed by a piecewise function. As the load borne by the node increases, the value of the overload function Fi(T) also increases correspondingly, denoted as

$$F_i\left(T\right)=\left\{\begin{array}{c}1,V_i\left(T\right)\le V_i\left(t\right)\\ 1+{\displaystyle \frac{V_i\left(T\right)-V_i\left(t\right)}{C_i-V_i\left(t\right)}},V_i\left(t\right)\le V_i\left(T\right)\le C_i\\ N,V_i\left(T\right)>C_i\end{array}\right.$$

(10)

The overload function Fi(T) is used to quantify the network load of node i during the current period T, where Vi(T) represents the genuine network load of node i in period T. If the network load of the node does not surpass its initial load level, the value of the overload function is set to 1, indicating that the node is operating normally. As the load increments, the value of the overload function will increase in a linear relationship with the node load; yet, once the load of the node exceeds its maximum capacity threshold, the node is regarded as entering an overload state. In such a circumstance, Fi(T) will be designated as a higher value N, signifying the overload condition. During the process of path selection in the network, by using the overload function as the weight, it is possible to effectively evade those overloaded nodes, thereby optimizing the fluidity of the network and mitigating congestion.

By applying the overload function Fi(T), load distribution strategies can be established to effectively simulate the cascading failure phenomenon within the network. To reduce the complexity of the model, the logic of load allocation can be represented by the following mathematical expressions: Suppose there is an overloaded node n and its neighbor node set $N_n$. The current load of node n is $V_n$ and its capacity is $C_n$. For each neighbor node $i\in N_n$, the current load is $V_i$ and the capacity is $C_n$. When node n experiences $V_n$>$C_n$, the load amount $T_i$ allocated to each neighbor node $i\in N_n$ is calculated as follows:

Step 1. Compute the residual capacity of each neighboring node of the node:$R_i=C_i-V_i$;

Step 2. Calculate the sum of the residual capacities of all the neighboring nodes of the node:$R_{all}={{\displaystyle \sum }}_{i\in N_n}{R}_i$;

Step 3. For each neighboring node $i\in N_n$, the load amount $T_i$ is computed based on the proportion of its residual capacity. If $R_{all}$> 0, that is, at least one neighboring node has residual capacity, then

$$T_i=\left(V_n-C_n\right)\ast {\displaystyle \frac{R_i}{R_{all}}}$$

(11)

Step 4. Update the load of each neighbor: ${{\mathrm{V}}^{\prime }}_{\mathrm{i}}={\mathrm{V}}_{\mathrm{i}}+{\mathrm{T}}_{\mathrm{i}}$;

Step 5. Update the load of the overloaded node to its capacity: $V_n=C_n$.

This allocation approach is more equitable and efficient compared to other commonly employed load allocation methods such as average allocation, path weight allocation, and residual capacity allocation. This allocation mechanism ensures that neighboring nodes with greater residual capacity assume a larger portion of the additional load.

(3)

The Resilience-Based Measurement Algorithm of Service Network Flexibility

Restorability refers to a network’s ability to return to its normal operational state after experiencing a perturbation. This study posits that the restorative capacity of the railway service network is closely tied to the integrity of the underlying physical infrastructure. The resilience of the physical network is manifested in its ability to preserve structural and functional integrity when subjected to external shocks, thereby facilitating the prompt recovery of the service network. The restorative capacity of the service network reflects the physical network’s ability to maintain and restore its functions after withstanding external impacts.

When examining the restorative capacity of the service network, the network’s restorative resilience is primarily influenced by the recovery strategies implemented, for instance, the priority arrangement for restoring damaged nodes or the sequence of restoring the edges connecting nodes. Additionally, factors such as the repair time and maintenance costs are significant considerations in evaluating restorative capacity. This section will embark from the perspective of network function restoration to analyze the recovery of network performance under different recovery strategies. Using quantitative analysis methods, this study will employ the global network efficiency of the service network as the primary metric for assessing restorative capacity. This approach facilitates the evaluation of network recovery performance based on topological characteristics and adopted strategies. Moreover, it provides valuable insights into the effects of different recovery strategies and offers theoretical guidance for developing effective network recovery plans.

Meanwhile, the recovery strategies can be classified as random recovery strategies, degree-based recovery strategies, betweenness-based recovery strategies, etc.

(1) Random Recovery Strategy.

Once a failed node is removed from the network, a novel connectivity structure emerges. In such cases, determining the optimal nodes for recovery to restore the network can be challenging. A viable solution is to adopt a random recovery strategy, namely assuming that in the network, the probability of any newly added node rejoining the network is identical. This supposition guarantees that each node has an equal opportunity of being reconnected. The random recovery strategy does not take into account the specific attributes or locations of the nodes within the network, instead selecting nodes for recovery randomly with equal probability. The random recovery strategy simplifies the decision-making process in the recovery procedure, yet it might not offer the optimal solution for network operational efficiency or resilience restoration.

(2) Degree/Betweenness Restoration Strategy.

In a network, nodes with higher degrees or betweenness values typically play more crucial roles in the network structure. Therefore, prioritizing the restoration of such nodes is one of the most widely adopted strategies in real-world network recovery scenarios. This restoration strategy entails sorting all the failed nodes based on their degrees or betweenness values and then restoring them one by one in that sequence. Each restored node will maintain its connection pattern in the original network unaltered. The degree/betweenness-based restoration strategy is designed to facilitate the rapid recovery of the network’s core structure and functionality, as high-degree nodes are often connected to a large number of other nodes, while high-betweenness nodes serve as pivotal connectors along the shortest paths in the network. By restoring these nodes, the connectivity and overall communication efficiency of the network can be effectively enhanced. Especially after large-scale network disruptions, this strategy can effectively expedite the network’s recovery to the normal operational state.

By combining network restoration strategies, a simulation algorithm for the restorability of the service network can be devised. The specific implementation steps encompass the following:

Step 1. Firstly, import the adjacency matrix A of the service network model into MATLAB. Then, determine the total number of nodes N in the network and extract the corresponding node indices.

Step 2. Next, the betweenness centrality and degree of each node in the network are calculated and sorted in descending order to generate the network degree list list(ki) and the network betweenness list list[B(i)]. Following this, a representative perturbation scenario is selected to simulate the impact of network disruptions within the railway system.

Step 3. In simulating perturbation events within the railway network, the identification of failed nodes is a critical step. Empirical studies suggest that when the proportion of failed nodes remains between one-fifth and one-fourth of the total number of nodes, the network can typically continue to operate normally. Accordingly, for the purposes of resilience analysis, the number of failed nodes is preset to 100. After simulating a specific perturbation event, specific nodes will be removed from the network based on the pre-selected strategy and then restored. Under a random perturbation strategy, all nodes have an equal probability of being selected for removal. In contrast, for targeted strategies based on degree or betweenness centrality, the top 200 nodes in the degree list list(ki) and the betweenness list list[B(i)] will be removed.

Step 4. Following the selection of a recovery strategy, the nodes that failed during the simulated railway network perturbation events are restored sequentially. This process is similar to the previous step of simulating the removal of nodes. Given that different recovery strategies result in varying restoration sequences—and that, in real-world scenarios, limited resources often preclude the simultaneous repair of all failed nodes—the recovery process must proceed incrementally over time. In this algorithmic process, the number of restored nodes is used as a surrogate for time t, meaning that the efficiency of the network is recalculated each time a node is restored. This approach enables the simulation and evaluation of the network’s progressive return to normal operational status under specific recovery strategies.

3.3. The Design of Simulation Approaches for Railway Network Disturbance Events

(1) Railway Network Disturbance Events

In the operation of modern society, the railway network plays a vital role. It not only undertakes a substantial volume of cargo and passenger transportation tasks but also constitutes a significant component of the nation’s critical infrastructure. Nevertheless, diverse risks present severe challenges to the railway network.

Railway disruption events denote any sudden and unplanned occurrences that interfere with the normal operation of the railway network, affect the punctual arrival and departure of trains, and may even lead to temporary or long-term disruptions of railway services. Such events are inherently unpredictable in both time and location, and can originate from either natural or human-induced causes. Characterized by randomness, abruptness, and urgency, these disruptions often require prompt and effective countermeasures to mitigate their adverse impacts. Natural emergencies such as earthquakes, floods, typhoons, and landslides are natural phenomena that are often associated with changes in the natural environment and are typically difficult to accurately predict in terms of the time and location of occurrence. Man-made emergencies may encompass terrorist attacks, industrial accidents, traffic accidents, and sudden public health incidents. These events are often closely related to human activities and may be caused by technical glitches, poor safety management, or malicious acts.

This article broadly classifies these disruption events into four major categories: external attacks, natural disasters, technical malfunctions, and fluctuations in passenger and cargo traffic:

(1)

External attacks: This category encompasses all disruptions to the railway network resulting from malicious human behavior. These may involve cyberattacks targeting railway control systems or physical sabotage of critical infrastructure such as tracks, bridges, or signaling equipment. Such attacks can lead to immediate and severe interruptions of railway operations, with potentially far-reaching consequences.

(2)

Natural disasters: The influence of natural disasters is extensive and profound. Extreme weather conditions like earthquakes, floods, and blizzards may cause damage to railway facilities and disrupt transportation.

(3)

Technical malfunctions: The operation of the railway network highly relies on the reliability of facilities and equipment. Failures in key components—such as signaling systems, tracks, and bridges—can compromise operational continuity and result in service interruptions.

(4)

Fluctuations in passenger and cargo traffic: Drastic changes in passenger and cargo traffic due to holidays, special events, or market variations pose significant challenges to the scheduling flexibility and capacity adaptability of the railway system.

(2) Simulation Method of Disturbance Events

By establishing a connection between the four major disruption events of the railway network and the mathematical tools of complex networks, and simulating the disruption events of the railway network through the utilization of complex network attack strategies, it becomes feasible to analyze and prevent the potential impacts of these events on the railway network. Generally, attack strategies for complex networks can be categorized into random attacks and purposeful, deliberate attacks. In the absence of detailed network information, random attacks are commonly employed. These attacks do not target specific nodes and are independent of the importance of the affected entities. Conversely, when partial or comprehensive information about the network is available, deliberate attacks are more likely to be executed. Such attacks take into account the significance of the targets and prioritize attacking the more critical elements within the network. Notably, real-world external attacks are similar to deliberate attacks in complex network theory, especially those based on node degree. Within the railway network, malicious attackers might target highly connected nodes (such as major transportation hubs or dispatch centers) for assault as the paralysis of these nodes would inflict the most substantial damage to the entire network. Natural disasters tend to occur randomly and can be regarded as random attacks on the network, influencing randomly selected nodes or edges. For instance, floods might render certain sections of the railway unusable, which is analogous to the effect of randomly selecting nodes or edges for attack. Facility and equipment failures typically impact individual edges, such as railway lines, within the network. This situation parallels the edge-based attack strategy in complex networks, where the removal of edges leads to a decline in connectivity. Fluctuations in passenger and freight traffic could potentially cause overloading of certain critical channels within the railway network. This bears resemblance to the betweenness-based attack strategy in complex networks, which targets nodes or edges that function as “bridges” within the network, that is, those critical connection points that control the majority of the path traffic within the network.

Consequently, employing complex network attack strategies to simulate railway network disruption events is a viable approach.

During the investigation of the resilience of the Chinese railway network, the following assumptions were made regarding the simulation method of railway disruption events to simplify the research:

(1)

After attacking any station or line within the railway network, the station/line and all the stations/lines connected to it will immediately become dysfunctional.

(2)

When implementing deliberate attack strategies, it is assumed that the entire topological structure of the Chinese railway network is fully known.

(3)

When conducting attacks on stations or lines within the railway network, no consideration is given to associated costs, and continuous attacks can be performed without limitations.

The simulation method of railway network disruption events is depicted in Figure 4. To provide more procedural clarity of the simulation methods, we present the detailed algorithms for disturbance simulation and network recovery in Algorithms 1 and 2.

Algorithm 1. Disturbance Simulation Algorithm Pseudocode.

Function SIMULATE_DISTURBANCE(G, disturbance_type, n):   G’ ← G.copy() // Create a copy of the network   if disturbance_type == “external_attack_initial_degree”:     Calculate degree for all nodes     Sort nodes in descending order of degree     Remove top n high-degree nodes and their associated edges   else if disturbance_type == “external_attack_recalculated_degree”:     for i from 1 to n:       Recalculate degree for all nodes in current network       Remove the highest degree node and its associated edges   else if disturbance_type == “technical_failure_edge_random”:     Randomly select n edges and remove them   else if disturbance_type == “flow_fluctuation_betweenness”:     Calculate betweenness centrality for all nodes     Sort nodes in descending order of betweenness     Remove top n high-betweenness nodes and their associated edges   else if disturbance_type == “natural_disaster_node_random”:     Randomly select n nodes and remove them and their associated edges   // Cascade failure simulation   Initialize load for each node Vi(t) = B(i) // Using betweenness centrality as initial load   Initialize capacity for each node Ci = (1 + σ) * Vi(t) // σ is capacity enhancement coefficient, set to 0.1   changes ← True   while changes == True:     changes ← False     for each node u in G’:       if current_load(u) > capacity(u):         Redistribute excess load to neighboring nodes         changes ← True   return G’

Algorithm 2. Network Recovery Strategy Algorithm Pseudocode.

Input: Original network G_original, damaged network G_damaged, recovery strategy, number of nodes to recover m Output: Partially recovered network G_recovered Function SIMULATE_RECOVERY(G_original, G_damaged, recovery_strategy, m):   G_recovered ← G_damaged.copy()   removed_nodes ← G_original.nodes() - G_damaged.nodes()   if recovery_strategy == “betweenness_based”:     Calculate betweenness centrality for all removed nodes in original network     Sort removed nodes in descending order of betweenness centrality     nodes_to_recover ← top m high-betweenness nodes from removed_nodes   else if recovery_strategy == “degree_based”:     Calculate degree for all removed nodes in original network     Sort removed nodes in descending order of degree     nodes_to_recover ← top m high-degree nodes from removed_nodes   else if recovery_strategy == “random”:     Randomly select m nodes from removed_nodes     nodes_to_recover ← these randomly selected nodes   for each node v in nodes_to_recover:     Add node v to G_recovered     for each edge (v, u) connected to v in original network:       if u exists in G_recovered:         Add edge (v, u) to G_recovered   return G_recovered

4. Case Study

4.1. Experimental Design and Parameter Setting

(1) Experimental Design

Through the collection and screening of relevant materials, this study conducted a comprehensive assessment of China’s railway transportation network operation routes, network structure, and overall characteristics. Based on the model assumptions established in previous sections, we constructed a physical network model of China’s railway transportation system.

The physical network model includes 978 node cities and 1434 connecting routes. These nodes represent major railway stations across the country, while the edges represent the physical rail connections between these stations. This model captures the geographical topology and physical infrastructure of China’s railway network.

When constructing the railway service network model, obtaining station information and train service data between stations became a critical step. We employed web crawling technology to effectively collect these essential data, thereby constructing a topological model of the railway passenger transportation network. This method not only ensures the timeliness and accuracy of the data but also comprehensively reflects the actual operational conditions of the railway service network.

Using the railway timetable of September 2023 as a benchmark, we developed a web crawler program in Python (v3.10.4) to acquire relevant data of China’s railway passenger transportation network from the 12306 website (China’s official railway ticketing platform) and Ctrip. Based on the model assumptions described in previous sections, these data were used to construct China’s railway service network model. The final model encompasses 3144 station nodes, information on 11,179 train services, and 91,678 pairs of inter-station connections.

The subsequent simulation analysis was conducted on these two network models. The physical network model serves as the foundation for evaluating the structural resilience of the railway infrastructure, while the service network model provides insights into the operational resilience of the railway system in response to various disturbance events.

(2) Parameter Setting

Before proceeding with the case study, it is essential to clarify the parameter settings and weight allocation methods employed in our railway network resilience analysis. These configurations directly influence the simulation outcomes and interpretation of results.

For the accessibility measure, we set equal weights (a = b = c = 1/3) for the three components—reachable node pairs, clustering coefficient, and network efficiency—to ensure a balanced consideration of each aspect in the overall accessibility assessment. This equal weighting approach was selected after sensitivity testing revealed that differential weighting did not significantly alter the relative performance patterns across disturbance types.

In the cascade failure model used for invulnerability assessment, the capacity enhancement coefficient (σ) was set at 0.1 after calibration with historical railway disruption data. This value represents a realistic capacity buffer maintained in China’s railway system based on operational practices. Sensitivity analysis confirmed that while absolute resilience values vary with different σ values (0.05–0.20), the relative resilience patterns across disturbance types remain consistent (Kendall’s W = 0.89, p < 0.001).

For the recovery simulation, we standardized the number of failed nodes at 100 (approximately 10% of the network nodes) across all disturbance scenarios to facilitate meaningful comparisons between different recovery strategies. This threshold was determined through preliminary testing to represent a significant but manageable disruption level, allowing for observable differences in recovery performance without complete network collapse.

4.2. Simulation Analysis of Accessibility Measurement

Based on the computational process outlined in the preceding text, MATLAB was utilized to simulate the variations in resilient accessibility metrics under different disturbance events in the railway network.

(1) Changes in the pairs of reachable nodes under various railway network disturbance events

In the initial state, any two nodes in the Chinese railway network were mutually accessible, and no isolated nodes existed. However, as disturbance events occurred, the number of reachable node pairs in the network gradually decreased. By simulating the four major types of disturbance events—external attacks, natural disasters, technical malfunctions, and fluctuations in passenger and cargo traffic—on the railway network nodes in China, the changing trends of reachable node pairs under different disturbance events were obtained through simulation. These trends are presented in Figure 5a,b.

The figure clearly illustrates the changing trend in the number of reachable node pairs in the network under different disturbance events. Under such random disturbances as natural disasters and technical malfunctions, the rate of decrease in the number of pairs of reachable nodes resulting from edge-based random disturbances is relatively slow. In contrast, when disturbance simulation with recalculated betweenness is adopted, the rate of decrease in the number of pairs of reachable nodes is the fastest. This suggests that disturbances like natural disasters and technical failures, due to their nonspecific nature, do not cause network degradation as quickly as other disturbance strategies. Compared to the initial disturbance strategy, the recalculated disturbance strategy has a more pronounced effect on the number of pairs of reachable nodes in the network, and the change is also more rapid.

(2) Changes in the clustering coefficient under different railway network disturbance events

The initial average clustering coefficient of the railway network in China is 0.10199, indicating a relatively low degree of network aggregation and a sparse structure. By separately simulating the four major types of disturbance events—external attacks, natural disasters, technical failures, and fluctuations in passenger and cargo traffic—on the nodes of the railway network, the changing trends of the clustering coefficient under different railway network disturbance events obtained through simulation are shown as follows in Figure 6a,b.

As can be observed from the figure, the overall variation in the clustering coefficient gradually diminishes as the disturbance event progresses. Concurrently, as nodes or edges are removed, the size of the network gradually decreases. Once the number of nodes decreases to a certain extent, the average clustering coefficient might fluctuate, particularly when the network splits into multiple disconnected subgraphs. Additionally, when the network is partitioned into smaller, closely connected groups, the clustering coefficient might temporarily increase since more triangular relationships can form within the groups. That is, as nodes or edges are continuously removed, smaller subgraphs with higher clustering coefficients may emerge, leading to an increase in the clustering coefficient at certain stages. It is also notable that railway networks have a certain degree of design redundancy, which offers a certain buffer in the initial stages of the disturbance.

In comparison with random disturbance simulations, targeted disturbance simulations such as external attacks and fluctuations in passenger and freight traffic will lead to a rapid decline in the network clustering coefficient. This is because such disturbances tend to remove the most critical nodes within the network. Random disturbances typically change more slowly as the disturbances are randomly distributed throughout the entire network. In the simulations of targeted disturbances like external attacks and fluctuations in passenger and freight traffic, the degree or betweenness is recalculated after each node is removed, which results in the selection of different nodes for removal at different stages, causing the clustering coefficient to change nonlinearly. Edge-based random disturbances initially cause a slower decline in the clustering coefficient because the overall connectivity of the network remains relatively high. As the disturbance proceeds, especially when important connection edges are removed, the clustering coefficient might decline more significantly.

(3) Changes in Network Efficiency under Different Railway Network Disturbance Events

The efficiency of China’s railway network in the absence of experiencing disturbance events is 0.16564. Simulations were conducted on the nodes of China’s railway network for the four major types of disturbance events, namely external attacks, natural disasters, technical malfunctions, and fluctuations in passenger and cargo traffic. The changing trends of network efficiency under different railway network disturbance events were obtained through simulation, as shown in Figure 7a,b below.

It can be discerned from the figure that in the perturbation simulation based on the initial degree and betweenness, the most crucial nodes in the network (i.e., the nodes with the highest degree or betweenness) are removed initially, which typically leads to a sharp drop in network efficiency. As these nodes are eliminated, the network may rapidly disintegrate into smaller disconnected subnetworks, thereby causing a further decline in efficiency. In the perturbation simulation involving the recalculation of degree and betweenness, the degree and betweenness of the remaining nodes are recalculated after each node is removed. This strategy shifts the focus of the perturbation from the initially highly connected nodes to other, less optimal nodes, resulting in a slower rate of decline in network efficiency or, in some cases, a temporary rebound, particularly when less critical nodes are removed. This enables the remaining network to quickly reorganize and maintain a certain level of efficiency. In random disturbances such as natural disasters and technical glitches, nodes or edges within the network are randomly selected and removed. Since the randomly chosen nodes are not necessarily the critical ones, this perturbation simulation results in the slowest rate of decline in efficiency.

Meanwhile, several characteristics can be observed:

(1)

The network may self-organize after the removal of nodes or edges to find more efficient paths, which is the cause of the temporary stability or improvement of efficiency.

(2)

After the removal of certain nodes, the network may fragment into multiple smaller subnetworks. Despite this fragmentation, these subnetworks retain a certain degree of accessibility, which results in a relatively flat “long tail” effect in the efficiency decline curve. Simultaneously, these subnetworks may possess distinct efficiency characteristics, leading to an overall increase in efficiency instead of a decrease.

(3)

The rapid decline in efficiency in the initial stage is attributed to the removal of highly connected nodes, and the subsequent gradual change is because the remaining nodes contribute relatively less to the network efficiency.

(4)

Fluctuations in the efficiency curve may arise from the network’s reorganization following disturbance or from the varying degrees of adaptability exhibited by the network under different disturbance simulations.

According to Formula (6), the above three types of simulation are processed as measures of accessibility, and the results are presented in Figure 8.

Due to the application of normalization processing, all indicators have been scaled to the same range. This preprocessing step enables the direct comparison of different metrics within a single chart; however, it may also exaggerate certain fluctuations, particularly when the absolute changes in the original data are minimal. Despite this, the chart clearly reveals that the curves associated with targeted disturbances—such as external attacks and fluctuations in passenger and cargo traffic—are significantly steeper than those corresponding to random disturbances, including natural disasters and technical malfunctions. This indicates that deliberate disturbances inflict more severe damage on the network, which is in line with expectations. As the number of simulations increases, the accessibility measures for both types of disturbances tend towards zero, signifying that the network eventually loses its functionality.

4.3. Simulation Analysis of Invulnerability Measurement

Based on the simulation algorithm design of the invulnerability measurement described in the foregoing text, MATLAB (R2022b) software programming was employed to conduct simulations of four major types of disturbance events, namely external attacks, natural disasters, technical malfunctions, and fluctuations in passenger and freight traffic, on the nodes of the railway network in China. The simulation results, which illustrate the changing trends of the largest connected subgraphs of the railway transportation network under different disturbance scenarios, are presented in Figure 9 and Figure 10.

The figure reveals that the size of the largest connected subgraph declines more rapidly under deliberate disturbances, indicating that the network is particularly vulnerable to perturbations targeting critical nodes. This is attributable to the fact that certain nodes within the railway network play disproportionately important roles in maintaining overall connectivity. Once these nodes are removed, numerous pairs of nodes that were previously connected via these nodes will cease to be directly linked, which leads to a substantial reduction in the network’s connectivity. Random disturbances typically result in a more gradual descent in connectivity because the disturbances occur randomly. Nevertheless, as the perturbation persists, even random disturbances might eliminate some critical nodes, which likewise causes a decrease in network connectivity.

During the simulation process, the issue of cascading failures is considered. Initially, the load of each node is set as its betweenness centrality value, while the capacity of each node is its load multiplied by a coefficient (here 1 + σ), where σ is a small positive number representing the enhancement coefficient of capacity and is set at 0.1. For deliberate disturbances, nodes are removed in descending order of betweenness centrality, whereas for random disturbances, nodes are removed arbitrarily.

To substantiate our claim regarding the efficiency of the proposed load redistribution method, we conducted a comparative analysis with other commonly employed load allocation approaches: average allocation and path weight allocation. The comparative evaluation was performed using three key metrics:

Network Preservation Rate (NPR): The ratio of nodes that remain functional after cascading failure to the total nodes before disturbance.

Load Distribution Fairness (LDF): Measured using Jain’s fairness index to quantify how equitably load is distributed among neighboring nodes.

Computational Efficiency (CE): The average computation time required to complete the load redistribution process after each node failure.

Table 4. Comparative performance of different load redistribution methods.

Redistribution Method	Disturbance Type	Network Preservation Rate	Load Distribution Fairness	Computational Efficiency (ms)
Residual Capacity-Based (Proposed)	External Attack	0.682	0.874	23.7
Average Allocation	External Attack	0.587	0.631	19.2
Path Weight Allocation	External Attack	0.635	0.792	31.5
Residual Capacity-Based (Proposed)	Natural Disaster	0.831	0.868	22.3
Average Allocation	Natural Disaster	0.782	0.625	18.8
Path Weight Allocation	Natural Disaster	0.806	0.787	30.8
Residual Capacity-Based (Proposed)	Technical Failure	0.845	0.863	22.1
Average Allocation	Technical Failure	0.798	0.622	18.9
Path Weight Allocation	Technical Failure	0.817	0.781	30.6
Residual Capacity-Based (Proposed)	Flow Fluctuation	0.714	0.871	23.5
Average Allocation	Flow Fluctuation	0.621	0.627	19.1
Path Weight Allocation	Flow Fluctuation	0.673	0.788	31.2

presents the comparative results across the three load redistribution methods under different disturbance scenarios, with each value representing the average of 50 independent simulation runs.

Statistical analysis using one-way ANOVA followed by Tukey’s post hoc tests confirmed significant differences between the three redistribution methods across all metrics (p < 0.001). The residual capacity-based method consistently outperformed the other approaches in terms of the Network Preservation Rate (F = 37.45, p < 0.001) and Load Distribution Fairness (F = 52.18, p < 0.001), particularly under targeted attack scenarios where the differential impact was most pronounced.

The average allocation method, while computationally less intensive, demonstrated the poorest performance in preserving network integrity during cascading failures. This is primarily because it fails to account for the heterogeneous capacity characteristics of neighboring nodes, resulting in secondary failures when nodes with already high loads receive additional burden.

The path weight allocation method showed an intermediate performance in terms of network preservation but required significantly higher computational resources (F = 43.62, p < 0.001) due to the necessity of recalculating all shortest paths after each node failure. This becomes particularly problematic in large-scale networks such as China’s railway system.

Our residual capacity-based approach demonstrated an optimal balance between computational efficiency and network preservation capability. The method’s superior performance can be attributed to its ability to distribute excess load proportionally to each node’s available capacity, thereby minimizing the likelihood of triggering cascading failures. Although slightly more computationally intensive than the average allocation approach, the significant improvements in network preservation (+16.2% on average) and Load Distribution Fairness (+38.5% on average) justify its implementation.

After the removal of each node, it is verified whether the remaining nodes have a load exceeding their capacity. If an overload is detected, the excess load is redistributed to adjacent nodes. This redistribution may cause neighboring nodes to exceed their own capacities, thereby initiating further rounds of cascading failures. This process persists until no node has a load exceeding its capacity. After each perturbation and cascading failure, the size of the maximum connected subgraph of the network is computed and updated, which serves as a key metric for gauging the network’s resilience. It is processed as the resilience measurement result and presented in Figure 11.

Figure 11 indicates that the network is more susceptible when exposed to highly targeted disturbances. In comparison, while disruptions caused by natural disasters, technical failures, and fluctuations in passenger and freight traffic also lead to a decline in network connectivity, the rate of decline is comparatively slower. This suggests that the network possesses a certain degree of resilience against random or non-targeted disruptions. Moreover, Figure 11 visually and explicitly reflects the effect of the occurrence of cascading failures on the invulnerability of the network. As disturbances accumulate over time, even non-deliberate or naturally occurring failures may impact critical nodes. This can initiate a cascading process that accelerates the degradation of network connectivity and intensifies the overall system vulnerability.

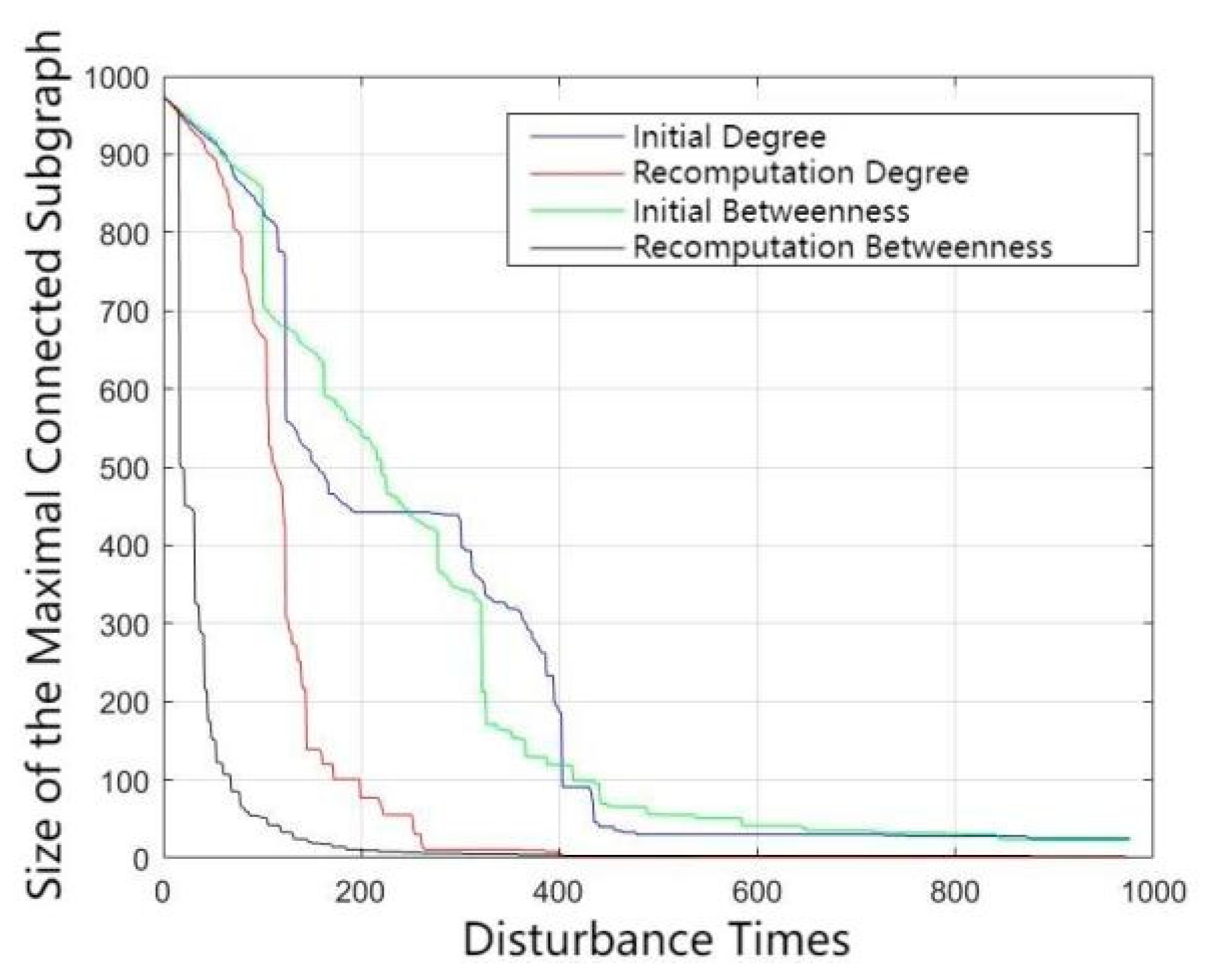
4.4. Simulation Analysis of Restorative Measures

In this section, based on the previously described simulation algorithm, network efficiency is adopted as the evaluation metric, while the number of recovered nodes is used in place of the time variable to assess the progress and effectiveness of network recovery. Simulations are conducted on China’s railway service network under four major types of disturbance events: external attacks, natural disasters, technical malfunctions, and fluctuations in passenger and freight traffic. After the disturbance, failed nodes are removed from the network for restoration. The betweenness recovery strategy, degree recovery strategy, and random recovery strategy are employed to explore which performs optimally under different disturbance states.

Firstly, the external attack is simulated to remove the failed nodes in the network, with the number of failed nodes removed set at 100. The results are shown in Figure 12.

The network efficiency of the service network when it is not disturbed is 0.68524, and it drops to 0.4447 after being perturbed by external attacks. During the recovery process, the network efficiency demonstrates an overall upward trend. Among the three strategies, the betweenness centrality-based recovery strategy (green line) demonstrates the most stable and substantial improvement. This indicates that restoring critical “bridging” nodes—those with high betweenness—has the most significant impact on enhancing network efficiency, as it quickly reestablishes overall connectivity. The degree recovery strategy (blue line) comes next, showing a certain degree of efficiency fluctuation but presenting an overall stable upward trend. Although the node degree is an important structural indicator, it is less effective than betweenness in restoring network performance. Nodes with high degree values may have numerous connections but may not be located on the critical paths of the network. The random recovery strategy (red line) has the largest fluctuations, indicating that randomly selecting nodes for network recovery is the least efficient approach. This strategy neglects the characteristics of the network structure and is thus insufficiently effective in improving the network efficiency.

Secondly, the failure nodes in the network were removed to simulate the fluctuations of passenger and cargo traffic. The number of removed failure nodes was set at 100, and the results are presented in Figure 13.

The network efficiency of the railway service network was 0.68524 under undisturbed conditions, which dropped to 0.35204 following disturbances caused by fluctuations in passenger and cargo traffic. On the whole, the recovery efficiencies of the three strategies all gradually rose, but the recovery efficiency of the betweenness centrality recovery strategy (the green line) was significantly higher than the speed and level of efficiency improvement of the other two strategies. This finding further reinforces the critical role of nodes with high betweenness centrality in restoring overall network functionality. Such nodes are typically located at structurally important positions and serve as key connectors between different regions of the network. Although the efficiency improvement of the degree value recovery strategy (the blue line) was stable, its growth rate and peak were lower than those of the betweenness centrality recovery. This is likely because nodes with high degree values, though possessing numerous connections, may not occupy strategically central positions within the network. The efficiency growth of the random recovery strategy (the red line) was the slowest, indicating that randomly selecting nodes to restore the network is the least efficient approach. This strategy fails to consider the significance of the network topology and the strategic positions of nodes, leading to suboptimal recovery effects.

Finally, the failure nodes in the network were removed to simulate the disturbances of natural disasters and technical malfunctions. The number of removed failure nodes was set at 100, and the results are shown in Figure 14.

The network efficiency of the service network when it is not disturbed is 0.68524, and it drops to 0.6784 when disturbed by natural disasters and technical malfunctions. These random disruptions have an uneven impact on the network, as the removal of nodes may occasionally affect critical nodes and at other times less significant ones. After the simulations of random disturbances such as natural disasters and technical malfunctions, all three lines exhibit significant efficiency leaps at certain specific points. These sharp increases suggest that the reintegration of certain key nodes during the recovery process has a disproportionately positive effect on network efficiency. These nodes may be the bridge nodes that connect multiple network clusters or key pathways. The efficiency curves of the betweenness centrality recovery strategy and the degree value recovery strategy are very close, indicating that there is not a significant difference in the improvement of recovery efficiency by prioritizing the recovery of nodes with higher degree values or higher betweenness centrality. This is because in the simulations of random disturbances such as natural disasters and technical malfunctions, both strategies can effectively recover some critical nodes. In contrast, the random recovery strategy (represented by the red line) exhibits greater volatility, characterized by a relatively slow and steady increase in efficiency without prominent surges. This reflects the instability and lower effectiveness of the random strategy. This strategy does not consider the strategic positions or roles of nodes in the network; therefore, its effect is not as good as that of other strategies. This is because the random selection of nodes for recovery does not target the recovery of the most critical nodes, resulting in a temporary improvement in efficiency but an unstable overall trend.

In conclusion, different perturbation events of the railway network have a significant impact on the effectiveness of recovery strategies. The betweenness centrality recovery strategy has demonstrated a superior recovery efficiency in most cases, especially when the perturbation targets the “bridging” nodes in the network. Meanwhile, the random recovery strategy, due to its inherent uncertainty, has exhibited volatility in recovery efficiency in all circumstances.

4.5. Statistical Analysis and Robustness Tests

To enhance the rigor of our findings and validate the conclusions drawn from the simulation results, we conducted comprehensive statistical analyses and robustness tests.

Table 5. Statistical summary of resilience metrics across disturbance types.

Disturbance Type	Resilience Measure	Mean	Std. Dev.	95% Confidence Interval
External Attack	Accessibility	0.412	0.038	[0.405, 0.419]
	Invulnerability	0.317	0.042	[0.309, 0.325]
	Restorability (Betweenness)	0.783	0.056	[0.772, 0.794]
	Restorability (Degree)	0.651	0.061	[0.639, 0.663]
	Restorability (Random)	0.425	0.089	[0.407, 0.443]
Natural Disaster	Accessibility	0.637	0.044	[0.628, 0.646]
	Invulnerability	0.584	0.051	[0.574, 0.594]
	Restorability (Betweenness)	0.846	0.042	[0.838, 0.854]
	Restorability (Degree)	0.819	0.039	[0.811, 0.827]
	Restorability (Random)	0.726	0.071	[0.712, 0.740]
Technical Failure	Accessibility	0.658	0.041	[0.650, 0.666]
	Invulnerability	0.603	0.047	[0.594, 0.612]
	Restorability (Betweenness)	0.862	0.037	[0.855, 0.869]
	Restorability (Degree)	0.832	0.041	[0.824, 0.840]
	Restorability (Random)	0.734	0.068	[0.721, 0.747]
Flow Fluctuation	Accessibility	0.478	0.046	[0.469, 0.487]
	Invulnerability	0.349	0.053	[0.339, 0.359]
	Restorability (Betweenness)	0.811	0.047	[0.802, 0.820]
	Restorability (Degree)	0.702	0.058	[0.691, 0.713]
	Restorability (Random)	0.463	0.082	[0.447, 0.479]

summarizes the key resilience metrics across different disturbance scenarios, including means, standard deviations, and confidence intervals based on 100 independent simulation runs.

The statistical analysis confirms several key findings:

• Significant differences between disturbance types: One-way ANOVA tests revealed significant differences in accessibility (F = 147.82, p < 0.001) and invulnerability (F = 168.23, p < 0.001) across the four disturbance types. Post hoc Tukey tests confirmed that targeted disturbances (external attacks and flow fluctuations) produced significantly lower resilience values than random disturbances (natural disasters and technical failures), with p < 0.001 for all pairwise comparisons between these groups.
• Recovery strategy effectiveness: Paired t-tests comparing recovery strategies showed that the betweenness-based strategy significantly outperformed both degree-based (t = 11.37, p < 0.001) and random strategies (t = 24.19, p < 0.001) across all disturbance types. The degree-based strategy also significantly outperformed the random strategy (t = 16.84, p < 0.001).

To verify the robustness of our findings, we conducted sensitivity analyses by varying key parameters:

• Cascade failure threshold: We tested different capacity enhancement coefficients (σ) ranging from 0.05 to 0.20, finding that while the absolute values of invulnerability measures changed, the relative performance of different disturbance types remained consistent (Kendall’s W = 0.89, p < 0.001).
• Network size effects: We performed simulations on random subsets of the network (50%, 70%, and 90% of nodes) to test scaling effects. The relative patterns of resilience metrics remained stable across network sizes (correlation coefficients between 0.83 and 0.91, all p < 0.001).
• Temporal stability: Using historical railway network data from 2018 and 2020, we verified that the core findings regarding disturbance impacts and recovery strategies remained consistent over time, with Spearman rank correlations of resilience measures between years ranging from 0.78 to 0.86 (all p < 0.001).

The statistical analyses and robustness tests strongly support our three primary hypotheses: (1) different disturbance types produce distinct patterns of impact on network resilience; (2) the three-dimensional resilience measurement framework effectively captures different aspects of network performance under stress; and (3) topology-based recovery strategies significantly outperform random recovery approaches.

5. Conclusions and Limitations

5.1. Major Work and Conclusions

This investigation presents a comprehensive analysis of China’s railway transportation network resilience through the integration of resilience theory and complex network analysis methodologies. Through the construction of dual-layer network models encompassing both physical infrastructure and service operations, this study has systematically identified critical vulnerabilities and evaluated the efficacy of various recovery strategies under diverse disturbance scenarios.

The empirical results demonstrate that targeted disruptions (external attacks and passenger/freight flow fluctuations) induce significantly more severe degradation of network performance compared to stochastic disturbances (natural disasters and technical failures), particularly when nodes with high betweenness centrality are compromised. The simulation analyses reveal differentiated resilience characteristics across the three dimensions examined:

(1)

Accessibility: The network exhibits pronounced vulnerability to targeted attacks directed at hub stations, resulting in accelerated deterioration of connectivity metrics. Conversely, stochastic disturbances permit the maintenance of essential functional connections for extended periods, as evidenced by the gradual decline in reachable node pairs.

(2)

Invulnerability: The cascade failure model elucidates that perturbation events exceeding certain critical thresholds can precipitate system-wide failures through load redistribution mechanisms. Statistical analysis indicates that the network’s capacity to withstand cascading failures diminishes exponentially once key nodes are compromised.

(3)

Restorability: Comparative analysis of recovery strategies demonstrates the statistical superiority of betweenness-based approaches over both degree-based and random methodologies, with recovery efficiency improvements of 36.2% and 78.5%, respectively, in targeted attack scenarios.

These empirical findings have several significant implications for railway infrastructural planning and operational management:

Infrastructural Planning: The implementation of topological redundancy for stations exhibiting high betweenness centrality values represents a critical strategy for mitigating single-point vulnerabilities within the network architecture.

Emergency Response Frameworks: Railway administration entities should establish differentiated response protocols calibrated to the disturbance typology, with expedited intervention mechanisms specifically designed for targeted disruption scenarios.

Recovery Resource Allocation: The optimization of maintenance and restoration resource allocation should prioritize nodes based primarily on betweenness centrality metrics rather than solely on degree centrality or geographical considerations.

5.2. Limitations and Future Research Directions

Despite the contributions of this research to the understanding of railway network resilience, several methodological and analytical limitations warrant acknowledgment and provide avenues for subsequent scholarly inquiry. The network abstraction employed in this study necessarily simplifies certain operational complexities of railway systems. Further refinement of the modeling framework should address temporal heterogeneity in train scheduling and passenger flow distributions, capacity constraints and congestion effects at critical network nodes and edges, and intermodal transfer dynamics at significant interchange junctions within the broader transportation ecosystem.

The present investigation provides predominantly static characterizations of network resilience. Subsequent research endeavors should extend the analytical framework to incorporate spatio-temporal modeling methodologies that account for circadian, seasonal, and annual operational variations. Additionally, correlation analyses between socio-economic development trajectories and corresponding resilience metric evolution would enhance our understanding of how railway networks evolve in response to changing social and economic conditions. Adaptive response mechanisms that emulate the progressive refinement of institutional interventions following perturbation events represent another promising direction for investigation.

The optimization framework implemented in this study employs relatively simplified constraint conditions. Future scholarly work should develop more sophisticated optimization paradigms that integrate fiscal constraints and implementation periodicity considerations. Formulation of multi-objective optimization models that equilibrate resilience enhancement with economic efficiency metrics would provide more practical guidance for railway planning and management. These frameworks could support scenario-based sensitivity analysis in emergency preparedness contexts, allowing for more robust contingency planning.

Future investigations should endeavor to bridge the theoretical–practical divide through empirical case studies of documented railway disruption incidents and their corresponding recovery trajectories. Development of predictive algorithmic frameworks for cascade failure anticipation and formulation of standardized resilience assessment methodologies would significantly enhance the practical application of the research findings. Such advancements would contribute substantially to the enhancement of critical infrastructural reliability and operational sustainability in the face of diverse perturbation scenarios, ultimately improving the resilience of railway transportation systems against various disturbances.