G-Pre: A Graph-Theory-Based Matrix Preconditioning Algorithm for Finite Element Simulation Solutions
Abstract
1. Introduction
2. Methods
2.1. Problems in Solving Systems of Linear Equations in Finite Element Analysis
2.1.1. Asymmetric Matrix Solution Problem
2.1.2. Symmetric Matrix Solution Problem
2.2. Matrix Solving Algorithm
| Algorithm 1: GMRES. |
| Input: Initial value u0, Convergence boundary Ɛ > 0, Maximum number of iterations IterMax 1: r0 = b − Au0, β = ||r0||2 2: υ1 = r0/β 3: for j = 1, …, IterMax: 4: w = Avj 5: for i = 1, …, j: 6: hi,j = (vj,w) 7: w = w − hi,j vi 8: end for 9: hj+1,j = ||w||2 10: if hj+1,j = 0: 11: m = j, break 12: end if 13: vj+1 = w/hj+1,j 14: relres = ||rj||2/β 15: if relres < Ɛ: 16: m = j, break 17: end if 18: end for |
| Algorithm 2: CG. |
| Input: stiffness matrix A, load vector b, initial value x0, convergence bound Ɛ, Maximum number of iterations IterMax. 1: r0 = Ax0 − b, P0 = − r0 2: α0 = ||r0||/P0TAP0 3: while || Axk − b ||/||rk|| > Ɛ: 4: for k = 1, …, IterMax: 5: xk = xk−1 + αk−1Pk−1 6: rk = rk−1 − αk−1APk−1 7: βk−1 = ||rk||/||rk−1|| 8: Pk = rk + βk−1Pk−1 9: end for 10: end while |
2.3. Matrix Preconditioning Algorithm
- Multilevel incomplete factorization (ILU(l)): This approach, denoted as ILU(l), is based on symbolic factorization, which computes the hierarchical level l of the non-zero elements in the factorization from the non-zero structure of the original matrix A. Elements with a hierarchical level l greater than a specified threshold are discarded [51]. The hierarchical value of the non-zero elements in the factorization is solely dependent on the distribution of the non-zero elements in A and is independent of their actual values. If matrix A is diagonally dominant, the elements at higher levels in the factorization tend to have smaller absolute values during LU factorization. Thus, in incomplete factorization, elements with level values exceeding a given threshold can be discarded [50]. However, for matrices without diagonal dominance, this relationship does not hold, and discarding elements based purely on their hierarchical level may result in unreliable preconditioners due to ignoring the impact of element values [34].
- Threshold rounding strategy: Another approach involves using a threshold rounding strategy based on the numerical magnitude of the elements in the factorization [52]. Given a threshold value τ > 0, non-zero elements in the factorization are discarded if their absolute value is less than τ; otherwise, they are retained. Although the relationship between the magnitude of discarded elements and the number of iterative steps required for convergence is complex, generally, discarding fill-in elements with smaller absolute values produces higher-quality preconditioners compared to discarding elements with larger values [27].
3. Graph Theory and G-Pre Preconditioning Algorithm Design
3.1. Graph Theory
3.2. G-Pre Preconditioning Algorithm Design
- Preconditioning division and reordering stage: This stage divides and reorders the matrix using a graph partitioning algorithm.
- Preconditioning factorization stage: In this phase, the ILU algorithm is employed to factorize the matrix.
- Parallel solving stage: The preprocessed matrix is then solved through parallel iterations.
| Algorithm 3: G-Pre code process. |
| Input: Non-symmetric matrix A, right-hand side vector b, initial guess x0, tolerance tol, max iterations max_iter Output: Approximate solution x 1: Step 1: Graph theory preconditioning 2: function preprocess_with_METIS(A): 3: graph = extract_graph(A) 4: n_partitions = calculate_optimal_partitions(A) 5: partition_result = METIS_PartGraph(graph, n_partitions) 6: P = construct_permutation_matrix(partition_result) 7: A_permuted = P.T @ A @ P 8: preconditioners = [] 9: for i in 0 to n_partitions − 1: 10: block = extract_block(A_permuted, i) 11: M_i = ILU(block) 12: preconditioners.append(M_i) 13: return P, preconditioners 14: Step 2: Preconditioned GMRES solver 15: function METIS_preconditioned_GMRES(A, b, x0, tol, max_iter): 16: P, preconditioners = preprocess_with_GRF(A) 17: b_permuted = P.T @ b 18: x = P.T @ x0 19: r = b_permuted − A_permuted @ x 20: beta = norm(r) 21: Q = [r/beta] 22: H = empty_matrix 23: for j in 0 to max_iter − 1: 24: v = apply_preconditioner(Q[j], preconditioners) 25: w = A_permuted @ v 26: for i in 0 to j: 27: H[i, j] = dot(Q[i], w) 28: w = H[i, j] ∗ Q[i] 29: H[j + 1, j] = norm(w) 30: Q.append(w/H[j + 1, j]) 31: e1 = [beta, 0, …, 0].T 32: y = solve_least_squares(H [0:j + 2, 0:j + 1], e1) 33: residual = norm(H [0:j + 2, 0:j + 1] @ y − e1) 34: if residual < tol: 35: break 36: x_update = P @ (Q [0:j + 1] @ y) 37: x = x0 + x_update 38: return x 39: function apply_preconditioner(v, preconditioners): 40: z = zeros_like(v) 41: for i in 0 to len(preconditioners) − 1: 42: block_indices = get_block_indices(i) 43: z[block_indices] = preconditioners[i].solve(v[block_indices]) 44: return z |
4. Numerical Experimental Simulation and Analysis
4.1. Introduction to Test Models
4.2. Comparison of Results
- A comparison and analysis of condition numbers;
- Solving time comparisons;
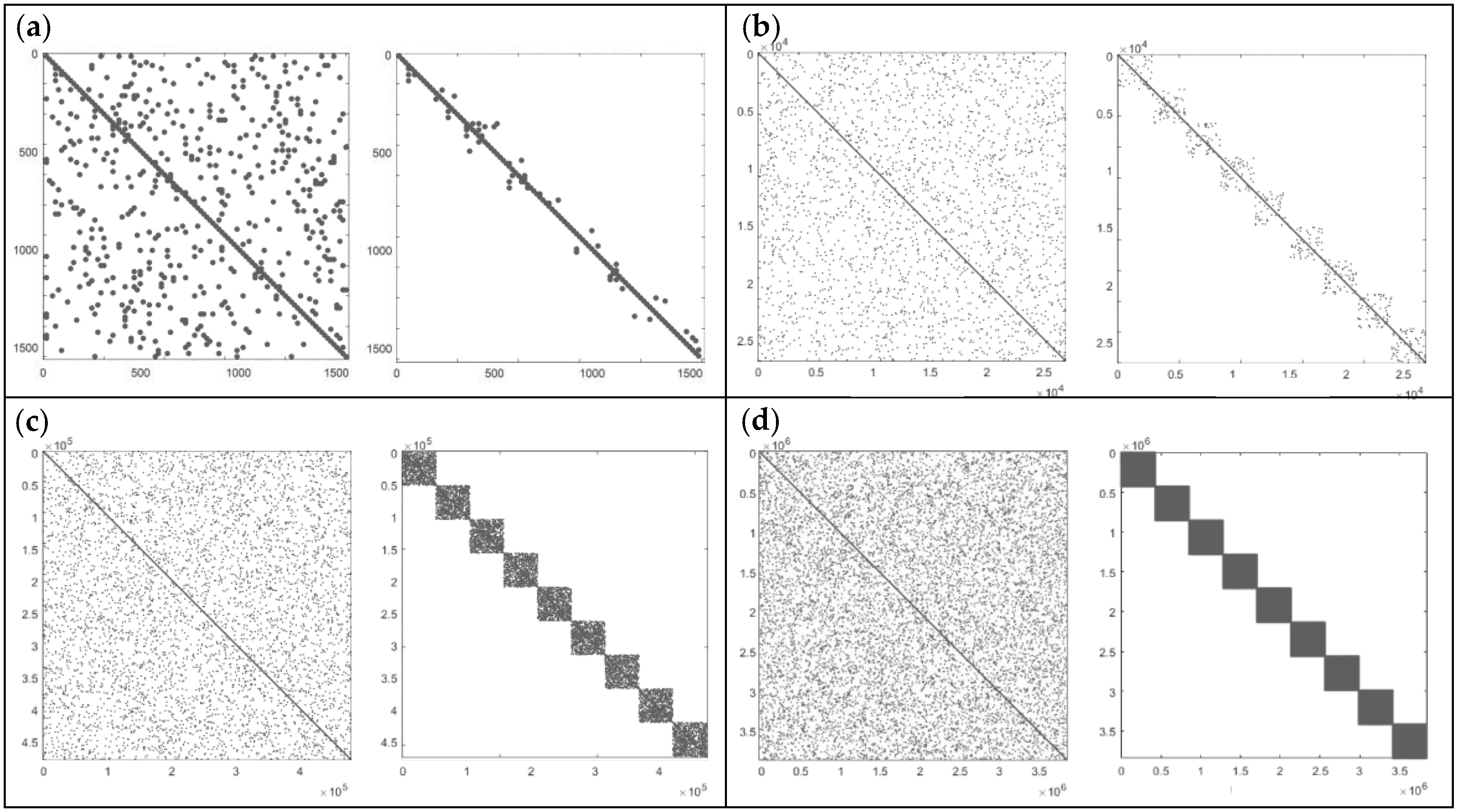
- Analysis of the distribution of matrices after preconditioning;
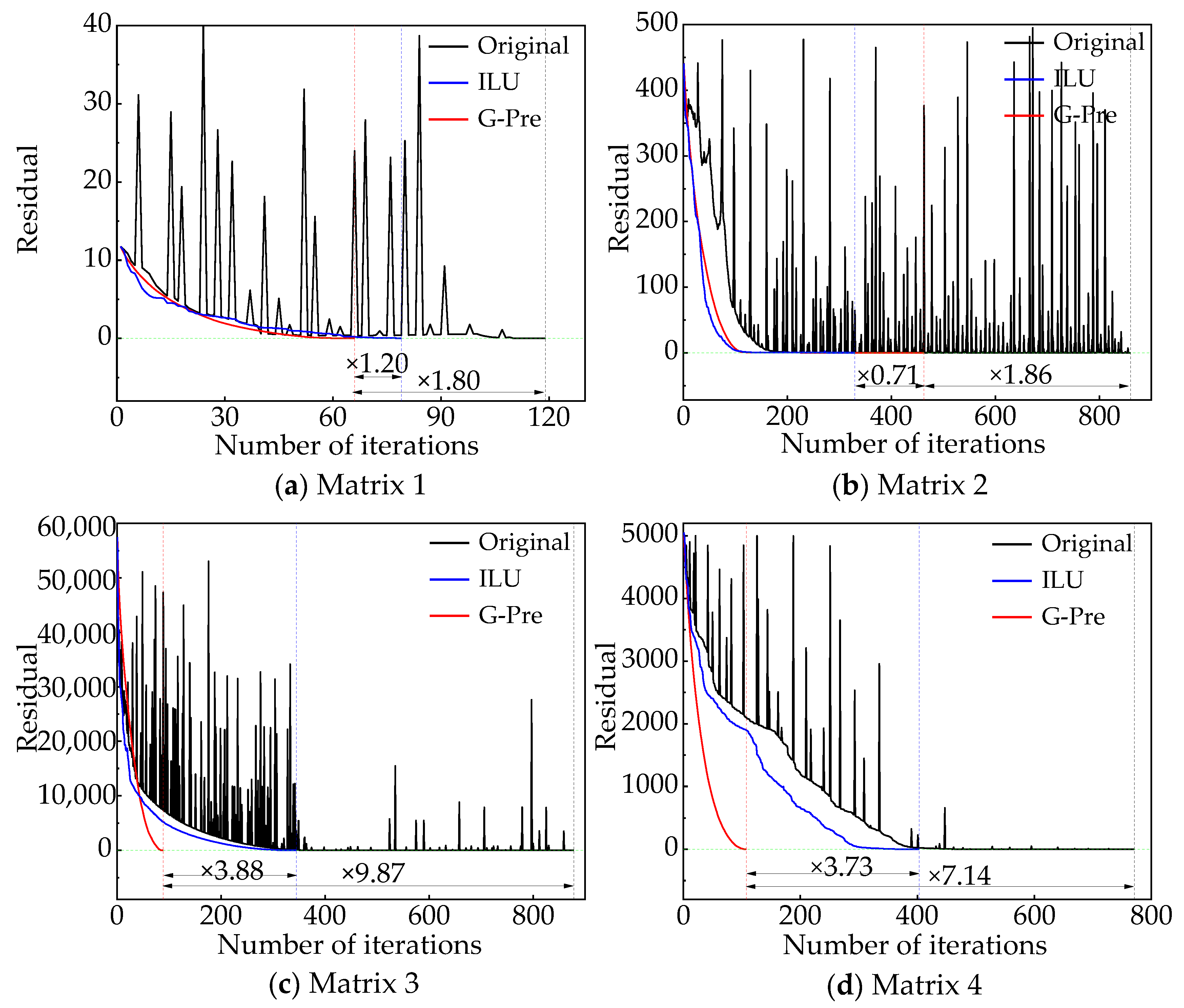
- Convergence performance during the matrix solving process;
- Accuracy of the matrix solving results.
4.3. Algorithm Performance Analysis
4.3.1. Comparison of Matrix Condition Numbers
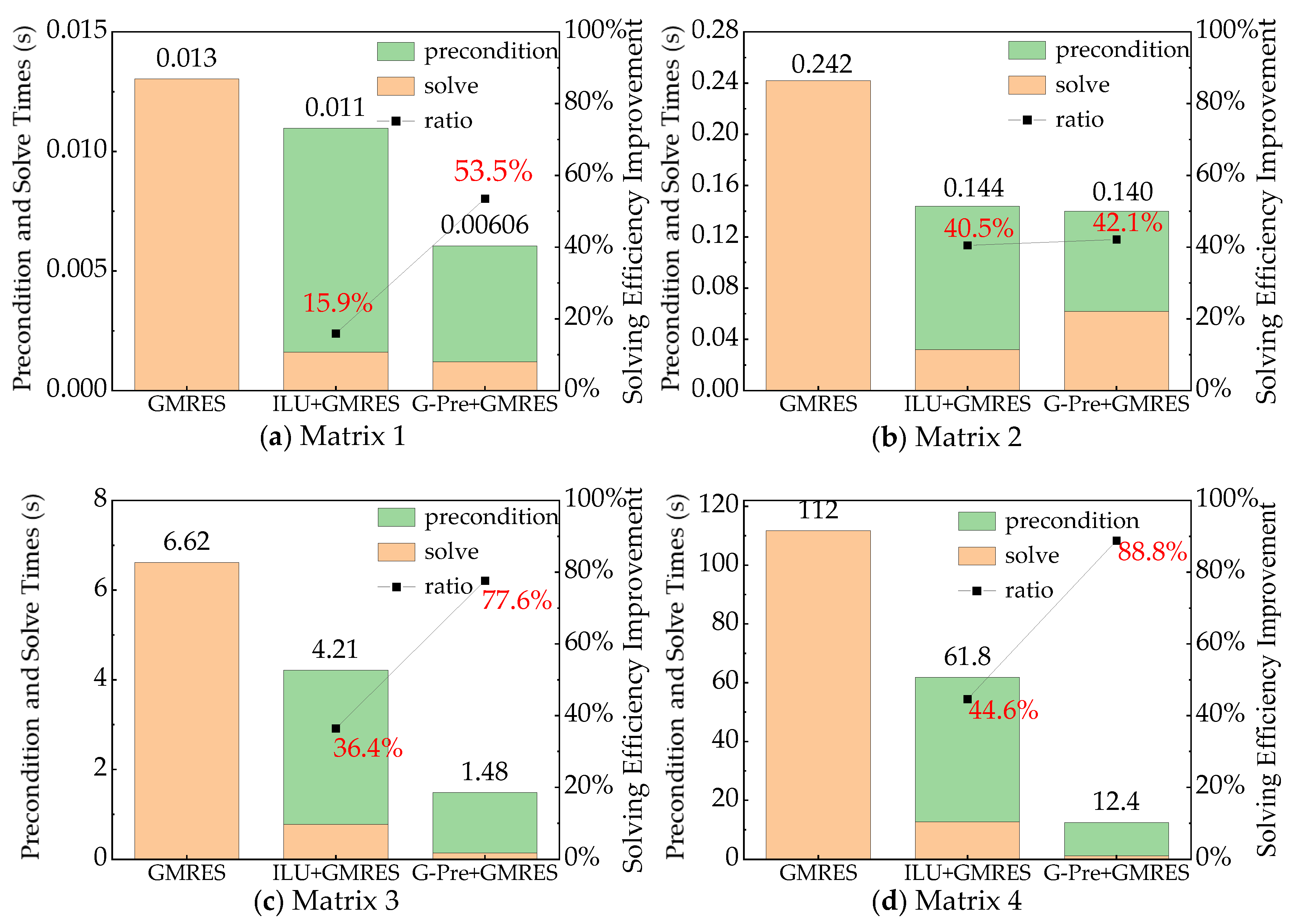
4.3.2. Comparative Analysis of Solving Time After Preconditioning Optimization
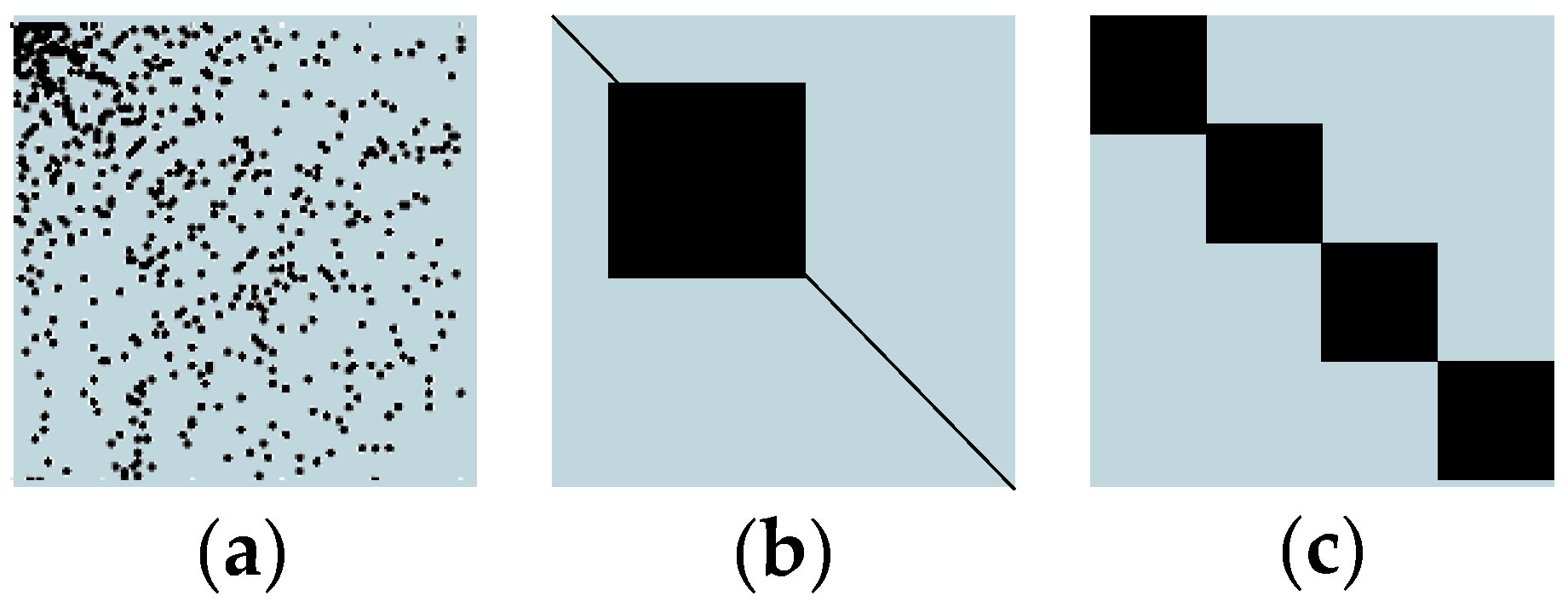
4.3.3. Comparison of Distribution Change After Matrix Preconditioning
4.3.4. Comparison of the Convergence Performance in the Matrix Solving Process
4.3.5. Comparison of the Accuracy of Matrix Solving Results
4.4. Application Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ILU | Incomplete LU |
| GMRES | Generalized minimum residual |
| SIMD | Single instruction–multiple data |
| CVD | Chemical vapor deposition |
| MEMSs | Microelectromechanical systems |
| FEM | Finite element method |
| FEA | Finite element analysis |
| MOSFETs | Metal-oxide-semiconductor field-effect transistors |
References
- Tan, X.; Chen, T. A Mixed Finite Element Approach for A Variational-Hemivariational Inequality of Incompressible Bingham Fluids. J. Sci. Comput. 2025, 103, 36. [Google Scholar] [CrossRef]
- Caucao, S.; Gatica, G.N.; Gatica, L.F. A posteriori error analysis of a mixed finite element method for the stationary convective Brinkman–Forchheimer problem. Appl. Numer. Math. 2025, 211, 158–178. [Google Scholar] [CrossRef]
- Rahman, H.A.; Ghani, J.A.; Rasani, M.R.M.; Mahmood, W.M.F.W.; Yaaqob, S.; Abd Aziz, M.S. Application of Finite Element Analysis and Computational Fluid Dynamics in Machining AISI 4340 Steel. Tribol. Int. 2025, 207, 110616. [Google Scholar] [CrossRef]
- Deng, G.; Chen, L.; Zhu, S.; Deng, G.; Chen, L.; Zhu, S.; Yun, Z.; Fan, H.; Chen, Y.; Hou, X.; et al. Preparation and quasi-static compressive behavior of fiber-reinforced truncated conical shells. Thin-Walled Struct. 2025, 210, 113035. [Google Scholar] [CrossRef]
- Özdemir, A.M. Experimental evaluation and 3D finite element simulation of creep behaviour of SBS modified asphalt mixture. Constr. Build. Mater. 2025, 460, 139821. [Google Scholar] [CrossRef]
- Wu, D.; Xue, Z.; Ni, Z.; Li, Y.; Chen, Z.; Zhu, X.; Xu, Y.; Lu, P.; Zhang, L.; He, J. Deformation Mechanisms of Nanoporous Oxide Glasses: Indentations and Finite Element Simulation. Acta Mater. 2025, 287, 120779. [Google Scholar] [CrossRef]
- Jellicoe, M.; Yang, Y.; Stokes, W.; Simmons, M.; Yang, L.; Foster, S.; Aslam, Z.; Cohen, J.; Rashid, A.; Nelson, A.L. Continuous Flow Synthesis of Copper Oxide Nanoparticles Enabling Rapid Screening of Synthesis-Structure-Property Relationships. Small 2025, 21, 2403529. [Google Scholar] [CrossRef]
- Lu, Y.; Hong, W.; Wu, W.; Zhang, J.; Li, S.; Xu, B.; Wei, K.; Liu, S. The impact of temperature regulation measures on the thermodynamic characteristics of bee colonies based on finite element simulation. Biosyst. Eng. 2025, 250, 306–316. [Google Scholar] [CrossRef]
- Lee, J.S.; Ramos-Sebastian, A.; Yu, C.; Kim, S.H. A multi-focused electrospinning system with optimized multi-ring electrode arrays for the wasteless parallel fabrication of centimeter-scale 2D multilayer electrospun structures. Mater. Today Adv. 2025, 25, 100563. [Google Scholar] [CrossRef]
- Fialko, S. Parallel Finite Element Solver for Multi-Core Computers with Shared Memory. Comput. Math. Appl. 2021, 94, 1–14. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Cai, Y.; Wang, G.; Li, G. Fully Parallel and Pipelined Sparse Direct Solver for Large Symmetric Indefinite Finite Element Problems. Comput. Math. Appl. 2024, 175, 447–469. [Google Scholar] [CrossRef]
- Zheng, S.; Xu, R. ZjuMatrix: C++ Vector and Matrix Class Library for Finite Element Method. SoftwareX 2024, 27, 101825. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, S.; Gu, J.; Zhang, Y. Efficient Blocked Symmetric Compressed Sparse Column Method for Finite Element Analysis. Front. Mech. Eng. 2025, 20, 5. [Google Scholar] [CrossRef]
- Jang, Y.; Grigori, L.; Martin, E.; Content, C. Randomized Flexible GMRES with Deflated Restarting. Numer. Algorithms 2024, 98, 431–465. [Google Scholar] [CrossRef]
- Thomas, S.; Carson, E.; Rozložník, M.; Carr, A.; Świrydowicz, K. Iterated Gauss–Seidel GMRES. SIAM J. Sci. Comput. 2024, 46, S254–S279. [Google Scholar] [CrossRef]
- Rump, S.M.; Ogita, T. Verified Error Bounds for Matrix Decompositions. SIAM J. Matrix Anal. Appl. 2024, 45, 2155–2183. [Google Scholar] [CrossRef]
- Mejia-Domenzain, L.; Chen, J.; Lourenco, C.; Moreno-Centeno, E.; Davis, T.A. Algorithm 1050: SPEX Cholesky, LDL, and Backslash for Exactly Solving Sparse Linear Systems. ACM Trans. Math. Softw. 2025, 50, 1–29. [Google Scholar] [CrossRef]
- Dai, S.; Zhao, D.; Wang, S.; Li, K.; Jahandari, H. Three-Dimensional Magnetotelluric Modeling in A Mixed Space-Wavenumber Domain. Geophysics 2022, 87, E205–E217. [Google Scholar] [CrossRef]
- Meijerink, J.A.; Van, D.V. An Iterative Solution Method for Linear Systems of Which the Coefficient Matrix is a Symmetric M-Matrix. Math. Comput. 1977, 31, 148–162. [Google Scholar] [CrossRef]
- Cerdán, J.; Marín, J.; Mas, J. A two-level ILU preconditioner for electromagnetic applications. J. Comput. Appl. Math. 2017, 309, 371–382. [Google Scholar] [CrossRef]
- Li, W.; Chen, Z.; Ewing, R.E.; Huan, G.; Li, B. Comparison of the GMRES and ORTHOMIN for the black oil model in porous media. Int. J. Numer. Methods Fluids 2005, 48, 501–519. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Zhang, X.F.; Xiao, M.L.; He, Z.H. Orthogonal Block Kaczmarz Inner-Iteration Preconditioned Flexible GMRES Method for Large-Scale Linear Systems. Appl. Math. Lett. 2025, 166, 109529. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, S.; Zhao, X.; Tian, M.; Lin, Z.; Zhang, Y. A Parallel Direct Finite Element Solver Empowered by Machine Learning for Solving Large-Scale Electromagnetic Problems. IEEE Trans. Antennas Propag. 2025, 73, 2690–2695. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J. Solving Graph Laplacians via Multilevel Sparsifiers. SIAM J. Sci. Comput. 2024, 46, S378–S400. [Google Scholar] [CrossRef]
- Bioli, I.; Kressner, D.; Robol, L. Preconditioned Low-Rank Riemannian Optimization for Symmetric Positive Definite Linear Matrix Equations. SIAM J. Sci. Comput. 2025, 47, A1091–A1116. [Google Scholar] [CrossRef]
- Luo, Z.; Zhong, Y.; Wu, F. A review of preprocessing techniques in the solution of sparse systems of linear equations. Comput. Eng. Sci. 2010, 32, 89–93. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; SIAM: Philadelphia, PA, USA, 2003; pp. 326–330. [Google Scholar]
- Benson, M.W.; Paul, O.; Frederickson. Iterative Solution of Large Sparse Linear Systems Arising in Certain Multidimensional Approximation Problems. Util. Math. 1982, 22, 127–140. [Google Scholar]
- Wang, Z.D.; Huang, T.Z. Comparison Results Between Jacobi and Other Iterative Methods. J. Comput. Appl. Math. 2004, 169, 45–51. [Google Scholar] [CrossRef]
- Lynn, M.S. On the Round-Off Error in the Method of Successive Over Relaxation. Math. Comput. 1964, 18, 36–49. [Google Scholar] [CrossRef]
- Xu, T.; Li, R.P.; Osei, K.D. A two-level GPU-accelerated incomplete LU preconditioner for general sparse linear systems. Int. J. High Perform. Comput. Appl. 2025, 39, 10943420251319334. [Google Scholar] [CrossRef]
- Van Der Vorst, H.A. Iterative Krylov Methods for Large Linear Systems; Cambridge University Press: Cambridge, UK, 2003; pp. 183–185. [Google Scholar]
- Saad, Y. ILUT: A dual threshold incomplete LU factorization. Numer. Linear Algebra Appl. 1994, 1, 387–402. [Google Scholar] [CrossRef]
- Li, N.; Saad, Y.; Chow, E. Crout versions of ILU for general sparse matrices. SIAM J. Sci. Comput. 2003, 25, 716–728. [Google Scholar] [CrossRef]
- Suzuki, K.; Fukaya, T.; Iwashita, T. A novel ILU preconditioning method with a block structure suitable for SIMD vectorization. J. Comput. Appl. Math. 2023, 419, 114687. [Google Scholar] [CrossRef]
- Osei-Kuffuor, D.; Li, R.; Saad, Y. Matrix reordering using multilevel graph coarsening for ILU preconditioning. SIAM J. Sci. Comput. 2015, 37, A391–A419. [Google Scholar] [CrossRef]
- Zheng, Q.; Xi, Y.; Saad, Y. Multicolor low-rank preconditioner for general sparse linear systems. Numer. Linear Algebra Appl. 2020, 27, e2316. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Q.; Wang, Z.; Cheng, X. A review of power battery cooling technologies. Renew. Sustain. Energy Rev. 2025, 213, 115494. [Google Scholar] [CrossRef]
- Qu, Z.; Xie, Y.; Zhao, T.; Xu, W.; He, Y.; Xu, Y.; Sun, H.; You, T.; Han, G.; Hao, Y.; et al. Extremely Low Thermal Resistance of β-Ga2O3 MOSFETs by Co-integrated Design of Substrate Engineering and Device Packaging. ACS Appl. Mater. Interfaces. 2024, 16, 57816–57823. [Google Scholar] [CrossRef]
- Lin, Y.; Cao, L.; Tan, Z.; Tan, W. Impact of Dufour and Soret effects on heat and mass transfer of Marangoni flow in the boundary layer over a rotating disk. Int. Commun. Heat Mass Transf. 2024, 152, 107287. [Google Scholar] [CrossRef]
- Ma, C.W.; Yu, S.H.; Fang, J.K.; Yang, P.F.; Chang, H.C. The physical improvement of copper deposition uniformity with the simulation models. J. Electroanal. Chem. 2023, 948, 117790. [Google Scholar] [CrossRef]
- Majeed, A.H.; Mahmood, R.; Liu, D. Finite element simulations of double diffusion in a staggered cavity filled with a power-law fluid. Phys. Fluids. 2024, 36, 3. [Google Scholar] [CrossRef]
- Yu, B.; Li, Y.; Liu, J. A Positivity-Preserving and Robust Fast Solver for Time Fractional Convection-Diffusion Problems. J. Sci. Comput. 2024, 98, 59. [Google Scholar] [CrossRef]
- Feron, J.; Latteur, P.; Pacheco de Almeida, J. Static Modal Analysis: A Review of Static Structural Analysis Methods Through a New Modal Paradigm. Arch. Comput. Methods Eng. 2024, 31, 3409–3440. [Google Scholar] [CrossRef]
- Oliker, L.; Li, X.; Husbands, P.; Biswas, R. Effects of Ordering Strategies and Programming Paradigms on Sparse Matrix Computations. Siam Rev. 2002, 44, 373–393. [Google Scholar] [CrossRef]
- Edalatpour, V.; Hezari, D.; Salkuyeh, D.K. A Generalization of the Gauss–Seidel Iteration Method for Solving Absolute Value Equations. Appl. Math. Comput. 2017, 293, 156–167. [Google Scholar] [CrossRef]
- De, S.B.; De, M.B. The QR Decomposition and the Singular Value Decomposition in the Symmetrized Max-Plus Algebra Revisited. Siam Rev. 2002, 44, 417–454. [Google Scholar]
- Chen, Q.X.; Huang, G.X.; Zhang, M.Y. Preconditioned BiCGSTAB and BiCRSTAB methods for solving the Sylvester tensor equation. Appl. Math. Comput. 2024, 466, 128469. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Li, X. Efficient Solution and Parallel Computing of Sparse Systems of Linear Equations; Hunan Science and Technology Press: Changsha, China, 2004. [Google Scholar]
- D’Azevedo, E.F.; Forsyth, P.A.; Tang, W.-P. Towards a cost effective ILU preconditioner with high level fill. BIT Numer. Math. 1992, 32, 442–463. [Google Scholar] [CrossRef]
- D’Azevedo, E.F.; Forsyth, P.A.; Tang, W.-P. Ordering methods for preconditioned conjugate gradient methods applied to unstructured grid problems. SIAM J. Matrix Anal. Appl. 1992, 13, 944–961. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. Parallel multilevel k-way partitioning scheme for irregular graphs. In Proceedings of the 1996 ACM/IEEE Conference on Supercomputing, Pittsburgh, PA, USA, 1 January 1996; IEEE: Washington, DC, USA; ACM: New York, NY, USA, 1996; p. 35-es. [Google Scholar]
- Grama, A. An Introduction to Parallel Computing: Design and Analysis of Algorithms, 2/e; Pearson Education India: Delhi, India, 2008; pp. 125–133. [Google Scholar]
- Karypis, G.; Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1998, 20, 359–392. [Google Scholar] [CrossRef]
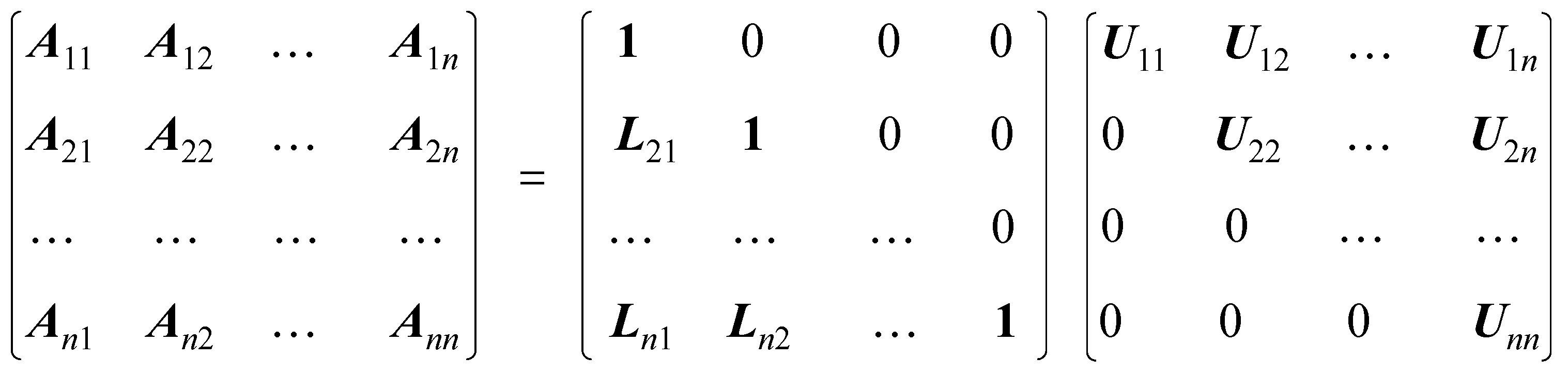



| No. | Matrix Dimension | Non-Zero Elements |
|---|---|---|
| 1 | 1565 | 78,425 |
| 2 | 26,742 | 1,362,615 |
| 3 | 475,750 | 24,262,002 |
| 4 | 3,843,405 | 196,012,424 |
| Matrix | Original | ILU | G-Pre |
|---|---|---|---|
| Matrix 1 | 1.2297 × 108 | 7.8489 × 105 | 6.5499 × 102 |
| Matrix 2 | 2.5738 × 1029 | 1.3881 × 1021 | 9.8851 × 104 |
| Matrix 3 | 4.6577 × 1043 | 3.5248 × 1032 | 1.3415 × 1015 |
| Model | Model File Size | Nodes | Matrix Dimension | Non-Zero Elements | Matrix File Size |
|---|---|---|---|---|---|
| Model 1 | 6 KB | 60 | 180 | 6298 | 190 KB |
| Model 2 | 965 KB | 10,863 | 32,589 | 1,996,613 | 67.4 MB |
| Model 3 | 20 MB | 463,874 | 532,146 | 38,501,924 | 1.34 GB |
| Model 4 | 205 MB | 3,648,656 | 4,824,972 | 371,365,956 | 13.6 GB |
| Model | Original | ILU | G-Pre |
|---|---|---|---|
| Model 1 | 0.0692 | 0.0227 | 0.0396 |
| Model 2 | 0.327 | 0.242 | 0.155 |
| Model 3 | 15.2 | 4.56 | 1.45 |
| Model 4 | 64.8 | 49.6 | 28.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Li, J.; Li, L.; Liang, K.; Wu, G.; Shen, W. G-Pre: A Graph-Theory-Based Matrix Preconditioning Algorithm for Finite Element Simulation Solutions. Appl. Sci. 2025, 15, 5130. https://doi.org/10.3390/app15095130
Chen M, Li J, Li L, Liang K, Wu G, Shen W. G-Pre: A Graph-Theory-Based Matrix Preconditioning Algorithm for Finite Element Simulation Solutions. Applied Sciences. 2025; 15(9):5130. https://doi.org/10.3390/app15095130
Chicago/Turabian StyleChen, Min, Jingyan Li, Lijie Li, Kang Liang, Gai Wu, and Wei Shen. 2025. "G-Pre: A Graph-Theory-Based Matrix Preconditioning Algorithm for Finite Element Simulation Solutions" Applied Sciences 15, no. 9: 5130. https://doi.org/10.3390/app15095130
APA StyleChen, M., Li, J., Li, L., Liang, K., Wu, G., & Shen, W. (2025). G-Pre: A Graph-Theory-Based Matrix Preconditioning Algorithm for Finite Element Simulation Solutions. Applied Sciences, 15(9), 5130. https://doi.org/10.3390/app15095130





