Soft Fuzzy Reinforcement Neural Network Proportional–Derivative Controller

Abstract

Controlling systems with highly nonlinear or uncertain dynamics present significant challenges, particularly when using conventional Proportional–Integral–Derivative (PID) controllers, as they can be difficult to tune. While PID controllers can be adapted for such systems using advanced tuning methods, they often struggle with lag and instability due to their integral action. In contrast, fuzzy Proportional–Derivative (PD) controllers offer a more responsive alternative by eliminating reliance on error accumulation and enabling rule-based adaptability. However, their industrial adoption remains limited due to challenges in manual rule design. To overcome this limitation, Fuzzy Neural Networks (FNNs) integrate neural networks with fuzzy logic, enabling self-learning and reducing reliance on manually crafted rules. However, most fuzzy neural network PD (FNNPD) controllers rely on mean square error (MSE)-based training, which can be inefficient and unstable in complex, dynamic systems. To address these challenges, this paper presents a Soft Fuzzy Reinforcement Neural Network PD (SFPD) controller, integrating the Soft Actor–Critic (SAC) framework into FNNPD control to improve training speed and stability. While the actor–critic framework is widely used in reinforcement learning, its application to FNNPD controllers has been unexplored. The proposed controller leverages reinforcement learning to autonomously adjust parameters, eliminating the need for manual tuning. Additionally, entropy-regularized stochastic exploration enhances learning efficiency. It can operate with or without expert knowledge, leveraging neural network-driven adaptation. While expert input is not required, its inclusion accelerates convergence and improves initial performance. Experimental results show that the proposed SFPD controller achieves fast learning, superior control performance, and strong robustness to noise, making it effective for complex control tasks.

1. Introduction

Proportional–Integral–Derivative (PID) controllers [1] are widely used in the field of control systems. However, their control performance is suboptimal for strongly nonlinear, high-order, and hysteresis systems [2]. Especially in the presence of noise, traditional control systems can face challenges in maintaining optimal performance. To address these issues, various advanced technologies have emerged. Among these, fuzzy PID controllers that integrate fuzzy logic have gained widespread applications (e.g., robotic trajectory tracking [3], brushless DC motors [4]) since their emergence [5,6]. These model-free controllers provide improved handling of nonlinearities, enhanced robustness, and greater flexibility compared to traditional PID controllers [7]. However, fuzzy PID controllers rely on fixed parameters derived from human expertise, making them less adaptable to system variations and highly dependent on prior knowledge [8].

While the integral term in PID controllers helps reduce steady-state errors, it also introduces lag and increases computational complexity. Unlike PID controllers, which accumulate past errors through integral action, Proportional–Derivative (PD) controllers [9] focus solely on the current error and its rate of change, allowing for quicker adaptation to dynamic system variations. However, their fixed parameters still limit adaptability in highly nonlinear or uncertain environments. Fuzzy PD controllers present an alternative to traditional PD controllers, providing greater flexibility while preserving the benefits of PD control. Their simpler fuzzy rule design [10] allows for easier implementation, while their rule-based adaptability enables them to deliver performance comparable to fuzzy PID controllers [11]. By leveraging fuzzy logic, they improve responsiveness and adaptability, making them well suited for applications that require fast reaction times without the drawbacks of integral action [12,13].

However, they still rely on rule-based methods, which can become inadequate in highly complex or uncertain environments. To enhance performance in such challenging scenarios, reinforcement learning (RL) algorithms, such as Soft Actor–Critic (SAC) [14], offer a model-free approach that learns optimal control policies directly through interaction with the environment. Unlike traditional model-based control methods, RL algorithms like SAC do not require an explicit system model, making it more adaptable to complex and dynamic environments. SAC, in particular, employs entropy maximization to promote exploration and prevent premature convergence, effectively balancing exploration and exploitation, which makes it a powerful tool for continuous control tasks. It also aims to maximize the cumulative reward (CR) while maintaining this balance. This differentiates it from classical control approaches, which typically rely on predefined control laws and system models. By leveraging an actor–critic framework and experience replay, SAC enhances sample efficiency and stability, making it well suited for complex, high-dimensional control problems.

Several studies have explored the integration of Soft Actor–Critic (SAC) with PID control, leveraging the replay buffer to enhance sample efficiency and improve system performance. He et al. [15] applied SAC-based deep reinforcement learning for online PID tuning in hydraulic servo control systems, showcasing its effectiveness in real-time applications by improving the system’s responsiveness and stability. Yu et al. [16] proposed a self-adaptive SAC-PID control approach for mobile robots, emphasizing its capability to dynamically adjust to unpredictable environments. Song et al. [17] investigated SAC-based PID parameter tuning for unmanned surface vehicle (USV) path following, optimizing control performance through automated and real-time tuning. While these approaches take advantage of SAC’s model-free adaptability, they must also address a major challenge in reinforcement learning (RL), experience replay, which stores and reuses past transitions to improve sample efficiency [18]. More specifically, in PID controllers, the integral term introduces a dependency on historical errors, which conflicts with the Markov property and can lead to unstable learning dynamics when combined with experience replay. While training with PID controllers and experience replay is not inherently incapable of convergence, it tends to exhibit instability, with successful convergence occurring inconsistently across multiple training attempts [19]. In contrast, fuzzy PD controllers do not suffer from this issue, as they rely solely on the current error and its derivative.

Existing studies on auto-tuning fuzzy PD controllers using neural networks and reinforcement learning present several limitations. Some approaches utilize Q-learning to adjust fuzzy PD parameters [20], but without a replay buffer, the learning process is inefficient and less effective compared to SAC. Additionally, certain methods employ neural networks as a compensation mechanism for PD controllers [21,22], requiring a predefined PD controller while still lacking a replay buffer, which limits sample efficiency. Other studies explored the use of neural networks to tune fuzzy rule parameters through supervised learning, necessitating pre-collected training data [23]. However, obtaining high-quality training data can be challenging, as it often requires extensive expert knowledge, precise system modeling, or costly real-world experiments. Additionally, the collected data may not fully represent the system’s operating conditions, leading to poor generalization when applied to new scenarios. Reddy K. H. [24] combined neural networks with fuzzy PD controllers to control the speed of BLDC motors, using the mean square error (MSE) for training without a critic network or experience replay, leading to suboptimal learning. Similarly, McCutcheon L. [25] applied model-based reinforcement learning with a State-Buffer State Prediction (SBSP) framework to auto-tune PD parameters for systems with large time delays. However, their approach employed a fully connected neural network within RL to tune the parameters of a fuzzy PD controller, but this is less effective than using a fuzzy neural network (FNN) [26], which is inherently better at capturing nonlinear relationships and adapting to system variations. While fuzzy logic itself can incorporate expert knowledge, relying solely on a standard neural network for parameter tuning limits its effectiveness, leading to poor initial performance and slow convergence. Moreover, FNNs offer a degree of interpretability by explicitly representing fuzzy rules and membership functions, making it easier to understand and analyze the decision-making process compared to standard neural networks [27]. These limitations highlight the need for a more effective approach that integrates fuzzy logic, neural networks, and reinforcement learning within a structured framework, ensuring better adaptability, interpretability, and sample efficiency for fuzzy PD controller optimization.

To the best of our knowledge, no studies have leveraged the SAC framework for fuzzy neural network PD controllers. This paper explores this novel application, marking the first known attempt to integrate SAC with fuzzy neural network PD controllers. We propose employing a fuzzy neural network to automatically adjust the PD controller’s parameters. Through reinforcement learning, the fuzzy neural network’s parameters are learned and adapted autonomously. By leveraging an actor–critic architecture, the parameter adjustments of the fuzzy neural network are guided by the critic network. The backpropagation algorithm is utilized to fine-tune the fuzzy neural network parameters, enabling the PD controller to achieve the desired performance. To enhance exploration efficiency, a stochastic output is employed during training.

In summary, this paper makes the following contributions:

• A model-free SAC framework for fuzzy neural network PD controllers that uses reinforcement learning to automatically adjust fuzzy rules for optimal control.
• Incorporation of expert knowledge: the partial interpretability of FNNs allows expert knowledge to be included during initialization, enabling faster convergence early in training.
• Enhanced training efficiency: the controller uses stochastic optimization and integrates entropy during training, improving exploration efficiency and significantly reducing training time.
• Superior performance: experimental results show that the SFPD controller achieves faster convergence and superior control performance compared to both SAC and traditional PD controllers.

2. Preliminaries

2.1. Reinforcement Learning (RL)

RL is a model-free approach where the controller continuously interacts with the environment to receive feedback and iteratively learns control strategies [28]. The goal of RL is to maximize the cumulative reward (CR). Based on the current state, the RL agent selects an action, which the environment then responds to by providing a reward and transitioning to the next state. Through this cyclic training process, the agent learns to determine the optimal actions that yield the highest CR given the current state.

As shown in Figure 1, the agent and the environment together constitute the RL framework. The agent is determined by the policy, $\pi$, which is a mapping from the state space S to the action space A ($\pi :S\to A$). At each time step, the policy selects an action ($a_t$) based on the current state ($s_t$), which is then applied to the environment to obtain a reward ($r_t$). The goal of RL is to find an optimal policy, denoted as ${\pi }^{*}$, that maximizes the cumulative reward (CR) over an epoch.

However, relying solely on the current reward r to train the policy makes it challenging to achieve the maximum CR because we need to consider long-term rewards, not just the immediate reward ($r_t$). This is where the critic network comes into play, evaluating the quality of the current state–action pair. This forms the basis of the actor–critic algorithm. Among these, the Soft Actor–Critic (SAC) [29] algorithm stands out due to its efficient exploration–exploitation trade-off, off-policy learning, and superior stability in continuous action spaces.

The SAC algorithm uses an experience replay buffer to store tuples of (state, action, reward, next state). It resamples batches of these tuples from the buffer and trains the neural network using stochastic gradient descent (SGD) [30]. Additionally, the SAC algorithm incorporates entropy into the exploration process to balance exploration and exploitation, which introduces stochasticity into the decision-making process. Consequently, the cost function of the policy in SAC is:

$$J\left(\pi \right)=\mathbb{E}\left[R\right(\tau )+\alpha H(\pi \left)\right]$$

(1)

where

• $J\left(\pi \right)$: the objective function of the policy network.
• $\mathbb{E}\left[R\right(\tau \left)\right]$: the expected return of a trajectory.
• $\alpha$: a hyperparameter used to balance the weights of return and entropy.
• $H\left(\pi \right)$: the entropy of the policy network distribution.

SAC is an actor–critic architecture with a critic network that consists of a state–action value (Q-value) network and a state value (V-value) network. The objective functions for these networks involve maximizing the CR and entropy, leading to what is known as the soft Q-value function and the soft V-value function. The objective functions for these networks involve maximizing the CR and entropy, leading to what is known as the soft Q-value function and the soft V-value function.

$$Q_{\theta }^{\pi }(s,a)={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)+\alpha \sum _{t=1}^{\infty }{\gamma }^{t}H\left(\pi (·|s_t)\right)|s_0=s,a_0=a\right]$$

(2)

$$V_{\psi }\left(s_t\right)={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}\left[Q_{\theta }^{\pi }(s,a)-\alpha log{\pi }_{\phi }\left(a_t\right|s_t)\right]$$

(3)

where $\gamma$ is a hyperparameter known as the discount factor, and $\alpha$ is the temperature factor. Based on the Bellman equation and (1)–(3), the loss functions for the policy, Q-value, and V-value can be derived as follows:

$$J_{\pi }\left(\phi \right)={\mathbb{E}}_{s_t\sim D,ϵ\sim N}\left[{\displaystyle \frac{1}{2}}{\left(\alpha log{\pi }_{\phi }(f_{\phi }({ϵ}_t,s_t)\mid s_t)-Q_{\theta }(s_t,f_{\phi }({ϵ}_t,s_t))\right)}^2\right]$$

(4)

$$J_Q\left(\theta \right)={\mathbb{E}}_{(s_t,a_t,s_{t+1})\sim D,a_t\sim {\rho }_{\pi }}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\theta }(s_t,a_t)-\left(r+\gamma Q_{\theta }(s_{t+1},a_{t+1})\right)\right)}^2\right]$$

(5)

$$J_V\left(\psi \right)={\mathbb{E}}_{(s_t,a_t,s_{t+1})\sim D,a_t\sim {\rho }_{\pi }}\left[{\displaystyle \frac{1}{2}}{\left(V_{\psi }\left(s_t\right)-{\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}\left[Q_{\theta }^{\pi }(s_{t+1},a_{t+1})-\alpha log{\pi }_{\phi }\left(a_t\right|s_t)\right]\right)}^2\right]$$

(6)

In (4), $f_{\phi }({ϵ}_t,s_t)$ employs the reparameterization trick [31] as shown in (7). This technique ensures the differentiability of the policy function while expanding the exploration range.

$$f_{\phi }({ϵ}_t,s_t)=f_{\phi }^{\mu }\left(s_t\right)+ϵf_{\phi }^{\sigma }\left(s_t\right)$$

(7)

where

• $f_{\phi }^{\mu }\left(s_t\right)$: the output of the policy network, which serves as the mean of a Gaussian distribution.
• $f_{\phi }^{\sigma }\left(s_t\right)$: the standard deviation of the Gaussian distribution.
• $ϵ$: a sample from the standard normal Gaussian distribution.

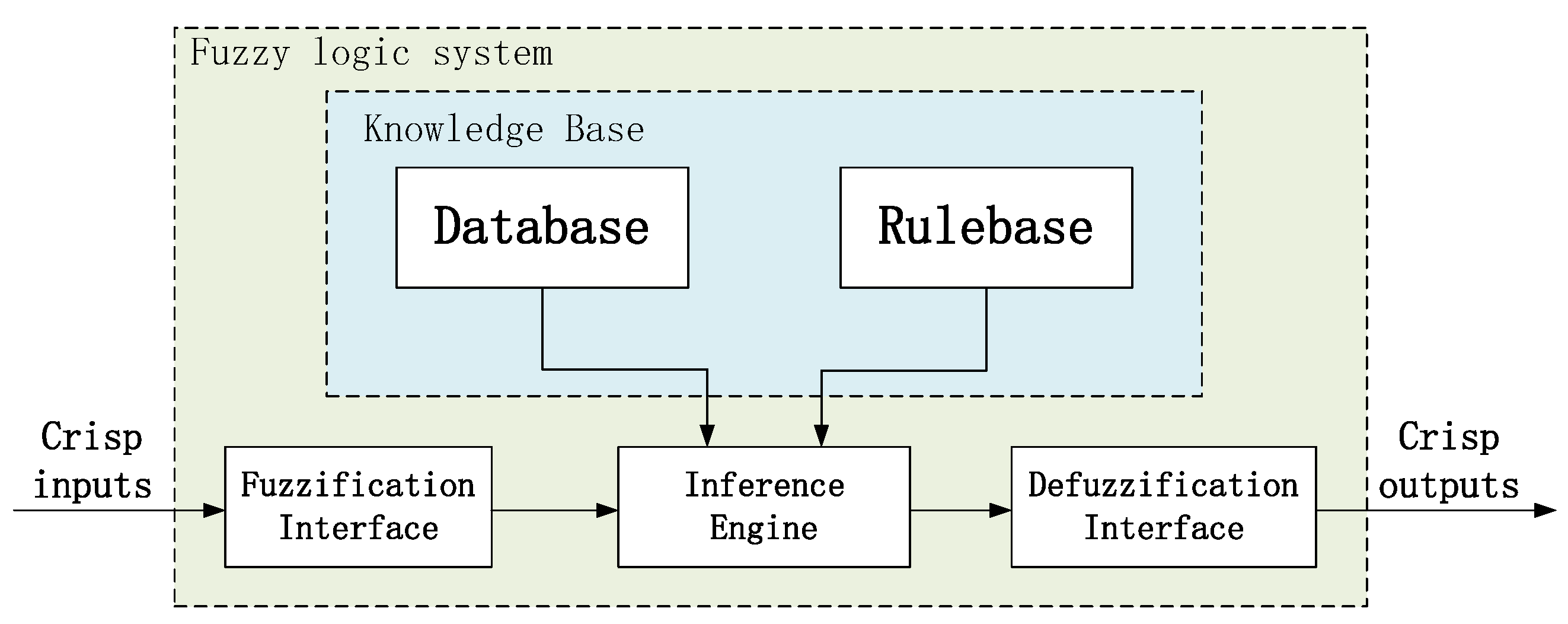
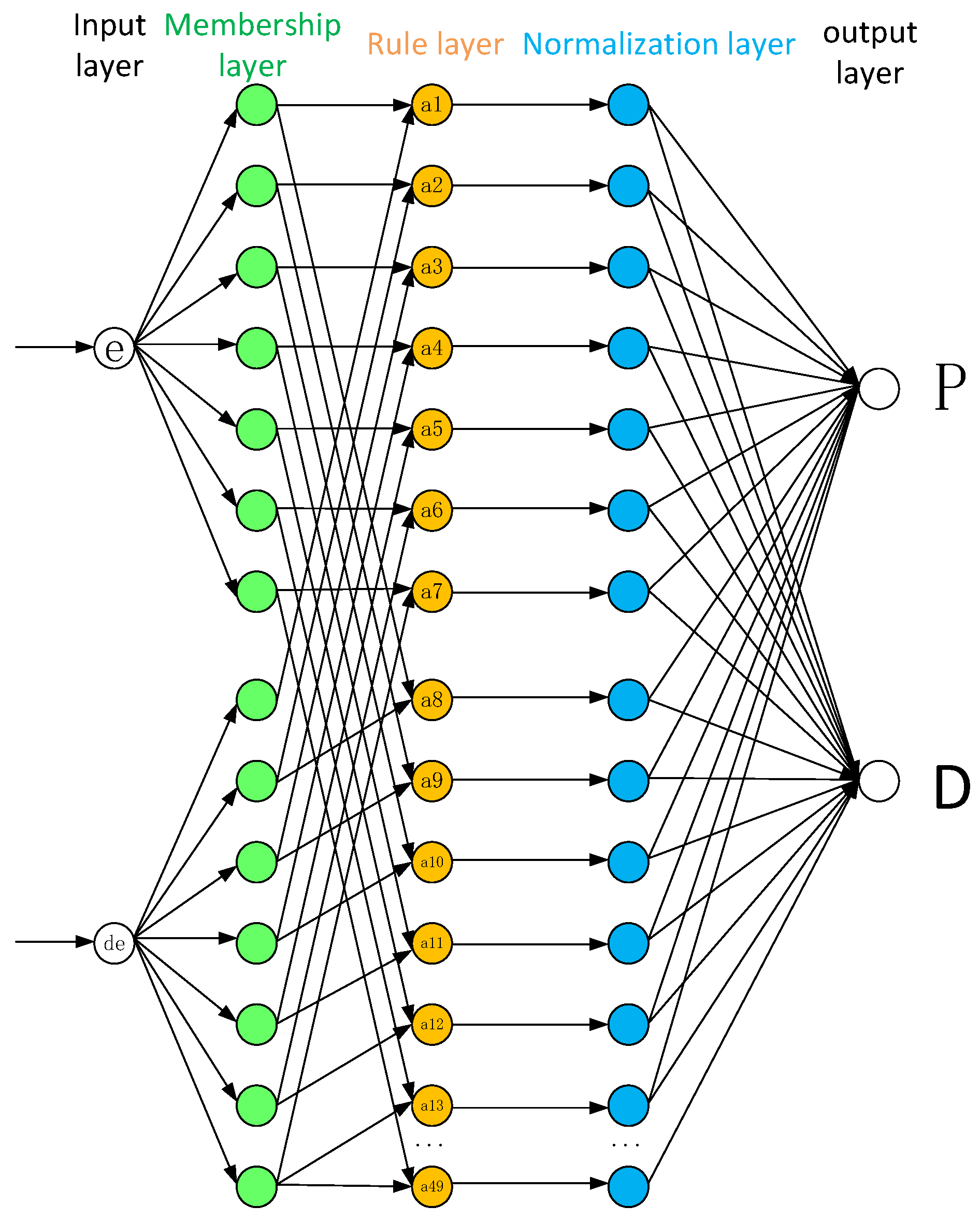
2.2. Fuzzy Neural Network PD (FNNPD) Controller

A fuzzy logic system (FLS) [32] is a control system that utilizes expert knowledge and fuzzy logic. The fuzzy control system consists of fuzzification interface, inference engine (including database and rule base), and defuzzification interface, as shown in Figure 2. With fuzzy rules designed based on expert experience, an FLS can effectively identify and control systems [33]. However, the quality of control heavily relies on the expert-designed fuzzy rules.

A fuzzy neural network (FNN) [34] combines the learning capabilities of neural networks with the advantages of an FLS. Its structure is depicted in Figure 3, where the FNN outputs the coefficients for a PD controller, using the system error e and the derivative error de as inputs. With seven membership functions per input variable, two input variables generate a total of 49 (7 × 7) fuzzy rules.

As shown in Figure 3, FNNs have basically five layers: the input layer, membership layer, rule layer, normalization layer, and output layer [35]. The membership layer transfers the input signal to fuzzy input sets according to fuzzy memberships. In the rule layer, each neuron represents a fuzzy rule, which transfers the fuzzy input sets to fuzzy output sets. The normalization layer conducts normalization operations. Finally, the output layer transfers the fuzzy output set into crisp output.

The traditional PD controller [36] is a classical controller widely used in industry due to its simple structure and effective control performance. The formula for the PD controller is as follows:

$$u=K_p\times e+K_d\times \dot{e}$$

(8)

where $K_p$ and $K_d$ are PD parameters, e represents the system error, while $\dot{e}$ represents the rate of error change.

However, its effectiveness diminishes in nonlinear systems, and adjusting PD parameters can be challenging. Combining fuzzy neural networks with the PD controller forms the fuzzy neural network PD controller (FNNPD) [20], which exhibits significant advantages. By utilizing a fuzzy neural network, the PD parameters can be automatically adjusted based on the system’s current state. It not only has learning capabilities and utilizes expert knowledge but also retains the robustness of the PD controller.

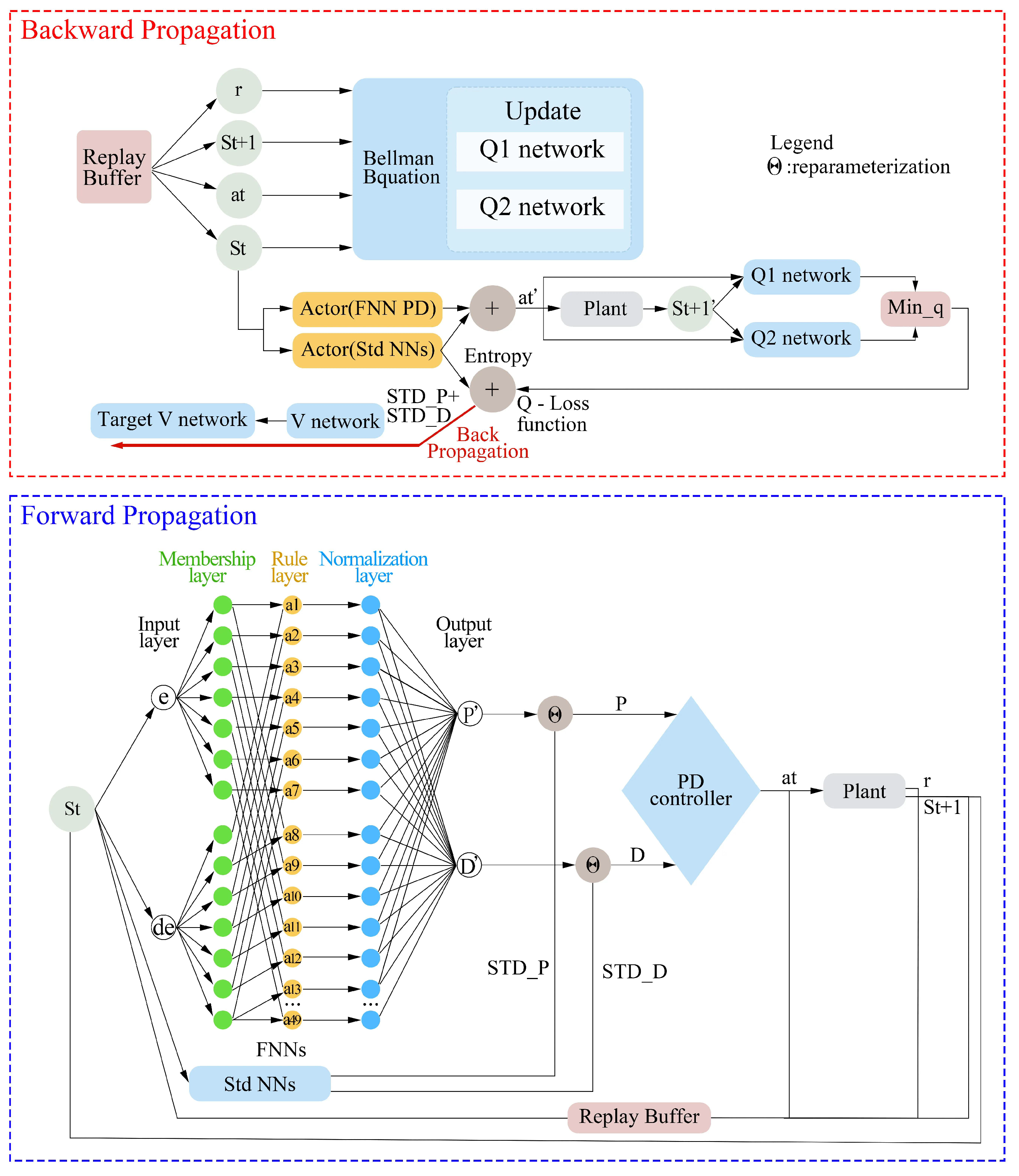
3. Proposed Soft Fuzzy Reinforcement Neural Network PD (SFPD) Controller

The proposed SFPD method in this paper is built on the SAC framework, with the policy network employing an FNNPD controller. Leveraging SAC enhances learning speed and stability. While FNNs enable the integration of expert knowledge through fuzzy rules, the proposed method starts with an imperfect fuzzy rule as a foundation and refines it through learning, demonstrating the controller’s ability to effectively enhance expert knowledge. The system diagram is shown in Figure 4.

3.1. Forward Propagation

The lower part of Figure 4 depicts the interaction between SFPD and the environment, representing the forward propagation. Based on the current state $S_t$, FNNs provide the PD control parameters. Each PD parameter, along with the standard deviation provided by standard neural networks (Std NNs), is then transformed into the final PD controller using the reparameterization technique. The PD controller subsequently calculates the current action a, which is applied to the environment (plant). The plant provides a reward, and the process continues to the next state $S_{t+1}$. The loop keeps going until the current epoch ends. The tuple ($S_t$, a, r, $S_{t+1}$) is stored in the replay buffer for parameter updates. Inputs are processed through tanh before being passed to the neural network to enhance convergence by normalizing values, maintaining a zero-centered distribution, and improving gradient flow.

In FNNs, the first layer is the input layer, which receives the inputs x. The tanh transformation is applied before training, as a preprocessing step to normalize the inputs into the range $[-1,1]$, which facilitates stable and efficient convergence. While tanh is not part of the model architecture and does not affect gradient flow during training, this bounded and smooth transformation helps reduce the impact of outliers and brings the input data into a scale that aligns well with the model’s initialization and training dynamics, thereby improving stability and robustness.

$$x=tanh\left([e,e^{\prime }]\right)$$

(9)

The second layer is the fuzzification layer and consists of fuzzy memberships. Each neuron represents one membership. The Gaussian function is used to transform the input into the fuzzy sets, as shown below [37]:

$${\mu }_i^j=e^{-{\displaystyle \frac{{(x_i-c_{ij})}^2}{{\sigma }_{ij}^2}}}$$

(10)

where $x_i$ is the input, and $c_{ij},{\sigma }_{ij}$ represent the center and width of the distribution. The notation $i=2,j=7$ indicates that there are two crisp inputs, each associated with seven fuzzy memberships. The partial interpretability of Fuzzy Neural Networks (FNNs) enables the integration of expert knowledge during the initialization phase. By setting initial parameters such as the centers and widths of the Gaussian membership functions based on domain expertise, the model can achieve a more informed starting point. This approach leads to faster convergence early in the training process, as the network starts with parameters that are more aligned with the underlying system behavior.

The third layer is the multiplication of all the input fuzzy sets, which represents the fuzzy inference:

$${\alpha }_j={\mu }_1^{i_1}{\mu }_1^{i_2}\cdots {\mu }_1^{i_n}$$

(11)

where $n=2$ represents the fuzzy membership functions associated with this rule:

The fourth layer is the normalization layer.

$${\beta }_j={\displaystyle \frac{{\alpha }_j}{{\sum }_{j=1}^m{\alpha }_j}},j=1,2,\cdots ,m$$

(12)

where $m=ji=49$ indicates that there are 49 fuzzy rules.

The fifth layer is the defuzzification layer:

$$y_i=\sum _{j=1}^r{\omega }_{ij}{\beta }_j,j=1,2,\cdots ,m$$

(13)

where $y_i$ includes the two parameters of the PD controller, $P^{\prime }$ and $D^{\prime }$, and ${\omega }_{ij}$ indicates the connection weight. Subsequently, $P^{\prime }$ and $D^{\prime }$ are reparameterized with the outputs from the standard neural network to obtain the final outputs P and D of the PD controller:

$$P=P^{\prime }+ϵf_{\varphi }^P\left(s_t\right)$$

(14)

$$D=D^{\prime }+ϵf_{\varphi }^D\left(s_t\right)$$

(15)

where $\varphi$ denotes the parameters of the standard neural networks.

Then, the PD controller computes the action output using (8).

3.2. Backward Propagation

The upper part of Figure 4 represents the update process, specifically the backpropagation phase. Backpropagation is a key algorithm in training neural networks, where the model’s error is propagated backward through the network. During this phase, the gradients of the loss function with respect to each weight are calculated, allowing the model to update its weights to minimize the error. This iterative process helps the network learn from the data and improve its performance over time. Initially, data $(s_t,a_t,r,s_{t+1})$ of batch size are retrieved from the replay buffer to update various network parameters. For enhanced stability during training, this study employed two state–action value neural networks (QNNs), using the minimum of their outputs, $min(Q_1,Q_2)$, and incorporated a target state value network (VNNs). The QNNs were updated using the Bellman equation as shown in (5). The loss function for the VNNs is depicted in (6), where the calculation of $Q_{\theta }^{\pi }(s_{t+1},a_{t+1})$ selects the minimum output between the two QNNs, while $log{\pi }_{\varphi }\left(a_t\right|s_t)$ represents the sum of the logarithms of the parameters P and D output by the Std NNs, as shown below:

$$log{\pi }_{\varphi }\left(a_t\right|s_t)=log{\pi }_{\varphi }{f}_{\varphi }^P\left(s_t\right)+log{\pi }_{\varphi }{f}_{\varphi }^D\left(s_t\right)$$

(16)

The loss function for FNNs and the Std NNs, as shown in (4), similarly involves selecting the minimum Q value and incorporating the aforementioned logarithm.

The forward and backward propagation are summarized in Algorithm 1.

Algorithm 1 SFPD

1:  Initialize all the NNs, including $Q_1$, $Q_2$, V, FNNs, Std NNs. 2:  Initialize target VNNs, with ${\theta }_{v^{\prime }}\leftarrow {\theta }_v$ 3:  Initialize the parameters ${\omega }_{ij}$, $c_{ij}$, and ${\sigma }_{ij}$ in FNNs. 4:  Set a replay buffer R 5:  for episodes $k=1$ to E 6:        while this episode is not completed or the maximum steps >N 7:               Obtain an action $a\left(t\right)$ from the PD controller, with parameters derived from the FNNs and Std NNs based on the current state s(t), according to the forward propagation 8:               Apply action $a\left(t\right)$ to interact with the environment, obtaining the next state $s(t+1)$ and reward $r\left(t\right)$ 9:               Put the $\left(s\right(t),a(t),s(t+1),r(t\left)\right)$ into the replay buffer  Updating part: 10:               Sample N samples from the replay buffer R 11:               for all the N samples 12:                      Update two QNNs, $Q_1$ and $Q_2$ based on Bellman’s equation according to (5) 13:                      Based on the sampled states $s\left(t\right)$, calculate the action $a\left(t\right)$ from the FNNs and the log probability from Std NNs 14:                      Based on the states $s\left(t\right)$ and actions $a\left(t\right)$, calculate $Q_1$, $Q_2$, and ${\min }_q\left(\min (Q_1,Q_2)\right)$ 15:                      Update the VNNs based on the loss function as described in (6) 16:                      Update all the parameters ${\omega }_{ij}$, $c_{ij}$, and ${\sigma }_{ij}$ in FNNs according to the loss function, represented by (4) 17:                      Update all the parameters $\phi$ in Std NNs according to the loss function, represented by (4) 18:                      Update target VNNs, ${\theta }_{v^{\prime }}\leftarrow {\theta }_v$ 19:               end for 20:        end while 21:  end for

4. Results and Discussion

4.1. Experimental Setup

Our algorithm was tested on two systems: the pendulum and the Continuous Stirred Tank Reactor (CSTR). The pendulum was chosen because it is a classic nonlinear system with unstable dynamics, making it a standard benchmark for control algorithms. The CSTR was selected due to its large control input space, requiring extensive exploration, and its strong nonlinear characteristics, which pose significant control challenges. These two systems ensured our algorithm was tested in both mechanical and process control domains. The SFPD controller used in the simulations was implemented in Python 3.9. The pendulum system leveraged the gym-pendulum-v1 environment from Python’s Gym library, while the CSTR model was built using MATLAB/Simulink R2023a. The simulations were performed on a personal computer with an Intel(R) Core(TM) i7-12700H processor (2.30 GHz), 64 GB of RAM, and a 64-bit operating system. The proposed controller exhibited low memory usage (peak $<0.4\mathrm{MB}$), demonstrating its memory efficiency. While edge deployment was not the focus of this study, previous works (e.g., Prado et al. [38]) have demonstrated the feasibility of similar lightweight controllers on embedded hardware such as FPGAs.

The commonly used metrics IAE (Integral of Absolute Error) and ISE (Integral of Squared Error) were adopted to evaluate the performance of the control system [39]. These metrics help quantify the deviation between the desired output (setpoint) and the actual system response. The definitions of IAE and ISE are shown in (17).

$$\begin{array}{c}\hfill IAE=\sum _{k=0}^n\left|e\left(k\right)\right|\\ \hfill ISE=\sum _{k=0}^n{e}^2\left(k\right)\end{array}$$

(17)

where n denotes the total number of steps, and $e\left(k\right)$ represents the system error at step k.

The fuzzy neural network utilized seven fuzzy memberships [40] for each input, leading to seven means and standard deviations for both the error and the error rate, resulting in a total of 28 trainable parameters in the membership layer. The choice of seven memberships ensured a balance between accuracy and computational efficiency, providing sufficient granularity to capture nonlinear relationships while avoiding excessive complexity. Seven memberships were sufficient to capture the underlying nonlinear relationships in the data, offering adequate granularity without introducing excessive model complexity. This ensured the network could generalize well while keeping computational costs manageable. Additionally, a fully combinatorial fuzzy rule design (also known as the Rule Cartesian Product) was adopted, where each of the seven input membership functions for the two input variables was paired to form $7\times 7=49$ fuzzy rules. These rules were directly mapped to 49 corresponding weights in the defuzzification layer, enhancing the network’s generalization ability while keeping computational costs low. To assess the robustness of the method, we initialized the centers (means) of the Gaussian membership functions uniformly within their respective value ranges, while the variances were fixed at 0.5, ensuring that the initialization was adaptable across different systems.

Table 1. Parameters and hyperparameters.

Notation	Description	Case 1: Pendulum	Case 2: CSTR
P	Number of training episodes	10	50
R	Replay buffer size	20,000	20,000
B	Batch size	32	32
A	Action space	[−10, 10]	[50, 420]
-	Learning rate	0.001	0.001
-	Length of steps for testing	200	1200
-	Optimizer	Adam	Adam
-	P/D parameter range	[−100, 100]/[−20, 20]	[−5, 5]/[−2, 2]

summarizes the hyperparameter settings.

The comparison methods in this paper included SAC and traditional PD algorithms. SAC was chosen as a baseline since the proposed method built upon it, enabling a direct comparison to highlight improvements in convergence and exploration efficiency in large action spaces. The traditional PD algorithm served as a benchmark to demonstrate the benefits of dynamic PD parameter adjustment, which enhances adaptability and robustness while eliminating the need for manual tuning [15].

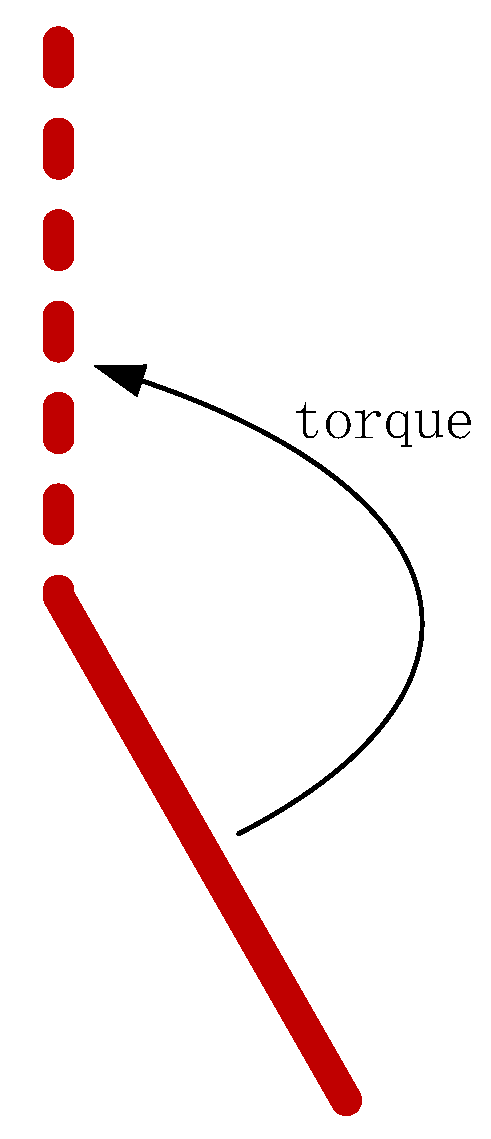
4.1.1. Case 1: Pendulum-v1

The pendulum is a classic test environment where one end is fixed, and the other end can move freely. By applying appropriate torque, the goal is to balance the pendulum upright and maintain its position as shown in Figure 5.

System Model

The following equations represent the pendulum system model:

$$\ddot{\theta }={\displaystyle \frac{3g}{2l}}sin\left(\theta \right)+{\displaystyle \frac{3}{m{l}^2}}u$$

(18)

where $\theta$ represents the angle of the pendulum. The angular velocity and angle of the pendulum are obtained through integration. The parameters for the pendulum system are detailed in

Table 2. Parameters for the pendulum.

Notation	Description	Value
g	Gravity acceleration	10
l	The length of the pendulum	1.0
m	The mass of the pendulum	1.0
u	The applied torque	[−10,10]
$\theta$	The current angle of the pendulum	[$-\pi ,\pi$]
$\dot{\theta }$	The current angular velocity of the pendulum	[−8,8]

.

Reward Function

The reward function was designed to guide the agent toward the desired behavior. It was formulated as follows:

$$r={\theta }^2+0.1{\dot{\theta }}^2+0.01u^2$$

(19)

where $\theta$ is the angle of the pendulum relative to the vertical position, $\dot{\theta }$ is the velocity, and u is the control input. The reward function was designed to balance stability and control efficiency. It penalized deviations from the desired upright position, high velocities, and excessive control efforts. By discouraging large angle deviations, fast movements, and unnecessary control actions, the function guided the agent to maintain the pendulum in a stable position with minimal control effort, ensuring efficient and effective performance.

4.1.2. Case 2: CSTR System

The Continuous Stirred Tank Reactor (CSTR) is widely used in industrial applications. Due to its high degree of nonlinearity, it imposes stringent requirements on controllers. This paper tested the effectiveness of the proposed method on a CSTR model.

System Model

In a CSTR model, the jacket temperature is the control variable, the reactor temperature is the process variable, and the feed temperature is the disturbance variable. The system equations for the CSTR are as follows [41]. The energy conservation equation within the vessel is

$${\displaystyle \frac{d{C}_A}{dt}}={\displaystyle \frac{F}{V}}\left(C_A^f\left(t\right)-C_A\left(t\right)\right)-r\left(t\right)$$

(20)

where

$$r\left(t\right)=k_0{e}^{-{\displaystyle \frac{E}{RT\left(t\right)}}}{C}_A\left(t\right)$$

(21)

where E represents the activation energy, R stands for the Boltzmann ideal gas constant, T denotes the temperature inside the reactor, and $k_0$ is an unspecified nonthermal constant.

The change in temperature within the vessel is

$${\displaystyle \frac{dT\left(t\right)}{dt}}={\displaystyle \frac{F}{V}}\left(T_f\left(t\right)-T\left(t\right)\right)-{\displaystyle \frac{\mathrm{\Delta }H}{\rho C_p}}r\left(t\right)-{\displaystyle \frac{UA}{\rho C_{p}V}}\left(T\left(t\right)-T_c\left(t\right)\right)$$

(22)

where

• $\mathrm{\Delta }H$ represents the heat of the reaction per mole;
• $C_p$ denotes the heat capacity coefficient;
• $\rho$ stands for the density coefficient;
• U represents the overall heat transfer coefficient;
• A denotes the area for heat exchange, specifically the interface area between the coolant and vessel.

The initial value of $C_A^f\left(t\right)$ was constant at 1 kcal/m³, $T_f\left(t\right)$ was constant at 350 K, and $T_c\left(0\right)$ = 50 K with the range $50\le T_c\le 420\mathrm{K}$. The values of the various parameters are shown in

Table 3. Parameters of CSTR model.

Param	Value	Unit	Description
F	1	m³/h	Liquid flow rate in the vessel
V	1	m³	Reactor volume
R	1.985875	kcal/(kmol·K)	Boltzmann’s ideal gas constant
$\mathrm{\Delta }H$	−5.960	kcal/kmol	Heat of chemical reaction
E	11,843	kcal/kmol	Activation energy
$k_0$	34,930,800	1/h	Pre-exponential nonthermal factor
$\rho C_p$	500	kcal/(m³·K)	Density multiplied by heat capacity
$UA$	150	kcal/(K·h)	Overall heat transfer coefficient multiplied by vessel area

.

Reward Function

The reward function for the CSTR (Continuous Stirred Tank Reactor) system was designed to guide the system towards minimizing the error e while preventing large gradients during the learning process. It was defined as follows:

$$r=\left\{\begin{array}{cc}-\beta e^2+1,\hfill & \mathrm{if}\left|e\right|<0.01\hfill \\ -\beta e^2,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(23)

where $\beta =0.0025$ is a small scale factor that ensures the penalty does not become too large, helping to prevent gradient explosion during training. When the error $\left|e\right|$ is small (i.e., less than 0.01), the function provides a positive reward of $1-\beta e^2$ to encourage the system to stay close to the desired state. This positive reward helps the system to fine-tune its performance and maintain small errors. However, for larger errors, the reward becomes negative and increases quadratically with the error. This quadratic increase discourages significant deviations from the target, promoting convergence toward the desired state and penalizing large errors. By balancing small positive rewards for minor errors and strong penalties for large errors, the function ensures the system remains stable and learns efficiently without excessive fluctuations or instability.

4.2. Experimental Results

This section presents the test results and analysis conducted on the Pendulum-v1 and CSTR models, demonstrating the effectiveness and performance of the proposed approach.

4.2.1. Case 1: Pendulum-v1

Training Performance Evaluation

Figure 6 represents the training processes of SFPD and SAC, evaluated by the cumulative reward (CR) per episode [42]. The definition of cumulative reward (CR) is as follows:

$$CR=\sum _{t=1}^{T}r\left(t\right)$$

(24)

The training process spanned 10 epochs. The policy network parameters for SAC were randomly initialized, while the fuzzy membership initialization parameters for SFPD’s FNNs were uniformly distributed within values.

Figure 6a shows the variation in cumulative rewards with training episodes for two algorithms (SFPD and SAC) in the pendulum control task. It suggested that the SFPD algorithm improved cumulative rewards rapidly during the early episodes, with a significantly faster convergence speed than the SAC algorithm. Additionally, the cumulative rewards of SFPD exhibited greater stability, with almost no significant regressions. In contrast, the SAC algorithm experienced significant fluctuations during the early stage and showed noticeable negative trends in the mid-training phase (around episodes 50 to 70), indicating potential instability in its policy updates. Overall, SFPD outperformed SAC, demonstrating faster convergence and higher stability.

Figure 6b describes the changes in policy gradient loss per episode for both algorithms. It can be observed that the policy loss of SFPD trended toward zero during the early training stage and remained stable throughout the process, indicating a smooth and well-converged policy optimization. In contrast, the SAC algorithm exhibited severe fluctuations in policy loss during the initial training stage, with significant negative gradients observed around episodes 50 to 70, which may reflect instability in its policy updates. While the policy loss of SAC gradually stabilized later, its overall performance remained less stable compared to SFPD.

Figure 6c presents the loss trends of the Q networks (Q1 and Q2) for both algorithms across training episodes. Results show that the Q network loss of SFPD decreased rapidly in the early training stage and stabilized thereafter, indicating effective control of value function estimation errors. On the other hand, the Q network loss of SAC showed large fluctuations during the early stages, and dramatic oscillations occurred around episodes 50 to 70. This aligned with the fluctuations observed in SAC’s cumulative rewards and policy loss, further indicating instability in value function estimation during that phase. Overall, SFPD exhibited superior stability and performance in Q network updates.

Figure 6d displays the trends in V network loss across episodes for the two algorithms. The V network loss of SFPD declined rapidly in the early training stage and remained at a low level throughout the process, suggesting a stable and efficient value function learning process. In contrast, the SAC algorithm experienced significant peaks in V network loss around episodes 50 to 70, reflecting instability in value function learning. This phenomenon was consistent with the fluctuations observed in SAC’s policy and Q network performance, further confirming its overall optimization instability.

The comparative analysis suggested that SFPD outperformed SAC in terms of cumulative rewards, policy loss, Q network loss, and V network loss. Its primary advantages lay in the rapid convergence and high stability during the training process. This suggests that SFPD is better suited than SAC for solving complex dynamic optimization problems in pendulum control tasks.

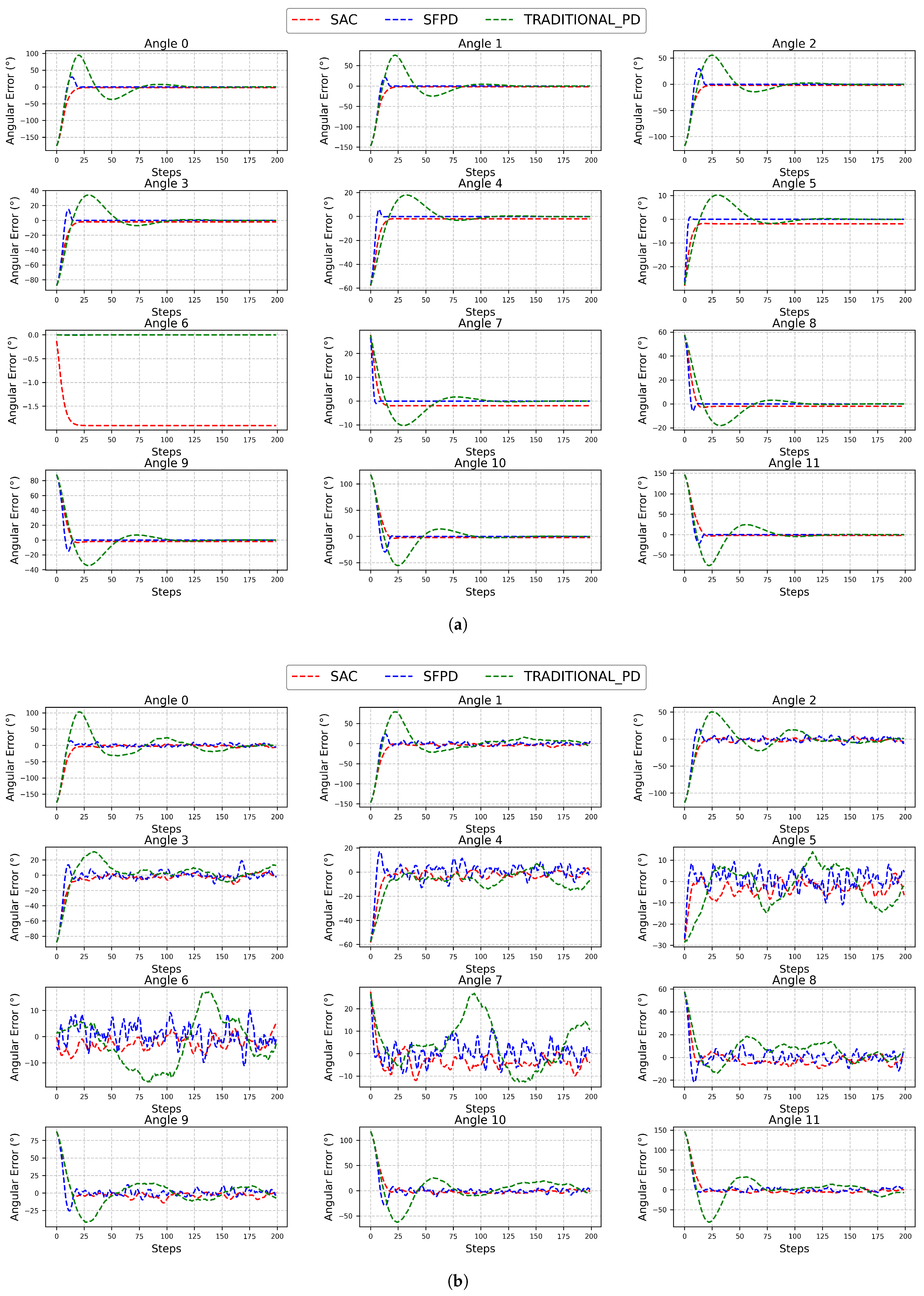
Testing Performance Evaluation

To evaluate the effectiveness of the proposed method, a series of controlled experiments were conducted, comparing its performance with Soft Actor–Critic (SAC) and traditional Proportional–Derivative (PD) controllers. The experiments were designed to assess response speed, accuracy, stability, noise robustness, and disturbance rejection capability. The initial evaluation was conducted under fixed initial conditions ($\theta =-{135}^{\circ }$, $\dot{\theta }=2$ rad/s) to ensure a controlled comparison. The control parameters of the traditional PD algorithm were determined using the Ziegler–Nichols tuning method ($K_p=5.708$, $K_d=9.510$). As shown in Figure 7a, the proposed SFPD algorithm exhibited superior speed, accuracy, and stability compared to SAC and traditional PD.

To analyze the impact of sensor noise on control performance, a Gaussian white noise measurement disturbance with $\mu \sim \mathcal{N}(0,0.1^2)$ was introduced. Figure 7b demonstrates that SFPD exhibited strong resilience to noise, owing to its Markov-based control strategy, which ensured decisions were made based on the current state, thereby mitigating the accumulation of errors over time. To further assess disturbance rejection capability, an external torque perturbation was applied [43] between steps 100 and 102. As shown in Figure 7c, SFPD demonstrated the fastest recovery with minimal oscillations, highlighting its exceptional robustness. SAC maintained stability but exhibited a slower response, while traditional PD showed significant overshoot and oscillations, indicating its limited disturbance rejection capability.

A detailed quantitative analysis of the control performance is presented in

Table 4. Quantitative metrics of testing process on the pendulum (Note: WGN = with Gaussian noise).

WGN	SFPD		SAC		Traditional PD
	ISE	IAE	ISE	IAE	ISE	IAE
No	104,046	1158	341,062	3062	138,813	2659
Yes	108,167	1852	351,541	3267	153,669	3399

. In noise-free conditions, SFPD achieved a 12.15% reduction in Integral of Squared Error (ISE) and a 40.19% reduction in Integral of Absolute Error (IAE) compared to SAC. Additionally, SFPD exhibited a 59.16% improvement in ISE and a 74.20% improvement in IAE over traditional PD, highlighting its superior error minimization. Even under measurement noise interference, SFPD remained highly effective, achieving a 7.54% reduction in ISE over SAC. Although SAC outperformed SFPD in IAE under these conditions (SAC: 1231, SFPD: 1368), SFPD still significantly outperformed traditional PD, achieving improvements of 53.69% in ISE and 51.70% in IAE, further demonstrating its robustness in noisy environments.

Overall, the experimental results demonstrated that SFPD outperformed SAC and traditional PD across various control scenarios. The proposed method achieved faster response, reduced steady-state errors, superior robustness to measurement noise, and enhanced disturbance rejection, making it a more effective solution for nonlinear control applications.

Test with Randomized Initial Conditions

In previous experiments, fixed initial conditions were used to provide a controlled assessment of the proposed method’s performance. To further evaluate its robustness and generalization capability, we then introduced randomized initial conditions [44]. This allowed for a more comprehensive assessment by ensuring the controller could adapt to a wider range of operating conditions and disturbances. Figure 8 presents a comparative analysis of the angular error performance of the SAC, SFPD, and traditional PD controllers under varying initial conditions and noise, highlighting the superior adaptability of the proposed method in handling uncertainties.

Across all 12 angles in Figure 8a, the SFPD (blue curve) consistently demonstrated faster convergence to near-zero angular error compared to the SAC (red curve) and traditional PD (green curve). For most angles, the SFPD algorithm showed reduced oscillations and overshoot during the initial error correction phase, highlighting its stability and precision. SAC displayed comparable performance but generally lagged slightly in terms of convergence speed. Traditional PD exhibited slower response times and significant overshoots, especially for larger initial angles.

Noise introduced noticeable fluctuations in angular error across all controllers as shown in Figure 8b. However, SFPD continued to maintain superior convergence performance with minimal oscillations compared to SAC and traditional PD. SAC showed improved noise tolerance compared to traditional PD, but its fluctuations remained larger than those of SFPD. Traditional PD suffered from larger amplitude oscillations and slower stabilization under noisy conditions, indicating its vulnerability to measurement noise.

4.2.2. Case 2: CSTR System

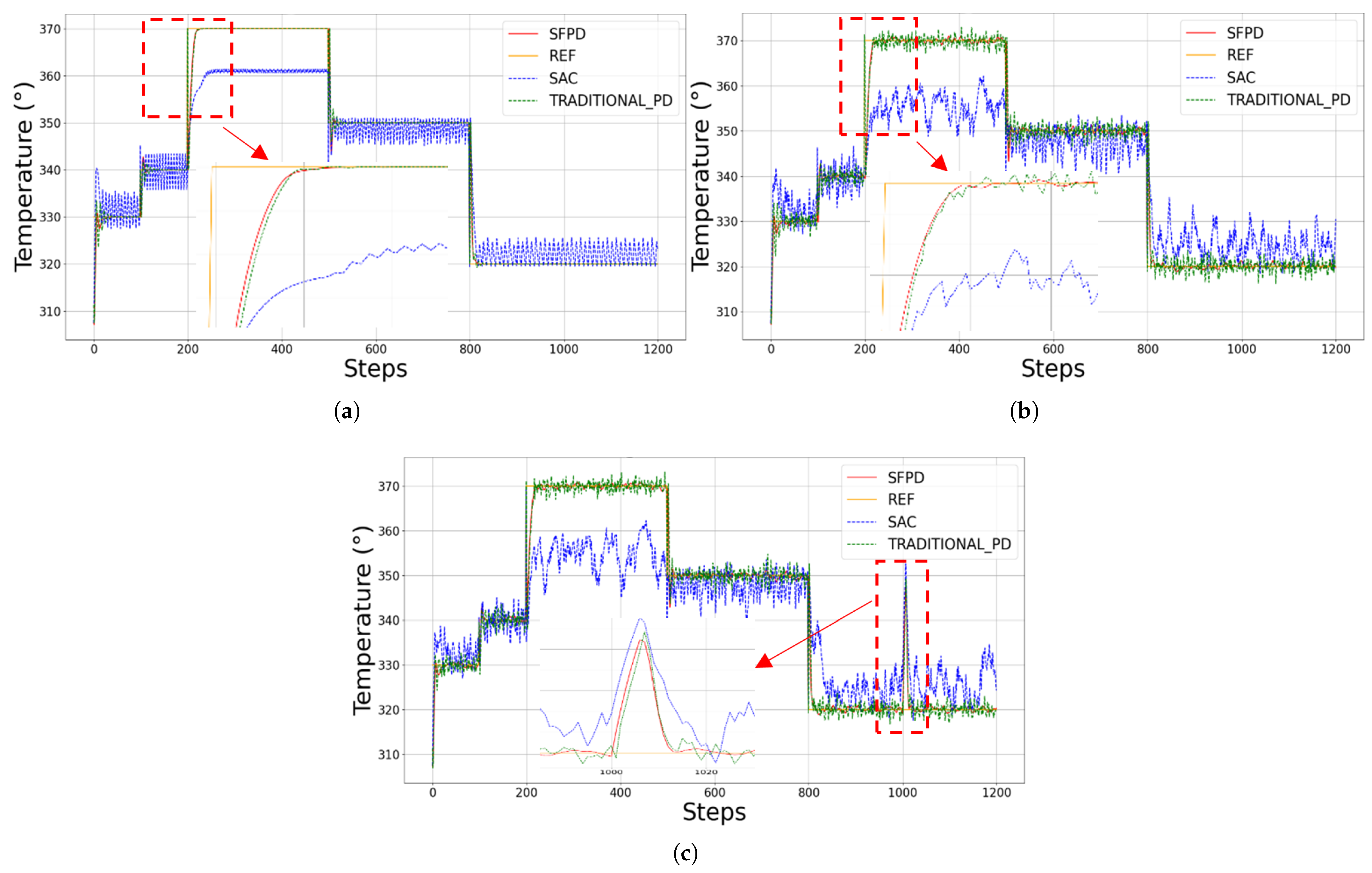
Training Performance Evaluation

The training process, as shown in Figure 9, involved 50 epochs for both the SFPD and SAC algorithms. The fuzzy membership initialization parameters for SFPD’s FNNs were uniformly distributed within their respective value ranges, with the number of fuzzy memberships set to seven.

From Figure 9, the training process on the CSTR system highlighted the significant advantages of SFPD over SAC. In Figure 9a, the cumulative reward (CR) for SFPD remained stable, consistently approaching 1000, while SAC exhibited substantial fluctuations and slower convergence, revealing instability in its learning process. Regarding policy loss, SFPD quickly minimized the loss and maintained stability, whereas SAC experienced higher losses and a slower decline, emphasizing SFPD’s superior efficiency in policy optimization. As shown in Figure 9b, the Q-network loss for SFPD was consistently low and stable from the outset, while SAC began with high losses that gradually decreased but still exhibited noticeable errors, underscoring SFPD’s accuracy in value function estimation. Similarly, Figure 9c illustrates that SFPD maintained low and stable V-network loss throughout, while SAC exhibited significant initial fluctuations before stabilizing, further demonstrating SFPD’s advantages in state-value function estimation and policy stability. Overall, SFPD outperformed SAC in terms of stability, convergence speed, and loss control, proving to be a more effective solution for complex dynamic system control tasks. Notably, when the exploration space is large, such as with vast action spaces, SAC’s convergence becomes significantly slower or may even fail entirely, whereas the proposed method continues to exhibit robust and reliable convergence performance.

Testing Performance Evaluation

Figure 10 presents the testing results, comparing the performance of the SAC, SFPD, and traditional PD algorithms. To evaluate noise robustness, a Gaussian white noise measurement disturbance signal with $\mu \sim \mathcal{N}(0,1^2)$ was introduced, as depicted in Figure 10b. Additionally, to assess disturbance rejection capability, an external torque disturbance was applied [45] between steps 1000 and 1005, as shown in Figure 10c. Unlike previous tests that employed a positional PD controller, this experiment utilized a traditional incremental PD controller. The mathematical formulation of the incremental PD controller is given below:

$$T_c(t+1)=T_c\left(t\right)+K_p\times e+K_d\times e^{\prime }$$

(25)

where $T_c(t+1)$ denotes the next time step’s control signal, while $T_c\left(t\right)$ denotes the current time’s control signal. The parameters for the PD algorithm were determined using the Ziegler–Nichols method, with $K_p=6.690$ and $K_d=1.842$.

From Figure 10, it can be observed that the SAC algorithm struggled with stability, showing significant oscillations. In contrast, both the SFPD and traditional PD algorithms managed to control the system effectively. Figure 10b illustrates that the SFPD algorithm demonstrated higher robustness compared to the traditional PD algorithm.

Table 5. Quantitative metrics of testing results on CSTR (Note: SI = sampling interval, WGN = with Gaussian noise).

SI	WGN	SFPD		SAC		Traditional PD
		ISE	IAE	ISE	IAE	ISE	IAE
0–100 s	No	1757	115	2121	320	1667	132
	Yes	1746	140	3003	408	1896	206
100–200 s	No	252	38	751	230	252	45
	Yes	272	66	875	242	461	128
200–500 s	No	4351	218	30,832	2939	4349	219
	Yes	4539	309	69,403	4449	4596	462
500–800 s	No	1031	78	1659	512	957	80
	Yes	1043	189	3885	859	1190	329
800–1200 s	No	2644	122	7584	1074	2622	125
	Yes	2777	242	16,036	2008	3518	520

provides the quantitative data. From Figure 10c, it is evident that SFPD (red line) demonstrated superior control stability, maintaining the temperature close to the reference value (yellow line) with minimal fluctuations. In contrast, SAC (blue dashed line) exhibited significant instability, with large oscillations and a pronounced peak around step 1000, exceeding 350 °C. Traditional PD (green dashed line) performed better than SAC but still showed noticeable deviations and slower recovery.

From the analysis of the data in Table 5, it can be observed that the SFPD algorithm showed significant improvements in both the absence and presence of Gaussian noise interference. In the absence of noise, the SFPD algorithm showed substantial improvements in ISE across different sampling intervals when compared to the SAC algorithm, with percentage gains of 17.14%, 66.44%, 85.88%, 37.84%, and 65.14%. However, when compared to the traditional PD algorithm, the improvements were less pronounced, with percentage changes of −5.40%, 0%, −0.05%, −7.73%, and −0.84%, indicating some negative improvements in specific cases.

When noise was introduced, the SFPD algorithm’s performance in ISE remained strong relative to the SAC algorithm, achieving improvements of 41.88%, 68.93%, 93.46%, 73.15%, and 82.68%. Comparatively, the improvements over the traditional PD algorithm were more moderate, with percentage gains of 7.94%, 41.00%, 1.24%, 12.35%, and 21.06%.

Similarly, the SFPD algorithm exhibited significant improvements in IAE. Without noise, the percentage improvements over the SAC algorithm were 64.06%, 83.48%, 92.58%, 84.77%, and 88.63%. Compared to the traditional PD algorithm, the gains were more modest, with percentage changes of 12.88%, 15.56%, 0.46%, 2.50%, and 2.40%. Under noisy conditions, the SFPD algorithm continued to outperform the SAC algorithm, with percentage improvements in IAE of 65.69%, 72.73%, 93.05%, 77.99%, and 87.94%. The enhancements over the traditional PD algorithm in this scenario were 32.04%, 48.44%, 33.12%, 42.45%, and 53.46%.

Overall, the SFPD algorithm excelled in both ISE and IAE metrics, particularly in challenging conditions with noise interference. While the advantages of the SFPD algorithm over the traditional PD algorithm were less pronounced in some instances, it required no human intervention and demonstrated greater robustness. The SFPD algorithm consistently outperformed the SAC algorithm, making it a strong candidate for applications where robustness and stability are crucial.

4.3. Complexity Analysis

4.3.1. Space Complexity Analysis

The space complexity of each layer in the model is as follows:

• For the input layer, the space required to store the input data x, where there are n input features, is $O\left(n\right)$.
• In the fuzzification layer, each input $x_i$ computes j fuzzy membership values (since there are j fuzzy membership functions per input). The total space required for these fuzzy membership values is $O(i·j)$.
• In the multiplication layer (fuzzy inference), we store the fuzzy inference result $\alpha$ for each rule. With m rules, the space complexity is $O\left(m\right)$.
• The normalization layer generates a new vector ${\beta }_j$, requiring $O\left(m\right)$ space to store the values.
• The defuzzification layer calculates the output $y_i$, and for r outputs, the space required is $O\left(r\right)$.

Thus, the overall space complexity is:

$$O\left(n\right)+O(i·j)+O\left(m\right)+O\left(m\right)+O\left(r\right)$$

(26)

Simplified, this becomes:

$$O(n+i·j+m+r)$$

(27)

As the system’s input dimensionality i increases, the number of fuzzy rules m grows exponentially (i.e., $m=j^i$), leading to a rapid increase in space requirements. Moreover, when increasing the number of fuzzy membership functions j, space complexity increases exponentially. Therefore, as the system complexity grows, the number of fuzzy rules increases significantly, potentially making real-time implementation more challenging due to the high space demands.

4.3.2. Time Complexity Analysis

The time complexity of each layer in the model is as follows:

• In the input layer, applying the tanh function to each input element has a time complexity of $O\left(1\right)$. For n input features, the overall time complexity is $O\left(n\right)$.
• In the fuzzification layer, we compute j fuzzy membership values for each input $x_i$, and each computation takes $O\left(1\right)$ time. Therefore, for i inputs and j memberships, the total time complexity is $O(i·j)$.
• The multiplication layer (fuzzy inference) calculates the fuzzy inference result $\alpha$ for each rule by multiplying n fuzzy memberships. The time complexity for each rule is $O\left(n\right)$, and for m rules, the total time complexity is $O(n·m)$.
• The normalization layer involves summing m fuzzy inference results and normalizing each ${\alpha }_j$, which takes $O\left(m\right)$ time.
• The defuzzification layer computes the output $y_i$, with a time complexity of $O(m·r)$, as there are r outputs requiring summation of m values.

Thus, the overall time complexity is:

$$O\left(n\right)+O(i·j)+O(n·m)+O\left(m\right)+O(m·r)$$

(28)

Simplified, this becomes:

$$O(n·m+i·j+m·r)$$

(29)

When increasing the number of fuzzy membership functions j, the number of fuzzy rules m increases, which leads to an exponential increase in time complexity. For high-dimensional systems, this can result in a significant increase in computational time per step, which could pose a challenge for real-time implementation. Thus, adding more input variables or membership functions could drastically increase the computational load, impacting system performance.

5. Conclusions

This paper introduced a novel SFPD controller that integrated the SAC framework with an FNN-based PD controller, leveraging reinforcement learning to enable automatic fuzzy rule adjustment for optimal PD control. The partial interpretability of FNNs allowed expert knowledge to be incorporated during initialization, facilitating faster convergence early in training. The controller employed stochastic optimization and integrated entropy during training, enhancing exploration efficiency and significantly reducing training time. Experimental results demonstrated that the SFPD controller achieved faster convergence and superior control performance compared to both SAC and traditional PD controllers. In large exploration spaces, SAC often struggles with convergence or fails entirely, whereas the proposed method maintains high performance and robustness. A key challenge in applying SAC to PID control is its inability to incorporate the integral (I) component, as this introduces dependence on past states, violating the Markov property. This limitation reduces the effectiveness of replay buffers, potentially causing instability and slower convergence. Therefore, our future work will focus on finding ways to isolate and compute the integral term separately in order to maintain stability and guarantee convergence. Additionally, addressing limitations in high-noise environments, complex nonlinear relationships, and large action spaces can further enhance the model’s robustness. In noisy environments, excessive disturbances can destabilize training, while complex relationships and large action spaces may not only increase computational complexity but also heighten the risk of overfitting. Furthermore, incorporating type-2 fuzzy control could further enhance adaptability and robustness.