The Pseudoinverse Gradient Descent Method with Eight Branch Directions (8B-PGDM): An Improved Dead Reckoning Algorithm Based on the Local Invariance of Navigation
Abstract
1. Introduction
- High-frequency data dependence: traditional inertial navigation systems (INS) require IMU sampling rates above 10 Hz to suppress integral drift, but in noncooperative scenarios, target observation frequencies are often lower than 5 Hz (such as satellite remote sensing revisit periods), leading to the failure of conventional Kalman filtering frameworks.
- Dynamic model mismatch: existing methods often assume that the target follows a linear motion model, but in fact, ships often perform nonlinear avoidance maneuvers [23].
- Obstacles to multi-source heterogeneous data fusion include spatiotemporal asynchrony and coordinate system homogeneity in multimodal data such as radar, AIS, EO/IR in non cooperative scenarios.
- Theoretical Foundation: We establish the first formal connection between motion invariance principles and dead reckoning methodologies through Lie group analysis. This theoretical bridge enables the derivation of system observability conditions under sparse sampling regimes.
- Algorithmic Breakthrough: An innovative methodology is established that leverages geometric invariants to reformulate the original non-convex parameter estimation problem into a tractable convex optimization framework.
- Engineering Implementation: The proposed dual-stage predictor-corrector architecture achieves continuous trajectory prediction.
2. Problem Formulation and Modeling
2.1. Time-Invariance of Motion Parameters
2.2. Time-Invariant Parameters in Optimal Control
2.3. Geometric Properties of Trajectory
2.4. Convex Function Construction
3. Methods
3.1. Pseudoinverse Gradient Descent Method
3.2. Intermediate Complexity of Methods
- For all and , (linearity).
- (conjugate symmetry), where denotes the complex conjugate of .
- For all , and if and only if (positive definiteness).
| Algorithm 1 Iterative Optimization Solver for 8B-PGDM |
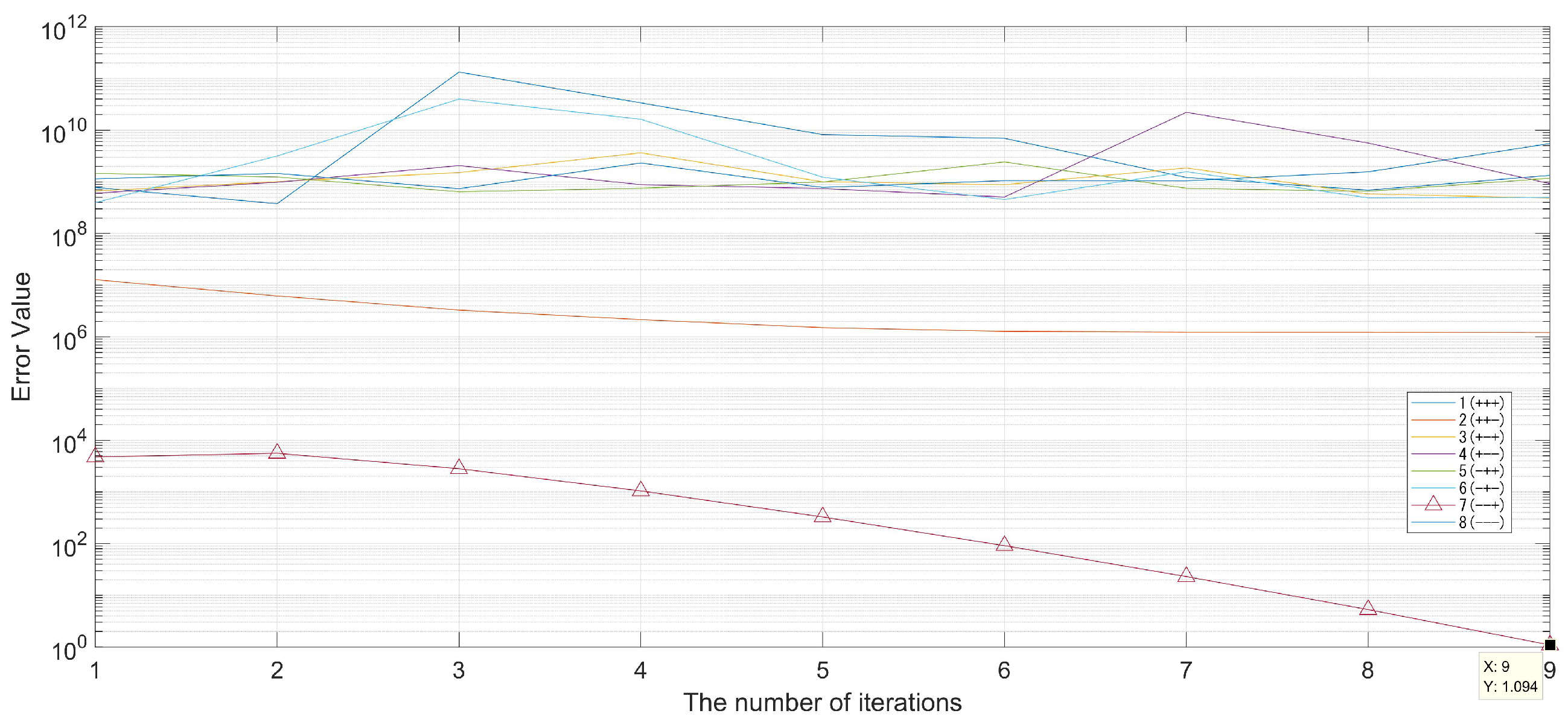
3.3. Convergence Analysis
3.4. 8B-PGDM
4. Results
4.1. Design of Experiments
4.2. Method Validation
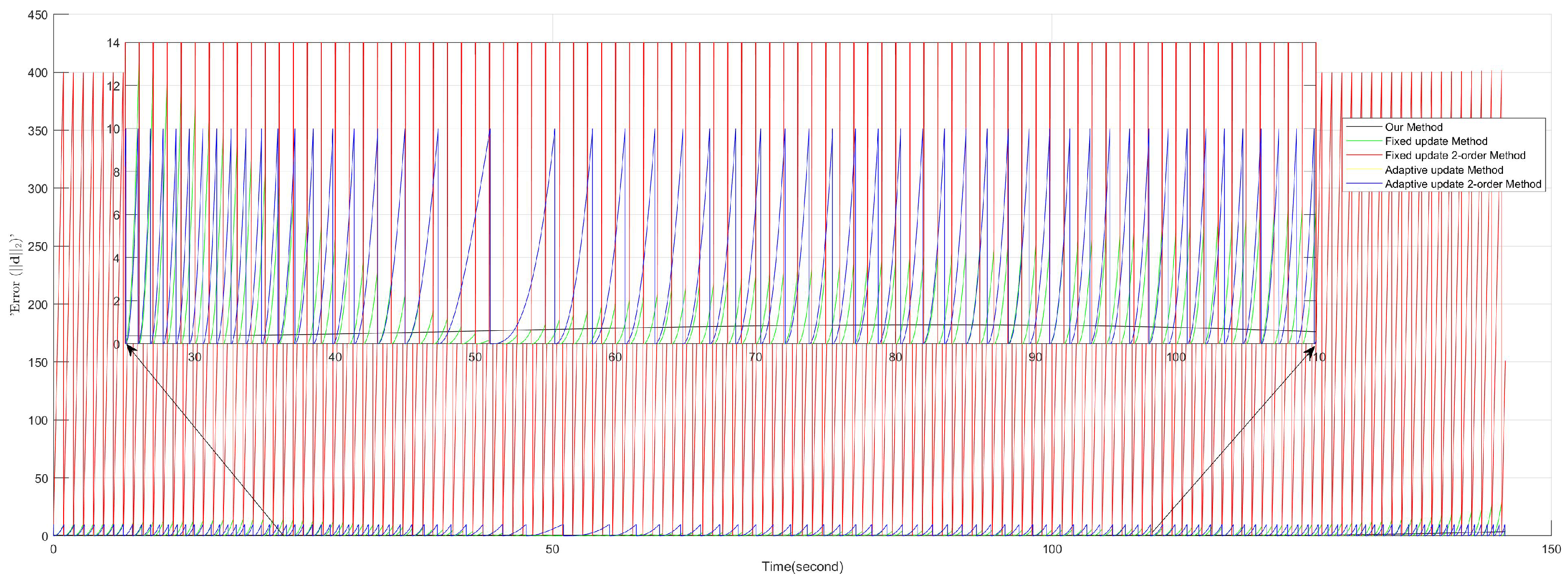
4.3. Performance Comparison
4.4. Limitations
5. Conclusions
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gogendeau, P.; Bonhommeau, S.; Fourati, H.; Oliveira, D.D.; Taillandier, V.; Goharzadeh, A.; Bernard, S. Dead-reckoning configurations analysis for marine turtle context in a controlled environment. IEEE Sens. J. 2022, 22, 12298–12306. [Google Scholar] [CrossRef]
- Kuang, J.; Liu, T.; Wang, Y.; Meng, X.; Niu, X. Magnetic vector constraint pedestrian dead reckoning based on foot-mounted and waist-mounted imu. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Vaughan, D. Dead Reckoning: Air Traffic Control, System Effects and Risk; University of Chicago Press: Chicago, IL, USA, 2021; ISBN 978-0-226-82032-3. [Google Scholar]
- Mori, D.; Kamekawa, M.; Fujieda, N.; Mizuno, Y. Robust vehicle state estimation from urban driving to the limits of handling. IEEE Trans. Intelligent Transp. Syst. 2024, 26, 892–905. [Google Scholar] [CrossRef]
- Gunner, R.M.; Holton, M.D.; Scantlebury, D.M.; Hopkins, P.; Shepard, E.L.; Fell, A.J.; Garde, B.; Quintana, F.; Gómez-Laich, A.; Yoda, K.; et al. How often should dead-reckoned animal movement paths be corrected for drift? Anim. Biotelemetry 2021, 9, 43. [Google Scholar] [CrossRef] [PubMed]
- Feigl, T.; Kram, S.; Woller, P.; Siddiqui, R.H.; Philippsen, M.; Mutschler, C. Rnn-aided human velocity estimation from a single imu. Sensors 2020, 20, 3656. [Google Scholar] [CrossRef]
- Canbek, K.O.; Yalcin, H.; Baran, E.A. Drift compensation of a holonomic mobile robot using recurrent neural networks. Intell. Serv. Robot. 2022, 15, 399–409. [Google Scholar] [CrossRef]
- Toskovic, A.; Petrovic, A.; Jovanovic, L.; Bacanin, N.; Zivkovic, M.; Dobrojevic, M. Marine Vessel Trajectory Forecasting Using Long Short-Term Memory Neural Networks Optimized via Modified Metaheuristic Algorithm; AIS Algorithms for Intelligent Systems; Springer: Singapore, 2024; pp. 51–66. [Google Scholar]
- Lin, J.; Zou, C.; Lan, L.; Gu, S.; An, X. Deep heading estimation for pedestrian dead reckoning. J. Phys. Conf. Ser. 2020, 1656, 012009. [Google Scholar] [CrossRef]
- Hurwitz, D.; Cohen, N.; Klein, I. Deep-learning-assisted inertial dead reckoning and fusion. IEEE Trans. Instrum. Meas. 2025, 74, 2501009. [Google Scholar] [CrossRef]
- Brossard, M.; Barrau, A.; Bonnabel, S. Ai-imu dead-reckoning. IEEE Trans. Intell. Veh. 2020, 5, 585–595. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Li, N.; Huang, Y.; Zhao, Y. A novel pedestrian dead-reckoning algorithm with self-estimates of imu biases. IEEE Trans. Instrumentation Meas. 2025, 74, 8503709. [Google Scholar] [CrossRef]
- Niu, Z.; Cong, L.; Qin, H.; Cao, S. Pedestrian dead reckoning based on complex motion mode recognition using hierarchical classification. IEEE Sens. J. 2024, 24, 4935–4947. [Google Scholar] [CrossRef]
- Li, H.; Guo, H.; Qi, Y.; Deng, L.; Yu, M. Research on multi-sensor pedestrian dead reckoning method with ukf algorithm. Measurement 2021, 169, 108524. [Google Scholar] [CrossRef]
- Li, L.; Wei, Z.; Zhang, T.; Cai, D. Three-dimensional dead reckoning of wall-climbing robot based on information fusion of compound extended kalman filter. J. Field Robot. 2023, 40, 505–520. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Zhuang, Y.; Wang, Y.; Shi, M.; Xu, Y. ulidr: An inertial-assisted unmodulated visible light positioning system for smartphone-based pedestrian navigation. Inf. Fusion 2025, 113, 102579. [Google Scholar] [CrossRef]
- Yang, X.; Huang, X.; Zhang, Y.; Liu, Z.; Pang, Y. Multi-sensor fusion and semantic map-based particle filtering for robust indoor localization. Measurement 2025, 242, 115874. [Google Scholar] [CrossRef]
- Wu, L.; Guo, S.; Han, L.; Anil Baris, C. Indoor positioning method for pedestrian dead reckoning based on multi-source sensors. Measurement 2024, 229, 114416. [Google Scholar] [CrossRef]
- Lin, F.; Cai, Q.; Liu, Y.; Chen, Y.; Huang, J.; Peng, H. Pedestrian dead reckoning method based on array imu. IEEE Sens. J. 2024, 24, 37753–37763. [Google Scholar] [CrossRef]
- Bergmann, X.H.J. Rocip: Robust continuous inertial position tracking for complex actions emerging from the interaction of human actors and environment. Appl. Intell. 2025, 55, 494. [Google Scholar]
- Ji, S.; Zhang, C.; Tian, L.; Ran, L.; Yang, Y. Dead reckoning method for tracking wellbore trajectories constrained by the drill pipe length. IEEE Trans. Instrum. Meas. 2024, 73, 8509512. [Google Scholar] [CrossRef]
- Chai, R.; Chen, K.; Hua, B.; Lu, Y.; Xia, Y.; Sun, X.M.; Liu, G.P.; Liang, W. A two phases multiobjective trajectory optimization scheme for multi-ugvs in the sight of the first aid scenario. IEEE Trans. Cybern. 2024, 54, 5078–5091. [Google Scholar] [CrossRef]
- Gharib, M.R.; Fard, M.A.; Koochi, A. Error analysis of dead reckoning navigation system by considering uncertainties in an underwater vehicle’s sensors. J. Navig. 2024, 77, 18–36. [Google Scholar] [CrossRef]



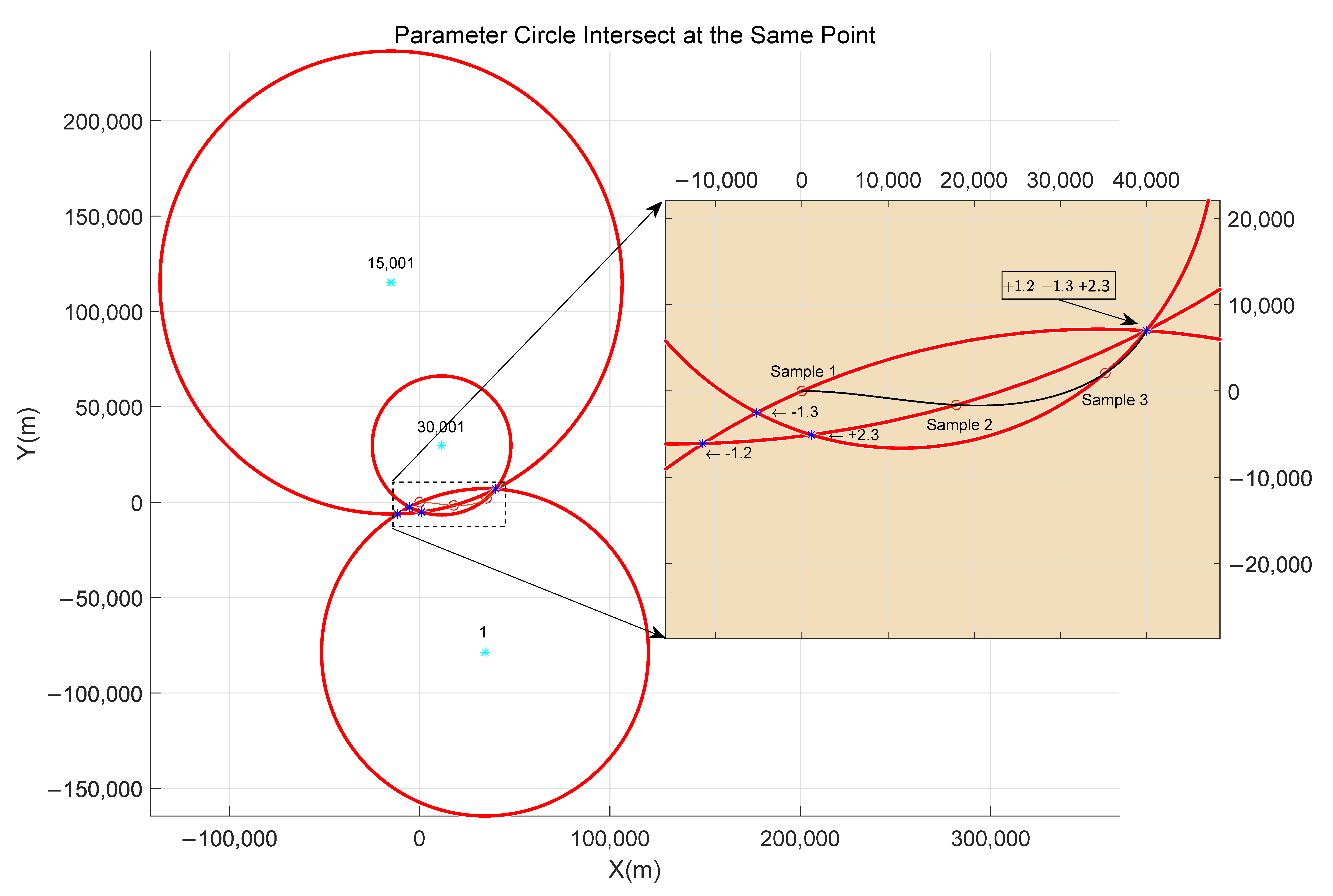
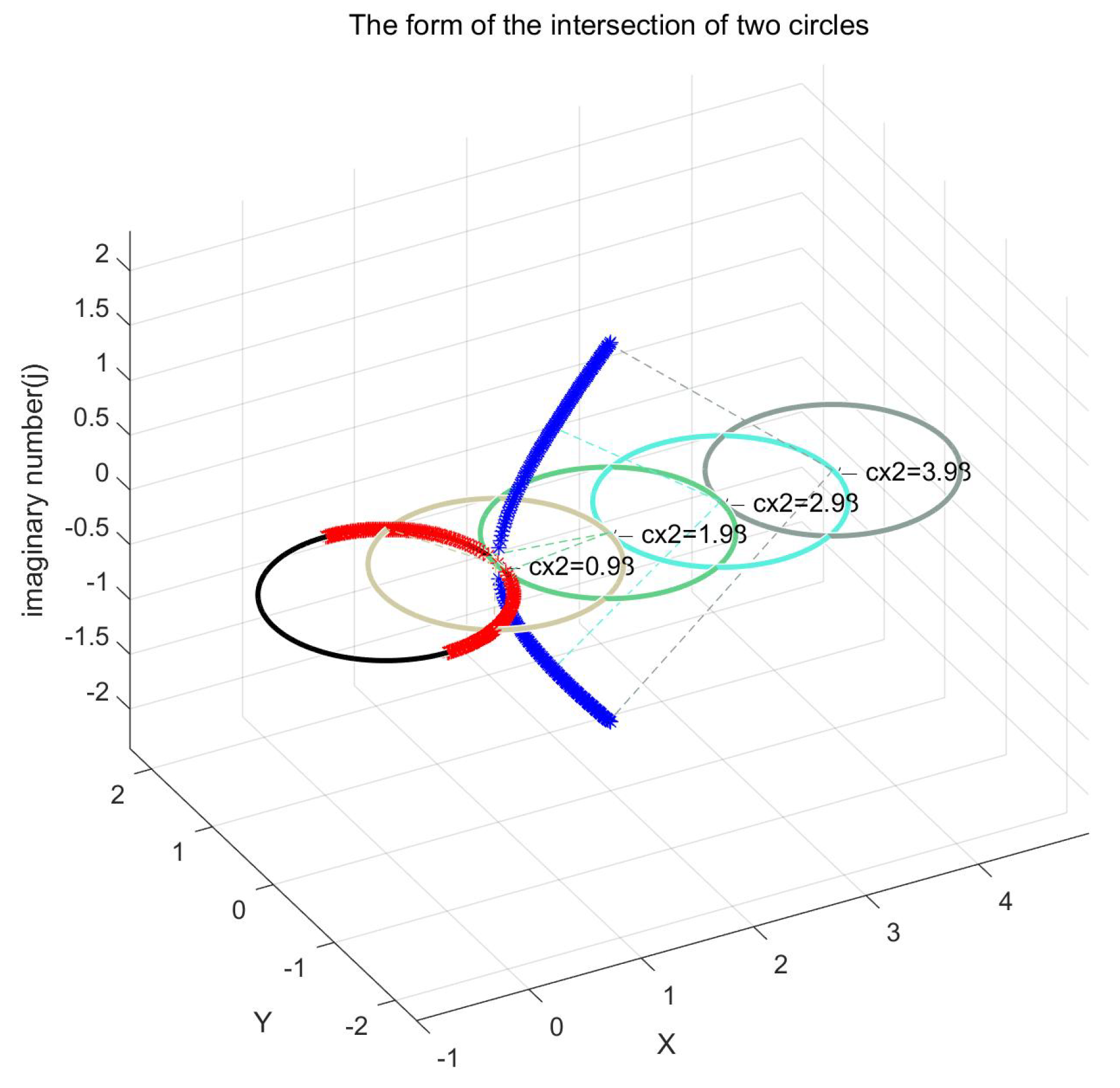
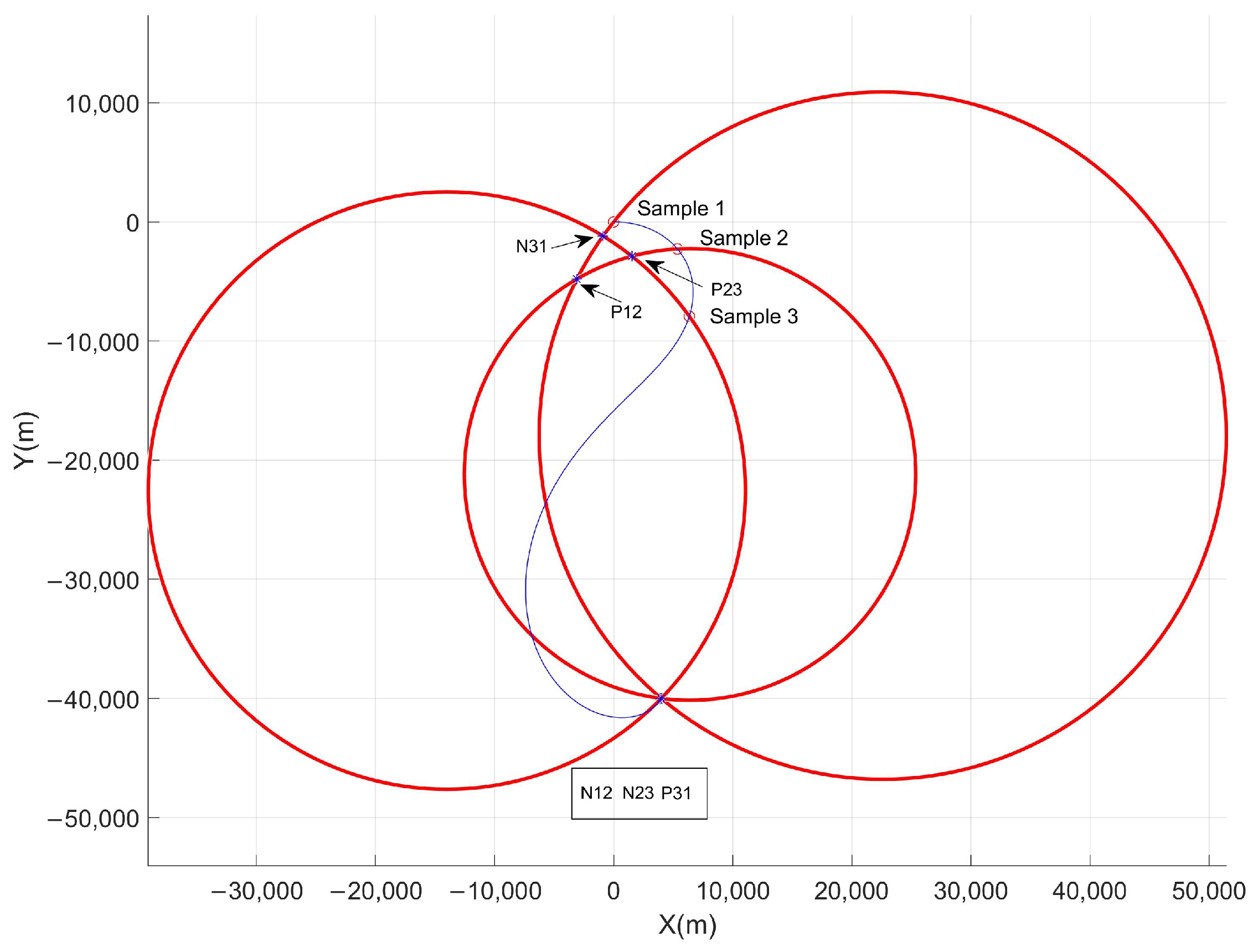
| Symbol | Description |
|---|---|
| Position vector in global coordinates | |
| Rotation matrix from world frame to body frame | |
| Rotation vector (axis-angle representation) | |
| Skew-symmetric matrix of angular velocity | |
| , | Linear velocity/acceleration in body frame |
| Discrete time step increment | |
| Time derivative operator | |
| J | Total cost function |
| Terminal state error penalty | |
| Energy consumption function | |
| X | State vector |
| A, B | Coefficients for calculating intersection coordinates of two parametric circles. |
| U | Control input vector |
| Expected endpoint coordinate position on a 2-D coordinate plane | |
| Bearing angle: | |
| r | Radial distance: |
| Final desired heading angle | |
| , | Initial and final time instants |
| Integration time variable |
| Method | Update Criterion | Samples | MSE | in X | in Y | STD |
|---|---|---|---|---|---|---|
| 8B-PGDM | - | 3 | 0.7906 | |||
| 1st-order DR | 1 s | 146 | 18.053 | |||
| 2nd-order DR | 1 s | 146 | 53176 | |||
| 1st-order DR | m | 122 | 19.913 | |||
| 2nd-order DR | m | 122 | 19.913 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Liu, Q.; Deng, H.; Sun, L.; Huang, J.; Lei, M. The Pseudoinverse Gradient Descent Method with Eight Branch Directions (8B-PGDM): An Improved Dead Reckoning Algorithm Based on the Local Invariance of Navigation. Appl. Sci. 2025, 15, 5049. https://doi.org/10.3390/app15095049
Gao J, Liu Q, Deng H, Sun L, Huang J, Lei M. The Pseudoinverse Gradient Descent Method with Eight Branch Directions (8B-PGDM): An Improved Dead Reckoning Algorithm Based on the Local Invariance of Navigation. Applied Sciences. 2025; 15(9):5049. https://doi.org/10.3390/app15095049
Chicago/Turabian StyleGao, Jialong, Quan Liu, Hanqiang Deng, Lei Sun, Jian Huang, and Ming Lei. 2025. "The Pseudoinverse Gradient Descent Method with Eight Branch Directions (8B-PGDM): An Improved Dead Reckoning Algorithm Based on the Local Invariance of Navigation" Applied Sciences 15, no. 9: 5049. https://doi.org/10.3390/app15095049
APA StyleGao, J., Liu, Q., Deng, H., Sun, L., Huang, J., & Lei, M. (2025). The Pseudoinverse Gradient Descent Method with Eight Branch Directions (8B-PGDM): An Improved Dead Reckoning Algorithm Based on the Local Invariance of Navigation. Applied Sciences, 15(9), 5049. https://doi.org/10.3390/app15095049






