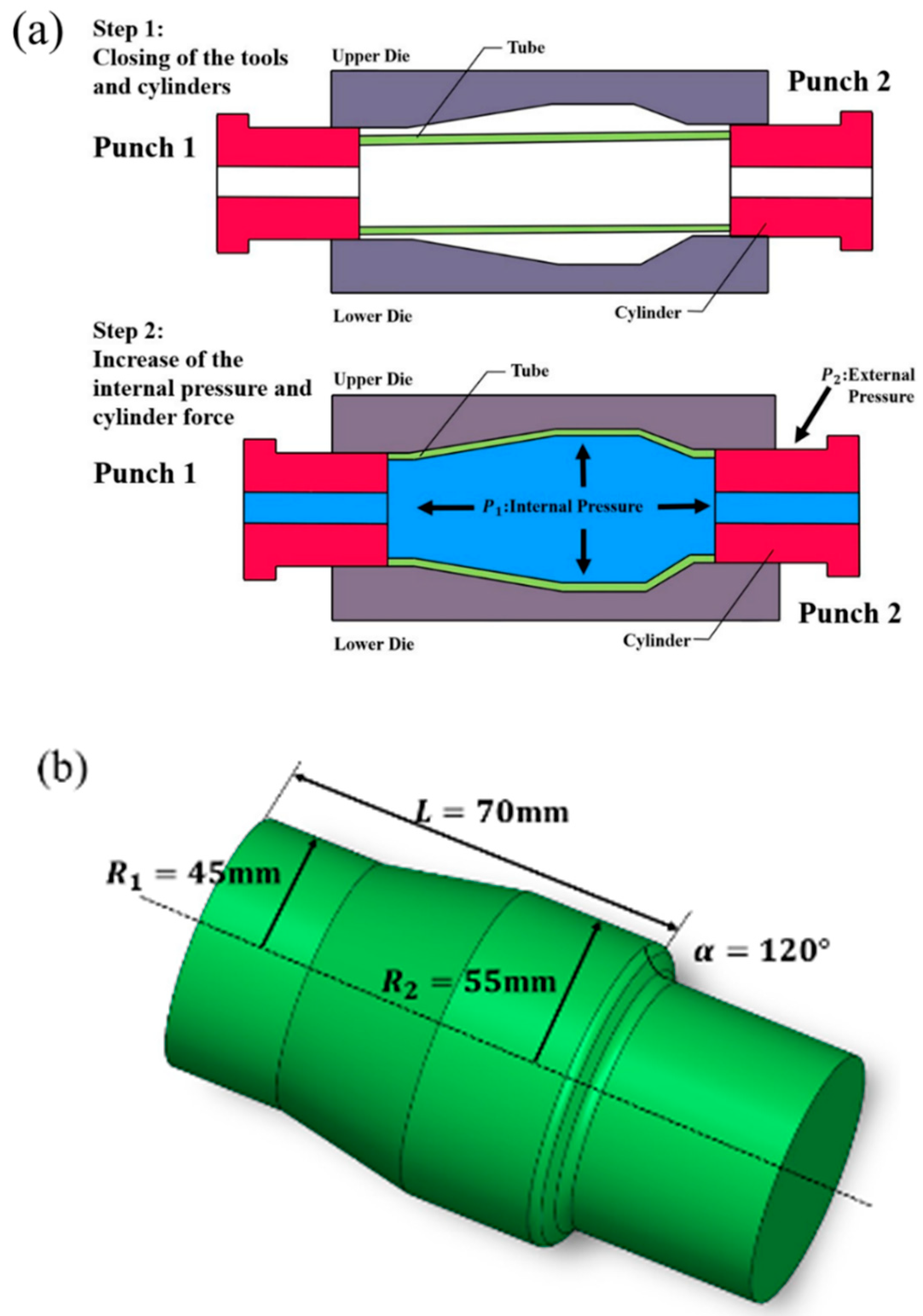
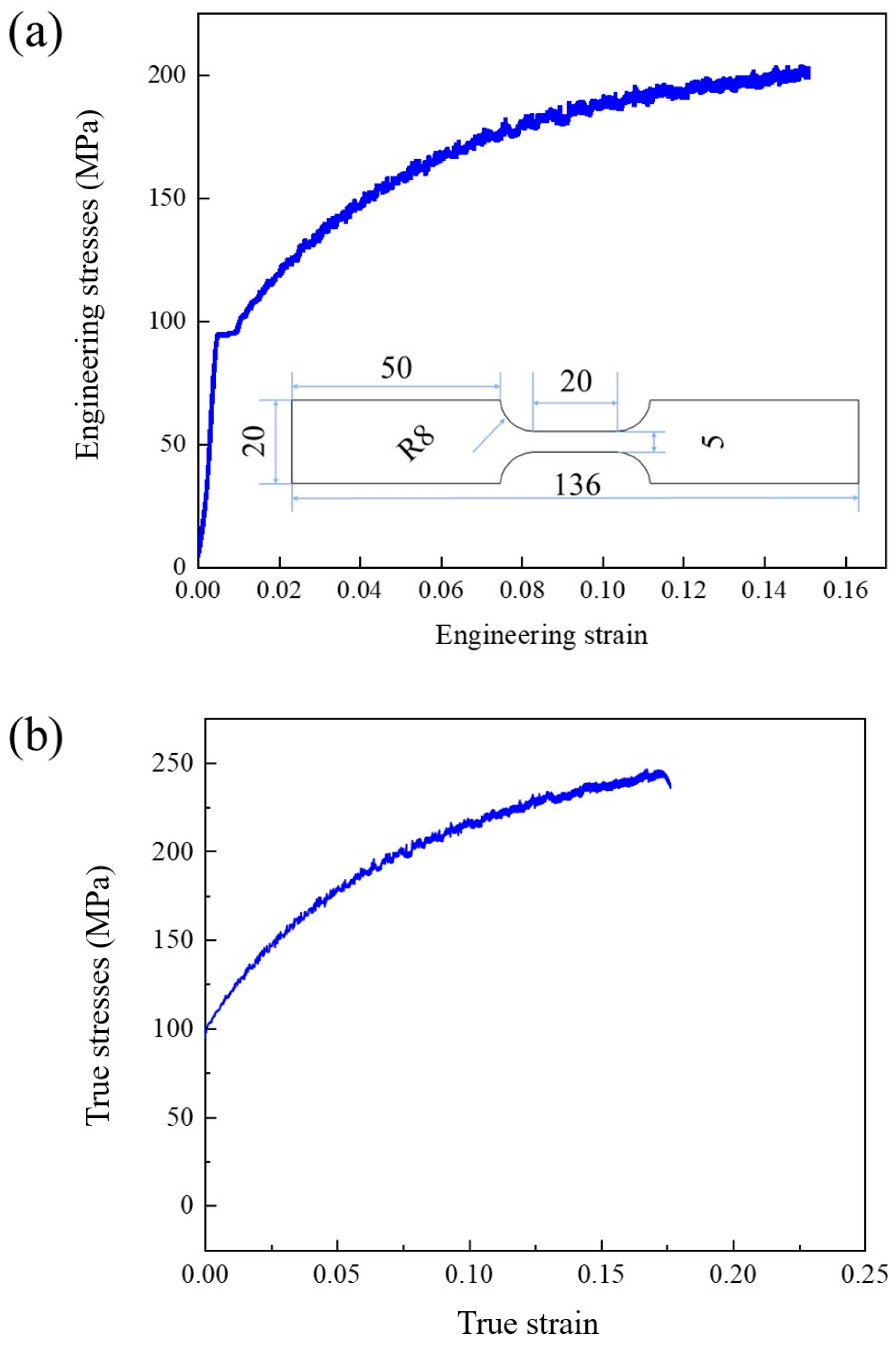
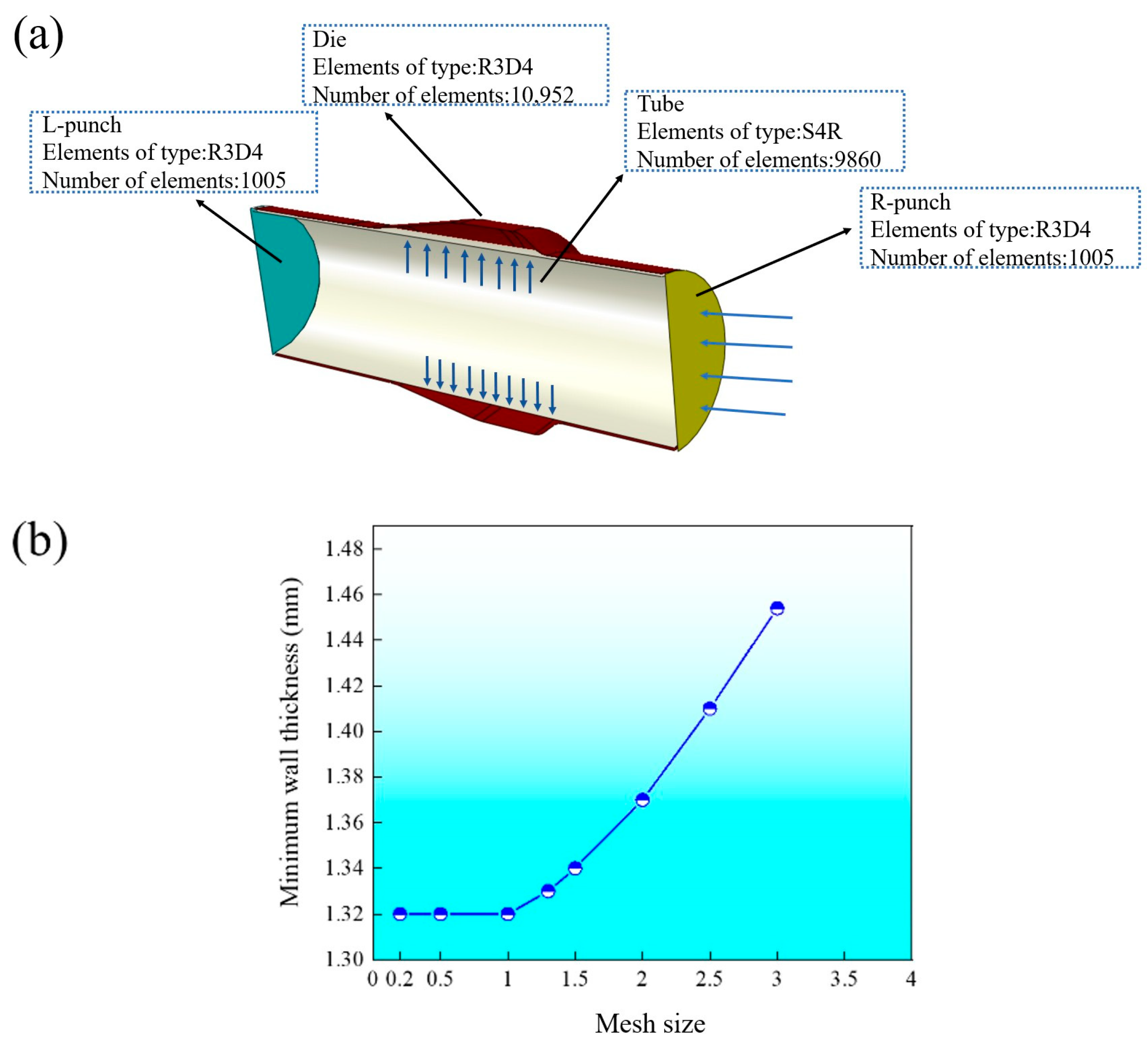
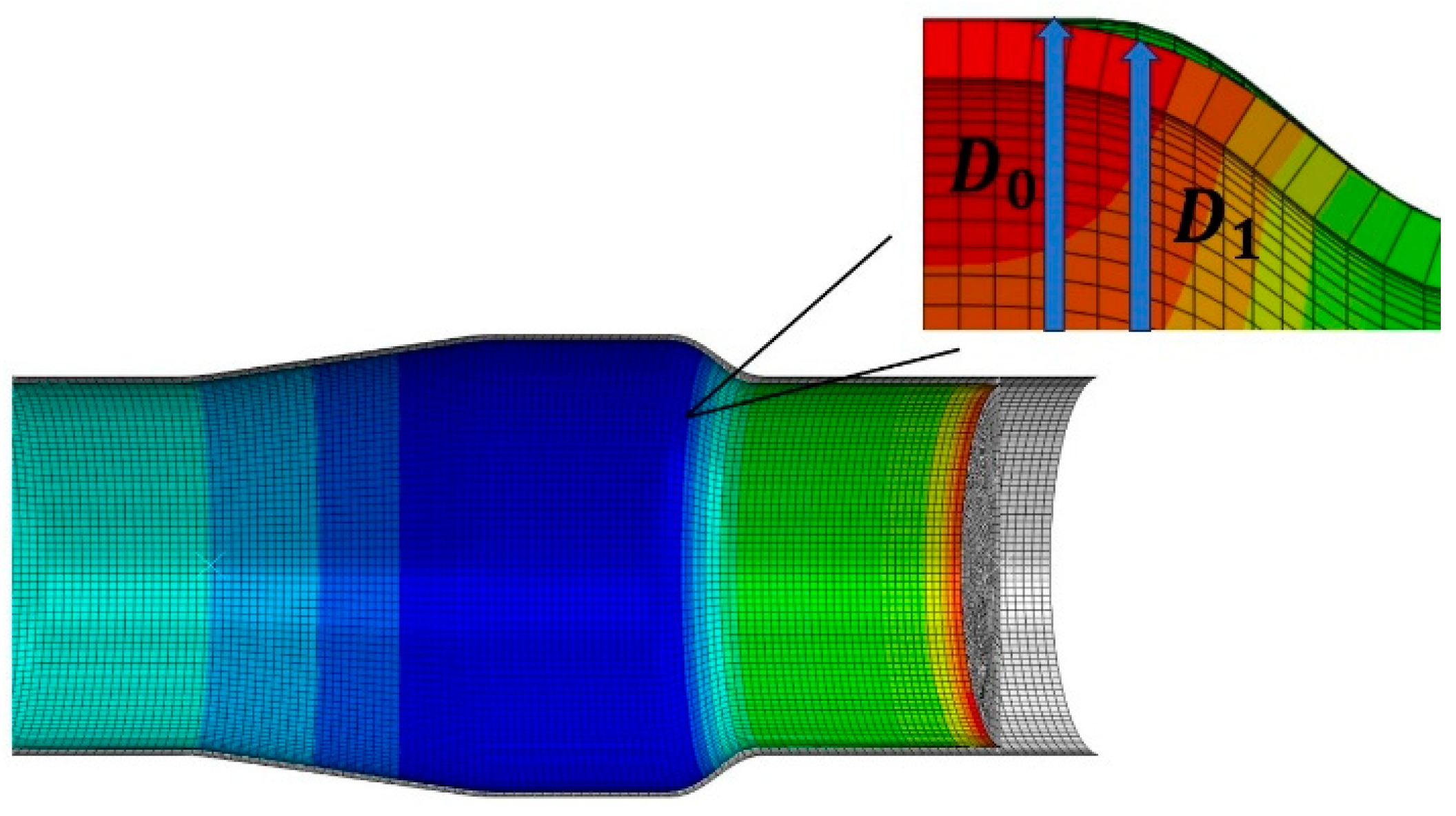
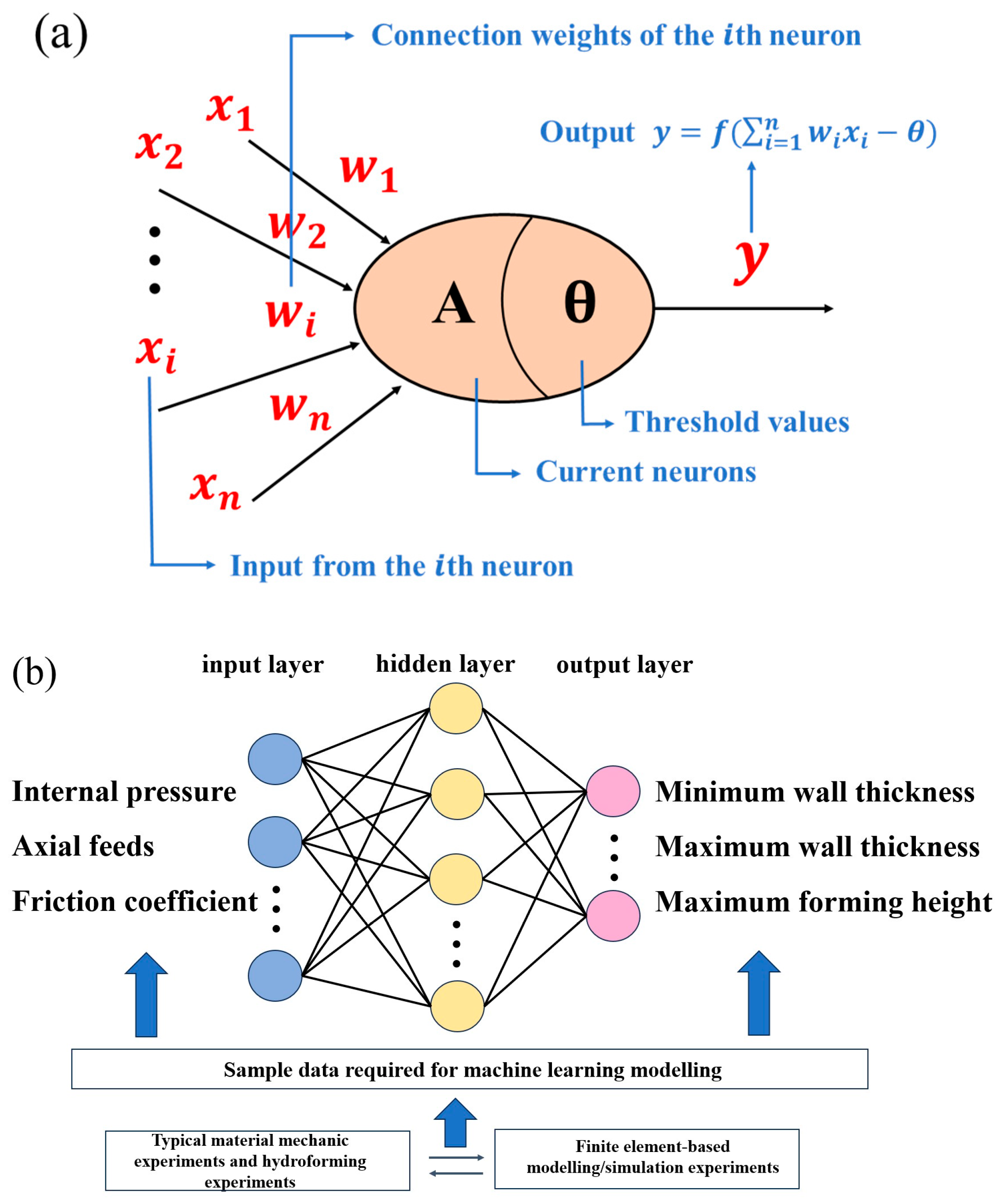
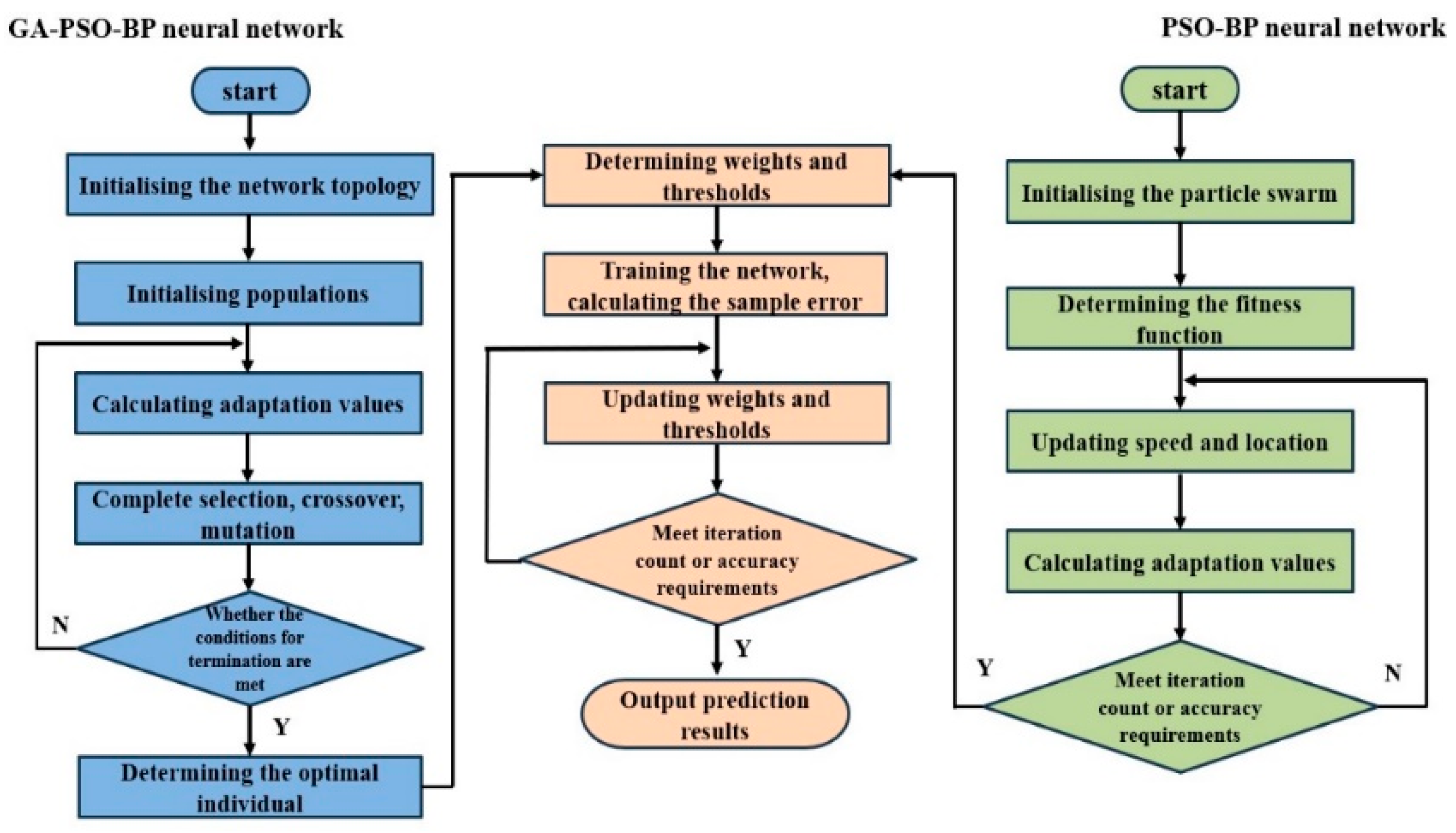
BP neural networks can approximate non-linear functions with arbitrary accuracy, but there are some drawbacks in use. In essence, the thresholds and weights are continuously adjusted by error back propagation and gradient descent, but, due to the cumbersome and slow error transfer process, the simulation results are unstable and prone to form local minima instead of global optimal solutions. There is also the problem that the selection of the number of hidden layer nodes and initial threshold weights is not supported by theoretical guidance. In this paper, two prediction models based on the particle swarm (PSO) optimisation of conventional BP neural network algorithms and the improvement of PSO-BP neural networks by introducing the hybridisation link in genetic algorithms (GA) are proposed for predicting the hydroforming effect.
4.3. GA-PSO-BP Model Accuracy Analysis
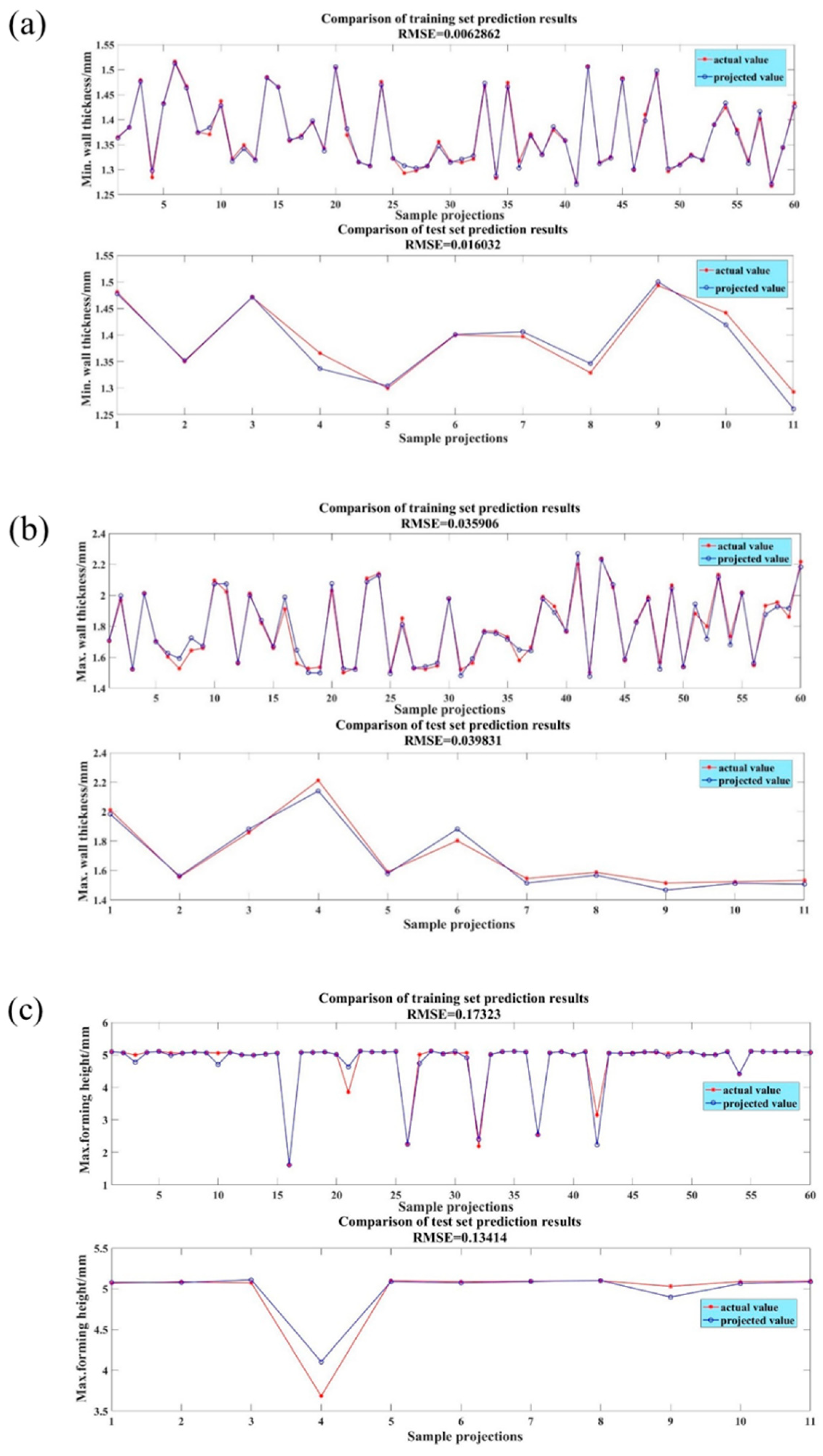
Comparison of the error results of the three prediction indexes (minimum wall thickness, maximum wall thickness, and maximum expansion height) based on the GA-PSO-BP neural network and the network performance evaluation results is shown in
Figure 9 and
Figure 10. Cross-validation was not utilised in the model construction for this research. The model accuracy was assessed through an evaluation of prediction errors across multiple forming quality metrics.
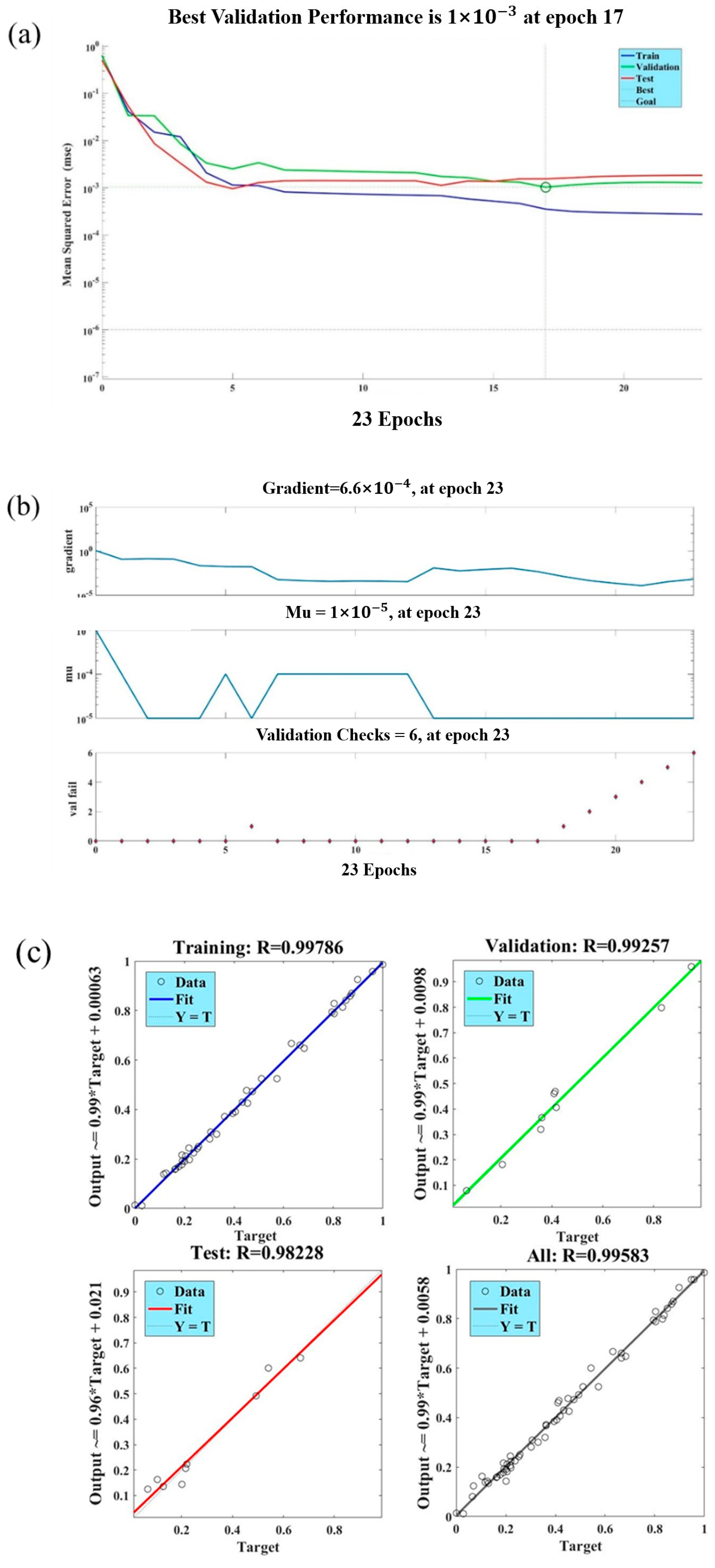
As shown in
Figure 9 and
Figure 10, the optimisation error is very small: the BP neural network was stopped for a total of 20 iterations and reached the optimal validation result at the 17th iteration with an MSE of 0.0010366. These errors indicate the accuracy of the proposed method in determining the optimal solution. An accurate prediction of tube hydroforming parameters is provided by the THF model based on the GA-PSO-BP neural network, which provides an effective tool for optimising tube hydroforming process parameters in the shortest possible time.
Figure 10c shows a plot of the predicted values of the neural network versus the actual values of the output patterns of the design matrix through the regression of training, validation, and test data. The coefficients of determination
for the training and test sets are 0.99786 and 0.98228. The artificial neural network-based THF model provides accurate predictions of the aluminium alloy variable diameter tubes, forming parameters with 98% confidence level. Therefore, there is a good correlation between measured and predicted values. Based on neural network analysis, axial feeds and forming pressure have a greater effect on tube thinning and the accuracy of dimensions.
4.4. Comparison of BP, PSO-BP, and GA-PSO-BP Calculation Accuracy
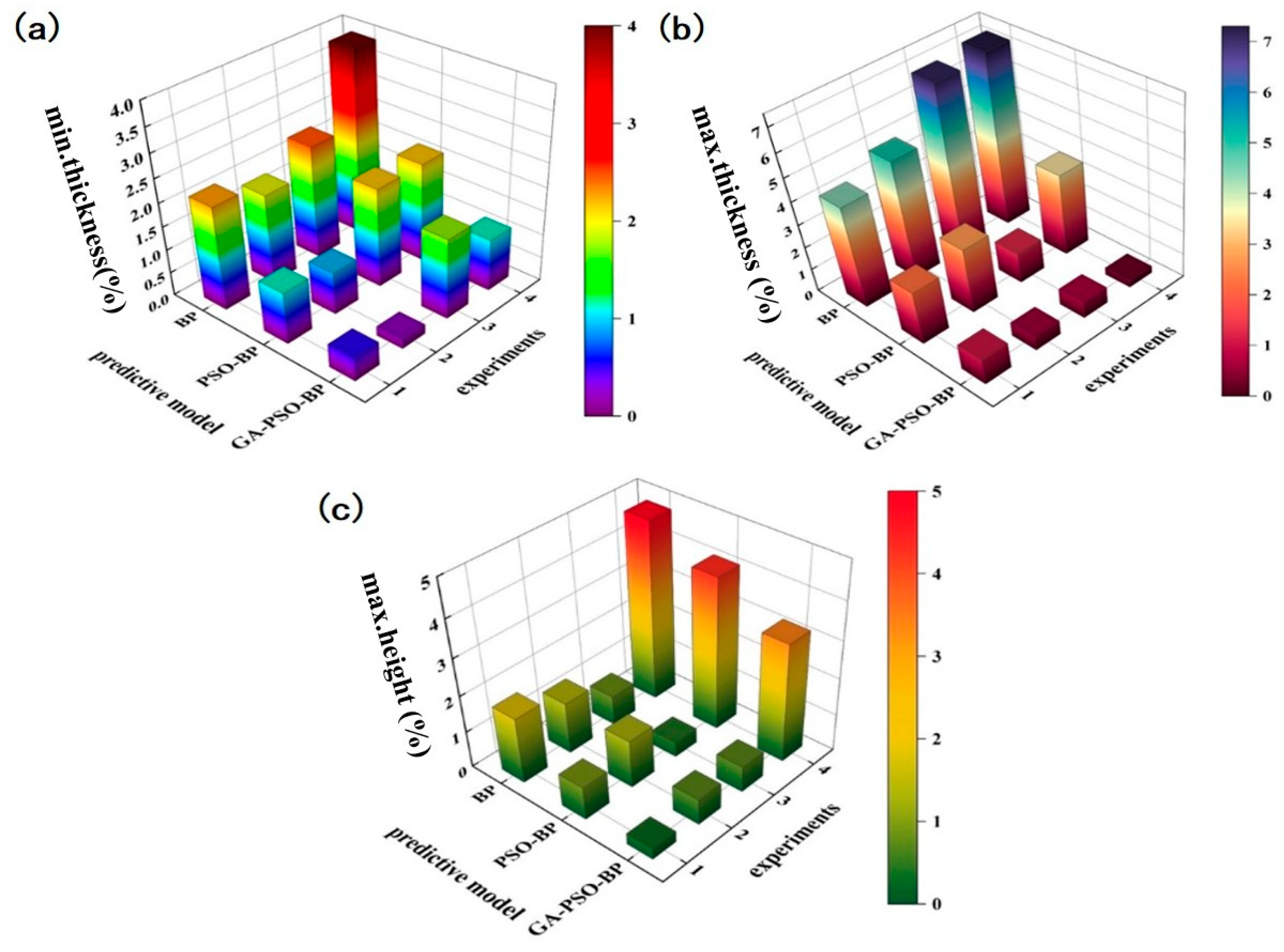
In order to further validate the prediction performance of the three machine learning prediction models, we combined these models with the simulation model of the EN AW 5052 aluminium alloy variable diameter tubes hydroforming constructed in the previous finite element simulation software. A comparison of the computational accuracy of models constructed based on BP neural networks and PSO-BP particle swarm optimisation neural network algorithms and models was based on genetically improved PSO-BP neural networks. The four sets of randomly selected data within the range of forming parameters need to be combined with the actual production experience of the aluminium alloy variable diameter tubes hydroforming and to avoid duplication with the database established in the previous section. The final set process parameters are shown in
Table 7. The error analysis of the prediction and simulation results using the three models is shown in
Figure 11.
Comparing the neural network prediction results and the finite element simulation results, it can be found that the neural network prediction model based on the GA-PSO-BP algorithm is in better agreement with the finite element simulation results. However, the second set of experiments shows from the input parameters and the forming effect that the condition is far from making the model reach the better-filled rate, and the deformation results of the tubes are not very informative. Therefore, the prediction result of the maximum expansion height of forming has a large error with the simulation result, and one of the reasons for the inaccurate prediction result is also related to the composition of the training set of the neural network model. In addition to this, the overall prediction accuracy is over 98%, which is a high prediction accuracy. It is fully demonstrated that the GA-PSO-BP neural network model for the prediction of hydraulic forming accuracy of the aluminium alloy variable diameter tubes established in this paper has good performance in the prediction of various parameters after forming, and it also verifies the reliability of the model in practical use.
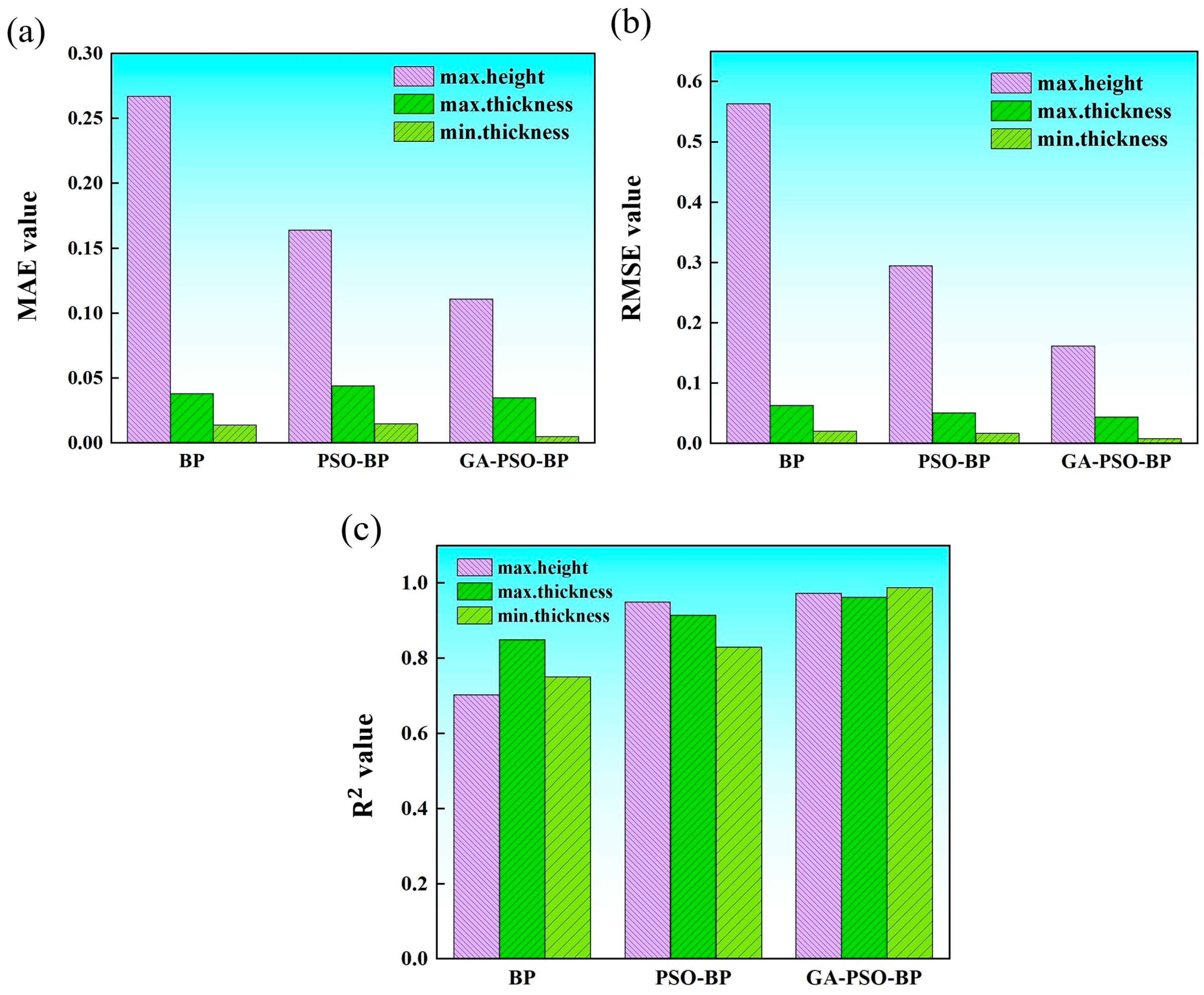
In order to more accurately judge the accuracy of the constructed model, in this paper, we will use the three performance metrics MAE, RMSE, and
mentioned in the previous section to compare the performance of BP, PSO-BP, GA-PSO-BP models, respectively. The error comparisons of the three specific forming parameters using the three different algorithms are shown in
Figure 12.
As can be seen from
Figure 12, the neural network model established directly based on the BP algorithm, when forming results are predicted for the four groups of randomly selected data, the results for the minimum wall thickness and the maximum wall thickness forming parameters with respect to the
evaluation indexes are 0.75 and 0.853, with a high prediction precision. However, the result for the maximum forming height with respect to the
evaluation index is 0.703, which is still a large error. The introduction of the particle swarm optimisation algorithm is used to replace the initialised weights in the former by iterative optimisation search, so that the results of the three shaping parameter
evaluation indexes of the improved model are 0.83, 0.915, and 0.950, and the prediction accuracy is effectively improved. However, the mean error function (MAE) is not greatly improved compared to the BP neural network. In order to balance the model’s ability to improve prediction accuracy while remaining as close as possible to the fitness obtained by fitting using the original test set, the hybridisation aspect of the genetic algorithm is introduced into the particle swarm iterative optimisation search process. Avoiding the phenomenon of the model falling into local search, it solves the problem that the model can easily fall into premature convergence and is unable to continue to iterate to seek the optimal solution when dealing with multi-dimensional problems, and it also achieves a balance between prediction accuracy and computational efficiency.
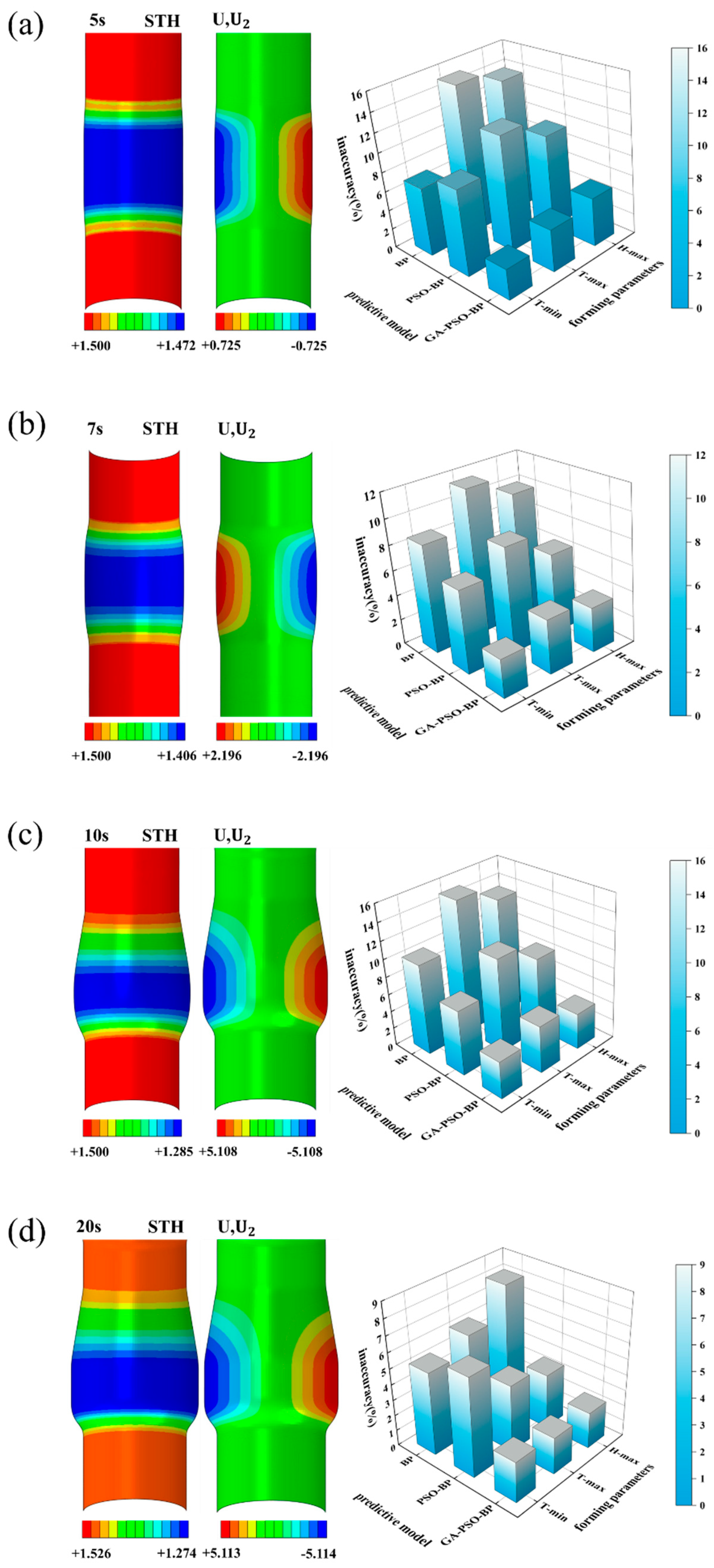
The process parameter combination for the hydroforming of aluminium alloy variable diameter tubes, which yielded the highest prediction accuracy, was determined using the GA-PSO-BP hybrid algorithm: The internal pressure is 40 MPa, the axial feed is 4 mm, and the friction coefficient is 0.15. After forming, the minimum wall thickness of the part is 1.27 mm, the maximum wall thickness is 1.53 mm, and the maximum height of forming is 5.11 mm. The finite element simulation results are shown in
Figure 13.
The specific forming process was divided into four stages of 5 s, 7 s, 10 s, and 20 s. The three neural network algorithms mentioned above were used to predict the three forming parameters, respectively, and, finally, the predicted values at different stages were compared with the simulated real values in terms of error. From the combined error comparison results, it was observed that the maximum expansion height parameter predictions exhibited larger errors across all three models. It was verified that the factors influencing expansion height were more complex during the initial hydroforming phase, when the tube first reached the state of plastic deformation, and before the tube reached the better-filled rate, as mentioned in the previous section. The influence of the aluminium large-section rate-of-change tube was included, which resulted in increased difficulty in achieving a linear relationship between the charge and internal pressure. Furthermore, the error comparison across different forming stages demonstrated that the forming parameter prediction errors of the GA-PSO-BP neural network model were maintained within ±4.5% for all stages.
4.5. Experimental Validation of Simulation Results
Hydroforming equipment and forming dies are shown in
Figure 14. The equipment is 315 t special hydraulic moulding equipment, driven by servo motors. The forming die mainly consists of left and right push heads, upper and lower dies, and the experimental process uses tensile oil as a lubricant between the tube and the die [
10].
Experimental testing of the simulation results used the previously mentioned machine learning forming parameters for aluminium alloy variable diameter tubes based on the GA-PSO-BP algorithm. The results were compared with the wall thickness and expansion height of the tube by selecting seven and five points at different locations on the outer contour of the axial profile of the tube. The results are shown in
Figure 15, and the experimental and simulation results for the maximum thinning and thickening rates after tube forming are 15.3%, 3.3%, 14%, and 1.7%. The error between the experimental results and the simulation results is within ±5% with high accuracy, and the feasibility of combining finite element simulation on the intelligent control method of the aluminium alloy large section rate of change tube hydroforming was also verified.
Friction plays a crucial role in tube hydroforming [
17]. Different coefficients of friction were achieved in the experiments through active lubrication or artificial roughness treatment. When the tube blank was left untreated, a coefficient of friction of approximately 0.12 was obtained. With active lubrication applied, the coefficient was reduced to about 0.05 [
18], whereas artificial roughness treatment resulted in a coefficient of 0.2. Additionally, the coefficient of friction could be adjusted by varying both the type of lubrication employed and the degree of roughness introduced through artificial treatment.