Short-Term Power Load Prediction of VMD-LSTM Based on ISSA Optimization
Abstract
1. Introduction
- (1)
- This study proposes a novel approach to determine the correlation between meteorological factors and the power load based on the Maximum Information Coefficient (MIC) combined with Variational Mode Decomposition (VMD) for decomposing power load series. Specifically, permutation entropy (PE) is employed to identify the optimal decomposition scale of VMD. PE is a method that can better adapt to the characteristics of signals and improve the accuracy and efficiency of signal decomposition, which can effectively mitigate the volatility and complexity of load data.
- (2)
- The Hilbert transform is applied to analytically transform the decomposed input signals, which is followed by constructing a variational problem. By introducing quadratic penalty terms and the Lagrange multiplier method, the augmented Lagrangian function is formulated to transform the constrained variational problem into an unconstrained one, which is then solved via iterative sequence updates.
- (3)
- To mitigate the subjective bias and prior knowledge dependency in LSTM networks, an Improved Sparrow Search Algorithm (ISSA) is developed to optimize four key hyperparameters, the learning rate (), number of hidden layer neurons (, ), and training batch size (), thereby enhancing short-term power load forecasting accuracy.
- (4)
- Experiments are conducted using datasets with varying input horizons and seasonal patterns from Detu’an City and a region in Australia, aiming to validate the proposed model’s stability and flexibility in short-term power load forecasting.
2. Fundamentals of the Model
2.1. Maximal Information Coefficient
2.2. Variational Mode Decomposition
2.3. Permutation Entropy
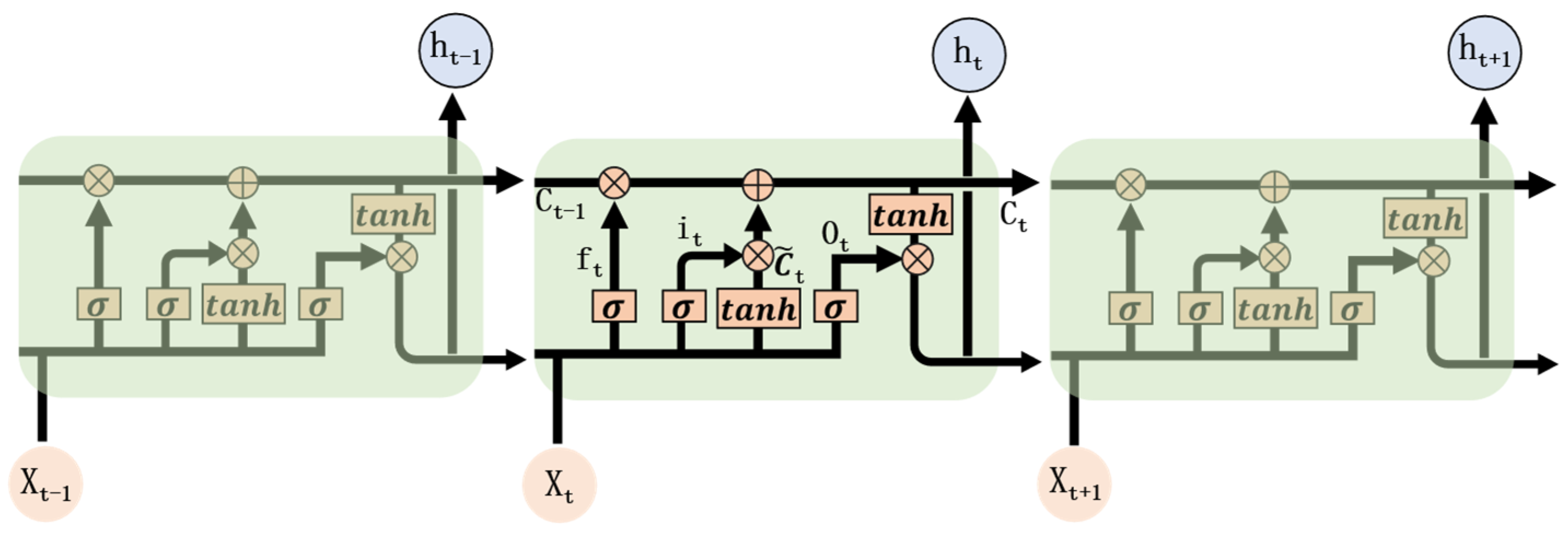
2.4. Long Short-Term Memory
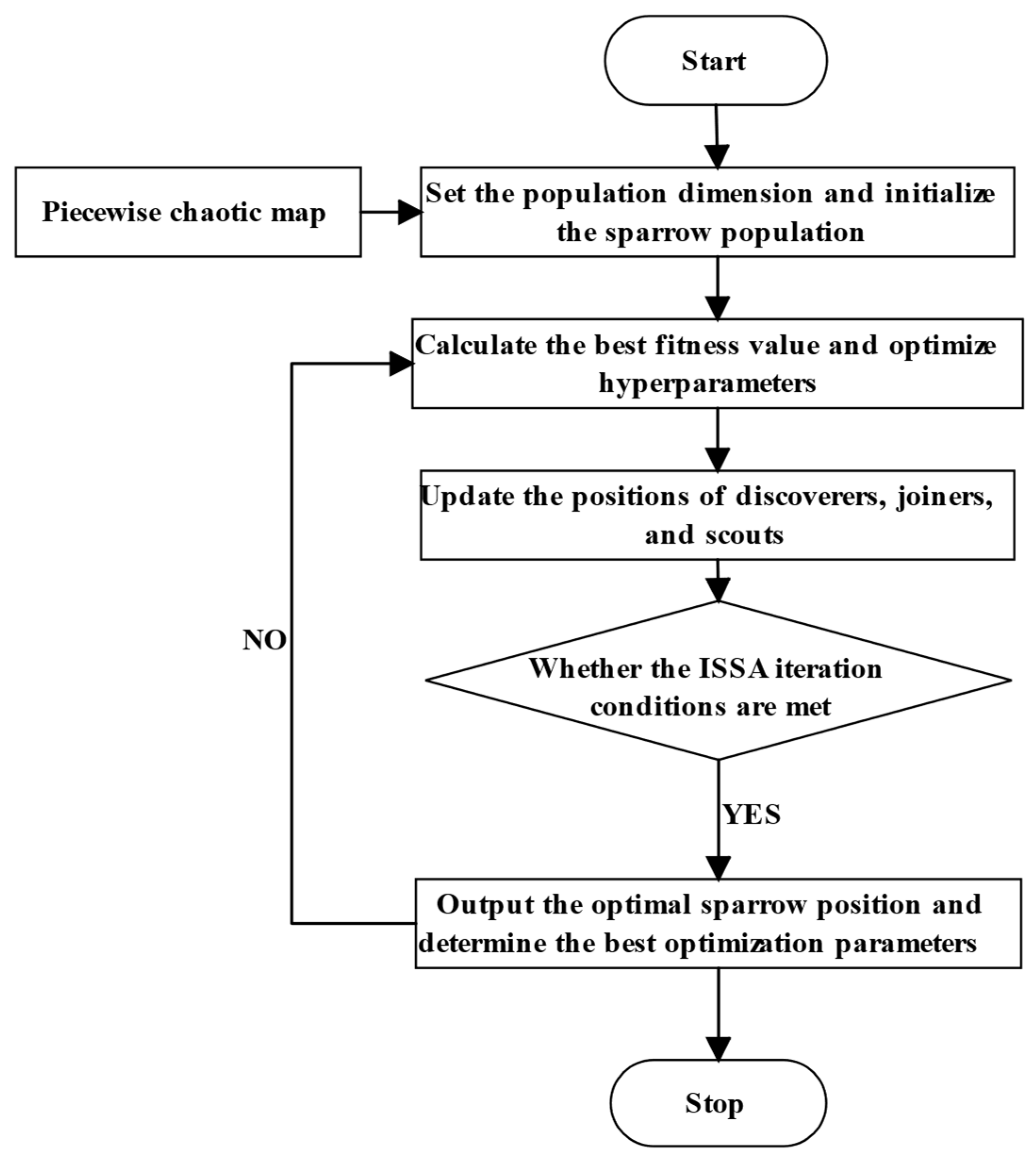
2.5. Sparrow Search Algorithm
| Algorithm 1: The framework of the SSA |
| Input: G: the maximum iterations |
| PD: the number of the producers |
| SD: the number of the sparrows who perceive the danger Establish an objective function ,where variable |
| Initialize a population of N sparrows and define its relevant parameters |
| Output: , 1: when the maximum iterations G is not met do 2: Rank the fitness values and find the current best individual and the current worst individual 3: 4: for 5: Using Equations (3) and (4) update the sparrow’s location 6: end for 7: for 8: Using Equations (3)–(5) update the sparrow’s location 9: end for 10: for 11: Using Equations (3)–(6) update the sparrow’s location 12: end for 13: Obtain the current new location 14: If the new location is better than before, update it 15: 16: end while 17: return |
2.6. Piecewise Chaos Mapping
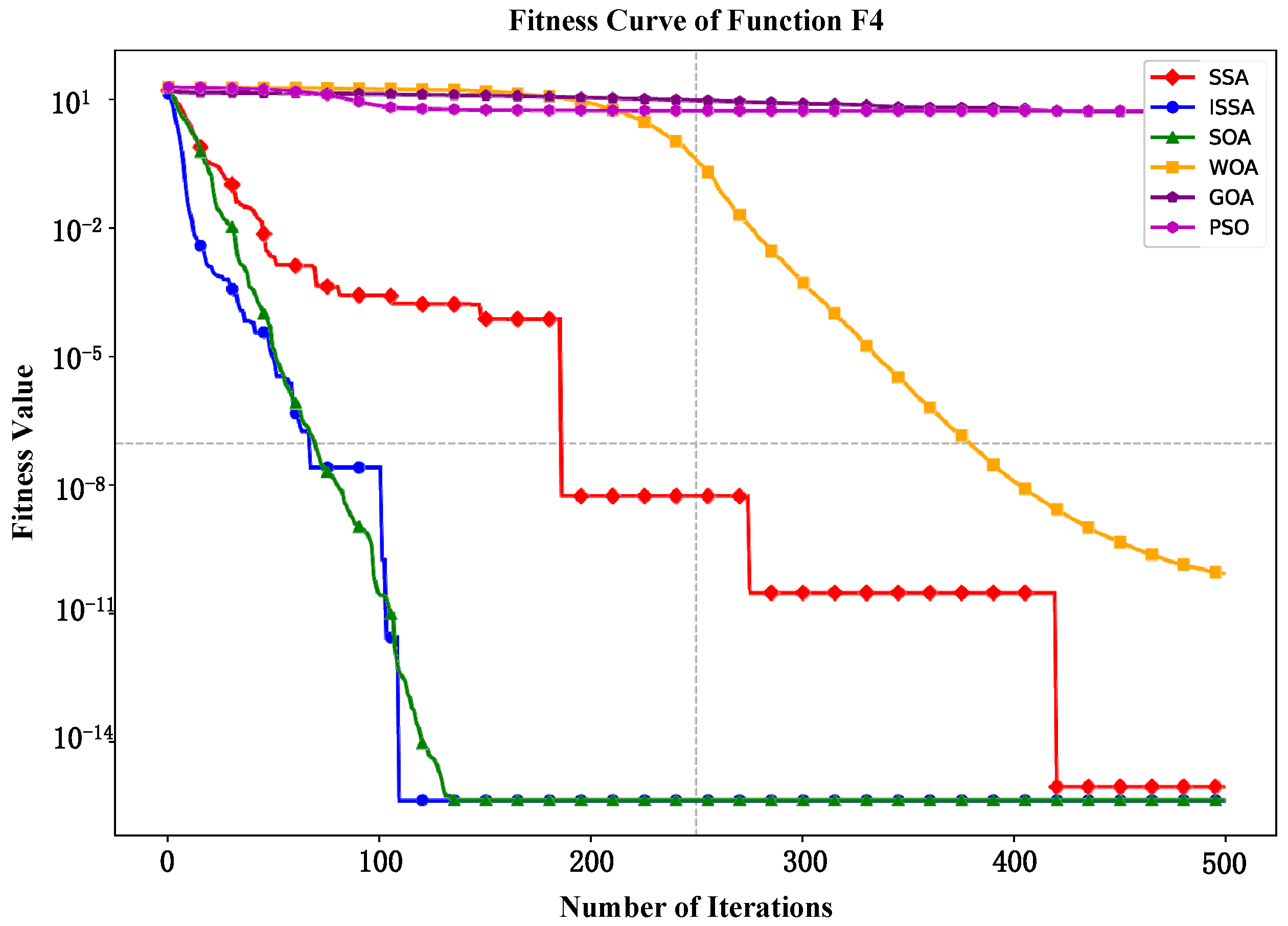
2.7. Testing the Performance of the ISSA Functions
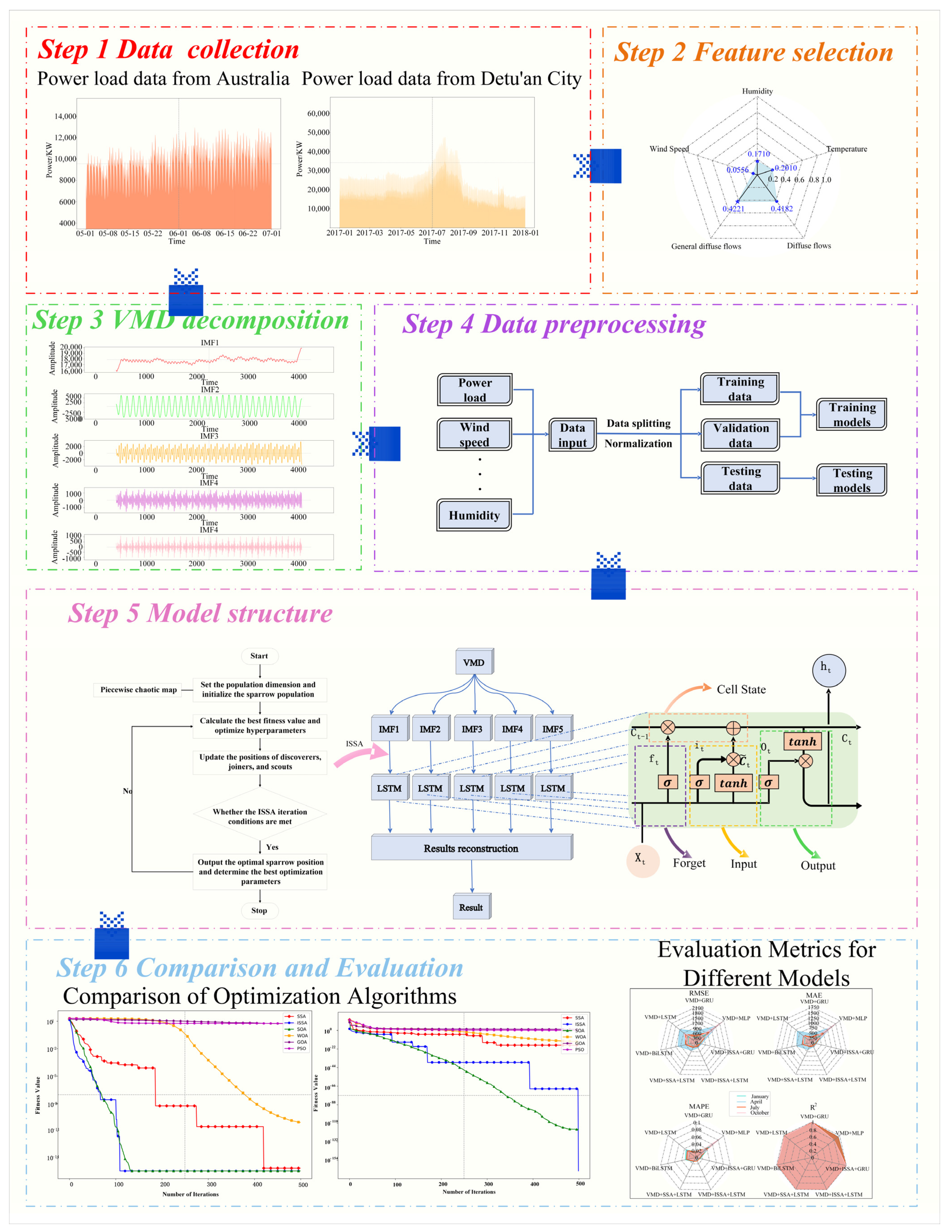
3. Structure of Prediction Model
4. Performance Indicators
5. Experiment and Analysis
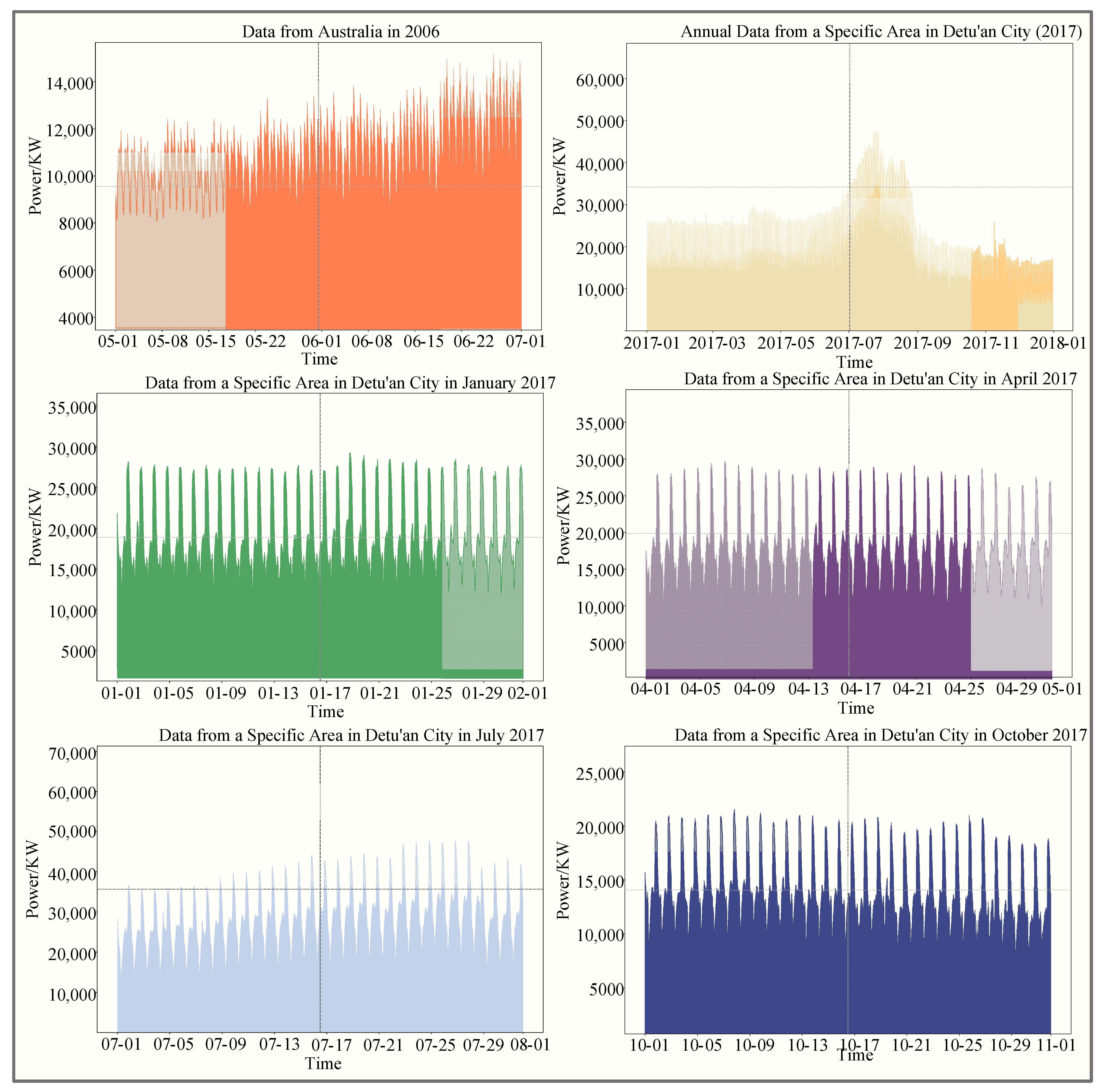
5.1. Data Description and Preprocessing
5.2. Parameter Settings
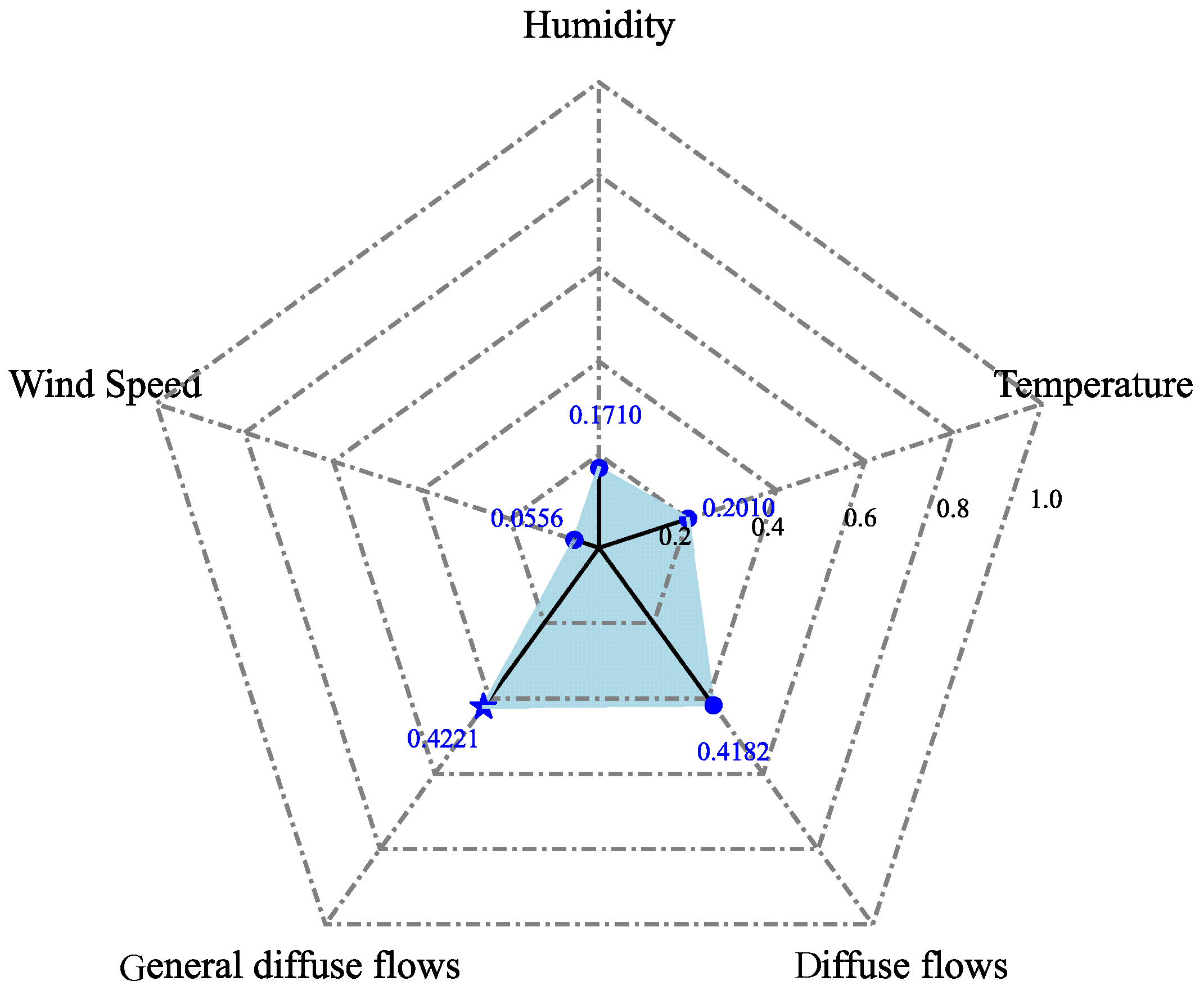
5.3. Feature Selection
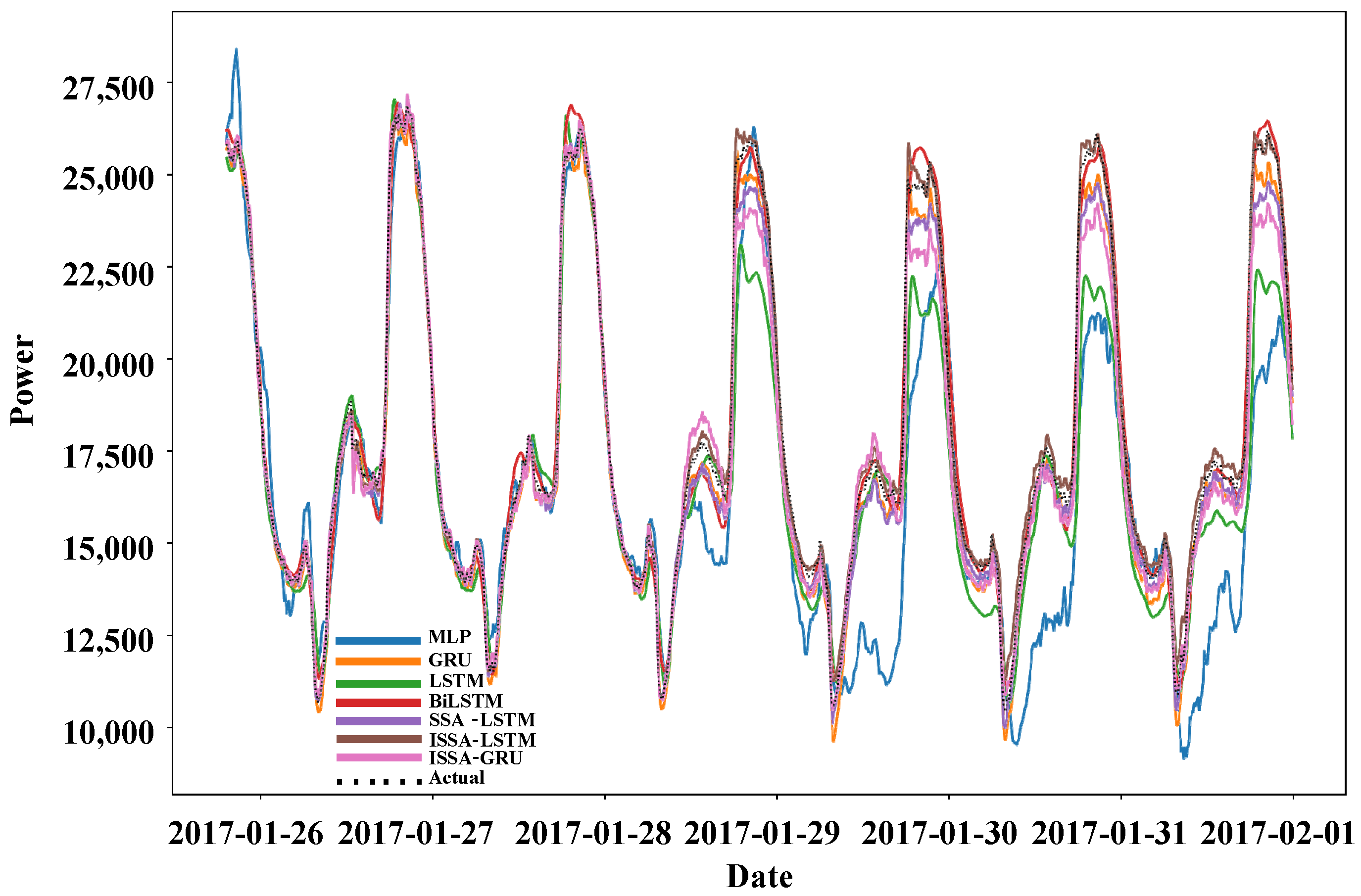
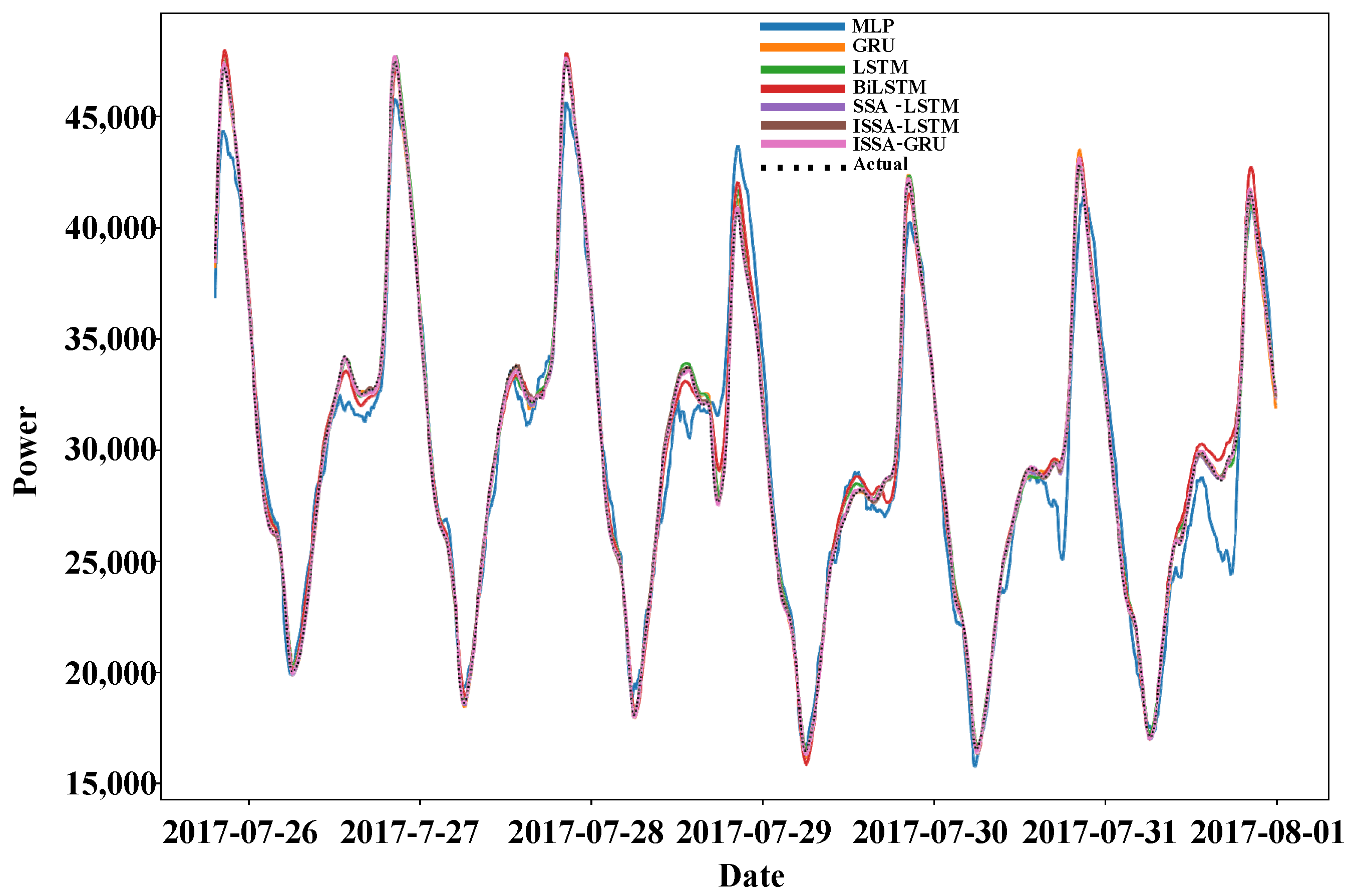
5.4. Example 1 Experiment
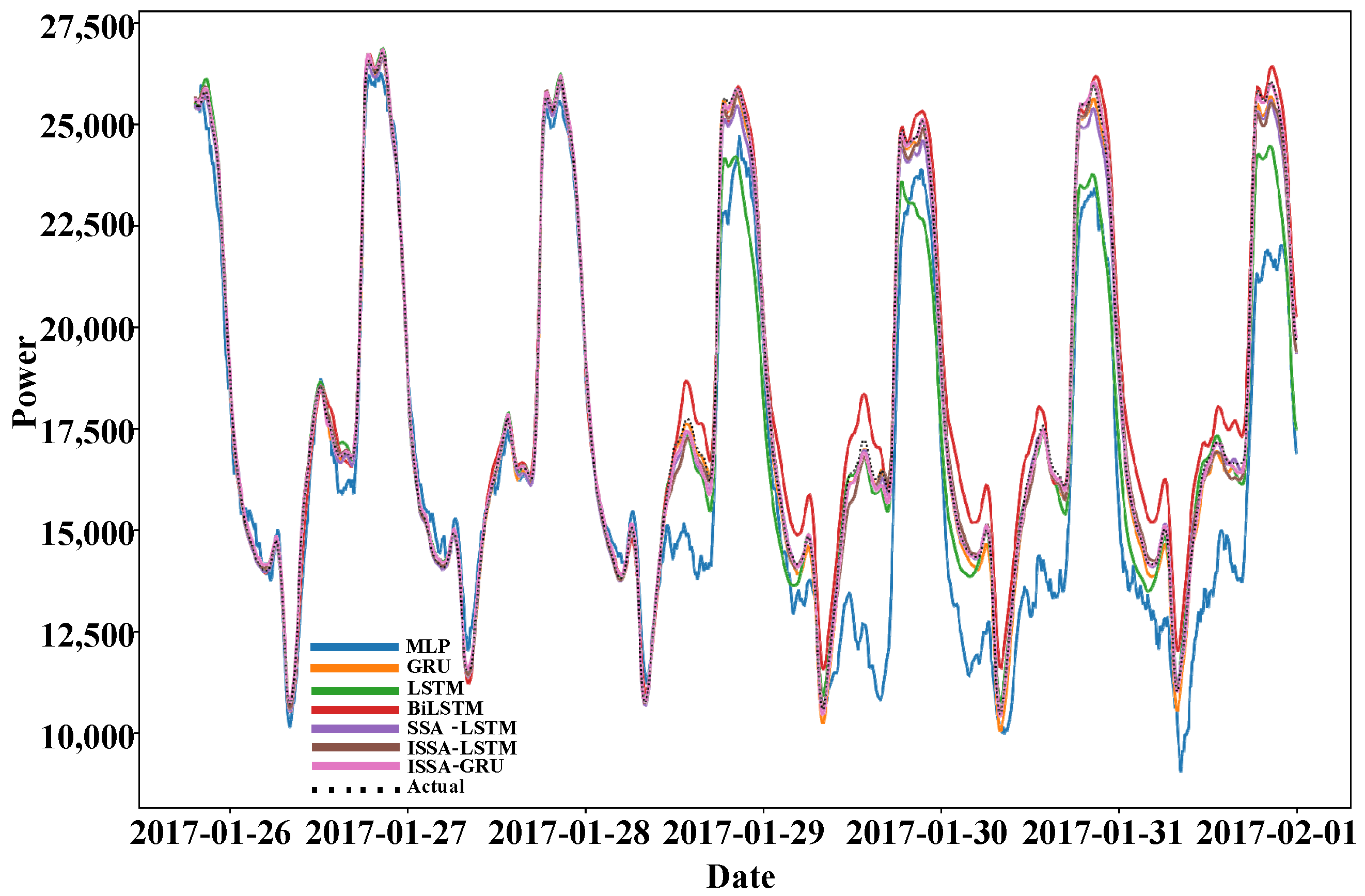
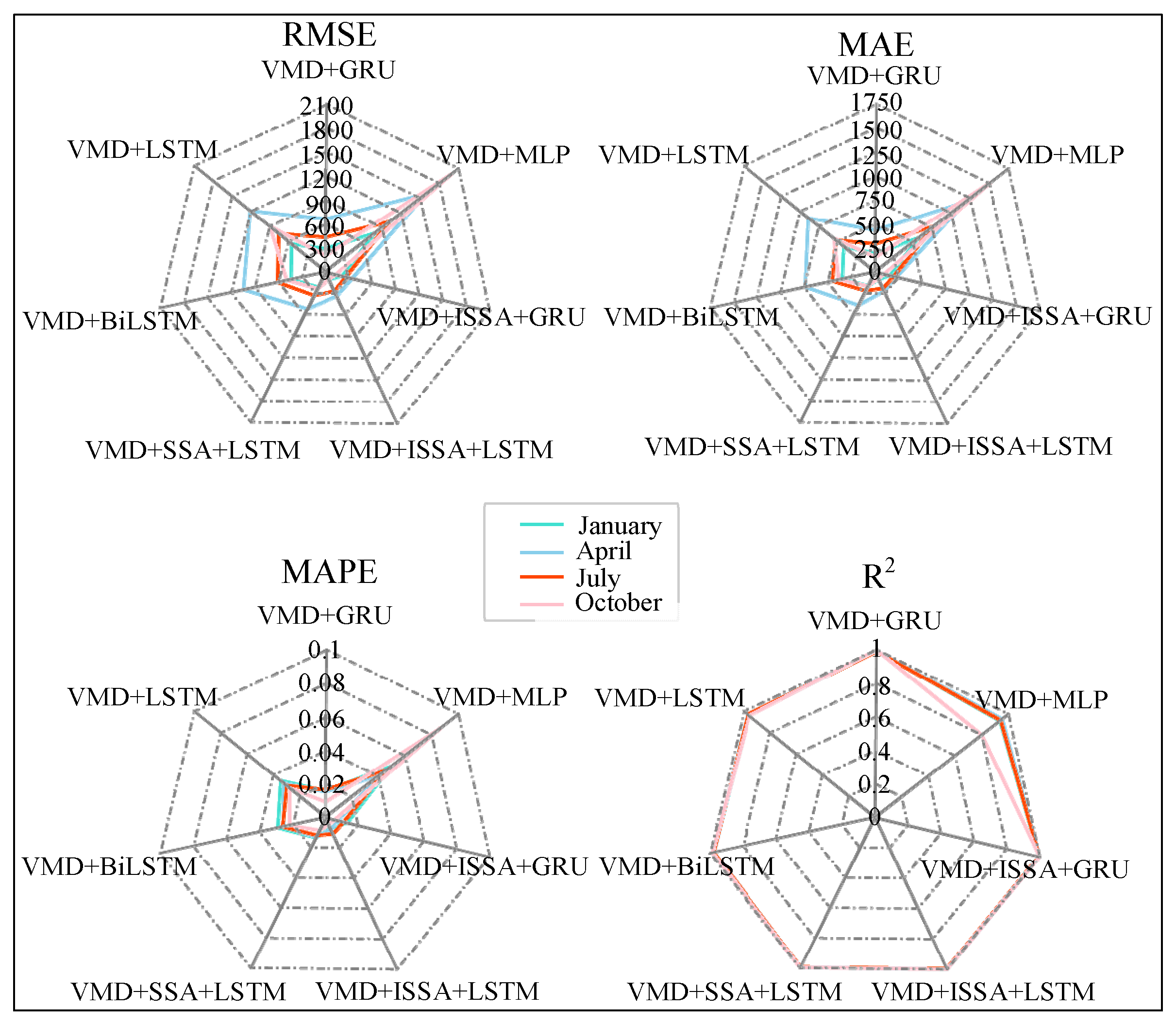
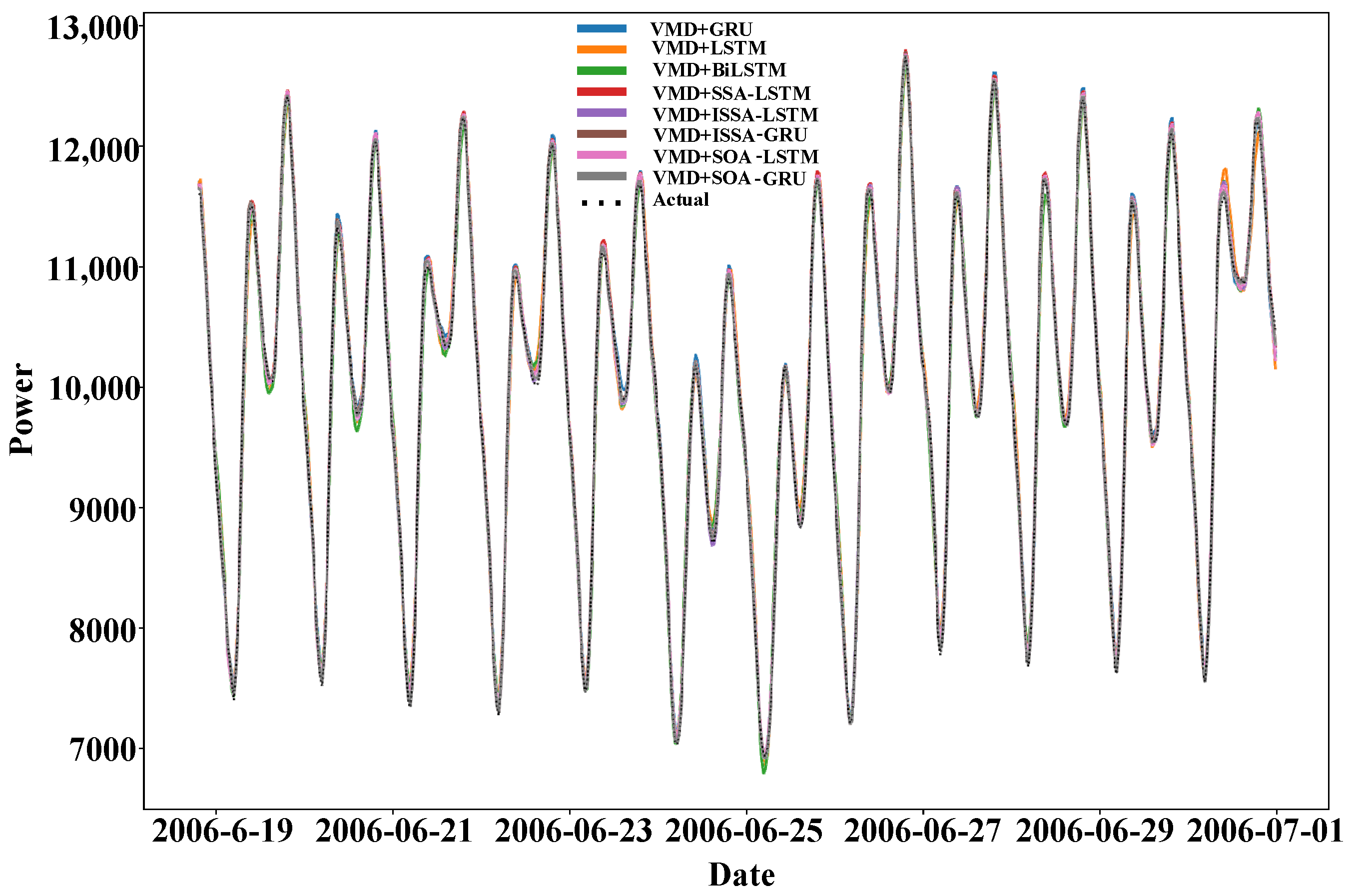
5.5. Example 2 Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Mi, J.; Fan, L.; Duan, X.; Qiu, Y. Short-term power load forecasting method based on improved exponential smoothing grey model. Math. Probl. Eng. 2018, 2018, 3894723. [Google Scholar] [CrossRef]
- Li, J.; Deng, D.; Zhao, J.; Cai, D.; Hu, W.; Zhang, M.; Huang, Q. A novel hybrid short-term load forecasting method of smart grid using MLR and LSTM neural network. IEEE Trans. Ind. Inform. 2020, 17, 2443–2452. [Google Scholar] [CrossRef]
- Yang, Z.; Ce, L.; Lian, L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA and kernel-based extreme learning machine methods. Appl. Energy 2017, 190, 291–305. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2017, 9, 5271–5280. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy 2019, 187, 115804. [Google Scholar] [CrossRef]
- Lv, L.; Wu, Z.; Zhang, J.; Zhang, L.; Tan, Z.; Tian, Z. A VMD and LSTM based hybrid model of load forecasting for power grid security. IEEE Trans. Ind. Inform. 2021, 18, 6474–6482. [Google Scholar] [CrossRef]
- Zhang, X.; Chau, T.K.; Chow, Y.H.; Fernando, T.; Iu, H.H.C. A novel sequence to sequence data modelling based CNN-LSTM algorithm for three years ahead monthly peak load forecasting. IEEE Trans. Power Syst. 2023, 39, 1932–1947. [Google Scholar]
- Li, C.; Tang, G.; Xue, X.; Saeed, A.; Hu, X. Short-term wind speed interval prediction based on ensemble GRU model. IEEE Trans. Sustain. Energy 2019, 11, 1370–1380. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-term electricity load forecasting model based on EMD-GRU with feature selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Chiu, M.C.; Hsu, H.W.; Chen, K.S.; Wen, C.Y. A hybrid CNN-GRU based probabilistic model for load forecasting from individual household to commercial building. Energy Rep. 2023, 9, 94–105. [Google Scholar] [CrossRef]
- Pang, S.; Zou, L.; Zhang, L.; Wang, H.; Wang, Y.; Liu, X.; Jiang, J. A hybrid TCN-BiLSTM short-term load forecasting model for ship electric propulsion systems combined with multi-step feature processing. Ocean Eng. 2025, 316, 119808. [Google Scholar] [CrossRef]
- Xu, H.; Fan, G.; Kuang, G.; Song, Y. Construction and application of short-term and mid-term power system load forecasting model based on hybrid deep learning. IEEE Access 2023, 11, 37494–37507. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, J.; Ning, E.; Zhang, C.; Wang, Z.; Jiang, E. Short-term power load forecasting: An integrated approach utilizing variational mode decomposition and TCN–BiGRU. Energies 2023, 16, 6625. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, P.; Ma, N.; Liu, G. Robust wavelet transform neural-network-based short-term load forecasting for power distribution networks. Sustainability 2022, 15, 296. [Google Scholar] [CrossRef]
- Wu, Y.; Cong, P.; Wang, Y. Charging load forecasting of electric vehicles based on VMD-SSA-SVR. IEEE Trans. Transp. Electrif. 2023, 10, 3349–3362. [Google Scholar] [CrossRef]
- Li, S.; Cai, H. Short-Term Power Load Forecasting Using a VMD-Crossformer Model. Energies 2024, 17, 2773. [Google Scholar] [CrossRef]
- Tang, Y.; Cai, H. Short-term power load forecasting based on vmd-pyraformer-adan. IEEE Access 2023, 11, 61958–61967. [Google Scholar] [CrossRef]
- Sun, Q.; Cai, H. Short-term power load prediction based on VMD-SG-LSTM. IEEE Access 2022, 10, 102396–102405. [Google Scholar] [CrossRef]
- Liu, J.; Cong, L.; Xia, Y.; Pan, G.; Zhao, H.; Han, Z. Short-term power load prediction based on DBO-VMD and an IWOA-BILSTM neural network combination model. Power Syst. Prot. Control 2024, 52, 123–133. [Google Scholar]
- Mounir, N.; Ouadi, H.; Jrhilifa, I. Short-term electric load forecasting using an EMD-BI-LSTM approach for smart grid energy management system. Energy Build. 2023, 288, 113022. [Google Scholar] [CrossRef]
- Deng, D.; Li, J.; Zhang, Z.; Teng, Y.; Huang, Q. Short-term Electric Load Forecasting Based on EEMD-GRU-MLR. Power Syst. Technol. 2020, 44, 593–602. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, Z.; Zhang, H.; Wang, X.; Guo, Y. A short-term wind power prediction model based on CEEMD and WOA-KELM. Renew. Energy 2022, 189, 188–198. [Google Scholar] [CrossRef]
- Liu, J.; Jin, Y.; Tian, M. Multi-Scale Short-Term Load Forecasting Based on VMD and TCN. J. Univ. Electron. Sci. Technol. China 2022, 51, 550–557. [Google Scholar] [CrossRef]
- Wang, X.; Sun, N.; Su, H.; Zhang, N.; Zhang, S.; Ji, J. Ultra-short-term wind speed prediction based on sample entropy-based dual decomposition and ssa-lstm. Acta Energiae Solaris Sin. 2025, 46, 611–618. [Google Scholar]
- Zhang, H.; He, S. Analysis and comparison of permutation entropy, approximate entropy and sample entropy. In Proceedings of the 2018 International Symposium on Computer, Consumer and Control (IS3C), Taichung, Taiwan, 6–8 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 209–212. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef]
- Yao, W.-P.; Liu, T.-B.; Dai, J.-F.; Wang, J. Multiscale permutation entropy analysis of electroencephalogram. Acta Phys. Sin. 2014, 63, 078704. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Tang, Y.; Li, C.; Song, Y.; Chen, C.; Cao, B. Adaptive mutation sparrow search optimization algorithm. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 681–692. (In Chinese) [Google Scholar] [CrossRef]
- Yang, H.Z.; Tian, F.M.; Zhang, P. Short-term load forecasting based on CEEMD-FE-AOA-LSSVM. Power Syst. Prot. Control 2022, 50, 126–133. [Google Scholar]




| Reference | Model | Limitations | Optimization |
|---|---|---|---|
| Wang Y, Guo P et al. [15] | Wavelet Transform-LSTM | Manually adjust the model parameters | No |
| Mounir N, Ouadi H et al. [21] | EMD-BiLSTM | High computational cost, modal aliasing | No |
| DENG Daiyu, LI Jian et al. [22] | EEMD-GRU-MLR | Residual noise | No |
| Ding Y, Chen Z, Zhang H et al. [23] | CEEMD-WOA-KELM | Prone to local optima, sensitive to initial parameters | Yes |
| LIU Jie, JIN Yongjie et al. [24] | VMD-TCN- Multi-Scale | Complex preprocessing, high implementation requirements | No |
| Function | Definition | Minimum Value | |
|---|---|---|---|
| Unimodal function | [−100,100] | 0 | |
| [−10,10] | 0 | ||
| Multimodal function | [−5.12,5.12] | 0 | |
| [−32,32] | 0 | ||
| [−5,5] | −1.0316 |
| Function | Algorithms | |||||
|---|---|---|---|---|---|---|
| ISSA | SSA | SOA | WOA | GOA | PSO | |
| 0 | 3.44 × 10−57 | 3.6 × 10−194 | 6.01 × 10−20 | 35.8871 | 0.1803 | |
| 2.9 × 10−167 | 3.12 × 10−18 | 8 × 10−118 | 6.18 × 10−14 | 20.8136 | 1.5318 | |
| 0 | 0 | 0 | 8.88 × 10−16 | 97.5923 | 25.2767 | |
| 4.44 × 10−16 | 9.18 × 10−16 | 4.44 × 10−16 | 8.92 × 10−11 | 5.4898 | 5.7464 | |
| −1.0316 | −1.0314 | −1.0316 | −1.0318 | −1.0318 | −1.0319 | |
| Model | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|
| MLP | 2507.245 | 1750.557 | 0.0964 | 0.6881 |
| GRU | 595.862 | 481.433 | 0.0275 | 0.9824 |
| LSTM | 1618.641 | 1081.296 | 0.0562 | 0.87 |
| BiLSTM | 614.801 | 457.115 | 0.0288 | 0.9811 |
| SSA-LSTM | 568.124 | 413.67 | 0.0219 | 0.984 |
| ISSA-LSTM | 350.546 | 252.363 | 0.0156 | 0.9939 |
| ISSA-GRU | 378.244 | 284.721 | 0.0159 | 0.9929 |
| K | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| mean | 0.9571 | 0.9546 | 0.9964 | 1.0314 | 1.06 | 1.0954 |
| Model | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|
| VMD+MLP | 2001.793 | 1526.295 | 0.087 | 0.7991 |
| VMD+GRU | 194.987 | 150.36 | 0.009 | 0.9981 |
| VMD+LSTM | 901.112 | 552.269 | 0.0276 | 0.9593 |
| VMD+BiLSTM | 501.163 | 386.788 | 0.0221 | 0.9875 |
| VMD-SSA-LSTM | 236.234 | 168.452 | 0.0087 | 0.9972 |
| VMD+ISSA-LSTM | 104.982 | 78.848 | 0.0047 | 0.9994 |
| VMD+ISSA-GRU | 141.247 | 100.078 | 0.0059 | 0.999 |
| Season | April | July | October | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE |
| VMD+MLP | 1018.263 | 770.78 | 0.0451 | 1584.604 | 1186.17 | 0.0402 | 781.282 | 574.361 | 0.0498 |
| VMD+GRU | 430.194 | 291.529 | 0.0164 | 663.289 | 433.022 | 0.0153 | 287.508 | 188.909 | 0.0156 |
| VMD+LSTM | 754.787 | 526.324 | 0.0299 | 1212.44 | 891.908 | 0.0322 | 550.135 | 417.819 | 0.0346 |
| VMD+BiLSTM | 614.344 | 452.81 | 0.0263 | 1047.672 | 740.127 | 0.0258 | 444.559 | 347.524 | 0.0292 |
| VMD+SSA+LSTM | 329.864 | 221.714 | 0.0119 | 516.604 | 389.036 | 0.0131 | 214.702 | 164.894 | 0.0135 |
| VMD+ISSA-LSTM | 267.966 | 191.303 | 0.0109 | 337.406 | 222 | 0.008 | 107.452 | 87.668 | 0.0072 |
| VMD+ISSA-GRU | 269.221 | 200.741 | 0.0114 | 348.445 | 229.263 | 0.008 | 223.079 | 161.535 | 0.0135 |
| Model | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|
| VMD+GRU | 64.964 | 52.356 | 0.0053 | 0.9977 |
| VMD+LSTM | 110.84 | 88.078 | 0.0089 | 0.9933 |
| VMD+BiLSTM | 97.052 | 76.839 | 0.0078 | 0.9949 |
| VMD+SSA-LSTM | 51.457 | 42.298 | 0.0043 | 0.9986 |
| VMD+ISSA-LSTM | 28.892 | 23.527 | 0.0024 | 0.9995 |
| VMD+ISSA-GRU | 31.62 | 26.01 | 0.0026 | 0.9995 |
| VMD+SOA-LSTM | 32.366 | 26.274 | 0.0026 | 0.9994 |
| VMD+SOA-GRU | 49.082 | 40.303 | 0.0041 | 0.9987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Cai, H. Short-Term Power Load Prediction of VMD-LSTM Based on ISSA Optimization. Appl. Sci. 2025, 15, 5037. https://doi.org/10.3390/app15095037
Wu S, Cai H. Short-Term Power Load Prediction of VMD-LSTM Based on ISSA Optimization. Applied Sciences. 2025; 15(9):5037. https://doi.org/10.3390/app15095037
Chicago/Turabian StyleWu, Shuai, and Huafeng Cai. 2025. "Short-Term Power Load Prediction of VMD-LSTM Based on ISSA Optimization" Applied Sciences 15, no. 9: 5037. https://doi.org/10.3390/app15095037
APA StyleWu, S., & Cai, H. (2025). Short-Term Power Load Prediction of VMD-LSTM Based on ISSA Optimization. Applied Sciences, 15(9), 5037. https://doi.org/10.3390/app15095037






