A Deep Reinforcement Learning-Based Decision-Making Approach for Routing Problems
Abstract
1. Introduction
- We propose a DRL-based decision-making approach designed to address routing problems across varying problem sizes and node distributions.
- We develop a dynamic-aware context embedding that explicitly captures state transitions and graph variations during route construction, enhancing the model’s ability to adapt to changing environments.
- We conduct extensive experiments demonstrating that our approach achieves substantial improvements in both solution quality and computational efficiency, establishing a new benchmark for learning-based routing optimization.
2. Related Work
2.1. Traditional Methods
2.2. DRL-Based Methods
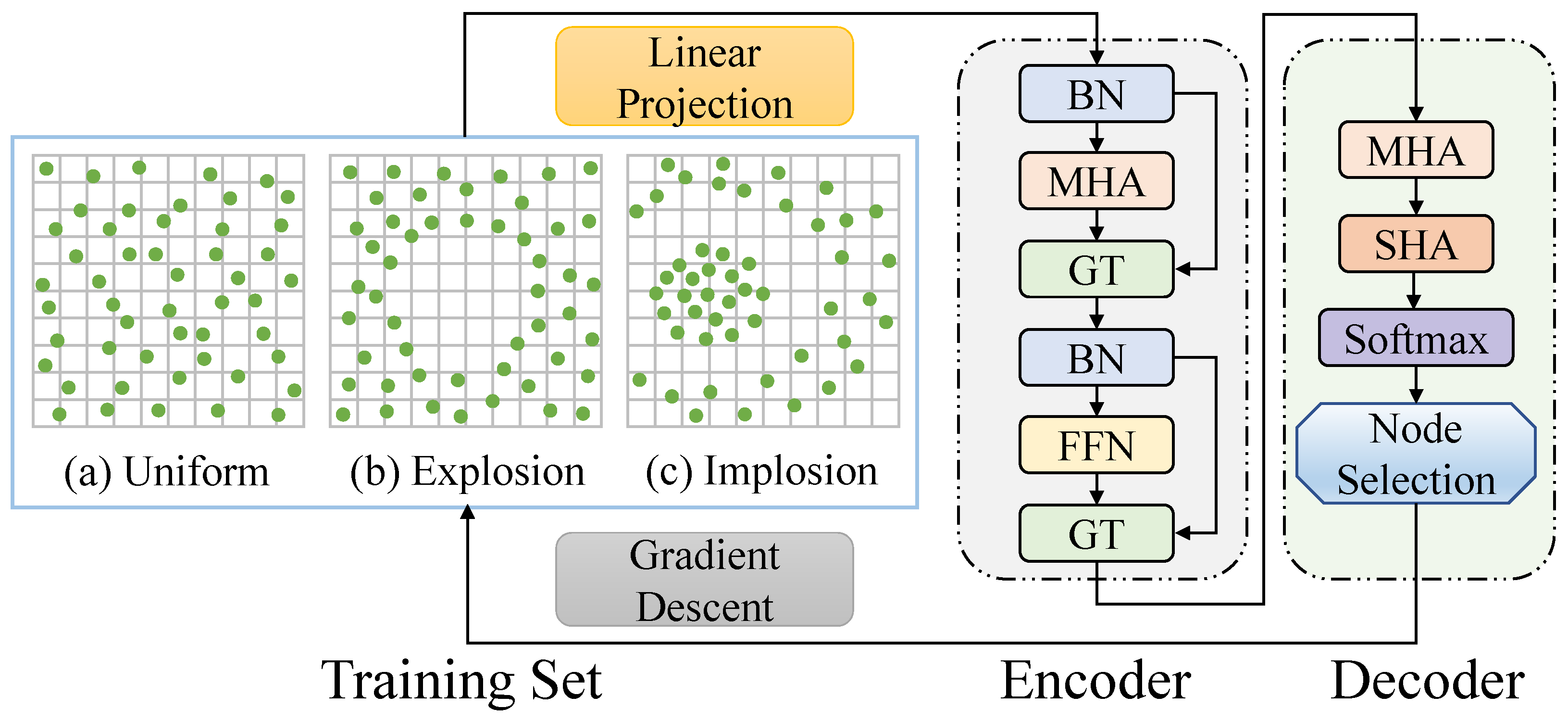
3. Methodology
3.1. Mathematical Framework
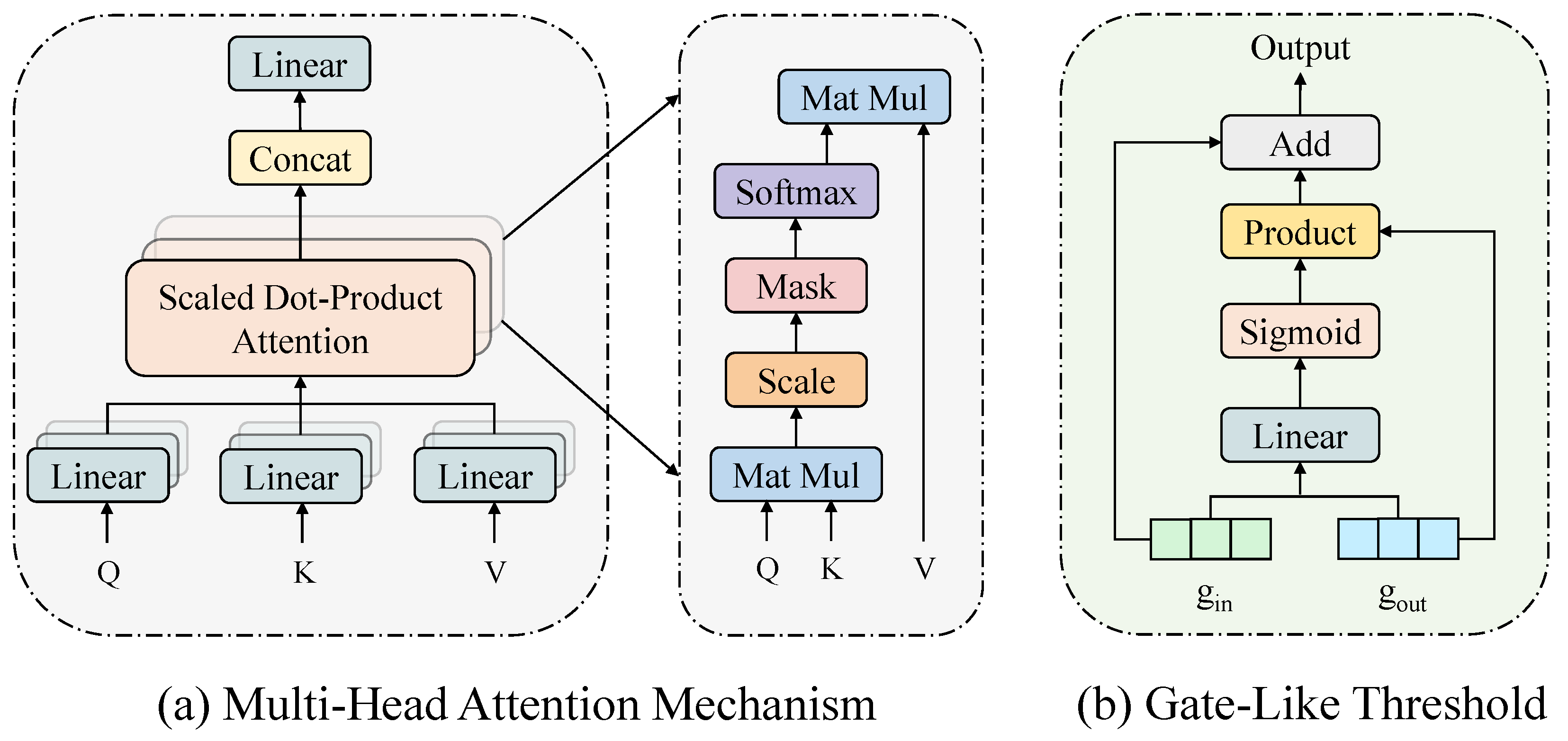
3.2. Encoder
3.3. Decoder
3.4. Trainer
4. Experiments
4.1. Experimental Settings
4.2. Comparison Analysis
- (1)
- Concorde [14]: A mature exact solver tailored for TSPs, which has been applied to scenes like vehicle routing, gene mapping, and so on.
- (2)
- Gurobi [28]: A most powerful commercial optimizer that models routing problems as mathematical programming and attains excellent solutions.
- (3)
- LKH-3 [29]: The practical decision-making technique that achieves state-of-the-art performance in a variety of routing problems.
- (4)
- Google OR Tools (v9.11) [30]: A fast and portable software specialized for combinatorial optimization problems.
- (5)
- GA [31]: The genetic algorithm which utilizes crossover and mutation operations to search for optimal solutions based on natural selection.
- (6)
- SA [32]: The simulated annealing approach that involves heating and controlled cooling strategies to approximate the global optimum in TSPs and CVRPs.
- (7)
- ACO [33]: The ant colony optimization that uses artificial ants to explore the entire environment via pheromone-based communication, thereby ultimately finding satisfactory routing results.
- (8)
- AM [22]: A milestone DRL-based method that, for the first time, introduces a transformer-based encoder–decoder framework to tackle different kinds of routing problems.
- (9)
- Wu et al. [24]: A DRL-based approach that learns improvement heuristics to handle routing problems.
- (10)
- DACT [25]: The improvement-based DRL model which exploits the circularity attribute inherent in traversal routes and designs a dual-aspect attention mechanism to find optimal solutions.
- (11)
- Neural-2-Opt [34]: The DRL-based model that learns to select 2-opt operators for local search and exhibits near-optimal results with relatively fast solving speed.
- (12)
- POMO [23]: A state-of-the-art DRL-based approach that learns parallel policies with multiple optima and achieves superior performance in various routing problems.
- (13)
- NeuRewritter [35]: A neural-based method that learns an elaborated policy to iteratively rewrite local components of the current route and improves it until convergence.
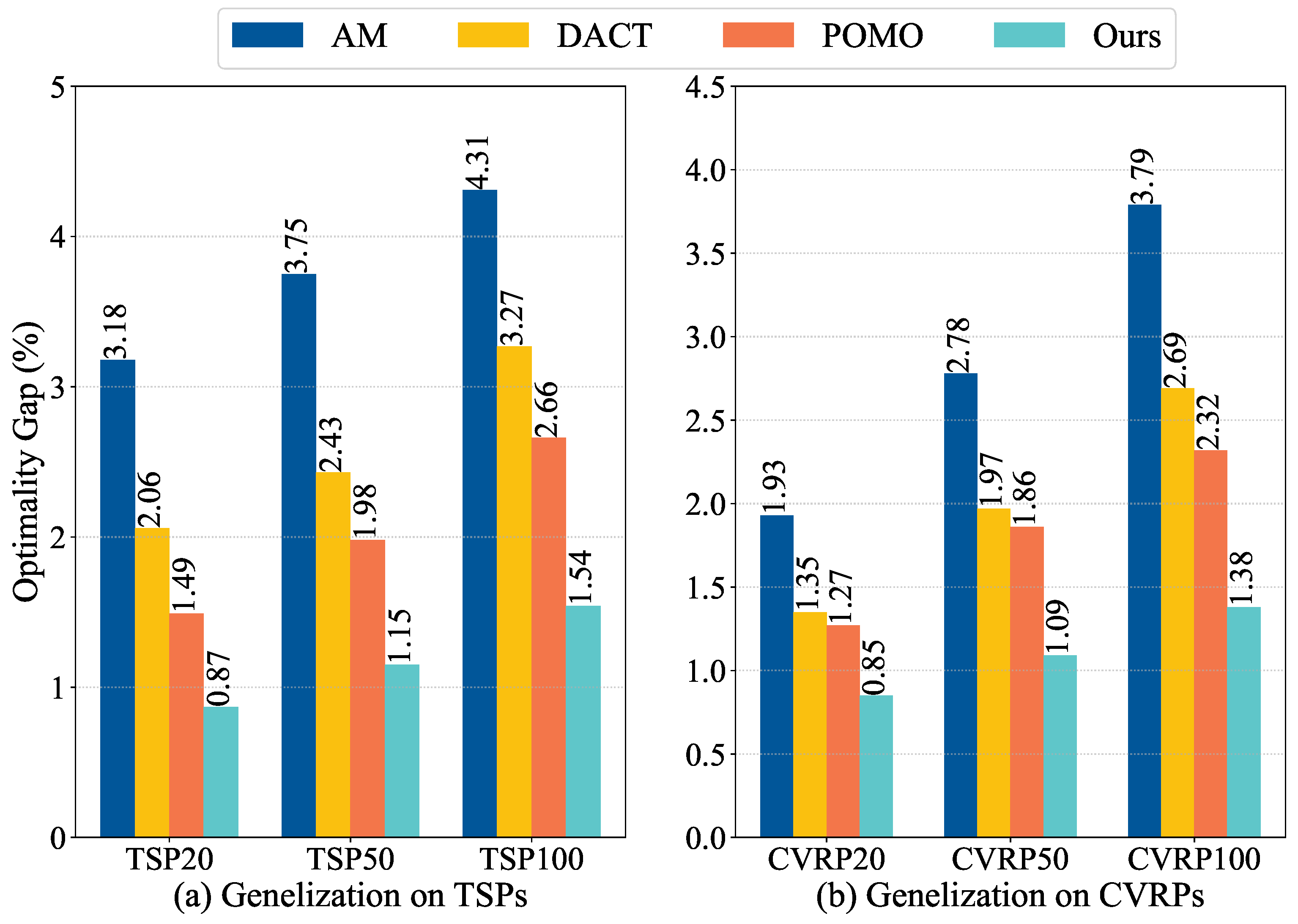
4.3. Generalization Study
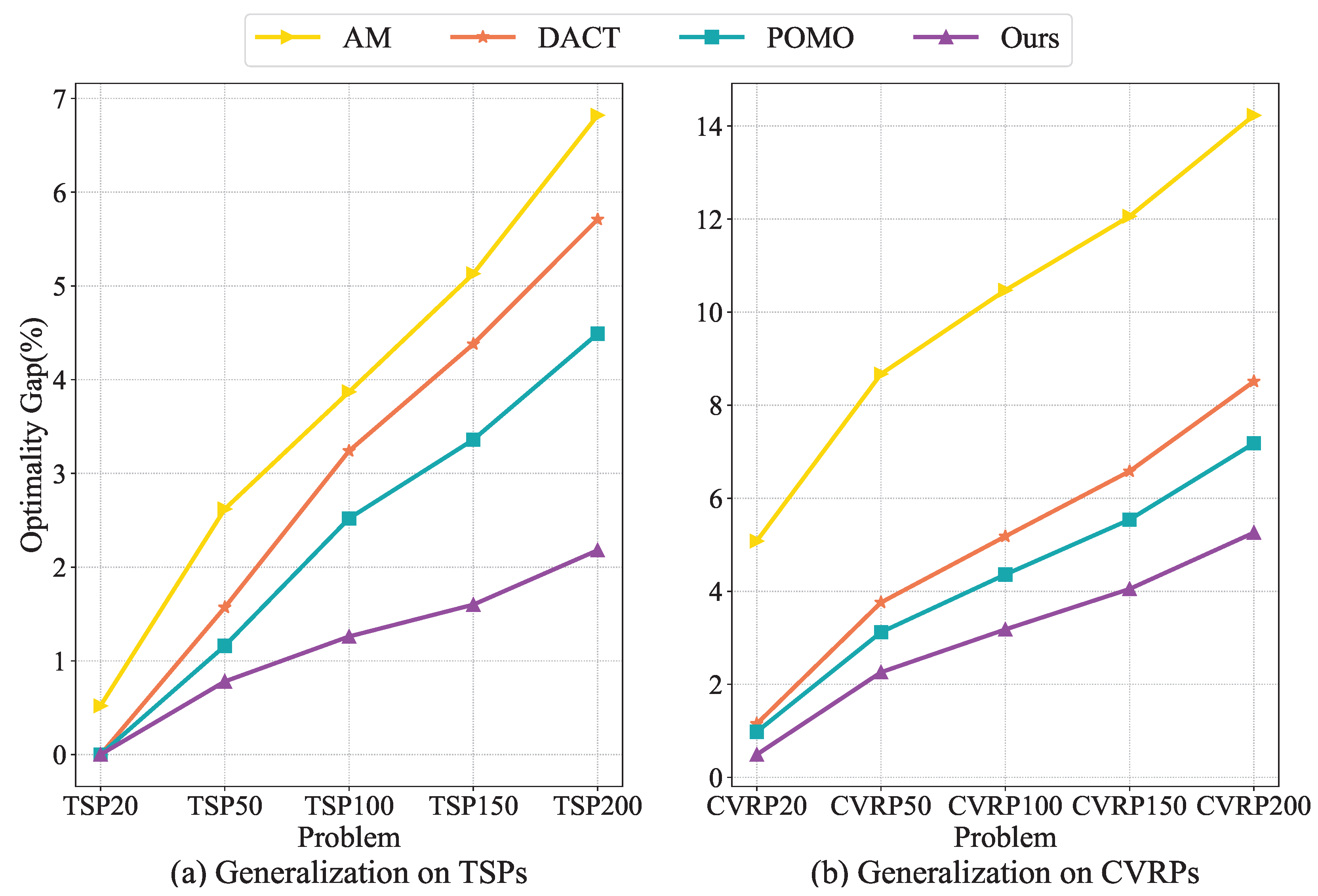
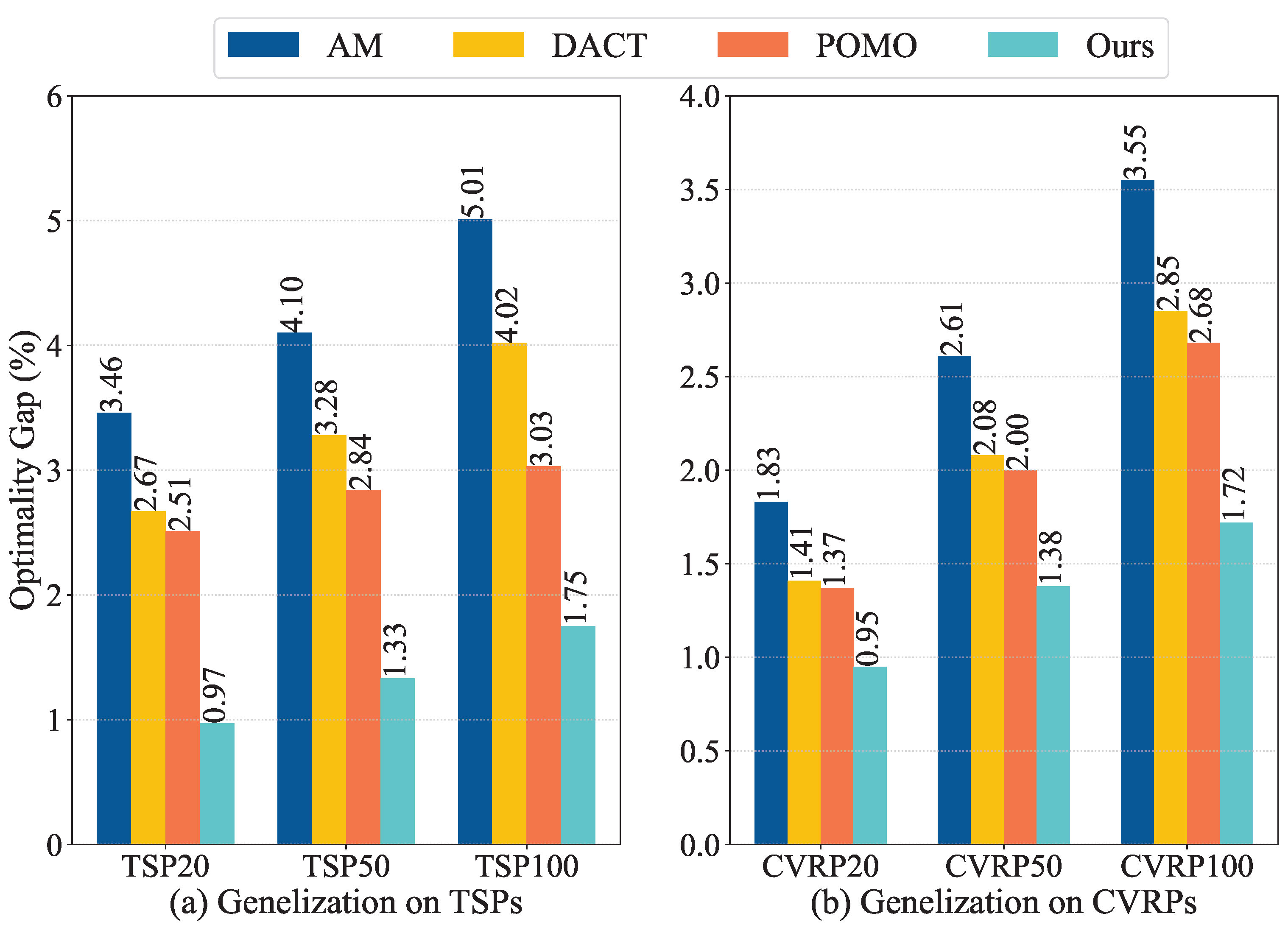
4.3.1. Cross-Size Generalization
4.3.2. Cross-Distribution Generalization
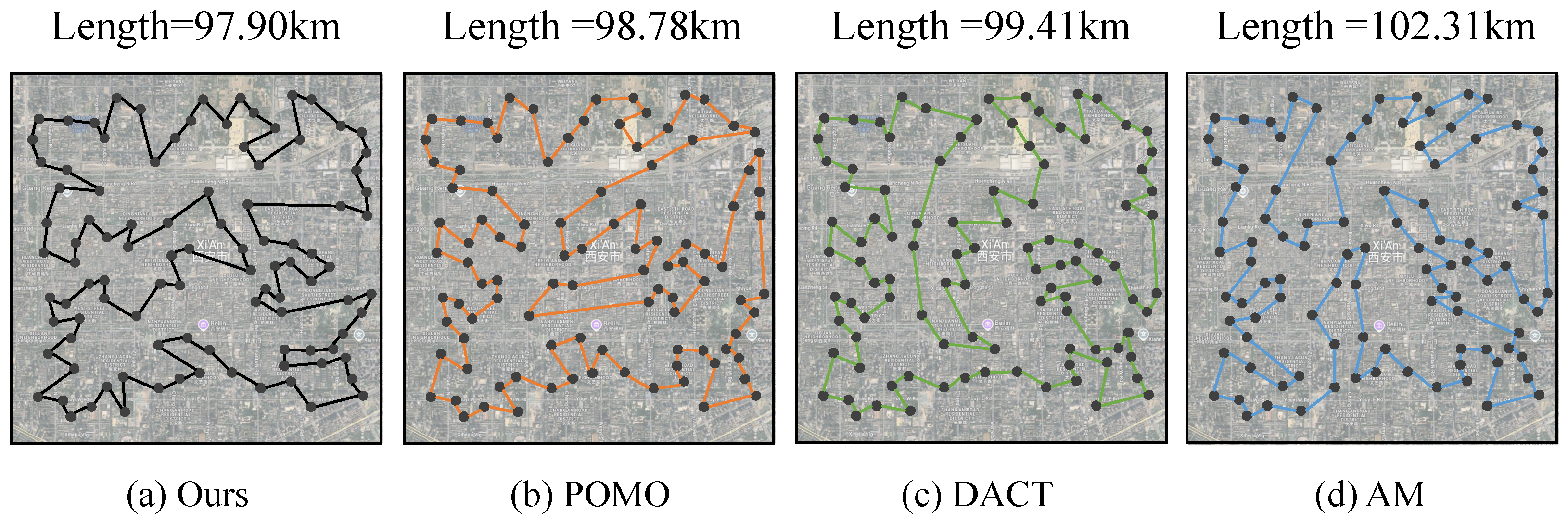
4.3.3. Generalization on Real-World Benchmarks
4.4. Ablation Study
4.5. Sensitive Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DRL | Deep reinforcement learning |
| DRL-DM | Deep reinforcement learning-based decision-making |
| TSP | Traveling salesman problem |
| CVRP | Capacitated vehicle routing problem |
| GPU | Graphics processing unit |
| AM | Attention model |
| MHA | Multi-head attention |
| FFN | Feedforward network |
| BNF | Batch normalization fronting |
| GT | Gate-like threshold |
| ReLU | Rectified linear unit |
| SHA | Single-head attention |
| GA | Genetic algorithm |
| SA | Simulated annealing |
| ACO | Ant colony optimization |
References
- Guan, Q.; Cao, H.; Jia, L.; Yan, D.; Chen, B. Synergetic attention-driven transformer: A Deep reinforcement learning approach for vehicle routing problems. Expert Syst. Appl. 2025, 274, 126961. [Google Scholar] [CrossRef]
- Guan, Q.; Hong, X.; Ke, W.; Zhang, L.; Sun, G.; Gong, Y. Kohonen self-organizing map based route planning: A revisit. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 7969–7976. [Google Scholar]
- Hao, Y.; Chen, Z.; Sun, X.; Tong, L. Planning of truck platooning for road-network capacitated vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2025, 194, 103898. [Google Scholar] [CrossRef]
- Guan, Q.; Cao, H.; Zhong, X.; Yan, D.; Xue, S. Hisom: Hierarchical Self-Organizing Map for Solving Multiple Traveling Salesman Problems. Networks, 2025; early view. [Google Scholar]
- Zhou, G.; Li, D.; Bian, J.; Zhang, Y. Two-echelon time-dependent vehicle routing problem with simultaneous pickup and delivery and satellite synchronization. Comput. Oper. Res. 2024, 167, 106600. [Google Scholar] [CrossRef]
- Shi, W.; Wang, N.; Zhou, L.; He, Z. The bi-objective mixed-fleet vehicle routing problem under decentralized collaboration and time-of-use prices. Expert Syst. Appl. 2025, 273, 126875. [Google Scholar] [CrossRef]
- Xia, Y.; Zeng, W.; Zhang, C.; Yang, H. A branch-and-price-and-cut algorithm for the vehicle routing problem with load-dependent drones. Transp. Res. Part B Methodol. 2023, 171, 80–110. [Google Scholar] [CrossRef]
- Hou, Y.; Guo, X.; Han, H.; Wang, J. Knowledge-driven ant colony optimization algorithm for vehicle routing problem in instant delivery peak period. Appl. Soft Comput. 2023, 145, 110551. [Google Scholar] [CrossRef]
- Tan, J.; Xue, S.; Guan, Q.; Niu, T.; Cao, H.; Chen, B. Unmanned aerial-ground vehicle finite-time docking control via pursuit-evasion games. Nonlinear Dyn. 2025, 113, 16757–16777. [Google Scholar] [CrossRef]
- Tan, J.; Xue, S.; Guan, Q.; Qu, K.; Cao, H. Finite-time Safe Reinforcement Learning Control of Multi-player Nonzero-Sum Game for Quadcopter Systems. Inf. Sci. 2025, 712, 122117. [Google Scholar]
- Wang, Y.; Hong, X.; Wang, Y.; Zhao, J.; Sun, G.; Qin, B. Token-based deep reinforcement learning for Heterogeneous VRP with Service Time Constraints. Knowl.-Based Syst. 2024, 300, 112173. [Google Scholar]
- Wang, C.; Cao, Z.; Wu, Y.; Teng, L.; Wu, G. Deep reinforcement learning for solving vehicle routing problems with backhauls. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 4779–4793. [Google Scholar]
- Yan, D.; Ou, B.; Guan, Q.; Zhu, Z.; Cao, H. Edge-Driven Multiple Trajectory Attention Model for Vehicle Routing Problems. Appl. Sci. 2025, 15, 2679. [Google Scholar] [CrossRef]
- Applegate, D.L.; Bixby, R.E.; Chvátal, V.; Cook, W.J. Concorde TSP Solver. 2020. Available online: http://www.math.uwaterloo.ca/tsp/concorde/ (accessed on 12 March 2020).
- Khachai, D.; Sadykov, R.; Battaia, O.; Khachay, M. Precedence constrained generalized traveling salesman problem: Polyhedral study, formulations, and branch-and-cut algorithm. Eur. J. Oper. Res. 2023, 309, 488–505. [Google Scholar] [CrossRef]
- Hintsch, T.; Irnich, S.; Kiilerich, L. Branch-price-and-cut for the soft-clustered capacitated arc-routing problem. Transp. Sci. 2021, 55, 687–705. [Google Scholar] [CrossRef]
- Pereira, A.H.; Mateus, G.R.; Urrutia, S.A. Valid inequalities and branch-and-cut algorithm for the pickup and delivery traveling salesman problem with multiple stacks. Eur. J. Oper. Res. 2022, 300, 207–220. [Google Scholar] [CrossRef]
- Yang, Y. An exact price-cut-and-enumerate method for the capacitated multitrip vehicle routing problem with time windows. Transp. Sci. 2023, 57, 230–251. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Y.; Wang, X.; Wang, Z.; Wang, H. A clustering-based extended genetic algorithm for the multidepot vehicle routing problem with time windows and three-dimensional loading constraints. Appl. Soft Comput. 2023, 133, 109922. [Google Scholar] [CrossRef]
- Vincent, F.Y.; Anh, P.T.; Gunawan, A.; Han, H. A simulated annealing with variable neighborhood descent approach for the heterogeneous fleet vehicle routing problem with multiple forward/reverse cross-docks. Expert Syst. Appl. 2024, 237, 121631. [Google Scholar]
- Jia, Y.H.; Mei, Y.; Zhang, M. A bilevel ant colony optimization algorithm for capacitated electric vehicle routing problem. IEEE Trans. Cybern. 2021, 52, 10855–10868. [Google Scholar] [CrossRef]
- Kool, W.; van Hoof, H.; Welling, M. Attention, Learn to Solve Routing Problems! In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019.
- Kwon, Y.D.; Choo, J.; Kim, B.; Yoon, I.; Gwon, Y.; Min, S. Pomo: Policy optimization with multiple optima for reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 21188–21198. [Google Scholar]
- Wu, Y.; Song, W.; Cao, Z.; Zhang, J.; Lim, A. Learning improvement heuristics for solving routing problems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5057–5069. [Google Scholar] [CrossRef]
- Ma, Y.; Li, J.; Cao, Z.; Song, W.; Zhang, L.; Chen, Z.; Tang, J. Learning to Iteratively Solve Routing Problems with Dual-Aspect Collaborative Transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 11096–11107. [Google Scholar]
- Labatie, A.; Masters, D.; Eaton-Rosen, Z.; Luschi, C. Proxy-normalizing activations to match batch normalization while removing batch dependence. Adv. Neural Inf. Process. Syst. 2021, 34, 16990–17006. [Google Scholar]
- Parisotto, E.; Song, F.; Rae, J.; Pascanu, R.; Gulcehre, C.; Jayakumar, S.; Jaderberg, M.; Kaufman, R.L.; Clark, A.; Noury, S.; et al. Stabilizing transformers for reinforcement learning. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual, 13–18 July 2020; pp. 7487–7498. [Google Scholar]
- Optimization, Gurobi and LLC. Gurobi Optimizer Reference Manual. 2022. Available online: https://www.gurobi.com/ (accessed on 28 June 2022).
- Helsgaun, K. An extension of the Lin-Kernighan-Helsgaun TSP solver for constrained traveling salesman and vehicle routing problems. Roskilde Rosk. Univ. 2017, 12, 966–980. [Google Scholar]
- Gunjan, V.K.; Kumari, M.; Kumar, A.; Rao, A.A. Search engine optimization with Google. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 206. [Google Scholar] [CrossRef]
- Hussain, A.; Muhammad, Y.S.; Nauman Sajid, M.; Hussain, I.; Mohamd Shoukry, A.; Gani, S. Genetic algorithm for traveling salesman problem with modified cycle crossover operator. Comput. Intell. Neurosci. 2017, 2017, 7430125. [Google Scholar] [CrossRef]
- Ilhan, I.; Gökmen, G. A list-based simulated annealing algorithm with crossover operator for the traveling salesman problem. Neural Comput. Appl. 2022, 34, 7627–7652. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z. Ant colony optimization for traveling salesman problem based on parameters optimization. Appl. Soft Comput. 2021, 107, 107439. [Google Scholar] [CrossRef]
- d O Costa, P.R.; Rhuggenaath, J.; Zhang, Y.; Akcay, A. Learning 2-opt heuristics for the traveling salesman problem via deep reinforcement learning. In Proceedings of the Asian Conference on Machine Learning. PMLR, Bangkok, Thailand, 18–20 November 2020; pp. 465–480. [Google Scholar]
- Chen, X.; Tian, Y. Learning to perform local rewriting for combinatorial optimization. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Reinelt, G. TSPLIB—A traveling salesman problem library. ORSA J. Comput. 1991, 3, 376–384. [Google Scholar] [CrossRef]
- Uchoa, E.; Pecin, D.; Pessoa, A.; Poggi, M.; Vidal, T.; Subramanian, A. New benchmark instances for the capacitated vehicle routing problem. Eur. J. Oper. Res. 2017, 257, 845–858. [Google Scholar] [CrossRef]
- Luo, J.; Li, C.; Fan, Q.; Liu, Y. A graph convolutional encoder and multi-head attention decoder network for TSP via reinforcement learning. Eng. Appl. Artif. Intell. 2022, 112, 104848. [Google Scholar] [CrossRef]
- Liu, H.; Zong, Z.; Li, Y.; Jin, D. NeuroCrossover: An intelligent genetic locus selection scheme for genetic algorithm using reinforcement learning. Appl. Soft Comput. 2023, 146, 110680. [Google Scholar] [CrossRef]

| Method | TSP20 | TSP50 | TSP100 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Length | Gap | Time | Length | Gap | Time | Length | Gap | Time | |
| Concorde [14] | 3.84 | 0.00% | 6 min | 5.70 | 0.00% | 15 min | 7.76 | 0.00% | 1 h |
| Gurobi [28] | 3.84 | 0.00% | 8 s | 5.70 | 0.00% | 3 min | 7.76 | 0.00% | 19 min |
| LKH-3 [29] | 3.84 | 0.00% | 45 s | 5.70 | 0.00% | 8 min | 7.76 | 0.00% | 28 min |
| Nearest Search | 4.33 | 12.76% | 1 s | 6.78 | 18.95% | 3 s | 9.47 | 22.04% | 8 s |
| Random Search | 4.01 | 4.43% | 1 s | 6.15 | 7.89% | 2 s | 8.55 | 10.18% | 3 s |
| Farthest Search | 3.95 | 2.86% | 1 s | 6.03 | 5.79% | 4 s | 8.37 | 7.86% | 9 s |
| OR Tools [30] | 3.87 | 0.78% | 1 min | 5.86 | 2.81% | 6 min | 8.09 | 4.25% | 25 min |
| GA [31] | 3.86 | 0.52% | 1 min | 5.84 | 2.46% | 5 min | 8.05 | 3.74% | 24 min |
| SA [32] | 3.86 | 0.52% | 1 min | 5.83 | 2.28% | 5 min | 8.03 | 3.48% | 23 min |
| ACO [33] | 3.86 | 0.52% | 1 min | 5.82 | 2.11% | 4 min | 8.02 | 3.35% | 22 min |
| AM [22] | 3.86 | 0.52% | 2 s | 5.80 | 1.75% | 5 s | 7.96 | 2.58% | 14 s |
| Wu et al. [24] | 3.85 | 0.26% | 13 min | 5.78 | 1.40% | 18 min | 7.94 | 2.32% | 28 min |
| DACT [25] | 3.84 | 0.00% | 9 s | 5.74 | 0.70% | 23 s | 7.92 | 2.06% | 1 min |
| Neural-2-Opt [34] | 3.84 | 0.00% | 16 min | 5.73 | 0.53% | 32 min | 7.89 | 1.68% | 45 min |
| POMO [23] | 3.84 | 0.00% | 5 s | 5.72 | 0.35% | 22 s | 7.83 | 0.90% | 1 min |
| Ours | 3.84 | 0.00% | 5 s | 5.71 | 0.18% | 19 s | 7.80 | 0.52% | 49 s |
| Method | CVRP20 | CVRP50 | CVRP100 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Length | Gap | Time | Length | Gap | Time | Length | Gap | Time | |
| Concorde [14] | 6.10 | 0.00% | 12 h | - | - | - | - | - | - |
| Gurobi [28] | 6.10 | 0.00% | 5 h | 10.37 | 0.00% | 16 h | - | - | - |
| LKH-3 [29] | 6.10 | 0.00% | 2 h | 10.37 | 0.00% | 7 h | 15.65 | 0.00% | 14 h |
| OR Tools [30] | 6.47 | 6.07% | 2 min | 11.29 | 8.87% | 15 min | 17.15 | 9.58% | 51 min |
| GA [31] | 6.40 | 4.92% | 2 min | 11.12 | 7.23% | 15 min | 16.87 | 7.80% | 49 min |
| SA [32] | 6.36 | 0.52% | 2 min | 11.05 | 2.28% | 14 min | 16.78 | 7.22% | 47 min |
| ACO [33] | 6.32 | 3.61% | 2 min | 10.98 | 5.88% | 13 min | 16.70 | 6.71% | 45 min |
| AM [22] | 6.41 | 5.08% | 3 s | 10.99 | 5.98% | 8 s | 16.82 | 7.48% | 23 s |
| Wu et al. [24] | 6.19 | 1.48% | 24 min | 10.72 | 3.38% | 49 min | 16.32 | 4.28% | 1 h |
| DACT [25] | 6.17 | 1.15% | 1 min | 10.63 | 2.51% | 4 min | 16.19 | 3.45% | 12 min |
| NeuRewritter [35] | 6.16 | 0.98% | 31 min | 10.58 | 2.03% | 56 min | 16.12 | 3.00% | 1 h |
| POMO [23] | 6.16 | 0.98% | 15 s | 10.52 | 1.45% | 1 min | 15.93 | 1.79% | 4 min |
| Ours | 6.13 | 0.49% | 14 s | 10.44 | 0.68% | 1 min | 15.78 | 0.83% | 3 min |
| Instance | Opt. | AM [22] | DACT [25] | POMO [23] | Ours |
|---|---|---|---|---|---|
| eil51 | 426 | 439 | 438 | 436 | 427 |
| berlin52 | 7542 | 8361 | 8062 | 7864 | 7549 |
| st70 | 675 | 693 | 688 | 684 | 682 |
| rat99 | 1211 | 1342 | 1310 | 1289 | 1232 |
| KroA100 | 21,282 | 42,661 | 40,238 | 38,624 | 25,163 |
| KroB100 | 22,141 | 36,035 | 34,526 | 33,521 | 26,591 |
| KroC100 | 20,749 | 32,937 | 31,456 | 30,468 | 23,627 |
| KroD100 | 21,294 | 33,826 | 31,011 | 29,135 | 23,668 |
| KroE100 | 22,068 | 29,036 | 27,415 | 26,335 | 24,257 |
| rd100 | 7910 | 8256 | 8209 | 8178 | 8034 |
| lin105 | 14,379 | 15,153 | 15,016 | 14,926 | 14,658 |
| pr107 | 44,303 | 53,849 | 53,252 | 52,855 | 47,562 |
| ch150 | 6528 | 6931 | 6882 | 6849 | 6702 |
| rat195 | 2323 | 2611 | 2576 | 2553 | 2406 |
| KroA200 | 29,368 | 35,638 | 35,210 | 34,926 | 33,282 |
| Avg. Gap | 0.00% | 27.40% | 23.39% | 20.70% | 7.12% |
| Instance | Opt. | AM [22] | DACT [25] | POMO [23] | Ours |
|---|---|---|---|---|---|
| X-n101-k25 | 27,591 | 36,248 | 32,262 | 29,605 | 28,967 |
| X-n106-k14 | 26,362 | 27,936 | 27,568 | 27,323 | 27,296 |
| X-n110-k13 | 14,971 | 16,318 | 16,060 | 15,889 | 15,219 |
| X-n115-k10 | 12,747 | 14,056 | 13,990 | 13,946 | 13,834 |
| X-n120-k6 | 13,332 | 14,453 | 14,392 | 14,352 | 14,231 |
| X-n125-k30 | 55,539 | 72,349 | 70,676 | 69,562 | 62,384 |
| X-n129-k18 | 28,940 | 30,896 | 30,458 | 30,167 | 30,026 |
| X-n134-k13 | 10,916 | 13,561 | 13,288 | 13,107 | 12,805 |
| X-n139-k10 | 13,590 | 14,756 | 14,403 | 14,169 | 13,856 |
| X-n143-k7 | 15,700 | 18,137 | 18,003 | 17,915 | 17,623 |
| X-n153-k22 | 21,220 | 29,034 | 27,434 | 26,368 | 25,103 |
| X-n157-k13 | 16,876 | 21,966 | 20,345 | 19,265 | 18,236 |
| X-n181-k23 | 25,628 | 27,865 | 27,596 | 27,418 | 27,048 |
| X-n190-k8 | 16,980 | 23,028 | 21,443 | 20,387 | 19,339 |
| X-n200-k36 | 58,578 | 76,035 | 74,289 | 73,126 | 67,238 |
| Avg. Gap | 0.00% | 19.43% | 15.47% | 12.82% | 8.91% |
| Components of Our DRL-DM | TSP20 | TSP50 | TSP100 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BNF | GT | Context | Length | Gap | Time | Length | Gap | Time | Length | Gap | Time |
| 3.86 | 0.52% | 2 s | 5.80 | 1.75% | 5 s | 7.96 | 2.58% | 14 s | |||
| ✓ | 3.86 | 0.52% | 2 s | 5.79 | 1.58% | 8 s | 7.94 | 2.32% | 21 s | ||
| ✓ | 3.85 | 0.26% | 3 s | 5.77 | 1.23% | 10 s | 7.90 | 1.80% | 26 s | ||
| ✓ | 3.85 | 0.26% | 3 s | 5.76 | 1.05% | 11 s | 7.88 | 1.55% | 30 s | ||
| ✓ | ✓ | 3.85 | 0.26% | 4 s | 5.76 | 1.05% | 13 s | 7.87 | 1.42% | 33 s | |
| ✓ | ✓ | 3.85 | 0.26% | 4 s | 5.74 | 0.70% | 14 s | 7.86 | 1.29% | 37 s | |
| ✓ | ✓ | 3.84 | 0.00% | 5 s | 5.73 | 0.53% | 16 s | 7.83 | 0.90% | 42 s | |
| ✓ | ✓ | ✓ | 3.84 | 0.00% | 5 s | 5.71 | 0.18% | 19 s | 7.80 | 0.52% | 49 s |
| Components of Our DRL-DM | CVRP20 | CVRP50 | CVRP100 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BNF | GT | Context | Length | Gap | Time | Length | Gap | Time | Length | Gap | Time |
| 6.41 | 5.08% | 3 s | 10.99 | 5.98% | 8 s | 16.82 | 7.48% | 23 s | |||
| ✓ | 6.37 | 4.43% | 5 s | 10.91 | 5.21% | 18 s | 16.66 | 6.45% | 54 s | ||
| ✓ | 6.31 | 3.44% | 7 s | 10.80 | 4.15% | 26 s | 16.46 | 5.18% | 1 min | ||
| ✓ | 6.27 | 2.79% | 8 s | 10.72 | 3.38% | 31 s | 16.30 | 4.15% | 2 min | ||
| ✓ | ✓ | 6.26 | 2.62% | 9 s | 10.70 | 3.18% | 37 s | 16.28 | 4.03% | 2 min | |
| ✓ | ✓ | 6.23 | 2.13% | 10 s | 10.63 | 2.51% | 42 s | 16.14 | 3.13% | 2 min | |
| ✓ | ✓ | 6.17 | 1.15% | 12 s | 10.52 | 1.45% | 50 s | 15.93 | 1.79% | 3 min | |
| ✓ | ✓ | ✓ | 6.13 | 0.49% | 14 s | 10.44 | 0.68% | 1 min | 15.78 | 0.83% | 3 min |
| Value | TSP20 | TSP50 | TSP100 | CVRP20 | CVRP50 | CVRP100 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Length | Time | Length | Time | Length | Time | Length | Time | Length | Time | Length | Time | |
| 3.86 | 4 s | 5.74 | 15 s | 7.85 | 42 s | 6.17 | 11 s | 10.51 | 1 min | 15.89 | 2 min | |
| 3.85 | 5 s | 5.72 | 17 s | 7.82 | 46 s | 6.15 | 12 s | 10.47 | 1 min | 15.82 | 3 min | |
| 3.84 | 5 s | 5.71 | 19 s | 7.80 | 49 s | 6.13 | 14 s | 10.44 | 1 min | 15.78 | 3 min | |
| 3.84 | 6 s | 5.71 | 21 s | 7.80 | 53 s | 6.13 | 16 s | 10.44 | 2 min | 15.78 | 4 min | |
| 3.84 | 7 s | 5.71 | 24 s | 7.79 | 58 s | 6.13 | 19 s | 10.43 | 2 min | 15.77 | 5 min | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, D.; Guan, Q.; Ou, B.; Yan, B.; Zhu, Z.; Cao, H. A Deep Reinforcement Learning-Based Decision-Making Approach for Routing Problems. Appl. Sci. 2025, 15, 4951. https://doi.org/10.3390/app15094951
Yan D, Guan Q, Ou B, Yan B, Zhu Z, Cao H. A Deep Reinforcement Learning-Based Decision-Making Approach for Routing Problems. Applied Sciences. 2025; 15(9):4951. https://doi.org/10.3390/app15094951
Chicago/Turabian StyleYan, Dapeng, Qingshu Guan, Bei Ou, Bowen Yan, Zheng Zhu, and Hui Cao. 2025. "A Deep Reinforcement Learning-Based Decision-Making Approach for Routing Problems" Applied Sciences 15, no. 9: 4951. https://doi.org/10.3390/app15094951
APA StyleYan, D., Guan, Q., Ou, B., Yan, B., Zhu, Z., & Cao, H. (2025). A Deep Reinforcement Learning-Based Decision-Making Approach for Routing Problems. Applied Sciences, 15(9), 4951. https://doi.org/10.3390/app15094951






